Pressure and temperature (kinetic theory of gases)

In this article, learn more about the relationship between pressure and temperature in connection with the kinetic theory of gases.

Introduction

In order to connect the macroscopically observed state variables of a gas such as temperature, volume and pressure with the microscopic variables such as particle mass and particle velocity, the kinetic theory of gases was developed. With its help it is possible, for example, to deduce the temperature or the pressure of a gas from the mean kinetic energy of the molecules.

For (ideal) gases, the kinetic theory of gases provides important relationships between macroscopically measurable state variables (e.g. temperature, pressure, volume, gas mass, etc.) and microscopic variables (e.g. particle velocity, mean kinetic energy, number of particles, partial mass, etc.)!

Assumptions

In order to develop a model of the behaviour of gas particles, some assumptions must first be made about the properties of gases or the molecules they contain. First, it is assumed that the gases are ideal gases. This means in particular:

1. the gas particles are considered as mass points,
2. the gas particles do not exert any binding forces on each other,
3. collisions between gas particles are completely elastic as well as collisions between molecules and surfaces (i.e. no loss of energy)
4. all gas particles move completely randomly, i.e. they have no preferred direction and are therefore statistically distributed in space (i.e. the influence of gravity on the molecules is neglected).

Microscopic interpretation of the gas pressure

Formation of the gas pressure

In the article “Gas pressure“, the formation of the gas pressure has already been explained in detail using the particle model. The macroscopically measurable gas pressure (“force per unit of surface area”) can be explained at a microscopic level by means of collisions. If the gas particles collide with a surface (e.g. the wall of a container), they exert forces similar to tennis balls thrown against a racket.

The pressure in gases is caused on a microscopic level by collisions of the particles contained therein, which collide with adjacent surfaces and thus exert impact forces!

If, for example, a gas under high pressure is enclosed in a cylinder, the particles contained in it collide constantly with the cylinder wall and exert forces. These impact forces can be clearly felt when, the cylinder is closed with a piston.

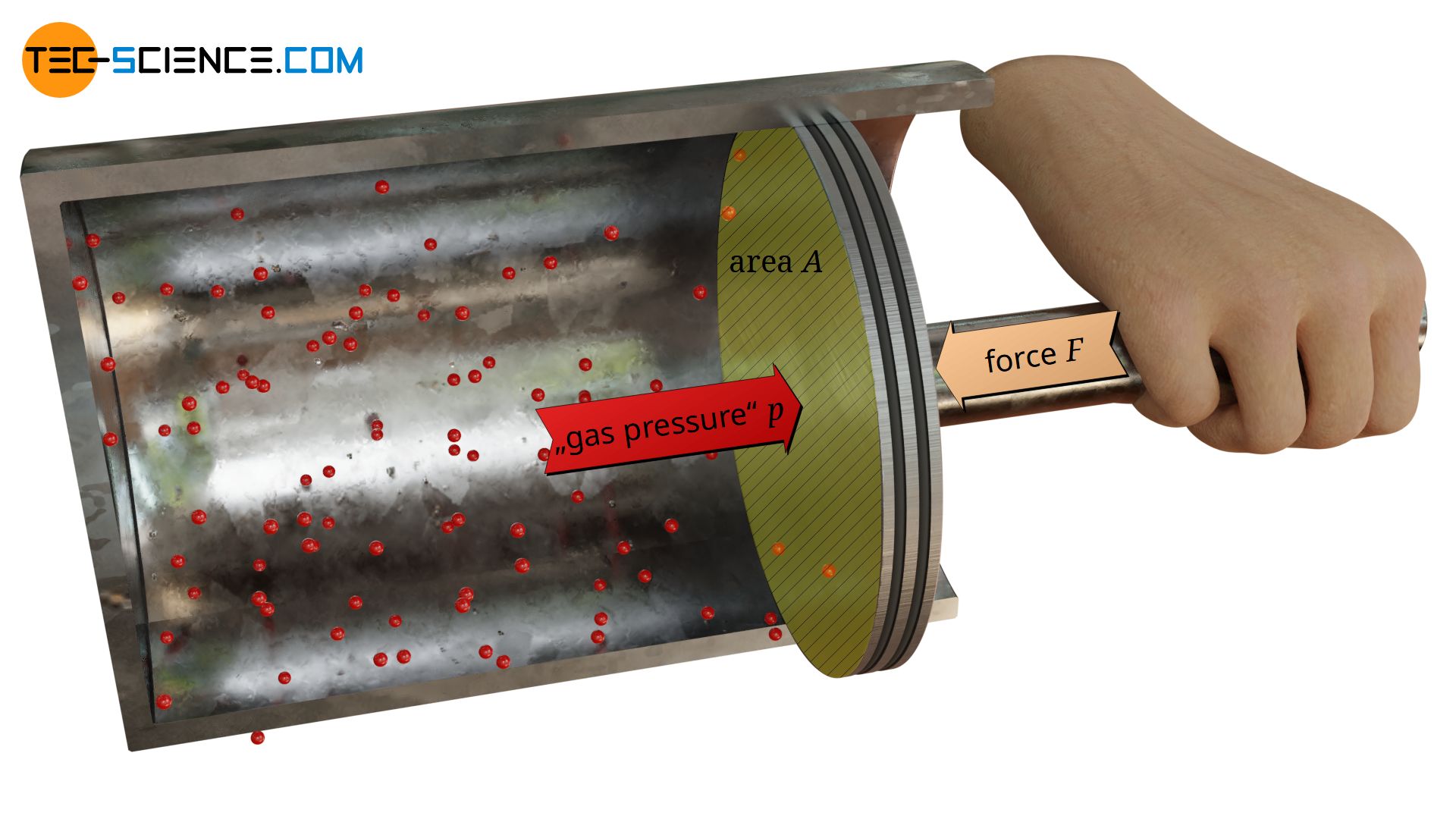
The animation below schematically shows the collisions between the gas molecules and the piston surface. In contrast to the animation, due to the large number of particles normally contained in a gas, one will not feel a “hammering” of the particles but will perceive a constant force.

The force F required to keep the piston in position is solely due to collisions between the gas particles and the piston surface A, i.e. the gas pressure! From the definition of pressure as “force per unit surface area”, the gas pressure p can finally be determined as follows:

\begin{align}
\label{p}
&\boxed{p = \frac{F}{A}} \\[5px]
\end{align}

Note: Not only the molecules inside the cylinder collide with the piston surface and thus exert an outward force. The surrounding air outside the cylinder also contains particles. These particles therefore additionally exert an opposite force on the piston, which is directed inwards. Only the difference between the two forces corresponds to the force required to hold the piston in position. For the sake of simplicity, a vacuum outside the cylinder is assumed in the following, so that the force F in the equation (\ref{p}) can be attributed exclusively to the gas particles inside the cylinder.

Variables influencing the gas pressure

The gas pressure in the cylinder will be higher the more particles collide with the piston within a certain time. This depends on the number of particles in the cylinder. This is because the more particles there are in total, the more can collide with the piston surface and will exert (impact) forces. This is already shown by everyday experience when inflating a bicycle tyre: the more air is pumped into the tyre (i.e. the more particles it contains), the greater the pressure!

On the other hand, the gas pressure depends on the speed at which the particles hit the piston surface. The greater the speed, the more intense the collisions and the greater the impact forces or the associated pressure. This, too, is shown by everyday experience: If a bottle filled with air is placed in the sun, the pressure in the bottle will increase as the temperature rises, since the speed of the molecules increases with higher temperature.

Calculation of the gas pressure

In order to determine the gas pressure in the cylinder, the number of particles that collide with the piston within a certain time Δt must first be determined. Only those molecules can hit the piston which on the one hand actually fly towards the piston and on the other hand are close enough to the piston surface.

In general, the velocity of a particle consists of three components (x-, y- and z-components), whereby only the velocity component with which the particle hits the piston surface is relevant for the formation of the pressure, i.e. the speed in the x-direction.

First, it is assumed that the x-component of the velocity is identical for all particles (|v_x|). Since no direction is preferred by the particles, half of all particles will move at this speed |v_x| in the positive x-direction and the other half in the negative x-direction.

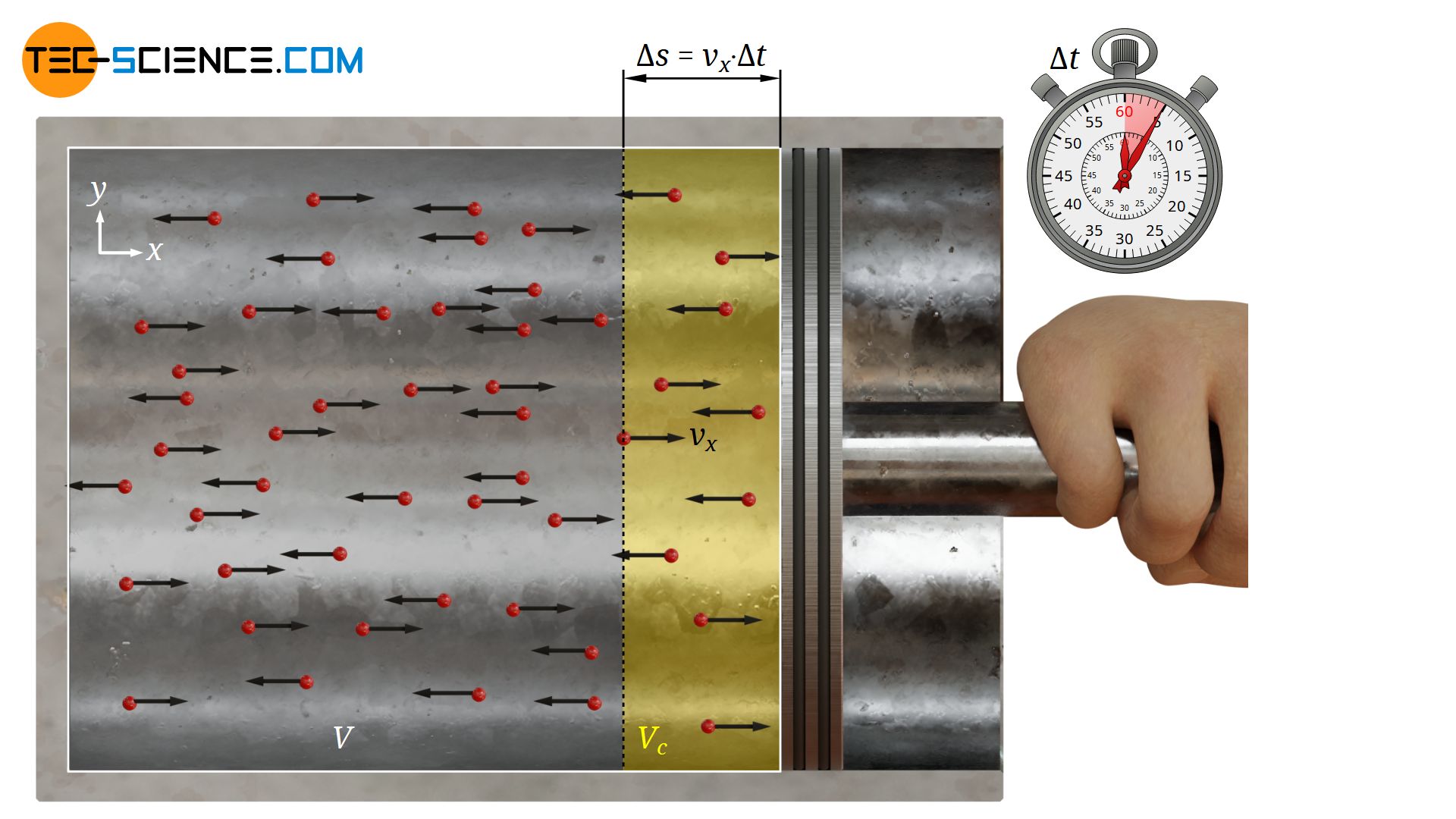
However, not all particles moving in positive direction can actually reach the surface of the piston within the given time Δt. With the assumed constant velocity |v_x| the particles can only cover a maximum distance Δs within the time Δt:

\begin{align}
&\Delta s = |v_x| \cdot \Delta t \\[5px]
\end{align}

This means, conversely, that only particles less than Δs away from the piston can hit the surface (see yellow volume V_c in the figure above). All other particles will simply not have the time to reach the piston within the time Δt.

Since the particles are evenly distributed in the cylinder, the particle density in the cylinder N/V (ratio of total number of particles N and total cylinder volume V) can be used to determine the number of particles N_c contained in the pressure relevant collision volume V_c as follows:

\begin{align}
&N_c = \frac{N}{V} \cdot V_c \\[5px]
\end{align}

Now it must be considered that only half of the particles in the collision volume actually move towards the piston in the positive x-direction. For the number of particles N_x in the collision volume that actually flies in the direction of the piston, the following applies:

\begin{align}
&N_x = \frac{1}{2} \cdot N_c = \frac{1}{2} \cdot \frac{N}{V} \cdot V_c \\[5px]
\end{align}

The collision volume V_c relevant for the formation of the pressure results from the product of the piston area A and the distance Δs. Thus, the pressure relevant number of particles N_x in the collision voume can be calculated as follows:

\begin{align}
&N_x = \frac{1}{2} \cdot \frac{N}{V} \cdot \overbrace{A \cdot \Delta s}^{V_c} = \frac{1}{2} \cdot \frac{N}{V} \cdot A \cdot \overbrace{|v_x| \cdot \Delta t}^{\Delta s} \\[5px]
\end{align}

Each of the total N_x particles will change its momentum by a certain amount |Δp| (impuls) when it collides with the piston. The total impuls |Δp_tot| of all particles over the time period considered Δt corresponds to the force |F_tot| that the particles exert on the piston surface:

\begin{align}
\require{cancel}
\label{force}
&|F_{tot}| = \frac{|\Delta p_{tot}|}{\Delta t} = \frac{N_x \cdot |\Delta p|}{\Delta t} = \frac{\frac{1}{2} \cdot \frac{N}{V} \cdot A \cdot |v_x| \cdot \bcancel{\Delta t} \cdot |\Delta p|}{\bcancel{\Delta t}} = \frac{1}{2} \cdot \frac{N}{V} \cdot A \cdot |v_x|\cdot |\Delta p| \\[5px]
\end{align}

Equation (\ref{force}) shows that the force on the piston is not dependent on the time period considered Δt! If this were the case, the pressure would have to change over time. Everyday experience shows, however, that the pressure in gases remains constant as long as no changes such as an increase in temperature or a reduction in volume are made!

The impuls |Δp| is identical for each particle, since it was assumed that all particles move at the same speed |v_x| and that the collisions with the piston are completely elastic without (kinetic) energy loss. A particle that moves towards the piston with the speed |v_x| will move after the collision in the opposite direction with the same speed |v_x|. Since the momentum of a particle before the collision is +m⋅|v_x| and after the collision -m⋅|v_x|, the momentum has changed by double the value:

\begin{align}
\label{momentum}
&|\Delta p| = 2 \cdot m \cdot |v_x| \\[5px]
\end{align}

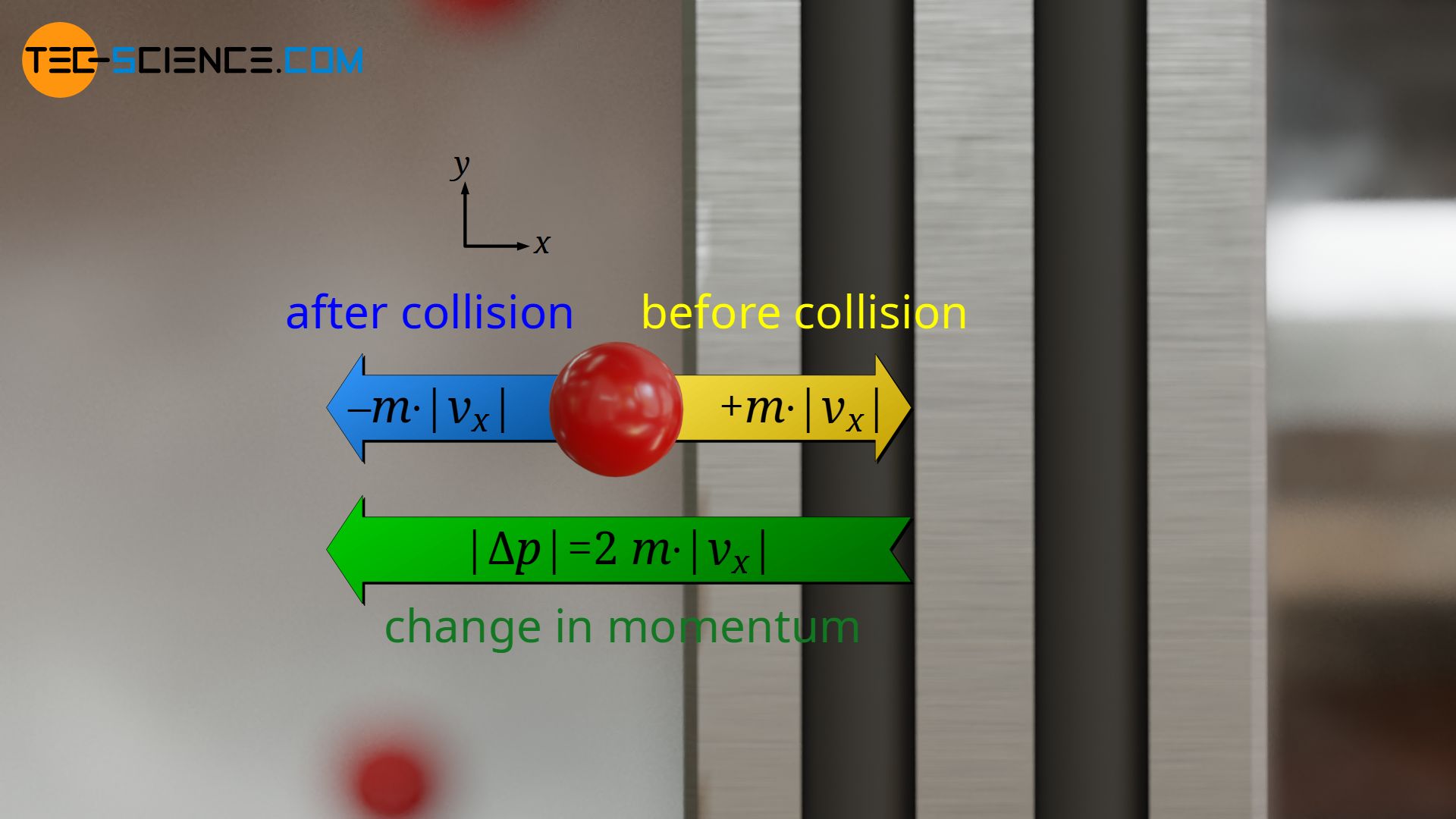
(Analogy: If the temperature changes from -20 °C to +20 °C, then it has changed by 40 °C in total, i.e. by twice the value).

If equation (\ref{momentum}) is now used in equation (\ref{force}), then the total force F_tot that the gas exerts on the piston can be calculated with the following formula:

\begin{align}
\label{f}
&|F_{tot}| = \frac{1}{2} \cdot \frac{N}{V} \cdot A \cdot |v_x|\cdot \overbrace{2 \cdot m \cdot |v_x|}^{|\Delta p|} =\frac{N}{V} \cdot A \cdot m \cdot |v_x|^2 =\frac{N}{V} \cdot A \cdot m \cdot v_x^2 \\[5px]
\end{align}

Note: Since the speed v_x is squared in equation (\ref{f}), it is no longer necessary to calculate the absolute value, since the square of a negative number is always positive.

Since the force |F_tot| is exerted on the piston surface A, the following gas pressure p is obtained by equation (\ref{p}):

\begin{align}
\require{cancel}
\label{pp}
& p = \frac{|F_{tot}|}{A} =\frac{\frac{N}{V} \cdot \bcancel{A} \cdot m \cdot v_x^2}{\bcancel{A}} = \frac{N}{V} \cdot m \cdot v_x^2 \\[5px]
\end{align}

Now it must be considered that even in ideal gases not all molecules have the same speed in x-direction, but is statistically (randomly) distributed. Therefore, according to the equation (\ref{pp}), the arithmetic mean of the squares of the speeds must be calculated:

\begin{align}
\label{ppp}
& \boxed{p =\frac{N}{V} \cdot m \cdot \overline{v_x^2}} \\[5px]
\end{align}

Not the average speed (arithmetic mean speed) of the particles may be squared but the squares of the individual speeds must be averaged. Therefore one speaks also of the mean square speed.

As an example the table below shows for 5 particles the results, if once the average speed (arithmetic mean speed) is squared and once the squares of the speeds are averaged (mean square speed). So the average speed in this case is 3 m/s and the square is 9 m²/s². If, on the other hand, the average of the speed squares is calculated, a value of 11.8 m²/s² is obtained.

Particle	Speed v (m/s)	Square of the speeds v² (m²/s²)
A	1	1
B	3	9
C	3	9
D	2	4
E	6	36
arithmetic mean	3 m/s	11.8 m²/s²

Note the different notation between the square of the average speed \(\overline{v~}^2\) and the average of the square of the speed \(\overline{v^2}\).

Relation between the motion in x-direction and the total motion

Kinematic approach

The speed v of a molecule can basically be determined as follows from its velocity components in the x, y and z direction:

\begin{align}
& v = \sqrt{v_x^2 + v_y^2 + v_z^2}~~~~~\text{} \\[5px]
\end{align}

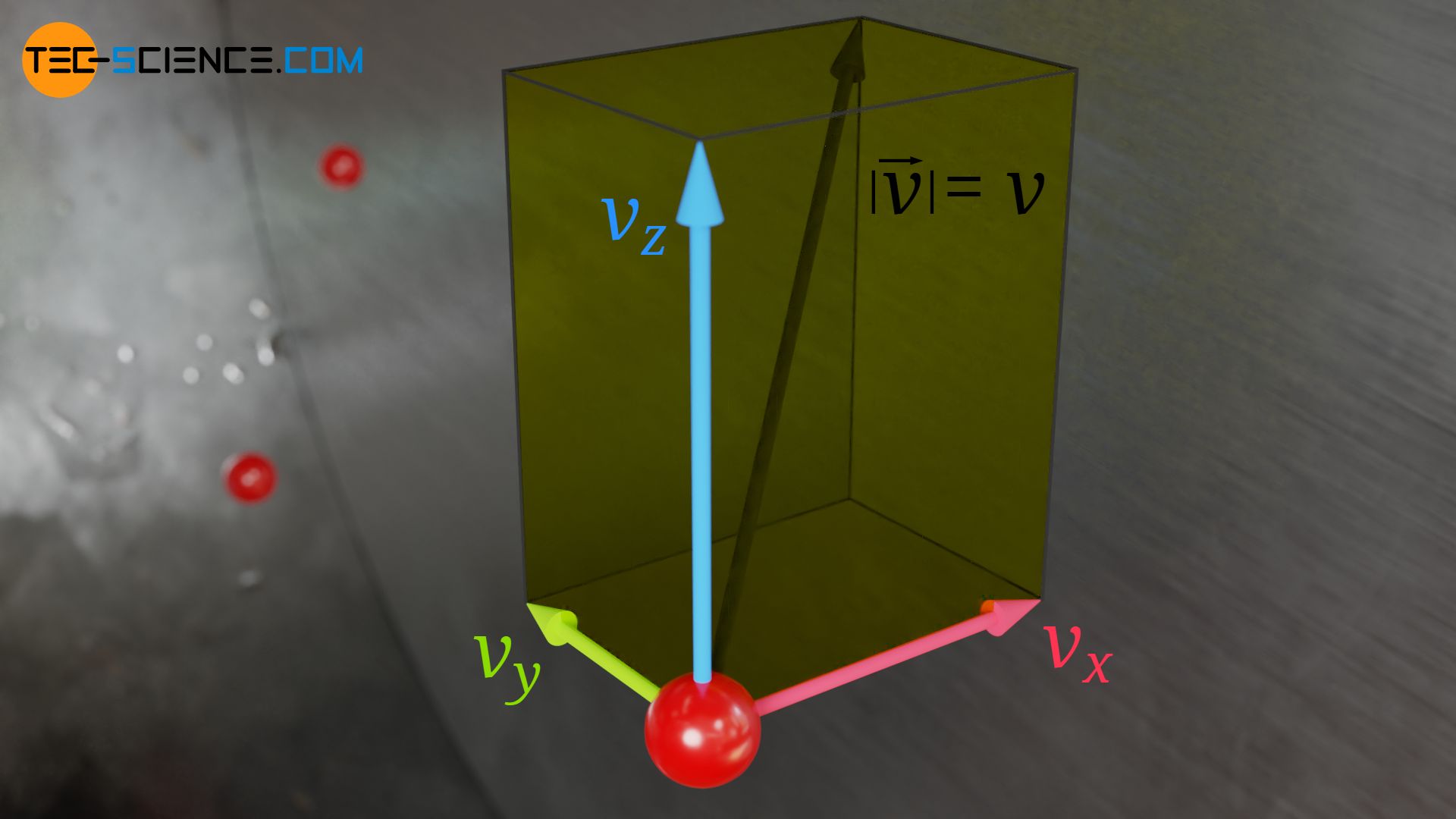
For the square of the speed v² therefore applies:

\begin{align}
& v^2= v_x^2 + v_y^2 + v_z^2 \\[5px]
\end{align}

The average of the squared speed can then be determined from the mean value of the individual squared velocity components as follows:

\begin{align}
& \overline{v^2}= \overline{v_x^2} + \overline{v_y^2} + \overline{v_z^2} \\[5px]
\end{align}

The velocity components of the molecules are statistically distributed and no direction is preferred. The mean value of the speed squares will thus be identical for all velocity components:

\begin{align}
&\overline{v_x^2} = \overline{v_y^2} = \overline {v_z^2} \\[5px]
\end{align}

Thus the following relation between the average of the squared speeds of the particles \(\overline{v^2}\) and the mean value of the squared velocity components in x-direction (\(\overline{v_x^2}\)) is obtained:

\begin{align}
& \overline{v^2}= \overline{v_x^2} + \overline{v_x^2} + \overline{v_x^2} = 3 \cdot \overline{v_x^2} \\[5px]
\end{align}

The average of the squared speeds in the x-direction thus corresponds to one third of the squared speeds of the individual particles:

\begin{align}
\label{x}
& \boxed{\overline{v_x^2} = \frac{\overline{v^2}}{3}} \\[5px]
\end{align}

If equation (\ref{x}) is applied in equation (\ref{ppp}), then the following relationship between the gas pressure p and the average of the speed squares \(\overline{v^2}\) of the individual particles becomes evident:

\begin{align}
\label{yy}
& \boxed{p =\frac{1}{3} \cdot \frac{N}{V} \cdot m \cdot \overline{v^2}} \\[5px]
\end{align}

Note that the speed v is no longer limited to the x-direction but represents the total speed of a particle (to be precise: to the mean of the speed squares of all molecules)!

Energetic approach

The same relations as are expressed in equation (\ref{yy}) can also be obtained by an energetic consideration. Starting point is again equation (\ref{ppp}). If equation (\ref{ppp}) is expanded with factor 2, then the term \(\frac{1}{2}m \overline{v_x^2}\) can be interpreted as the mean kinetic energy \(\overline{W_{kin,x}}\) of the particles that is related to the x-direction:

\begin{align}
& p =\frac{2}{2} \cdot \frac{N}{V} \cdot m \cdot \overline{v_x^2} =
2 \cdot \frac{N}{V} \cdot \overbrace{\frac{1}{2} m \cdot \overline{v_x^2}}^{\overline{W_{kin,x}}} \\[5px]
\label{druck}
& \boxed{p = 2 \cdot \frac{N}{V} \cdot \overline{W_{kin,x}}} \\[5px]
\end{align}

Since the velocities are randomly distributed and no direction is preferred, the same speed distribution is obtained for any direction. This in turn means that the mean kinetic energy of the particles in each direction is identical (i.e. the mean kinetic energy that would result if the motion of the particles were only observed along one spatial direction):

\begin{align}
& \overline{W_{kin,x}} = \overline{W_{kin,y}} = \overline{W_{kin,z}}\\[5px]
\end{align}

However, the particles do not only move in one direction but in three-dimensional space. The mean total kinetic energy \(\overline{W_{kin}}\), which the molecules have during their three-dimensional motion, is then the sum of the kinetic energies along the three spatial directions. Since the mean kinetic energy along the different spatial directions is identical, the total energy corresponds to three times the kinetic energy in one spatial direction (e.g. in the x-direction):

\begin{align}
& \overline{W_{kin}} = \overline{W_{kin,x}} + \overline{W_{kin,y}} + \overline{W_{kin,z}} = 3 \cdot \overline{W_{kin,x}} \\[5px]
\label{kine}
&\overline{W_{kin,x}} = \frac{1}{3}\cdot \overline{W_{kin}} \\[5px]
\end{align}

Thus the pressure is linked as follows to the mean kinetic energy of a particle (insert equation (\ref{kine}) in (\ref{druck})):

\begin{align}
&p = 2 \cdot \frac{N}{V} \cdot \frac{1}{3} \overline{W_{kin}} \\[5px]
\label{y}
& \boxed{p = \frac{2}{3} \cdot \frac{N}{V} \cdot \overline{W_{kin}}} \\[5px]
\end{align}

The pressure of a gas depends beside the number of particles and the volume only on the average kinetic energy of a particle!

Note that the mean kinetic energy of a particle refers only to the translational motion. The particles of a gas generally also have a rotational motion and therefore rotational energy, but this has no effect on the pressure!

Since the mean kinetic energy of the particles is linked by their mass to the mean of the speed squares (\(\overline{W_{kin}}=\frac{1}{2}m\cdot \overline{v^2}\)), whereby the speed v no longer refers only to a spatial direction but to the total speed, then the same relationship as in equation (\ref{yy}) becomes evident:

\begin{align}
& p = \frac{2}{3} \cdot \frac{N}{V} \cdot \overbrace{\overline{W_{kin}}}^{\frac{1}{2}m \overline{v^2}} \\[5px]
& \boxed{p =\frac{1}{3} \cdot \frac{N}{V} \cdot m \cdot \overline{v^2}} \\[5px]
\end{align}

Microscopic interpretation of temperature

In the article “Ideal gas law” the following equation was derived experimentally:

\begin{align}
\label{1}
& p \cdot V = N \cdot k_B \cdot T \\[5px]
\end{align}

In this equation, k_B denotes the so-called Boltzmann constant and T the thermodynamic temperature of the gas. If you now bring the gas volume V in equation (\ref{y}) on the left side…

\begin{align}
\label{2}
& p \cdot V =\frac{2}{3} \cdot N \cdot \overline{W_{kin}} \\[5px]
\end{align}

… and then equating equations (\ref{1}) and (\ref{2}), then the relationship between the mean kinetic energy of a particle and temperature of the gas becomes apparent:

\begin{align}
\require{cancel}
& \frac{2}{3} \cdot \bcancel{N} \cdot \overline{W_{kin}} = \bcancel{N} \cdot k_B \cdot T \\[5px]
\label{kin}
& \boxed{\overline{W_{kin}} = \frac{3}{2} k_B \cdot T} \\[5px]
\end{align}

The average kinetic energy of the particles depends only on the temperature!

Also at this point, the kinetic energy again refers only to the translatory motion and not to the rotational motion. Rotational energies (angular kinetic energy) do not influence the temperature at all!

Internal energy of an ideal gas

Since according to equation (\ref{kin}) each particle carries (on average) a kinetic energy of 3/2⋅k_BT, the total energy of all the particles and thus the energy of the gas can be obtained by multiplying the mean kinetic energy of a particle with the total number of particles N. This total energy inside the gas is also called the internal energy U:

\begin{align}
\label{u}
& \boxed{U = \frac{3}{2} N k_B T} \\[5px]
\end{align}

If the expression N⋅k_BT is replaced by p⋅V according to the equation (\ref{1}), then the pressure can also be determined from the energy density u_v of the gas (in order to avoid confusion with the specific internal energy u as a mass-related quantity, a “v” is added to the volumetric energy density in the index):

\begin{align}
& U = \frac{3}{2} N k_B T = \frac{3}{2} pV\\[5px]
& p = \frac{2}{3} \cdot \underbrace{\frac{U}{V}}_{\text{energy density } u_v} \\[5px]
& \boxed{p = \frac{2}{3} u_v} ~~~~~ u_v=\frac{U}{V}
\end{align}

The pressure of an ideal gas only depends on the energy density, i.e. the internal energy in the gas per unit volume!