The Magnus effect refers to the lateral force acting on rotating round bodies in a flow!
Introduction
Anyone who has ever played football has most likely already had to deal with the Magnus effect. If you give the ball a rotation (spin), it moves on a curved path. The direction in which the ball is deflected is the same as the direction of the spin. This phenomenon is called Magnus effect.
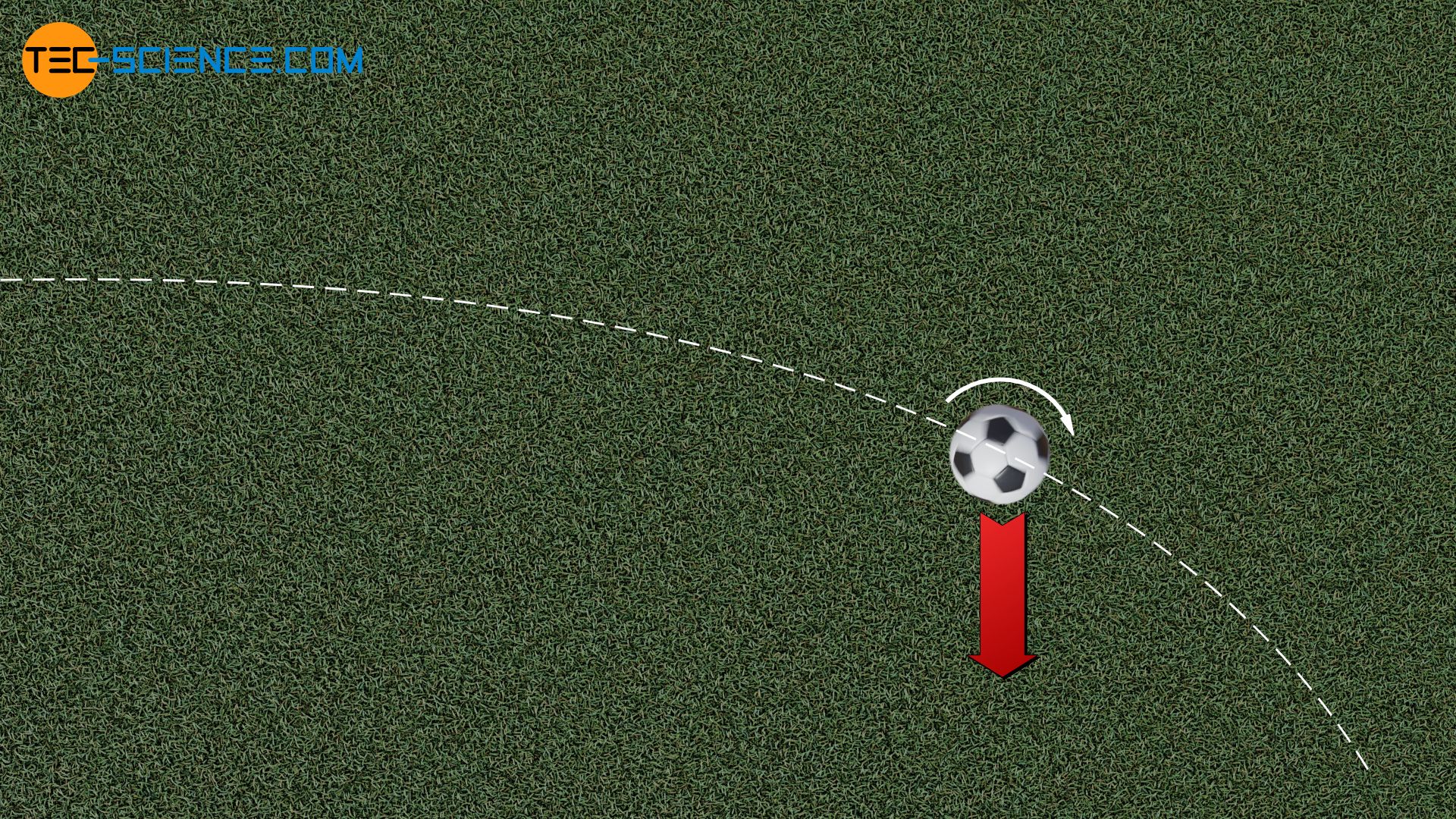
The Magnus effect is referred to as the lateral force exerted by a flow on a rotating round body!
The Magnus effect is not only present when playing football, but also when playing tennis. For example, topspin ensures that the ball falls down as quickly as possible after crossing the net. The opposite to topspin is slice, which is also based on the Magnus effect. The Magnus Effect is also used in technical applications, for example in the form of Flettner rotors (more about this later).
Superposition of two motions
So how does such a deflecting force come about. To answer this question, we take a closer look at the flow around a rotating cylinder at a fixed position. Note that it is irrelevant whether a body is moving in a resting fluid (e.g. a flying football in resting air) or a resting body is flowed around by a fluid (e.g. a resting football in the wind). What matters is only the relative speed between body and fluid.
The flow field around a straight moving and rotating cylinder finally results from two superimposed flows:
- Flow of a non-rotating cylinder around which a fluid flows
- Flow of a fixed rotating cylinder in a resting fluid
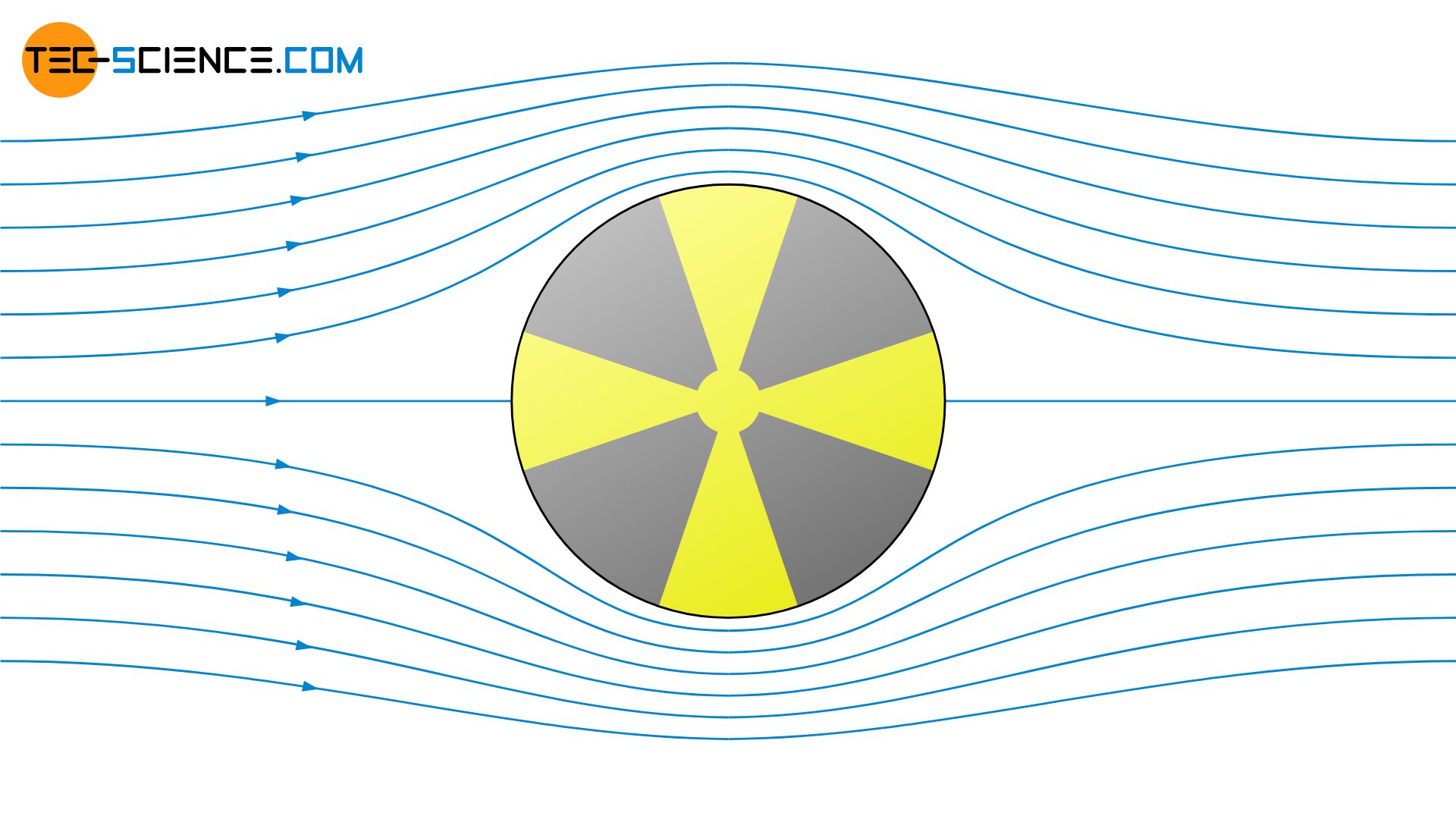
For the sake of simplicity, we assume a completely laminar flow around the cylinder, neglecting friction (potential flow). If the cylinder does not rotate, a symmetrical flow around the cylinder is obtained. The streamlines are equally displaced upwards and downwards. The denser streamlines clearly show an increase in flow velocity (see also the article Streamlines, pathlines, streaklines and timelines). Physically, this is based on the conservation of mass. A constriction of the flow cross-section inevitably means an increase in flow velocity, since the same mass must still flow through the considered cross-section.
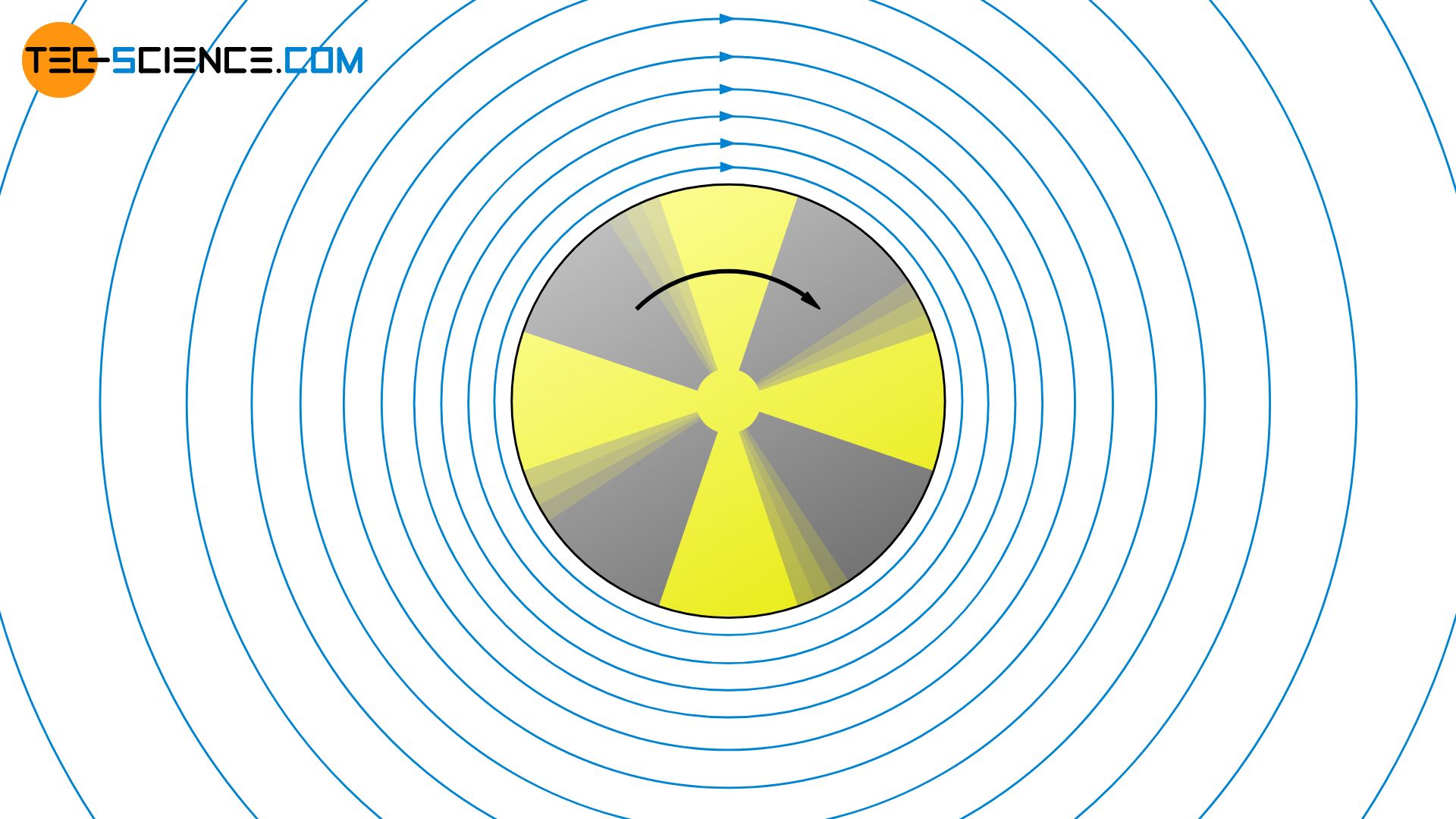
Now we look at the flow field of a stationary rotating cylinder in a resting fluid. The fluid particles located directly on the cylinder adhere to the wall due to the adhesion forces (no-slip condition). The fluid particles there rotate with the cylinder at the same speed. Depending on the viscosity of the fluid, the fluid particles also exert forces on the adjacent concentric fluid layers. These are thus also set in rotation. A so-called circulation is formed.
Explanation by the Bernoulli Effect
If you superimpose the two flow fields mentioned above, you finally obtain the flow field that is present when the cylinder rotates and a fluid flows around it simultaneously. In this case the flow around the cylinder is no longer symmetrical. In the above area the cylinder, the cylinder rotates with the direction of flow. The fluid particles are thus additionally accelerated. In the area below the cylinder, however, the rotational movement is directed against the direction of flow. The fluid particles are thus slowed down. The flow velocity is therefore greater in the area where the rotation is directed with the flow than in the area where the cylinder rotates in the opposite direction to the flow.
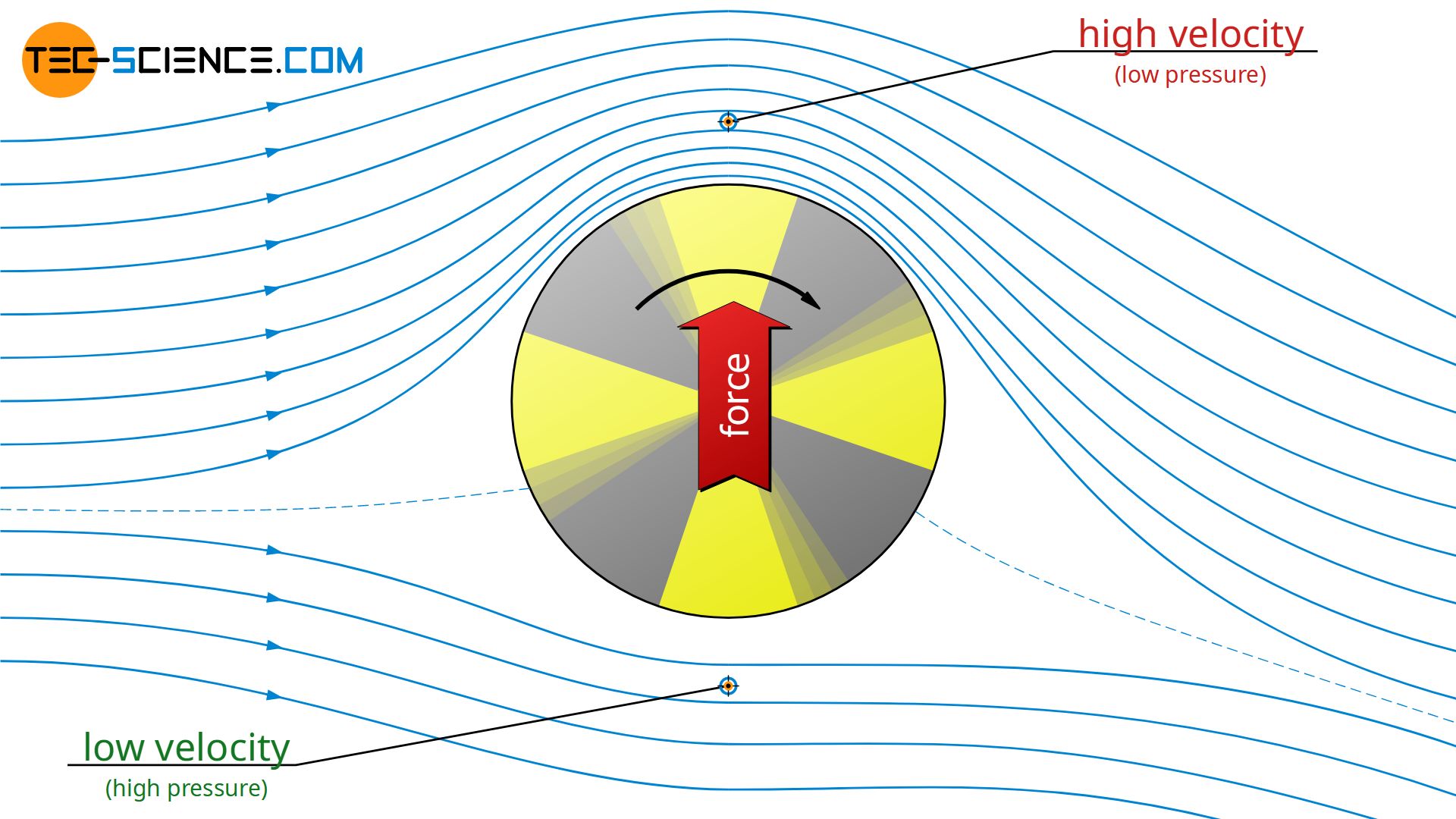
According to the Bernoulli equation, different flow speeds are associated with different pressures. The higher the flow velocity, the lower the pressure (also called Venturi effect). Consequently, the pressure in the area where the flow is directed with the rotation of the cylinder is lower than at the opposite area where the flow is directed against the rotation of the cylinder. In total, a lateral deflecting force (with regard to the direction of flow) thus acts on the rotating cylinder. This is the Magnus effect.
Explanation by the boundary layer separation
In fact, flow separation (boundary layer separation) also plays a role for the Magnus effect. In practice, the laminar flow around a cylindrical body is completely attached to the body. Due to the deceleration of the fluid after passing the thickest point of the cylinder (widening of the streamlines!), the pressure rises again according to the Bernoulli equation. This increase in pressure (called adverse pressure gradient) causes the fluid to flow back inside the boundary layer. As a result, the flow separates from the cylinder.
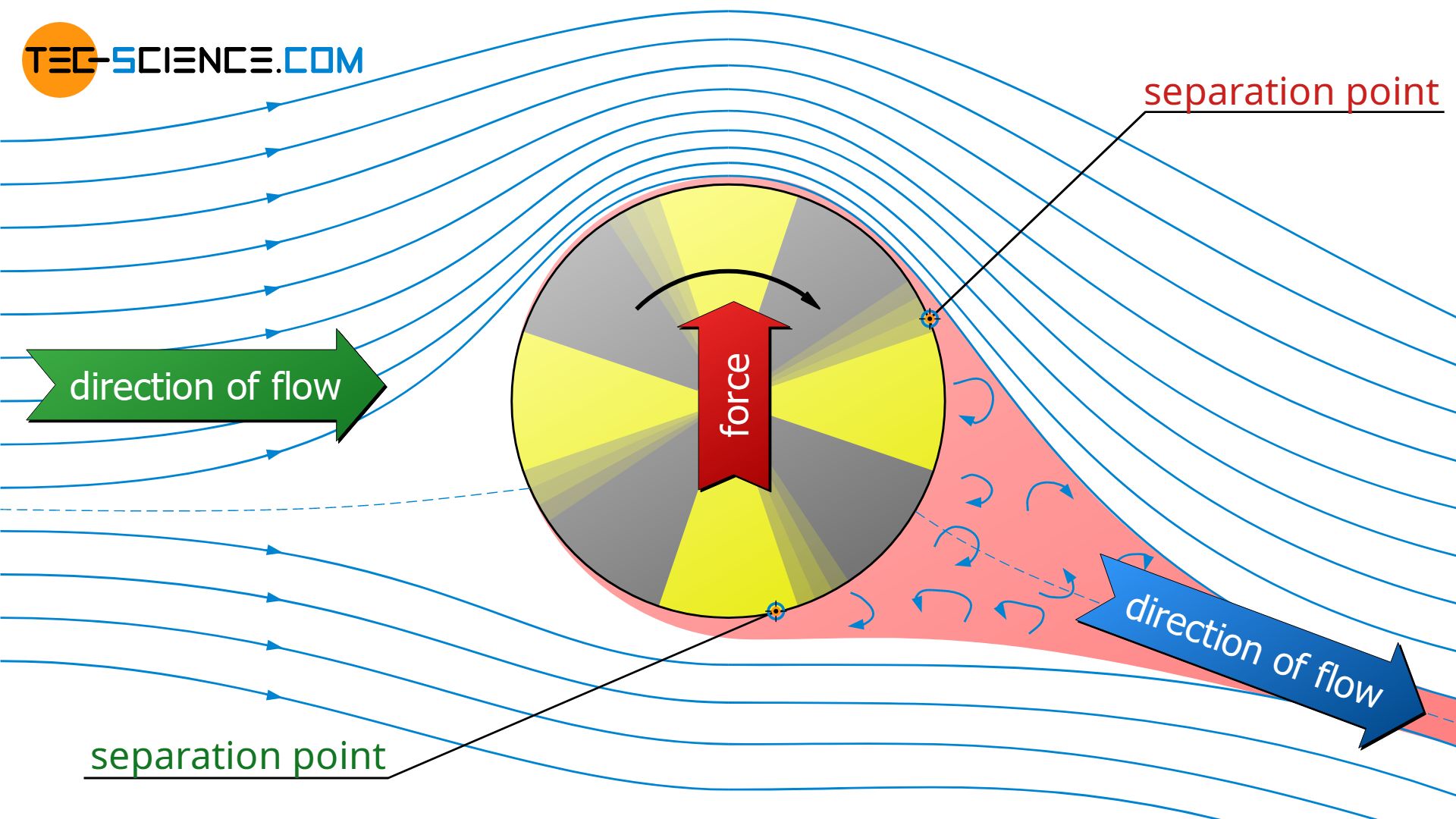
Due to the rotation of the cylinder, however, the flow speed on the side rotating with the flow is higher. The higher kinetic energy means that the flow can follow the cylinder longer despite the increase in pressure. As a result, the flow around the cylinder is longer attached to the body and flow separation occurs later on the cylinder. The flow separation is no longer symmetrical, but shifts to the side that rotates against the flow.
The fluid is thus deflected when flowing around the rotating cylinder. Obviously, the cylinder causes a lateral momentum to the flow, which must be the result of force. According to Newton’s third law (action=reaction), this means that, conversely, a lateral force is also exerted on the cylinder by the flow. The Magnus Effect.
Flettner rotor
The technical application of the Magnus Effect can be found, for example, in so-called Flettner rotors. These were/are used in shipping and consist of vertically rotating cylinders. These cylinders are driven by electric motors. When the wind blows around them, the rotating cylinders generate a force due to the Magnus Effect, which serves as propulsion. The driving force for the ship is the sum of the force created by the Magnus Effect and the force created by the air resistance.







