The Venturi effect describes the decrease of (static) pressure in flowing fluids with increasing flow velocity due to a constricted section.
Pressure as volume specific energy
Pressure is usually measured in the unit N/m² (force per unit area). If this quotient is extended by the unit meter (m), then the pressure can also be interpreted formally as energy per unit volume:
\begin{align}
& [p] = \frac{\text{N}}{\text{m²}} \cdot \frac{\text{m}}{\text{m}} = \frac{\text{Nm}}{\text{m³}}=\frac{\text{J}}{\text{m³}} \\[5px]
\end{align}
How can pressure be depicted as volume-specific energy? For this purpose we consider a water tank which we fill with a pump from the bottom. Filling the tank with water requires energy, because the water in the tank has to be pressed upwards against gravity. The work necessary to lift the water is done by the pump.

We imagine a manually operated piston pump. The pump presses the water through the pipe with a piston. We can determine the force required for a pump stroke from the stroke length of the piston Δs and from the pressure p acting on the piston surface area A. We assume that the tank is sufficiently large so that the water level practically does not change during a stroke. In this case we can assume a constant force during the stroke. The work done per stroke (ΔW) can be calculated using the following formula:
\begin{align}
& \Delta W = F \cdot \Delta s = p ~\underbrace{\cdot A \cdot \Delta s}_{\Delta V} \\[5px]
\label{w}
& \Delta W = p \cdot \Delta V \\[5px]
\end{align}
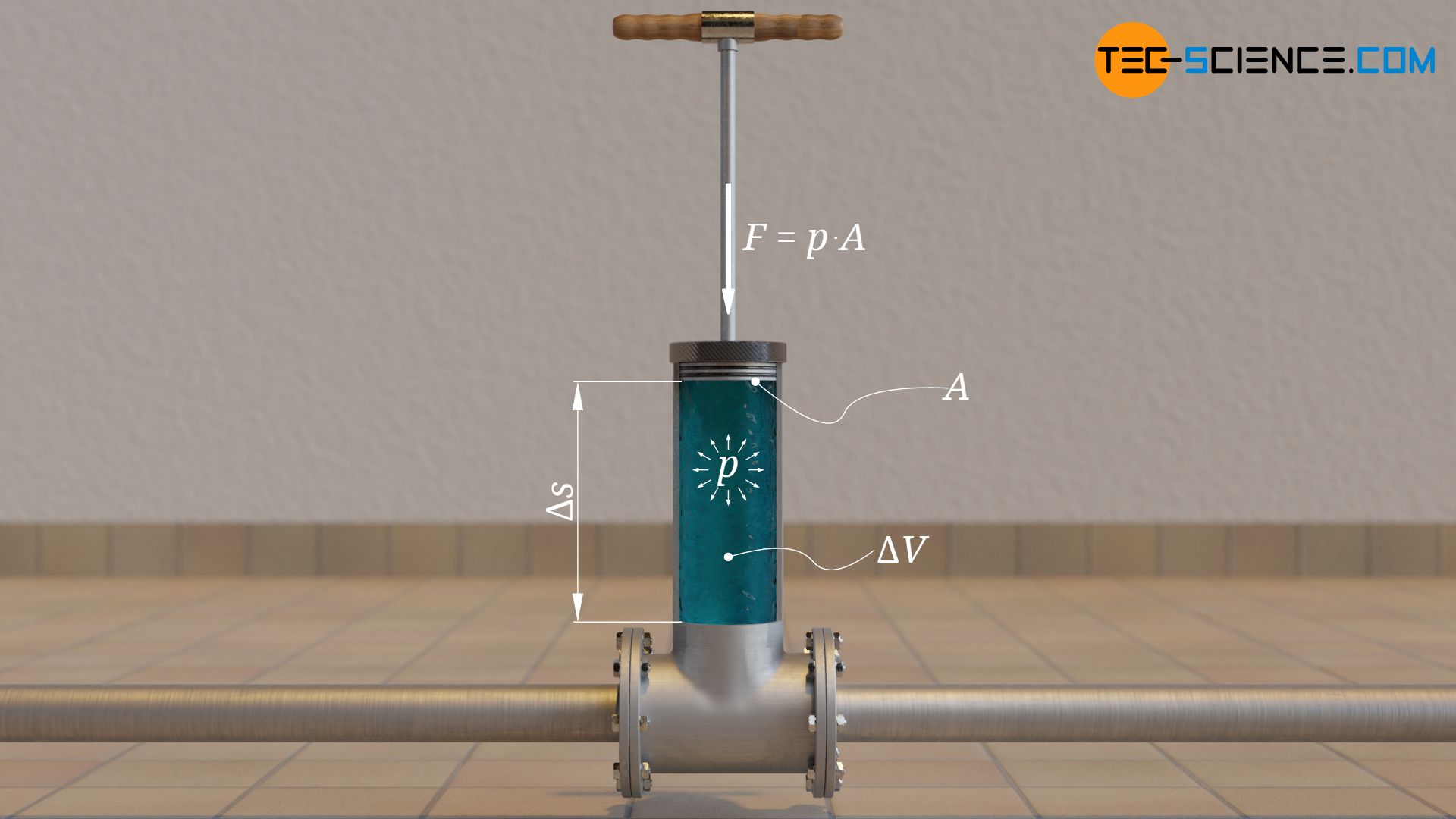
The product of piston area and stroke length corresponds to the pushed in volume ΔV (displaced volume). The work ΔW performed by the pump was converted into potential energy of the fluid. Let us now reverse this process in our thoughts. In this case, the water pressure p pushes the piston back by the distance Δs and performs work ΔW on the piston. The fluid volume ΔV with the pressure p was obviously able to do the work ΔW. If you rearrange equation (\ref{w}), then the pressure obviously also makes a statement how much energy per unit volume is present in a fluid and can be converted into mechanical work accordingly:
\begin{align}
\label{p}
& \boxed{p= \frac{\Delta W}{\Delta V}} \\[5px]
\end{align}
Pressure can be interpreted as volume-specific energy (energy per unit volume), which indicates how much potential energy is contained in a volume of a fluid and can be converted into mechanical work!
Venturi effect
The energetic interpretation of the pressure has far-reaching consequences. Let us consider a pipe through which water flows without friction. At a reducer the pipe is brought to a smaller diameter. The same mass that flows into the reducer must also flow out on the reduced side, because mass cannot accumulate or be destroyed in the reducer (continuity equation). However, the same mass can only be transported through a reduced pipe section if the flow velocity increases accordingly. This is exactly what happens inside the reducer, i.e. the fluid is inevitably accelerated.
Acceleration means an increase in the kinetic energy of the fludis. However, energy can not increase out of nothing (inside the reducer there is no pump installed, which could have delivered that energy). Knowing about energetic interpretation of pressure, only one answer remains: increase of kinetic energy can only come from pressure. However, this also means that the pressure in the constricted section with the higher kinetic energy must be lower. That this is indeed the case can be confirmed by pressure gauges attached to the pipes.
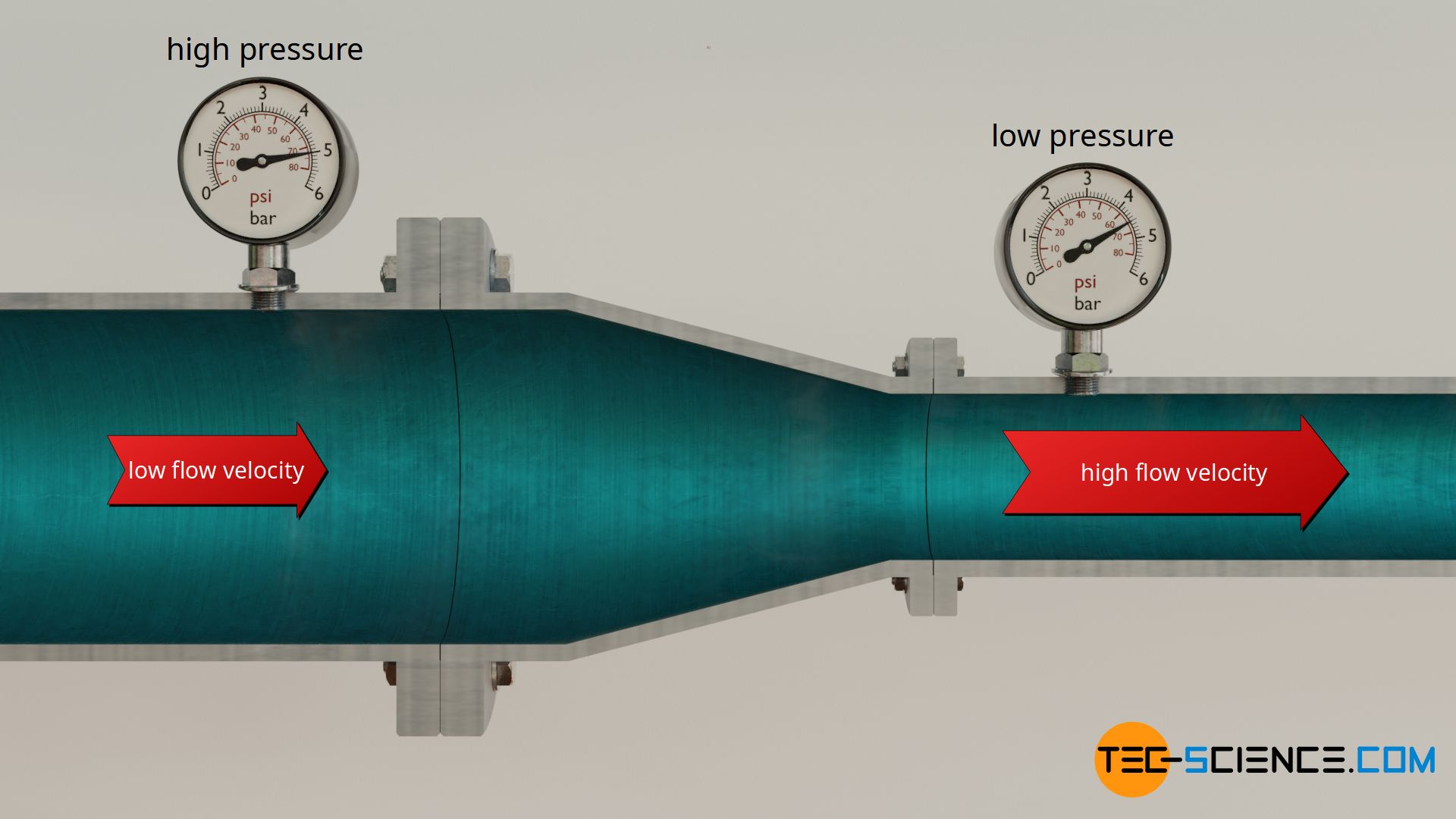
Contrary to the supposed everyday experience, the pressure decreases with increasing flow velocity! Why this misleading experience occurs, we will explain later. This (paradoxical) phenomenon of pressure decrease with increasing flow velocity is also called Venturi effect. The Venturi effect is ultimately a consequence of energy conservation.
The Venturi Effect refers to the decrease of static pressure in flowing fluids with increasing flow velocity due to energy conservation!
Demonstration of the Venturi effect
The Venturi effect can be demonstrated impressively on a vertical tube mounted on a plate with a hole. Another plate with additional weight is held against this plate from below. When air is blown through the pipe, the lower plate is not pressed down but upwards! The reason for this is the Venturi effect. Because of the small gap between the two plates, the air flows very fast. The static pressure between the plates decreases. So on the top side of the lower plate there is a lower pressure than on the bottom side. The plate is therefore pressed upwards by the greater ambient pressure at the bottom.

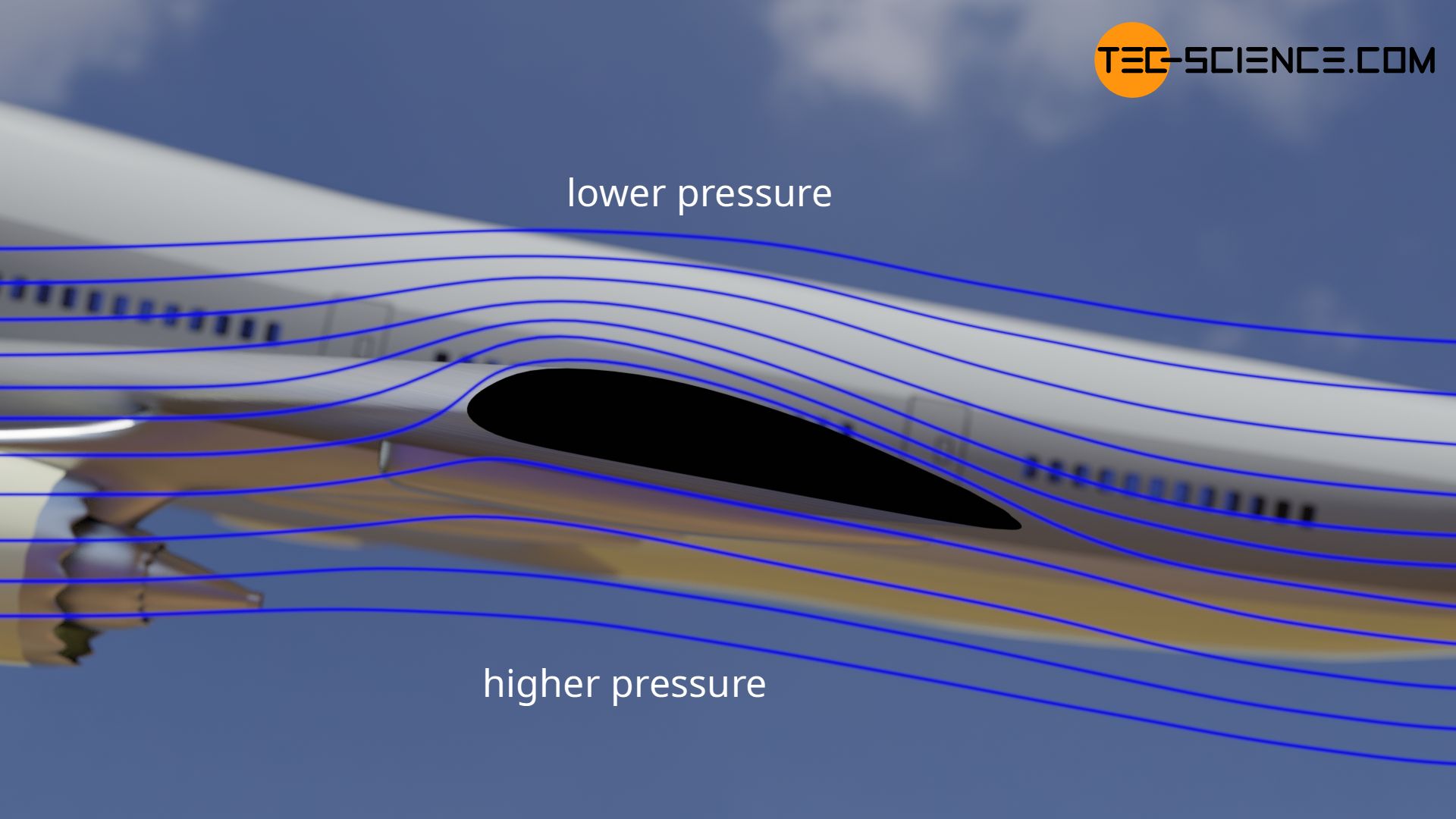
In the same way, the Venturi effect on the wings of aircraft provides a lifting force. Carburetors or pneumatic suction devices as well as decanters also use the Venturi effect. Likewise, the blowing off of a roof during a severe storm is a result of the Venturi effect. The article Examples of applications of the Venturi effect deals with this in more detail.
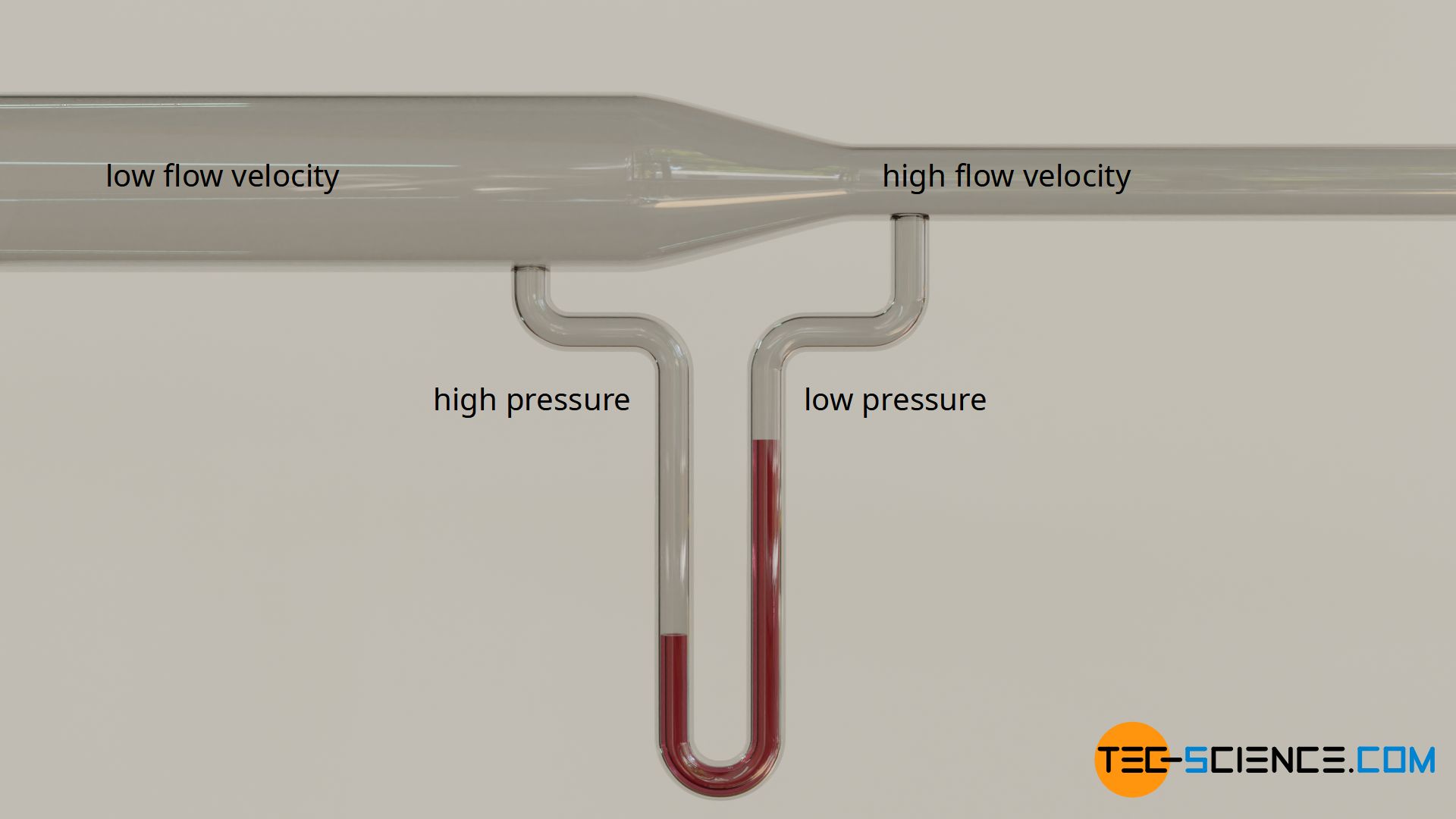
Venturi tube and de Laval nozzle
The pressure drop with increasing flow velocity can be clearly shown for gas flows. For this purpose, the pipe sections of different sizes are connected to a liquid-filled U-pipe. The higher pressure in the pipe section with the slow flowing gas pushes the liquid in the direction of the lower pressure pipe section with the faster flowing gas. Such an arrangement for generating a pressure difference, in particular the generation of a negative pressure, is also called a venturi tube or venturi nozzle. This principle is used to operate pneumatic suction cups, for example.
By the way: If the flow velocity in a tapering pipe section reaches the speed of sound, the flow velocity in the supersonic range can only be further increased if the cross-section increases again. Such a pipe shape is also referred to as a de Laval nozzle. The typical constriction and subsequent enlargement of the cross section to generate supersonic flows can be seen in rocket engines, for example. The outer visible part of the rocket engine is the supersonic part of the de Laval nozzle.

Where does the apparent contradiction come from?
So where does the apparent contradiction come from, that the pressure decreases with increasing speeds. In this context one often imagines a jet of water directed at one. Experience shows that the higher the speed of the water jet, the greater the force and thus the pressure we feel. There is nothing wrong about this observation, but the conclusion is!
Because in this argumentation one wrongly assumes that one feels the pressure in a flowing state. But this is not the case, because the liquid jet is slowed down on impact. You feel the pressure in the already decelerated state, so to speak, and not in a flowing state!
While the pressure decreases in favor of kinetic energy when a flow is accelerated, the pressure increases during the deceleration, i.e. kinetic energy is converted back into pressure energy. This increase in pressure due to the energy conversion during deceleration is what leads us to believe that the static pressure in flowing fluids is higher. In fact, this argument is based on the already decelerated state.
The same argument applies if, for example, we hold a plate in a water current and then claim that the pressure increases with increasing flow velocity. The pressure that we feel is not the pressure in the flowing state, but the pressure that is created when the flow slows down the plate. If you want to measure the static pressure in a flowing fluid, the flow itself must not be slowed down. This is exactly what the Venturi tube does by measuring the pressure sideways as it flows past. This principle is also used to determine the dynamic pressure using a Prandtl tube.
Static, dynamic and hydrostatic pressure
The kinetic energy contained in the flowing fluid can also be related to the volume of the fluid. According to the equation (\ref{p}), the kinetic energy can thus also be assigned a pressure. In contrast to the static pressure in a fluid at rest, the pressure associated with the kinetic energy is called dynamic pressure. The increase in dynamic pressure (increase in kinetic energy) is thus at the expense of static pressure.
A further reduction in static pressure occurs if the pipe is not aligned horizontally but inclined upwards. In this case the fluid must not only be accelerated, but also pressed upwards against gravity. The gravitational potential energy required for this also comes from the static pressure. The static pressure thus continues to drop as the height increases! This part of the pressure that is due to lift the fluid (gravitational potential energy) is called hydrostatic pressure.
| static pressure | pressure energy per volume unit |
| dynamic pressure | kinetic energy per volume unit |
| hydrostatic pressure | gravitational potential energy per volume unit |
Static pressure thus comes up by random movement of particles, so to speak, while dynamic pressure comes up by ordered bulk motion (macroscopic flow). The relationship between pressure energy (static pressure), kinetic energy (dynamic pressure) and gravitational positional energy (hydrostatic pressure) are described mathematically by the Bernoulli equation. This is discussed in more detail in the linked article.






