Mittlere freie Weglänge & Stoßzahl (Herleitung)

Als mittlere freie Weglänge bezeichnet man die durchschnittliche Strecke, die ein Teilchen ohne Kollision mit anderen Teilchen zurücklegt!

Einleitung

Im Artikel Maxwell-Boltzmann-Verteilung wurde gezeigt, dass sich die mittlere Geschwindigkeit (Durchschnittsgeschwindigkeit) der Teilchen eines idealen Gases mit folgender Formel ermitteln lässt:

\begin{align}
\label{v}
&\boxed{ \bar{v} = \sqrt{\frac{8 k_B T}{\pi m}}  } \\[5px]
\end{align}

Mit dieser Formel lässt sich bspw. die mittlere Geschwindigkeit von Luftteilchen abschätzen. Da Luft zu 78 % aus Stickstoff besteht, berechnet man hierzu einfach die Durchschnittsgeschwindigkeit der Stickstoffmoleküle (N₂) in einem reinen Stickstoffgas. Ein solches Stickstoffteilchen hat eine Masse von 4,65⋅10^-26 kg. Bei einer Temperatur von 20° C (293 K) ergibt sich auf diese Weise eine mittlere Geschwindigkeit von etwa 470 m/s.

Im Durchschnitt bewegen sich die Luftteilchen also mit Überschallgeschwindigkeit. Aufgrund der statistischen Verteilung der Geschwindigkeiten sind aber auch deutlich höhere Geschwindigkeiten vorhanden. Etwa 1 % der Teilchen hat sogar eine Geschwindigkeit von über 1000 m/s. Ein Teilchen aus einer Milliarde erreicht sogar eine Geschwindigkeit von 2000 m/s.

Wenn Gasteilchen im Allgemeinen so hohe Geschwindigkeiten besitzen, weshalb nimmt man dann den Duft einer geöffneten Parfümflasche am anderen Endes eines Raumes nicht sofort wahr, wie man es bei Geschwindigkeiten von mehreren hundert Metern pro Sekunde erwarten würde. Die Erfahrung zeigt, dass es offensichtlich einige Zeit dauert, bis der Duft wahrgenommen wird.

Der scheinbare Widerspruch liegt darin, dass die Gasteilchen keine „freie Bahn“ bei ihrer Bewegung haben. Die Gasmoleküle werden permanent mit anderen Teilchen zusammenstoßen und dabei ihre Bewegungsrichtungen in chaotischer Weise ändern. Die Strecke die ein Teilchen im Mittel ohne Kollision mit anderen Teilchen zurücklegen kann, wird mittlere freie Weglänge genannt. Die relativ geringe mittlere freie Weglänge der Duftteilchen sorgt in diesem Fall dafür, dass der Parfümduft nicht sofort wahrgenommen wird.

Als mittlere freie Weglänge bezeichnet man die durchschnittliche Strecke, die ein Teilchen ohne Kollision mit anderen Teilchen zurücklegt!

Dass dennoch relativ rasche Wahrnehmen des Duftes ist hauptsächlich auf die vorhandenen Luftströmungen (Konvektionen) zurückzuführen, die die Teilchen über größere Distanzen „mittragen“. Beachte, dass es sich bei Konvektionen nicht mehr um eine völlig ungeordnete Teilchenbewegungen mehr handelt. Die Moleküle werden in diesem Fall über makroskopische Distanzen hinweg in eine bestimmte Richtung bewegt, z.B. zu den Sinneszellen unserer Nase.

Berechnung der mittleren freien Weglänge

Um die mittlere freie Weglänge eines Teilchens in einem Gas zu ermitteln, wird ein Gas betrachtet, welches nur aus einer einzigen Teilchensorte besteht. Die Teilchen werden dabei als Kugeln mit einem Durchmesser d angenommen. Verfolgt man nun in Gedanken ein Teilchen aus diesem Gas (rot dargestellt), so wird dieses in unregelmäßigen Abständen mit anderen Teilchen zusammenstoßen (schwarz dargestellt). Die im Durchschnitt zurückgelegte Wegstrecke zwischen zwei aufeinanderfolgenden Kollisionen entspricht der mittleren freien Weglänge λ.

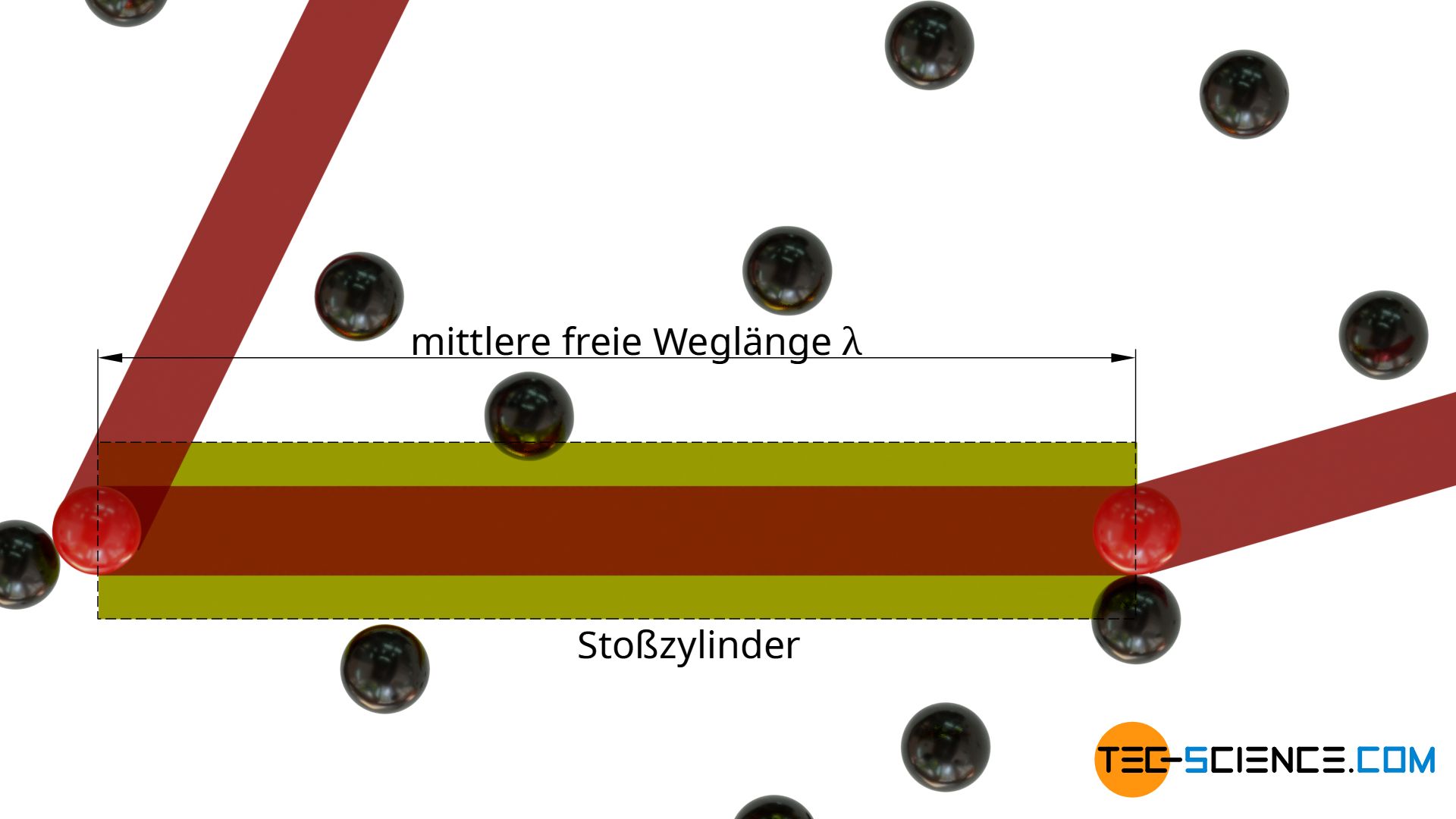
Mit Ausnahme des in Gedanken verfolgten Teilchens werden der Einfachheit halber alle anderen Teilchen zunächst als in Ruhe betrachtet. Das verfolgte Teilchen bewegt sich also durch ein „Meer“ von ruhenden Teilchen und ändert nach jeder freien Weglänge seine Richtung.

Zwischen dem sich bewegenden Teilchen und den ruhenden Teilchen wird es immer dann zu einer Kollision kommen, wenn sich die Oberflächen der kugelförmig angenommen Teilchen berühren. Dies wird dann der Fall sein, wenn der Schwerpunktsabstand geringer ist als der zweifache Teilchenradius.

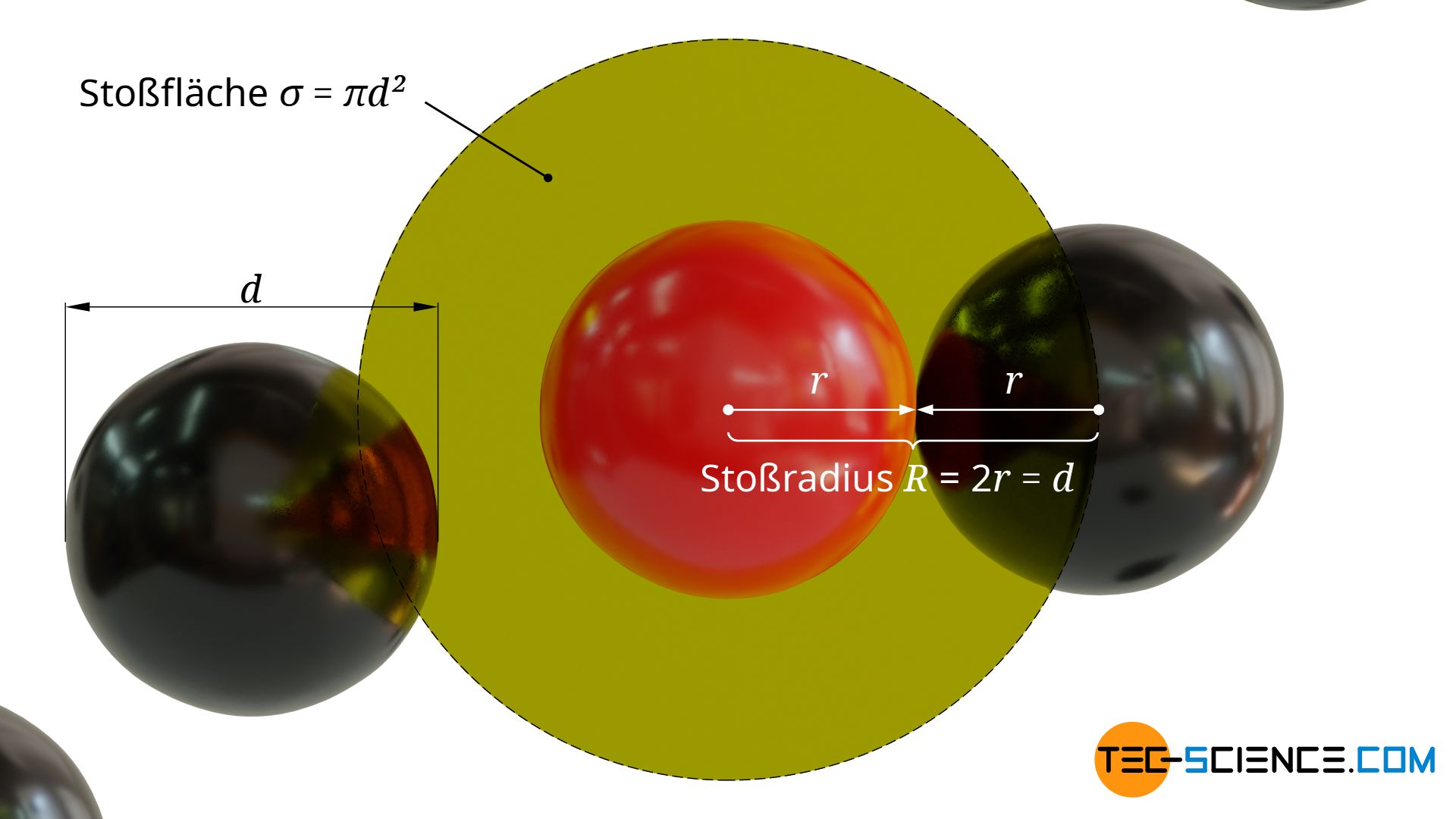
Rundum den Schwerpunkt des sich bewegenden Teilchens kann somit senkrecht zur Bewegungsrichtung eine kreisförmige Stoßfläche σ mit dem Radius R=2r=d definiert werden, innerhalb dessen der Schwerpunkt des ruhenden Teilchens liegen muss, damit es zu einer Kollision kommt. Diese Stoßfläche wird auch Wirkungsquerschnitt genannt:

\begin{align}
&\sigma = \pi R^2 = \pi d^2 ~~~~~\text{Wirkungsquerschnitt} \\[5px]
\end{align}

In Bewegungsrichtung ergibt sich auf diese Weise ein gedachter Stoßzylinder, welcher letztlich ein Kollisionsvolumen kennzeichnet. Sobald sich der Schwerpunkt eines Teilchens innerhalb dieses Stoßzylinders befindet, kommt es zur Kollision mit diesem Teilchen. Die Länge des Stoßzylinders entspricht dabei der freien Weglänge λ.

Das (mittlere) Volumen des Stoßzylinders V_S ergibt sich aus dem Produkt von Stoßfläche σ und (mittlerer) freier Weglänge λ:

\begin{align}
& V_S = \sigma \cdot \lambda = \pi d^2 \cdot \lambda~~~~~\text{Stoßzylinder} \\[5px]
\end{align}

In jedem zylindrischen Stoßvolumen V_S=σ⋅λ befindet sich per Definition gerade ein Teilchen; nämlich jenes Teilchen mit dem das bewegende Teilchen kollidiert. Anschließend wird das Teilchen seine Richtung ändern und ein neues Stoßvolumen definieren, mit wiederum einem Teilchen mit dem es kollidieren wird.

Die Aussage, dass sich innerhalb eines Stoßzylinders nur ein einziges Teilchen befindet, bezieht sich letztlich auf den Schwerpunkt der Teilchen. Im Allgemeinen wird es zwar mehrere Teilchen geben, die mit ihrer Oberfläche in das Stoßvolumen hinein reichen, aber nur wenn sich auch der Schwerpunkt innerhalb des Stoßzylinders befindet, wird tatsächlich eine Kollision stattfinden. Dies wird eben nur für ein Teilchen der Fall sein, da ab dann ein neues Stoßvolumen definiert wird, bis es schließlich wieder zu einer neuen Kollision kommt. Diese Betrachtung des Schwerpunktes ist auch insofern sinnvoll, als dass man sich die Teilchen weiterhin als Massepunkte vorstellen kann, die von einer kugelförmigen „Kollisionshülle“ umgeben sind. Mit dieser Betrachtung als Massepunkte wird deutlich, dass sich tatsächlich nur ein Teilchen im Stoßvolumen befindet (siehe Abbildung unten).

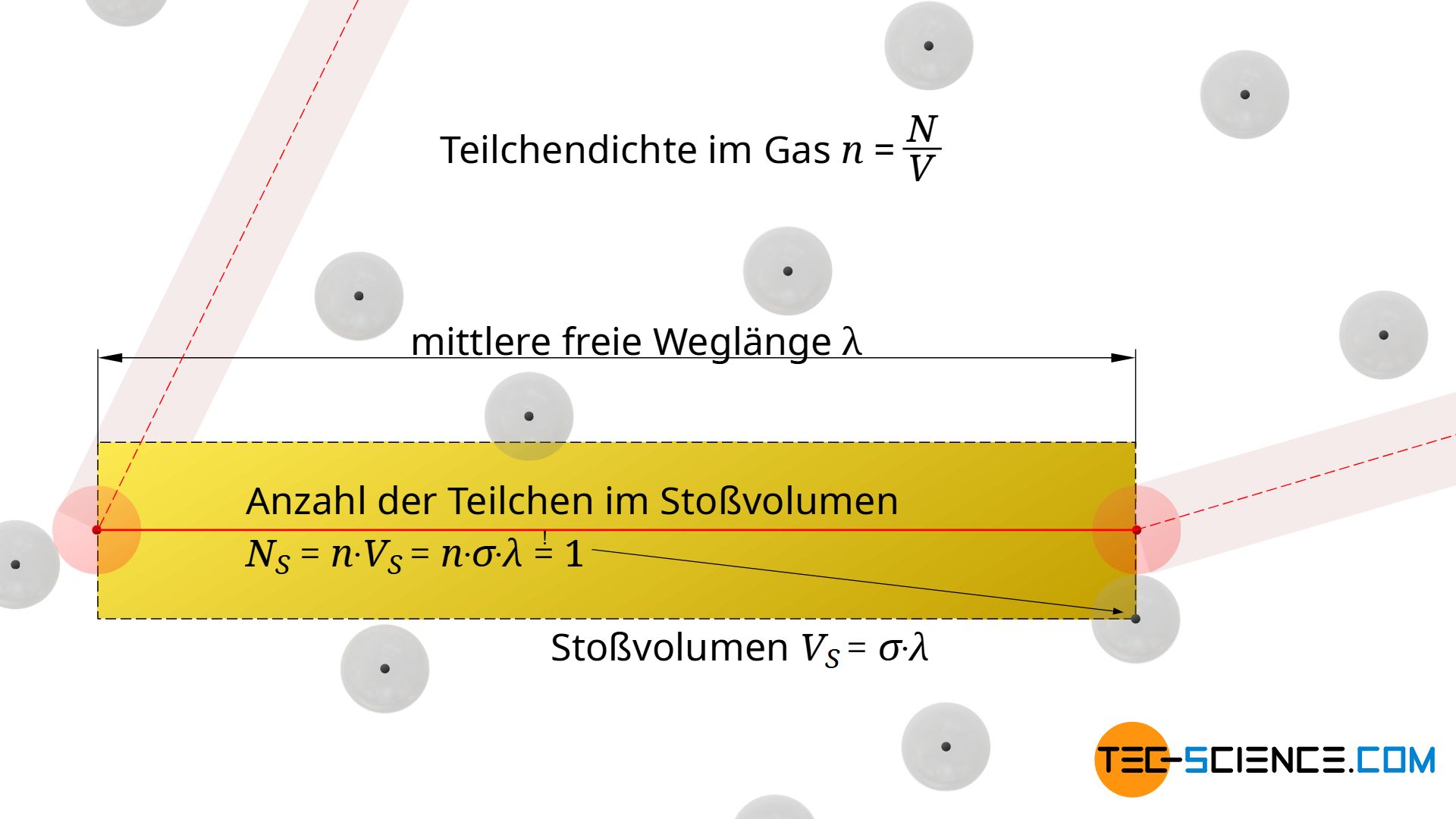
Wie viele Teilchen sich in einem bestimmten Volumenbereich befinden, kann aber auch ganz Allgemein über die Teilchendichte n im Gas ermittelt werden. Diese Teilchendichte n bestimmt sich dabei über den Quotienten aus Teilchenanzahl N und Gasvolumen V:

\begin{align}
& n = \frac{N}{V} ~~~~~\text{Teilchendichte}\\[5px]
\end{align}

Die Teilchendichte gibt anschaulich die Teilchenanzahl pro Volumeneinheit an. Multipliziert man diese Teilchendichte n mit einem beliebigen Volumen V_S, so erhält man dann die darin im Mittel befindliche Teilchenanzahl N_S. Für das Stoßvolumen beträgt diese Teilchenzahl gerade 1, sodass über diese Bedingung (!) die mittlere freie Weglänge λ ermittelt werden kann:

\begin{align}
& N_S = n \cdot V_S =n \cdot 2 \pi d^2 \lambda \overset{!}{=} 1~~~~~(\text{Teilchenanzahl im Stoßvolumen } V_S)\\[5px]
& \underline{\lambda = \frac{1}{n \pi d^2}}
\end{align}

Die mittlere freie Weglänge ist also nur von der Teilchendichte und dem Teilchendurchmesser abhängig! Bei dieser Betrachtung wurde jedoch von ruhenden Teilchen ausgegangen. Tatsächlich werden sich die einzelnen Teilchen jedoch relativ zueinander bewegen. Es ist davon auszugehen, dass dies dann zu vermehrten Kollisionen führen wird und sich deshalb die mittlere freie Weglänge verkürzt. Unter Berücksichtigung der Maxwell-Boltzmann-Geschwindigkeitsverteilung ergibt sich dann eine um den Faktor 1/√2 verkürzte mittlere freie Weglänge (auf die genaue Herleitung dieses Faktors wird im letzen Abschnitt näher eingegangen):

\begin{align}
\label{l}
& \boxed{\lambda = \frac{1}{\sqrt{2}n \pi d^2}} ~~~~~\text{mit }n=\frac{N}{V}
\end{align}

Für ein ideales Gas, kann die Teilchendichte n=N/V gemäß der idealen Gasgleichung auch über die Temperatur T und den Druck p ausgedrückt werden:

\begin{align}
&pV=N k_B T ~~~~~\text{ideale Gasgleichung}\\[5px]
\label{n}
&n=\frac{N}{V}=\frac{p}{k_B T}\\[5px]
\end{align}

Wird Gleichung (\ref{n}) in Gleichung (\ref{l}) eingesetzt, dann kann die mittlere freie Weglänge auch wie folgt ermittelt werden:

\begin{align}
\label{lam}
& \boxed{\lambda = \frac{k_B T}{\sqrt{2} p \pi d^2}}
\end{align}

Wird für ein Stickstoffmolekül ein Teilchenduchmesser von etwa d = 370 pm zugrunde gelegt (dies entspricht einer Stoßfläche von σ = 4,3·10^-19 m²), dann ergibt sich bei 20 °C (T=293 K) und einem Druck von p=1 bar eine mittlere freie Weglänge von λ = 67 nm. Die mittlere freie Weglänge ist in diesem Fall etwa um den Faktor 10 geringer als die Wellenlänge des sichtbaren Lichts!

Berechnung der Stoßzahl

Ist neben der (mittleren) freien Weglänge λ auch die (mittlere) Geschwindigkeit \(\overline{v}\) der Teilchen bekannt, dann lässt sich die (mittlere) Zeitdauer τ zwischen zwei Kollisionen ermitteln:

\begin{align}
& \text{Geschwindigkeit } \overline{v}= \frac{\text{Strecke }\lambda}{\text{Zeit } \tau} \\[5px]
\label{t}
& \boxed{\tau = \frac{\lambda}{\overline{v}}} ~~~~~\text{Zeitdauer zwischen zwei Stößen}
\end{align}

Diese mittlere Zeitdauer τ hat letztlich die Bedeutung einer Periodendauer, da sie angibt in welchen sich wiederholenden Zeitabständen im Mittel Stöße zwischen einem Teilchen und seinen Stoßpartnern stattfinden. Insofern kann der Kehrwert der Zeitdauer τ als Stoßfrequenz f aufgefasst werden, die die Anzahl der Stöße pro Zeiteinheit angibt. Diese Stoßfrequenz wird häufig auch als Stoßzahl Z bezeichnet.

\begin{align}
& Z = f = \frac{1}{\tau} \\[5px]
\label{zz}
& \boxed{Z = \frac{\overline{v}}{\lambda}} ~~~~~\text{Stoßzahl}
\end{align}

Als Stoßzahl oder Stoßfrequenz bezeichnet man die pro Zeiteinheit stattfindenden Stöße zwischen einem Teilchen und seinen Stoßpartnern!

Wird Gleichung (\ref{v}) für die mittlere Geschwindigkeit und Gleichung (\ref{lam}) für die mittlere freie Weglänge in die Formel für die Stoßzahl eingesetzt, dann ergibt sich folgende Formel:

\begin{align}
&Z = \frac{\overline{v}}{\lambda}
= \frac{\sqrt{\frac{8 k_B T}{\pi m}} }{\frac{k_B T}{\sqrt{2} p \pi d^2} }
= \sqrt{\frac{8 k_B T}{\pi m}} \frac{\sqrt{2} p \pi d^2 }{k_B T}
= \sqrt{\frac{8 k_B T}{\pi m}} \sqrt{\left(\frac{\sqrt{2} p \pi d^2 }{k_B T}\right)^2} \\[5px]
&= \sqrt{\frac{8 k_B T}{\pi m} \left(\frac{\sqrt{2} p \pi d^2 }{k_B T}\right)^2}
= \sqrt{\frac{8 k_B T}{\pi m} \frac{2 p^2 \pi^2 d^4 }{k_B^2 T^2}}
= \sqrt{\frac{16 \pi p^2 d^4}{k_B T m}} \\[5px]
\label{z}
&\boxed{Z=\sqrt{\frac{16 \pi p^2 d^4}{k_B T m}} } \\[5px]
\end{align}

Für das bereits betrachtete Stickstoffmoleküle ergibt sich bei 20 °C (293 K) und einem Druck von 1 bar, eine Stoßzahl von Z = 7·10⁹ 1/s, d.h. innerhalb von einer Sekunde wird ein einziges Stickstoffteilchen im Mittel mit 7 Milliarden Teilchen kollidieren!

Um die Gesamtzahl der Stöße pro Volumeneinheit zu erhalten, muss die Stoßzahl Z lediglich mit der Teilchendichte n („Teilchenanzahl pro Volumen“) multipliziert werden. Dabei muss beachtet werden, dass jeweils zwei Teilchen einen Stoß ausführen, sodass noch ein Faktor ½ berücksichtigt werden muss. Wird die Teilchendichte n nach Gleichung (\ref{n}) durch die Temperatur und den Druck ausgedrückt, dann bestimmt sich die Gesamtstoßzahl pro Volumeneinheit z wie folgt:

\begin{align}
&z=\frac{1}{2} \cdot n \cdot Z = \frac{1}{2} \cdot \frac{p}{k_BT} \cdot \sqrt{\frac{16 \pi p^2 d^4}{k_B T m}} = \sqrt{\frac{4 \pi p^4 d^4}{k_B^3 T^3 m}} \\[5px]
&\boxed{z= \sqrt{\frac{4 \pi p^4 d^4}{k_B^3 T^3 m}} } ~~~~~\text{Gesamtstoßzahl pro Volumeneinheit}
\end{align}

Für Stickstoff erhält man auf diese Weise eine Gesamtstoßzahl von 8,7·10³⁴ 1/sm³, d.h. in einem Volumen von einem Kubikmeter finden innerhalb von einer Sekunde 8,7·10³⁴ Kollisionen statt.

Herleitung des Faktors 1/√2

In diesem Abschnitt soll die Frage geklärt werden, wie es genau zu dem Faktor 1/√2 in der Gleichung (\ref{lam}) für die mittlere freie Weglänge kommt. Ausgangssituation war zunächst die Annahme, dass sich die Stoßpartner eines Teilchens alle in Ruhe befinden.

Modellvorstellung

In Analogie kann man sich eine Marktplatz mit vielen Personen vorstellen, welchen man zu Fuß überqueren möchte. Alle Personen bleiben dabei aber zunächst in Ruhe stehen. Nun beginnt man geradeaus zu laufen. Jedesmal wenn man auf eine Person trifft, ändert man in zufälliger Weise seine Richtung und läuft anschließend wieder geradeaus. Die Wegstrecke die man im Mittel zurücklegen kann, ohne dass man auf eine Person trifft, entspricht im übertragenen Sinne der mittlere freien Wegstrecke.

Man kann die freie Wegstrecke auf dem Marktplatz wie folgt bestimmen. Hierzu muss man zum einen die Zeitdauer zwischen zwei Zusammenstößen messen und zum anderen benötig man die Geschwindigkeit mit der man sich bewegt. Aus dem Produkt von (mittlerer) Zeitdauer τ₀ und (mittlerer) Geschwindigkeit \(\overline{v}\) ergibt sich dann die (mittlere) freie Weglänge λ:

\begin{align}
& \lambda_0 = \overline{v} \cdot \tau_0 ~~~~~\text{mittlere freie Weglänge für ruhende Stoßpartner}
\end{align}

Nun gehen wir davon aus, dass sich die Personen auf dem Marktplatz in chaotischer Weise selbst bewegen, wenn wir diesen überqueren. Die Zeitdauer τ zwischen zwei Zusammenstößen kann wiederum durch einfaches Messen ermittelt werden. Obwohl man nach wie vor mit derselben Geschwindigkeit über den Marktplatz läuft, wird man nun aber feststellen, dass sich die Zeitdauer zwischen zwei Zusammenstößen im Mittel verkürzt (τ<τ₀). Hierdurch wird auch folglich auch die mittlere freie Weglänge verkürzen (λ<λ₀):

\begin{align}
& \lambda = \overline{v} \cdot \tau ~~~~~\text{mittlere freie Weglänge für sich bewegende Stoßpartner}
\end{align}

Die Verkürzung der Zeitdauer (bzw. der mittleren Wegstrecke) ist letztlich darin begründet, dass nicht nur die eigene Geschwindigkeit den Zeitabstand zwischen zwei Kollisionen bestimmt, sondern die Relativgeschwindigkeit mit der man sich auf einen Stoßpartner zubewegt. Es ist also auch die Geschwindigkeit der umgebenden Personen relevant. Die Relativgeschwindigkeit ist im Grunde genommen auch für den Fall von ruhenden Stoßpartnern entscheidend, da diese aber als ruhend betrachtet werden entspricht die Relativgeschwindigkeit der Geschwindigkeit mit der man sich selbst bewegt!

Übertragung der Modellvorstellung auf Gase

Überträgt man diese Modellvorstellung auf ein Gas, dann darf man also für die mittlere Zeitdauer zwischen zwei Kollisionen nicht die mittlere Geschwindigkeit \(\overline{v}\) eines Teilchens zugrunde legen, sondern die mittlere Relativgeschwindigkeit \(\overline{v_{rel}}\), mit der sich die Teilchen im Mittel annähern. Aus statistischen Überlegungen heraus, kann ein Zusammenhang zwischen diesen beiden Geschwindigkeiten hergeleitet werden.

Hierzu werden zwei Teilchen betrachtet, die sich annähern und miteinander kollidieren werden. Die Geschwindigkeitsvektoren der beiden Teilchen können dabei in beliebiger Weise angeordnet sein (siehe Abbildung unten). Aus Sicht des Teilchens 1 ergibt sich die Relativgeschwindigkeit mit der sich Teilchen 2 bewegt aus der Differenz der Geschwindigkeitsvektoren:

\begin{align}
\label{rel1}
& \vec{v_{rel}} = \vec{v_2} – \vec{v_1} \\[5px]
\end{align}

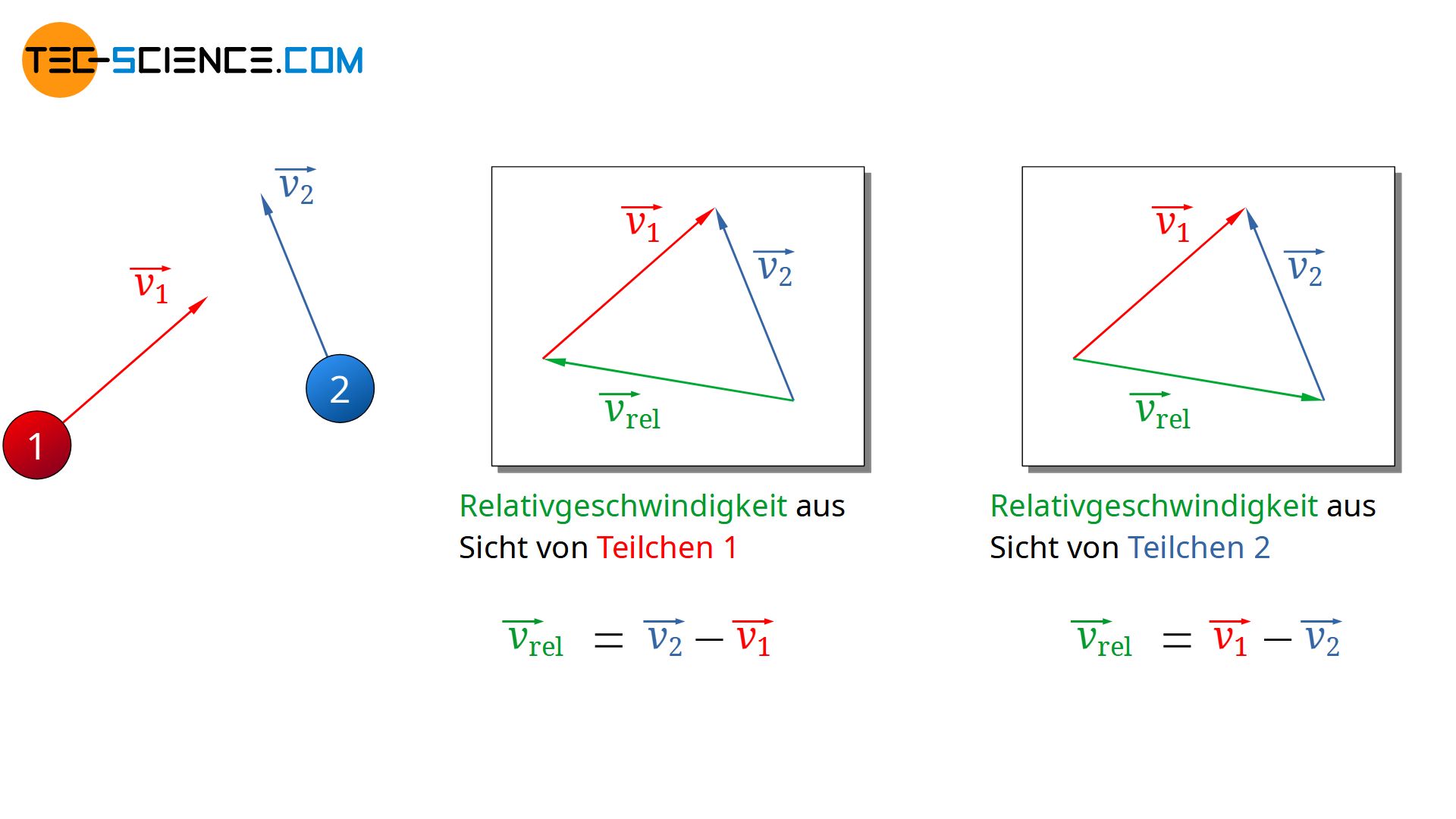
Da später ohnehin nur der Betrag der (mittleren) Relativgeschwindigkeit für die (mittlere) freie Weglänge relevant ist, hätte es an dieser Stelle keinen Unterschied gemacht in welcher Reihenfolge die Geschwindigkeitsvektoren voneinander abgezogen worden wären. Man hätte die Indizes in der oberen Gleichung also auch vertauschen können. Auf diese Weise hätte man dann die Annäherung der Teilchen aus Sicht des Teilchens 2 beschrieben.

Grundsätzlich macht es aus mathematischer Sicht keinen Unterschied ob man den Betrag eines Vektors quadriert (v²) oder ob man den Vektor selbst quadriert (\(\vec{v}^2\)). Man erhält in beiden Fällen dasselbe skalare Ergebnis:

\begin{align}
\label{mat}
& v^2 = \vec{v}^2\\[5px]
\end{align}

Anmerkung: Der Übersichtlichkeit halber wird im Folgenden auf die Betragsstriche verzichtet und nur das Formelsymbol v angegeben, wenn der Betrag der Geschwindigkeit gemeint ist. Ist hingegen der Geschwindigkeitsvektor \(\vec{v}\) gemeint, dann wird explizit ein Pfeil über das Symbol gestellt.

Der Betrag der Relativgeschwindigkeit v_rel lässt sich somit wie folgt durch den entsprechenden Vektor \(\vec{v_{rel}}\) ausdrücken:

\begin{align}
\label{rel2}
& v_{rel}^2 = \vec{v_{rel}}^2\\[5px]
\end{align}

Wird nun Gleichung (\ref{rel1}) in Gleichung (\ref{rel2}) eingesetzt, dann ergibt sich folgende Beziehung zwischen der Relativgeschwindigkeit und den Geschwindigkeiten der einzelnen Teilchen:

\begin{align}
& v_{rel}^2= \vec{v_{rel}}^2 =\left(\vec{v_2} – \vec{v_1} \right)^2 =\vec{v_2}^2 + \vec{v_1}^2 – 2\vec{v_1}\vec{v_2} \\[5px]
\end{align}

Um diese Gleichung etwas übersichtlicher zu gestalten, kann gemäß Gleichung (\ref{mat}) für das Quadrat der Geschwindigkeitsvektoren wiederum das Quadrat der Geschwindigkeitsbeträge verwendet werden:

\begin{align}
& v_{rel}^2= v_2^2 + v_1^2 – 2\vec{v_1}\vec{v_2} \\[5px]
\end{align}

Mit dieser Gleichung lässt sich bisher nur die Relativgeschwindigkeit einzelner Kollision bestimmen. Eine Aussage über den Mittelwert der Relativgeschwindigkeit ist nur möglich, wenn alle möglichen Stöße betrachtet werden und hieraus der Mittelwert gebildet wird. Man muss also theoretisch die Relativgeschwindigkeit für jede erdenkliche Kollision nach oberer Formel ausrechnen und dann den Mittelwert bestimmen:

\begin{align}
& \overline{v_{rel}^2}= \overline{v_2^2 + v_1^2 – 2\vec{v_1}\vec{v_2}} \\[5px]
\end{align}

Da es sich bei der rechten Seite der Gleichung um den Mittelwert einer Summe handelt, kann anstelle dessen auch der Mittelwert der einzelnen Summanden gebildet werden:

\begin{align}
\label{term}
& \overline{v_{rel}^2}= \underbrace{\overline{v_2^2}}_{\text{Term 1}} +
\underbrace{\overline{v_1^2}}_{\text{Term 2}} –
\underbrace{\overline{2\vec{v_1}\vec{v_2}}}_{\text{Term 3}} \\[5px]
\end{align}

Der erster Term, der das Quadrat der Geschwindigkeit des gestoßen Teilchens 2 enthält, wird sich im Mittelwert grundsätzlich nicht von dem zweiten Term unterscheiden, der das Quadrat der Geschwindigkeit des Teilchens 1 enthält. Aufgrund der ungeordneten Bewegungen werden die Geschwindigkeit im Mittel von beiden Stoßpartnern identisch sein. Es wurde ja bereits erwähnt, dass die Indizes auch einfach hätten vertauscht werden können. Dies ist nur eine Frage ob der Stoß von dem einen Teilchen oder dem anderen Teilchen aus betrachtet wird. Die Mittelwerte der Geschwindigkeiten v₁ und v₂ werden somit identisch sein und entsprechen der mittleren Geschwindigkeit \(\overline{v}\) eines Teilchens. Somit gilt:

\begin{align}
& \overline{v_{1}^2}=\overline{v_{2}^2}=\overline{v^2} \\[5px]
\end{align}

Der dritte Term in Gleichung (\ref{term}) enthält das Skalarprodukt aus den Geschwindigkeitsvektoren der Stoßpartner. Wie bei einem Skalarprodukt üblich werden dabei die einzelnen Geschwindigkeitskomponenten miteinander multipliziert und anschließend aufsummiert. Die einzelnen Komponenten können dabei sowohl negativ als auch positiv sein. Da es sich dabei aber um eine völlig statistische Verteilung der Komponenten handelt, werden im selben Maße positive wie negative Werte für das Skalarprodukt erhalten. Bei Betrachtung hinreichend vieler Teilchen bzw. Stöße (dies ist bei einer Stoßrate in der Größenordnung von 10³⁴ Stöße pro Sekunde und Kubikmeter wohl mehr als gegeben!) werden sich im Mittel die positiven Terme mit den im selben Maße negativen Terme kompensieren. Im statistischen Mittel wird der dritte Term in Gleichung (\ref{term}) also Null sein:

\begin{align}
& \overline{2\vec{v_1}\vec{v_2}} = 0 \\[5px]
\end{align}

Für Gleichung (\ref{term}) gilt also im Mittelwert:

\begin{align}
& \overline{v_{rel}^2}= \underbrace{\overline{v_2^2}}_{\overline{v^2}} +\underbrace{\overline{v_1^2}}_{\overline{v^2}} –
\underbrace{\overline{2\vec{v_1}\vec{v_2}}}_{=0} \\[5px]
\label{vrel}
& \underline{\overline{v_{rel}^2}= 2 \cdot \overline{v^2}} \\[5px]
\end{align}

Gemäß der Maxwell-Boltzmann-Geschwindigkeitsverteilung steht der Mittelwert der Geschwindigkeitsquadrate \(\overline{v^2}\) in einem konstanten Verhältnis zum Quadrat der mittleren Geschwindigkeit (dies gilt auch für die Relativgeschwindigkeit, denn ein Gas ändert ja nicht seine Temperatur, nur weil man es aus Sicht eines Gasmoleküls beschreibt). Somit gilt ganz allgemein:

\begin{align}
\boxed{\frac{ \sqrt{\overline{v^2}} }{\overline{v}}=\sqrt{\frac{3\pi}{8}}}\\[5px]
\end{align}

\begin{align}
\frac{ \overline{v^2} }{\overline{v}^2}&=\frac{3\pi}{8}\\[5px]
\overline{v^2} &=\frac{3\pi}{8} \cdot \overline{v}^2 \\[5px]
\end{align}

Deshalb kann Gleichung (\ref{vrel}) auch durch das Quadrat der mittleren Geschwindigkeit ausgedrückt werden. Folglich stehen die Geschwindigkeiten über den Faktor √2 in Zusammenhang:

\begin{align}
\require{cancel}
\overline{v_{rel}^2}&= 2 \cdot \overline{v^2} \\[5px]
\cancel{\frac{3\pi}{8}} \cdot \overline{v_{rel}}^2 &= 2 \cdot \cancel{\frac{3\pi}{8}} \cdot \overline{v}^2 \\[5px]
\end{align}

\begin{align}
&\boxed{\overline{v_{rel}}= \sqrt{2} \cdot \overline{v}} \\[5px]
\end{align}

Schlussfolgerung

Die Relativgeschwindigkeit der Teilchen in einem Gas ist also im Mittel um den Faktor √2 größer als die mittlere Geschwindigkeit der Teilchen. Die tatsächliche Annäherungsgeschwindigkeit zweier Teilchen ist also um den Faktor √2 größer als wenn nur die eigene Geschwindigkeit bei der Annäherung zugrunde gelegt werden würde (dies entspräche im Prinzip dem Fall, dass alle anderen Teilchen sich in Ruhe befänden).

Die höhere Annäherungsgeschwindigkeit bei der Relativbewegung verkürzt die Zeitdauer zwischen zwei Kollisionen folglich um den Faktor 1/√2. Im Vergleich zur ruhenden Betrachtung wird deshalb die mittlere freie Weglänge ebenfalls um den Faktor 1/√2 geringer ausfallen! Aus diesem Grund wird in Gleichung (\ref{l}) der Faktor 1/√2 eingeführt, da die Betrachtung davor auf ruhenden Teilchen basierte.