In diesem Artikel betrachten wir Temperaturverläufe und Wärmeströme durch eine ebene Wand, durch ein zylindrisches Rohr und durch eine Hohlkugel.
Einleitung
Temperaturdifferenzen verursachen Wärmeströmen. Diese Wärmeströme wiederum sorgen im stationären Fall je nach Geometrie für unterschiedliche Temperaturverläufe im Inneren des betrachteten Materials. Als Beispiel soll im Folgenden der Temperaturverlauf bei Wärmeleitung innerhalb einer ebenen Gefäßwand, innerhalb eines zylindrischen Rohres (Hohlzylinder) und einer Hohlkugel berechnet werden.
Wärmeströme durch eine ebene Wand ist wahrscheinlich der häufigste Fall. Als Beispiel sei der Wärmestrom durch eine Gebäudewand oder durch die Gefäßwand eines ebenen Behälters mit heißem Wasser genannt.


Wärmeströme durch Hohlzylinder finden sich ganz allgemein bei Rohrleitungen wieder. Die Heizrippen mancher Heizkörper haben eine solche zylindrische Form.


In seltenen Fällen hat eine wärmeleitende Geometrie auch die Form einer Hohlkugel. Dies ist bei einigen Speicherkollektoren der Fall, die in einem Kugelförmigen Tank Warmwasser speichern.

Gemäß des Fourier’sches Gesetzes ist der Wärmestrom Q* durch ein Flächenelemente A wie folgt von dem dort vorhandenen Temperaturgradienten dT/dr abhängig:
\begin{align}
&\dot Q = – \lambda \cdot A \cdot \frac{\text{d}T}{\text{d}r} \\[5px]
\end{align}
Für die infinitesimale Temperaturänderung dT entlang eines Streckenabschnitts dr gilt folglich ganz allgemein:
\begin{align}
\label{q}
&\boxed{ \text{d}T = – \frac{\dot Q}{\lambda \cdot A} \cdot \text{d}r} \\[5px]
\end{align}
Der Quotient aus Wärmestrom und Fläche, kann also Wärmestromdichte q* aufgefasst werden, d.h. als Wärmestrom pro Flächeneinheit. Somit lässt sich obere Gleichung auch wie folgt darstellen:
\begin{align}
\label{qq}
&\boxed{ \text{d}T = – \frac{\dot q}{\lambda} \cdot \text{d}r} \\[5px]
\end{align}
Temperaturprofile
Temperaturverlauf innerhalb einer ebenen Wand
Bei einer ebenen Wand ist die Fläche A in Richtung des Wärmestroms stets konstant und damit keine Funktion der Variablen r. Der Wärmestrom Q* bezeichnet dabei den Wärmestrom der auf die Innenseite der Wand übertragen und durch die Wand geleitet wird. Aufgrund der Energieerhaltung tritt dieser Wärmestrom im stationären Zustand auch im selben Maße durch jede gedachte Zwischenebene.
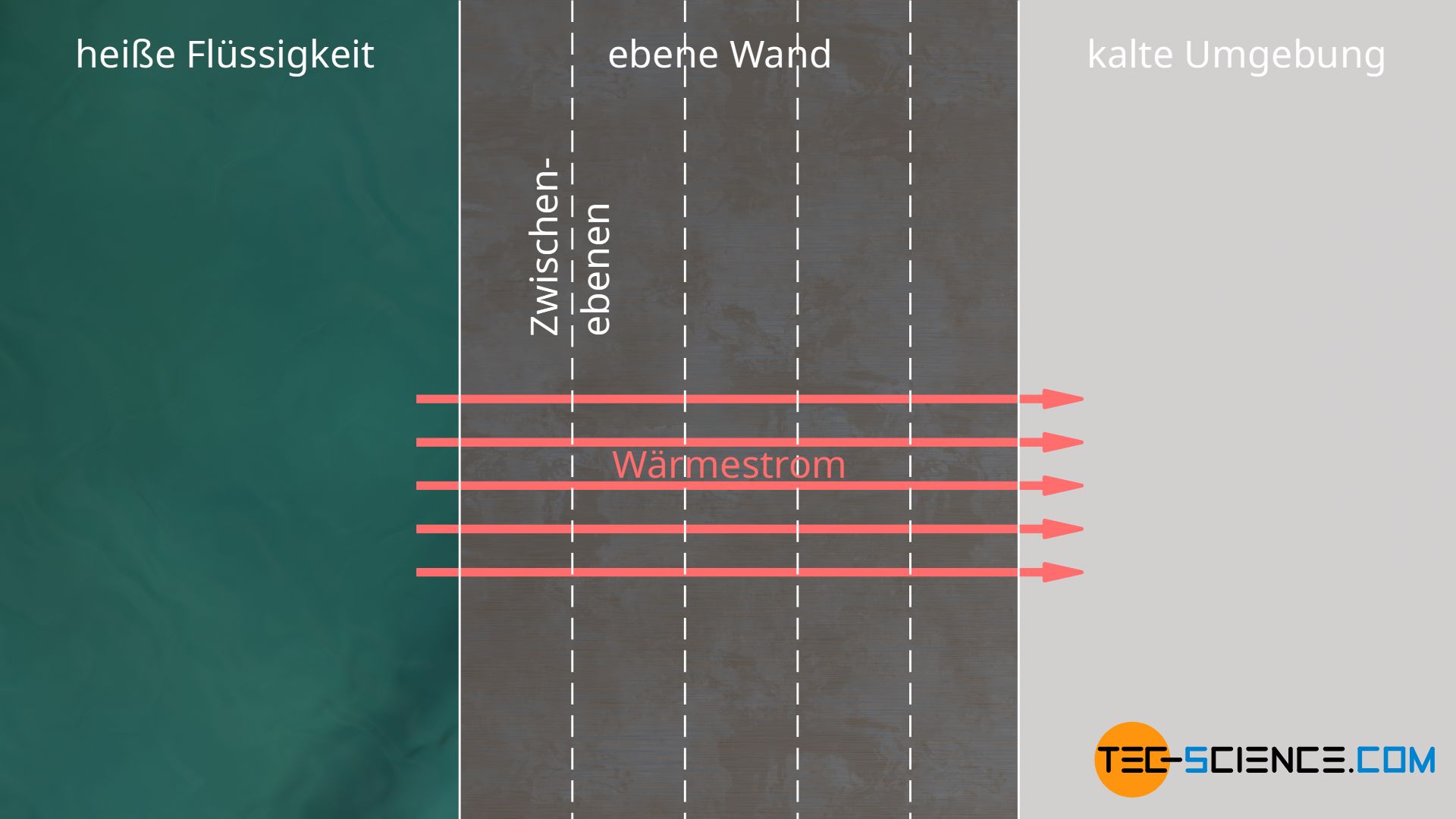
Wäre dies nicht der Fall, dann würde sich die Wand entweder durch „Anhäufung“ von Wärme erwärmen oder durch „Entzug“ von Wärme abkühlen. Wir möchten aber ausschließlich den stationären Fall betrachten, bei dem sich der Temperaturverlauf zeitlich nicht ändert. Aufgrund des konstanten Wärmestroms und die konstante Fläche durch die dieser tritt, erhält man folglich eine konstante Wärmestromdichte q*. Dies wiederum bedeutet gemäß Gleichung (\ref{qq}), dass sich die Temperatur pro Streckenabschnitt dr immer um denselben Betrag dT ändert. Folglich ergibt sich bei einer ebenen Wand eine lineare Temperaturänderung.
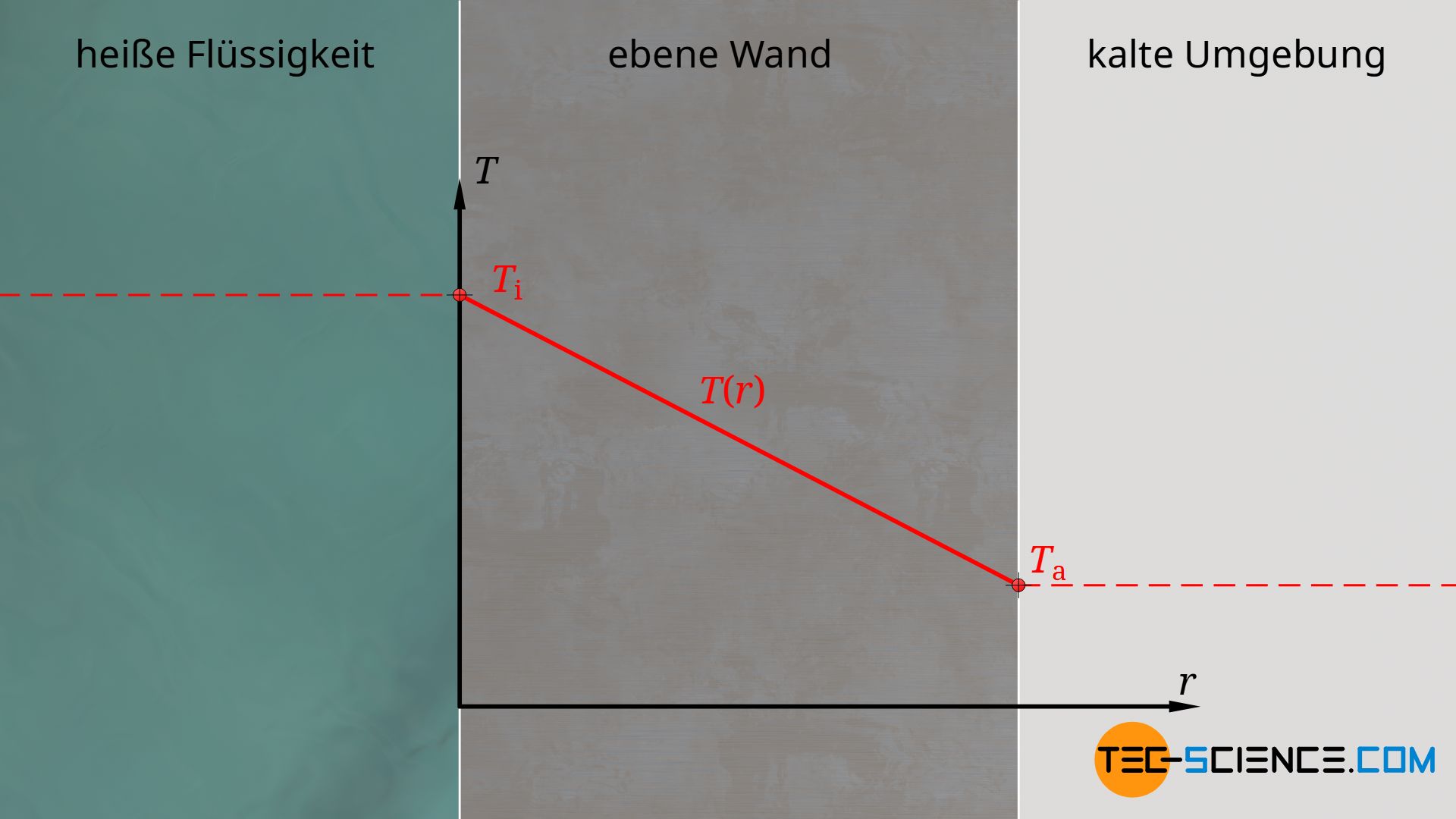
Den genauen Verlauf der Temperatur T(r) kann man durch Integration von Gleichung (\ref{q}) ermitteln, wobei die Wärmeleitfähigkeit als konstant vorausgesetzt wird. Dabei bezeichnet Ti die Temperatur an der Innenseite der Wand bei r=0:
\begin{align}
& \text{d}T = – \frac{\dot Q}{\lambda \cdot A} \cdot \text{d}r \\[5px]
& \int \limits_{T_i}^{T}\text{d}T = – \frac{\dot Q}{\lambda \cdot A} \cdot \int \limits_{0}^{r}\text{d}r \\[5px]
& [T]_{T_i}^{T}= – \frac{\dot Q}{\lambda \cdot A} \cdot [r]_{0}^{r}\\[5px]
& T-T_i= – \frac{\dot Q}{\lambda \cdot A} \cdot r \\[5px]
\label{e}
&\boxed{T(r) = T_i – \frac{\dot Q}{\lambda \cdot A} \cdot r} \\[5px]
\end{align}
Die Temperatur ändert sich durch eine ebene Wand linear!
Temperaturverlauf innerhalb eines zylindrischen Rohres
Auch bei einer zylindrischen Wand tritt im stationären Zustand durch jede gedachte Zwischenebene im selben Maße der von Innen auf die Wand übertragene Wärmestrom. Ansonsten käme es insgesamt wieder zu einer Erwärmung oder Abkühlung des Rohrs. Der Wärmestrom Q* durch die zylindrische Wand ist somit wiederum keine Funktion der Koordinate r, sondern stets konstant.
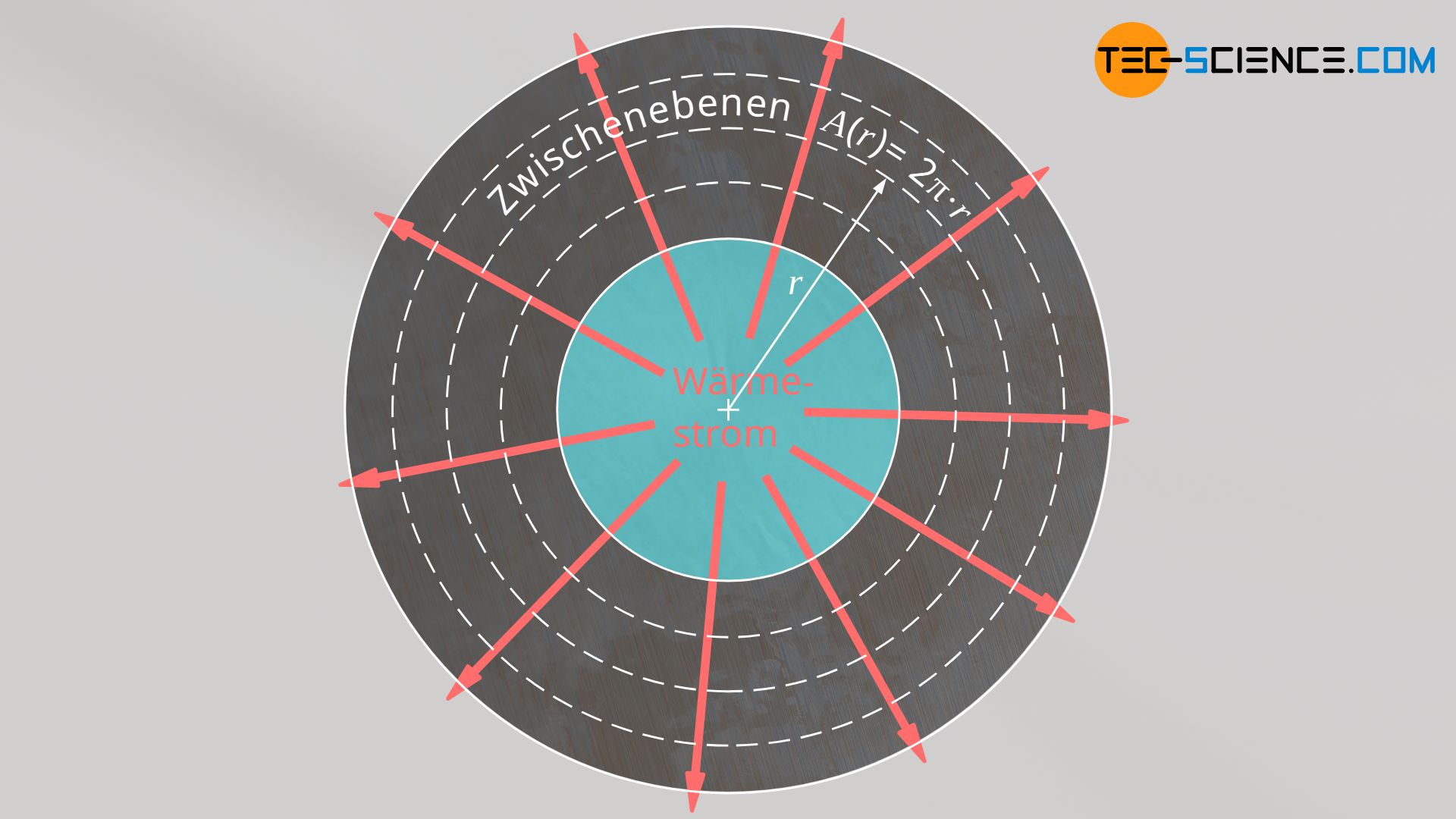
Anders als bei der ebenen Wand, ändert sich jedoch die Fläche (der Zwischenebene), durch die der Wärmestrom jeweils tritt. Mit größerem Radius r nimmt die Fläche linear zu. Dies wiederum bedeutet, dass sich der Wärmestrom auf eine immer größere Fläche verteilt, d.h. die Wärmestromdichte nimmt mit zunehmendem Abstand r ab. Gemäß Gleichung (\ref{qq}) bedeutet dies, dass sich die Temperatur mit zunehmender Entfernung von der Innenwand immer weniger stark ändert. Der Temperaturverlauf flacht also ab.
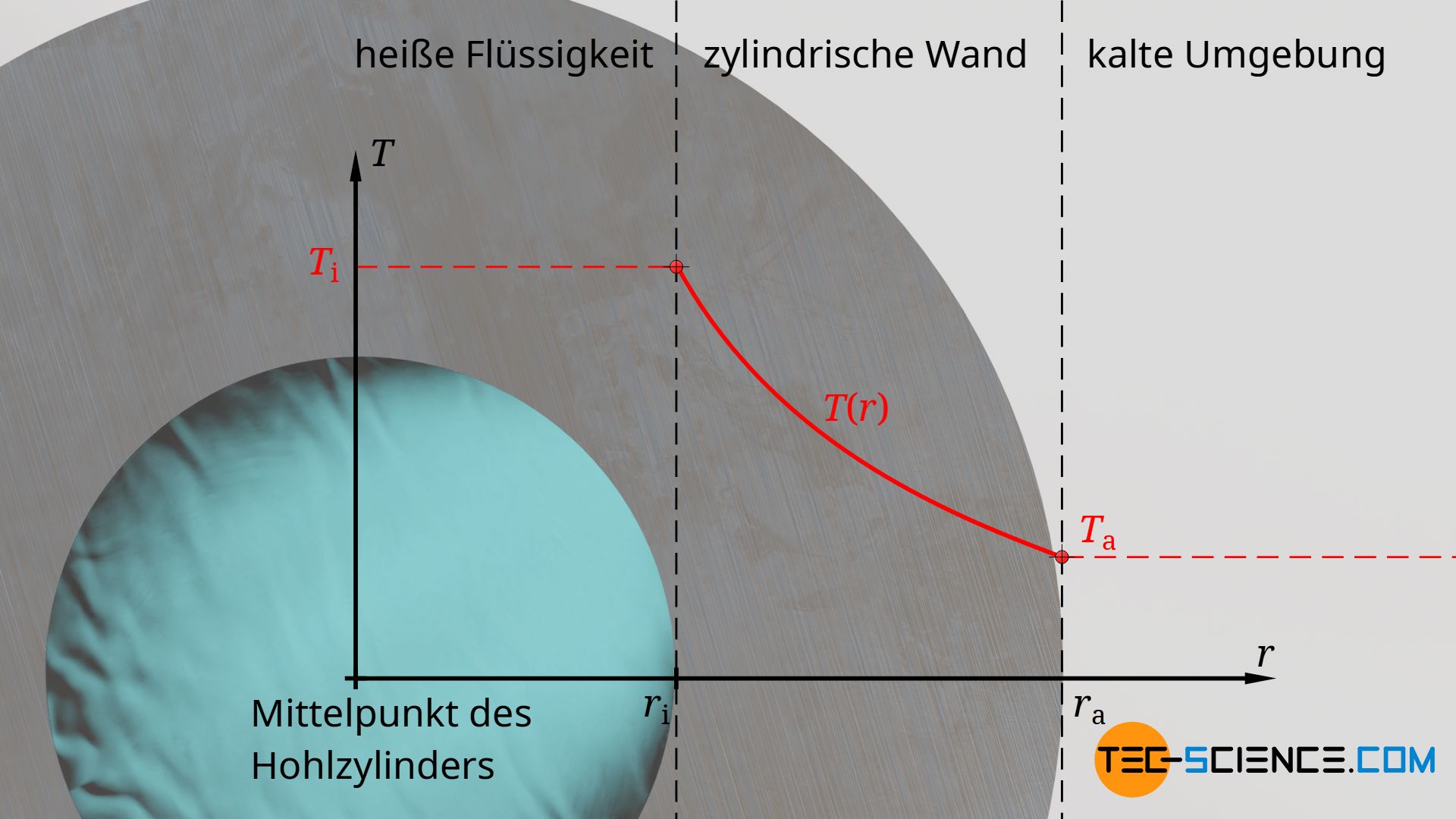
Den genauen Verlauf der Temperatur T(r) erhält man durch Integration von Gleichung (\ref{q}), wobei die Wärmeleitfähigkeit wieder als konstant vorausgesetzt wird. Dabei muss allerdings beachtet werden, dass die Fläche nun eine Funktion des Radius ist. Mit l als Länge des zylindrischen Rohres lässt sich die Fläche A in einem Abstand r wie folgt bestimmen:
\begin{align}
& A(r) = 2\pi \cdot l \cdot r \\[5px]
\end{align}
Diese Funktion in Gleichung (\ref{q}) eingesetzt und anschließend integriert, liefert dann schließlich folgenden Temperaturverlaufs im Inneren des Rohres:
\begin{align}
& \text{d}T = – \frac{\dot Q}{\lambda \cdot A(r)} \cdot \text{d}r \\[5px]
& \int \limits_{T_i}^{T}\text{d}T = – \frac{\dot Q}{\lambda \cdot 2\pi \cdot l } \cdot \int \limits_{r_i}^{r} \frac{\text{d}r}{r} \\[5px]
& [T]_{T_i}^{T}= – \frac{\dot Q}{ \lambda \cdot 2\pi \cdot l } \cdot \left[\ln(r)\right]_{r_i}^{r}\\[5px]
& T-T_i= – \frac{\dot Q}{\lambda \cdot 2\pi \cdot l} \cdot \left[\ln(r)-\ln(r_i)\right] \\[5px]
& T-T_i= – \frac{\dot Q}{\lambda \cdot 2\pi \cdot l} \cdot \ln\left( \frac{r}{r_i}\right) \\[5px]
\label{z}
& \boxed{T(r)= T_i – \frac{\dot Q}{\lambda \cdot 2\pi \cdot l} \cdot \ln\left( \frac{r}{r_i}\right)} \\[5px]
\end{align}
Die Temperatur durch eine zylindrische Wand ändert sich logarithmisch!
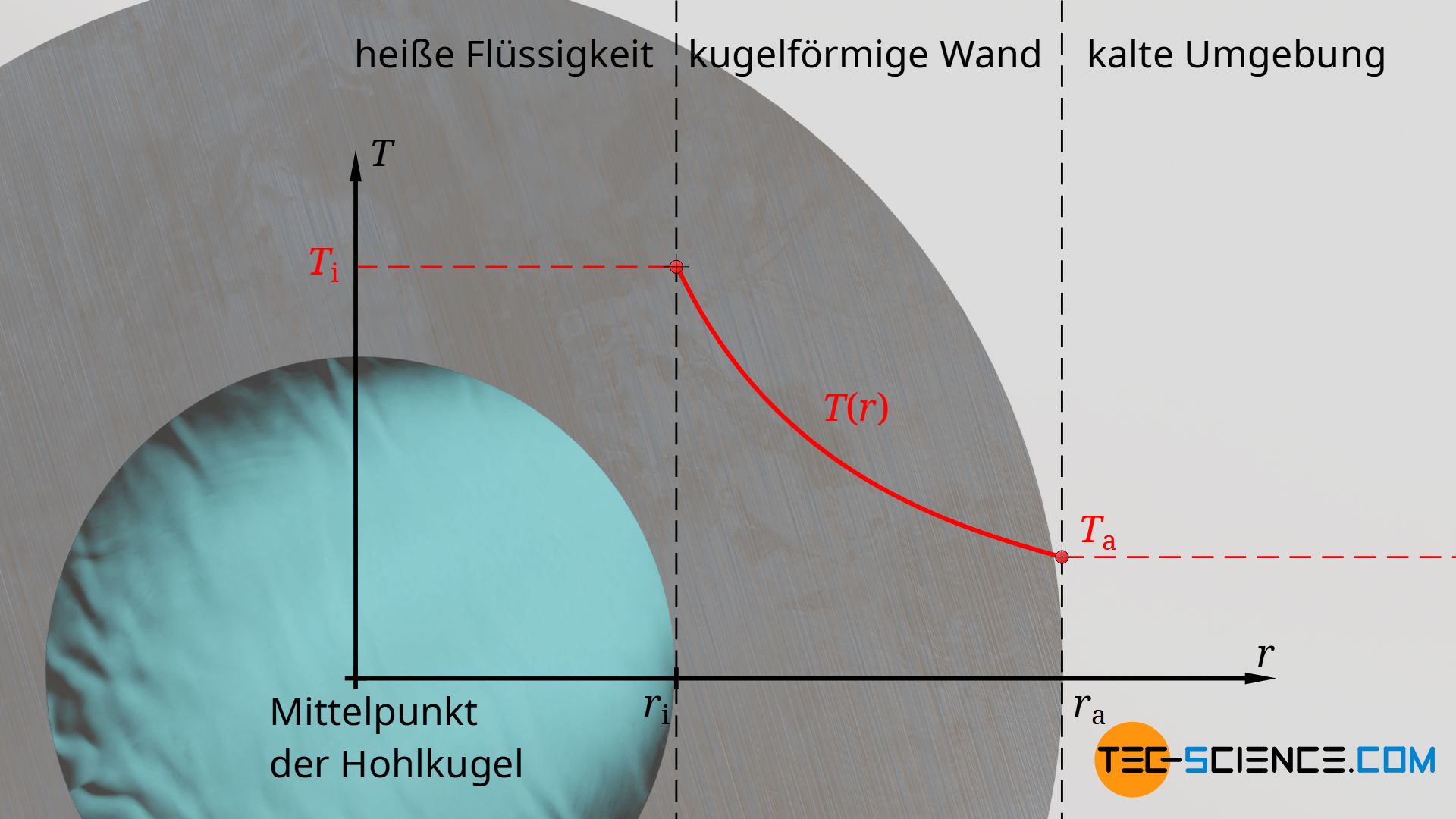
Temperaturverlauf innerhalb einer Hohlkugel
Befindet sich bspw. eine heiße Flüssigkeit im Inneren eines kugelförmigen Gefäßes, dann dringt Wärme durch die Wand der Kugel nach außen. Für den stationären Fall gilt wieder, dass der von der Flüssigkeit abgegebene Wärmestrom im selben Maße durch jede gedachte Zwischenebene tritt und anschließend auf die Umgebung übergeht. Jedoch nimmt die Fläche, durch die der Wärmestrom tritt, mit zunehmendem Radius zu, sodass die Wärmestromdichte entsprechend abnimmt.

Wie bereits bei einem zylindrischen Rohr, so ist also auch in diesem Fall davon auszugehen, dass sich die Temperatur mit zunehmendem Radius immer geringer ändert (Abflachung der Temperaturkurve). Der Einfluss des Radius auf eine betrachtete Fläche ist jedoch kein linearer mehr, sondern ein quadratischer:
\begin{align}
& A(r) = 4\pi \cdot r^2 \\[5px]
\end{align}
Dies führt nach Integration von Gleichung (\ref{q}) schließlich zu einem hyperbolischen Temperaturprofil:
\begin{align}
& \text{d}T = – \frac{\dot Q}{\lambda \cdot A(r)} \cdot \text{d}r \\[5px]
& \int \limits_{T_i}^{T}\text{d}T = – \frac{\dot Q}{\lambda \cdot 4\pi } \cdot \int \limits_{r_i}^{r} \frac{\text{d}r}{r^2} \\[5px]
& [T]_{T_i}^{T}= – \frac{\dot Q}{ \lambda \cdot 4\pi} \cdot \left[-\frac{1}{r}\right]_{r_i}^{r}\\[5px]
& T-T_i= – \frac{\dot Q}{\lambda \cdot 4\pi} \cdot \left(\frac{1}{r_i} -\frac{1}{r} \right)\\[5px]
\label{k}
& \boxed{T(r)= T_i – \frac{\dot Q}{\lambda \cdot 4\pi} \cdot \left(\frac{1}{r_i} -\frac{1}{r} \right) } \\[5px]
\end{align}
Die Temperatur durch eine kugelförmige Wand ändert sich hyperbolisch!
Berechnung der Wärmeströme anhand der Temperaturen
Flächenspezifischer Wärmestrom durch eine ebene Wand
In der Praxis interessiert man sich häufig nicht so sehr für den Temperaturverlauf, sondern viel mehr für den Wärmestrom den man bei gegebenen Temperaturen je nach Geometrie erhält. So ist man bspw. bei Gebäudewänden häufig daran interessiert, wie viel Wärme pro Zeit bei vorhandener Temperaturdifferenz durch die Wände nach außen tritt. Für eine ebene Wand der Dicke t lässt sich dieser Wärmestrom durch Umstellen von Gleichung (\ref{e}) ermitteln. Mit T(r=t) als Temperatur an der Außenseite (Ta) und Ti als Temperatur an der Innenseite der Wand folgt:
\begin{align}
& T_a = T_i – \frac{\dot Q}{\lambda \cdot A} \cdot t \\[5px]
\label{ee}
& \underbrace{\frac{\dot Q}{A}}_{\dot q_A} =(T_i-T_a) \cdot \frac{\lambda}{t} \\[5px]
& \boxed{\dot q_A =(T_i-T_a) \cdot \frac{\lambda}{t}} \\[5px]
\end{align}
Der Quotient aus Wärmestrom und Fläche wurde in der oberen Gleichung zum sogenannten flächenspezifischen Wärmestrom q*A zusammengefasst (auch als Wärmestromdichte bezeichnet). Dieser gibt den Wärmestrom pro Flächeneinheit an.
Durch Umstellen von Gleichung (\ref{ee}) nach dem Ausdruck Q*/(A⋅λ) und Einsetzen in Gleichung (\ref{e}), erhält man den Verlauf der Temperatur in Abhängigkeit der Außentemperatur Ta bzw. Innentemperatur Ti. Der Temperaturverlauf ist also unabhängig vom Wärmestrom, der Wärmeleitfähigkeit und der Fläche (natürlich kann der Verlauf nicht von diesen Größen abhängen, da der lineare Verlauf bereits vollständig durch die Innen- und Außentemperatur definiert ist)!
\begin{align}
& \frac{\dot Q}{A \cdot \lambda} = \frac{T_i-T_a}{t} ~~~~~\text{eingesetzt in}~~~~~ T(r) = T_i – \frac{\dot Q}{\lambda \cdot A} \cdot r ~\text{:}\\[5px]
&\boxed{T(r) = T_i – \frac{T_i-T_a}{t} \cdot r} \\[5px]
\end{align}
Längenspezifischer Wärmestrom durch ein zylindrisches Rohr
Auch bei einem zylindrischen Rohr interessiert in der Praxis häufig der Wärmestrom und nicht die sich einstellenden Temperaturen. Man stelle sich hierzu den bereits erwähnten röhrenförmigen Heizkörper vor. Im Rohrinneren strömt warmes Wasser, welches auf eine bestimmte Temperatur aufgeheizt ist. Aus der Temperaturdifferenz zwischen Außen- und Innenseite des Heizkörpers, lässt sich durch Umstellen von Gleichung (\ref{z}), dann der auf die Raumluft übertragene Wärmestrom ermitteln. Mit T(r=ra) als Temperatur an der Außenseite (Ta) des Heizkörpers und Ti als Temperatur an der Innenseite (Wassertemperatur) folgt:
\begin{align}
& T_a = T_i – \frac{\dot Q}{\lambda \cdot 2\pi \cdot l} \cdot \ln\left( \frac{r_a}{r_i}\right) \\[5px]
\label{zz}
&\underbrace{\frac{\dot Q}{l}}_{\dot q_L}= (T_i-T_a) \cdot \frac{ 2 \pi \lambda }{\ln\left( \frac{r_a}{r_i}\right) } \\[5px]
&\boxed{\dot q_L= (T_i – T_a) \cdot \frac{ 2 \pi \lambda }{\ln\left( \frac{r_a}{r_i}\right) }} \\[5px]
\end{align}
Der Quotient aus Wärmestrom und Rohrlänge wurde in der oberen Gleichung zum sogenannten längenspezifischen Wärmestrom q*L zusammengefasst. Dieser gibt den Wärmestrom pro Längeneinheit des Rohres an.
Auch an dieser Stelle erhält man wieder durch Umstellen von Gleichung (\ref{zz}) nach dem Ausdruck Q*/(2⋅π⋅l⋅λ) und anschließendes Einsetzen in Gleichung (\ref{z}), den Verlauf der Temperatur in Abhängigkeit der Außentemperatur Ta bzw. Innentemperatur Ti:
\begin{align}
& \frac{\dot Q}{ 2 \pi l \lambda } = \frac{T_i-T_a}{ \ln\left( \frac{r_a}{r_i}\right) } ~~~~~\text{eingesetzt in}~~~~~ T(r)= T_i – \frac{\dot Q}{2\pi l \lambda } \cdot \ln\left( \frac{r}{r_i}\right) ~\text{:}\\[5px]
&\boxed{T(r) = T_i – \frac{T_i-T_a}{ \ln\left( \frac{r_a}{r_i}\right) } \cdot \ln\left( \frac{r}{r_i}\right) } \\[5px]
\end{align}
Raumwinkelspezifischer Wärmestrom durch eine Hohlkugel
Der Wärmestrom durch eine Hohlkugel bei gegebener Innen- bzw. Außentemperatur bestimmt sich durch Umstellen von Gleichung (\ref{k}) wie folgt:
\begin{align}
& T_a= T_i – \frac{\dot Q}{\lambda \cdot 4\pi} \cdot \left(\frac{1}{r_i} -\frac{1}{r_a} \right) \\[5px]
\label{kk}
& \frac{\dot Q}{4\pi} = (T_i-T_a) \cdot \frac{\lambda}{ \frac{1}{r_i} -\frac{1}{r_a} } \\[5px]
& \underbrace{\frac{\dot Q}{4\pi}}_{\dot q_R} = (T_i-T_a) \cdot \lambda \cdot \frac{ r_a \cdot r_i}{ r_a -r_i} \\[5px]
& \boxed{ \dot q_R = (T_i-T_a) \cdot \lambda \cdot \frac{ r_a \cdot r_i}{ r_a -r_i}} \\[5px]
\end{align}
Der Quotient aus Wärmestrom und dem Ausdruck 4π wurde in der oberen Gleichung zum sogenannten raumwinkelspezifischen Wärmestrom q*R zusammengefasst. Dieser gibt den Wärmestrom pro Raumwinkeleinheit an. Für eine vollständige Kugel beträgt der Raumwinkel 4π und für eine Halbkugel 2π.
Für den Verlauf der Temperatur gilt nach Umstellen von Gleichung (\ref{kk}) und anschließendes Einsetzen in Gleichung (\ref{k}):
\begin{align}
& \frac{\dot Q}{ 4 \pi \lambda } = \frac{ T_i-T_a }{ \frac{1}{r_i} -\frac{1}{r_a} } ~~~~~\text{eingesetzt in}~~~~~ T(r)= T_i – \frac{\dot Q}{4\pi \lambda } \cdot \left(\frac{1}{r_i} -\frac{1}{r} \right) ~\text{:}\\[5px]
&\boxed{T(r) = T_i – \frac{ T_i-T_a }{ \frac{1}{r_i} -\frac{1}{r_a} } \cdot \left(\frac{1}{r_i} -\frac{1}{r} \right) } \\[5px]
\end{align}
Berechnung des Wärmestrom mit Hilfe der mittleren Fläche
Man kann die Berechnung des Wärmestroms durch die oben beschriebenen Geometrien auf eine gemeinsame Formel reduzieren, wenn man für die Flächen die sogenannte mittlere Fläche A einsetzt:
\begin{align}
&\boxed{\dot Q = – \lambda \cdot \bar A \cdot \frac{\text{d}T}{\text{d}r}} \\[5px]
\end{align}
Je nach Geometrie gilt für die mittlere Fläche:
\begin{align}
&\bar A_{\text{ ebene Wand}} = A_i = A_a \\[5px]
&\bar A_{\text{ Hohlzylinder}} = \frac{A_a-A_i}{\ln\left(\frac{A_a}{A_i}\right)} \\[5px]
&\bar A_{\text{ Hohlkugel}} = \sqrt{A_i \cdot A_a} \\[5px]
\end{align}
Die Fläche Ai bezeichnet dabei die Fläche an der Innenseite der Geometrie und Aa die Fläche der Außenseite der Geometrie.