Thermodynamische Herleitung des Stefan-Boltzmann-Gesetzes

In diesem Artikel wird das Stefan-Boltzmann-Gesetz mit Hilfe der Gesetzmäßigkeiten der Thermodynamik hergeleitet.

Einleitung

Für die Herleitung des Stefan-Boltzmann-Gesetzes müssen zunächst grundlegende Zusammenhänge geklärt werden. Auf diese wird in den folgenden Abschnitten näher eingegangen.

Zusammenhang zwischen Energiedichte und Druck

Kinetische Gastheorie mit klassischen Teilchen

Mithilfe der kinetischen Gastheorie wurde im Artikel Druck und Temperatur folgender Zusammenhang zwischen dem Druck eines Gases p und der Geschwindigkeit v der darin enthaltenen Teilchen hergeleitet werden:

\begin{align}
\label{p}
&\boxed{p = \frac{1}{3}\frac{N}{V}m\cdot \overline{v^2}} \\[5px]
\end{align}

Dabei bezeichnet N die Anzahl der Gasteilchen in einem Volumen V und m die Teilchenmasse. Die Geschwindigkeit bezieht sich dabei auf die quadratisch gemittelte Geschwindigkeit.

Bei einer klassischen Betrachtung von idealen Gasen, bei der die Teilchengeschwindigkeiten weit unterhalb der Lichtgeschwindigkeit liegen, kann die mittlere kinetische Energie der Teilchen in sehr guter Näherung mit ½⋅m⋅v² beschrieben werden (Beachte, dass diese Formel tatsächlich nur für die klassische, nicht-relativistische Mechanik gilt!) Dabei wird dann folgender Zusammenhang zwischen dem Druck und der mittlere Energie eines Teilchens offensichtlich:

\begin{align}
p &= \frac{2}{3} \cdot \frac{N}{V} \cdot \overbrace{\frac{1}{2} m \overline{v^2}}^{\overline{W_{kin}}} = \frac{2}{3} \cdot \frac{N}{V} \cdot \overline{W_{kin}} \\[5px]
&= \frac{2}{3} \cdot \frac{\overbrace{N \cdot \overline{W_{kin}}}^{\text{innere Energie } U}}{V}
= \frac{2}{3}\cdot \overbrace{\frac{U}{V}}^{\text{Energiedichte } u_v}
= \frac{2}{3}\cdot u_v \\[5px]
&\boxed{p = \frac{2}{3} u_v} ~~~~~\text{gilt nur für ein klassisches Gas}
\end{align}

Bei der oberen Herleitung wurde ausgenutzt, dass das Produkt von Teilchenanzahl N und mittlerer kinetischer Energie eines Teilchens, der im Gas enthaltenen Gesamtenergie entspricht; d.h. der sogenannten inneren Energie U. Der Quotient von innerer Energie U und Volumen V kann deshalb als (volumetrische) Energiedichte u_v aufgefasst werden (um Missverständnisse mit der spezifischen inneren Energie u als massebezogene Größe zu vermeiden, ist bei der Energiedichte im Index ein „v“ hinzugefügt).

Aufgrund der Tatsache, dass für die Herleitung die klassische Mechanik unter der Annahme der Gültigkeit von W_kin=½⋅m⋅v² genutzt wurde, gilt der beschriebene Zusammenhang zwischen Druck und Energiedichte nur bei klassischen idealen Gasen.

Kinetische Gastheorie mit relativistischen Teilchen (Photonen)

Aufgrund des Welle-Teilchen-Dualismus von elektromagnetischer Strahlung, kann man sich diese auch als ein Strahl von Photonen vorstellen, so wie bei der Herleitung des Strahlungsdrucks bereits geschehen. Auf diese Weise kann man nun auch die Strahlung eines schwarzen Körpers mathematisch beschreiben. Im Artikel Schwarzkörperstrahlung wurde die Realisierung eines solchen Schwarzen Körpers bereits ausführlich erläutert. Hierzu wird einfach ein kleines Loch in einen Gegenstand gebohrt, der in einen Hohlkörper führt.

Alle einfallende Strahlung wird vom Hohlraum absorbiert, wobei der Hohlraum auch selbst Strahlung emittiert. Im thermodynamischen Gleichgewicht, ist die emittierte und absorbierte Strahlungsenergie gleich, sodass sich im Hohlraum im Prinzip ein Gas von Photonen bildet. Anstelle von massebehafteten Teilchen, hat man es in diesem also Fall mit masselosen, relativistischen Photonen zu tun. Auch dabei wird man im Hohlraumvolumen V einen Druck p durch die Strahlung bzw. aufgrund der Photonen feststellen können, der sogenannte Strahlungsdruck.

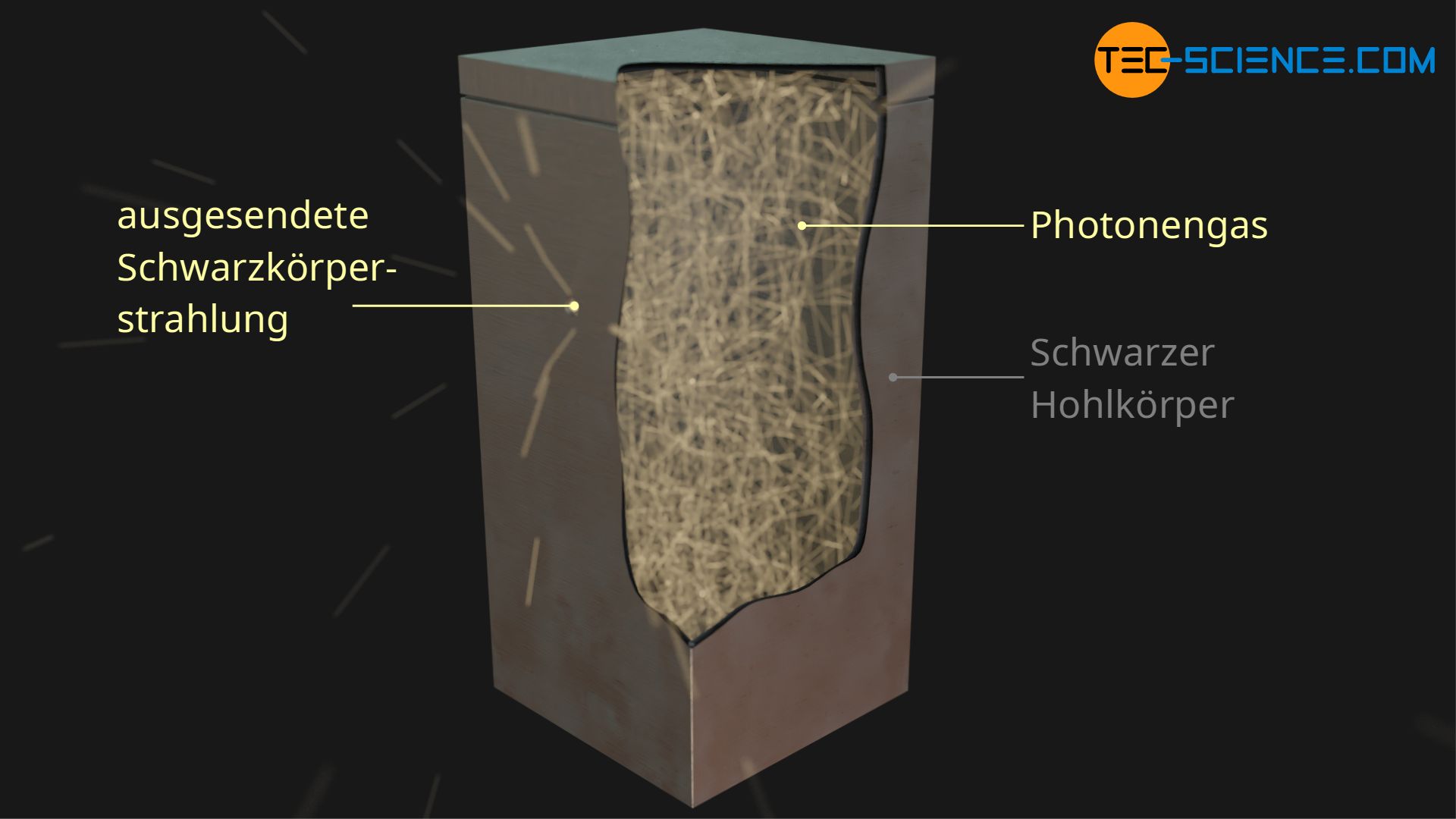
Gleichung (\ref{p}) kann nun auch an dieser Stelle wieder verwendet werden, sie muss lediglich vor dem Hintergrund der Relativitätstheorie interpretiert werden. Die Geschwindigkeit der Teilchen v entspricht bei Photonen offensichtlich der Lichtgeschwindigkeit c und die Masse m muss als relativistische Masse m_rel betrachtet werden. An dieser Stelle muss nicht zwischen dem Mittelwert der Geschwindigkeitsquadrate \(\overline{c^2}\) und dem Geschwindigkeitsquadrat c² unterschieden werden, da es in diesem Fall keine klassische Geschwindigkeitsverteilung gibt sondern alle Photonen mit derselben Lichtgeschwindigkeit unterwegs sind. Beide Werte sind deshalb identisch.

\begin{align}
\label{pp}
&p = \frac{1}{3}\frac{N}{V}\cdot m_{rel} \cdot c^2 \\[5px]
\end{align}

Beachte, dass Photonen zwar keine Ruhemasse besitzen, aber dennoch eine relativistische Masse. So zeigte Einstein mit seiner berühmten Energie-Masse-Äquivalenz-Gleichung, dass jedem mit Energie behafteten Teilchen eine entsprechende (relativistische) Masse m_rel zugeordnet werden kann:

\begin{align}
\label{e}
&\boxed{E =mc^2} ~~~~~\text{bzw.}~~~~~ \boxed{W=m_{rel}\cdot c^2} \\[5px]
\end{align}

Gemäß der Quantenmechanik ergibt sich die Energie eines Photons aus dem Produkt von Frequenz f und Planckschem Wirkungsquantum h, sodass hieraus die relativistische Masse ermittelt werden kann:

\begin{align}
&W = h\cdot f \\[5px]
\end{align}

Das in Gleichung (\ref{pp}) enthaltene Produkt aus (relativistischer) Masse m (=m_rel) und Quadrat der Lichtgeschwindigkeit c² entspricht nach der Einsteingleichung (\ref{e}) gerade der Energie eines Photons W. Somit gilt zwischen dem Strahlungsdruck p des Photonengases und dessen Energiedichte u_v folgender Zusammenhang:

\begin{align}
&p = \frac{1}{3}\frac{N}{V}\cdot \overbrace{ m_{rel}\cdot c^2}^{W}=\frac{1}{3}\frac{N}{V}\cdot W =\frac{1}{3}\frac{\overbrace{N\cdot W}^{\text{„innere“ Energie } U}}{V} =\frac{1}{3} \cdot \overbrace{\frac{U}{V}}^{\text{Energiedichte }u_v} = \frac{1}{3} u_v \\[5px]
\label{h}
&\boxed{p = \frac{1}{3} u_v } ~~~~~\text{gilt nur für ein Photonengas (homogene Strahlung)}
\end{align}

Bei der Herleitung wurde wiederum ausgenutzt, dass das Produkt von Photonenenergie und Photonenanzahl der im Photonengas insgesamt enthaltenen (inneren) Energie entspricht, d.h. der Strahlungsenergie (Photonengasenergie). Der Quotient von Strahlungsenergie und Hohlraumvolumen lässt sich wiederum als Energiedichte des Photonengases bzw. als Energiedichte der Strahlung auffassen.

Der Zusammenhang zwischen Druck und Energiedichte eines klassischen Gases unterscheidet sich also um den Faktor 2 von dem eines relativistischen Photonengases.

Herleitung aus dem Strahlungsdruck

Den Zusammenhang zwischen Strahlungsdruck und Energiedichte für ein homogenes Photonengas kann man auch aus dem Strahlungsdruck einer gerichteten Strahlung herleiten. Im Artikel Strahlungsdruck wurde gezeigt, dass der Strahlungsdruck p_St, den eine gerichtete Strahlung auf einen Gegenstand bei vollständiger Reflexion ausübt, dem doppelten Wert der Energiedichte entspricht:

\begin{align}
\label{s}
&\boxed{p_{St} =2 \cdot u_v} ~~~~~\text{gilt nur bei vollständiger Reflexion einer gerichteten Strahlung} \\[5px]
\end{align}

Diese Gleichung steht nicht im Widerspruch zu Gleichung (\ref{h})! Denn Gleichung (\ref{s}) gilt nur bei gerichteter Strahlung, d.h. wenn sich alle Photonen in dieselbe Richtung bewegen und auf eine Grenzfläche treffen. Im Falle der Hohlraumstrahlung, handelt es sich aber um eine Strahlung, die im Inneren permanent reflektiert, absorbiert und emittiert wird, d.h. die Photonen bewegen sich alle in völlig zufällige Richtungen; es handelt sich eben um ein Photonengas.

Um aus einer gerichteten Strahlung eine völlig zufällige Photonenbewegung zu machen, müssten sich alle darin enthaltenen Photonen plötzlich in unterschiedliche Richtungen bewegen. Bei der Annahme einer homogenen statistischen Verteilung, würden sich demnach insgesamt ein Sechstel der Photonen nach oben bewegen, ein Sechstel nach unten, wiederum ein Sechstel nach links und ein Sechstel nach rechts sowie ein Sechstel nach hinten und schließlich würden sich ein Sechstel der Photonen nach vorne auf die betrachtete Grenzfläche zubewegen, auf die ein Druck ausgeübt wird.

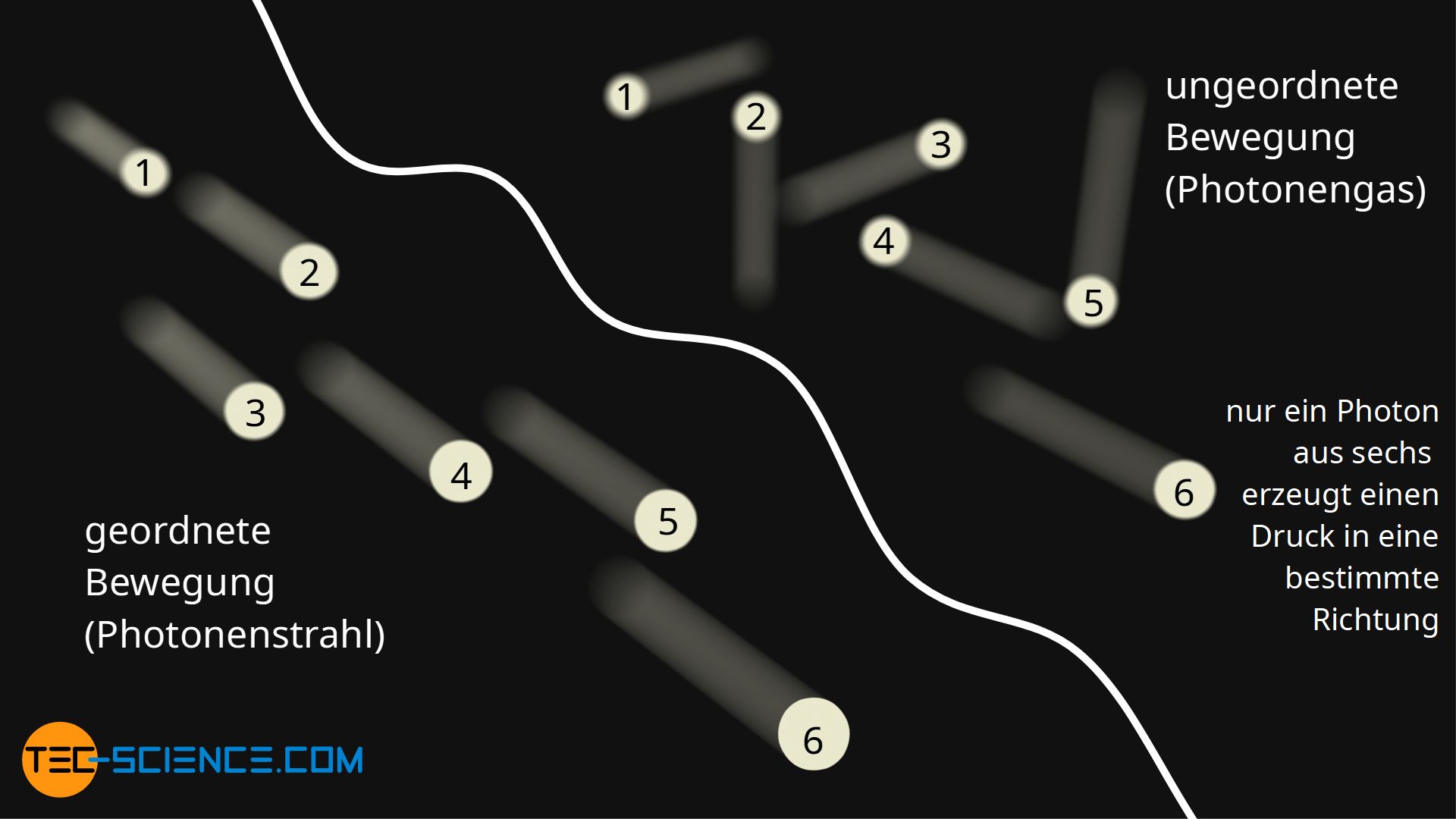
Bei gleicher Energiedichte (Photonendichte) ist der Druck bei einem homogenen Photonengas somit um ein Sechstel geringer im Vergleich zu einem gerichteten Photonenstrahl, da eben nur ein Sechstel der Photonen effektiv auf die Grenzfläche prallen. Somit kommt man für ein homogenes Photonengas wieder zum identischen Zusammenhang:

\begin{align}
& p = \frac{1}{6} \cdot p_{St} = \frac{1}{6} \cdot 2 \cdot u_v= \frac{1}{3} \cdot u_v \\[5px]
\end{align}

Man könnte an dieser Stelle nun argumentieren, dass der Hohlraumstrahlung doch keine vollständige Reflexion zugrunde liegt und damit Gleichung (\ref{s}) gar nicht gültig ist. Vielmehr handelt es sich bei einem Schwarzen Körper bzw. einer Hohlraumstrahlung doch um eine vollständige Absorption der Strahlung. Dies ist zwar richtig, jedoch werden im thermodynamischen Gleichgewicht genau dieselbe Anzahl an Photonen absorbiert wie emittiert. Hieraus stellt sich ja schließlich das thermodynamische Gleichgewicht ein.

Kinematisch betrachtet, ist eine Reflexion aber nichts anderes als eine Absorption („Aufprall“) mit unmittelbarer Emission („Rückprall“). Nur weil Absorption und Emission im Falle der Hohlraumstrahlung nicht zu identischen Zeiten stattfinden, bleiben sie vom Wesen her identisch wie die Reflexion, bei der beide Vorgänge im Prinzip unmittelbar nacheinander stattfinden. Deshalb muss bei der Hohlraumstrahlung im thermodynamischen Gleichgewicht von einem vollständig reflektierenden Verhalten ausgegangen werden!

Zusammenhang zwischen einer Volumenänderung und der Änderung der Photonengasenergie

Wie bereits die experimentelle Untersuchung der Schwarzkörperstrahlung ergeben hat, hängt die Energie der abgegebenen Strahlung nur von der Temperatur hab. Die Energiedichte ist somit nur eine Funktion der Temperatur. Bei konstanter Temperatur und damit konstanter Energiedichte u_v, bedeutet eine Vergrößerung des Hohlraumvolumens um dV somit eine entsprechende Vergrößerung der Photonengasenergie dU:

\begin{align}
& U(T,V) = u_v(T) \cdot V \\[5px]
& \frac{\text{d}U(T,V)}{\text{d}V} =\frac{\text{d}(u_v(T) \cdot V )}{\text{d}V} = \overbrace{\underbrace{\frac{\partial{u_v(T)}}{\partial{V}}}_{=0} \cdot V +\underbrace{\frac{\partial{V} }{\partial{V}}}_{=1} \cdot u_v(T)}^{\text{Produktregel}} = u_v(T) = u_v \\[5px]
\label{t}
&\boxed{\left(\frac{\partial{U}}{\partial{V}}\right)_T = u_v = 3p} \\[5px]
\end{align}

Beachte, dass die (partielle) Ableitung der Energiedichte nach dem Volumen Null ergibt, da die Energiedichte keine Funktion des Volumens ist. Bezüglich der Variablen V handelt sich also um die Ableitung einer Konstanten. Zudem wurde im letzten Schritt ausgenutzt, dass der Strahlungsdruck einem Drittel der Energiedichte entspricht bzw. die Energiedichte u_v dem dreifachen Wert des Drucks p [siehe Gleichung (\ref{h})].

Dass die Photonengasenergie bei konstanter Energiedichte im selben Maße steigt wie das Volumen wird auch anschaulich klar, denn eine konstante Energiedichte bedeutet schließlich auch eine konstante Photonendichte. Vergrößert man das Volumen des Hohlraumes, dann befinden sich bei gleichbleibender Photonendichte nun insgesamt mehr Photonen darin (der Hohlraum emittiert dann verstärkt Photonen bis sich wieder ein thermodynamische Gleichgewicht einstellt). Da jedes Photon mit einer bestimmten Energie verbunden ist, ist somit also auch die im Volumen enthaltene Gesamtenergie gestiegen.

Erster Hauptsatz der Thermodynamik

Da das Photonengas analog zu einem klassischen idealen Gas betrachtet wird, kann an dieser Stelle auch der erste Hauptsatz der Thermodynamik zur Anwendung kommen. In differentieller Form stellt sich dieser wie folgt dar (darin bezeichnet S die Entropie):

\begin{align}
&\boxed{\text{d}U = T \cdot \text{d}S – p \cdot \text{d}V } ~~~~~\text{Erster Hauptsatz der Thermodynamik} \\[5px]
\end{align}

Wird diese Gleichung durch dV geteilt erhält man bei konstanter Temperatur folgende Beziehung:

\begin{align}
\label{ss}
& \left(\frac{\partial{U}}{\partial{V}}\right)_T = T \left(\frac{\partial{S}}{\partial{V}}\right)_T – p \\[5px]
\end{align}

Ohne tiefer auf die Herleitung der sogenannten Maxwell-Beziehungen der Thermodynamik einzugehen, liefern diese an dieser Stelle einen weiteren wichtigen Zusammenhang. So steht eine Entropieänderung und eine Volumenänderung bei konstanter Temperatur im selben Zusammenhang wie eine Druckänderung und eine Temperaturänderung bei konstantem Volumen. Mathematisch wird dies wie folgt ausgedrückt:

\begin{align}
&\boxed{\left(\frac{\partial{S}}{\partial{V}}\right)_T = \left(\frac{\partial{p}}{\partial{T}}\right)_V} ~~~~~\text{Maxwell-Relation} \\[5px]
\end{align}

Diese Maxwell-Beziehung kann nun in Gleichung (\ref{ss}) eingesetzt werden, sodass gilt:

\begin{align}
\label{x}
& \left(\frac{\partial{U}}{\partial{V}}\right)_T = T \left(\frac{\partial{p}}{\partial{T}}\right)_V – p \\[5px]
\end{align}

Gemäß Gleichung (\ref{t}) kann der Ausdruck (∂U/∂V)_T durch die Energiedichte u_v ersetzt werden. Zudem entspricht der Druck p nach Gleichung (\ref{h}) gerade einem Drittel der Energiedichte, sodass insgesamt gilt:

\begin{align}
u_v &= T \left(\frac{\partial{\frac{1}{3}u_v}}{\partial{T}}\right)_V – \frac{1}{3} u_v \\[5px]
u_v &= \frac{1}{3} T \left(\frac{\partial{u_v}}{\partial{T}}\right)_V – \frac{1}{3} u_v \\[5px]
3 u_v &= T \left(\frac{\partial{u_v}}{\partial{T}}\right)_V – u_v \\[5px]
\end{align}

Da die Energiedichte nur eine Funktion der Temperatur ist, kann die partielle Ableitung der Energiedichte nach der Temperatur als gewöhnliches Differential ausgedrückt werden. Nach anschließender Trennung der Variablen folgt schließlich:

\begin{align}
3 u_v &= T \frac{\text{d}u_v}{\text{d}T} – u_v \\[5px]
4 u_v &= T \frac{\text{d}u_v}{\text{d}T} \\[5px]
\frac{\text{d}u_v}{u_v} &=4 \frac{\text{d}T}{T} \\[5px]
\end{align}

Beide Seiten der Gleichung können nun unbestimmt integriert werden, wobei bei der Bildung der Stammfunktionen jeweils eine Integrationskonstante zu berücksichtigen ist, die in der Konstanten a zusammengefasst werden (a steht in diesem Fall allgemein für eine Konstante, nicht für einen speziellen Wert!):

\begin{align}
\int \frac{\text{d}u_v}{u_v} &= \int 4 \frac{\text{d}T}{T} \\[5px]
\ln{u_v} &= 4 \cdot \ln{T} + a\\[5px]
e^{\ln{u_v}} &= e^{4 \cdot \ln{T}+a} \\[5px]
e^{\ln{u_v}} &= e^{4 \cdot \ln{T}} \cdot e^{a} \\[5px]
e^{\ln{u_v}} &= \left(e^{\ln{T}}\right)^4 \cdot a \\[5px]
&\underline{u_v = a \cdot T^4} \\[5px]
\end{align}

Die Energiedichte u_v ist also proportional zur vierten Potenz der absoluten Temperatur T. Ein mit Photonen gefülltes Volumen V (z.B. das Volumen des betrachteten Hohlraumes), welche von einem Schwarzen Körper bei der Temperatur T emittiert werden, enthält also folgende Gesamtenergie U:

\begin{align}
&U = u_v \cdot V = a \cdot T^4 \cdot V \\[5px]
\label{st}
&\boxed{U = a \cdot T^4 \cdot V} \\[5px]
\end{align}

Die Konstante a könnte nun experimentell bestimmt werden. In der Regel interessiert aber nicht die Energie eines Photonengases sondern die Leistung mit der ein Strahler die Photonen emittiert.

Strahlungsleistung

Im Folgenden wird nun ein Schwarzer Körper mit der Oberfläche A betrachtet, der sich im thermodynamischen Gleichgewicht bei der Temperatur T befindet. Dieser Schwarze Körper emittiert Photonen, die sich mit Lichtgeschwindigkeit c von der Oberfläche entfernen (bei einem Hohlkörper in den Hohlraum hinein und dann durch das Loch in die Umgebung, oder bei einem Vollkörper direkt in die Umgebung). Innerhalb der infinitesimalen Zeit dt legen diese Photonen dabei eine bestimmte Strecke ds zurück:

\begin{align}
& \text{d}s = c \cdot \text{d}t \\[5px]
\end{align}

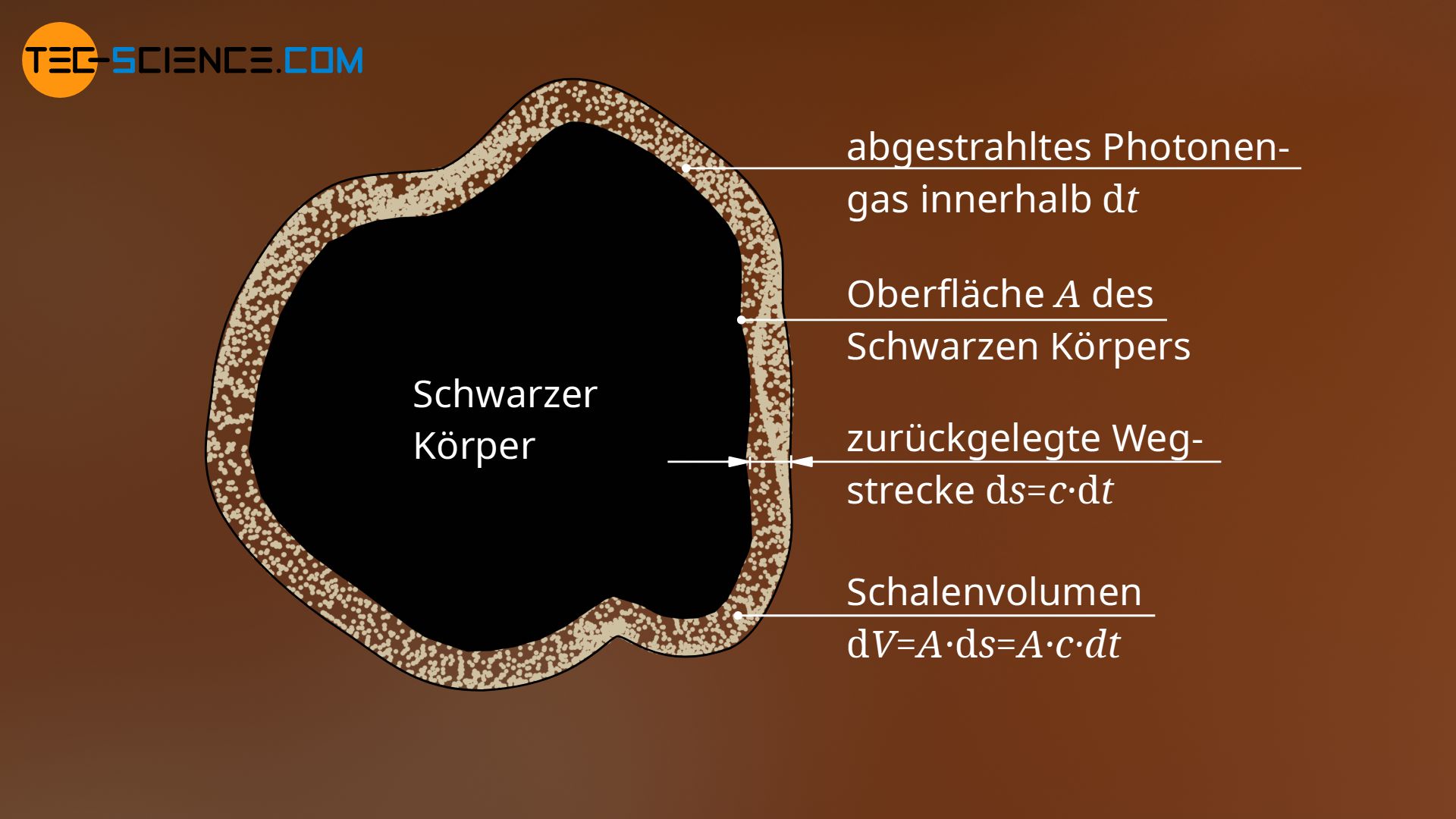
Da die Photonen aus der Oberfläche A des Schwarzen Körpers austreten, nehmen diese innerhalb der Zeit dt ein bestimmtes Schalenvolumen um den Schwarzen Körper herum ein. Aufgrund der infinitesimalen Strecke, ergibt sich das Volumen dV dieser emittierten Photonenschale aus dem Produkt von Grundfläche A und Höhe ds:

\begin{align}
& \text{d}V = A \cdot \text{d}s = A \cdot c \cdot \text{d}t \\[5px]
\end{align}

Bei gegebener Temperatur T ist die im ausgestoßenen Photonenvolumen dV enthaltene Energie dU durch Gleichung (\ref{st}) gegeben.

\begin{align}
&\text{d}U = a \cdot T^4 \cdot \text{d}V= a \cdot T^4 \cdot A \cdot c \cdot \text{d}t \\[5px]
\end{align}

Innerhalb der Zeit dt strahlt der Schwarze Körper also die Energie dU ab. Hieraus lässt sich dann die Strahlungsleistung Φ als abgegebene Strahlungsenergie pro Zeit ermitteln:

\begin{align}
\require{cancel}
&\Phi =\frac{\text{d}U}{\text{d}t} = \frac{a \cdot T^4 \cdot A \cdot c \cdot \bcancel{\text{d}t} }{\bcancel{\text{d}t}} =\underbrace{a\cdot c}_{\sigma} \cdot A \cdot T^4 \\[5px]
\end{align}

Die Konstante a und die ebenfalls konstante Lichtgeschwindigkeit c können zu einer neuen Konstanten zusammengefasst werden, der sogenannten Stefan-Boltzmann-Konstanten σ (nicht zu verwechseln mit der Boltzmann-Konstanten k_B). Damit ergibt sich die im thermodynamischen Gleichgewicht abgegeben Strahlungsleistung eines Schwarzen Körpers bei gegebener Temperatur T wie folgt:

\begin{align}
\label{bb}
&\boxed{\Phi = \sigma \cdot A \cdot T^4} ~~~~~ \sigma = 5,670 \cdot 10^{-8} \frac{\text{W}}{\text{m²K}^4} \\[5px]
\end{align}

Dieses Gesetzmäßigkeit wurde durch den Physiker Josef Stefan experimentell hergeleitet und später durch Ludwig Boltzmann mathematisch bewiesen. Dieses Gesetz wird deshalb als Stefan-Boltzmann-Gesetz bezeichnet.

Wird die Strahlungsleistung Φ an dieser Stelle auf die Fläche A des Schwarzen Körpers bezogen, dann erhält man die Strahlungsintensität I:

\begin{align}
&I=\frac{\Phi}{A} = \frac{\sigma \cdot A \cdot T^4}{A} = \sigma \cdot T^4\\[5px]
&\boxed{I = \sigma \cdot T^4 } \\[5px]
\end{align}

Bei der zunächst empirisch durch Experimente bestimmten Stefan-Boltzmann-Konstante σ, handelt es sich um eine Naturkonstante, die tatsächlich erst durch die Quantenmechanik aus anderen Naturkonstanten hergeleitet werden konnte:

\begin{align}
&\boxed{\sigma = \frac{2 \pi^5k_B^4}{15h^3c^2} } \\[5px]
\end{align}

Wie bereits zu Beginn des Artikels erläutert, gibt es Schwarze Körper nur in der Idealvorstellung. In der Realität strahlen Körper deshalb nicht mit der Intensität eines Schwarzen Körpers sondern mit geringerer Leistung. Dies wird durch den Emissionsgrad ε<1 erfasst:

\begin{align}
&I=\varepsilon \cdot \sigma \cdot T^4\\[5px]
\end{align}