Erfahre in diesem Artikel mehr über den Zusammenhang innerer Energie und und Wärmekapazität vor dem Hintergrund der kinetischen Gastheorie.
Innere Energie
Im Artikel Gleichverteilungssatz wurde bereits ausführlich erläutert, dass sich die Energie eines Gases auf die unterschiedlichen atomaren Energieformen gleichmäßig aufteilt. Bei einatomigen idealen Gasen fällt hierunter ausschließlich die Bewegungsenergie der Gasteilchen in Form der Translationsbewegung (Schwerpunktsbewegung). Im Gegensatz zu einatomigen idealen Gasen, können die Teilchen von mehratomigen Gasen auch Energie in Form einer Rotationbewegung speichern. Darüber hinaus sind die Atome von Gasmolekülen über „elastische“ Bindungskräfte miteinander verbunden. Diese Bindungskräfte können in gewissen Grenzen analog zu einer elastischen Feder betrachtet werden. Auf atomarer Ebene finden sich somit auch Schwingungsenergien wieder.

All die oben genannten Energieformen sind letztlich auf atomarer Ebene vorhanden, d.h. „im Inneren“ des Gases. Die Summe dieser Energien eines jeden einzelnen Teilchens tragen somit zum Energiegehalt des gesamten Gases bei. Man bezeichnet den Energiegehalt des Gases auch als innere Energie. Die Teilchen stellen sozusagen „Energiespeicher“ für die innere Energie dar.
Als innere Energie bezeichnet man den „atomaren“ Energiegehalt eines Stoffes, der unter anderem in der Bewegungsenergie der Teilchen steckt!
Tatsächlich werden noch weitere Energieformen zur inneren Energie gezählt, wie bspw. Ionisationsenergien oder chemisch gebundene Energien, die durch chemische Reaktionen frei werden können. Im Vergleich zu diesen Energieformen ist für die Translations,- Rotations- und Schwingungsenergie charakteristisch, dass es sich dabei um ungeordnete (statistisch verteilte) Bewegungen der Teilchen handelt. Deshalb zählt man diese ungeordneten Bewegungsenergien im engeren Sinne zur sogenannten thermischen Energie. Insofern ist die thermische Energie der ungeordneten Teilchenbewegung nur ein Teil der inneren Energie.
Die Energie die in der ungeordneten Bewegung der Moleküle steckt, wird als thermische Energie bezeichnet und ist Teil der inneren Energie!
Im Rahmen der kinetischen Gastheorie ist es jedoch völlig ausreichend die innere Energie auf die thermische Energie der ungeordneten Teilchenbewegung zu reduzieren, da weder Vorgänge mit chemischen Reaktionen noch Ionisierungen oder Ähnliches betrachtet werden. Wenn im Folgenden also von der inneren Energie die Rede ist, dann ist damit ausschließlich die thermische Energie der ungeordneten Teilchenbewegung gemeint.
Freiheitsgrade
Die einzelnen thermischen Energieformen können sogar noch weiter unterteilt werden. So kann sich ein Gasteilchen in drei unabhängige Raumrichtungen bewegen. Die Translationsenergie kann somit in die unterschiedlichen Richtungen aufgeteilt werden, d.h. salopp formuliert in eine Bewegungsenergie in x-Richtung, y-Richtung und z-Richtung. Für die Rotation kann analog eine Aufteilung der Rotationenergie erfolgen, die dann mit einer Bewegung um die die x-Achse, y-Achse bzw. z-Achse verknüpft ist. Ähnliches gilt auch für die Schwingungsenergie, die bei Molekülen auf unterschiedliche Weise erfolgen kann. Man spricht bei all diesen einzelnen Möglichkeiten der Energiespeicherung auch von sogenannten Freiheitsgraden.
Im thermodynamischen Sinne bezeichnet man als Freiheitsgrad die prinzipiellen „atomaren“ Möglichkeiten Energie in Form einer Translationsbewegung, Rotationsbewegung und Schwingungsbewegung zu speichern!
Die Translation besitzt insgesamt drei Freiheitsgrade, nämlich für jede Raumrichtung eine Möglichkeit Energie in Form einer Translationsbewegung zu speichern. Dasselbe gilt für die Rotation, bei der um jede der drei Raumachsen Energie in Form einer Rotationsenergie gespeichert werden kann. Somit besitzt auch die Rotation drei Freiheitsgrade.
Bei zweiatomigen Molekülen (bzw. bei linearen Molekülen im Allgemeinen, d.h. Moleküle deren Atome sich alle auf einer gemeinsamen Achse befinden) gibt es eine Besonderheit in den Freiheitsgraden der Rotation. Vordergründig würde man wahrscheinlich von drei Freiheitsgraden ausgehen, da das Molekül sowohl um die x-Achse und die y-Achse als auch um die z-Achse (Molekülachse) rotieren können sollte.
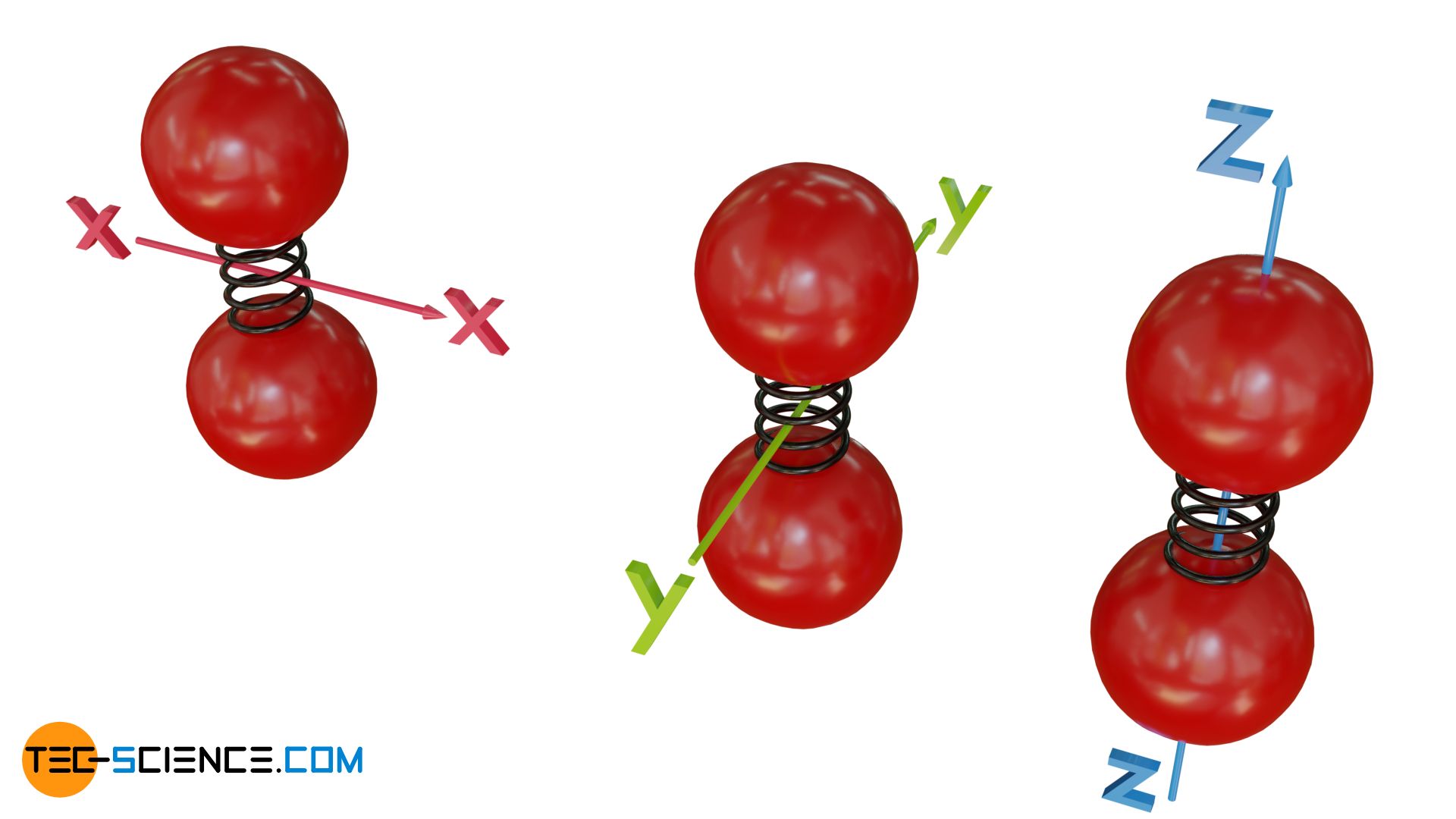
Tatsächlich werden lineare Moleküle jedoch nicht um die eigene Molekülachse rotieren und somit diesen Freiheitsgrad nicht zur Energiespeicherung nutzen können. Dies hat mit quantenmechanischen Effekten zu tun. Man kann sich diesen Sachverhalt aber auch durch die Idealisierung des Gases als ideales Gas verdeutlichen. Betrachtet man die Atome eines linearen Moleküls nämlich als Massepunkte, dann wird sich bei Rotation um die Molekülachse effektiv betrachtet auch keine Masse in Rotation befinden und damit keine Energie vorhanden sein (kein Trägheitsmoment, da die gesamte Masse in Drehzentrum konzentriert ist).
Anschaulich kann man das Fehlen des Rotationsfreiheitsgrades um die Molekülachse auch dadurch erklären, dass man bei Annahme der Atome als starre, reibungsfreie Kugeln keine Möglichkeit besitzt diese um die Molekülachse in Rotation zu versetzen. Jede Kollision mit anderen Teilchen wird aufgrund der Kugelform stets direkt auf die Molekülachse wirken (man würde sozusagen immer „abrutschen“). Somit ist kein Drehmoment möglich, das ein lineares Molekül um die Molekülachse in Drehung versetzen könnte. Deshalb fällt dieser Freiheitsgrad als Energiespeicher für lineare Atome weg.
Lineare Moleküle besitzen nur zwei Freiheitsgrade für die Rotation!
Neben der Translationsbewegung und Rotationsbewegung, können zwei- oder -mehratomige Moleküle auch schwingen. Die Schwingungsmöglichkeiten (auch Schwingungsmoden genannt) sind dabei abhängig von der Anzahl der Atome und der Form des Moleküls. Die Atome von zweiatomigen Molekülen können nur entlang ihrer Molekülachse schwingen und besitzen damit nur einen Schwingungsfreiheitsgrad (eine Schwingungsmode).

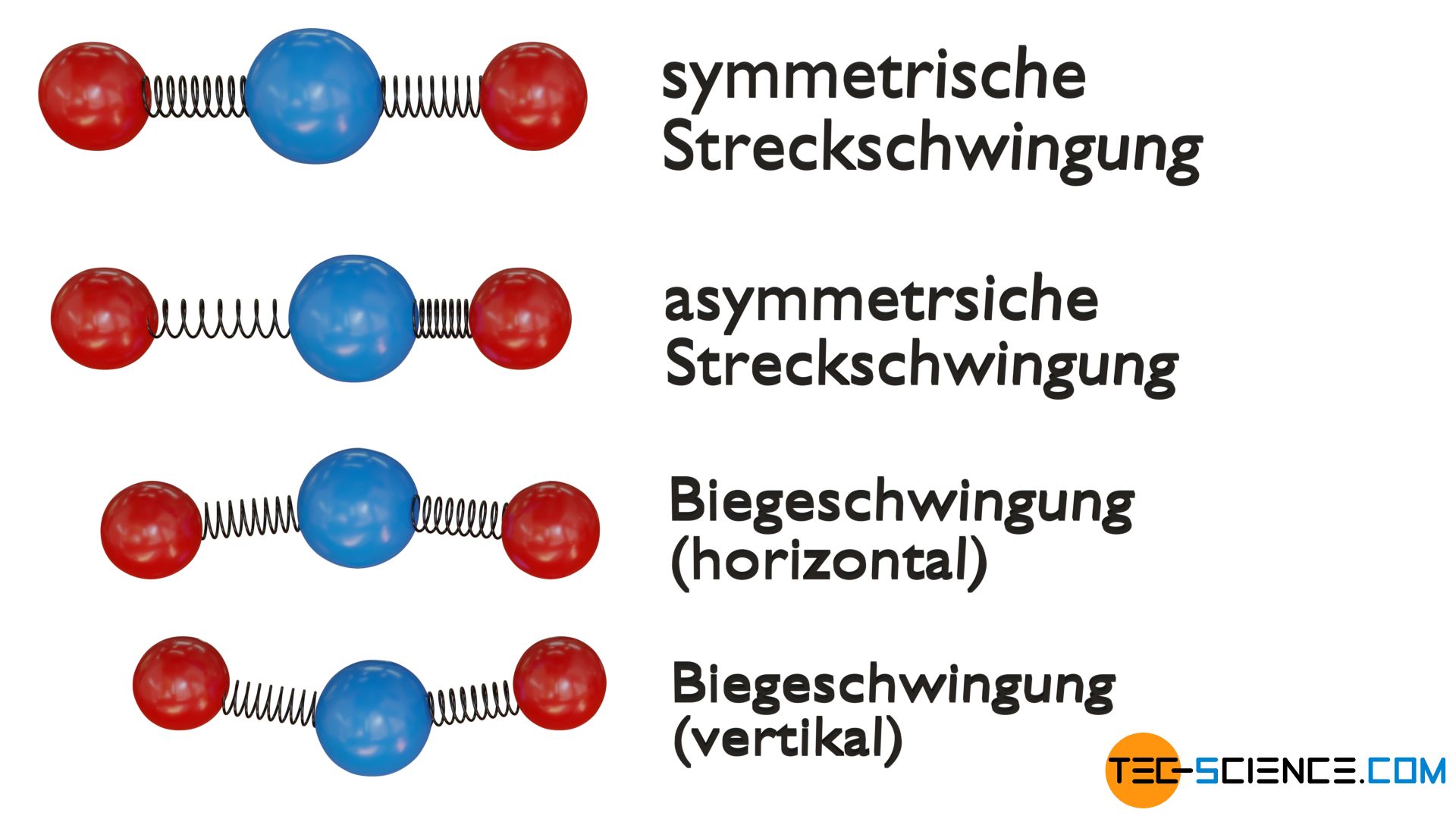
Dreiatomige lineare Moleküle haben hingegen vier Schwingungsfreiheitsgrade. Die Atome können zum einen symmetrisch entlang deren Bindungsachse schwingen (symmetrische Streckschwingung) oder zum anderen phasenverschoben (asymmetrische Streckschwingung). Beide Schwingungsmoden werden auch als Valenzschwingung bezeichnet. Zudem sind zwei Biegeschwingungen möglich, die jeweils zu einer Änderung des Bindungswinkels führen. Dabei wird zwischen einer Schwingung vertikal und horizontal unterschieden.
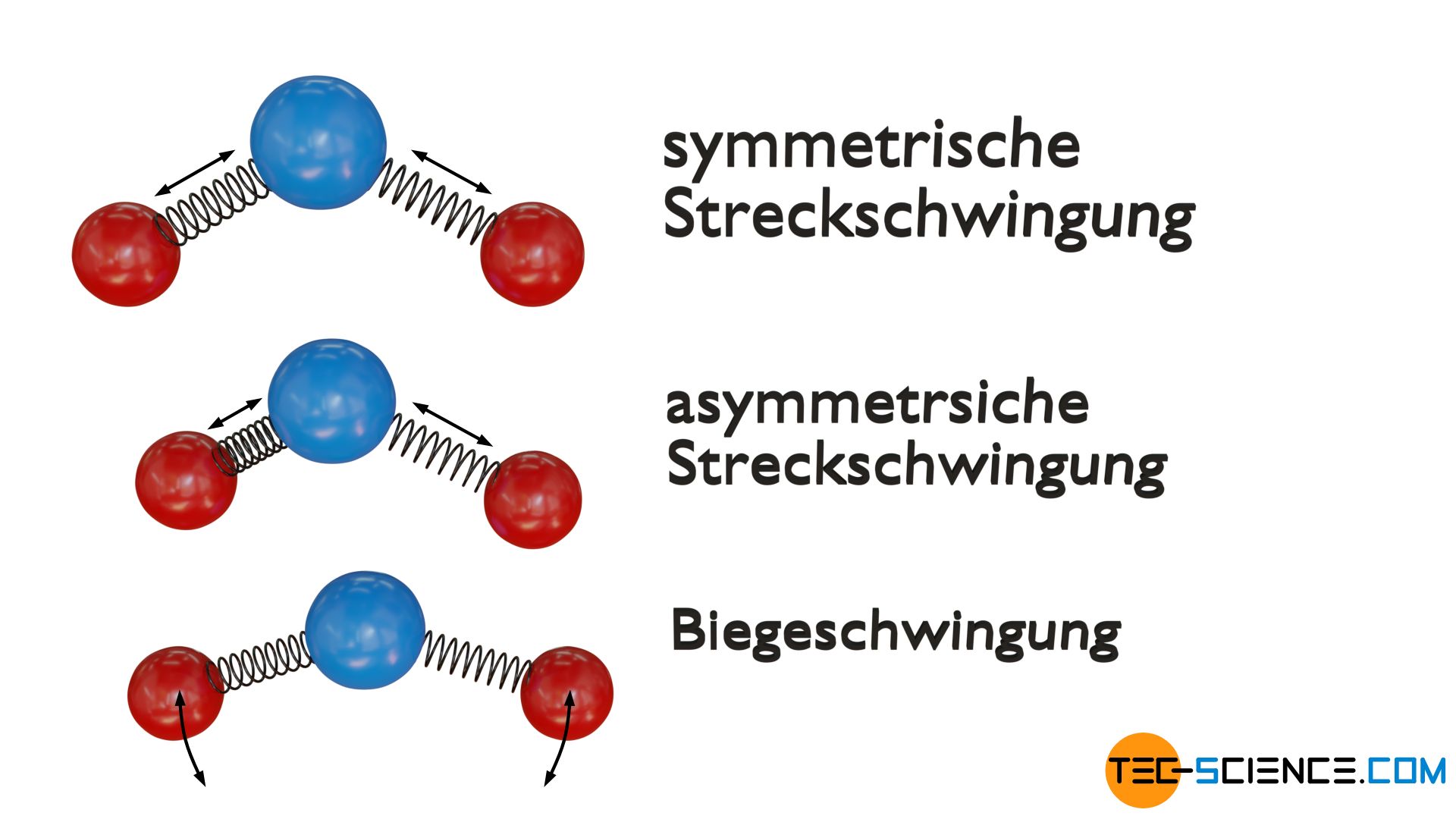
Bei dreiatomigen gewinkelten Molekülen existieren hingegen insgesamt drei Schwingungsfreiheitsgrade. Zum einen wiederum eine symmetrische Streckschwingung und zum anderen eine asymmetrische Streckschwingung entlang der Bindungsachsen. Zudem ist wiederum eine Biegeschwingung in der Molekülebene möglich.
Aus energetische Sicht muss bei allen Schwingungsfreiheitsgraden jedoch beachtet, werden, dass in einer Schwingung sowohl kinetische Energie als auch potentielle Energie steckt. Die Schwingungsenergie wird während einer Periode „umverteilt“, d.h. potentielle Energie wird nach und nach in kinetische Energie umgewandelt und umgekehrt; die Energiesumme als eigentliche Schwingungsenergie bleibt aber stets konstant. Somit besitzt eine Schwingungsmode also immer zwei Möglichkeiten Energie zu speichern. In Form von kinetischer und potentielle Energie. Deshalb muss aus energetischer Sicht jeder Schwingungsfreiheitsgrad doppelt gezählt werden!

Freiheitsgrade der Schwingung werden aus energetischer Sicht doppelt gezählt, da in einer Schwingung sowohl potentielle als auch kinetische Energie steckt!
Die untere Tabelle zeigt für ein-, zwei- und dreiatomige Moleküle die Anzahl der jeweiligen Freiheitsgrade f, aufgeteilt auf die verschiedenen Bewegungsformen.
| Teilchenart | Translation ftrans | Rotation frot | Schwingung fsch | Gesamt f |
| einatomig | 3 | 0 | 0 (x 2) | 3 |
| zweiatomig (linear) | 3 | 2 | 1 (x 2) | 7 |
| dreiatomig (nicht-linear) | 3 | 3 | 3 (x 2) | 12 |
| dreiatomig (linear) | 3 | 2 | 4 (x 2) | 13 |
Die Gesamtzahl der Freiheitsgrade f ergibt sich aus der Summe der einzelnen Freiheitsgrade für die Translation (ftrans), Rotation (frot) und die Schwingung (fsch):
\begin{align}
&\boxed{f = f_{trans} + f_{rot} + 2 \cdot f_{sch}} \\[5px]
\end{align}
Gleichverteilungssatz (Äquipartitionstheorem)
Eine solche Aufteilung der Energie in Freiheitsgrade hat einen besonderen Grund. Denn es hat sich gezeigt, dass sich die (innere) Energie eines Gases gleichmäßig auf alle Freiheitsgrade aufteilt (siehe auch hauptartikel Gleichverteilungssatz). Dieselbe Energie die bspw. in der Translationsbewegung der Teilchen in x-Richtung steckt, findet sich auch in Form der Rotationsenergie der Teilchen um die z-Achse wieder. Diese Energie wird sich im Mittel auch in der potentiellen Energie bzw. kinetischen Energie einer Schwingung wiederfinden.
Eine solche gleichmäßige Aufteilung der Energie auf die unterschiedlichen Freiheitsgrade wird auch als Gleichverteilungssatz oder Äquipartitionstheorem bezeichnet.
Der Gleichverteilungssatz (Gleichverteilungssatz) beschreibt die gleichmäßige Aufteilung der Energie auf die einzelnen Freiheitsgrade!
Im Artikel Druck und Temperatur zeigt sich, dass die Temperatur T eines Gases wie folgt mit der mittlere kinetischen Translationsenergie W eines Teilchens verknüpft ist (kB) ist die Boltzmann-Konstante):
\begin{align}
\label{bew}
&W_{kin} = \frac{3}{2} k_BT ~~~~~\text{mittlere kinetische Energie eines Teilchens}\\[5px]
\end{align}
Dieser Zusammenhang gilt zunächst nur zwischen der Temperatur und jener Energie, die in der (dreidimensionalen) Translationsbewegung eines Teilchens steckt. Auf jeden Freiheitsgrad der Translationsbewegung entfällt gemäß dem Gleichverteilungssatz damit im Mittel eine Energie von ½⋅kB⋅T.
Die Aussage des Gleichverteilungssatzes beschränkt sich aber prinzipiell nicht nur auf die Translationsenergie, sondern gilt für alle Energieformen gleichermaßen. Wenn ein Freiheitsgrad der Translationsbewegung im Mittel eine Energie von ½⋅kB⋅T besitzt, dann gilt dies gemäß dem Gleichverteilungssatz auch für die Freiheitsgrade der Rotation und der Schwingung (denn die Energie ist nun einmal gleich verteilt).
Jeder Freiheitsgrad, egal ob translatorisch, rotatorisch oder oszillatorisch, besitzt somit im Mittel die Energie ½⋅kB⋅T. Kennt man also die Anzahl der Freiheitsgrade f eines Moleküls, dann trägt dieses Teilchen bei einer gegebenen Temperatur T im Mittel die Energie W=f⋅½⋅kB⋅T:
\begin{align}
\label{frei}
&\boxed{W = \frac{f}{2} k_BT~} ~~\text{Energie eines Teilchens}\\[5px]
\end{align}
Ist darüber hinaus die Anzahl der Teilchen in einem Gas bekannt, dann kann hieraus die Gesamtenergie des Gases und damit dessen innere Energie ermittelt werden. Denn wenn ein Teilchen im Mittel die Energie W trägt, dann wird im Gas mit N Teilchen die Gesamtenergie U=N⋅W vorhanden sein:
\begin{align}
&\boxed{U = \frac{f}{2}Nk_BT~} ~~~~~\text{Innere Energie des Gases}\\[5px]
\end{align}
Die innere Energie des Gases kann nicht nur durch die Teilchenanzahl sondern auch durch die Stoffmenge n=N/NA ausgedrückt werden, d.h. durch die Anzahl der Mole (mit NA als Avogadro-Konstante):
\begin{align}
&U = \frac{f}{2} \cdot n \cdot \underbrace{N_A \cdot k_B}_{R_m} \cdot T \\[5px]
\end{align}
In der oberen Gleichung können die Avogadro-Konstante NA und die Boltzmann-Konstante kB zu einer neuen Konstante zusammengefasst werden, zur sogenannten molaren Gaskonstanten Rm (auch universelle Gaskonstante oder ideale Gaskonstante genannt):
\begin{align}
\label{inn}
&\boxed{U = \frac{f}{2} R_m n T~}~~~~~R_m = 8,314 \frac{\text{J}}{\text{mol}\cdot\text{K}} \\[5px]
\end{align}
Änderung der inneren Energie
Das Verständnis über die Freiheitsgrade und den Zusammenhang zur inneren Energie kann man nun nutzen, um die Temperaturänderung eines idealen Gases bei einer Energiezufuhr zu berechnen.
Hierzu wird ein ideales Gas betrachtet, dessen Freiheitsgrade f als bekannt vorausgesetzt werden. Ändert sich die innere Energie des Gases um einen Betrag ΔU, dann resultiert dies in eine entsprechenden Temperaturänderung ΔT, da alle anderen Größen in Gleichung (\ref{inn}) konstant sind.
\begin{align}
\label{du}
&\boxed{\Delta U = \frac{f}{2} R_m n ~ \Delta T~} ~~~~~\text{gilt für jeden thermodynamischen Prozess} \\[5px]
\end{align}
Dieser Sachverhalt wird auch anschaulich klar. Erhöht man bspw. die innere Energie des Gases durch eine Wärmezufuhr, denn wird sich die Erhöhung der Energie auf alle Energieformen gleichmäßig verteilen. Auch die translatorische Bewegungsenergie wird sich erhöhen, die gemäß Gleichung (\ref{bew}) direkt mit einer Temperaturerhöhung verbunden ist. Umgekehrt wird eine Verringerung der inneren Energie durch Wärmeabfuhr zu einer Erniedrigung der Bewegungsenergien führen und damit die Temperatur sich senken.
Auch die Temperaturerhöhung bei einem Kompressionsvorgang lässt sich mit dieser Gleichung anschaulich erläutern. Komprimiert man ein Gas unter Arbeitsaufwand, dann kommt diese aufgewendete Energie der inneren Energie des Gases zugute. Dies ist nach Gleichung (\ref{du}) folglich mit einer Temperaturerhöhung verbunden. Dieses Prinzip der Temperaturerhöhung durch Kompression wird bspw. in Dieselmotoren verwendet um das Treibstoff-Luft-Gemisch dabei so stark zu erhitzen, dass es sich von selbst entzündet.
Die untere Animation zeigt einen Versuch zur Demonstration der Temperaturerhöhung während einer Kompression. Hierzu wird ein Wattebausch in einem Zylinder aus Plexiglas platziert. Der Zylinder wird mit einem beweglichen Kolben verschlossen. Wird nun der Kolben schlagartig nach unten bewegt, dann erhitzt sich die darin befindliche Luft so stark, dass der Wattebausch sich entzündet.

Der Verdichtungsvorgang muss deshalb sehr schnell erfolgen, da ansonsten das Gas an den relativ kühlen Zylinderwänden sofort wieder abkühlen würde. Durch den raschen Vorgang wird eine Wärmeabfuhr aus dem Gas praktisch verhindert (sog. adiabater Prozess). Die Temperaturerhöhung während der Kompression kann auch anschaulich erklärt werden. Wird der Kolben in den Zylinder bewegt, dann stößt der Kolben auf Gasteilchen wie ein Tennisschläger auf entgegen fliegende Tennisbälle. Die Geschwindigkeit der Gasteilchen erhöht sich dabei, was direkt eine Zunahme der Temperatur bedeutet.
Tatsächlich benötigt man zur Demonstration der Temperaturerhöhung während einer Verdichtung kein derartig aufwendigen Versuchsaufbau. Bereits die tägliche Erfahrung beim Aufpumpen eines Fahrradreifens zeigt, dass sich Luft während einer Verdichtung erwärmt. Die Erwärmung der Luftpumpe ist dabei nicht etwa Reibungseffekten geschuldet sondern hauptsächlich auf die Energiezufuhr während der Kompression zurückzuführen! Auch die sehr starke Temperaturerhöhung von Kompressoren im Bereich der Drucklufterzeugung zeigt diesen Effekt.
Molare Wärmekapazität
Die qualitativen Aussagen über den Zusammenhang zwischen einer Energiezufuhr – im Speziellen einer Wärmezufuhr – und der resultierenden Temperaturerhöhung sollen im Folgenden etwas ausführlicher diskutiert werden.
Molare Wärmekapazität des isochoren Prozesses
Wird einem Gas eine bestimmte Wärmeenergie zugeführt – und gibt das Gas dabei selbst keine Energie durch mechanische Arbeit oder durch Wärmeabfuhr wieder ab (!) – dann kommt diese Wärmezufuhr wie bereits erwähnt vollständig der inneren Energie des Gases zugute (Energieerhaltungssatz). Die innere Energie des Gases wird also durch diesen Prozess folglich um den Betrag der zugeführte Wärme Q ansteigen, d.h. die Wärmezufuhr Q entspricht direkt der Änderung der inneren Energie ΔU:
\begin{align}
& Q \overset{!}{=} \Delta U \\[5px]
&\boxed{Q = \frac{f}{2}R_m n \cdot \Delta T~} ~~~~~\text{gilt nur für den isochoren Prozess} \\[5px]
\end{align}
Diese Gleichung gilt nicht nur für eine Wärmezufuhr, sondern auch für eine Wärmeabfuhr (die Wärmeenergie wird im thermodynamischen Sinne dann negativ gezählt). Wie bereits erläutert, führt eine Wärmeabfuhr in diesem Fall zur Verringerung der inneren Energie und damit zu einer Absenkung der Temperatur (negative Temperaturänderung).
Bemerkenswert an der oberen Gleichung ist, dass es für den Zusammenhang zwischen einer Wärmezufuhr und der resultierenden Temperaturerhöhung offensichtlich keine Rolle spielt um welche Gasart es sich genau handelt. Es kommt in dieser Gleichung keine gasartspezifische Größe vor. Es ist nur die Anzahl der Freiheitsgrade der Moleküle von Bedeutung, nicht aber aus welchen Atomen sich das Molekül genau zusammensetzt. Für ein ideales Gas kommt es somit nur auf die „Form“ der Gasmoleküle an, d.h. ob einatomig (f=3), zweiatomig bzw. linear (f=7) oder verzweigt (f=12), da hierdurch die Zahl der Freiheitsgrade vorgegeben ist (siehe Tabelle oben).
Die für eine bestimmte Anzahl an Freiheitsgraden konstante Größe f/2⋅Rm wird auch als molare Wärmekapazität Cm,v bezeichnet, da sie den quantitativen Zusammenhang zwischen einer Wärmezufuhr/-abfuhr und der Temperaturänderung bestimmt:
\begin{align}
\label{qv}
&\boxed{Q = C_{m,v} \cdot n \cdot \Delta T~} ~~~~~\text{mit}\\[5px]
\label{c}
&\boxed{C_{m,v} := \frac{f}{2}R_m} = \frac{Q}{n ~ \Delta T} ~~~~\left[C_{m,v}\right]=\frac{\text{J}}{\text{mol} \cdot \text{K}}\\[5px]
\end{align}
Wie aus Gleichung (\ref{c}) ersichtlich wird, gibt die molare Wärmekapazität anschaulich an, wie viel Wärmeenergie zugeführt werden muss um die Temperatur eines Gases mit einer Stoffmenge von einem Mol um ein Kelvin zu erhöhen.
Die molare Wärmekapazität gibt anschaulich an, wie viel Wärmeenergie notwendig ist um ein Mol einer Substance um ein Kelvin (ein Grad Celsius) zu erwärmen!
Gleichung (\ref{qv}) wurde unter der Bedingung hergeleitet, dass das Gas während der Wärmezufuhr keine Energie nach außen abgibt. Es stellt sich dann natürlich die Frage, wie ein solcher thermodynamischer Prozess in der Praxis konkret aussieht.
Ein einfaches Beispiel stellt ein mit Gas gefülltes, verschlossenes Gefäß dar, das mit einem Bunsenbrenner erwärmt wird. Zwar nimmt zum einen das Gefäß einen Teil der zugeführten Wärme auf, und zum anderen kann das Gas über das Gefäß wieder einen Teil der zugeführten Wärme an die Umgebung abgeben; Gleichung (\ref{qv}) behält jedoch dann weiterhin Gültigkeit, wenn als Wärmezufuhr Q der Nettobetrag der zugeführten Wärme zugrundegelegt wird, d.h. die dem Gas effektiv zugeführte Wärme.

Ein Gas kann aber nicht nur Energie in Form von Wärme an die Umgebung abgegeben sondern auch mechanische Arbeit verrichten. Man denke bspw. an einen Kolben in einem Motorzylinder, der durch den Gasdruck mit einer bestimmten Kraft nach unten gedrückt wird und dabei Arbeit verrichtet. Das Gas gibt dabei offensichtlich Energie in Form mechanischer Arbeit nach außen ab.
Ein Gas wird grundsätzlich immer dann mechanische Arbeit verrichten, wenn sich dessen Volumen vergrößert. Denn eine Volumenvergrößerung bedeutet immer, dass das Gas mit einer bestimmten Kraft (bedingt durch den herrschenden Druck an der Systemgrenze) entlang einer Strecke sein Volumen vergrößert. Eine wirkende Kraft entlang einer Strecke ist schließlich genau die Definition der mechanischen Arbeit. Deshalb ist eine Volumenänderung an einem Gas immer mit einem mechanischen Energieumsatz verbunden. Man spricht in diesem Zusammenhang auch oft von einer Volumenänderungsarbeit.
Als Volumenänderungsarbeit bezeichnet man die mechanische Energie die einem Gas während einer Kompression zugeführt wird bzw. die mechanische Energie die das Gas bei einer Expansion abgibt!
Für die Gültigkeit von Gleichung (\ref{qv}) muss deshalb unbedingt das Gasvolumen während der Wärmezufuhr konstant gehalten werden, ansonsten verliert diese Gleichung aufgrund der noch zu berücksichtigenden mechanischen Arbeit ihre Gültigkeit. Deshalb ist das eingangs betrachtete Gefäß mit einem Korken verschlossen. Man spricht bei dieser Art der Wärmezufuhr unter konstantem Volumen auch von einem sogenannten isochoren Prozess.
Eine thermodynamische Zustandsänderung bei konstantem Volumen, wird auch als isochorer Prozess bezeichnet!
Um deutlich zu machen, dass Gleichung (\ref{qv}) nur bei einem isochoren Prozess gilt (und Q als Nettowärmebetrag), wird im Index der molaren Wärmekapazität zusätzlich der Buchstabe v hinzugefügt („volumen konstant“). Beachte, dass bei einem isochoren Prozess die zugeführte Wärmeenergie vollständig der Erhöhung der inneren Energie zugute kommt bzw. eine abgeführte Wärmeenergie sich vollständig auf Kosten der inneren Energie vollzieht.

Wichtige Anmerkung
Mit der Definition der molaren Wärmekapazität des isochoren Prozesses Cm,v lässt sich rein formal (!!!) nun auch die Änderung der inneren Energie ΔU gemäß Gleichung (\ref{du}) ausdrücken:
\begin{align}
\label{du2}
&\boxed{\Delta U = C_{m,v} n ~ \Delta T~} ~~~~~\text{gilt für jeden thermodynamischen Prozess} \\[5px]
\end{align}
Gleichung (\ref{du2}) gilt im Gegensatz zu Gleichung (\ref{qv}) für jeden thermodynamischen Prozess eines idealen Gasen, auch wenn darin die molare Wärmekapazität des isochoren Prozesses auftritt! Für die Änderung der inneren Energie ist die Verwendung dieser Größe nur eine rein formale Schreibweise!
Molare Wärmekapazität des isobaren Prozesses
Während der betrachteten isochoren Wärmezufuhr des verschlossenen Gefäßes wird sich infolge der Temperaturerhöhung auch der Druck erhöhen. Entfernt man hingegen den Korken, dann kann das Gas während der Wärmezufuhr unter konstantem (Umgebungs-)Druck expandieren, d.h. sein Volumen vergrößern. Im Gegensatz zu einem isochoren Prozess spricht man bei einer thermodynamischen Zustandsänderung unter konstantem Druck von einem isobaren Prozess.
Eine thermodynamische Zustandsänderung bei konstantem Druck, wird auch als isobarer Prozess bezeichnet!
Auch für einen isobaren Prozess, lässt sich eine molare Wärmekapazität in Abhängigkeit der Freiheitsgrade definieren. Dies soll im Folgenden gezeigt werden.
Als Beispiel eines isobaren Prozesses wird ein Gas in einem senkrecht stehenden Zylinder betrachtet, der durch eine im Zylinder reibungsfrei gleitende Platte („Kolben“) verschlossen ist. Unter dem Gewicht der Platte wird das Gas zunächst komprimiert und der Druck erhöht sich, bis sich ein Gleichgewichtszustand einstellt.

In diesem Zustand wirkt der Gasdruck p auf die Plattenfläche A, sodass das Gas die Kraft Fp=p⋅A auf die Innenseite der Platte ausübt. Von außen wirkt zum einen die Gewichtskraft Fg=m⋅g auf die Plattenfläche (genauer gesagt: auf die Grenzfläche zum Gas, die auch als Systemgrenze bezeichnet wird) und zum anderen der Umgebungsdruck p0, der zusätzlich auf die Plattenfläche bzw. auf die Systemgrenze eine Kraft F0=p0⋅A verursacht.
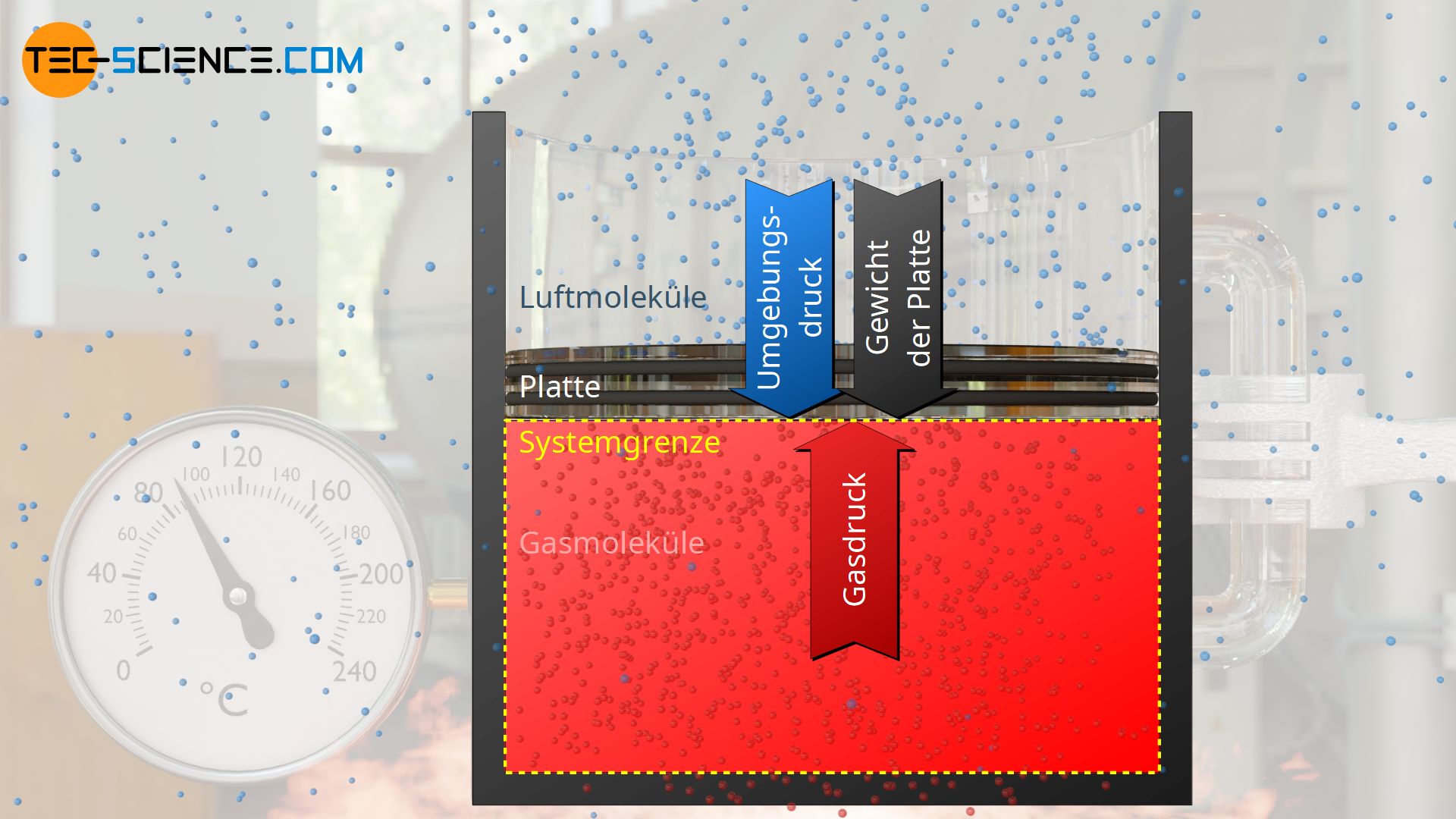
Im Gleichgewichtszustand stehen die äußeren Kräfte Fg und F0 mit der inneren, vom Gas verursachten Kraft Fp, im Gleichgewicht. Aus dieser Gleichgewichtsbetrachtung kann der Gasdruck p wie folgt ermittelt werden:
\begin{align}
&F_p \overset{!}{=} F_g + F_0 \\[5px]
&p \cdot A = mg + p_0A\\[5px]
&\boxed{p = \frac{mg}{A}+p_0} \\[5px]
\end{align}
Es zeigt sich, dass der Gasdruck offensichtlich nur durch die Masse der Platte und die Plattenfläche sowie des Umgebungsdrucks beeinflusst wird. Das Gewicht der Platte und der Umgebungsdruck zwingen dem Gas sozusagen den Druck auf. Auch wenn das Gas nun erwärmt wird, wird sich an diesem Sachverhalt prinzipiell nichts ändern. Der Druck wird immer durch das Gewicht der Platte und durch den Umgebungsdruck vorgegeben werden. Man erhält somit also eine Wärmezufuhr bei der sich der Druck nicht ändert!
Man könnten an dieser Stelle auch wie folgt argumentieren: Wird das Gas erwärmt, dann wird ein möglicher Druckanstieg durch ein Nachgeben der Platte nach oben ausgeglichen (Expansion), sodass der Druck stets konstant bleibt.
Bilanziert man nun die Energieumsätze, die am Gas getätigt werden, dann stellt sich die Situation wie folgt dar. Dem Gas wird auf der einen Seite Energie in Form von Wärme Q zugeführt, aber auf der anderen Seite gibt das Gas Energie in Form von mechanischer Arbeit W nach außen ab, nämlich durch Anheben des Gewichtes während der Expansion (das Gas verrichtet Hubarbeit). Das Gas erhöht seine innere Energie also um den Betrag der zugeführten Wärme Q und verringert ihn gleichzeitig wieder um den Betrag der verrichteten (abgegeben) Arbeit W, sodass die innere Energie effektiv um den Differenzbetrag ansteigt:
\begin{align}
\label{ees}
&\Delta U = Q – W \\[5px]
\end{align}

Während die Änderung der inneren Energie durch Gleichung (\ref{du}) bereits gegeben ist, kann die vom Gas verrichtete Arbeit W aus der konstanten Kraft Fp=p⋅A, mit der das Gas die Platte um eine Höhe Δh anhebt, bestimmt werden:
\begin{align}
&W = F_p \cdot \Delta h = p \cdot \underbrace{A \cdot \Delta h}_{\Delta V} = p \cdot \Delta V\\[5px]
&W = p \cdot \Delta V \\[5px]
\end{align}

Bei der oberen Herleitung wurde ausgenutzt, dass es sich bei dem Produkt aus Kolbenfläche und Anhebehöhe gerade um die Volumenänderung ΔV des Gases handelt. Die Arbeit als Produkt von Druck und Volumenänderung kann mithilfe der idealen Gasgleichung schließlich wie folgt durch die Temperaturänderung ΔT ausgedrückt werden:
\begin{align}
&p V =R_m \cdot n \cdot T ~~~~~~\text{für }p \text{=konstant gilt:} \\[5px]
&p \cdot \Delta V = R_m \cdot n \cdot \Delta T \\[5px]
\end{align}
Somit gilt zwischen der umgesetzten Arbeit und der Temperaturänderung folgender Zusammenhang:
\begin{align}
\label{w}
&W = p\cdot \Delta V= R_m \cdot n \cdot \Delta T \\[5px]
\end{align}
Werden die Gleichungen (\ref{du}) und (\ref{w}) in Gleichung (\ref{ees}) eingesetzt, zeigt sich folgender Zusammenhang zwischen der zugeführten Wärme und der resulteirenden Temperaturänderung bei einem isobaren Prozess:
\begin{align}
\Delta U &= Q – W \\[5px]
\frac{f}{2} R_m n ~ \Delta T &= Q – R_m \cdot n ~ \Delta T \\[5px]
Q &= \frac{f}{2} R_m n ~ \Delta T + R_m \cdot n ~ \Delta T \\[5px]
Q &= \underbrace{\left(\frac{f}{2} + 1\right)R_m}_{C_{m,p}} \cdot n ~ \Delta T \\[5px]
\end{align}
Der über der geschweiften Klammer gekennzeichnete Ausdruck kann nun als die molare Wärmekapazität des isobaren Prozesses Cm,p aufgefasst werden, die den Zusammenhang zwischen einer Wärmezufuhr bei konstantem Druck und der hieraus resultierenden Temperaturänderung beschreibt:
\begin{align}
\label{qp}
&\boxed{Q = C_{m,p} \cdot n \cdot \Delta T~} ~~~~~\text{mit}~~~~~ \boxed{C_{m,p} := \left(\frac{f}{2}+1\right)R_m} \\[5px]
\end{align}
Zusammenhang zwischen den molaren Wärmekapazitäten
Betrachtet man die molaren Wärmekapazitäten genauer, so zeigt sich, dass die des isobaren Prozesses stets um den Wert der molaren Gaskonstante größer ist als die molare Wärmekapazität für die isochoren Zustandsänderung:
\begin{align}
\require{cancel}
& C_{m,p} – C_{m,v} = \left(\tfrac{f}{2}+1\right)R_m – \tfrac{f}{2}R_m = \bcancel{\tfrac{f}{2}R_m} + R_m – \bcancel{\tfrac{f}{2} R_m} = R_m \\[5px]
\label{cc}
&\boxed{C_{m,p} = C_{m,v} + R_m}
\end{align}
Die stets größere molare Wärmekapazität Cm,p im Vergleich zu Cm,v bedeutet konkret, dass bei einem isobaren Prozess offensichtlich mehr Wärme zugeführt werden muss, um dieselbe Temperaturänderung zu erreichen. Dies wird auch anschaulich klar, denn die zugeführte Wärme wird bei einem isobaren Vorgang nicht vollständig zur Erhöhung der inneren Energie und damit zur Temperaturerhöhung genutzt, sondern ein Teil der Wärmeenergie wird in mechanische Arbeit umgewandelt (Beachte, dass eine Temperaturänderung gemäß Gleichung (\ref{du}) direkt mit einer Änderung der inneren Energie verknüpft ist!). Wollte man dennoch dieselbe Temperaturänderung hervorrufen, dann müsste man eine um den Betrag der vom Gas verrichteten Arbeit größere Wärmemenge zuführen.

Adiabater Prozess
Weitere wichtige Prozesse in der Thermodynamik sind Zustandsänderungen die so schnell ablaufen, dass im Prinzip keine Zeit für eine Wärmezufuhr oder Wärmeabfuhr bleibt. Aufgrund der hohen Drehzahlen in Motoren ist dies bspw. näherungsweise bei den dort stattfindenden Expansions- und Verdichtungsvorgängen der Fall. Solche Prozesse ohne Wärmeumsätze werden auch als adiabate Prozesse bezeichnet. Der bereits beschriebene Demonstrationsversuch bei dem ein Wattebausch durch rasche Kompression eines Gases zum Entzünden gebracht wurde, kann als näherungsweise adiabat betrachtet werden.
Zur Beschreibung dieser Vorgänge spielt das Verhältnis der molaren Wärmekapazitäten eine wichtige Rolle. Dieses Verhältnis wird auch als Adiabatenexponent oder Isentropenexponent κ bezeichnet:
\begin{align}
\require{cancel}
& \kappa:=\frac{C_{m,p}}{C_{m,v}} = \frac{\left(\tfrac{f}{2}+1\right)\bcancel{R_m}}{\tfrac{f}{2}\bcancel{R_m}}= 1+ \frac{2}{f} \\[5px]
&\boxed{\kappa = 1 + \frac{2}{f}}
\end{align}
Molare Wärmekapazitäten ausgewählter Gase
In der unteren Tabelle sind für ideale Gase und für ausgewählte reale Gase die molaren Wärmekapazitäten und die Isentropenexponenten bei Raumtemperatur angegeben. Man sieht, dass Helium einem einatomigen idealen Gas mit drei Freiheitsgraden sehr nahe kommt. Analog gilt dies für Stickstoff und Luft, welche einem zweiatomigen idealen Gas mit fünf Freiheitsgraden sehr nahe kommen.
| Gas | Molare Wärmekapazität des isochoren Prozesses Cm,v in J/(mol⋅K) | Molare Wärmekapazität des isobaren Prozesses Cm,p in J/(mol⋅K) | Isentropenexponent κ |
| ideal, einatomig (f=3) | 12,5 | 20,8 | 1,67 |
| Helium He | 12,6 | 20,9 | 1,66 |
| Argon Ar | 12,4 | 20,7 | 1,67 |
| ideal, zweiatomig* (f=5) | 20,8 | 29,1 | 1,40 |
| Wasserstoff H2 | 20,2 | 28,6 | 1,42 |
| Luft | 20,7 | 29,1 | 1,41 |
| Stickstoff N2 | 20,7 | 29,0 | 1,40 |
| Sauerstoff O2 | 21,0 | 29,3 | 1,40 |
*) Achtung: zweiatomige Gase können zwar theoretisch 7 Freiheitsgrade aufweisen, jedoch sind in der Praxis die beiden Freiheitsgrade der Schwingung bei Raumtemperatur meist eingefroren – im nächsten Abschnitt mehr dazu.
Beachte, dass man in der Praxis zudem zuerst die molare Wärmekapazität anhand der Temperaturänderung bei einer bestimmten Wärmezufuhr gemäß Gleichung (\ref{c}) bestimmt. Anschließend kann man dann auf die Zahl der Freiheitsgrade schließen. Es zeigt sich also, dass man durch makroskopisch messbare Größen auf den mikroskopischen Zustand in Form der Freiheitsgrade eines Gases schließen kann!
Abhängigkeit der molaren Wärmekapazitäten von der Temperatur
Betrachtet man die Gleichungen zur Bestimmung der molaren Wärmekapazitäten, dann hängen diese offensichtlich nur von der Zahl der Freiheitsgrade ab:
\begin{align}
&C_{m,v} := \frac{f}{2}R_m \\[5px]
&C_{m,p} := \left(\tfrac{f}{2}+1\right)R_m \\[5px]
\end{align}
Man könnten vordergründig annehmen, dass die molaren Wärmekapazitäten unabhängig von der Temperatur ist. Tatsächlich stellt man in der Praxis aber fest, dass die Wärmekapazitäten nur innerhalb bestimmter Temperaturbereiche weitgehend konstant sind. Trägt man bspw. die molare Wärmekapazität Cm,v über der Temperatur in einem Diagramm auf, dann zeigt sich, dass die molare Wärmekapazität mit sinkender Temperatur ebenfalls abnimmt.
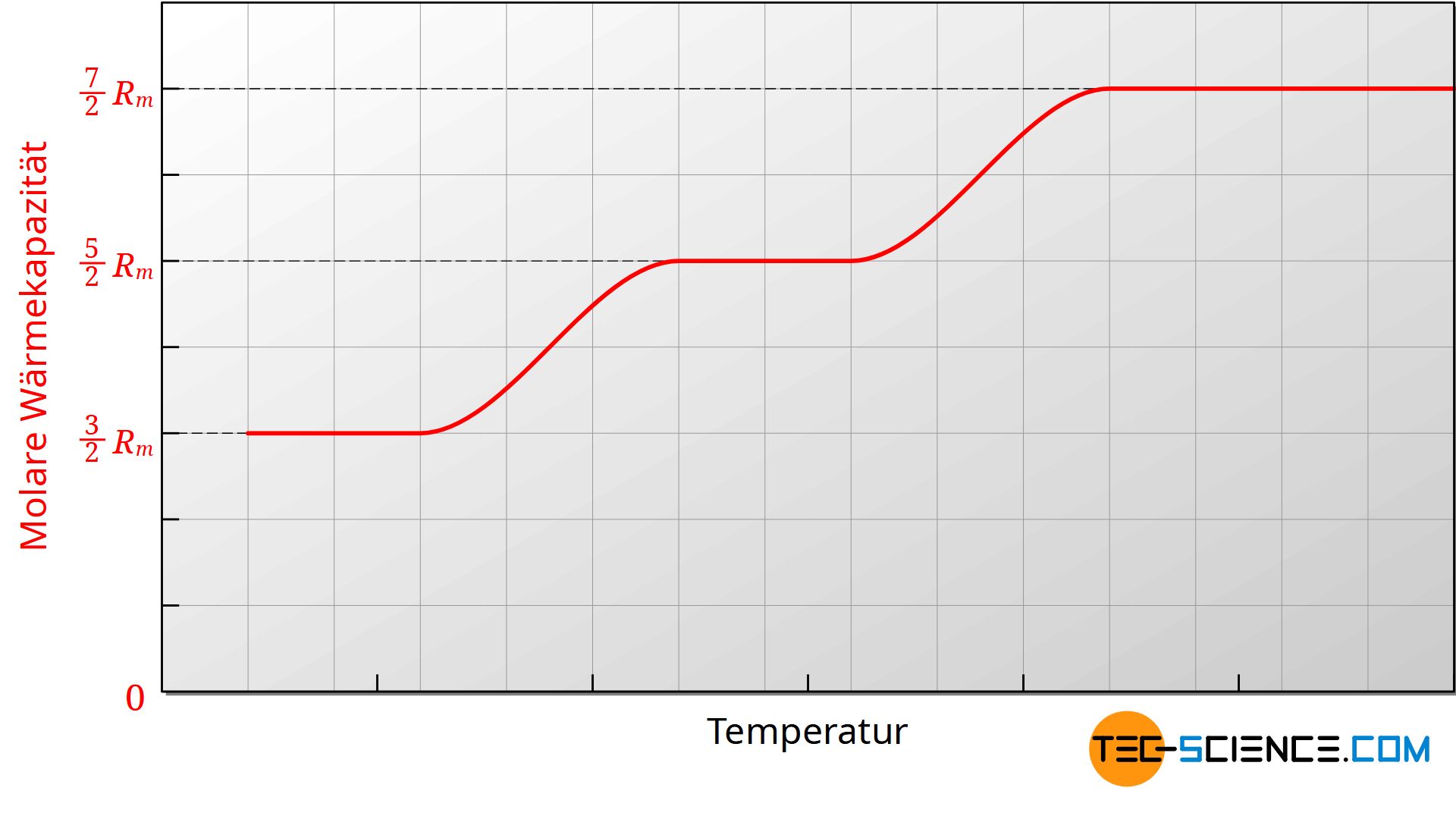
Die obere Abbildung zeigt exemplarisch für ein zweiatomiges ideales Gases den Verlauf der molaren Wärmekapazität des isochoren Prozesses in Abhängigkeit der Temperatur. Da die molare Gaskonstante eine Naturkonstante ist, muss die Änderung der Wärmekapazität auf die Zahl der Freiheitsgrade zurückzuführen sein. Offensichtlich verringert sich mit abnehmender Temperatur die Zahl der Freiheitsgrade.
Die Verringerung der Freiheitsgrade kann nur durch die Quantenmechanik erklärt werden, dessen Grundidee darauf basiert, dass Energien nicht beliebige Werte annehmen können, sondern nur diskrete Werte. Um einen bestimmten Energiezustand eines Moleküls anzuregen, sind bestimmte Mindestenergien notwendig. So erfordert bspw. die Schwingung eines zweiatomigen Moleküls entlang der Molekülachse eine bestimmte Mindestenergie. Ist diese Mindestenergie nicht vorhanden, dann kann die Schwingung auch nicht angeregt werden. Wenn keine Schwingung ermöglicht werden kann, dann steht dieser Freiheitsgrad natürlich auch nicht für die Energiespeicherung zur Verfügung. Aufgrund zu geringer Energie der Moleküle (gleichbedeutend mit zu geringen Temperaturen) ist dieser Freiheitsgrad praktisch eingefroren.
Ein Freiheitsgrad wird als „eingefroren“ bezeichnet, wenn aufgrund zu geringer Energie (d.h. zu geringer Temperatur) dieser Freiheitsgrad aus quantenmechanischen Gründen nicht angeregt werden kann und damit nicht zur Verfügung steht!
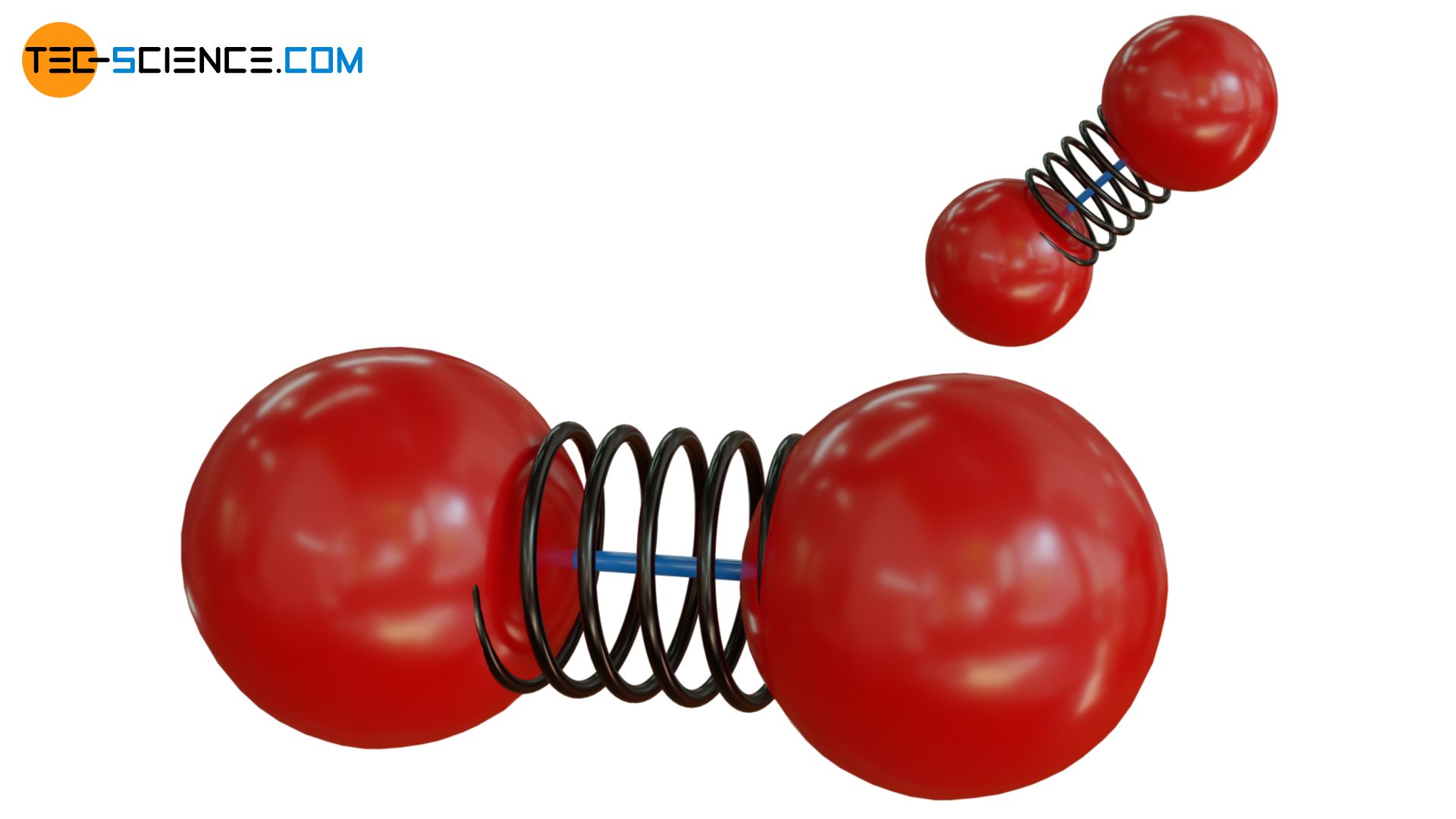
Man kann sich die Situation mit zwei Kugeln („Atome“) veranschaulichen, die zwar mit einer elastischen Feder („Bindungskräfte“) verbunden sind, aber zusätzlich noch durch einen dünnen, zerbrechlichen Stab. Bei geringen Bewegungsenergien des wird, der Stab somit eine Schwingung der Kugeln verhindern. Somit kann keine Energie in Form von Schwingungsenergie gespeichert werden. Ist die Bewegungsenergie hingegen hoch (dies entspricht im übertragenen Sinne einer hohen Temperatur), dann kann der Stab bei einer Kollision mit einem anderen Teilchen zerbrechen. Nun erst sind die Kugeln in der Lage zu schwingen und können dementsprechend Schwingungsenergie zu speichern.
Der Grund weshalb die molare Wärmekapazität innerhalb eines Temperaturbereichs abfällt und nicht plötzlich, ist der charakteristischen Geschwindigkeitsverteilung in einem idealen Gas geschuldet. Bei einer bestimmten Temperatur haben nicht alle Teilchen dieselbe Geschwindigkeit. Einige Teilchen sind langsamer und einige schneller. Sinkt die Temperatur dann wird also nicht bei allen Molekülen gleichzeitig der Freiheitsgrad eingefroren sondern nur bei jenen Teilchen deren Bewegungsenergien zu gering sind.
Bei einem zweiatomigen Gas wird mit sinkender Temperatur zuerst der Freiheitsgrad der Schwingung eingefroren. Anschließend erfolgt der Freiheitsgrad der Rotation.
Man sieht also, dass auch wenn ein Stoff als ideales Gas betrachtet wird, Freiheitsgrade in der Praxis eingefroren werden und sich dadurch die Wärmekapazitäten ändern. Werden im Sinne der Vereinfachung solche Änderungen in den Wärmekapazitäten vernachlässigt, dann spricht man auch von perfekten Gasen.
Als perfektes Gas bezeichnet man ein ideales Gas dessen Wärmekapazitäten als konstant betrachtet werden, d.h. insbesondere keine Freiheitsgrade mit abnehmender Temperatur eingefroren werden!
Molare Wärmekapazität von Feststoffen
Eine Unterscheidung zwischen einem isobare und einem isochoren Prozess muss für Flüssigkeiten und Festkörper im Allgemeinen nicht gemacht werden. Grund hierfür ist, dass Festkörper und Flüssigkeiten inkompressibel sind, d.h. ihr Volumen unter Druck oder bei einer Temperaturänderung (fast) nicht ändern. Die geringe Wärmeausdehnung ist dabei vernachlässigbar! Diese Stoffe sind also nicht in der Lage nennenswerte Volumenänderungsarbeit zu verrichten. Deshalb gleicht eine Wärmezufuhr immer einer isochoren Zustandsänderung.
Es zeigt sich durch empirische Untersuchungen, dass man die angestellten Überlegungen über die Freiheitsgrade von idealen Gasen in vielen Fällen auch auf Festkörper übertragen kann. Im Gegensatz zu Gasen können die Moleküle in Festkörper sich nicht frei bewegen sondern sind an bestimmte Orte gebunden. Auch eine Rotation fällt in diesen Fällen weg. Die Bewegungen der Moleküle in Festkörper beschränken sich somit auf Schwingungen um eine Gleichgewichtslage, wobei die Schwingungen in alle drei Raumrichtungen stattfinden können.
Es ergeben sich für die Moleküle in Festkörper damit drei Schwingungsfreiheitsgrade, die aufgrund der potentiellen und kinetischen Energie die einer Schwingung steckt, doppelt gezählt werden müssen. Mit also effektiv sechs Freiheitsgraden ergibt sich für Festkörper somit eine molare Wärmekapazität die theoretisch dem dreifachen Wert der molaren Gaskonstante entspricht:
\begin{align}
&C_{m} = \frac{f}{2}R_m = \frac{6}{2}R_m = 3 R_m \\[5px]
& \boxed{C_m = 25~\tfrac{\text{J}}{\text{mol}\cdot\text{K}} } ~~~~~\text{Dulong-Petit-Gesetz} \\[5px]
\end{align}
Und tatsächlich zeigen empirische Untersuchungen, dass diese einfache Betrachtung für viele Festkörper in guter Näherung gilt. Man bezeichnet diesen Zusammenhang auch als Dulong-Petit-Gesetz. Der Begriff „Gesetz“ ist an dieser Stelle nicht wirklich passend, da es sich dabei vielmehr um eine Abschätzung handelt.
Das Dulong-Petit-Gesetz besagt, dass die molare Wärmekapazität von Feststoffen in etwa dem dreifachen Wert der molare Gaskonstante entspricht!
Die untere Tabelle zeigt für ausgewählte Festkörper die tatsächliche molare Wärmekapazität bei Raumtemperatur. Man sieht aber auch, dass die Abschätzung nach dem Dulong-Petit-Gesetz für viele Stoffe eine gute Näherung darstellt.
| Stoff | Molare Wärmekapazität Cm in J/(mol⋅K) |
| Aluminium | 25 |
| Blei | 27 |
| Eisen | 26 |
| Kupfer | 25 |
| Zink | 25 |
| Zinn | 26 |
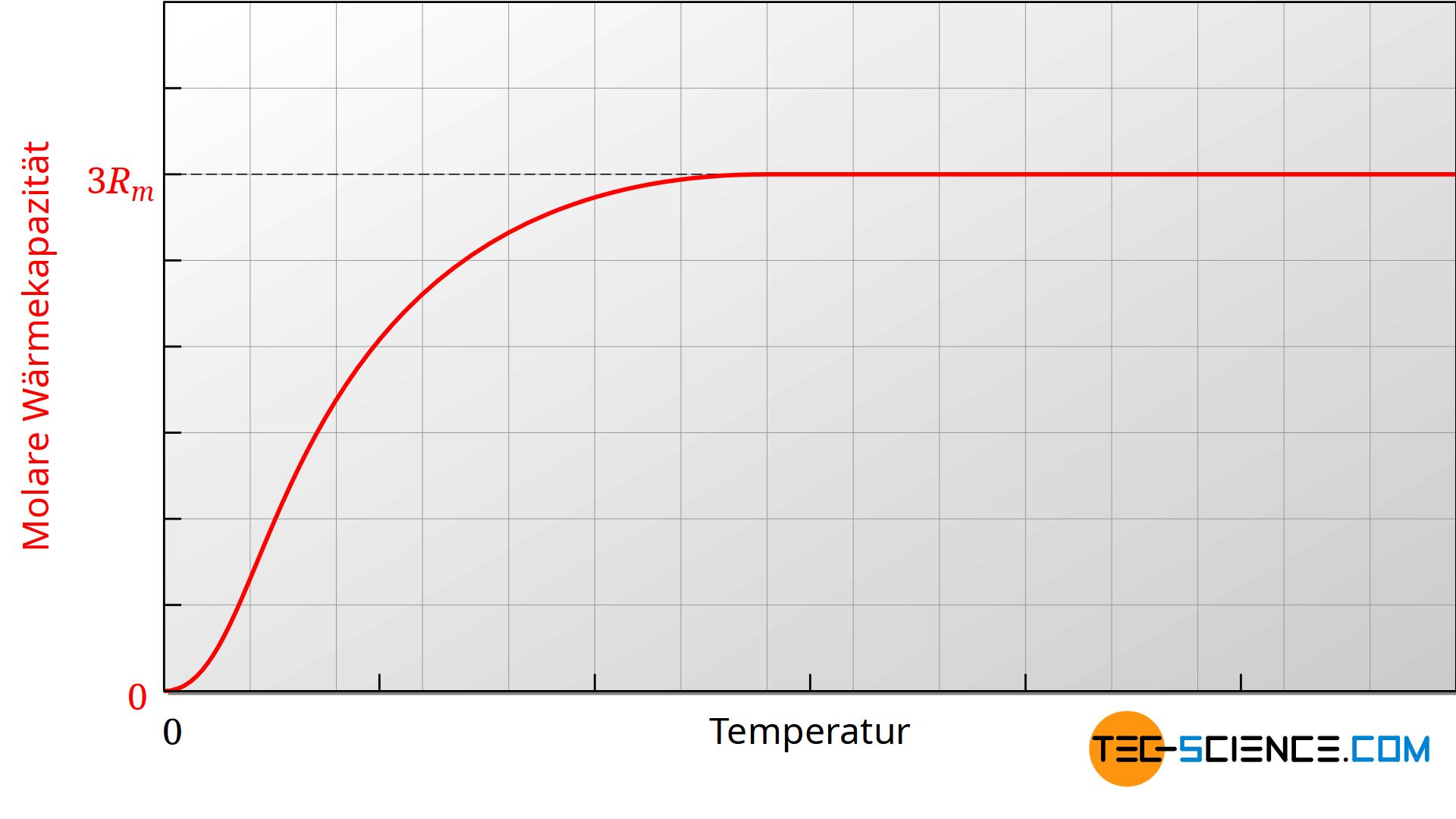
Beachte, dass auch bei Feststoffen mit geringer werdender Temperatur immer mehr Freiheitsgrade eingefroren werden. Dies gilt insbesondere in der Nähe des absoluten Nullpunktes, sodass spätestens in diesem Punkt alle Freiheitsgrade der Schwingung eingefroren sind. Dies gilt prinzipiell für alle Stoffe, da im absoluten Nullpunkt keine Energie vorhanden ist, aber jeder Freiheitsgrad prinzipiell eine bestimmte Mindestenergie benötigt, um überhaupt angeregt zu werden.
Die Wärmekapazität von Stoffen nimmt mit Annäherung der Temperatur an den absoluten Nullpunkt auf Null ab!
Spezifische Wärmekapazität
Wie bereits erläutert, gibt die molare Wärmekapazität anschaulich an wie viel Wärmeenergie zugeführt werden muss, um die Temperatur eines Stoffes mit einem Mol an Teilchen um ein Kelvin zu erwärmen. Möchten man die Temperaturänderung eines Stoffes bei einer Wärmezufuhr ermitteln, so muss die Stoffmenge n offensichtlich bekannt sein:
\begin{align}
& Q = C_m n \Delta T \\[5px]
\end{align}
In der Praxis misst man jedoch meistens nicht die Anzahl der Mole die in einem Stoff enthalten sind, sondern deren Masse. Es ist deshalb häufig üblich die Wärmekapazität nicht bezogen auf die Stoffmenge anzugeben sondern auf die Masse zu beziehen. Die Stoffmenge und Masse stehen dabei über die molare Masse in Zusammenhang. Die molare Masse M ist definiert als Quotient von Masse m und Stoffmenge n und gibt somit anschaulich an wie viel Masse pro Mol ein Stoff besitzt:
\begin{align}
& \boxed{M := \frac{m}{n}} \\[5px]
\label{n}
& n = \frac{m}{M} \\[5px]
\end{align}
Wird die Stoffmenge durch die Masse und die molare Masse ausgedrückt, dann folgt gilt folgender Zusammenhang zwischen der Wärmemenge und der Temperaturänderung:
\begin{align}
& Q = C_m \cdot \frac{m}{M} \cdot \Delta T = \underbrace{\frac{C_m}{M}}_{=c} \cdot m \cdot \Delta T =c \cdot m \cdot \Delta T \\[5px]
&\boxed{Q= c \cdot m \cdot \Delta T} \\[5px]
\end{align}
In der oberen Gleichung wurde der Quotient aus molarer Wärmekapazität und molare Masse (stoffabhängig!) zur spezifischen Wärmekapazität c zusammengefasst:
\begin{align}
& \boxed{c = \frac{C_m}{M}}=\frac{Q}{m \cdot \Delta T} ~~~~~[c]=\frac{\text{J}}{\text{kg} \cdot \text{K} } \\[5px]
\end{align}
Die spezifische Wärmekapazität ist eine stoffspezifische Größe und gibt anschaulich an wie viel Wärme notwendig ist um die Temperatur eines Stoffes mit einer Masse von einem Kilogramm um ein Kelvin zu erwärmen!
Auch bei der spezifischen Wärmekapazität muss für Gase zwischen einer isochoren und einer isobaren Wärmezufuhr unterschieden werden. Dementsprechend unterscheidet man zwischen der spezifischen Wärmekapazität des isochoren Prozesses cv und der spezifischen Wärmekapazität des isobaren Prozesses cp.
Der Zusammenhang zwischen den molaren Wärmekapazitäten Cm,v und Cm,p gemäß der Gleichung (\ref{cc}) kann nun genutzt werden, um auch einen Zusammenhang zwischen den entsprechenden spezifischen Wärmekapazitäten herzustellen:
\begin{align}
&C_{m,p} = C_{m,v} + R_m \\[5px]
&\frac{C_{m,p}}{M} = \frac{C_{m,v}}{M} + \underbrace{\frac{R_m}{M}}_{=R_S} \\[5px]
&\boxed{c_p=c_v+R_S} \\[5px]
\end{align}
Der stoffabhängige Quotient aus allgemeiner Gaskonstante Rm und molarer Masse wird zur sogenannten spezifischen Gaskonstante Rs zusammengefasst:
\begin{align}
&\boxed{R_S=\frac{R_m}{M}} \\[5px]
\end{align}
Die Änderung der inneren Energie kann anstelle der molaren Wärmekapazität Cm,v nun auch durch die spezifische Wärmekapazität cv ausgedrückt werden:
\begin{align}
&\boxed{\Delta U = c_{v} m ~ \Delta T~} \\[5px]
\end{align}