Der Wärmedurchgangskoeffizient (ugs. U-Wert) beschreibt den Wärmetransport durch einen festen Gegenstand, der sich zwischen zwei Fluiden (Gas oder Flüssigkeit) mit unterschiedlichen Temperaturen befindet.
Definition und Einheit des U-Werts
Der U-Wert U gibt an wie viel Wärmeenergie pro Zeit- und Flächeneinheit bei einem Temperaturunterschied der Fluide von 1 Kelvin (1 °C) durch den festen Gegenstand tritt. Angegeben wird der U-Wert folglich in der Einheit „Watt pro Quadratmeter und Kelvin“ W/(m²⋅K). Die pro Zeit- und Flächeneinheit übertragene Wärmeenergie wird auch als Wärmestromdichte q* bezeichnet.
\begin{align}
\label{def}
&\boxed{U := \frac{Q}{\Delta t \cdot A \cdot \Delta T}} \\[5px]
&U = \underbrace{\frac{Q}{\Delta t}}_{\text{Wärmeleistung }\dot Q} \cdot \frac{1}{A \cdot \Delta T} \\[5px]
&U = \underbrace{\frac{\dot Q}{A}}_{\text{Wärmestromdichte }\dot q} \cdot \frac{1}{\Delta T} \\[5px]
&\boxed{U := \frac{\dot q}{ \Delta T}}\\[5px]
\end{align}

Je größer der U-Wert, desto mehr Wärme strömt innerhalb einer bestimmten Zeit durch den Gegenstand und umso geringer ist die Dämmwirkung. Kleine U-Werte bedeuten folglich gute Wärmedämmeigenschaften.
Der U-Wert hängt im Wesentlichen von der Wärmeleitfähigkeit des Festkörpers ab (Wärmetransport durch Wärmeleitung), aber auch vom Wärmeübergangskoeffizient zwischen Fluid und Festkörper bzw. Festkörper und Fluid (Wärmetransport durch Konvektion). Zudem tritt auch eine Wärmeübertragung durch Strahlung auf. In der Praxis wird der U-Wert für verschiedene Bauteile allerdings nicht anhand der Wärmeleitfähigkeit oder des Wärmeübergangskoeffizienten bestimmt, sondern auf experimentellem Wege für verschiedene Bauteile ermittelt.

Gemäß Gleichung (\ref{def}) muss bei gegebenem Temperaturunterschied ΔT im stationären Zustand lediglich die innerhalb einer Zeit Δt durch eine Fläche A hindurchtretende Wärmemenge Q ermittelt werden. Zur Messung des Wärmestroms kommen spezielle Wärmestrommesser zum Einsatz.
Bedeutung und Verwendung des U-Werts
Besondere Bedeutung hat der U-Wert bei Gebäuden. In der Bautechnik handelt es sich bei den Fluiden um Luft. Als wärmeübertragende Festkörper dienen in diesem Fall bspw. Fenster, Mauerwerk, Putz oder sonstige Dämmmaterialien (Gebäudehülle). Es handelt sich dabei also um jene Bauteile, die einen Wärmedurchgang zwischen Hausinnerem und Umgebung möglichst verhindern sollen. Der U-Wert wird deshalb umgangssprachlich auch als Dämmwert bezeichnet.
Im Hinblick auf die Wärmedämmung ist es dabei stets das Ziel Materialien mit möglichst niedrigen U-Werten zu verwenden, um eine größtmögliche Dämmwirkung zu erzielen. Die Dämmwirkung steht dabei jedoch immer auch im Spannungsfeld zwischen Stabilität, Schallschutz, Brandschutz, Umweltschutz und Kosten.
Mit Hilfe des U-Werts von Gegenständen kann schließlich die durch ein Bauteil hindurchtretende Wärmestromdichte q* anhand der vorhandenen Temperaturdifferenz ΔT ermittelt werden:
\begin{align}
&\boxed{\dot q = U \cdot \Delta T} ~~~\text{Wärmestromdichte (Wärmeleistung pro Flächeneinheit)} \\[5px]
\end{align}
Ist zudem die Fläche A des Gegenstandes bekannt, dann kann die durch den Körper transportierte Wärmeleistung Q* bestimmt werden:
\begin{align}
&\boxed{\dot Q = U \cdot A \cdot \Delta T} ~~~\text{Wärmeleistung} \\[5px]
\end{align}
Die über eine Zeit Δt hindurchgetretene Wärmemenge Q ergibt sich dann schließlich wie folgt:
\begin{align}
&\boxed{Q = U \cdot A \cdot \Delta T \cdot \Delta t} ~~~\text{hindurchgeströmte Wärmeenergie} \\[5px]
\end{align}
Berechnung des U-Werts (Wärmewiderstände)
Für die Berechnung des U-Wertes ist es sinnvoll, je nach Wärmeübertragungsart verschiedene Wärmewiderstände zu definieren. Dies Summe dieser Widerstände ergibt den gesamten Wärmedurchgangswiderstand, dessen Kehrwert dann schließlich dem Wärmedurchgangskoeffizient (U-Wert) entspricht.
Wärmedurchlasskoeffizient und Wärmedurchlasswiderstand der Wärmeleitung
Die Wärmeleitfähigkeit λ eines Festkörpers beschreibt wie viel Wärme pro Zeit- und Flächeneinheit bei gegebener Temperaturdifferenz ΔT durch den Querschnitt des Gegenstandes strömt.
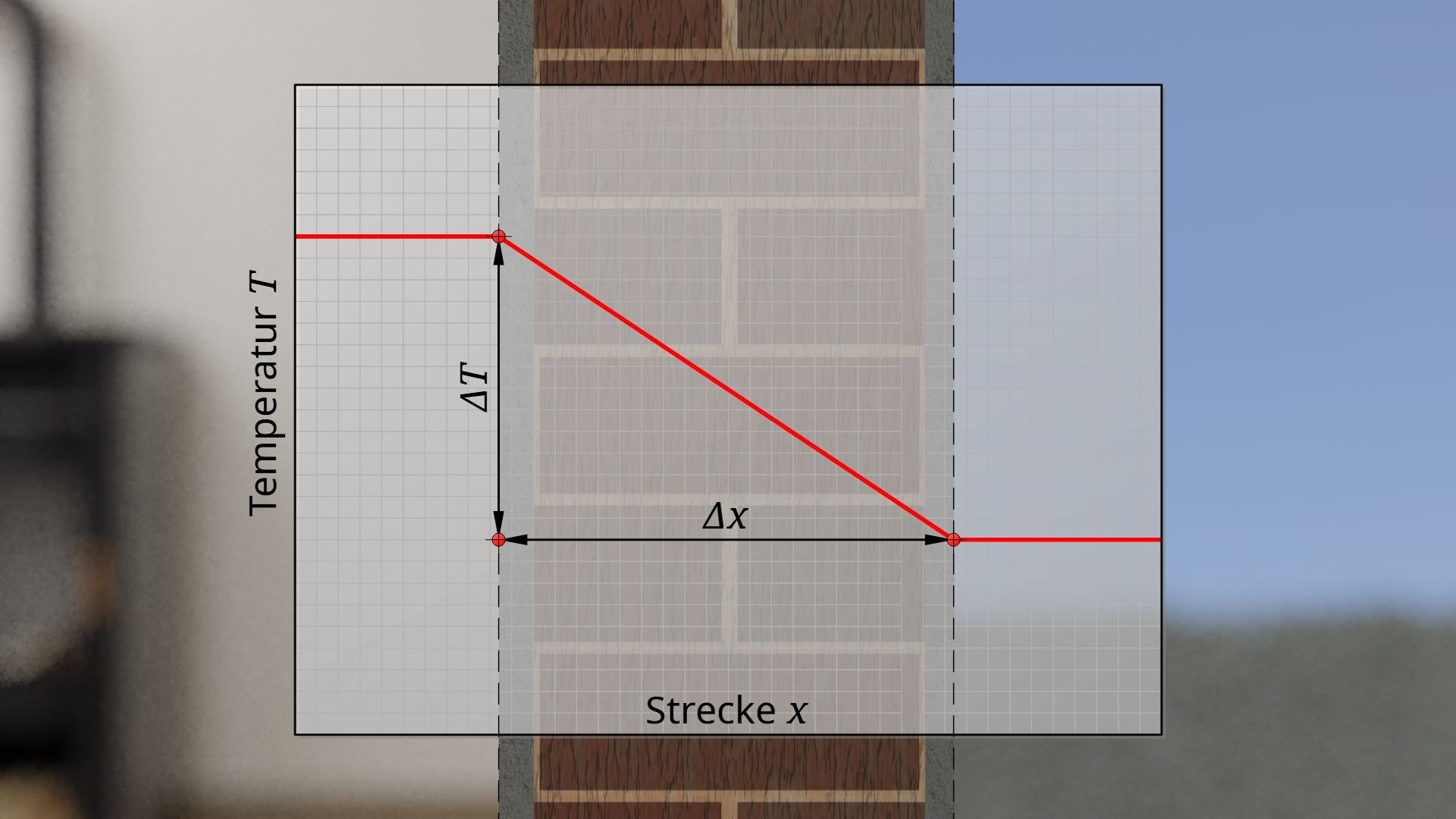
Je größer die Wärmeleitfähigkeit des Materials, desto stärker ist der Wärmetransport infolge der Wärmeleitung. Dabei ist bei gegebener Temperaturdifferenz die resultierende Wärmestromdichte q*λ maßgeblich von der Dicke Δx des Bauteils abhängig (siehe Fouriersches Gesetz), denn schließlich tritt bspw. innerhalb einer bestimmten Zeit durch eine dicke Wand deutlich weniger Wärme als durch eine dünne Wand.
\begin{align}
&\boxed{\dot q_\lambda = \lambda \cdot \frac{\Delta T}{\Delta x}}~~~~~\text{Fourier’sches Gesetz} \\[5px]
&\dot q_\lambda = \underbrace{\frac{\lambda}{\Delta x}}_{\text{Wärmedurchlass-}\\{\text{koeffizient }\Lambda}} \cdot \Delta T \\[5px]
\end{align}
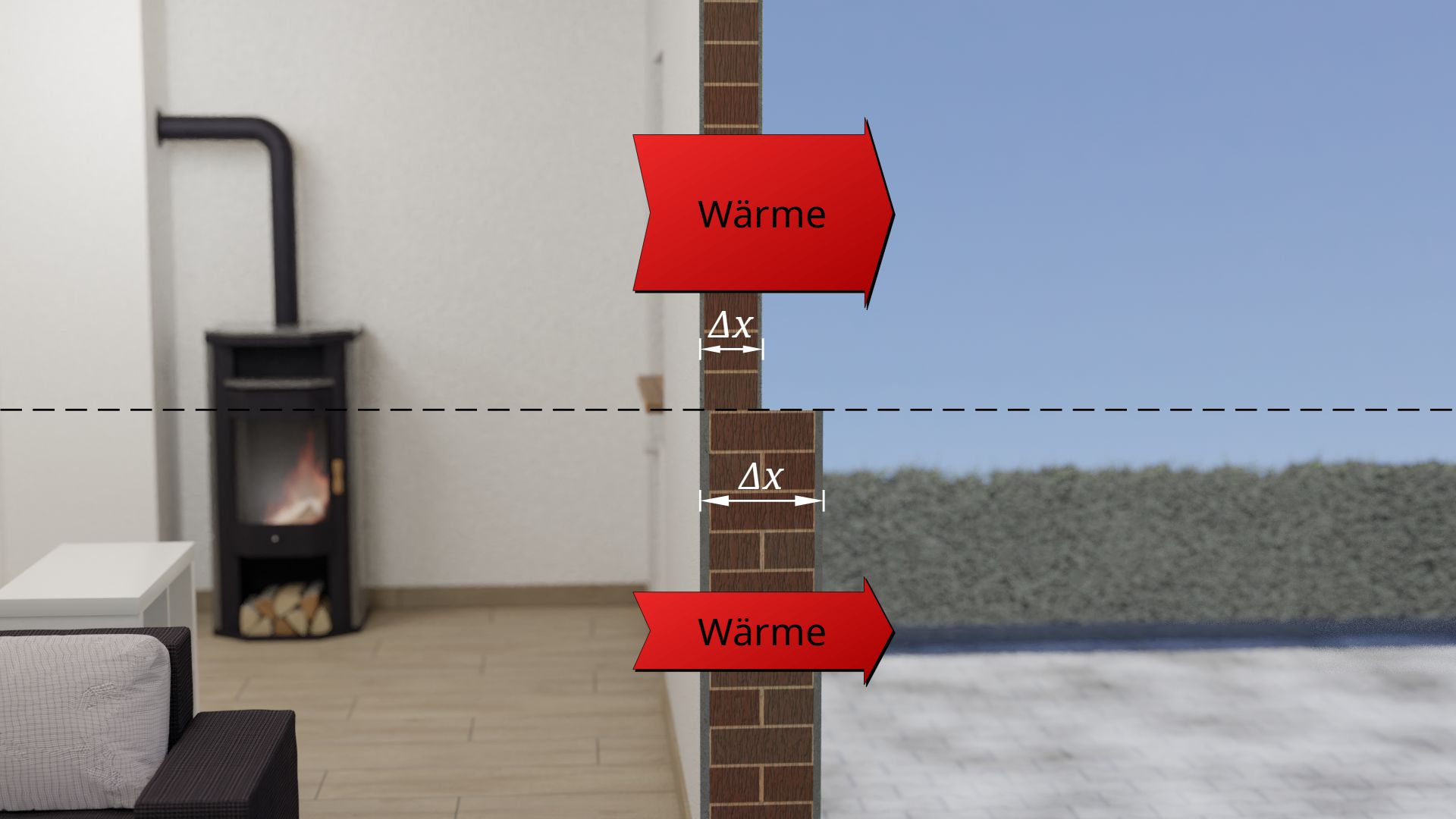
Da die Kombination von Wärmeleitfähigkeit und Dicke des Materials eine Bauteileigenschaft ist, werden diese Größen zu einer neuen bauteilabhängigen Größe zusammengefasst: dem Wärmedurchlasskoeffizienten Λ (auch Wärmedurchlasskoeffizient oder Wärmedurchlasszahl genannt):
\begin{align}
\label{ql}
&\boxed{\dot q_\lambda = \Lambda \cdot \Delta T}~~~\text{mit}~~ \boxed{\Lambda=\frac{\lambda}{\Delta x}}~~\text{als Wärmedurchlasskoeffizient} \\[5px]
\end{align}
Der Wärmedurchlasskoeffizient (Wärmedurchlasszahl) beschreibt als bauteilabhängige Größe den Wärmetransport durch ein Bauteil infolge der Wärmeleitung!
Je größer der Wärmedurchlasskoeffizient, desto stärker der Wärmetransport durch Leitung und umso geringer die Dämmwirkung. Der Kehrwert der Wärmedurchlasszahl ist folglich ein Maß für den Widerstand gegenüber Wärmeleitung und wird Wärmedurchlasswiderstand R genannt:
\begin{align}
&R:=\frac{1}{\Lambda} \\[5px]
\label{a}
&\boxed{R=\frac{\Delta x}{\lambda}}~~[R]=\frac{\text{m²K}}{\text{W}} ~~~\text{Wärmedurchlasswiderstand} \\[5px]
\end{align}
Der Wärmedurchlasswiderstand beschreibt als bauteilabhängige Größe die Dämmwirkung eines Bauteils bezüglich der Wärmeleitung (Widerstand gegenüber Wärmeleitung)!
Wärmeübergangskoeffizient und Wärmeübergangswiderstand der Wärmeströmung (Konvektion)
Der Wärmeübergangskoeffizient α zwischen einem Fluid und einem Festkörper beschreibt wie viel Wärme pro Zeit- und Flächeneinheit bei gegebener Temperaturdifferenz ΔT durch die Grenzfläche zwischen Fluid und Festkörper strömt.
Anders als die Wärmeleitung, die den Wärmetransport im Inneren eines Festkörpers durch Wärmeleitung beschreibt, beschreibt der Wärmeübergangskoeffizient den Wärmetransport durch Konvektion and der Grenzfläche zwischen Fluid und Feststoff! Je größer der Wärmeübergangskoeffizient, desto stärker ist der Wärmetransport infolge der Konvektion (Wärmeströmung). Für die Wärmestromdichte q*s gilt dabei:
\begin{align}
\label{qk}
&\boxed{\dot q_\text{s} = \alpha \cdot \Delta T} ~~~\text{mit}~~ \alpha~~\text{als Wärmeübergangskoeffizient}\\[5px]
\end{align}
Der Index s bei der Wärmestromdichte steht für das englische Wort für Oberfläche (surface), und bringt zum Ausdruck, dass sich die Wärmestromdichte bei der Konvektion auf die Grenzfläche zwischen Fluid und Festkörper bezieht.
Der Wärmeübergangskoeffizient (Wärmeübergangszahl) beschreibt als bauteilabhängige Größe den Wärmetransport an der Grenzfläche zwischen Fluid und Festkörper infolge der Wärmeströmung (Konvektion)!
Anmerkung: Im Bauwesen wird der Wärmeübergangskoeffizient (engl.: heat transfer coefficient) gemäß Norm mit h bezeichnet anstelle von α.
An dieser Stelle wird nun die analoge Beschreibung der unterschiedlichen Wärmetransportvorgänge deutlich. Vergleiche hierzu die Formel (\ref{ql}) zur Beschreibung der Wärmeleitung und Formel (\ref{qk}) zur Beschreibung der Wärmeströmung. Beachte dabei, die unterschiedlichen Begrifflichkeiten:
Der WärmeDURCHLASSkoeffizient gilt für Wärmeleitung, und der WärmeÜBERGANGskoeffizient für Wärmeströmung (Konvektion)! Beide Arten der Wärmeübertragung treten im Allgemeinen gemeinsam auf.
Je größer der Wärmeübergangskoeffizient, desto stärker der Wärmetransport durch Konvektion und umso geringer die Dämmwirkung. Der Kehrwert der Wärmeübergangszahl ist folglich ein Maß für den Widerstand gegenüber Konvektion und wird Wärmeübergangswiderstand Rs genannt:
\begin{align}
\label{rk}
&\boxed{R_\text{s} =\frac{1}{\alpha}}~~[R_\text{s}]=\frac{\text{m²K}}{\text{W}} ~~~\text{Wärmeübergangswiderstand} \\[5px]
\end{align}
Der Wärmeübergangswiderstand beschreibt als bauteilabhängige Größe die Dämmwirkung eines Bauteils bezüglich der Wärmeströmung (Widerstand gegenüber Konvektion)!
Wärmetransport durch Wärmestrahlung
Die Beschreibung der Wärmestrahlung könnte im Prinzip nach den analogen Gesetzmäßigkeiten wie die der Wärmeleitung bzw. Konvektion beschrieben werden. In der Praxis wird bei der experimentellen Bestimmung der Wärmeübergangszahl für Konvektion immer auch die Wärmestrahlung ungewollt mitberücksichtigt.
Die Wärmestromdichte bei der Wärmeübertragung durch Konvektion ergibt sich somit aus jenem Anteil, der tatsächlich auf die Konvektion zurückzuführen ist (αc; engl. convection) und der ungewollt enthaltenen Wärmestrahlung (αr; engl. radiation):
\begin{align}
\label{qs}
&\boxed{\dot q_\text{s} = \left(\alpha_\text{c} +\alpha_\text{r} \right)\cdot \Delta T} \\[5px]
\end{align}
Insofern ist die Wärmestrahlung bereits im Wärmeübergangswiderstands nach Gleichung (\ref{rk}) enthalten:
\begin{align}
&\boxed{R_\text{s} =\frac{1}{\alpha}=\frac{1}{\alpha_\text{c}+\alpha_\text{r}}} \\[5px]
\end{align}
Im Bauwesen spielt die Wärmestrahlung meist nur bei großen Temperaturunterschieden eine merkliche Rolle. Diese Situation ist bei der Gebäudehülle eines Hauses in der Regel nicht gegeben. Die Wärmestrahlung hat in diesem Fall nur eine untergeordnete Bedeutung. Im Falle von Warmwasserleitungen kann aufgrund der großen Temperaturdifferenz zwischen Wasser und Umgebung die Wärmestrahlung jedoch eine größere Bedeutung einnehmen und muss dann explizit berücksichtigt werden.
Um auch Maßnahmen zur Eindämmung des Wärmeverlustes durch Strahlung zu ergreifen, sind Warmwasserrohre deshalb neben einer wärmedämmenden Schicht meist noch mit reflektierender Folie umwickelt. Dies minimiert durch Reflektionen das Austreten der Strahlung und unterbindet damit weitestgehend ein Wärmetransport durch Strahlung.

Wärmedurchgangswiderstand und Wärmedurchgangskoeffizient (U-Wert)
Strömt Wärme nun von einem Fluid auf ein anderes Fluid, wobei beide durch einen Festkörper voneinander getrennt sind, dann muss der Wärmestrom zunächst den Wärmewiderstand durch Konvektion an der Innenseite des Festkörpers überwinden. Dies entspricht dem Widerstand zwischen Fluid und Festkörper (Wärmeübergangswiderstand). Anschließend erfolgt der zu überwindende Wärmewiderstand durch Leitung innerhalb des Festkörpers (Wärmedurchlasswiderstand). Abschließend erfolgt ein nochmaliger Wärmeübergang zwischen Festkörper auf Fluid, der ebenfalls der Konvektion unterliegt (Wärmeübergangswiderstand).
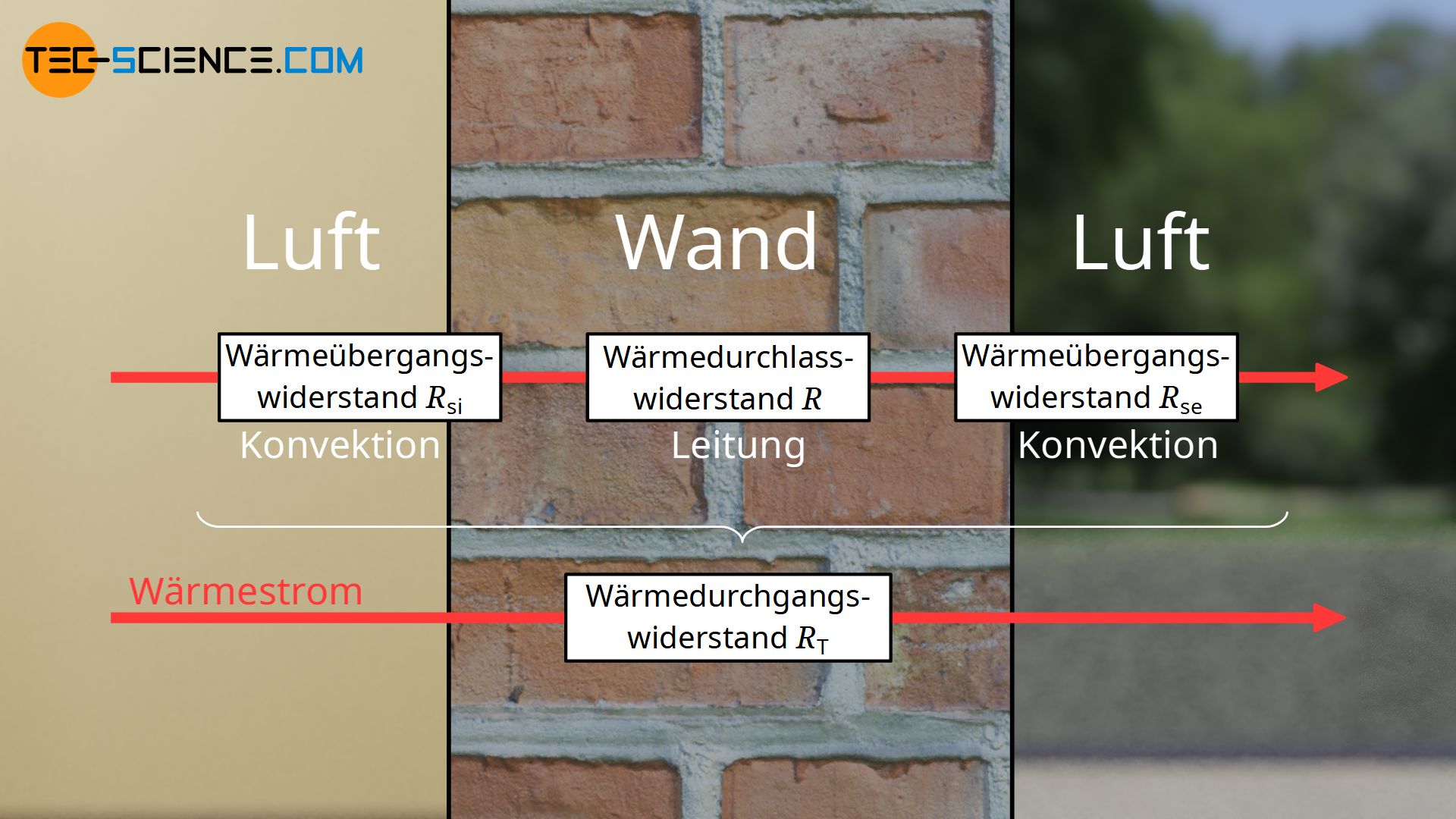
Beachte, dass der Wärmeübergangswiderstand an der Innenseite in der Regel ein anderer ist als an der Außenseite des Festkörpers. Dies gilt insbesondere, wenn ein Bauteil aus unterschiedlichen Materialien aufgebaut ist und Außen- und Innenfläche damit aus unterschiedlichen Stoffen bestehen, die jeweils einen andere Wärmeübergang aufweisen. Vor allem bei Gebäuden spielen auch die Windgeschwindigkeiten eine Rolle, die im Gebäude offensichtlich andere sind als außerhalb des Gebäudes. Auch dies führt dazu, dass der konvektive Wärmeübergang an der Innenseite der Wand eine andere ist als an der Außenseite.
Diese Unterscheidung im Wärmeübergangswiderstand wird durch einen zusätzlichen Buchstaben im Index kenntlich gemacht. Der Wärmeübergangswiderstand Rsi beschreibt den Wärmewiderstand an der Innenseite (engl. internal) und der Wärmeübergangswiderstand Rse den Wärmewiderstand an der Außenseite (engl. external). Die Begriffe Innen bzw. Außen beziehen sich dabei auf die Richtung des Wärmestroms, d.h. von „kalt nach warm“.
Die Summe der beiden Wärmeübergangswiderstände an der Außen- und Innenseite (Rsi und Rse), sowie dem Wärmedurchlasswiderstand R ergibt dann schließlich den gesamten Wärmedurchgangswiderstand RT.
\begin{align}
&\boxed{R_\text{T} =R_\text{si} + R + R_\text{se}} ~~~\text{Wärmedurchgangswiderstand}\\[5px]
\end{align}
Besteht der Festkörper aus mehreren unterschiedlichen Materialien, dann muss die Summe der entsprechenden Wärmedurchlasswiderstände der einzelnen Schichten zugrunde gelegt werden (Beachte, dass es keine Konvektion zwischen den einzelnen Schichten gibt):
\begin{align}
&\boxed{R_\text{T} =R_\text{si} + \sum R + R_\text{se}} ~~~\text{Wärmedurchgangswiderstand}\\[5px]
\end{align}
Die einzelnen Widerstände gegenüber dem Wärmestrom können analog zu elektrischen Widerständen in der Elektrotechnik betrachtet werden. Dabei gilt bei einer Reihenschaltung von Widerständen, dass sich die Einzelwiderstände zum Gesamtwiderstand aufaddieren lassen. Der elektrische Strom kann dabei in Analogie zum Wärmestrom betrachtet werden.
Beachte auch an dieser Stelle wieder die unterschiedlichen Begrifflichkeiten:
| Bezeichnung | Bedeutung |
|---|---|
| WärmeÜBERGANGswiderstand | Wärmewiderstand gegenüber Konvektion |
| + WärmeDURCHLASSwiderstand | + Wärmewiderstand gegenüber Leitung |
| = WärmeDURCHGANGswiderstand | = gesamter Wärmewiderstand durch ein Bauteil |
Der Kehrwert des Wärmedurchgangswiderstands entspricht dann schließlich dem Wärmedurchgangskoeffizient bzw. dem U-Wert:
\begin{align}
&\boxed{U = \frac{1}{R_\text{T}} =\frac{1}{R_\text{si} + \sum R + R_\text{se}}} ~~~\text{U-Wert}\\[5px]
\end{align}
Beispiel zur vereinfachten Berechnung des U-Werts im Bauwesen
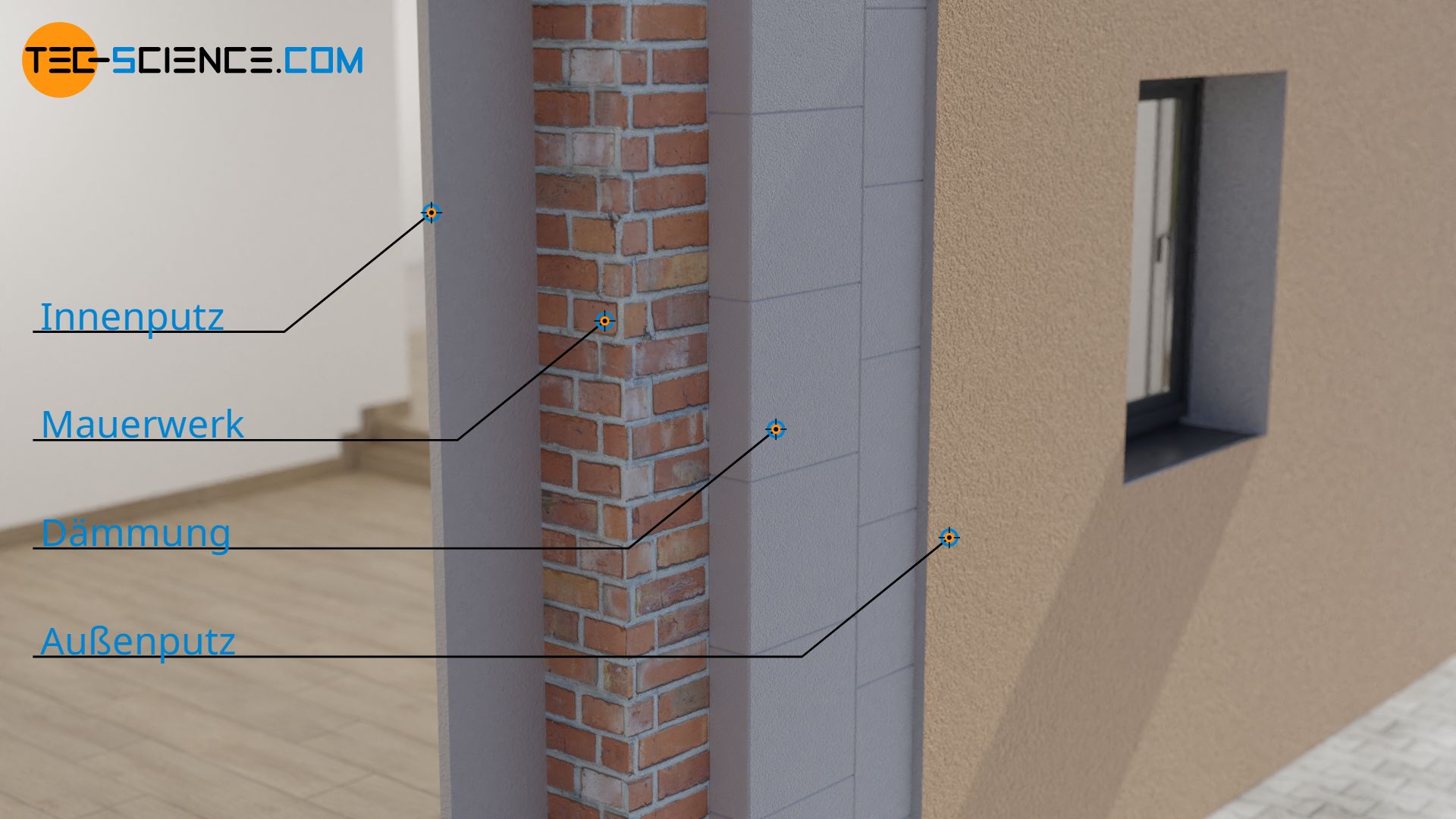
Im Folgenden soll exemplarisch der U-Wert einer Außenwand eines Gebäudes ermittelt werden. Von innen nach außen, ist die Wand wie folgt aufgebaut:
- Innenputz (2 cm)
- Mauerwerk aus Hochlochziegel (30 cm)
- Wärmedämmschicht (16 cm)
- Außenputz (2 cm)

Der Wärmeübergang zwischen Luft und Innenputz bzw. Außenputz und Luft hängt strenggenommen nicht nur von der Temperatur ab. Auch die Stärke Luftzirkulation, d.h. vor allem die Windgeschwindigkeit außerhalb des Gebäudes, beeinflusst den Wärmeübergang. Dadurch, dass es aufgrund der Dichte Unterschiede auch zur freien Konvektion kommt, beeinflusst die Richtung des Wärmestroms den Wärmeübergang. Es muss somit auch zwischen horizontal, aufwärts und abwärts gerichtetem Wärmestrom unterschieden werden.
Für eine vereinfachte Berechnung sind gemäß DIN EN 6946 folgende Bemessungswerte für die Wärmeübergangswiderstände je nach Richtung des Wärmestroms ausgewiesen:
| Wärmeübergangswiderstand in m²⋅K/W | seitwärts | aufwärts | abwärts |
|---|---|---|---|
| Rsi | 0,13 | 0,10 | 0,17 |
| Rse | 0,04 | 0,04 | 0,04 |
Die Wärmeleitfähigkeiten der angegeben Materialschichten finden sich in Tabellenbüchern wieder. Mit Hilfe der jeweiligen Schichtdicke können die Wärmedurchlasswiderstände gemäß Gleichung (\ref{a}) ermittelt werden:
| Material | Wärmeleit- fähigkeit λ in W/(m⋅K) | Schicht- dicke Δx in m | Wärmedurchlass- widerstand R in m²⋅K/W |
|---|---|---|---|
| Innenputz | 0,40 | 0,02 | 0,05 |
| Mauerwerk | 0,50 | 0,30 | 0,60 |
| Wärmedämmschicht | 0,032 | 0,16 | 5,00 |
| Außenputz | 0,25 | 0,02 | 0,08 |
Die Summe der einzelnen Wärmewiderstände ergibt den gesamten Wärmedurchgangswiderstands RT:
\begin{align}
R_\text{T}
&= R_\text{si} + \sum R + R_\text{se}\\[5px]
&= R_\text{si} + R_\text{Innenputz} + R_\text{Mauerwerk} + R_\text{Dämmung} + R_\text{Außenputz} +R_\text{se}\\[5px]
&= \left(0,13+ 0,05 + 0,60 + 5,00+ 0,08 + 0,04 \right) \tfrac{\text{m²}\cdot \text{K}}{\text{W}} \\[5px]
&= \underline{5,90 \tfrac{\text{m²}\cdot \text{K}}{\text{W}}}\\[5px]
\end{align}
Der Kehrwert dieses Wärmedurchgangswiderstandes entspricht nun schließlich dem U-Wert unserer Gebäudewand:
\begin{align}
&U = \frac{1}{R_\text{T}} =\frac{1}{5,90 \tfrac{\text{m²}\cdot \text{K}}{\text{W}}} = \underline {0,17 \tfrac{\text{W}}{\text{m²}\cdot \text{K}}} \\[5px]
\end{align}
Der U-Wert der Wand beträgt somit 0,17 (oft ohne Einheiten angegeben) und liegt damit unterhalb dem von der Energieeinsparverordnung (EnEV) vorgeschriebenem Wert von 0,24. Maßgeblich beeinflusst wird der U-Wert in diesem Fall von der Wärmedämmschicht, ohne diese der U-Wert 1,11 betragen würde. Ohne Wärmedämmung wäre der Wärmeverlust durch die Gebäudewand also rund 6,5-fach so groß.