Erfahren Sie in diesem Artikel mehr über die experimentelle Bestimmung der Wärmeleitfähigkeit von Stoffen mit Hilfe von Wasserdampf und Eis.
Wärmeleitfähigkeit
Die Wärmeleitfähigkeit ist ein Maß wie gut oder schlecht ein Material Wärme durch sich hindurch leitet. Konkret gibt die Wärmeleitfähigkeit λ den Zusammenhang zwischen einem Temperaturgefälle ΔT entlang einer Strecke Δx und dem hieraus resultierenden Wärmestrom Q* durch die Fläche A an:
\begin{align}
&\boxed{\dot Q =\lambda \cdot A \cdot \frac{\Delta T}{\Delta x}} ~~~~~\text{mit}~~~~~[\lambda]=\frac{\text{W}}{\text{m} \cdot \text{K}} ~~~~~\text{Wärmeleitfähigkeit}\\[5px]
\end{align}
Ausführlicher Informationen zu dieser Gleichung, die auch als als Fourier’sches Gesetz bekannt ist, finden Sie im Hauptartikel Wärmeleitfähigkeit. In diesem Artikel soll lediglich die experimentelle Bestimmung der Wärmeleitfähigkeit im Vordergrund stehen, die auf der oberen Gleichungen beruht:
\begin{align}
\label{a}
&\boxed{\lambda =\frac{\dot Q \cdot \Delta x}{\Delta T \cdot A}}
\end{align}
Um die Wärmeleitfähigkeit λ eines Materials mit der Dicke Δx und der Fläche A zu ermitteln, muss man diesem also eine Temperaturdifferenz ΔT aufzwingen und den hierfür benötigten Wärmestrom Q* bestimmen.
Messprinzip
Im Folgenden soll ein relativ einfaches Experiment vorgestellt werden, welches das Messprinzip der sogenannten Plattenmessverfahren verdeutlicht.
Hierzu nutzt man eine plattenförmige Probe, für dessen Material die Wärmeleitfähigkeit ermittelt werden soll. Im abgebildeten Fall, handelt es sich um eine Platte aus Metall. Diese Metallplatte hat die Dicke Δx = 10 mm und wird von der einen Seite erwärmt und von der anderen gekühlt. Die unteren Abbildungen zeigen hierzu den Versuchsaufbau.
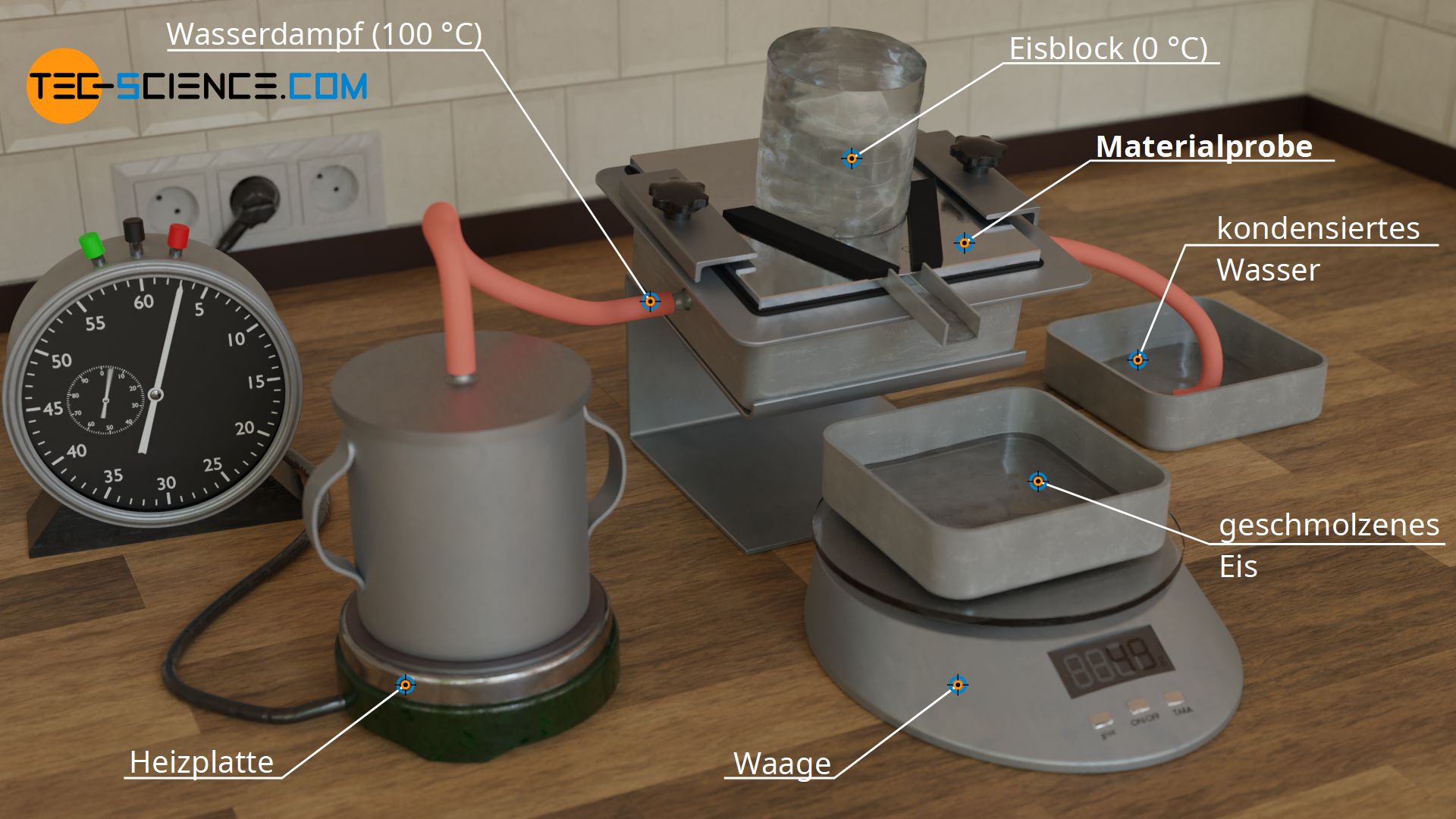

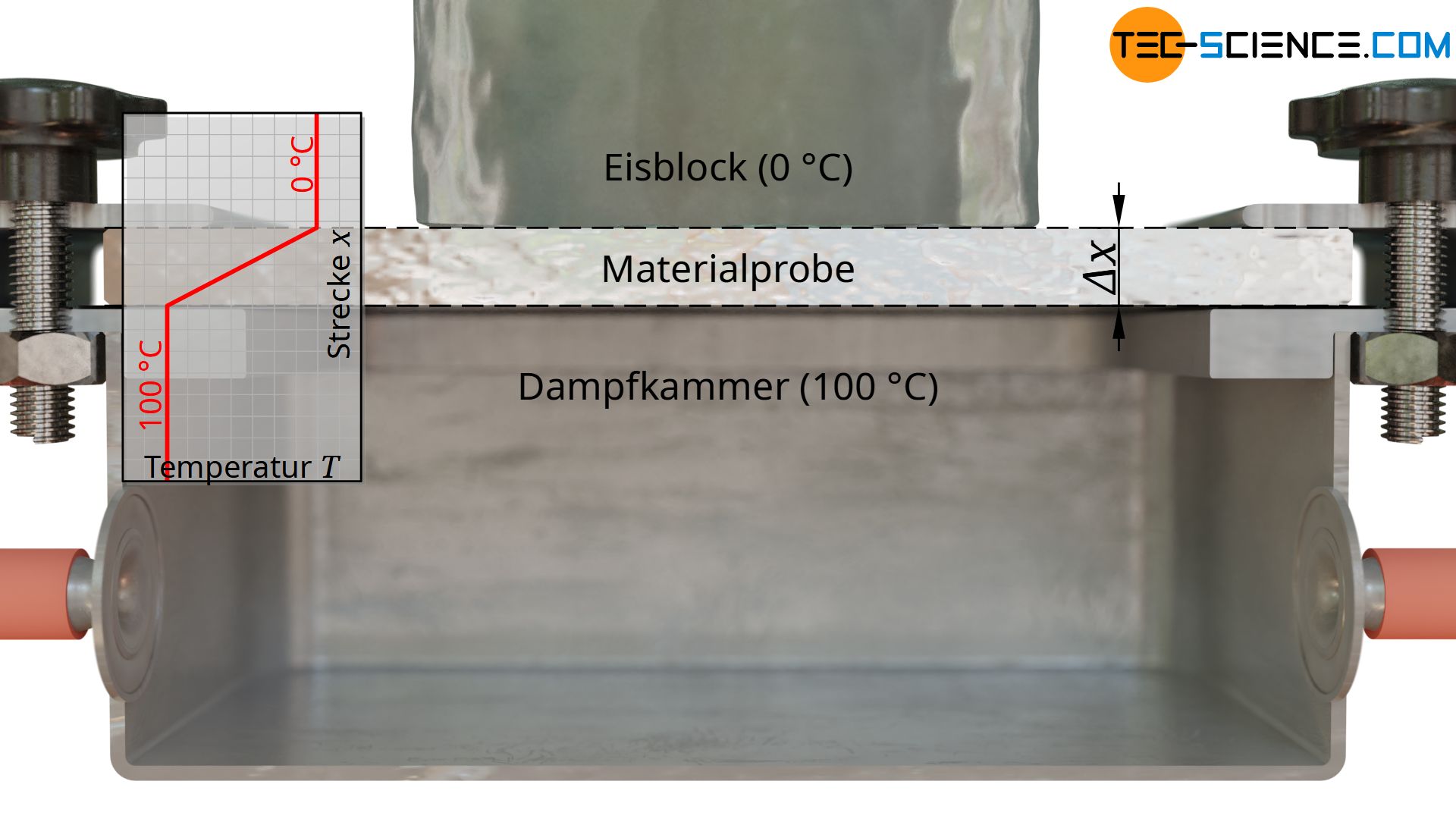
Die Erwärmung erfolgt mit heißem Wasserdampf, welcher beim Kondensieren an der Platte eine Temperatur von exakt 100 °C erzeugt. Zur Temperierung der kalten Seite nutzt man einen Eisblock, der beim Schmelzvorgang eine Temperatur von exakt 0 °C an der Platte entstehen lässt. Somit hat man über die Plattendicke hinweg einen Temperaturabfall von ΔT = 100 °C.
Der Wärmestrom bestimmt sich über die geschmolzene Wassermenge des Eisklotzes. Hierzu wird innerhalb einer bestimmten Zeit das geschmolzene Wasser aufgefangen und gewogen. Mit Hilfe der spezifischen Schmelzwärme des Eises von qs=334 kJ/kg und der innerhalb der Zeit Δt geschmolzenen Wassermenge m bestimmt sich der Wärmestrom Q* durch die Probenplatte wie folgt:
\begin{align}
&\dot Q=\frac{Q}{\Delta t} = \frac{q_s \cdot m}{\Delta t}
\end{align}
Schmilzt bspw. innerhalb von Δt = 17 s eine Eismasse von m = 50 g, so ergibt sich gemäß oberer Formel ein Wärmestrom von Q* = 982 J/s.
Die Zeitmessung und das Auffangen des geschmolzenen Wassers darf allerdings nicht sofort nach Aufsetzen des Eisklotzes begonnen werden. Zunächst muss sich ein stationärer Zustand einstellen, d.h. man muss einige Zeit warten, bis sich die Temperaturen im Material nicht mehr ändern und sich ein zeitlich konstantes Temperaturgefälle eingestellt hat. Die Wärmeleitfähigkeit bezieht sich grundsätzlich nur auf solche stationäre Zustände bei denen der Wärmestrom zeitlich konstant ist. Das Verhalten der Temperaturen während sich die Probe noch erwärmt wird hingegen durch die sogenannte Temperaturleitfähigkeit beschrieben (obwohl beide Größen in Zusammenhang stehen). Diese Temperaturausbreitung ist ein sogenannter instationärer Zustand bei dem der Wärmestrom zeitlich nicht konstant ist. Der stationäre Zustand ist in der unteren Simulation nach etwa 10 Sekunden erreicht.
Als weitere Größe zur Berechnung der Wärmeleitfähigkeit benötigt man noch die Fläche A, durch die der Wärmestrom tritt. Dies entspricht der Auflagefläche des Eisklotzes. Es darf an dieser Stelle also nicht die gesamte Plattenfläche zugrunde gelegt werden, denn der für das Schmelzen des Eisklotzes relevante Wärmestrom tritt schließlich nur durch den Bereich wo sich der Eisblock befindet. Die als eindimensional betrachteten Wärmeströme außerhalb dieses Bereichs gehen auf die Luft über und werden nicht über das Schmelzen berücksichtigt (später mehr dazu).
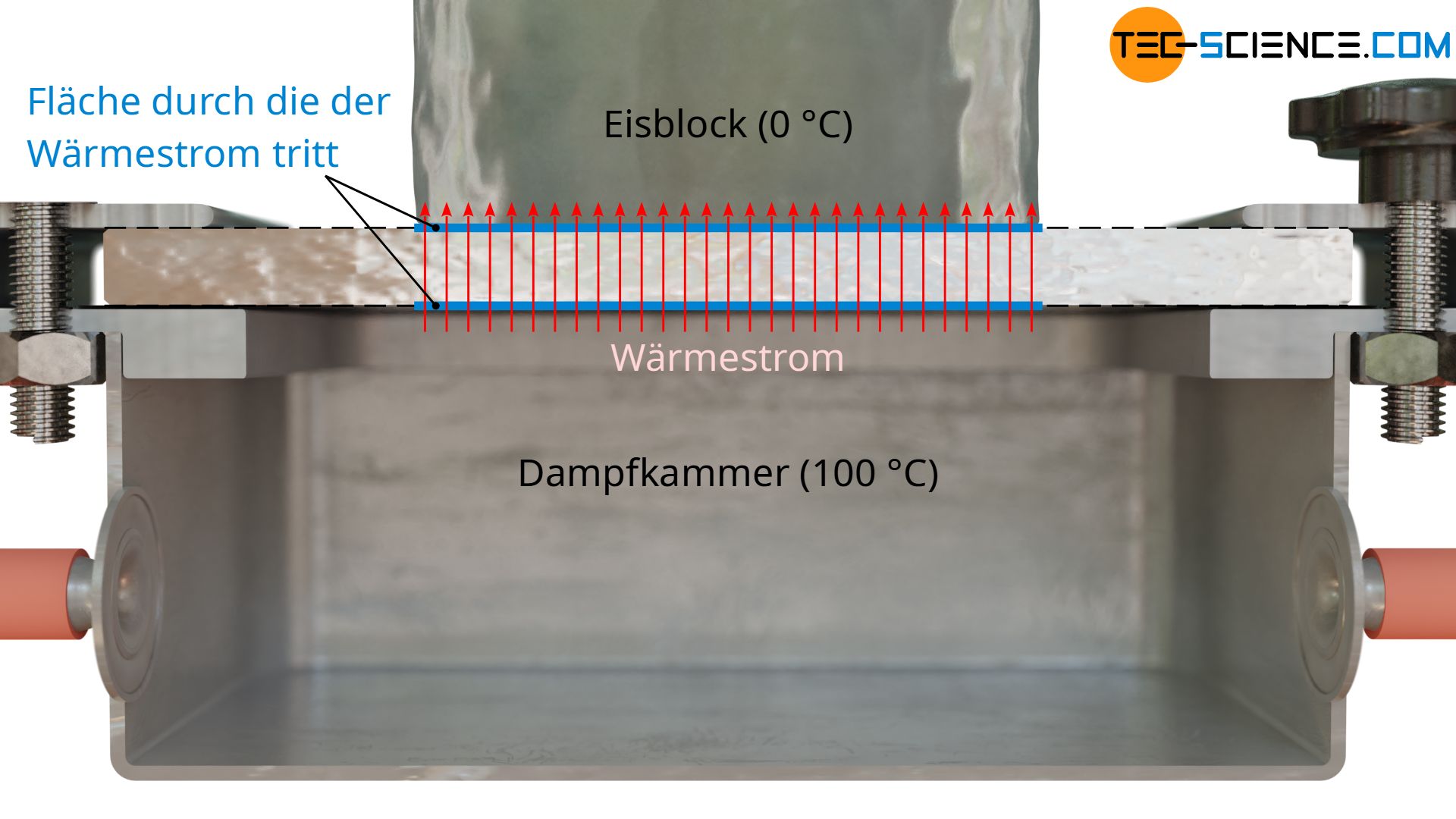
Mit einem Durchmesser des Eisklotzes von bspw. 5 cm, ergibt sich auf diese Weise eine Wärmestromfläche von A = 0,00196 m².
Nachdem nun alle relevanten Größen ermittelt sind (Probendicke, Temperaturgefälle, Fläche und Wärmestrom), kann die Wärmeleitfähigkeit der verwendeten Materialprobe schließlich nach Gleichung (\ref{a}) bestimmt werden. Mit den beispielhaft gegeben Werten erhält man somit eine Wärmeleitfähigkeit von λ= 50 W/(m⋅K).
\begin{align}
&\lambda =\frac{\dot Q \cdot \Delta x}{\Delta T \cdot A} = \frac{982 \frac{\text{J}}{\text{s}} \cdot 0,01 \text{ m}}{100 \text{ K} \cdot 0,00196 \text{ m²}} = 50 \frac{\text{W}}{\text{m}\cdot \text{K}}
\end{align}
Nachteile des Verfahrens
Keine reine Wärmeleitung
Zu beachten ist bei der experimentellen Bestimmung der Wärmeleifähigkeit grundsätzlich, dass sich die Wärmeleitfähigkeit definitionsgemäß nur auf die Wärmeübertragung durch Wärmeleitung bezieht, nicht auf Konvektion oder Wärmestrahlung! Bei Materialien, die Gase enthalten (z.B. Porenbeton), lässt sich in der Realität eine Wärmeströmung in den Gasporen aber nicht verhindern. Ebenfalls kann Wärmestrahlung unter Umständen das Material durchdringen. Insofern werden diese Wärmeübertragungsmechanismen bei der praktischen Bestimmung der Wärmeleitfähigkeit (ungewollter Weise) mitberücksichtigt. Der Einfluss der Wärmestrahlung auf das Ergebnis kann jedoch minimiert werden, wenn die Probe möglichst dick gewählt wird, sodass Wärmestrahlung die Probe kaum durchdringt. Dies birgt aber einen anderen Nachteil, wie sich gleich zeigt.
Kein eindimensionaler Wärmestrom
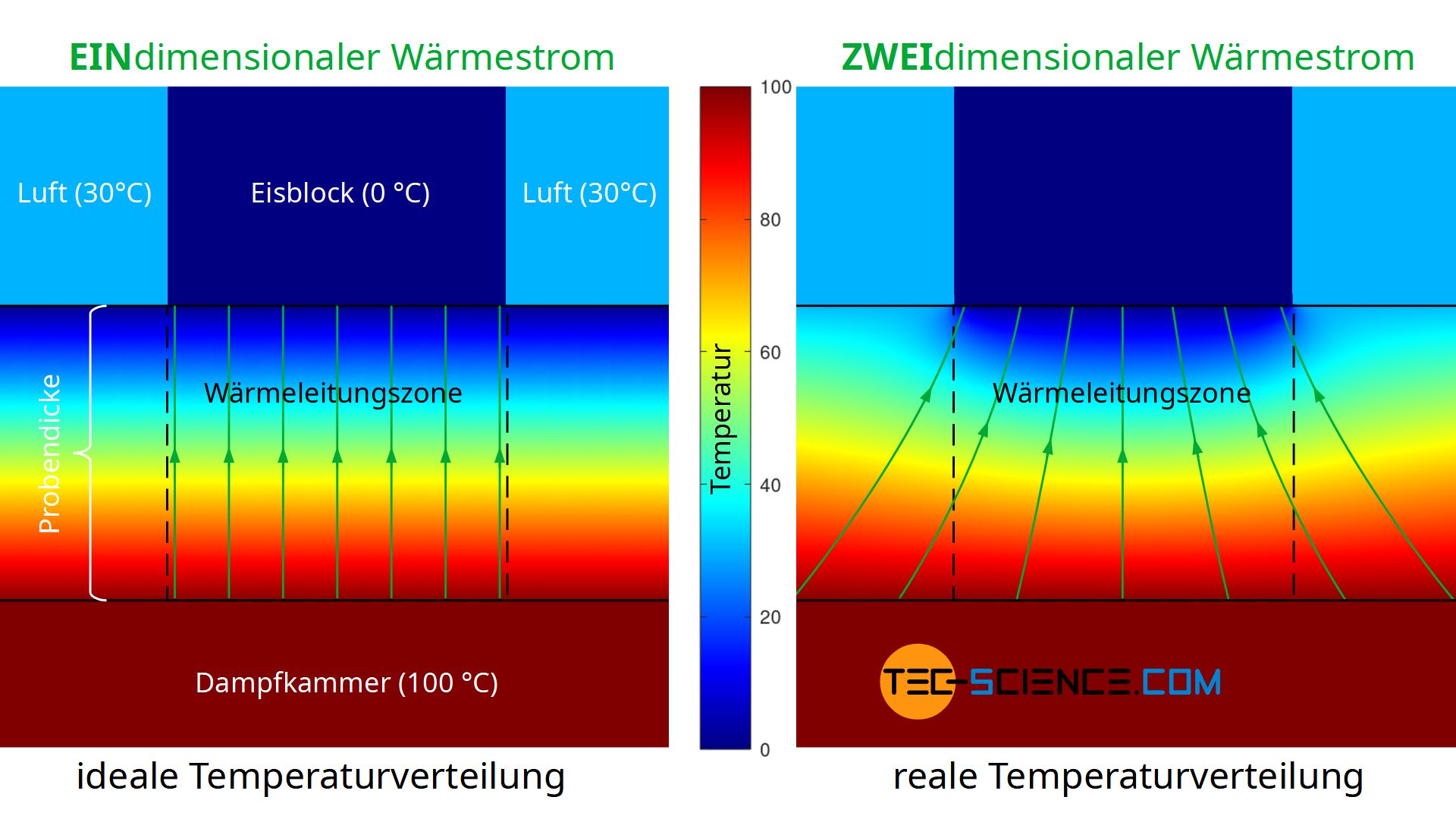
Ein weiterer Nachteil des beschriebenen Versuchs ist, dass es sich während der Durchführung strenggenommen nicht um einen eindimensionalen Wärmefluss durch das Material handelt, wie es das Fouriersche Gesetz im makroskopischen Maßstab aber voraussetzt. Wärme strömt sozusagen nicht geradlinig durch die Probe, sondern auch seitlich in die Wärmeleitungszone (Messzone) ein. Dem Wärmestrom liegt an der heißen Unterseite der Probe also eine größere effektive „Wärmefläche“ zugrunde als an der Oberseite wo sich der Eisblock befindet (siehe untere Abbildung). Dieser Effekt des zweidimensionalen Wärmestroms hat umso weniger Einfluss auf das Ergebnis, je dünner das Probenmaterial im Vergleich zur Fläche ist. Gleichzeitig steigt damit aber der Einfluss der Wärmestrahlung, da diese dünnen Proben stärker durchdringt als dicke.
Die untere Abbildung zeigt die vereinfachte Simulation der Temperaturverteilung und damit des Wärmestroms. Modelliert wurde mit einer konstanten Temperatur an der Unterseite der Platte und konstanten Temperaturen an der Oberseite. Die Temperaturen zum Eisblock hin bzw. zur Umgebung hin wurden als scharf begrenz angenommen. Die Simulation zeigt die Ausbildung eines zweidimensionalen Wärmestroms, wie sie auch in der Realität auftritt. Im Vergleich hierzu ist in der Abbildung ein eindimensionaler Wärmestrom gezeigt, wie eigentlich vom Fourier’schen Gesetz gefordert.
Temperaturabhängigkeit der Wärmeleitfähigkeit
Ein weiterer Nachteil des beschriebenen Verfahrens liegt in der Einstellung der Temperaturen. Die Wärmeleitfähigkeit ist strenggenommen keine Stoffkonstante, sondern von der Temperatur abhängig. Man misst mit dem Versuch also lediglich eine mittlere Wärmeleitfähigkeit im Bereich zwischen 0 °C und 100 °C. Eine genauere Untersuchung der Wärmeleitfähigkeit in Abhängigkeit der Temperatur, ist mit dem bisherigen experimentellen Aufbau nicht möglich. Die Temperaturen sind bei der Verwendung von Wasserdampf und Eis fest vorgegeben und können nicht geändert werden.
Erzeugung von eindimensionalen Wärmeströmen
Damit die Bestimmung der Wärmeleitfähigkeit nach Gleichung (\ref{a}) überhaupt Gültigkeit hat, muss grundsätzlich ein eindimensionaler Wärmestrom gewährleistet sein. Dies kann man bspw. dadurch erreichen, dass man die Probe auch außerhalb der eigentlichen Wärmeleitungszone temperiert. Die Temperatur ist dabei identisch mit der Temperatur der gekühlten Seite. Man müsste also die Oberseite der Platte um den Eisblock herum ebenfalls mit einer Temperatur von 0 °C temperieren.
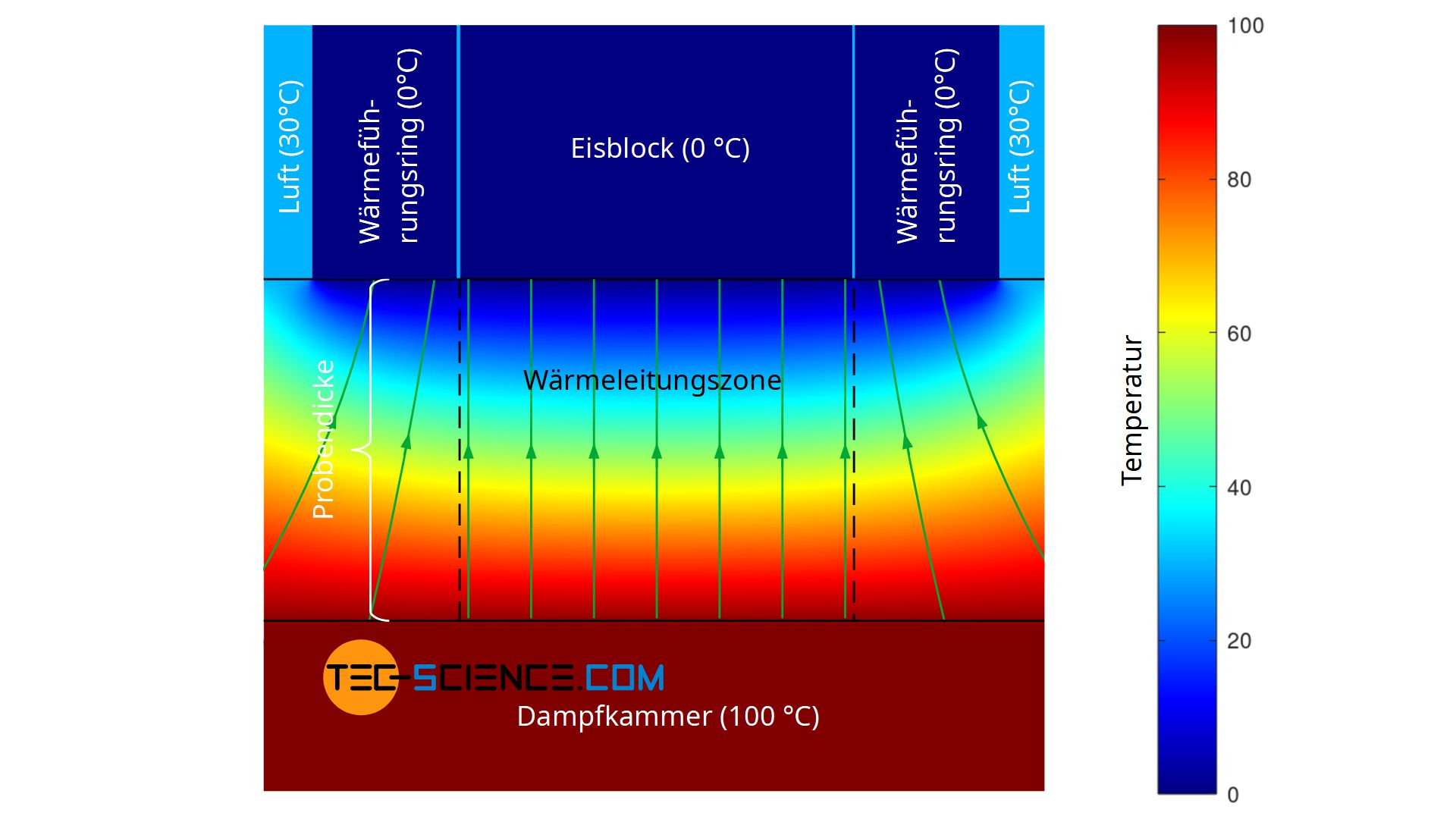
Ein Ring aus Eis kann dabei natürlich nicht verwendet werden, denn dieser würde ebenfalls schmelzen und somit mit in die Berechnung der Wärmeleitfähigkeit einfließen. Man hätte damit lediglich den ursprünglichen Eisblock vergrößert. Die zweidimensionalen Wärmeströmen an den Rändern der Wärmeleitungszone würden nach wie vor bestehen bleiben. Man könnte allerdings um den Eisblock einen Metallring anbringen, der mit Kühlflüssigkeit auf 0 °C temperiert wird. Auf diese Weise verlagert sich der zweidimensionale Wärmestrom in die Nähe des Metallrings und sorgen innerhalb der Wärmeleitungszone für einen nahezu eindimensionalen Wärmestrom.
Ein solch temperierter Ring, der den Wärmestrom in eindimensionaler Richtung führt, wird auch als Wärmefühungsring oder kurz als Wärmeführung bezeichnet (engl.: guard ring). Das Prinzip der Wärmeführung macht man sich bspw. beim sogenannten Guarded-Hot-Plate Verfahren (GHP) zunutze, das im verlinkten Artikel näher beschrieben ist.