Als spezifische Schmelzwärme (Schmelzenthalpie) bezeichnet man die zum Schmelzen einer Flüssigkeit notwendige Wärmeenergie pro Kilogramm des Stoffes!
Schmelzprozess
Wird ein Feststoff mehr und mehr erwärmt, dann wird irgendwann der Schmelzpunkt erreicht. In diesem Punkt ändert sich der Aggregatzustand und der Feststoff beginnt schließlich zu schmelzen. Während des Schmelzens beobachtet man für Reinstoffe keine weitere Temperaturzunahme, trotzt der weiterhin zugeführten Wärmeenergie. Die Energie kommt während des Schmelzens offensichtlich nicht mehr der Erhöhung der Schwingungsenergie der Teilchen zugute, welche sonst eine Temperaturzunahme bedeuten würde (siehe hierzu auch Artikel Temperatur und Teilchenbewegung).

Die zugeführte Energie führt beim Schmelzen zur Erhöhung der Inneren Energie in Form von geänderten Bindungsenergien zwischen festem und flüssigem Zustand. Die intermolekularen Bindungen im festen Zustand werden durch die zugeführte Wärmeenergie sozusagen aufgebrochen und erlauben somit den Übergang in den flüssigen Zustand. Im flüssigen Zustand sind die Moleküle aufgrund der geringeren Bindungskräfte weniger stark aneinander gebunden. Auf diese Weise sind die Moleküle nicht mehr an einen bestimmten Ort gebunden und können sich durchmischen. Deshalb haben Flüssigkeit auch keine feste Form.

Während des Schmelzens muss Energie für das Aufbrechen der intermolekularen Bindungen aufgebracht werden. Bei Reinstoffen bleibt die Temperatur dabei solange konstant bis der Schmelzvorgang vollständig abgeschlossen ist!
Ausführlichere Informationen hierzu finden sich auch im Artikel Warum bleibt die Temperatur bei einer Änderung des Aggregatzustandes konstant?
Es stellt sich die Frage, wie viel Wärme zugeführt werden muss, um eine bestimmte Menge eines Feststoffs vollständig zu schmelzen. Die hierfür erforderliche Wärme wird auch als Schmelzwärme oder Schmelzenthalpie bezeichnet. In dieser Schmelzwärme ist die für die Erwärmung des Stoffes auf Schmelztemperatur erforderliche Wärmemenge nicht berücksichtigt. Die Schmelzwärme beinhaltet somit nur jene zuzuführende Wärmeenergie während des Schmelzens, wenn der Festkörper bereits auf Schmelztemperatur erwärmt wurde.
Als Schmelzwärme (Schmelzenthalpie) bezeichnet man die am Schmelzpunkt eines Feststoffes zuzuführende Wärmeenergie, um eine bestimmte Menge des Stoffes vollständig zu schmelzen!
Da sich die zugeführte Schmelzwärme während des Schmelzens nicht direkt in einer Temperaturerhöhung bemerkbar macht, aber dennoch in Form von innerer Energie im geschmolzenen Stoff wiederzufinden ist, bezeichnet man die Schmelzwärme auch als latente Wärme. Der Begriff „latent“ kommt aus dem Lateinischen und bedeutet „verborgen sein“ oder „nicht direkt in Erscheinung tretend“.
Experimentelle Bestimmung der Schmelzwärme
Versuchsaufbau
Am Beispiel von gefrorenem Wasser (Eis) soll im Folgenden exemplarisch die Schmelzwärme experimentell ermittelt werden, die für das Schmelzen einer bestimmten Menge an Eis nötig ist. Hierzu wird gefrorenes Eis aus dem Kühlfach in ein elektrisch beheiztes Gefäß gegeben. Das Gefäß sollte bestmöglich wärmegedämmt sein, damit der Schmelzvorgang ausschließlich auf die Heizleistung zurückzuführen ist (und hierdurch ermittelt werden kann) und nicht auf die Wärmezufuhr der wärmeren Umgebung, die normalerweise zu einem Schmelzen des Eises führen würde. Durch ein kleines Loch am Boden des Gefäßes kann das geschmolzene Wasser aufgefangen werden und somit zeitliche Schmelzen des Eises anhand einer Waage beobachtet werden.

Die zugeführte Schmelzwärme kann über die elektrische Leistung der Heizwendel ermittelt werden, die vollständig in Wärmeleistung umgesetzt wird. Die bei einer Leistung P zugeführte Wärmeenergie QS (= Schmelzwärme) ergibt sich über die Betriebsdauer t der Heizung:
\begin{align}
\label{q}
Q_\text{S} = P \cdot t \\[5px]
\end{align}
Versuchsdurchführung
Zunächst wird das Wasser durch die Heizung auf Schmelztemperatur erwärmt. Beginnt das Wasser zu schmelzen, so kann nun zu einem beliebigen Zeitpunkt das Experiment gestartet werden. Hierzu wird die Waage auf null zurückgesetzt und die Zeitmessung gestartet. Das Eis schmilzt allmählich und die geschmolzene Masse wird an der Waage angezeigt. In regemäßigen Zeitabständen wird der angezeigte Wert der Waage erfasst. Zu jedem Zeitpunkt t kann mit Hilfe von Formel (\ref{q}) die bis dahin zugeführte Schmelzwärme QS ermittelt werden. Auf diese Weise erhalt man eine Aussage welche Wärmemenge zum Schmelzen welcher Masse mS führte.
Versuchsauswertung
Stellt man die geschmolzene Masse in Abhängigkeit der Schmelzwärme dar (Schmelzkurve), dann zeigt sich ein proportionaler Zusammenhang. Dies bedeutet anschaulich, dass beispielsweise das Schmelzen einer doppelten Menge an Eis auch die doppelte Schmelzwärme erfordert. So zeigt sich durch die Versuchsauswertung, dass für das Schmelzen einer Wassermasse von 100 g offensichtlich eine Schmelzwärme von rund 35 kJ zuzuführen ist. Bei einer zugeführten Wärmeenergie von etwa 70 KJ ist dann schließlich auch eine doppelte Menge Eis von 200 g geschmolzen.
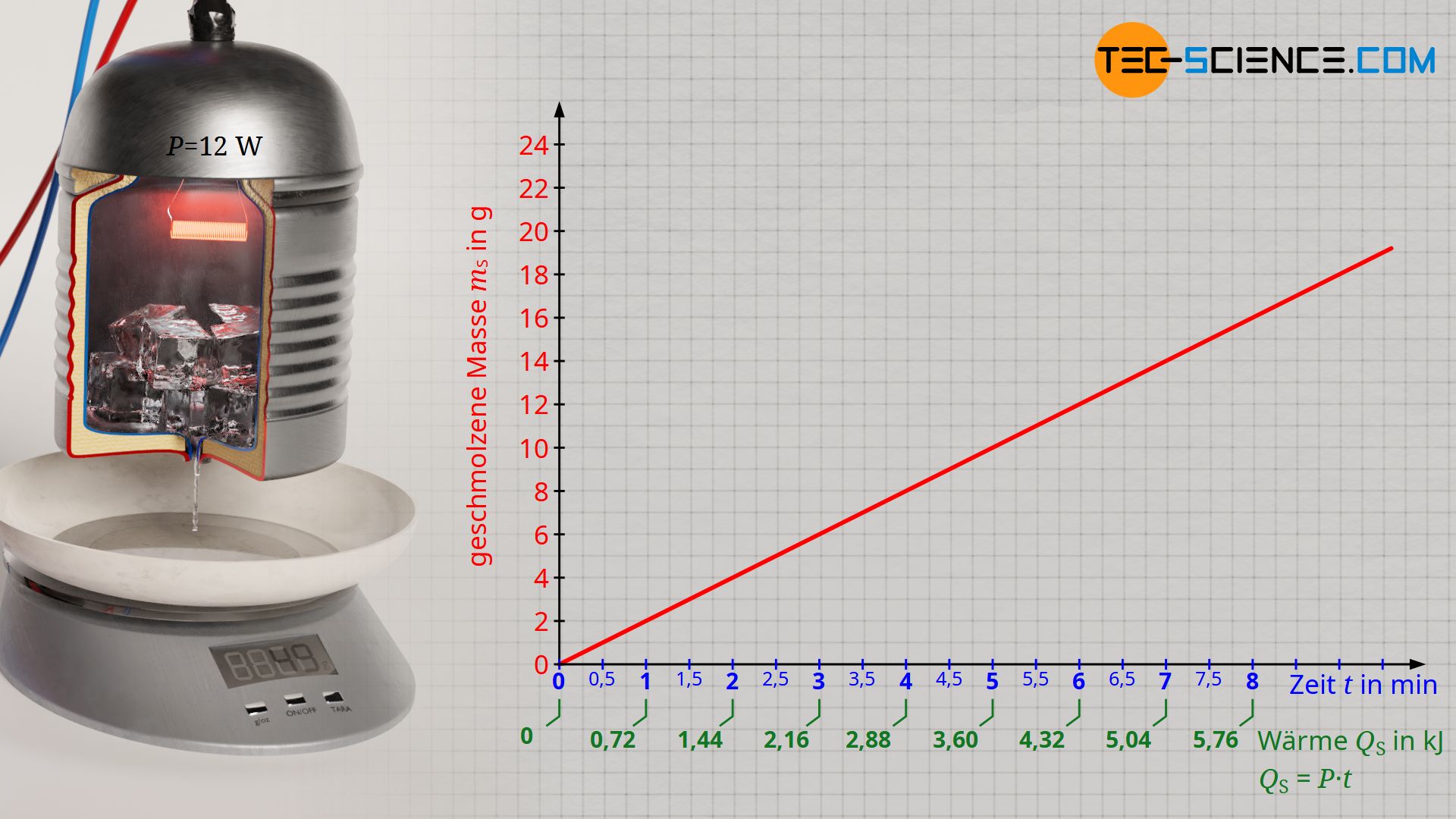
Vor allem im Hinblick auf die Vergleichbarkeit der Schmelzwärmen verschiedener Stoffe macht es deshalb Sinn, die Schmelzwärmen QS immer auf eine einheitliche zu schmelzende Menge mS zu beziehen (z.B. 1 Kilogramm). Dieses konstante Verhältnis zwischen von Schmelzwärme und zu schmelzender Masse wird als spezifische Schmelzwärme oder als spezifische Schmelzenthalpie qS bezeichnet:
\begin{align}
&\boxed{q_\text{S} = \frac{Q_\text{S}}{m_\text{S}}}~~~[q_\text{S}]=\frac{\text{J}}{\text{kg}}~~~~~\text{spezifische Schmelzwärme} \\[5px]
\end{align}
Aus dem Versuch erhält man für Wasser schließlich eine spezifische Schmelzwärme von rund qS=350 kJ/kg. Anschaulich bedeutet dies, dass für das Schmelzen einer Eismasse von 1 Kilogramm eine Wärmeenergie von 350 kJ nötig ist. Bei der experimentell ermittelten Schmelzwärme des Eises anhand des beschrieben Versuchsaufbaus muss jedoch beachtet werden, dass die abgegebene Wärme der Heizung nicht vollständig dem Schmelzen des Eises zugutekommt. Die Wärme wird teilweise auch für die Erwärmung des Gefäßes genutzt und geht somit als Wärmeverlust auf die Umgebung über. Für das reine Schmelzen des Eises ist folglich eine geringere Wärmemenge erforderlich als mit Formel (\ref{q}) zugrunde gelegt worden ist. Der Literaturwert für die spezifische Schmelzwärme von Wasser liegt deshalb mit qS = 334 kJ/kg etwas niedriger.

Als spezifische Schmelzwärme bezeichnet man die pro Kilogramm eines zu schmelzenden Feststoffes zuzuführende Schmelzwärme!
Im Falle von Eis ist die zum Schmelzen zuzuführende latente Wärme mit 334 kJ pro Kilogramm ungefähr so groß, wie jene Wärmemenge, die man bräuchte um das Wasser ausgehend von Raumtemperatur zum Kochen zu bringen. Es muss also sehr viel Wärme für das Schmelzen aufgewendet werden. Dies erklärt zum Beispiel warum Eiswürfel sich hervorragend zum Kühlen von Getränken eignen.
Schlussfolgerung
Die spezifische Schmelzwärme qS beschreibt den gesuchten Zusammenhang zwischen der zu schmelzenden Masse mS und der hierfür zuzuführenden Schmelzwärme QS:
\begin{align}
&\boxed{Q_\text{S} = q_\text{S} \cdot m_\text{S}} ~~~\text{Schmelzwärme} \\[5px]
\end{align}
Spezifische Schmelzwärme ausgewählter Flüssigkeiten
Führt man den oben beschriebenen Versuch anstelle mit gefrorenem Wasser mit anderen Feststoffen durch (z.B. Metalle, die geschmolzen werden), dann zeigt sich, dass die Stoffe unterschiedlich schnell schmelzen. Demzufolge ist mehr oder weniger Wärmeenergie erforderlich, um eine bestimmte Masse des jeweiligen Stoffes zu schmelzen. Die spezifische Schmelzwärme ist also stoffabhängig.
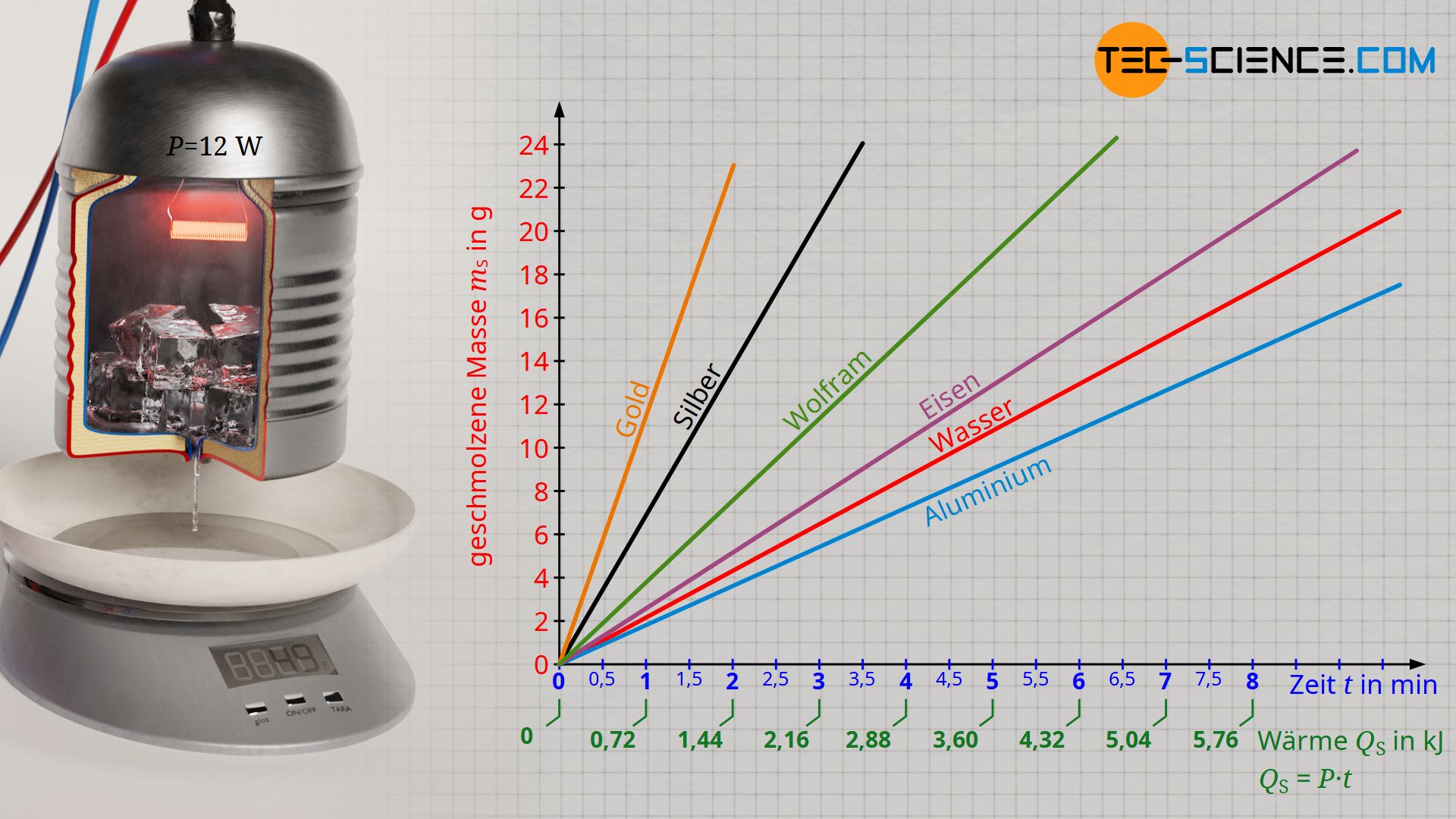
Je größer die spezifische Schmelzwärme eines Stoffes, desto mehr Wärme ist nötig, um eine bestimmte Masse zu schmelzen. Stoffe mit großen spezifischen Schmelzwärmen schmelzen also bei Wärmezufuhr nicht so schnell. Die Schmelzkurven im Diagramm verlaufen entsprechend flacher. In der unteren Tabelle sind die spezifischen Schmelzwärmen ausgewählter Stoffe angegeben.
| Stoff | Schmelztemperatur in °C | Spezifische Schmelzwärme in kJ/kg |
|---|---|---|
| Aluminium | 660 | 398 |
| Blei | 328 | 25 |
| Eisen | 1538 | 268 |
| Quecksilber | -39 | 12 |
| Silber | 962 | 105 |
| Wasser | 0 | 334 |
| Wolfram | 3422 | 191 |
| Zinn | 232 | 59 |
| Gold | 1064 | 63 |
Anmerkung: Die relativ hohe spezifische Schmelzwärme von Aluminium ist unter anderem ein Grund, weshalb die Herstellung von Aluminium, insbesondere das Einschmelzen, sehr energieintensiv und damit teuer ist!