Das Hagen-Poiseuille-Gesetz beschreibt das parabelförmige Geschwindigkeitsprofil von reibungsbehafteten, laminaren Rohrströmungen von inkompressiblen, newtonschen Fluiden.
Antrieb und Widerstand für Strömungsprozesse
Die Beschreibung von Rohrströmungen ist in vielen Fällen in der Natur und Technik von großer Bedeutung. In der chemischen Industrie hat man es bspw. oft mit Flüssigkeiten zu tun, die durch Rohre gefördert werden. Gerade wenn es um das korrekte Mischen von Reaktionspartnern geht, spielt der zugeführte Massenstrom eine große Rolle. Dieser anhand des erzeugten Förderdrucks der Pumpe und dem Rohrdurchmesser zu bestimmen, ist von zentraler Bedeutung für die Reaktionsführung.
Ursache für Rohrströmungen sind grundsätzlich Druckunterschiede, die das Fluid von Stellen höheren Drucks („Rohranfang“) zu Stellen mit niedrigeren Drucks („Rohrende“) drücken. In Strömungsrichtung bildet sich entlang des Rohres somit ein permanent abnehmender Druck aus. Je stärker dieser Druckunterschied auf einer bestimmten Länge ist, desto schneller strömt das Fluid durch das Rohr und umso größer ist der Massenstrom. Der Antrieb für eine Rohrströmung ist also ein Druckgradient dp/dx, d.h. der Druckunterschied pro Längeneinheit.
Antrieb für Strömungsprozesse in Rohren sind Druckgradienten!
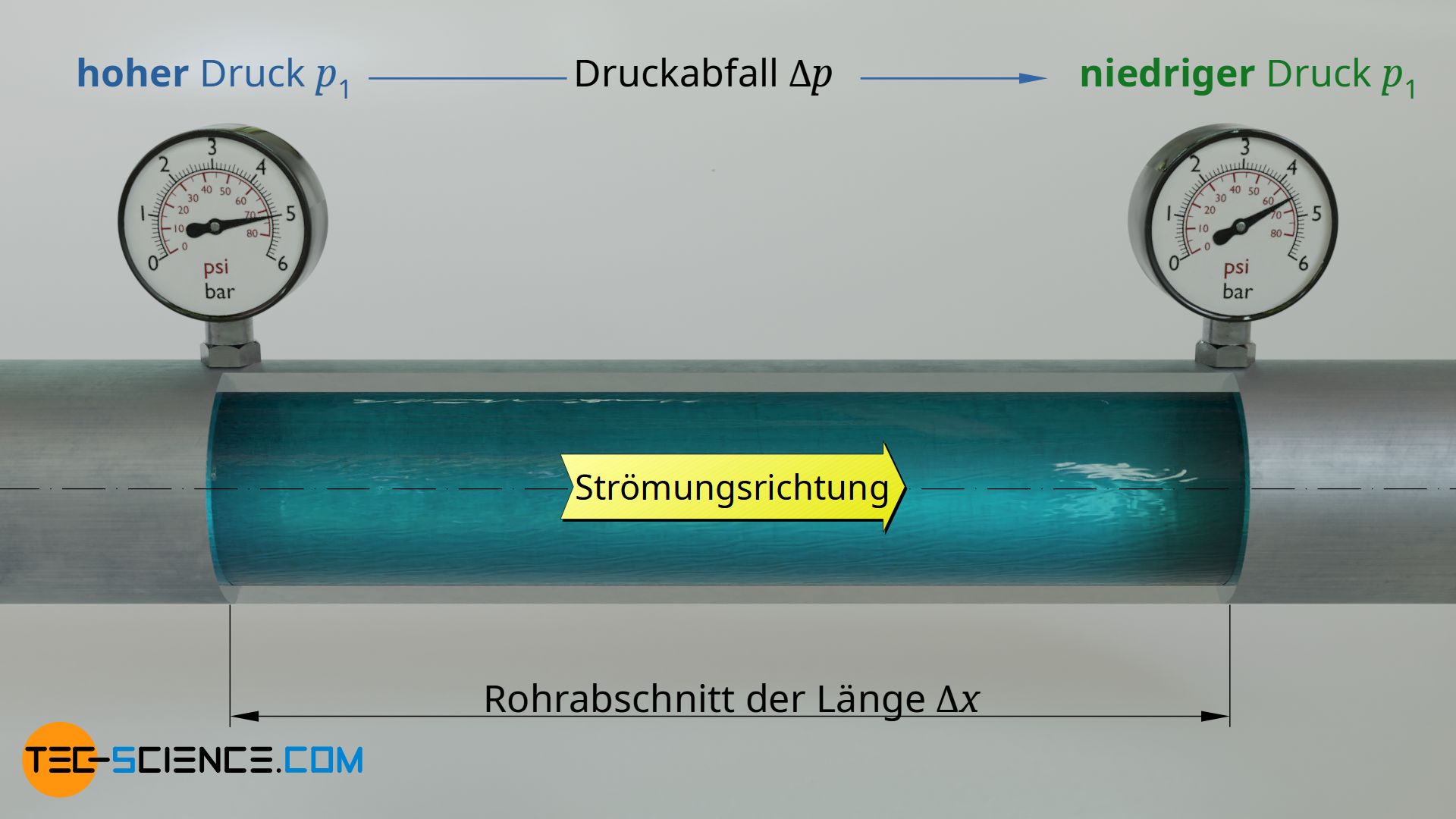
Diesem Antrieb wirken Reibungskräfte des Fluids entgegen, die sowohl zwischen Fluid und Rohr als auch innerhalb der strömenden Fluidschichten herrschen. Sie kommen durch die Viskosität des Fluids zustande.
Widerstände für Strömungsprozesse kommen durch die Viskosität des Fluids zustande!
Anhand beider Kräfte, Druckkräfte als Antrieb und Reibungskräfte als Widerstand, lassen sich laminare Rohrströmungen mathematisch beschreiben. Im Folgenden soll sowohl das Geschwindigkeitsprofil als auch der Volumenstrom einer solchen reibungsbehafteten Rohrströmung hergeleitet werden.
Herleitung des Gesetzes von Hagen-Poiseuille
Wirkende Druckkraft auf ein Volumenelement
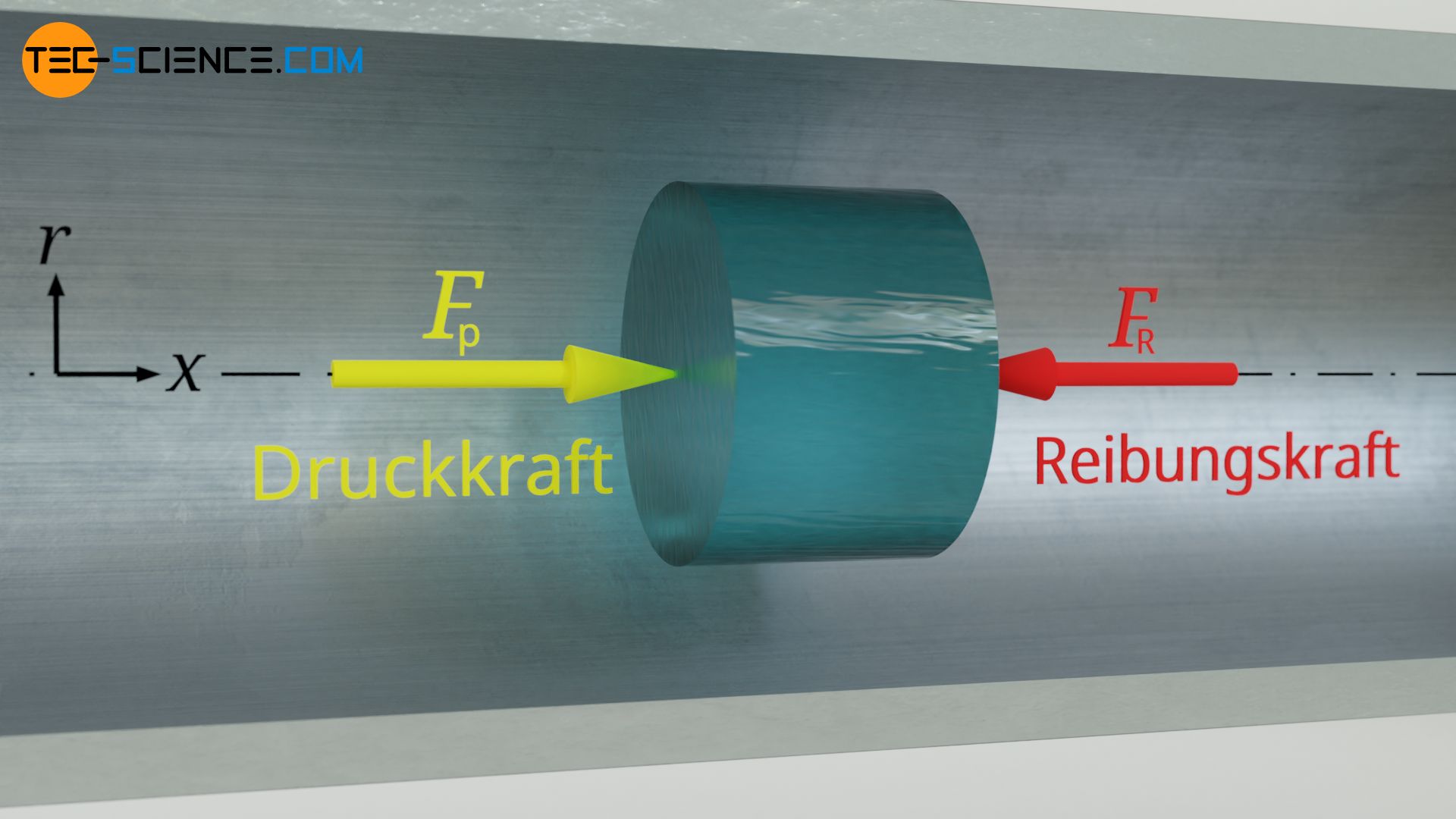
Betrachtet wird ein zylindrisches Fluidelement mit dem Radius r. Auf die Stirnflächen dieses Volumenelementes wirken Druckkräfte, die über den gesamten Rohrquerschnitt als konstant betrachtet werden (also keine Funktion von r sind). Diese Druckkräfte ergeben sich aus den Drücken im Fluid, die an den Stirnflächen des Volumenelements wirksam sind. An der Stelle x1 wirke der Druck p und an der Stelle x2 ein um dp<0 geringerer Druck. Für die wirkenden Druckkräfte auf das Volumenelement gilt folglich:
\begin{align}
&F_{\text{p}_1} = p \cdot \pi r^2 \\[5px]
&F_{\text{p}_2} = \left(p+\text{d} p\right) \cdot \pi r^2 \\[5px]
\end{align}

Die effektiv wirkende Kraft Fp auf das Volumenelement, mit der die Drücke versuchen das Fluid in Bewegung zu setzen, ergibt sich folglich aus der Differenz beider Kräfte:
\begin{align}
\require{cancel}
& F_\text{p}=F_{\text{p}_1} – F_{\text{p}_2} \\[5px]
& F_\text{p} = p \cdot \pi r^2 – \left(p+\text{d} p\right) \cdot \pi r^2 \\[5px]
& F_\text{p} = \cancel{p \cdot \pi \cdot r^2 } – \cancel{p \cdot \pi \cdot r^2 }- \text{d} p \cdot \pi r^2 \\[5px]
\label{fp}
&\boxed{ F_\text{p} = -\pi r^2 \cdot \text{d} p} \\[5px]
\end{align}
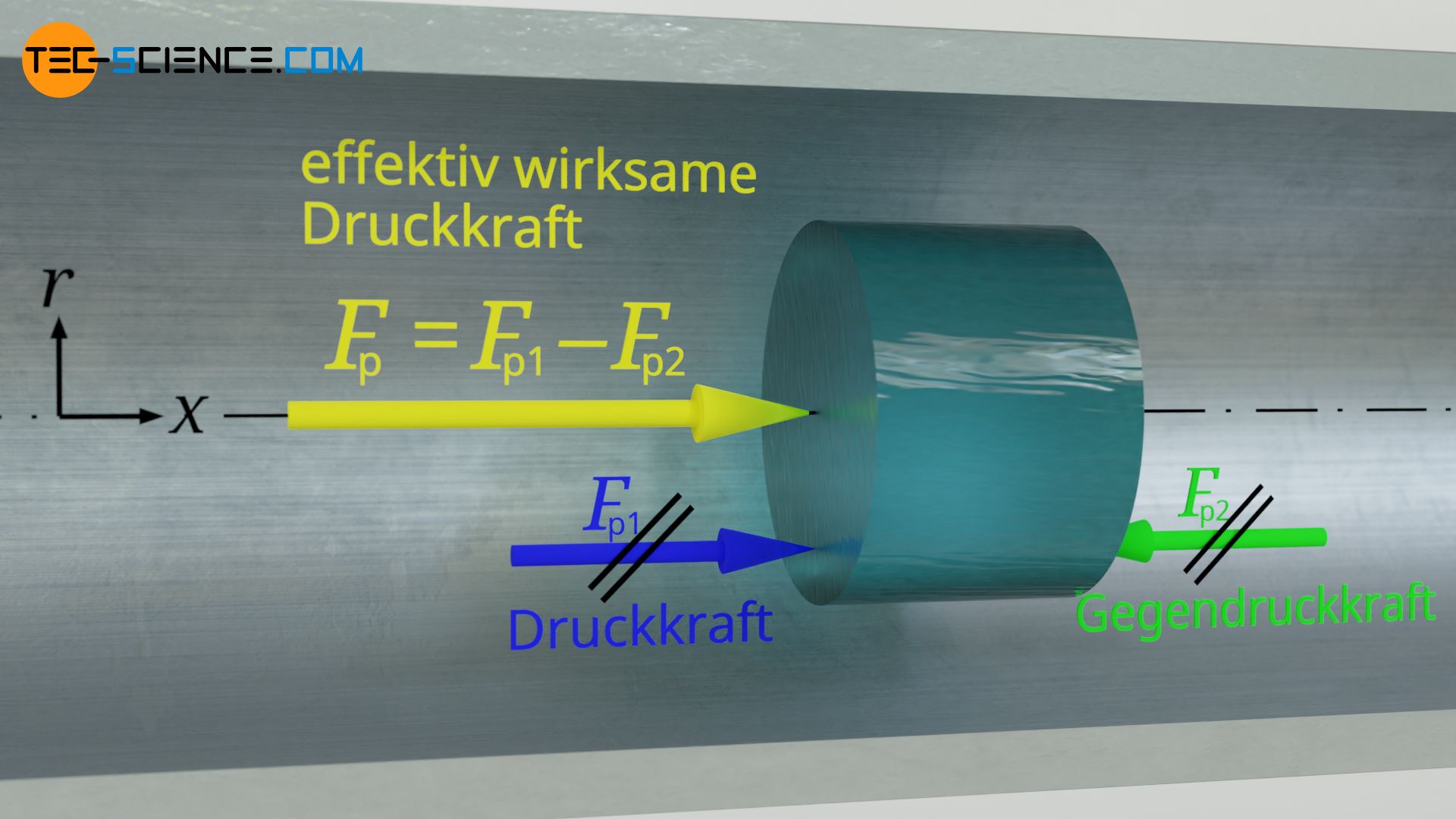
Die antreibende Kraft der Strömung ist somit nur auf den Druckunterschied und nicht auf die absolut wirkenden Drücke zurückzuführen! Beachte, dass bei einer Verringerung des Drucks entlang der positiven axialen Richtung, die Druckänderung dp negativ ist, und die effektive Kraft somit entlang der positiven axialen Richtung wirkt.
Wirkende Reibungskraft auf ein Volumenelement (Viskosität)
Grundsätzlich ist die Strömungsgeschwindigkeit im Rohr nicht über die gesamte Querschnittsfläche konstant. Das Fluid reibt an der Rohrwand, weshalb die Geschwindigkeit im Randbereich geringer ist als in der Mitte des Rohres. Am Rand haftet das Fluid aufgrund der Adhäsionskräfte sogar regelrecht an der Wand. Dies wird auch als Haftbedingung bezeichnet. Aber auch untereinander reiben die einzelnen Fluidschichten aufgrund der Viskosität des Fluids aneinander. Dies führt zur Ausbildung eines bestimmten Geschwindigkeitsprofils, dessen Verlauf noch zu bestimmen sein wird. Festzuhalten bleibt aber, dass die Strömungsgeschwindigkeit ist in der Mitte des Rohres maximal ist und dann bis zur Wand hin auf Null abfällt.
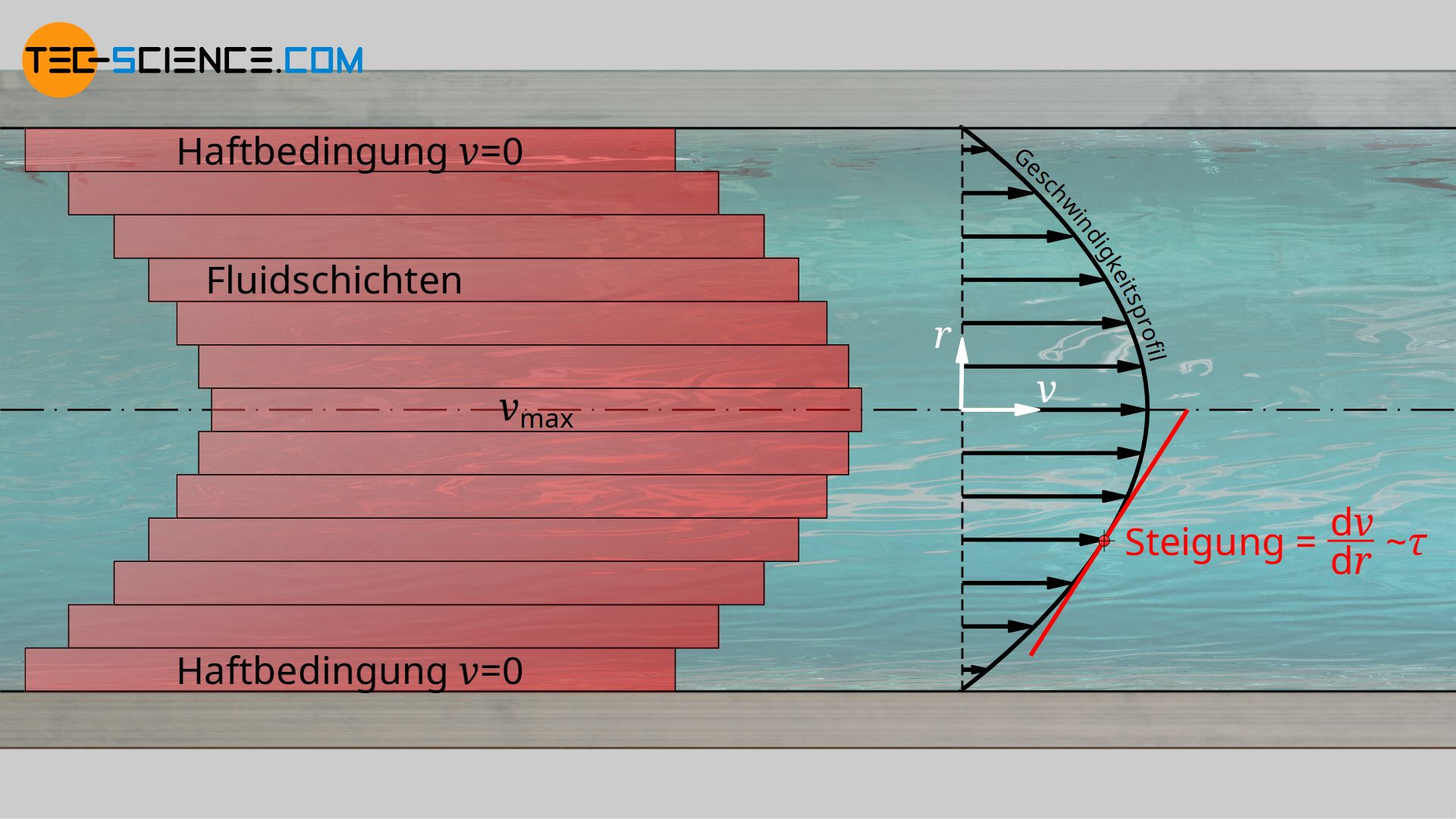
Der zu überwindende Fließwiderstand der nötig ist, um die einzelnen Fluidschichten gegeneinander abzuscheren, hängt von der Viskosität des Fluids ab. Der Fließwiderstand wird dabei durch die Scherspannung τ ausgedrückt, d.h. als Kraft pro Flächeneinheit, die nötig ist um eine Fluidschicht zu verschieben. Diese Scherspannung ist abhängig davon, wie stark die Fluidschichten gegeneinander verschoben werden. Dies wiederum wird ausgedrückt durch den Geschwindigkeitsgradienten senkrecht zur Strömungsrichtung, d.h. durch die Steigung des Geschwindigkeitsprofils in radialer Richtung dv(r)/dr (auch Schergeschwindigkeit genannt). Der mathematische Zusammenhang beider Größen wird über die Viskosität η hergestellt (Newtonsches Reibungsgesetz):
\begin{align}
\label{vis}
&\boxed{\tau= \eta \cdot \frac{\text{d}v(r)}{\text{d}r}} \\[5px]
\label{sch}
&\boxed{\tau:=\frac{F}{A}} ~~~\text{ Scherspannung} \\[5px]
\end{align}
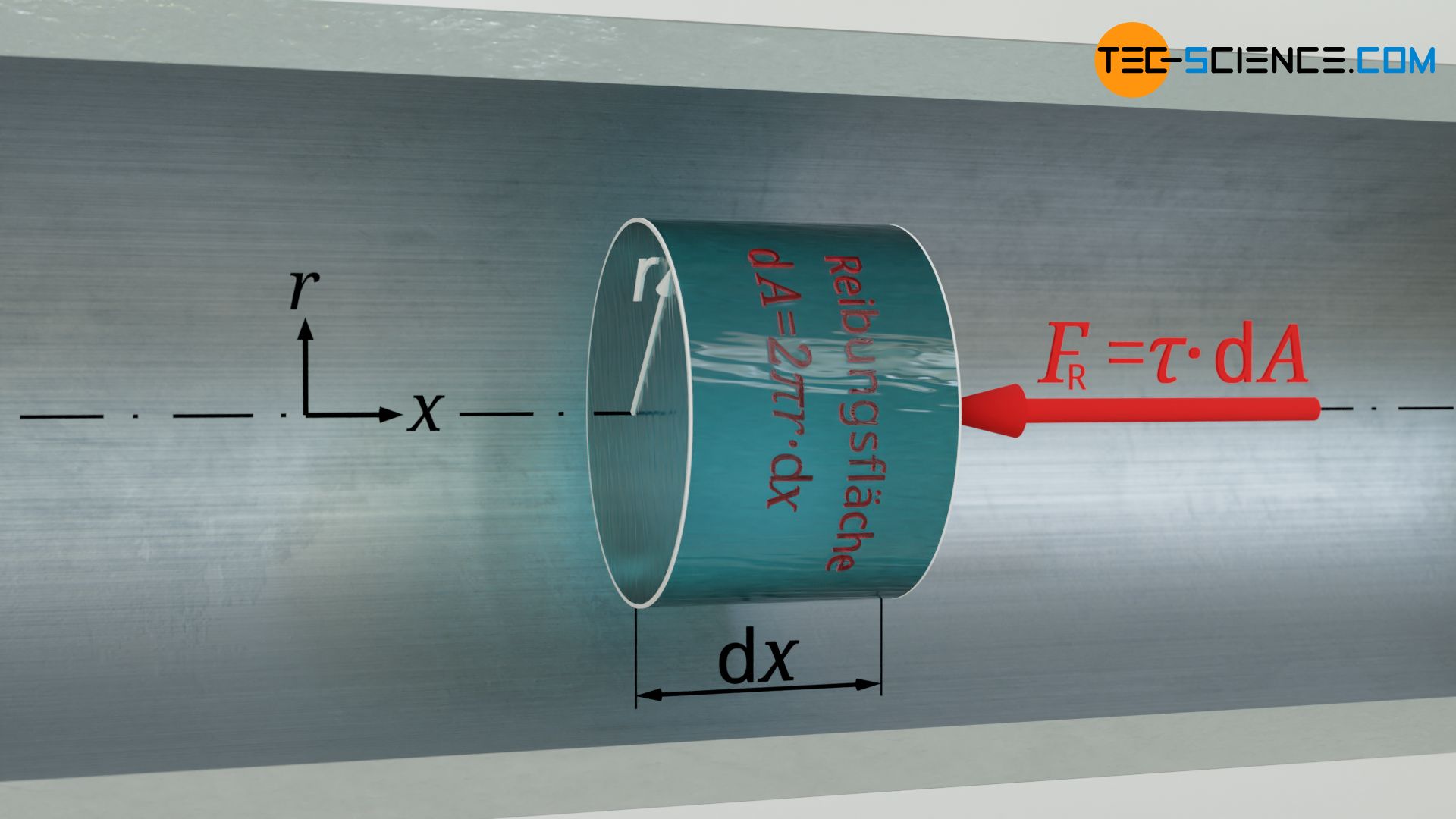
Der im Abschnitt zuvor hergeleiteten Antriebskraft aufgrund der wirkenden Druckkräfte steht die Reibungskraft zwischen dem betrachtetem Fluidvolumen und dem umgebenden Fluid entgegen. Mit τ als flächenbezogene Kraft kann diese Reibungskraft FR mit Hilfe der Mantelfläche des zylindrischen Volumenelements 2π⋅r⋅dx ermittelt werden. Die Scherspannung τ ist gemäß Gleichung (\ref{vis}) wiederum durch die Viskosität und den vorhandenen Geschwindigkeitsgradienten vorgegeben. Somit folgt für die Reibungskraft:
\begin{align}
& F_\text{R}=\tau \cdot \text{d}A = \tau \cdot 2 \pi r \cdot \text{d}x \\[5px]
\label{fr}
& \boxed{F_\text{R}= \eta \cdot \frac{\text{d}v(r)}{\text{d}r} \cdot 2 \pi r \cdot \text{d}x} \\[5px]
\end{align}
Geschwindigkeitsprofil
Für eine stationäre Strömung, bei der sich die Strömungsgeschwindigkeiten zeitlich nicht mehr ändern, gilt an dem betrachteten Volumenelement Kräftegleichgewicht. Die effektiv wirksame Druckkraft (\ref{fp}) und die entgegen wirkende Reibungskraft (\ref{fr}) können somit gleichgesetzt werden:
\begin{align}
\require{cancel}
& F_\text{R}= F_\text{p} \\[5px]
& \eta \cdot \frac{\text{d}v(r)}{\text{d}r} \cdot 2 \cancel{\pi r} \cdot \text{d}x = – \pi r^\cancel{2} \cdot \text{d} p \\[5px]
&\boxed{\frac{\text{d}v(r)}{\text{d}r}= – \frac{1}{2\eta} \frac{\text{d} p}{\text{d}x} \cdot r} \\[5px]
\end{align}
Auf der linken Seite der Gleichung steht der Geschwindigkeitsgradient der Strömung in radialer Richtung, d.h. die Steigung (Ableitung) des Geschwindigkeitsprofils. Auf der rechten Seite steht der Druckgradient in axialer Richtung und die Viskosität des Fluids. Beide Größen sind keine Funktion des Radius. Demzufolge ist also die Ableitung des Geschwindigkeitsprofils eine lineare Funktion. Das eigentliche Geschwindigkeitsprofil ist damit parabelförmig!
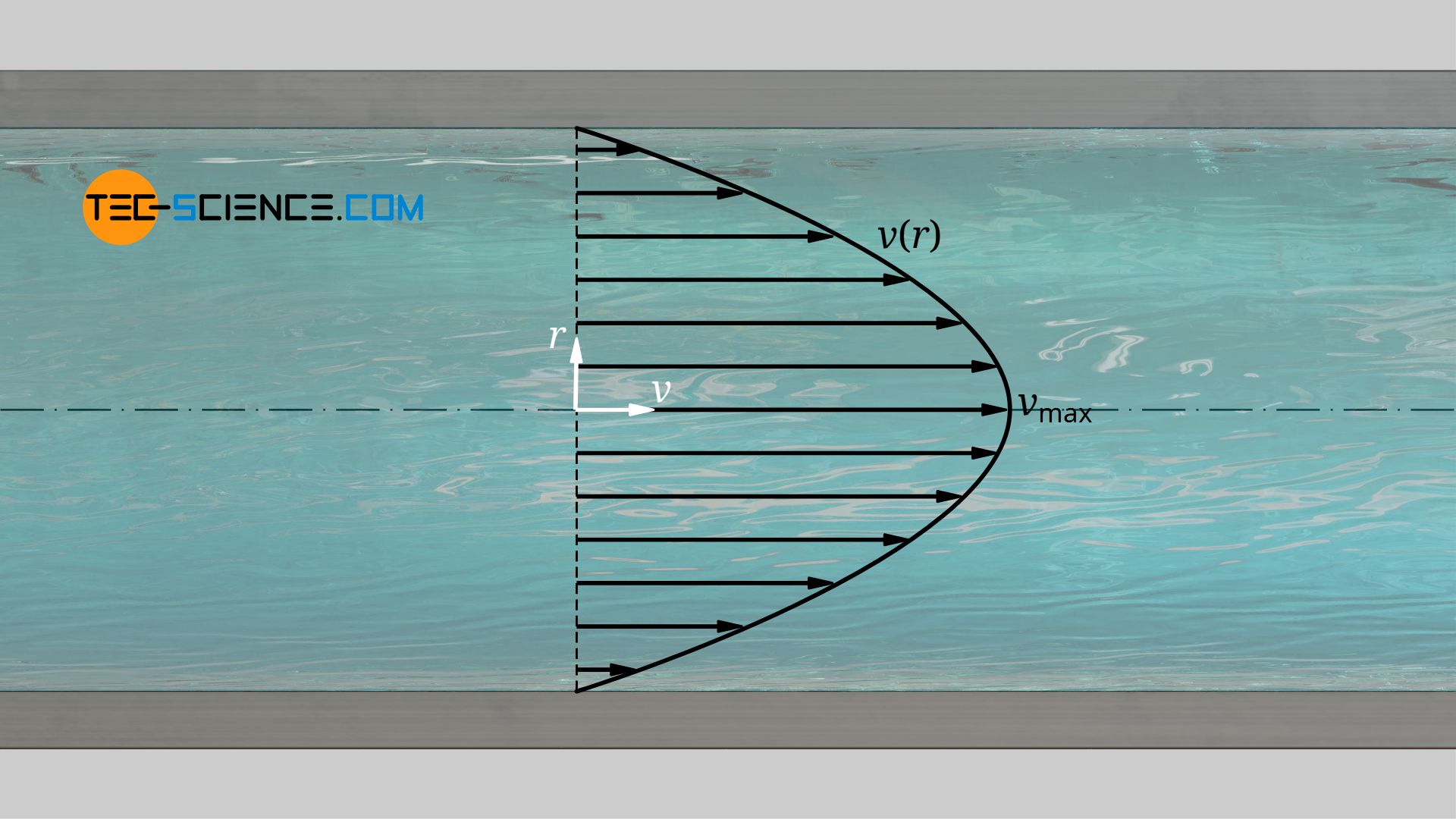
Die genaue Geschwindigkeitsfunktion v(r), erhält man durch Integration der oberen Gleichung:
\begin{align}
&v(r)=\int -\frac{1}{2\eta} \frac{\text{d} p}{\text{d}x} \cdot r ~~\text{d}r \\[5px]
&v(r)=-\frac{1}{4\eta} \frac{\text{d} p}{\text{d}x} \cdot r^2 + C \\[5px]
\end{align}
Die Integrationskonstante C lässt sich aus der Randbedingung erhalten, dass die Strömungsgeschwindigkeit an der Rohrwand bei r=R Null ist (Haftbedingung):
\begin{align}
&v(r=R)\overset{!}{=}0 \\[5px]
&-\frac{1}{4\eta} \frac{\text{d} p}{\text{d}x} \cdot R^2 + C = 0 \\[5px]
&\underline{C = \frac{1}{4\eta} \frac{\text{d} p}{\text{d}x} \cdot R^2} \\[5px]
\end{align}
Diese Konstante in die obere Gleichung eingesetzt, ergibt schließlich folgendes Geschwindigkeitsprofil:
\begin{align}
&v(r)=-\frac{1}{4\eta} \frac{\text{d} p}{\text{d}x} \cdot r^2 +\frac{1}{4\eta} \frac{\text{d} p}{\text{d}x} \cdot R^2 \\[5px]
&v(r)=-\frac{1}{4\eta} \frac{\text{d} p}{\text{d}x} \cdot \left(R^2-r^2\right) \\[5px]
\label{vr}
&\boxed{v(r)=-\frac{R^2}{4\eta} \frac{\text{d} p}{\text{d}x} \cdot \left[1-\left(\frac{r}{R}\right)^2\right]} \\[5px]
\end{align}
Maximale Strömungsgeschwindigkeit
Die maximale Strömungsgeschwindigkeit vmax liegt in der Mitte des Rohres vor. Sie kann durch Lösen der oberen Gleichung unter der Bedingung r=0 bestimmt werden:
\begin{align}
&v_{\text{max}}=v(r=0) \\[5px]
&v_{\text{max}}= -\frac{R^2}{4\eta} \frac{\text{d} p}{\text{d}x} \cdot \left[1-\left(\frac{0}{R}\right)^2\right] \\[5px]
\label{max}
&\boxed{v_{\text{max}}= -\frac{R^2}{4\eta} \frac{\text{d} p}{\text{d}x} } \\[5px]
\end{align}
Die maximale Geschwindigkeit entspricht also gerade dem Ausdruck vor den rechteckigen Klammern in Gleichung (\ref{vr}), sodass sich das Geschwindigkeitsprofil auch wie folgt darstellen lässt:
\begin{align}
\label{vrr}
&\boxed{v(r)=v_\text{max} \cdot \left[1-\left(\frac{r}{R}\right)^2\right]} ~~~\text{mit:}~~~\boxed{v_\text{max}=-\frac{R^2}{4\eta} \frac{\text{d} p}{\text{d}x}} \\[5px]
\end{align}
Die Gesetzmäßigkeit mit der die Strömungsgeschwindigkeit von außen nach innen quadratisch zunimmt, wird nach den Wissenschaftlern Hagen und Poiseuille auch als Gesetz von Hagen-Poiseuille bezeichent. Bei der Herleitung dieser Gesetzmäßigkeit wurde vorausgesetzt, dass die Viskosität unabhängig der Schergeschwindigkeit und somit keine Funktion des Radius ist. Folglich gilt diese Gleichung nur für sogenannte Newtonsche Fluide, bei denen die Viskosität stets konstant ist. Zudem muss für die Gültigkeit der Gleichung eine laminare Strömung vorausgesetzt werden (Schichtenströmung), da die Viskosität ansonsten ihre eigentliche Bedeutung verliert.
Ebenfalls verliert das Gesetz von Hagen-Poiseuille seine Gültigkeit, wenn die Viskosität des Fluids relativ gering im Vergleich zum Durchmesser des Rohres ist. Dies kann man auch anschaulich nachvollziehen. Hierzu stellen wir uns in Gedanken ein Rohr mit einem riesigen Radius von bspw. 6 Meter vor. Durch dieses Rohr strömt nun Wasser mit einer maximalen Strömungsgeschwindigkeit von bspw. 6 m/s. Gemäß des Gesetztes von Hagen-Poiseuille erhielte man dann in einer Entfernung von 10 cm zur Rohrwand gerade einmal eine Strömungsgeschwindigkeit von 20 cm/s. Bereits die Erfahrung zeigt, dass die Strömungsgeschwindigkeit in dieser doch recht großen Entfernung zur Rohrwand deutlich größer sein sollte (vgl. hierzu die Strömungsgeschwindigkeit in einem breiten Fluss, die ebenfalls bereits in relativ geringem Abstand zum Ufer nahezu maximal ist).
Würde man in Gedanken allerdings deutlich zähflüssigerer Honig durch das Rohr fließen lassen, so wäre die relativ geringe Strömungsgeschwindigkeit am Rand plötzlich gar nicht mehr so unrealistisch. Hohe Viskositäten beeinflussen die Strömung sozusagen über den gesamten Rohrquerschnitt, während sehr niedrigviskose Fluide die Strömung nur in eine relativ geringen Randbereich beeinflussen und gar nicht mehr den gesamten Querschnitt umfassen. Salopp formuliert gilt das Hagen-Poiseuille-Gesetz somit nur, wenn die Viskosität in der Lage ist den gesamten Strömungsquerschnitt zu beeinflussen (siehe hierzu auch den Artikel Grenzschichten). Dies setzt also voraus, dass die Viskosität in Relation zum Durchmesser nicht allzu niedrig ist.
Als Hagen-Poiseuille-Gesetz bezeichnet man das parabolische Geschwindigkeitsprofil einer reibungsbehafteten, laminaren Rohrströmung von Newtonschen Fluiden für Rohre deren Länge groß ist im Vergleich zum Durchmesser und die Viskositäten nicht zu gering sind! Die Strömung selbst wird deshalb auch als Hagen-Poiseuille-Strömung bezeichnet.
Einschränkung des Hagen-Poiseuille-Gesetz für kurze Rohre
Wie bereits erläutert, ist eine Druckdifferenz zwischen Rohranfang und der freien Umgebung (Rohrende) Antrieb für eine Strömung. Der sich über die Rohrlänge bildende Druckgradient hat im Prinzip aber zwei Aufgaben. Er muss nicht nur die Reibungskraft während des Strömens kompensieren (Aufbringen von Reibungsarbeit), sondern der Druckgradient muss die Strömung überhaupt erst auf das Strömungsprofil beschleunigen (Aufbringen von Beschleunigungsarbeit).
Man kann also die gesamte Druckdifferenz – und damit auch den Druckgradienten – aufteilen, in einen Anteil der auf das Beschleunigen der Strömung entfällt und in einen Anteil der für die Kompensation der Reibung notwendig ist. Wie eingangs bereits erläutert, ist in den oberen Gleichungen mit dem dort enthaltenen Druckgradienten dp/dx nur jener Anteil am gesamten Druckgradienten gemeint, der zur Überwindungen der Reibung notwendig ist.

Man darf zur Bestimmung dieses Druckgradienten im Allgemeinen also nicht einfach die Druckdifferenz zwischen Rohranfang und Rohrende nehmen und dann durch die Rohrlänge teilen. Deshalb war im Zusammenhang mit den oberen Gleichungen auch immer von einem Rohrabschnitt die Rede, bei dem stillschweigend davon ausgegangen wurde, dass sich das Strömungsprofil bereits vollständig ausgebildet hat.
Das Gesetz von Hagen-Poiseuille gilt nicht in der Anlaufströmung, innerhalb deren der Druckgradient zusätzlich zur Überwindung der Reibung auch noch die Strömung auf das typische parabelförmige Profil beschleunigen muss!
Unter bestimmten Umständen kann es zur Beschreibung von Rohrströmung dennoch gerechtfertigt sein, den Druckgradienten in den oberen Gleichungen einfach aus dem Quotienten von Druckdifferenz und Rohrlänge zu bestimmen. Nämlich immer dann, wenn die Beschleunigungsarbeit (und damit auch der hierfür verantwortliche Druckanteil) vernachlässigbar klein gegenüber der Reibungsarbeit ist. Dies wird immer dann der Fall sein, wenn das Rohr im Vergleich zu seinem Durchmesser relativ lang ist, d.h. bei vernachlässigbarer Anlaufstrecke, oder wenn die Strömungsgeschwindigkeit relativ gering ist. In solchen Fällen überwiegt die Reibungsarbeit aufgrund der großen Rohrlänge meist deutlich die relativ geringe Beschleunigungsarbeit.
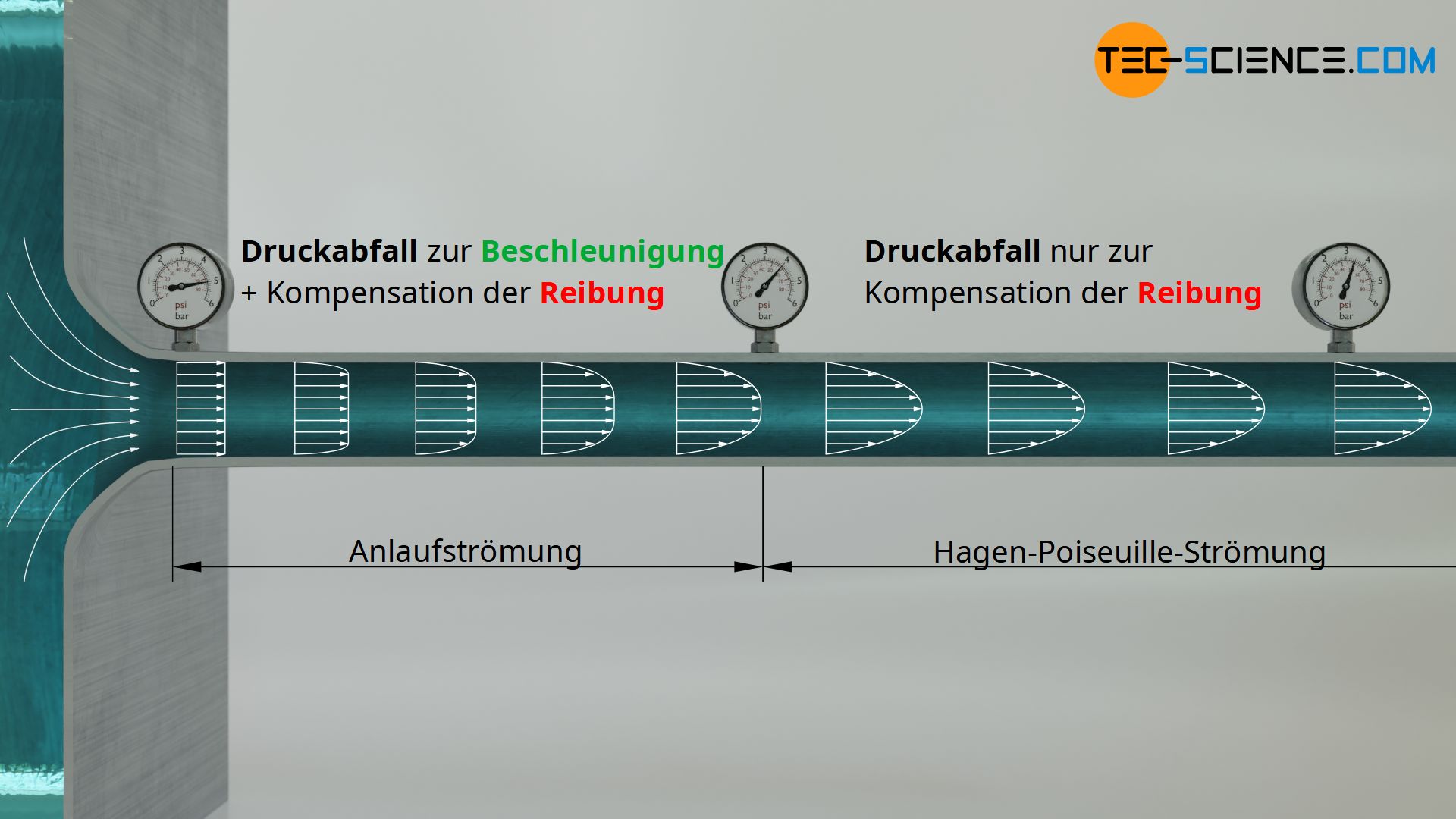
Bei relativ kurzen Rohren nimmt der Druckanteil zur Beschleunigung der Strömung hingegen einen nicht mehr zu vernachlässigenden Anteil an. In einem solchen Fall kann sich innerhalb des kurzen Rohrstücks das parabelförmige Geschwindigkeitsprofil nicht vollständig ausbilden. Das Hagen-Poiseuille-Gesetz ist in diesem Falle nicht mehr gültig (kein parabelförmiges Geschwindigkeitsprofil)! Mehr Informationen zu diesem Thema findet sich im Artikel Energetische Betrachtung des Hagen-Poiseuille-Gesetz.
Die Gesetzmäßigkeiten zur Hagen-Poiseuille-Strömung gelten nur für lange Rohre, deren Länge im Vergleich zum Durchmesser relativ groß ist.
Volumenstrom
Da das Geschwindigkeitsprofil nun also bekannt ist, kann auch der Volumenstrom ermittelt werden, der durch eine Rohrleitung strömt. Zur Herleitung des Volumenstroms betrachten wir in einem beliebigen Abstand r zur Rohrachse einen Kreisring mit der infinitesimalen Dicke dr. Die Fläche des betrachteten Ringelements dA lässt sich aus der „Länge“ des Rings 2π⋅r (Ringumfang) und der „Höhe“ dr (Dicke) ermitteln:
\begin{align}
\label{q}
&\text{d}A = 2\pi r \cdot \text{d}r \\[5px]
\end{align}

Die Geschwindigkeit mit der das Fluid im Abstand r durch diesen Kreisring strömt, ist durch Gleichung (\ref{vr}) gegeben. Dabei legt das Fluid innerhalb der Zeit dt die Strecke dx=v(r)⋅dt zurück. Somit gilt für das durchströmende Fluidvolumen dV bzw. für den infinitesimalen Volumenstrom dV*:
\begin{align}
&\text{d}V = \text{d}A \cdot \text{d}x = 2\pi r \cdot \text{d}r \cdot v(r) \cdot \text{d}t \\[5px]
&\text{d}V = -2\pi r \cdot \frac{R^2}{4\eta} \frac{\text{d} p}{\text{d}x} \cdot \left[1-\left(\frac{r}{R}\right)^2\right] \cdot \text{d}r \cdot \text{d}t \\[5px]
&\text{d}\dot V = \frac{\text{d}V}{\text{d}t} = – \frac{ 2\pi R^2}{4\eta} \frac{\text{d} p}{\text{d}x} \cdot \left[r-\frac{r^3}{R^2}\right] \cdot \text{d}r \\[5px]
\end{align}
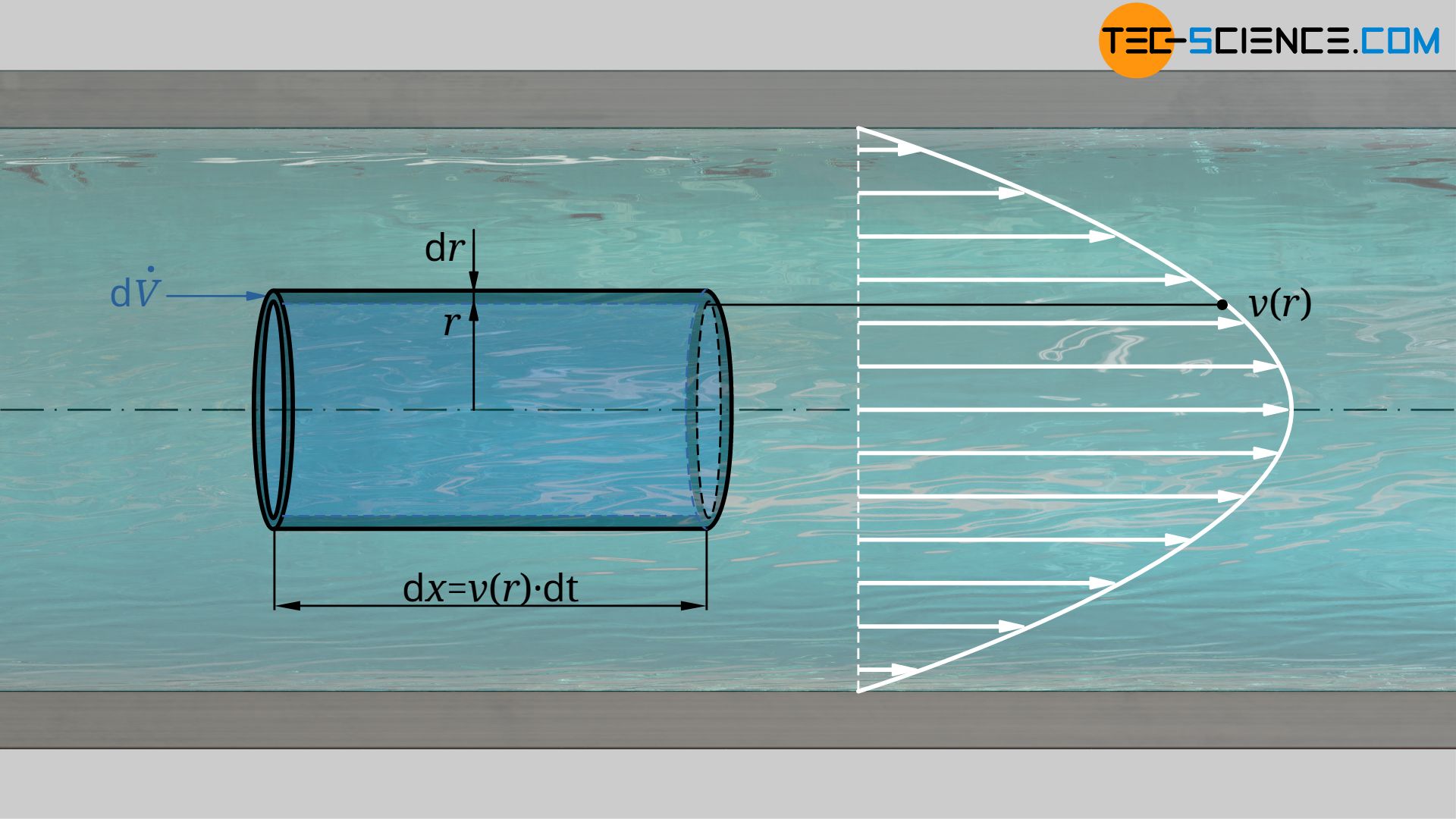
Den Volumenstrom V* durch das gesamte Rohr erhält man schließlich durch Integration dieser Gleichung über die gesamte Querschnittsfläche, d.h. innerhalb der Grenzen von r=0 bis r=R:
\begin{align}
&\dot V = \int\limits_{(A)}^{} \text{d} \dot V = \int\limits_0^R – \frac{ 2\pi R^2}{4\eta} \frac{\text{d} p}{\text{d}x} \cdot \left[r-\frac{r^3}{R^2}\right] \cdot \text{d}r \\[5px]
&\dot V = – \frac{ 2\pi R^2}{4\eta} \frac{\text{d} p}{\text{d}x} \cdot \left\vert \frac{r^2}{2}-\frac{r^4}{4R^2}\right\vert_0^R \\[5px]
&\dot V = – \frac{ 2\pi R^2}{4\eta} \frac{\text{d} p}{\text{d}x} \cdot \left(\frac{R^2}{2}-\frac{R^4}{4R^2}\right) = – \frac{ 2\pi R^2}{4\eta} \frac{\text{d} p}{\text{d}x} \cdot \frac{R^2}{4} \\[5px] \\[5px]
\label{dv}
&\boxed{\dot V = – \frac{\pi R^4}{8\eta} \frac{\text{d} p}{\text{d}x} } \\[5px]
\end{align}
Besonders erwähnenswert ist an diesem Ergebnis, dass der Radius des Rohres mit der vierten Potenz in die Formel zur Berechnung des Volumenstroms eingeht. Eine Verdopplung des Rohrradius bedeutet somit einen 16-fachen Volumenstrom! Beachte, dass dieser Zusammenhang nur für inkompressibel Stoffe gilt, deren Volumen sich nicht mit dem Druck ändert. Nach wie vor muss eine laminare Rohrströmung eines newtonschen Fluids vorausgesetzt werden.
Die Gesetzmäßigkeiten zum Volumenstrom haben in der Praxis noch eine ganz andere Bedeutung. Zum Einen hängt der Volumenstrom direkt von der Viskosität des Mediums ab und zum Anderen kann man den Volumenstrom sehr einfach und vor allem sehr genau bestimmen. Auf diese Weise ist es möglich mithilfe des Volumenstroms die Viskosität von Fluiden zu ermitteln. Auf diesem Prinzip beruht das Kapillarviskosimeter.
Anmerkung
Häufig wird an dieser Stelle auf das Beispiel der Verengung von Venen und auf feine Blutgefäße verwiesen, was laut dem Hagen-Poiseuille-Gesetz tatsächlich enorme Auswirkungen auf den Blutstrom bzw. auf den benötigten Blutdruck mit sich bringen würde. Blut ist in diesem Zusammenhang aber eher ein unpassendes Beispiel, auch wenn Poiseuille tatsächlich das Strömen des Blutes zum Anlass nahm solche Strömungsvorgänge näher zu untersuchen.
Blut ist nämlich kein Newtonsches Fluid, sondern ein scherverdünnendes (strukturviskoses) Fluid. Und gerade bei sehr feinen Blutgefäßen oder bei einer Verengung ist das Strömungsprofil ziemlich genau das Gegenteil einer Hagen-Poiseuille-Strömung! Bei sehr feinen Gefäßen bewegen sich die Blutkörperchen nämlich wie große Pfropfen mit nahezu konstanter Strömungsgeschwindigkeit über den gesamten Querschnitt hinweg. Man spricht deshalb auch von einer Pfropfenströmung.
Zudem können bei Verengungen und hohen Strömungsgeschwindigkeiten turbulente Strömungsanteile auftreten, was dann ebenfalls zu einem nahezu konstanten Geschwindikeitsprofil führen würde (siehe Abschnitt zur turbulenten Rohrströmung).
Mittlere Strömungsgeschwindigkeit
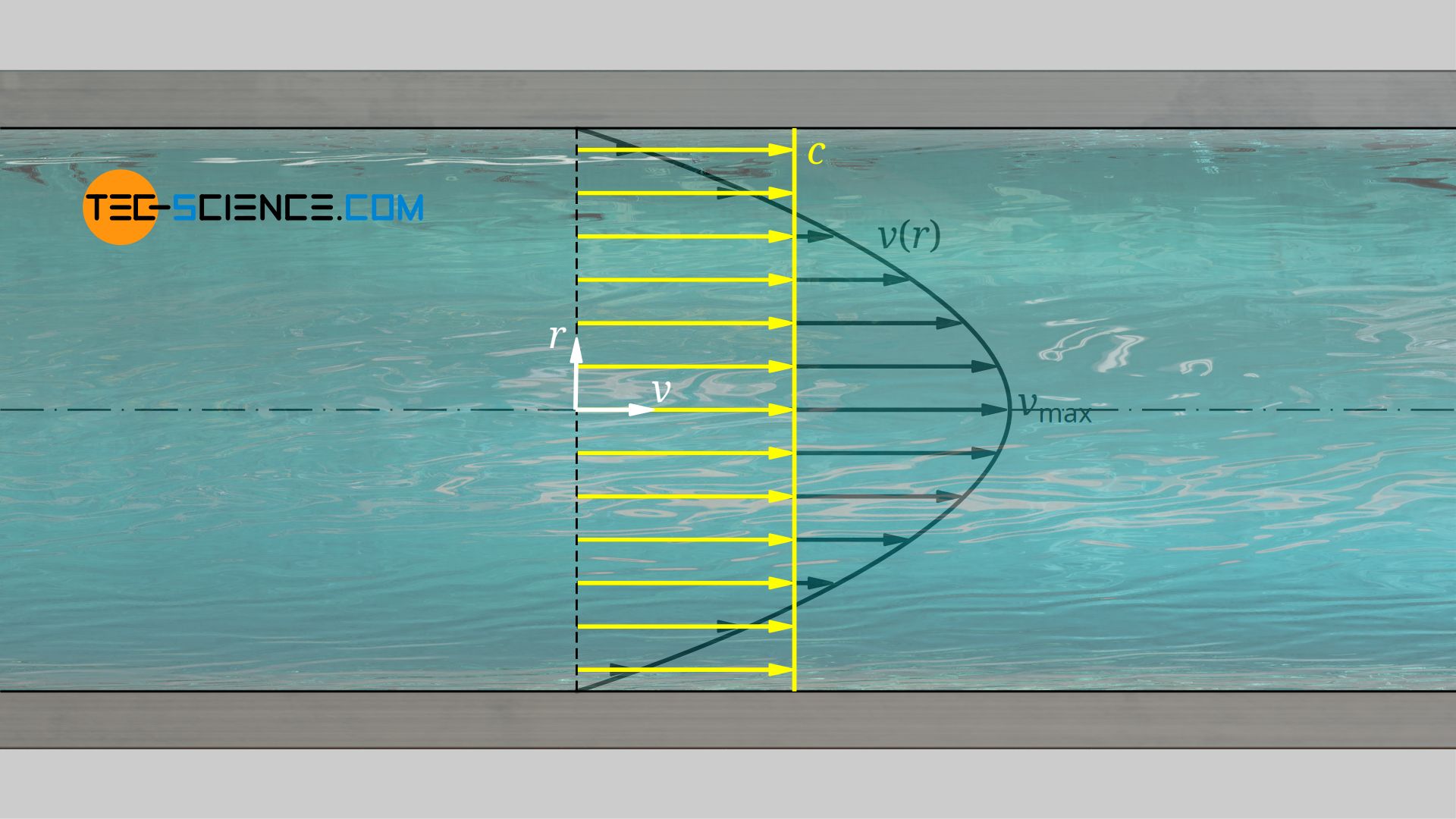
Eine reibungsbehaftete Rohrströmung besitzt mit ihrem parabolischen Geschwindigkeitsprofil im Prinzip keine charakteristische Geschwindigkeit. Man definiert zur Charakterisierung von Rohrströmungen deshalb häufig eine mittlere Strömungsgeschwindigkeit c. Diese ist definiert als eine über den gesamten Querschnitt hinweg konstante Geschwindigkeit, die denselben Volumenstrom liefert wie das reale Geschwindigkeitsprofil. Mit A=π⋅R2 als innerem Rohrquerschnitt und c als mittlere Strömungsgeschwindigkeit, gilt für den Volumenstrom V*:
\begin{align}
\label{dvv}
&\dot V = \frac{\Delta V}{\Delta t} = \frac{A \cdot \Delta x}{\Delta t} = \pi R^2 \cdot \frac{\Delta x}{\Delta t} = \pi R^2 \cdot c \\[5px]
\end{align}
Bei der oberen Herleitung wurde ausgenutzt, dass der Quotient aus Strömungsstrecke Δx und Zeitdauer Δt gerade der mittleren Strömungsgeschwindigkeit entspricht. Gleichsetzen der Gleichungen (\ref{dvv}) und (\ref{dv}) liefert schließlich folgende mittlere Strömungsgeschwindigkeit c:
\begin{align}
&\pi R^2 \cdot c =- \frac{\pi R^4}{8\eta} \frac{\text{d} p}{\text{d}x} \\[5px]
\label{c}
& \boxed{c =- \frac{R^2}{8\eta} \frac{\text{d} p}{\text{d}x}} ~~~\text{mittlere Strömungsgeschwindigkeit}\\[5px]
\end{align}
Zwischen der maximalen Strömungsgeschwindigkeit vmax und der mittleren Strömungsgeschwindigkeit c besteht folgender Zusammenhang:
\begin{align}
&\frac{c}{v_\text{max}} = \frac{ – \frac{R^2}{8\eta} \frac{\text{d} p}{\text{d}x} }{ -\frac{R^2}{4\eta} \frac{\text{d} p}{\text{d}x} } = \frac{1}{2}\\[5px]
&\boxed{c = \frac{1}{2} \cdot v_\text{max}}
\end{align}
Die mittlere Strömungsgeschwindigkeit ist halb so groß wie die maximale Strömungsgeschwindigkeit in der Mitte des Rohrs!
Förderdruck und Druckverlust
Wie bereits erläutert, stellt der Druckgradient dp/dx in den oberen Gleichungen den Antrieb für den reibungsbehafteten Strömungsprozess dar. Gemäß Gleichung (\ref{dv}) beeinflusst dieser direkt den geförderten Volumenstrom. Umgekehrt bedeutet dies, dass für einen gewünschten Volumenstrom ein entsprechender Druckgradient vorhanden sein muss. Hierfür ist eine Pumpe erforderlich, die letztlich diesen Druckgradienten erzeugt. Nach Umstellen von Gleichung (\ref{dv}) folgt für den Betrag des erforderlichen Druckgradienten (an dieser Stelle soll auf das Vorzeichen verzichtet werden, da ohnehin nur die Beträge entscheidend sind):
\begin{align}
& \frac{\text{d} p}{\text{d}x} = \frac{8\eta}{\pi R^4} \dot V \\[5px]
\end{align}
Aus der Definition des Druckgradienten als Druckänderung pro Längeneinheit kann für einen Rohrabschnitt der Länge ΔL die zur Förderung des Fluids benötigte Druckdifferenz ΔpF mit nachfolgender Formel bestimmt werden (im Folgenden Förderdruck genannt):
\begin{align}
\label{pv}
& \frac{\text{d}p}{\text{d}x} = \frac{\Delta p_F}{L} \\[5px]
& \Delta p_F = \frac{\text{d}p}{\text{d}x} \cdot \Delta L \\[5px]
& \underline{\Delta p_F = \frac{8\eta \cdot \Delta L}{\pi R^4} \dot V } \\[5px]
\end{align}
Für eine reibungsfreie Strömung hingegen müsste man im stationären Zustand keinen solchen Förderdruck aufbringen, um das Fluid am Strömen zu halten. Einmal in Bewegung versetzt, würde das Fluid ohne Geschwindigkeitsverlust von selbst durch die Rohrleitung strömen. Das Aufbringen des Förderdrucks ist also dem Reibungsverlust geschuldet, der gleichbedeutend mit einem Druckverlust ist. Der Förderdruck muss im stationären Fall den Druckverlust vollständig kompensieren, um das Fluid am Fließen zu halten. Obere Formel ist deshalb gleichbedeutend mit dem Druckverlust ΔpV, der über die Rohrlänge ΔL erfolgt:
\begin{align}
& \boxed{\Delta p_V = \frac{8\eta \cdot \Delta L}{\pi R^4} \dot V} ~~~\text{Druckverlust} \\[5px]
\end{align}
Man kann sich die Situation anschaulich an einem Rohr verdeutlichen, durch das eine Stange aus Schaumstoff gedrückt werden soll. Für das Durchschieben muss die Reibungskraft zwischen Schaumstoff und Rohr überwunden werden. Hierfür ist eine bestimmte Kraft erforderlich. Die von dieser Seite des Rohrs aufgebrachte Kraft entspricht aber nicht der Kraft, die eine zweite Person am Ende der Rohrleitung wahrnimmt. Diese Person misst abzüglich der Reibungskraft somit eine deutlich geringere Kraft.
Es tritt zum Ende der Rohrleitung hin also eine Kraftverlust auf, der umso größer ist je größer die Reibung und damit die Rohrleitung ist. Bezieht man die Kraft auf die Querschnittsfläche des Rohrs, dann entspricht dies letztlich einem Druck. Es tritt also ein Druckverlust entlang des Rohres auf. Im stationären Fall bei konstanter Durchschiebegeschwindigkeit herrscht Kräftegleichgewicht, sodass der Druckverlust ΔpV aufgrund der Reibungskraft gerade dem Förderdruck ΔpF entspricht, mit dem der Schaumstoff insgesamt durch die Rohrleitung geschoben wird (Druckdifferenz zwischen Rohranfang und -ende).
Der Volumenstrom in der oberen Gleichung kann gemäß Gleichung (\ref{c}) auch durch die mittlere Strömungsgeschwindigkeit ausgedrückt werden. Für den Druckverlust in Abhängigkeit der mittleren Strömungsgeschwindigkeit gilt somit:
\begin{align}
& \Delta p_V = \frac{8\eta \cdot \Delta L}{\pi R^4} \cdot \overbrace{\pi R^2 \cdot c}^{\dot V} \\[5px]
& \boxed{\Delta p_V = \frac{8\eta \cdot \Delta L}{R^2} \cdot c} ~~~\text{Druckverlust} \\[5px]
\end{align}
Der auftretende Druckverlust entlang einer Rohrleitung ist bei laminarer Strömung proportional zur mittleren Strömungsgeschwindigkeit! Für turbulente Strömungen gilt dieser Zusammenhang nicht mehr.
Beachte, dass der beschriebene Druckverlust rein auf der Viskosität beruht („viskoser Druckverlust“). Dieser Druckverlust muss durch eine Pumpe stets aufgebracht werden, um das Fluid am Strömen zu halten. Druckverluste, die bspw. durch Strömungsverluste in Rohrkrümmern auftreten, sind dabei nicht berücksichtigt. Die Gleichungen zeigen aber dennoch, dass der Rohrradius offensichtlich großen Einfluss auf den Druckverlust hat. Große Rohre führen im Allgemeinen zu einem geringeren (viskosen) Druckverlust. Durch Verwendung großer Rohre lässt sich somit die Pumpenleistung P bei gleichem Volumenstrom V* deutlich reduzieren:
\begin{align}
& P = \Delta p_V \cdot \dot V =\frac{8\eta \cdot \Delta L}{\pi R^4} \dot V^2\\[5px]
& \boxed{P =\frac{8\eta \cdot \Delta L}{\pi R^4} \dot V^2}\\[5px]
\end{align}
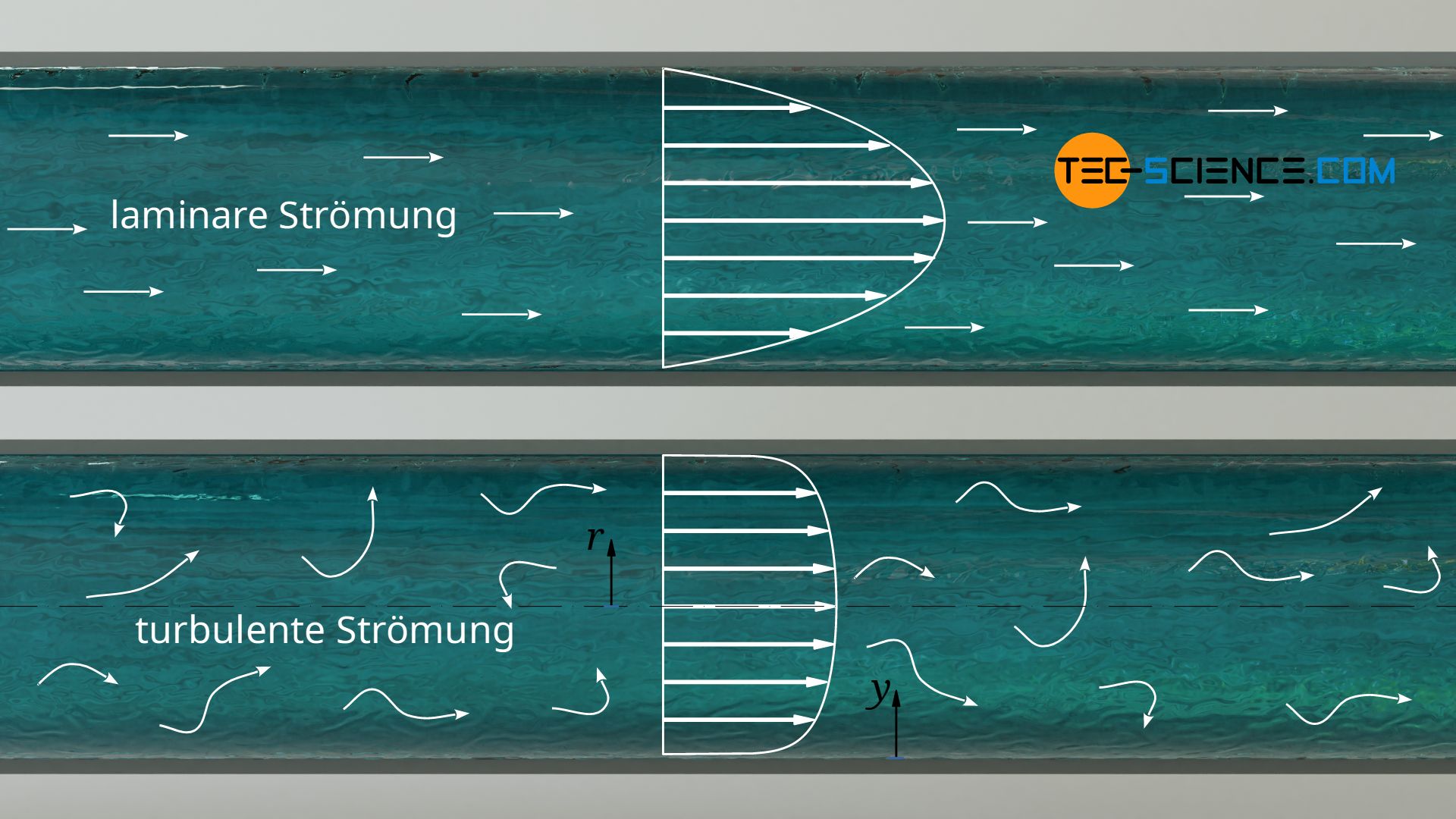
Geschwindigkeitsprofil bei turbulenten Strömungen
Ein parabelförmiges Geschwindigkeitsprofil bildet sich in Rohren nur aus, wenn eine laminare Strömung vorliegt. Würde die Strömung bei ansonsten gleichen Bedingungen in eine turbulente Strömungen übergehen, so ist aufgrund der Verwirbelungen die maximale Strömungsgeschwindigkeit in der Rohrmitte geringer. Gleichzeitig führt aber die erhöhte Durchmischung zu einem stärkeren Impulsaustausch zwischen den Fluidteilchen, sodass die Strömungsgeschwindigkeit im Randbereich schneller ansteigt. Für turbulente Strömungen mit Reynolds-Zahlen größer etwa 2300 wird mit Hilfe eines Fließindexes n deshalb häufig folgender Ansatz zur Beschreibung des Geschwindigkeitsprofils verwendet:
\begin{align}
&\boxed{v(r)=v_\text{max} \cdot \left(1-\frac{r}{R}\right)^\frac{1}{n}} ~~~\text{turbulente Strömung}~~~~~(\text{häufig } n=7)\\[5px]
\end{align}
Für ein Koordinatensystem, dessen Ursprung die Rohrwand ist, gilt folgende Funktion:
\begin{align}
&\boxed{v(z)=v_\text{max} \cdot \left(\frac{y}{R}\right)^\frac{1}{n}} ~~~~0<y<R\\[5px]
\end{align}
In der Praxis wird für den Fließindex häufig der Wert n=7 gewählt. Man bezeichnet dies auch als das 1/7-Potenzgesetz (Ein-Siebtel-Potenzgesetz). In diesem Fall gilt zwischen der mittleren und der maximalen Fließgeschwindigkeit folgender Zusammenhang:
\begin{align}
&\boxed{c = 0,817 \cdot v_\text{max}} ~~~\text{für } n=7\\[5px]
\end{align}
Der Fließindex ist dabei abhängig von der Reynoldszahl und von der relativen Rauheit des Rohres, d.h. vom Verhältnis zwischen Oberflächenrauigkeit und Durchmesser des Rohres.
Anmerkung: Das 1/7-Potenzgesetz findet bspw. auch bei der Beschreibung von turbulenten Grenzschichten Anwendung. Letztlich ist die gesamte Rohrströmung eine einzig große Grenzschicht.






