Die Viskosität von (idealen) Gasen beruht auf dem Impulstransport aufgrund von Diffusionsprozesse zwischen den einzelnen Fluidschichten
Definition der Viskosität
Im Artikel Viskosität wurde die Ursache der Viskosität hauptsächlich auf Anziehungskräfte zwischen den Schichten eines Fluids zurückgeführt. Diese wirken ähnlich wie Reibungskräfte, sodass es zu einer gegenseitigen Abbremsung der einzelnen Fluidschichten kommt. Zur anschaulichen Definition der Viskosität kann man ein Fluid zwischen zwei Platten betrachten. Die untere Platte ruht dabei und die oberen Platte wird mit konstanter Geschwindigkeit bewegt.
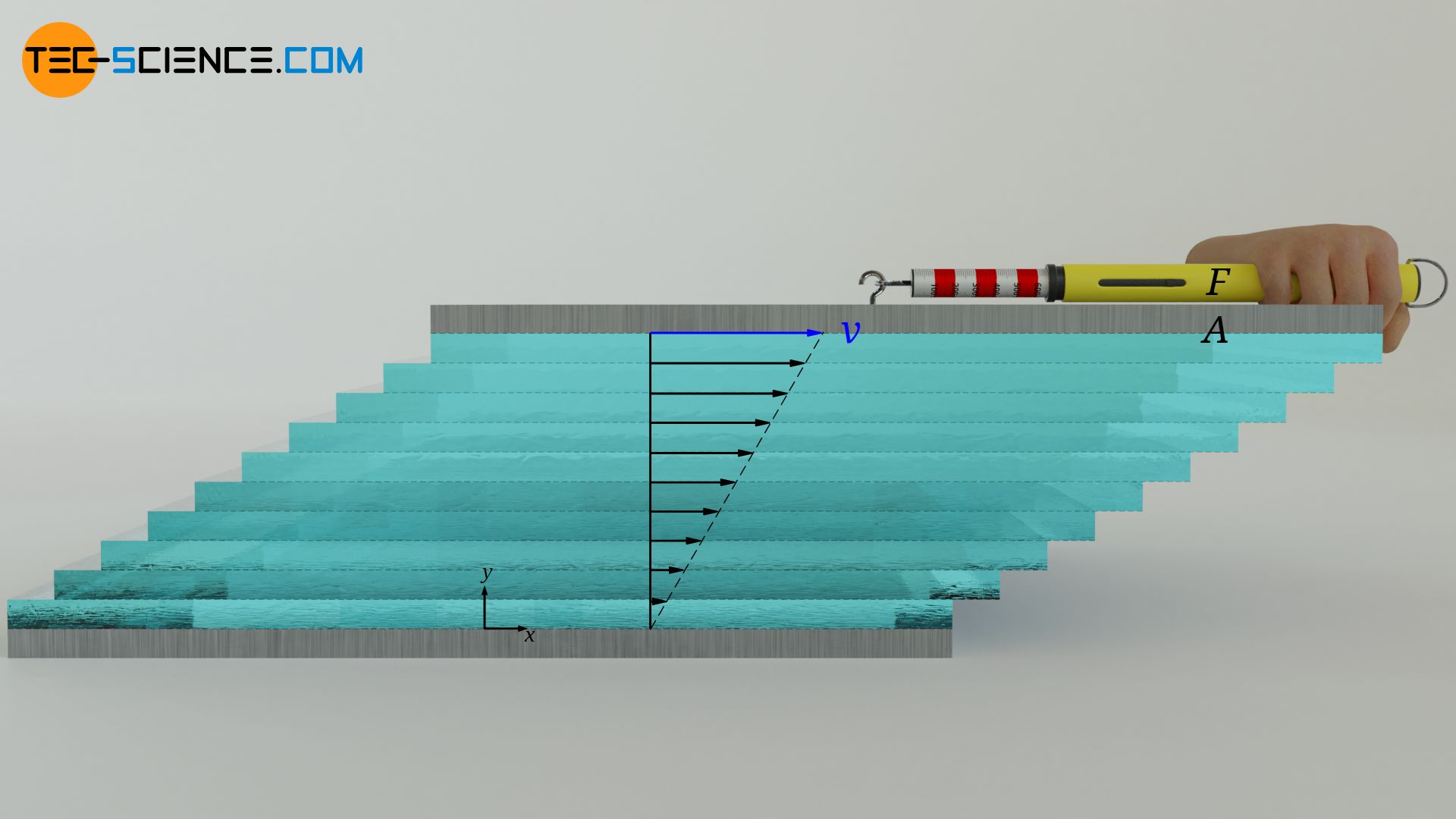
Aufgrund der Haftbedingung haftet sowohl die oberste als auch die unterste Fluidschicht jeweils an den Platten. Die untere Fluidschicht bleibt somit in Ruhe und die oberste Fluidschicht bewegt sich mit derselben Geschwindigkeit wie die obere Platte. Dazwischen bildet sich dann ein lineares Geschwindigkeitsprofil. Ein betrachtete Fluidschicht bewegt sich somit stets langsamer als die unmittelbar darüber befindliche Fluidschicht. Aufgrund der molekularen Anziehungskräfte ist somit eine untere Schicht immer versucht die darüber befindliche Schicht auszubremsen.
Diese Reibungskräfte zwischen den Schichten müssen entsprechend kompensiert werden, wenn die oberste Platte mit konstanter Geschwindigkeit gezogen werden soll. Je viskoser (zähflüssiger) ein Fluid ist, desto stärke innere Reibungskräfte wirken und umso größere Kräfte werden für das Verschieben der obersten Platte benötigt. Die Viskosität η gibt dabei den Zusammenhang zwischen der flächenbezogenen Kraft F/A (Schubspannung τ), die zur Verschiebung der Schichten notwendig ist, und der Steigung des Geschwindigkeitsprofils dv/dy (Geschwindigkeitsgradient) wieder:
\begin{align}
\label{t}
&\frac{F}{A}=\boxed{\tau= \eta \cdot \frac{\text{d} v}{\text{d} y}} ~~~~~\text{Newtonsches Reibungsgesetz}\\[5px]
\end{align}
Viskosität von Gasen durch Impulstransport
Das Zustandekommen der Viskosität durch wirkende Reibungskräfte zwischen den Fluidschichten ist bei Flüssigkeiten sehr anschaulich. In Gasen üben die Moleküle allerdings nahezu keinerlei Anziehungskräfte aufeinander aus. Reibungskräfte einzelner Fluidschichten durch intermolekulare Anziehungskräfte sind somit so gut wie nicht vorhanden. Die Praxis zeigt aber, dass selbst Gase eine beachtliche Viskosität aufweisen und es in Strömungen zur Abbremsung einzelner Fluidschichten kommt. Wie kann dieses Verhalten ohne Vorhandensein von Anziehungskräften erklärt werden?
Die abbremsende Wirkung der Fluidschichten kommt in Gasen hauptsächlich durch den Impulstransport der Gasmoleküle zustande, wenn diese von einer langsameren Schicht in eine schnellere Schicht eindiffundieren. In Flüssigkeiten findet dieser Prozess zwar auch statt; er ist aber im Vergleich zu dem Abbremseffekt aufgrund der wirkenden Anziehungskräften vernachlässigbar.
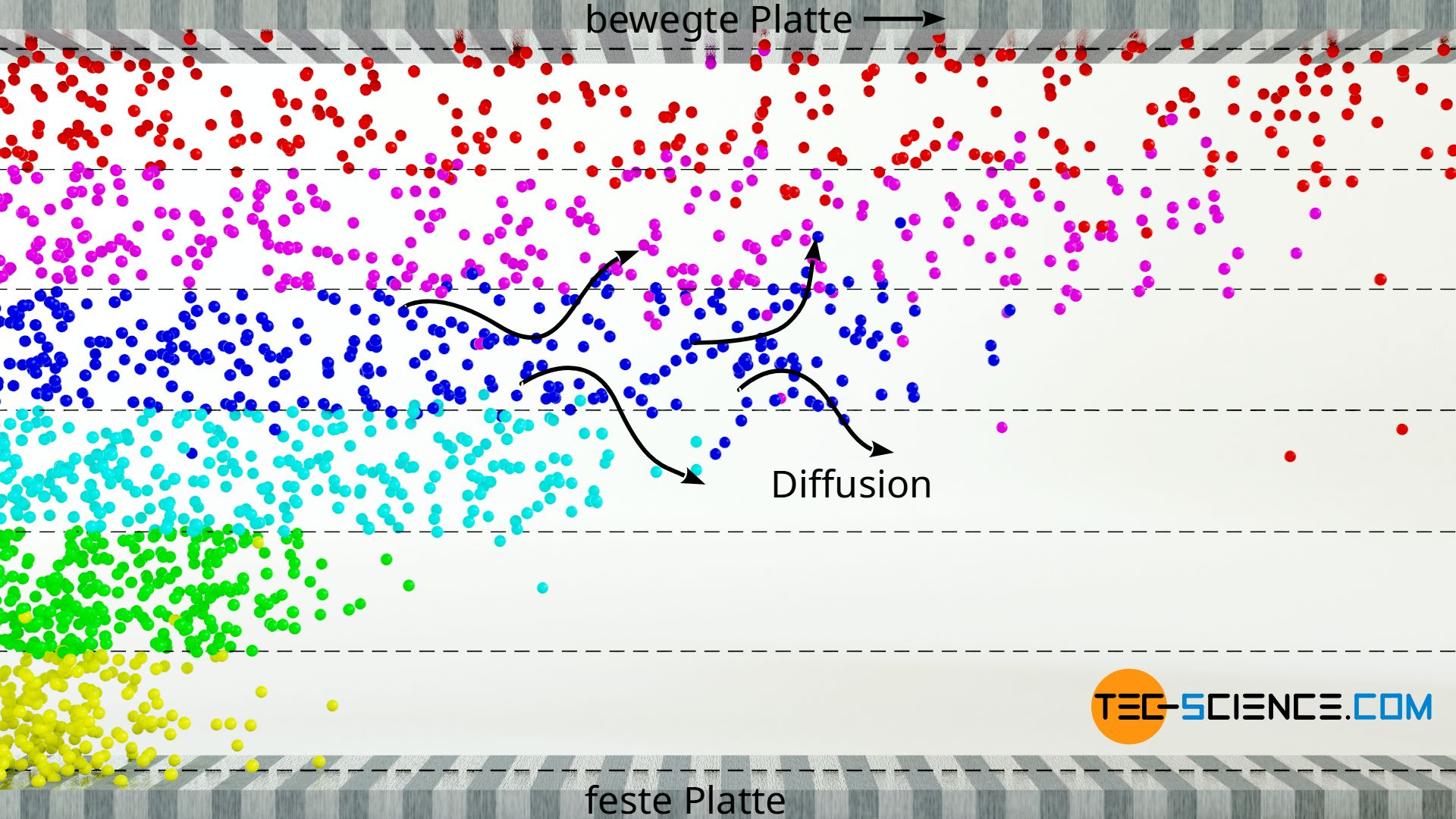
Betrachten wir hierzu nochmals die bereits angesprochene Schichtenströmung (laminare Strömung), die diesmal aus einem idealen Gas als Fluid besteht. Prallt in diesem Gas ein Gasmolekül mit einem anderen zusammen, dann findet ein Impulsaustausch statt, d.h. ein langsameres Molekül nimmt einen Teil des Impulses des schnelleren Moleküls auf. Ein solcher Impulstransport findet allerdings nicht nur innerhalb einer Fluidschicht statt. Aufgrund der ungeordneten Brown’schen Molekularbewegung diffundieren Moleküle auch in benachbarte Fluidschichten ein. Was passiert, wenn nun ein langsameres Molekül in eine Schicht aus schnelleren Teilchen eindiffundiert? Die schnellen Moleküle werden an diesem eindiffundierten Gasteilchen abgebremst und es kommt insgesamt zu einer Verlangsamung der Schicht.
Man kann sich die Situation mit einem Wagen und einer Kugel veranschaulichen. Der Wagen soll mit konstanter Geschwindigkeit gezogen werden, als beim Vorbeifahren plötzlich die schwere Kugel hineingelegt wird. Die Kugel steht dabei für das langsamere Gasmolekül (in diesem Fall sogar Stillstand), das in die schnelleren Fluidschicht eindiffundiert (veranschaulicht durch den Wagen). Da die Kugel beim Einlegen eine geringere Geschwindigkeit als der Wagen hat, muss die Kugel nach dem Einlegen auf die Geschwindigkeit des Wagens beschleunigt werden, sofern die Geschwindigkeit weiterhin konstant bleiben soll. Dies erfordert eine der Masse der Kugel entsprechende Kraft (Kraft = Masse x Beschleunigung). Das Einlegen der langsamen Kugel in den schnelleren Wagen verursacht somit einen Widerstand, der sich durch eine zusätzlich aufzubringende Kraft bemerkbar macht. Würde man diese Kraft nicht aufbringen, dann würde der Wagen an der langsameren Kugel abgebremst werden, ähnlich zu einer Reibungskraft.
Diffusionsprozesse von Gasmolekülen zwischen den einzelnen Schichten einer laminaren Strömung führt zu einem Impulstransport. Auf diesem Impulstransport beruht maßgeblich die Viskosität von Gasen!
Schnellere Schichten geben also ein Teil ihres Impulses durch Diffusion in langsamere Schichten weiter. Insgesamt findet als ein Impulstransport von der bewegten Platte hin zur ruhenden Platte statt. Dieser Impulsstrom, der letztlich einer Kraft zwischen den Schichten entspricht, fließt sozusagen in Richtung abnehmender Geschwindigkeit, d.h. entgegen des Geschwindigkeitsgradienten. Besonders anschaulich wird der Transport des Impulses, wenn die obere Platte aus der Ruhe heraus in Bewegung gesetzt wird. Zunächst wird lediglich die unmittelbar an der oberen Platte haftende Schicht in Bewegung gesetzt. Durch den Transport des Impulses auf die darunter befindliche Schicht, beginnt sich nun diese in Bewegung zu setzen, usw. Der Impuls breitet sich somit allmählich durch die Schichten aus.
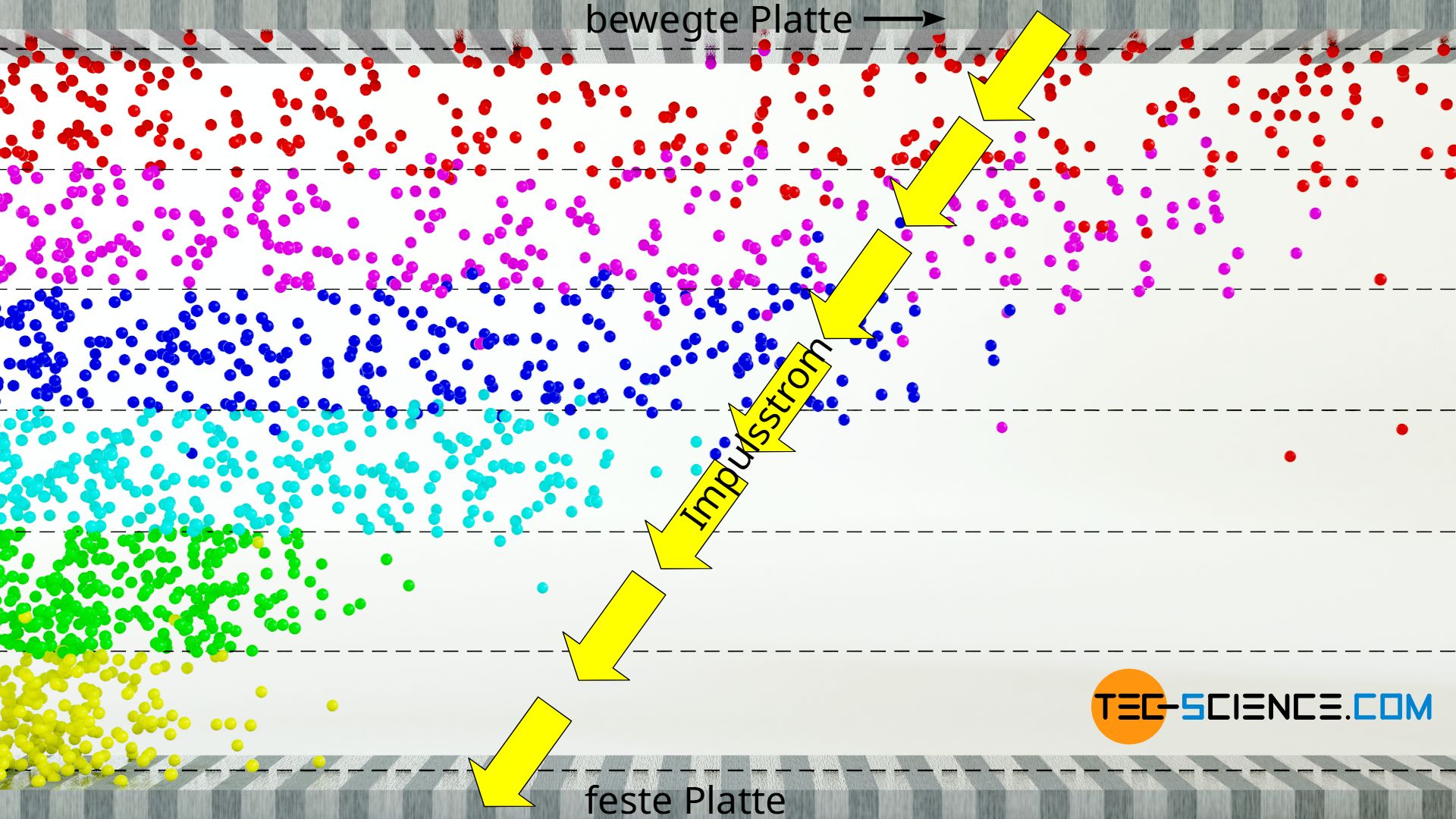
Die Widerstandskraft beim Bewegen der Platte kommt schließlich dadurch zustande, dass das in Bewegung setzen der Gasschichten dadurch behindert wird, dass die untere Platte fixiert ist. Das Festhalten der Platte erfordert letztlich dieselbe Kraft im Vergleich zur Aufrechterhaltung der Bewegung der oberen Platte. Der Impuls wird sozusagen an der oberen Platte eingeleitet und wird von Schicht zu Schicht übertragen und strömt an der unteren Platte schließlich wieder heraus. Im Gleichgewichtszustand findet schließlich keine Netto-Impulsstrom statt, der auf die Fluidschichten übertragen wird, sodass sich diese schließlich mit jeweils konstanter (aber unterschiedlicher) Geschwindigkeit bewegen.
Herleitung der Viskosität von idealen Gasen
Spannung als Impulsstromdichte
Die Kraft F lässt sich ganz allgemein aus der Änderung des Impulses pro Zeit ermitteln:
\begin{align}
&F= \frac{\text{d} p}{\text{d} t} = \dot p ~~~~~\Rightarrow~~~~~\boxed{\text{Kraft = Impulsstrom}}\\[5px]
\end{align}
Die Kraft auf die einzelnen Fluidschichten kommt also durch die Änderung des Impulses, verursacht durch den Impulstransport aufgrund von Diffusionsprozessen, zustande und lässt sich somit auch als Impulsstrom p* auffassen. Bezieht man die Kraft und damit den Impulsstrom auf die Fläche, so erhält man letztlich eine Schubspannung, die sich dann wiederum als Impulsstromdichte p*A interpretieren lässt (Änderung des Impulses pro Zeit- und Flächeneinheit):
\begin{align}
&\tau = \frac{F}{A}= \frac{\dot p}{A} = \dot p_\text{A} ~~~~~\Rightarrow~~~~~\boxed{\text{Spannung = Impulsstromdichte}}\\[5px]
\end{align}
Das Newton’sche Reibungsgesetz (\ref{t}) lässt sich somit auch wie folgt darstellen:
\begin{align}
\label{tt}
&\boxed{\dot p_\text{A} = – \eta \cdot \frac{\text{d} v}{\text{d} y}} \\[5px]
\end{align}
Das negative Vorzeichen wurde an dieser Stelle deshalb eingefügt, um der Tatsache gerecht zu werden, dass der Impulsstrom weg von schnelleren Schichten hin zu langsameren Schichten übertragen wird, d.h. in Richtung abnehmendem Geschwindigkeitsgradienten. An dieser Stelle lässt sich eine interessante Analoge zu anderen Transportvorgängen wie Wärmetransport und Stofftransport ziehen, die letztlich auf dieselbe Weise beschrieben werden:
| Wärmetransport | Stofftransport | Impulstransport | |
|---|---|---|---|
| Gesetz von | Fourier | Fick | Newton |
| \begin{align} \notag &\boxed{\dot q = – \lambda ~\frac{\text{d}T}{\text{d}y}} \end{align} | \begin{align} \notag &\boxed{\dot n = – D~ \frac{\text{d}c}{\text{d}y}} \end{align} | \begin{align} \notag &\boxed{\dot p_A = -\eta~ \frac{\text{d}v}{\text{d}y}} \end{align} | |
| Antrieb | Temperatur- gradient | Konzentrations- gradient | Geschwindigkeits- gradient |
| Charakteristische Größe | Wärmeleit- koeffizient | Diffusions- koeffizient | Viskosität |
| Stromdichte | Wärmestromdichte | Stoffstromdichte | Impulsstromdichte |
Impulstransport zwischen den Schichten
Mithilfe der kinetischen Gastheorie kann man die Viskosität von idealen Gasen rechnerisch ermitteln. Für die Herleitung der Formel betrachten wir die bereits angesprochene Schichtenströmung, bei der sich ein ideales Gas zwischen zwei Platten befindet. Die untere Platte ist dabei fixierst und die obere Platte bewegt sich mit einer konstanten Geschwindigkeit.
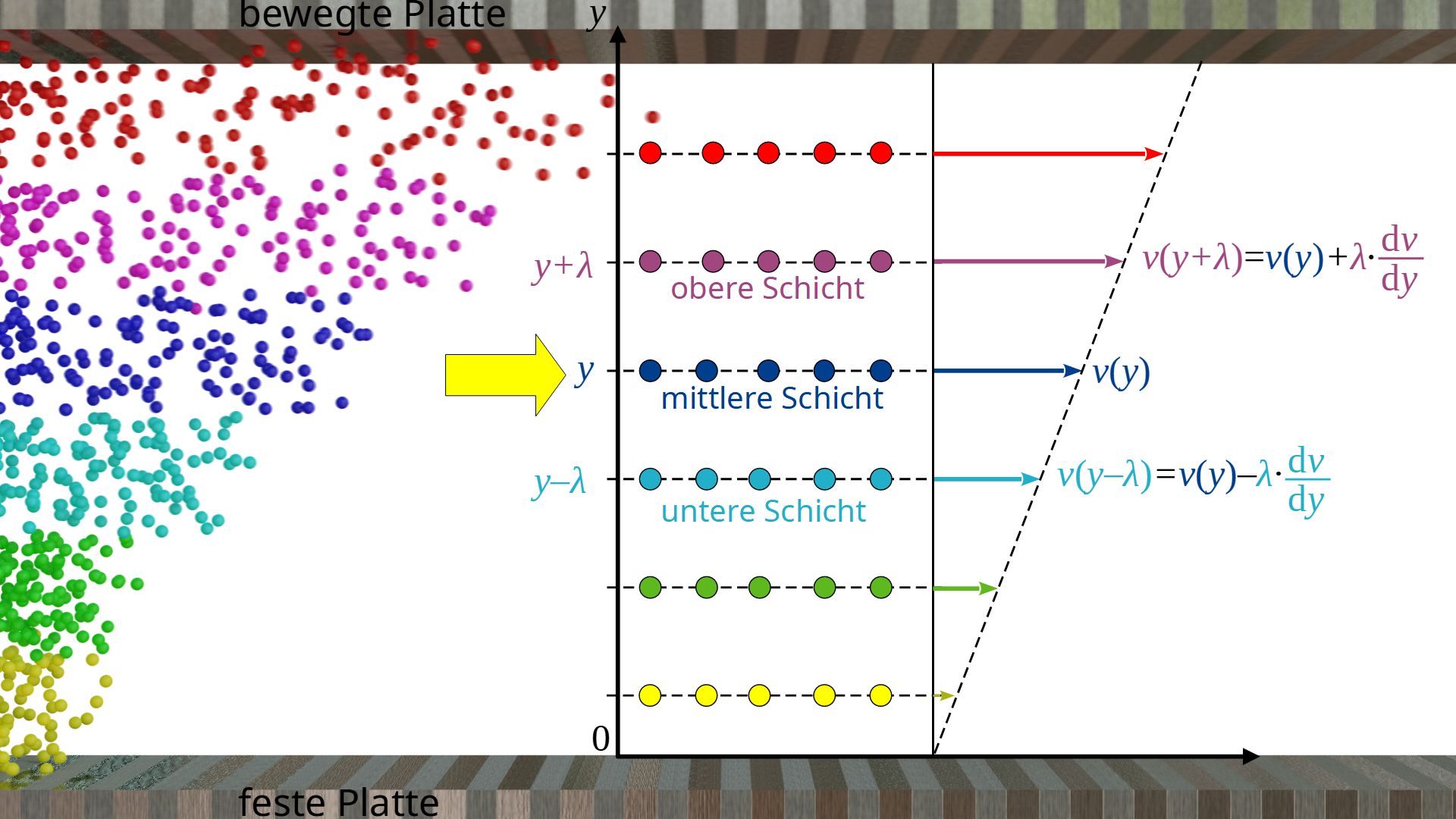
Wir betrachten die Strömung auf mikroskopischer Ebene und bewegen uns jeweils mit den einzelnen Fluidschichten mit. Die durchschnittliche Wegstrecke, die die Gasteilchen zwischen zwei Stößen zurücklegen, wird mittlere freie Weglänge λ genannt. Wir betrachten deshalb Gasschichten, die einen Abstand λ zueinander haben, sodass es bei Diffusionsprozessen jeweils innerhalb dieser Schichten zu einem Stoß und damit zu einem Impulstransport kommt. Wir betrachten nun eine Schicht in einer belieben Höhe y. Die mittlere Geschwindigkeit der Gasmoleküle in x-Richtung bzgl. eines ortsfesten Koordinatensystems (ruhende Platte) sei mit vx(y) bezeichnet.
Die mittlere Geschwindigkeit vx(y+λ)der Gasteilchen im Abstand λ in der darüber befindliche Schicht lässt sich über den Geschwindigkeitsgradienten dv/dy ermitteln:
\begin{align}
&v_{x}(y+\lambda)= v_{x}(y) + \lambda \cdot \frac{\text{d}v}{\text{d}y} \\[5px]
\end{align}
Analog lässt sich die mittlere Geschwindigkeit vx(y-λ) der Gasteilchen im Abstand λ in der darunter befindliche Schicht bestimmen:
\begin{align}
&v_{x}(y-\lambda)= v_{x}(y) – \lambda \cdot \frac{\text{d}v}{\text{d}y} \\[5px]
\end{align}
Bezeichnet n*A die Teilchenstromdichte, d.h. die Anzahl der Teilchen pro Zeit- und Flächeneinheit, die von der oberen Schicht bzw. unteren Schicht in die mittlere Schicht eindiffundiert, dann lassen sich die entsprechenden Impulsströme mit nachfolgender Formel bestimmen. Beachte, dass die Teilchenstromdichte für beide Schichten identisch ist, sofern wir von einer inkompressiblen Gasströmen ausgehen, bei der die Teilchendichte in jedem Punkt der Strömung dieselbe ist.
\begin{align}
&\dot p_{A}(y+\lambda) = \dot n_\text{A} \cdot \overbrace{m \cdot v_{x}(y+\lambda)}^{\text{Impuls eines Teilchens}} = \dot n_\text{A} \cdot m \cdot \left(v_{x}(y) + \lambda \cdot \frac{\text{d}v}{\text{d}y} \right) \\[5px]
&\dot p_{A}(y-\lambda) = \dot n_\text{A} \cdot m \cdot v_{x}(y-\lambda) = \dot n_\text{A} \cdot m \cdot \left(v_{x}(y) – \lambda \cdot \frac{\text{d}v}{\text{d}y} \right) \\[5px]
\end{align}
Der Netto-Impulsstrom p*A(y) in der Schicht auf der Höhe y ergibt sich schließlich aus der Summe beider Impulsströme. Gemäß des gewählten Koordinatensystems entspricht der von unten nach oben gerichtete Impulsstrom (in positive y-Richtung zeigten) auch einem positiven Wert und der nach unten gerichtete Impulsstrom einem negativen Wert. Für den Netto-Impulsstrom gilt deshalb:
\begin{align}
\dot p_\text{A}(y) &= \dot p_{A}(y-\lambda) ~-~ \dot p_{A}(y+\lambda) \\[5px]
&= \dot n_\text{A} \cdot m \cdot \left(v_{x}(y) – \lambda \cdot \frac{\text{d}v}{\text{d}y} \right)- \dot n_\text{A} \cdot m \cdot \left(v_{x}(y) + \lambda \cdot \frac{\text{d}v}{\text{d}y} \right) \\[5px]
&= \dot n_\text{A} \cdot m \cdot \left(v_{x}(y) ~- \lambda \cdot \frac{\text{d}v}{\text{d}y} ~-~ v_{x}(y) ~- \lambda \cdot \frac{\text{d}v}{\text{d}y}\right) \\[5px]
\end{align}
\begin{align}
&\boxed{\dot p_\text{A}= – 2~ \dot n_\text{A} \cdot m \cdot \lambda \cdot \frac{\text{d}v}{\text{d}y}} ~~~\text{Netto-Impulsstrom}\\[5px]
\end{align}
Viskosität von idealen Gasen in Abhängigkeit der Teilchenstromdichte
Gemäß obenstehender Gleichung ist der Netto-Impulsstrom offensichtlich keine Funktion der Variablen y mehr und somit in jedem Punkt der Strömung identisch! Vergleicht man diese Formel mit dem Newtonschen Reibungsgesetz (\ref{tt}), so zeigt sich sofort, dass der Ausdruck 2⋅n*A⋅m⋅λ offensichtlich der Viskosität η entspricht:
\begin{align}
&\dot p_\text{A} = – \eta \cdot \frac{\text{d} v}{\text{d} y} \\[5px]
&\dot p_\text{A}=- \underbrace{2~ \dot n_\text{A} \cdot m \cdot \lambda}_{\eta} \cdot \frac{\text{d}v}{\text{d}y} \\[5px]
\label{eta}
&\boxed{\eta= 2~ \dot n_\text{A} \cdot m \cdot \lambda} ~~~\text{Viskosität idealer Gase}\\[5px]
\end{align}
Die Viskosität eines (idealen) Gases ist also nur von der Masse eines Gasteilchens, der mittleren freien Weglänge und der Teilchenstromdichte abhängig. Der flächenbezogene Teilchenstrom n*A, der von einer darüber bzw. darunter befindlichen Schicht eindiffundiert, ist wiederum davon abhängig wie stark sich die Gasmoleküle aufgrund der ungeordneten Diffusionsbewegung bewegen (Brownsche Molekularbewegung). Dies ist wiederum durch die Temperatur bestimmt.
Ist die Temperatur hoch, dann finden Diffusionsprozesse vermehrt statt und es diffundieren vermehrt Teilchen zwischen den Schichten. Die Teilchenstromdichte ist entsprechend groß und somit auch der Impulstransport. Dies macht sich einer zunehmenden Kraft bemerkbar, die für das Aufrechterhalten der makroskopischen Strömung (Bewegung der Platte) erforderlich ist! Die Viskosität von Gasen nimmt deshalb im Allgemeinen mit der Temperatur zu und nicht wie bei Flüssigkeiten ab!
An dieser Stelle zeigt sich auch die Tatsache, dass bei idealen Gasen der Druck keinen Einfluss auf die Viskosität hat. Zwar steigt die Teilchendichte und damit der diffundierende Teilchenstrom proportional mit zunehmendem Druck, jedoch nimmt im selben Maße die mittlere freie Weglänge ab. Beide Effekte heben sich also gegenseitig auf.
Bei idealen Gasen ist die Viskosität unabhängig des Drucks und steigt mit zunehmender Temperatur an!
Viskosität von idealen Gasen in Abhängigkeit der Temperatur
An dieser Stelle möchten wir die quantitative Abhängigkeit der Viskosität idealer Gase von der Temperatur explizit herleiten. Hierfür muss ein Zusammenhang zwischen der senkrecht zur Strömung diffundierenden Teilchenstromdichte und der Temperatur gefunden werden.
Hierzu bewegen wir uns in Gedankten mit einer Schicht mit, sodass diese relativ zu uns als Beobachter ruht. Die Gasteilchen selbst sind auf mikroskopischer Ebene allerdings keinesfalls in Ruhe. Sie bewegen sich aufgrund der Brown’schen Molekularbewegung völlig ungeordnet in alle Richtungen gleichermaßen. Gemäß der Maxwell-Boltzmann-Verteilung ist die mittlere Geschwindigkeit eines Gasteilchens vT wie folgt mit der Temperatur T des Gases verknüpft:
\begin{align}
\label{a}
&\boxed{ \overline{v_\text{T}} = \sqrt{\frac{8 k_B T}{\pi m}}} ~~~\text{arithmetisch gemittelte Geschwindigkeit} \\[5px]
\end{align}
In dieser Gleichung bezeichnet m die Masse eines Gasteilchens und kB die Boltzmann-Konstante. Beachte, dass die Geschwindigkeit vT die mittlere Geschwindigkeit relativ zu den sich bewegenden Fluidschichten darstellt und nicht die Überlagerung der makroskopischen Strömungsbewegung beinhaltet. Letztere hat ohnehin keinen Einfluss auf die Temperatur; die Temperatur eines Gases ist schließlich nicht davon abhängig, ob sich das Gas in Ruhe befindet oder sich bewegt.
Betrachten wir nun zunächst eine gerichtete Strömung bei der sich alle Teilchen mit der (mittleren) Geschwindigkeit v in dieselbe Richtung bewegen. Die Anzahl der Teilchen die pro Zeit- und Flächeneinheit strömen (Teilchenstromdichte) lässt sich wie folgt ermitteln. Hierzu betrachten wir ein Flächenelement dA durch das die Teilchen innerhalb einer Zeit dt mit der (mittleren) Geschwindigkeit v strömen. Die Teilchen legen dabei die Strecke dl=v⋅dt zurück. Somit durchströmen die Teilchen offensichtlich folgendes Volumen dV:
\begin{align}
&\text{d}V =\text{d}A \cdot \text{d}l = \text{d}A \cdot \overline{v} \cdot \text{d}t \\[5px]
\end{align}
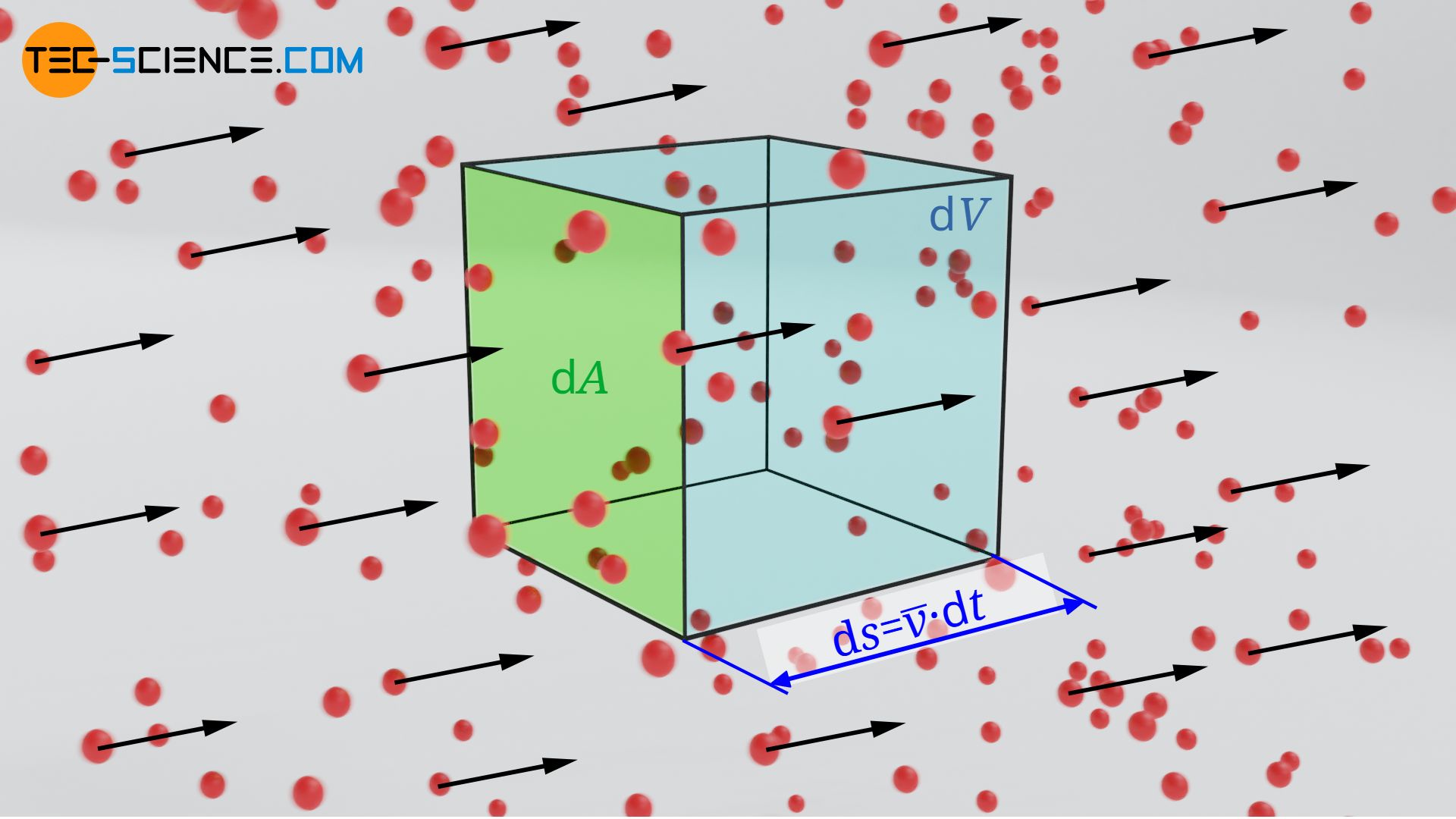
Bei einer gegeben Teilchendichte n (Anzahl Teilchen pro Volumeneinheit) sind in diesem Volumen bzw. durchströmen dieses Volumen somit folgende Anzahl an Teilchen dN:
\begin{align}
&\text{d}N = n \cdot \text{d}V =n \cdot \text{d}A \cdot \overline{v} \cdot \text{d}t \\[5px]
\end{align}
Die pro Zeit- und Flächeneinheit hindurchtretende Anzahl an Teilchen (Teilchenstromdichte n*A) durch eine senkrecht zur Strömung gerichtete Fläche ergibt sich somit wie folgt:
\begin{align}
&\dot n_\text{A} = \frac{\text{d}N}{\text{d}A \cdot \text{d}t} =n \cdot \overline{v} \\[5px]
&\boxed{\dot n_\text{A} =n \cdot \overline{v} } ~~~\text{Teilchenstromdichte einer gerichteten Bewegung}\\[5px]
\end{align}
Betrachten wir nun wieder unsere Schichtenströmung, mit der wir uns in Gedanken mitbewegen. Aus dieser Sichtweise ist die Strömung nicht mehr gerichtet, sondern mit einer mittleren Geschwindigkeit vT völlig ungeordnet. Die Teilchen bewegen sich in alle Raumrichtungen gleichermaßen. Dies bedeutet, dass sich nur ein Sechstel der Teilchen nach unten bewegt und in eine darunter befindliche Gasschicht eindiffundiert. Die senkrecht zur Hauptströmung gerichtete Teilchenstromdichte ist somit nur ein Sechstel so groß:
\begin{align}
\label{na}
&\boxed{\dot n_\text{A} = \frac{1}{6} n \cdot \overline{v_\text{T}} } ~~~\text{Teilchenstromdichte einer ungeordneten Bewegung}\\[5px]
\end{align}
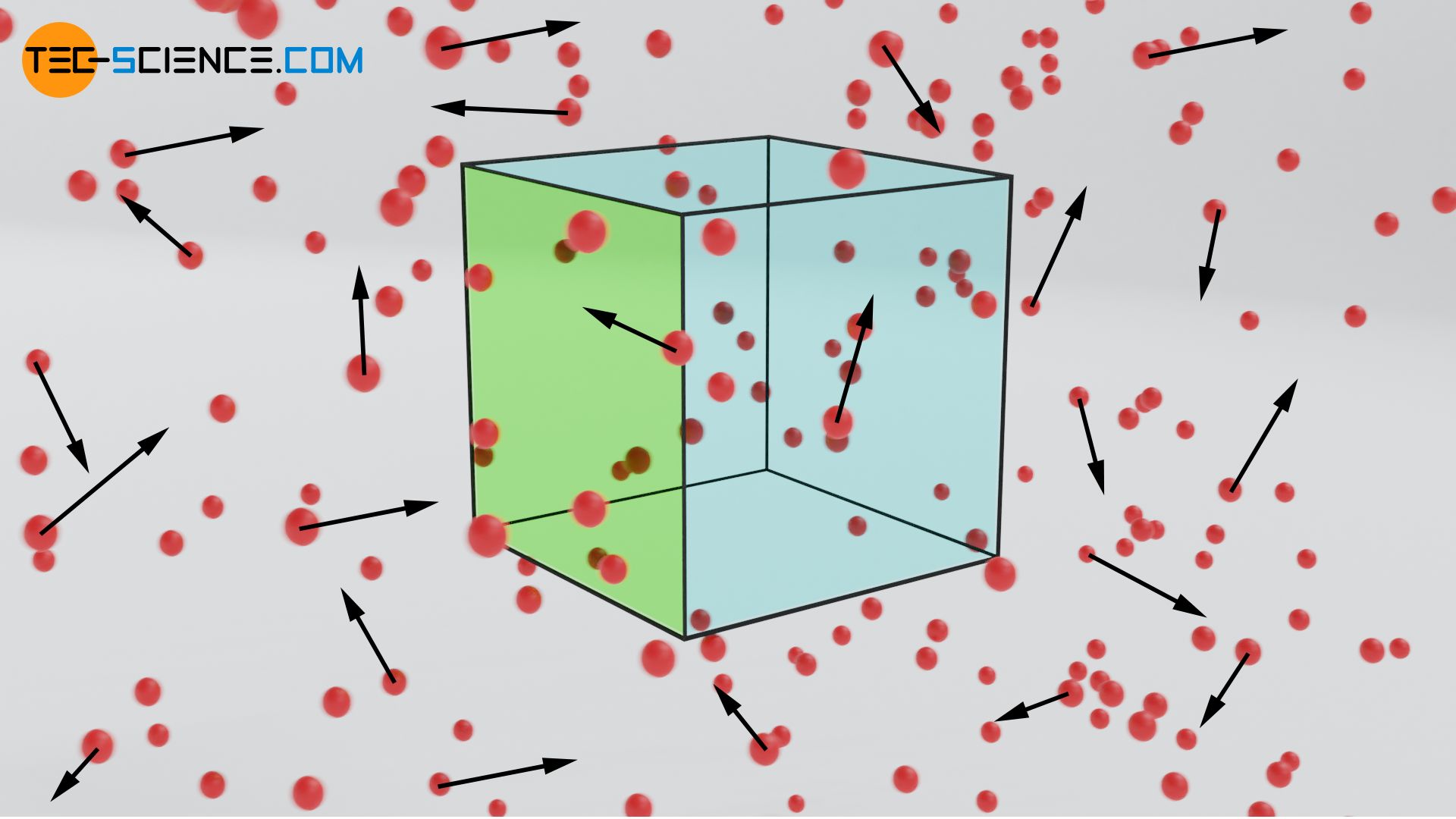
Einsetzen von (\ref{a}) in Gleichung (\ref{na}) ergibt schließlich folgende diffundierende Teilchenstromdichte in Abhängigkeit der Temperatur:
\begin{align}
&\dot n_\text{A} = \frac{1}{6} n \cdot \underbrace{\sqrt{\frac{8 k_B T}{\pi m}}}_{\overline{v_\text{T}}} \\[5px]
\end{align}
Diese Gleichung in Formel (\ref{eta}) eingesetzt, zeigt schlussendlich folgenden Zusammenhang zwischen der Viskosität und der Temperatur:
\begin{align}
&\eta= 2~ \dot n_\text{A} \cdot m \cdot \lambda \\[5px]
&\eta= 2~ \frac{1}{6} n \cdot \sqrt{\frac{8 k_B T}{\pi m}} \cdot m \cdot \lambda \\[5px]
\label{ac}
&\boxed{\eta= \frac{1}{3} n \cdot \sqrt{\frac{8 k_B m T}{\pi}} \cdot \lambda} \\[5px]
\end{align}
Als letzten kann noch die mittlere freie Weglänge λ durch die Teilchendichte n und den Durchmesser der Gasmoleküle d ausgedrückt werden (Herleitung siehe Artikel Mittlere freie Weglänge & Stoßzahl):
\begin{align}
& \boxed{\lambda = \frac{1}{\sqrt{2}~n ~\pi d^2}} \\[5px]
\end{align}
Setzt man diese Formel in Gleichung (\ref{ac}) ein, dann zeigt sich schließlich folgende Formel zur Berechnung der Viskosität von idealen Gasen:
\begin{align}
&\eta= \frac{1}{3} n \cdot \sqrt{\frac{8 k_B m T}{\pi}} \cdot \lambda \\[5px]
&\eta= \frac{1}{3} n \cdot \sqrt{\frac{8 k_B m T}{\pi}} \cdot \frac{1}{\sqrt{2}~n ~\pi d^2} \\[5px]
&\boxed{\eta= \sqrt{\frac{4 k_B m~T}{9\pi^3~d^4}}} \\[5px]
&\boxed{\eta \sim \sqrt{T}} \\[5px]
\end{align}
In dieser Formel wird offensichtlich, dass die Teilchendichte und damit der Druck keinen Einfluss auf die Viskosität von idealen Gasen nimmt. Lediglich die Temperatur als variable Größe beeinflusst die Viskosität. Die Viskosität steigt proportional mit der Wurzel der Temperatur!
Beachte, dass diese Formel nur für laminare Strömungen gilt, bei denen sich die Schichten makroskopisch nicht mischen und nur auf mikroskopischer Ebene Diffusionsprozesse zwischen den Schichten stattfinden. Bei turbulenten Strömungen ist der Impulsaustausch durch die Verwirbelungen größer und die Viskosität entsprechend höher.
Vergleich zwischen Viskosität und Wärmeleitfähigkeit
Gleichung (\ref{na}) kann auch direkt in die Formel (\ref{eta}) für die Viskosität eingesetzt werden, sodass folgt:
\begin{align}
&\eta= 2~ \dot n_\text{A} \cdot m \cdot \lambda \\[5px]
&\eta= 2~ \frac{1}{6} n \cdot \overline{v_\text{T}} \cdot m \cdot \lambda \\[5px]
&\eta= \frac{1}{3} \underbrace{n \cdot m}_{\rho} \cdot \lambda \cdot \overline{v_\text{T}} \\[5px]
&\boxed{\eta= \frac{1}{3} \cdot \rho \cdot \lambda \cdot \overline{v_\text{T}}} \\[5px]
\end{align}
Bei der Herleitung wurde ausgenutzt, dass das Produkt von Teilchendichte und Masse eines Teilchens gerade der Dichte ϱ des Gases entspricht. An dieser Stelle zeigt sich ein interessante Analogie zur Wärmeleitfähigkeit k von idealen Gasen (um Verwechslungen mit der mittleren freien Weglänge zu vermeiden, wurde die Wärmeleitfähigkeit nicht mit λ sondern mit k bezeichnet):
\begin{align}
& \boxed{k= \frac{1}{3} \cdot \rho \cdot \lambda \cdot c_v \cdot \overline{v_\text{T}} } \\[5px]
\end{align}
Die Wärmeleitfähigkeit folgt also im Prinzip denselben Gesetzmäßigkeiten wie die Viskosität, d.h. sie nimmt insbesondere mit steigender mittlerer Teilchengeschwindigkeit zu (steigender Temperatur). Dies ist insofern nicht verwunderlich, da mit der Diffusion von Teilchen nicht nur ein Impulstransport, sondern auch ein (Wärme-)Energietransport verbunden ist.






