In diesem Artikel sind ausgewählte Aufgaben mit Lösungen für die Anwendung der Bernoulli-Gleichung gegeben.
Bernoulli-Gleichung
Die Bernoulli-Gleichung beruht auf der Energieerhaltung von strömenden Fluiden. Die Herleitung wurde im Artikel Herleitung der Bernoulli-Gleichung ausführlich gezeigt. Für reibungsfrei strömende, inkompressible Fluide wie Flüssigkeiten besagt diese Gleichung, dass die Summe aus statischem Druck p, dynamischem Druck ½⋅ϱ⋅v² und hydrostatischem Druck ϱ⋅g⋅h entlang einer Stromlinie konstant ist:
\begin{align}
& \boxed{p + \frac{1}{2} \rho ~v^2 +\rho g h= \text{konstant}} ~~~\text{Bernoulli-Gleichung}\\[5px]
\end{align}
Zwei Punkte auf einer Stromlinie sind somit wie folgt miteinander verknüpft:
\begin{align}
& \boxed{p_1 + \frac{1}{2} \rho v_1^2 +\rho g h_1= p_2 + \frac{1}{2} \rho v_2^2 + \rho g h_2} \\[5px]
\end{align}
Im Folgenden sollen ausgewählte Beispiele für die Anwendung der Bernoulli-Gleichung gezeigt werden.
Horizontale Rohrströmung mit sich verengendem Querschnitt
Durch ein horizontales Rohr strömt Wasser mit einer Dichte von 1 g/cm³. Der Rohrquerschnitt verengt sich an einem Reduzierstück von 80 cm² auf 40 cm². Der statische Druck vor der Verengung betrage 4 bar und die Strömungsgeschwindigkeit 4 m/s. Die Strömung sei inkompressibel und reibungsfrei. Welcher statische Druck wird nach der Verengung gemessen?
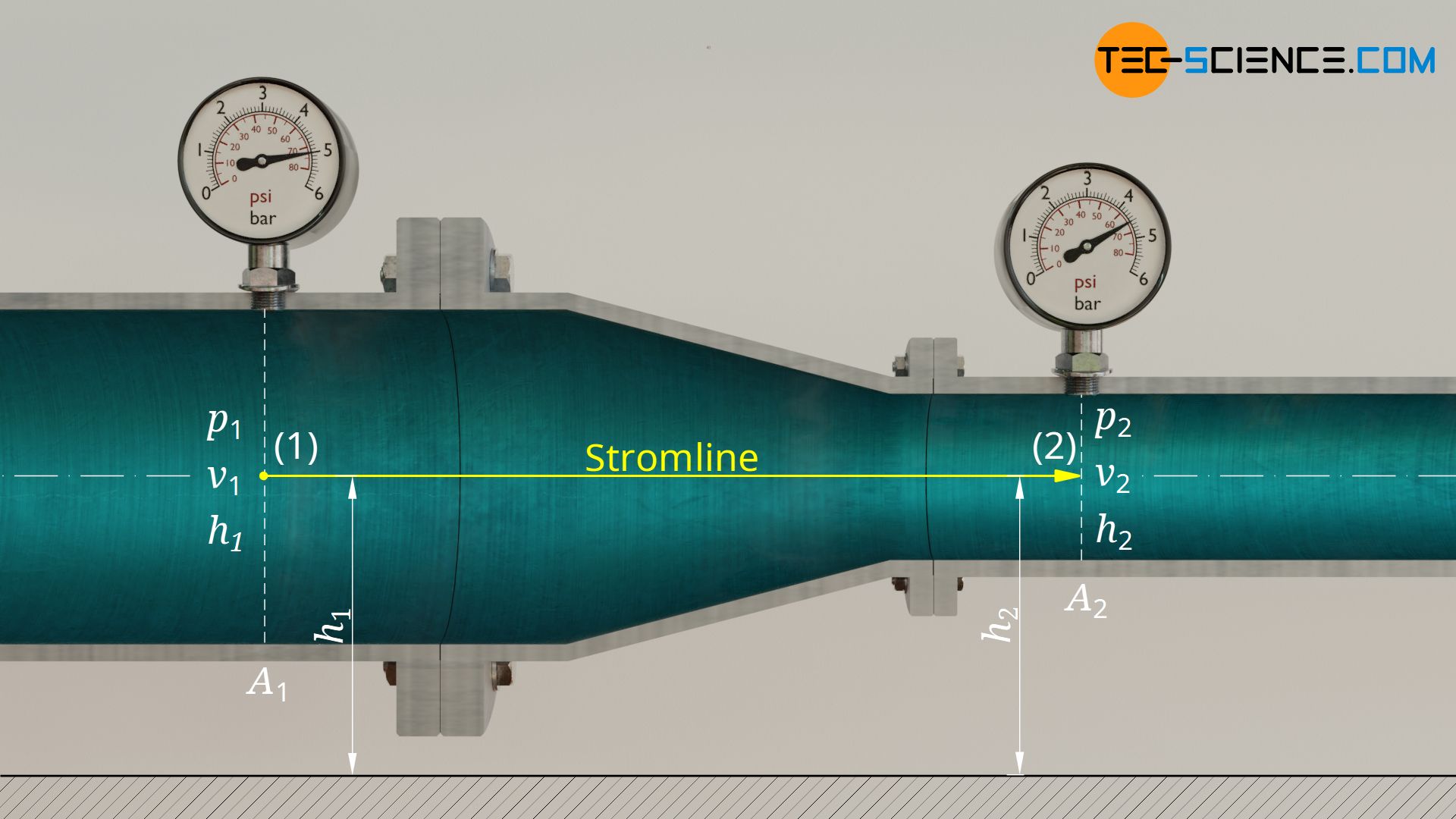
Um diese Frage zu beantworten, betrachten wir eine Stromlinie und jeweils einen Punkt vor der Verengung und nach der Verengung. Folgende Zustandsgrößen sind dabei bekannt:
| Zustand 1 (großes Rohr) | Zustand 2 (kleines Rohr) | |
| Höhe | h1 = h2 | h2 = h1 |
| Geschwindigkeit | v1 = 4 m/s | v2 = ? |
| Statischer Druck | p1 = 4 bar | p2 = gesucht |
Beachte, dass sich aufgrund der horizontalen Ausrichtung des Rohres beide Punkte auf derselben Höhe befinden (h2 = h1). Die Bernoulli-Gleichung vereinfacht sich folglich dahingehend, dass sich die damit verbundenen hydrostatischen Drücke gegenseitig aufheben. Für den statischen Druck p2 nach der Verengung gilt damit:
\begin{align}
\require{cancel}
&p_1 + \frac{1}{2} \rho v_1^2 + \cancel{\rho g h_1}= p_2 + \frac{1}{2} \rho v_2^2 + \cancel{\rho g h_2}\\[5px]
&p_1 + \frac{1}{2} \rho v_1^2 = p_2 + \frac{1}{2} \rho v_2^2 \\[5px]
\label{p2}
&\underline{p_2 = p_1 + \frac{1}{2} \rho v_1^2 -\frac{1}{2} \rho v_2^2} \\[5px]
\end{align}
Für die Berechnung des statischen Drucks benötigen wir noch die Strömungsgeschwindigkeit nach der Verengung. Diese erhalten wir durch die Bedingung der Massenerhaltung (Kontinuitätsbedingung). Innerhalb der Zeit Δt strömt das Fluid vor der Verengung mit der Geschwindigkeit v1 und legt damit die Strecke Δs1=v1⋅Δt zurück. Folgendes Fluidvolumen schiebt sich somit durch den Querschnitt A1:
\begin{align}
\label{1}
& \Delta V = A_1 \cdot \Delta s_1 = A_1 \cdot v_1 \cdot \Delta t \\[5px]
\end{align}
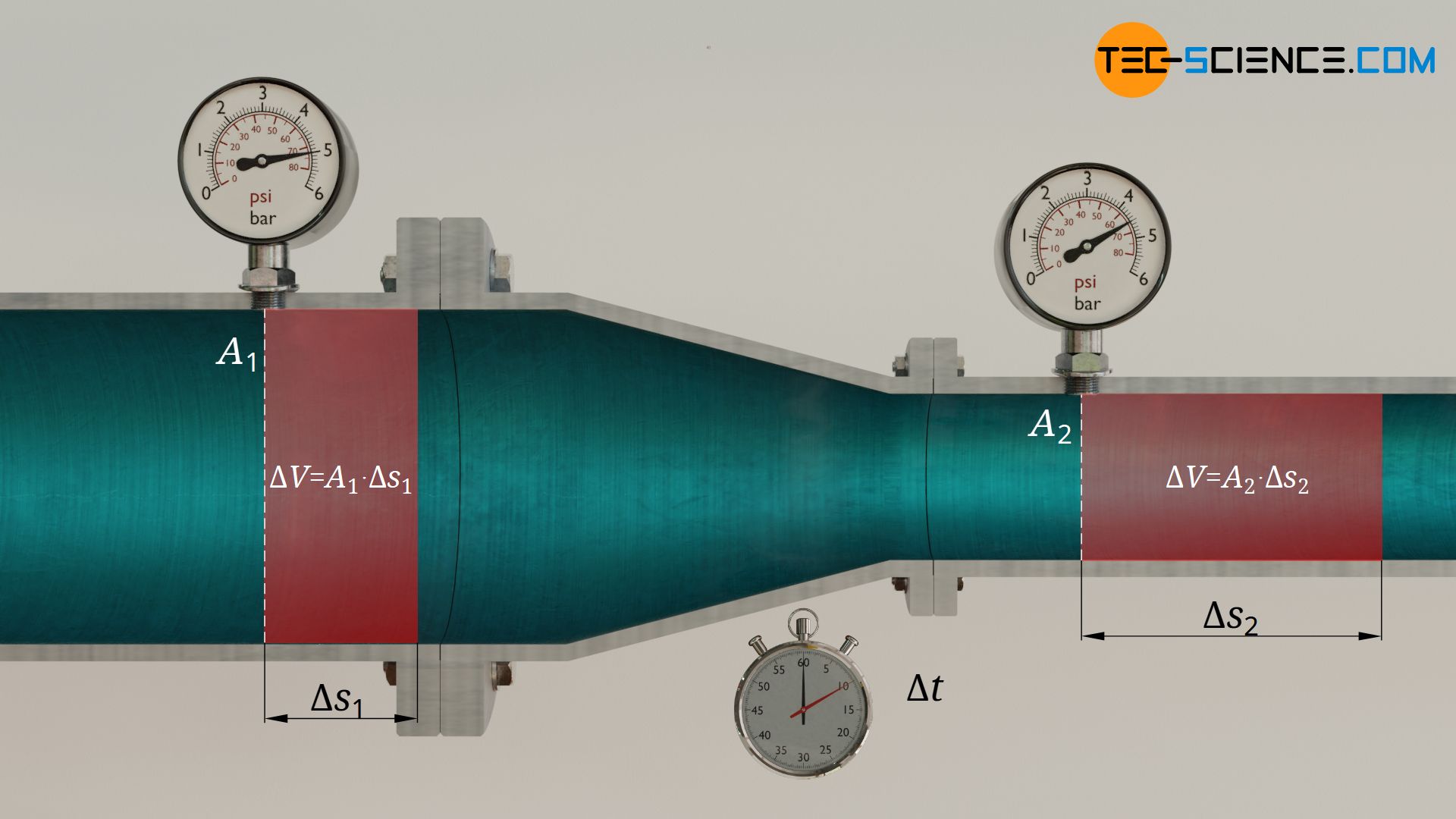
Aufgrund der Massenerhaltung und der Inkompressibilität des Wasser, muss innerhalb derselben Zeit Δt auch dasselbe Volumen ΔV durch den Querschnitt A2 geschoben werden. Da der Querschnitt kleiner ist, muss die zurückgelegte Strecke Δs2 des Fluidvolumens größer sein, was die höhere Strömungsgeschwindigkeit v2 erklärt:
\begin{align}
\label{2}
& \Delta V = A_2 \cdot \Delta s_2 = A_2 \cdot v_2 \cdot \Delta t \\[5px]
\end{align}
Gleichsetzung von Gleichung (\ref{1}) und (\ref{2}) und anschließendes Umstellen nach v2 liefert schließlich die gesuchte Strömungsgeschwindigkeit im verengten Querschnitt:
\begin{align}
\require{cancel}
& A_2 \cdot v_2 \cdot \cancel{\Delta t} = A_1 \cdot v_1 \cdot \cancel{\Delta t} \\[5px]
& \boxed{v_2 = \frac{A_1}{A_2} \cdot v_1} = \frac{80 \text{m²}}{40 \text{m²}} \cdot 4 \frac{\text{m}}{\text{s}} = \underline{\underline{8 \frac{\text{m}}{\text{s}}}} \\[5px]
\end{align}
Aufgrund der Verengung des Querschnitts auf nur noch die Hälfte vergrößert sich die Strömungsgeschwindigkeit folglich auf das Doppelte. Alle Werte können nun in Gleichung (\ref{p2}) eingesetzt werden. Beachte, dass der Druck in der Grundeinheit N/m² zu verwenden ist und die Dichte in der Einheit kg/m³.
\begin{align}
&p_2 = p_1 + \frac{1}{2} \rho v_1^2 -\frac{1}{2} \rho v_2^2 \\[5px]
&p_2 = 4 \cdot 10^5 \tfrac{\text{N}}{\text{m²}} + \frac{1}{2} 1000 \tfrac{\text{kg}}{\text{m³}} ~\left(4 \tfrac{\text{m}}{\text{s}} \right)^2 – \frac{1}{2} 1000 \tfrac{\text{kg}}{\text{m³}} ~\left(8 \tfrac{\text{m}}{\text{s}} \right)^2 =3,76 \cdot 10^5 \tfrac{\text{N}}{\text{m²}} \\[5px]
&\underline{\underline{p_2 = 3,76 ~\text{bar}}}\\[5px]
\end{align}
Die Zunahme der Strömungsgeschwindigkeit sorgt also für die eine Abnahme des statischen Druck von ursprünglich 4 bar auf 3,76 bar. Anschaulich kann dies damit erklärt werden, dass ein Teil der mit dem statischen Druck verbundenen Energie für die Beschleunigung des Wasser aufgewendet werden musste. Die Zunahme der kinetischen Energie des Wassers erfolgte zu Lasten des statischen Drucks. Ausführlichere Informationen zu diesem Phänomen finden sich im Artikel Bernoulli-Effekt.
Strömung in einem Wasserschlauch mit Düse
An einem Wasserhahn wird ein Schlauch mit einem Innenquerschnitt von 1,24 cm² angeschlossen. Der Schlauch führt in eine Höhe von 6 Metern, wo das Wasser aus einer Düse ins Freie strömt und in einen Pool läuft. Das Becken füllt sich dabei mit 30 Litern pro Minute. Ein Meter über dem Boden ist am Schlauch ein Druckmessgerät zur Messung des statischen Drucks angebracht. Dieser zeigt einen Wert von 2 bar an. Der Umgebungsdruck der Luft betrage 1 bar. Die Strömung sei inkompressibel und reibungsfrei. Mit welcher Geschwindigkeit tritt das Wasser aus der Düse?

Zur Beantwortung dieser Frage betrachten wir eine Stromlinie, die von der Messstelle zum Ausgang der Düse führt. In diesem Fall müssen die Terme für die Lageenergien (hydrostatische Drücke) in der Bernoulli-Gleichung mitberücksichtigt werden. Folgende Daten sind zunächst bekannt:
| Zustand 1 (Druckmessgerät) | Zustand 2 (Düse) | |
| Höhe | h1 = 1 m | h2 = 6 m |
| Geschwindigkeit | v1 = ? | v2 = gesucht |
| Statischer Druck | p1 = 2 bar | p2 = ? |
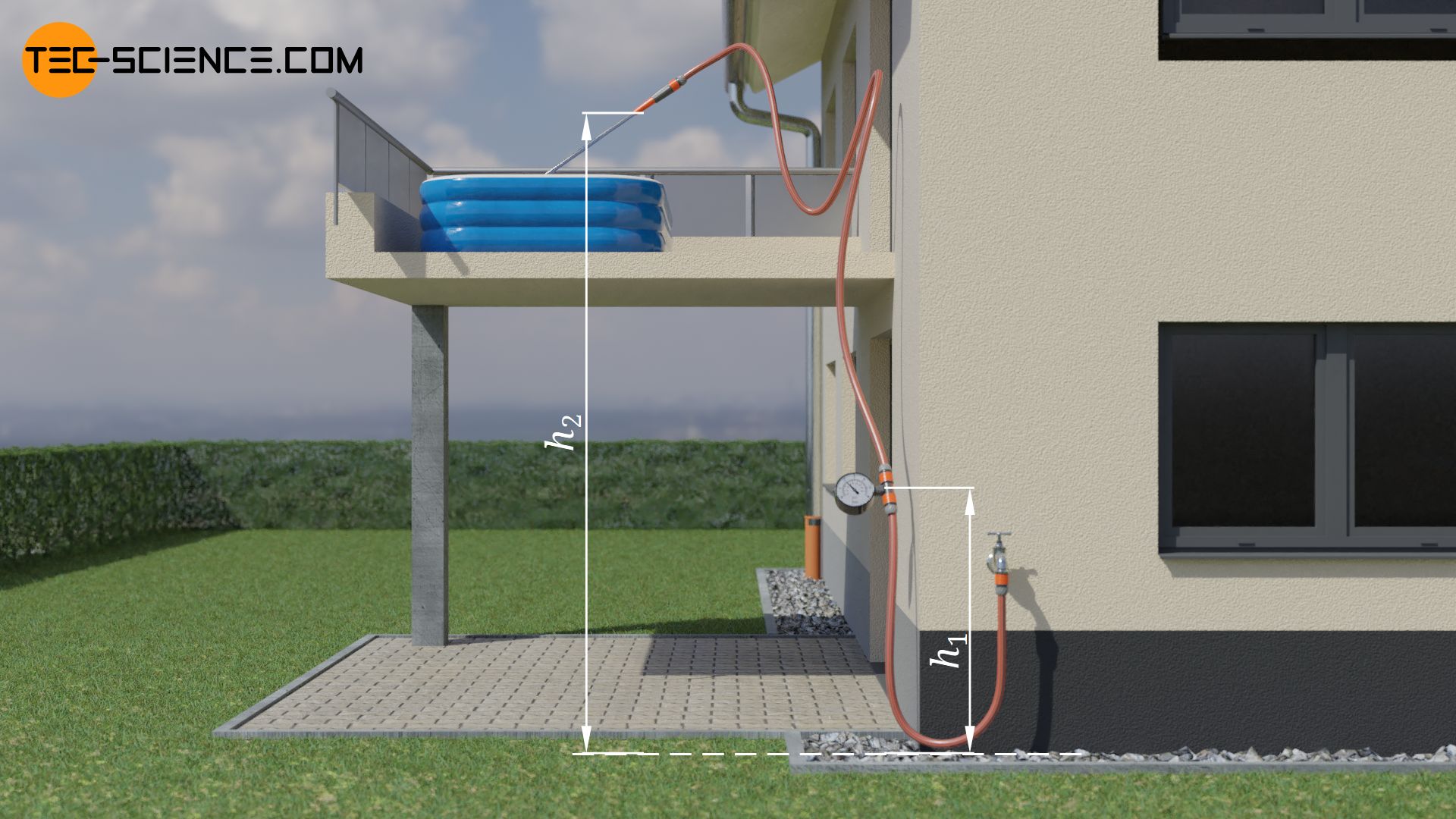
Die Strömungsgeschwindigkeit v1 an des Messstelle kann über den Volumenstrom bestimmt werden, mit dem sich das Becken füllt. Aufgrund der Inkompressibilität muss der Volumenstrom an der Messstelle genauso groß sein wie der Volumenstrom, der aus der Düse tritt und das Becken befüllt. Bei einer Strömungsgeschwindigkeit v1 tritt innerhalb der Zeit Δt folgendes Volumen durch den Schlauchquerschnitt A1:
\begin{align}
&\Delta V = A_1 \cdot v_1 \cdot \Delta t\\[5px]
\end{align}
Für den Volumenstrom V* als Quotient aus durchströmtem Volumen ΔV und hierfür benötigter Zeit Δt gilt somit:
\begin{align}
&\dot V = \frac{\Delta V}{\Delta t} = A_1 \cdot v_1 \\[5px]
\end{align}
Umstellen dieser Gleichung liefert für die Strömungsgeschwindigkeit v1 schließlich einen Wert von etwa 4,03 m/s. Beachte, dass der Volumenstrom bei Einsetzen in die Formel zunächst von der Einheit L/min in die Einheit m³/s umgerechnet werden muss:
\begin{align}
&v_1 = \frac{\dot V}{A_1} = \frac{5 \cdot 10^{-4} ~ \tfrac{\text{m³}}{\text{s}}}{1,24\cdot 10^{-4} ~\text{m²}}=\underline{\underline{4,03 \frac{\text{m}}{\text{s}}}} \\[5px]
\end{align}
Zuletzt fehlt noch der statische Druck p2 am Ausgang der Düse. Da das Wasser ungehindert ins Freie strömt, verspürt dieser nur den Druck der Umgebung. Der Umgebungsdruck zwingt dem frei strömenden Wasserstrahl somit seinen statischen Druck auf. Dies bezeichnet man auch als Freistrahlbedingung. Es gilt also:
\begin{align}
&p_2 = \underline{\underline{1~ \text{bar}}} \\[5px]
\end{align}
Als Freistrahlbedingung bezeichnet man das Aufprägen des Umgebungsdrucks einem frei auströmenden Fluids aus einer Öffnung!
Da nun alle Größen bekannt sind, können diese in die Bernoulli-Gleichung eingesetzt werden und nach der Strömungsgeschwindigkeit v2 aufgelöst werden:
\begin{align}
& p_1 + \frac{1}{2} \rho v_1^2 +\rho g h_1= p_2 + \frac{1}{2} \rho v_2^2 + \rho g h_2 \\[5px]
&v_2 = \sqrt{\frac{2~(p_1-p_2)}{\rho} + 2g (h_1-h_2) + v_1^2} = \underline{\underline{10,87 \frac{\text{m}}{\text{s}}}} \\[5px]
\end{align}
Das Wasser tritt also mit einer Geschwindigkeit von 10,87 m/s aus der Düse aus.
Ausflussgesetz von Torricelli
An einem oben offenen Becken mit Wasser ist seitlich ein Wasserhahn angebracht. Ein Schlauch wird mit einem Ende an den Hahn angeschlossen. Auf das andere Ende wird eine Düse mit verstellbarem Querschnitt montiert. Der Wasserstrahl tritt durch die Düse ins Freie. Das Becken sei so groß, dass sich der Wasserspiegel (fast) nicht ändert, während das Wasser aus der Düse spritzt. Die Strömung sei inkompressibel und reibungsfrei. Mit welcher Geschwindigkeit tritt das Wasser aus der Düse, wenn sich die Wasseroberfläche auf der Höhe h oberhalb als der Düsenöffnung befindet?

Um diese Aufgabe zu lösen, betrachten wir eine Stromlinie, die von der Wasseroberfläche bis zum Ausgang der Düse führt. Das Bezugsniveau für die Höhen zu Berechnung der hydrostatischen Drücke legen wird auf die Höhe der Düse. Somit sind folgende Werte bekannt:
| Zustand 1 (Wasseroberfläche) | Zustand 2 (Düse) | |
| Höhe | h1 = h | h2 = 0 |
| Geschwindigkeit | v1 ≈ 0 | v2 = gesucht |
| Statischer Druck | p1 = pu | p2 = pu |

Beachte, dass sich der Wasserspiegel laut Aufgabenstellung nicht merklich ändert, wenn das Wasser durch die Düse tritt. Die Sinkgeschwindigkeit bzw. die Strömungsgeschwindigkeit eines Fluidteilchens an der Wasseroberfläche beträgt deshalb ungefähr null (v1≈0).
Ferner entspricht der statische Druck an der Wasseroberfläche gerade dem Umgebungsdruck pu, da dieser der Wasseroberfläche seinen Druck aufprägt. Dies ist im Prinzip nichts anderes als die Freistrahlbedingung – lediglich mit dem Unterschied, dass sich die Wasseroberfläche nicht entgegen des Umgebungsdrucks bewegt, sondern mit dem Umgebungsdruck.
Ferner gilt die Freistrahlbedingung auch beim Austritt des Wassers aus der Düse. Dort wirkt als statischer Druck ebenfalls der Druck der Umgebung pu. Zur Lösung der Aufgabe ist der genaue Wert des Umgebungsdrucks nicht erforderlich, da sich dieser in der Bernoulli-Gleichung herauskürzt:
\begin{align}
\require{cancel}
& p_1 + \frac{1}{2} \rho v_1^2 +\rho g h_1= p_2 + \frac{1}{2} \rho v_2^2 + \rho g h_2 \\[5px]
& \cancel{p_u }+ \frac{1}{2} \rho \underbrace{v_1^2}_{=0} + \rho g\underbrace{h_1}_{=h}= \cancel{p_u} + \frac{1}{2} \rho v_2^2 + \rho g \underbrace{h_2}_{=0} \\[5px]
& \cancel{\rho} g h= \frac{1}{2} \cancel{\rho} v_2^2 \\[5px]
\label{aus}
&\boxed{v_2=\sqrt{2gh}} \\[5px]
\end{align}
Dieses Ergebnis ist in zweierlei Hinsicht bemerkenswert. Zum einen ist offensichtlich nur die Höhe des Wasserspiegels über der Düsenöffnung für die Ausstromgeschwindigkeit relevant. Der Querschnitt der Düse hat folglich keinen Einfluss auf diese Geschwindigkeit.
Zum anderen zeigt sich, dass die Ausströmgeschwindigkeit gerade der Fallgeschwindigkeit vF entspricht, wenn man ein Fluidteilchen ausgehend der Wasseroberfläche fallen lassen würde (man bezeichnet dies auch als Ausflussgesetz von Torricelli). Die Lageenergie eines Fluidteilchens mit der Masse m wandelt sich dabei vollständig in kinetische Energie um:
\begin{align}
\require{cancel}
&\cancel{m}~g~h=\frac{1}{2}\cancel{m}~v_\text{F}^2 \\[5px]
&\boxed{v_\text{F}=\sqrt{2gh}} ~~~\text{Ausflussgesetz von Torricelli}\\[5px]
\end{align}
Nun wird auch aus energetischer Sicht nochmals deutlich, dass die Ausströmgeschwindigkeit gar nicht höher sein kann als durch Formel (\ref{aus}) gegeben. Denn mit dieser Geschwindigkeit kann ein austretendes Fluidteilchen maximal wieder die Ausgangshöhe erreichen, d.h. die Höhe bis zur Wasseroberfläche. Wäre die Geschwindigkeit höher, dann widerspräche dies dem Energieerhaltungssatz. Denn dann könnte das Fluidteilchen eine größere Höhe erreichen. Man könnte dann mit einem Becken praktisch ohne Energieaufwand ein höher gelegenes Becken befüllen.
Druck in einer bestimmten Tiefe eines Sees
Tatsächlich gilt die Bernoulli-Gleichung nicht nur für ein strömendes Fluid. Auch bei einem ruhenden Fluid kann die Bernoulli-Gleichung angewendet werden. Betrachten wir hierzu einen stillen tiefen See. Welcher (statische) Druck herrscht in der Tiefe h unterhalb der Wasseroberfläche?
Um diese Aufgabe zu lösen betrachten wir eine Stromlinie von der Oberfläche des Wassers bis hin zur Tiefe h. Beachte, dass eine Stromlinie als Tangente an die Geschwindigkeitsvektoren definiert ist. Da bei einem ruhenden Fluid die gesamten Vektoren null sind, kann man eine Stromlinie letztlich auf beliebigen Wegen ziehen. Das Bezugsniveau für die Lageenergien legen wir in die betrachtete Tiefe, in der der Druck bestimmt werden soll. Dieser Tiefe ist also die Höhe null zugeordnet und der Wasseroberfläche die Höhe h. Der statische Druck an der Wasseroberfläche entspricht dem Umgebungsdruck pu. Damit sind folgende Werte bekannt:
| Zustand 1 (Wasseroberfläche) | Zustand 2 (Tiefe) | |
| Höhe | h1 = h | h2 = 0 |
| Geschwindigkeit | v1 = 0 | v2 = 0 |
| Statischer Druck | p1 = pu | p2 = gesucht |
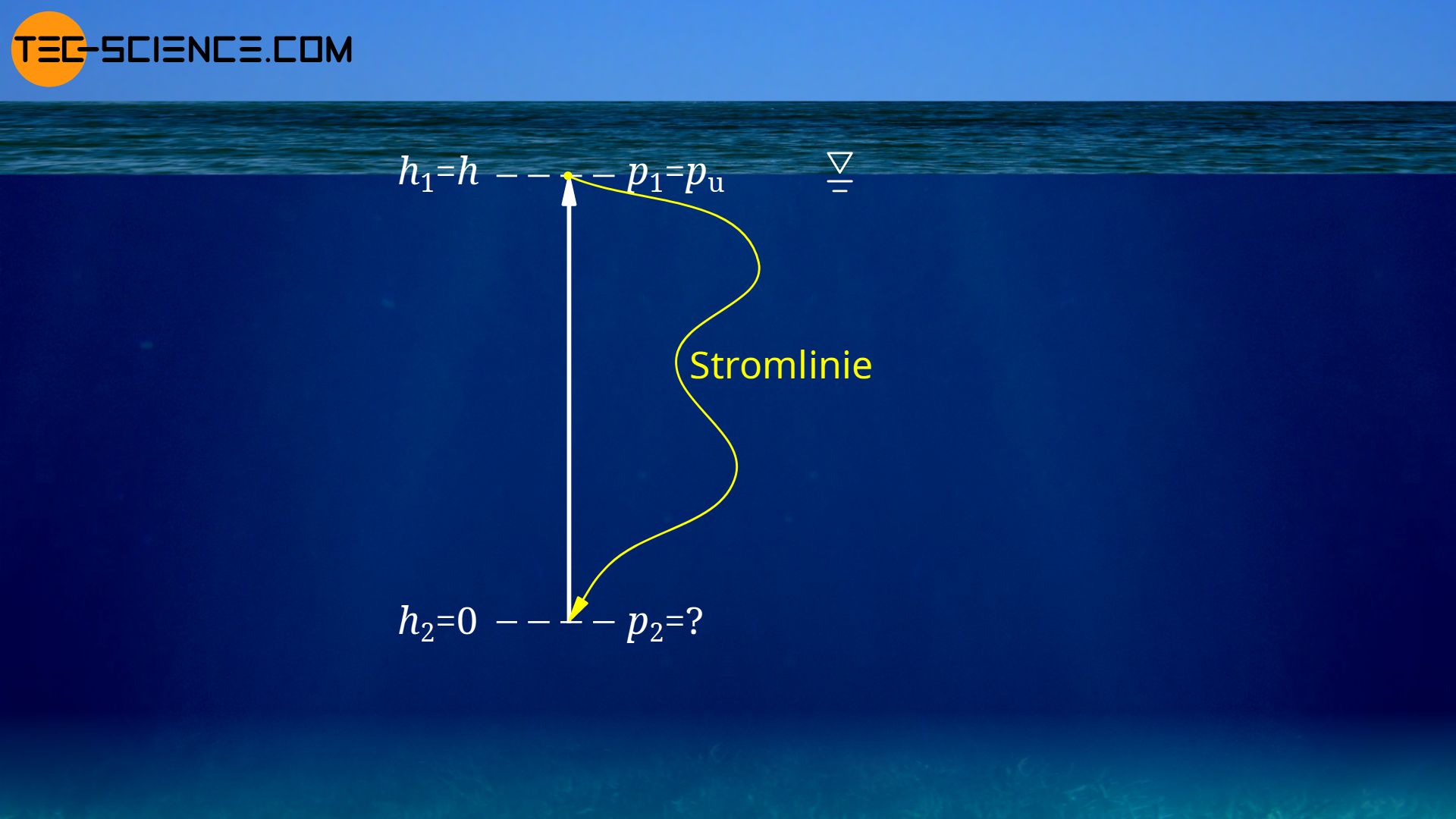
Diese Werte in der Bernoulli-Gleichung eingesetzt, liefern für den Wasserdruck p2 folgendes Ergebnis:
\begin{align}
\require{cancel}
& \underbrace{p_1}_{p_u} + \frac{1}{2} \rho \underbrace{v_1^2}_{=0} +\rho g \underbrace{h_1}_{=h}= p_2 + \frac{1}{2} \rho \underbrace{v_2^2}_{=0} + \rho g \underbrace{h_2}_{=0} \\[5px]
&\boxed{p_2=p_u + \rho g h} \\[5px]
\end{align}
Wie zu erwarten war, entspricht der Druck p2 in der Tiefe h dem Umgebungsdruck pu plus dem (hydrostatischen) Druck der durch die darüber befindliche Wassersäule zustande kommt!






