Bewegungsgleichung eines Fluids auf einer Stromlinie

In diesem Artikel leiten wir die Bewegungsgleichung eines Fluidelements auf einer Stromlinie und senkrecht dazu her.

Einleitung

Im Folgenden möchten wir die Bewegungsgleichung eines Fluidelements auf einer Stromlinie für eine ebene, laminare Strömung herleiten (zweidimensionale Strömung). Man kann sich hierzu bspw. eine Strömung in einem gekrümmten, tiefen Kanal vorstellen, der von oben betrachtet wird. Wir definieren in einer horizontalen Ebene parallel zur Erdoberfläche ein ortsfestes Koordinatensystem s, das in Richtung der Stromlinie verläuft. Der Krümmungsradius der Stromlinie ist mit r_K bezeichnet.

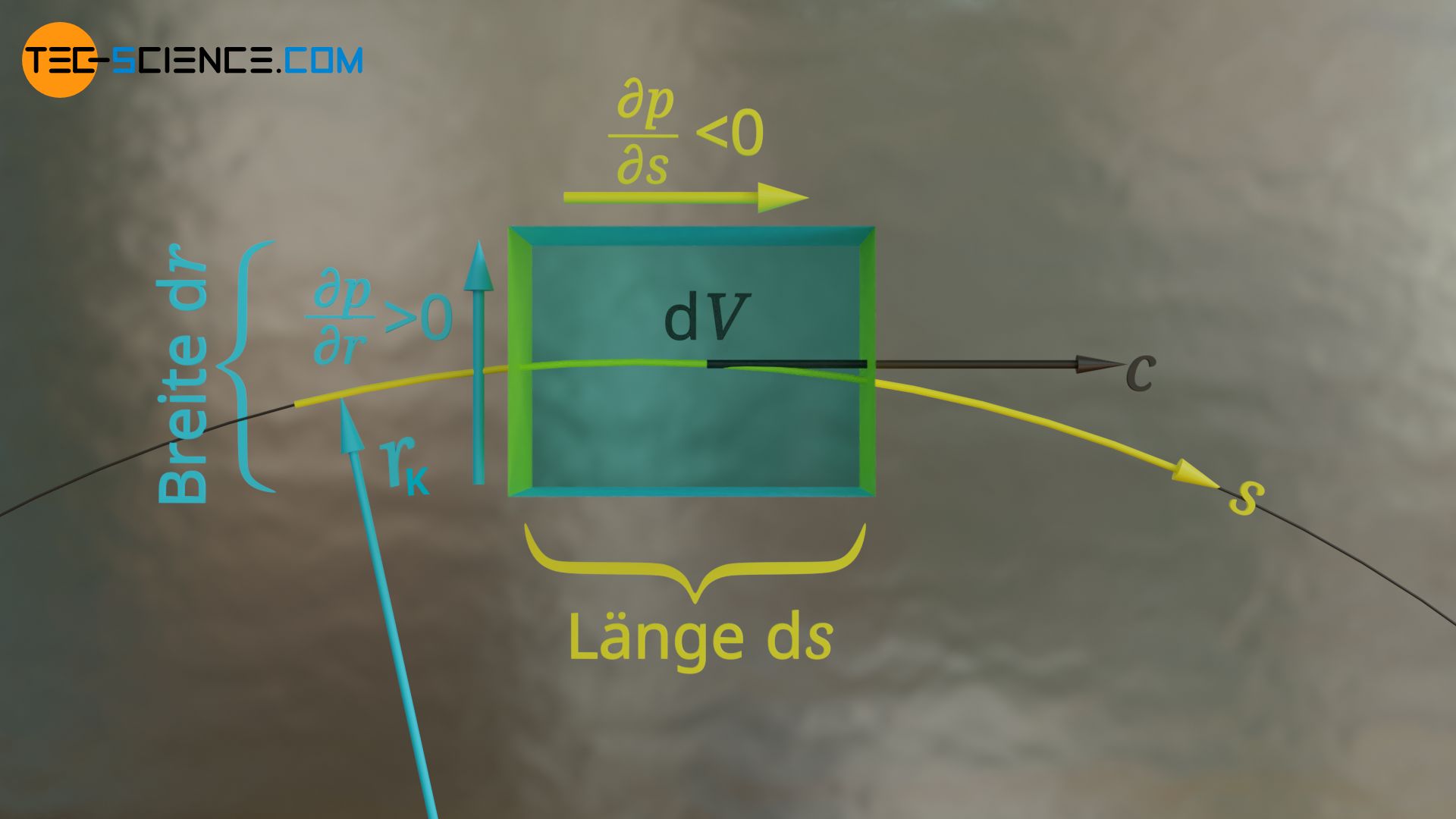
Das Fluidelement hat in radialer Richtung die Breite dr und in Richtung der Stromlinie die Länge ds. Der Druckgradient in Stromlinienrichtung beträgt ∂p/∂s<0 und in radialer Richtung ∂p/∂r>0. Das Fluidelement mit dem Volumen dV bewegt sich mit der Geschwindigkeit c auf der Stromlinie.

Bewegungsgleichung eines Fluidelements in Richtung der Stromlinie

Substantielle Beschleunigung

Zunächst betrachten wir die Kinetik eines Fluidelements nur in Richtung der Stromlinie. Das Fluidelement bewegt sich dabei mit der Geschwindigkeit c definitionsgemäß tangential zur Stromlinie. Da bei instationären Strömungen die Strömungsgeschwindigkeit c aber nicht nur von Ort zu Ort variiert, sondern sich auch zeitlich an einem festen Ort ändert (z.B. beim „Anlaufen“ der Strömung), entfallen auf die Beschleunigung eines betrachteten Fluidelements grundsätzlich zwei Anteile:

1. die lokale zeitliche Änderung der Geschwindigkeit an einem festen Ort (lokale Beschleunigung) und
2. die räumliche Änderung der Geschwindigkeit von Ort zu Ort (konvektive Beschleunigung).

Erster Anteil ergibt sich aus der bekannten Tatsache, dass jede zeitliche Änderung der Geschwindigkeit an einem festen Ort letztlich eine entsprechende Beschleunigung darstellt. Dies bedeutet: Ändert sich an einem festen Ort die Geschwindigkeit des Fluidelements, dann kann dies nur eine Folge einer entsprechenden Beschleunigung sein.

Der zweite Anteil ist darauf zurückzuführen, dass sich die Geschwindigkeit eben nicht nur ein einem festen Ort zeitlich ändert, sondern sich bei einem bestimmten Zeitpunkt auch von Ort zu Ort unterschiedet. Dies bedeutet: Ein Fluidelement muss bei Änderung seines Ortes sozusagen auf die neue Strömungsgeschwindigkeit beschleunigt werden. Beide Beschleunigungsanteile zusammen, bilden die sogenannte substantielle Beschleunigung, d.h. jene Beschleunigung die tatsächlich in Summe auf das Fluidelement wirkt (auch als materielle Beschleunigung bezeichnet).

Die substantielle Änderung der Geschwindigkeit dc erhält man also über die zeitliche Änderung der Geschwindigkeit ∂c/∂t innerhalb der Zeit dt und über eine räumliche Änderung der Geschwindigkeit ∂c/∂s (Gradient) innerhalb der Strecke ds:

\begin{align}
&\underbrace{\text{d}c}_{\text{substantielle Änderung}} = \underbrace{\frac{\partial c}{\partial t} \text{d}t}_{\text{lokale Änderung}} + \underbrace{\frac{\partial c}{\partial s} \text{d}s}_{\text{konvektive Änderung}}\\[5px]
\end{align}

Teilt man die obere Gleichung durch die Zeitdauer dt, so erhält man folgenden Ausdruck für die substantielle Beschleunigung a_t in tangentialer Richtung der Stromlinie:

\begin{align}
&a_t = \frac{\text{d}c}{\text{d}t} = \frac{\partial c}{\partial t} + \frac{\partial c}{\partial s} \underbrace{\frac{\text{d}s}{\text{d}t}}_{c}\\[5px]
& \underline{a_t = \frac{\partial c}{\partial t} + c\frac{\partial c}{\partial s}} \\[5px]
\end{align}

Beachte, dass der Term der konvektiven Beschleunigung von der Strömungsgeschwindigkeit abhängt ist. Dies wird auch anschaulich klar, denn strömt das Fluidelement sehr schnell, dann legt dieses innerhalb einer bestimmten Zeit eine relativ große Strecke zurück. Bei gegebenem Geschwindigkeitsgradienten ∂c/∂s bedeutet dies dann auch eine entsprechend große Änderung der Geschwindigkeit und somit eine große Beschleunigung.

Auf ein betrachtetes Fluidelement der Masse dm wirkt in Stromlinienrichtung somit die folgende beschleunigende Tangentialkraft F_t, wobei die Masse durch das Volumen dV des Fluidelementes und die Dichte ϱ ausgedrückt werden kann:

\begin{align}
\label{t}
& \boxed{F_t = \text{d}m \cdot a_t = \text{d}V \cdot \rho \cdot \left( \frac{\partial c}{\partial t} + c\frac{\partial c}{\partial s}\right)} ~~~~~\text{tangential beschleunigende Kraft} \\[5px]
\end{align}

Druckkräfte

Die obere Gleichung beschreibt letztlich nur die Wirkung einer örtlichen und zeitlichen Geschwindigkeitsänderung auf die Beschleunigung (Kinematik), nicht aber die Ursache dieser Beschleunigung (Kinetik). Ursache der beschleunigenden Kraft sind die am Fluidelement wirkenden Kräfte. Wir müssten deshalb die auf das Fluidelement wirkenden Kräfte näher betrachten und bilanzieren. Auch dabei betrachten wir zunächst nur die Bewegung bzw. die Kräfte in Richtung der Stromlinie.

Auf die Stirnflächen es Fluidelementes wirken Druckkräfte, die entlang der Stromlinie abnehmen. Beachte, dass sich ein Fluidteilchen nur in Richtung abnehmendes Druck bewegen kann, denn ein abnehmender Druckgradient ∂p/∂s<0 ist überhaupt erst der Antrieb für eine Strömung. Wirkt also auf die linke Stirnseite dA_s ein Druck p, dann ergibt sich über die Strecke ds auf der rechten Stirnseite ein um p+∂p/∂s⋅ds geringer Druck. Für die Kräfte auf die Stirnflächen gilt somit:

\begin{align}
& \underline{F_{p1} = p \cdot \text{d}A_s} \\[5px]
& \underline{F_{p2} = \left(p+\frac{\partial p}{\partial s}\cdot \text{d}s \right) \cdot \text{d}A_s} \\[5px]
\end{align}

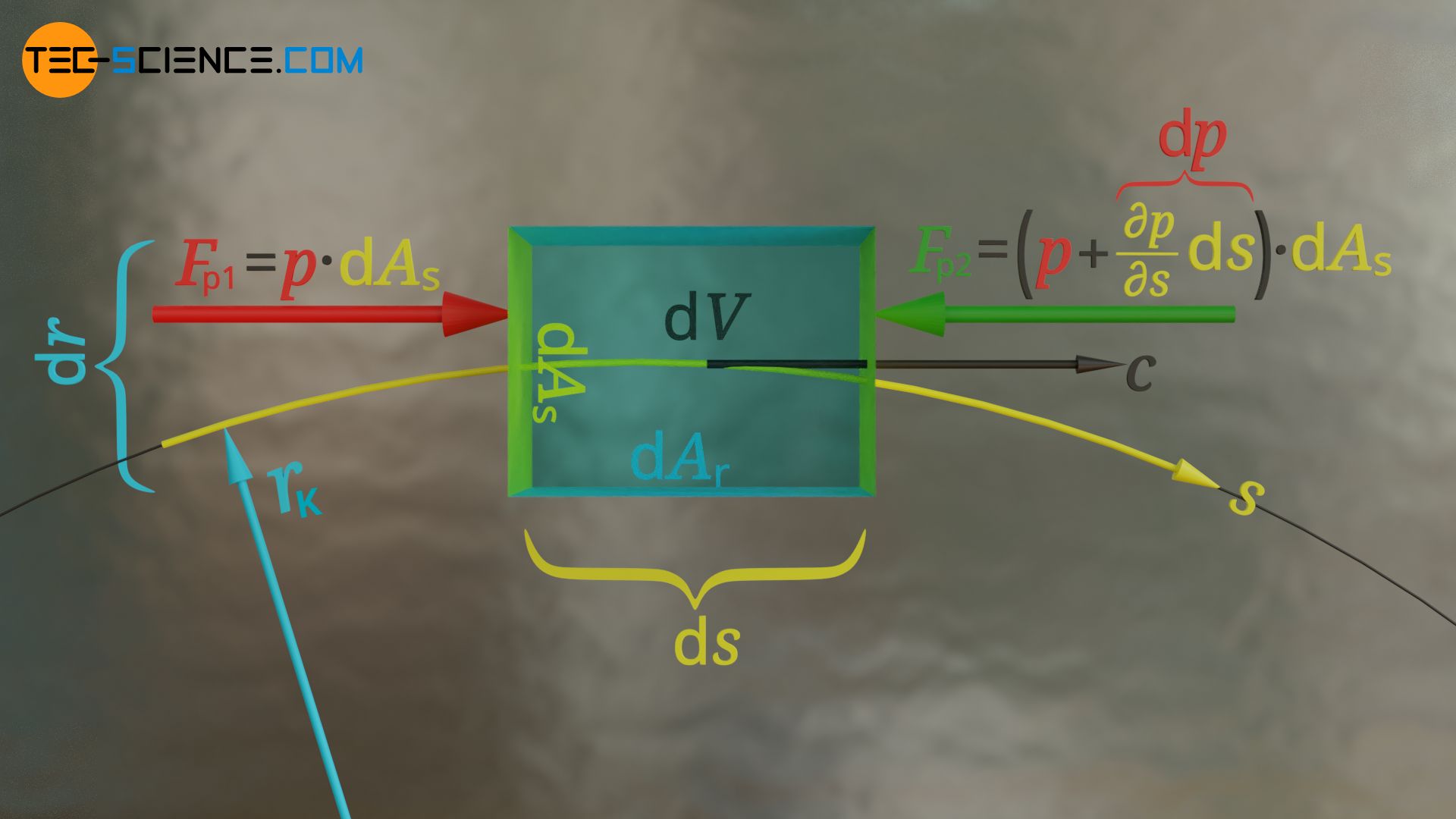
Die effektiv wirkende Druckkraft auf das Fluidelement F_p ergibt sich schließlich aus der Differenz beider Kräfte:

\begin{align}
\require{cancel}
F_p &= F_{p1} – F_{p2} \\[5px]
&=p \cdot \text{d}A_s – \left(p+\frac{\partial p}{\partial s}\cdot \text{d}s \right) \cdot \text{d}A_s \\[5px]
&=\cancel{p \cdot \text{d}A_s} – \cancel{p \cdot \text{d}A_s} – \frac{\partial p}{\partial s}\cdot \underbrace{\text{d}s \cdot \text{d}A_s}_{\text{d}V} \\[5px]
\end{align}

\begin{align}
\boxed{F_p = – \frac{\partial p}{\partial s}\cdot \text{d}V}~~~~~\text{effektiv wirkende Druckkraft} \\[5px]
\end{align}

Reibungskräfte

Des Weiteren wirken auf die seitlichen Flächen Reibungskräfte aufgrund der dynamischen Viskosität η des Fluids. Diese können mit dem Newtonschen Reibungsgesetz für Flüssigkeiten ermittelt werden:

\begin{align}
\label{n}
& \tau= \eta \cdot \frac{\partial c}{\partial r} \\[5px]
\end{align}

Darin bezeichnet τ die in der Fläche wirkende Scherspannung, die proportional zum radialen Geschwindigkeitsgradienten ∂c/∂r ist. Dieser Geschwindigkeitsgradient beschreibt die räumliche Geschwindigkeitsänderung senkrecht zur Stromlinie. Über die Breite dr des Fluidelementes hinweg, ändert sich dieser Geschwindigkeitsgradient jedoch im Allgemeinen. Somit wirken auf beiden Seiten auch unterschiedliche Schubspannungen.

Bezeichnet ∂τ/∂r die Änderung der Scherspannung in radialer Richtung (Scherspannungsgradient), dann ändert sich bei gegebener Breite des Fluidelements von dr die Schubspannung folglich um den Betrag ∂τ/∂r⋅dr. Für die seitlich wirkenden Scherkräfte gilt somit:

\begin{align}
& F_{R1} = \tau \cdot \text{d}A_r \\[5px]
& F_{R2} = \left(\tau+ \frac{\partial \tau}{\partial r}\text{d}r\right) \cdot \text{d}A_r \\[5px]
\end{align}

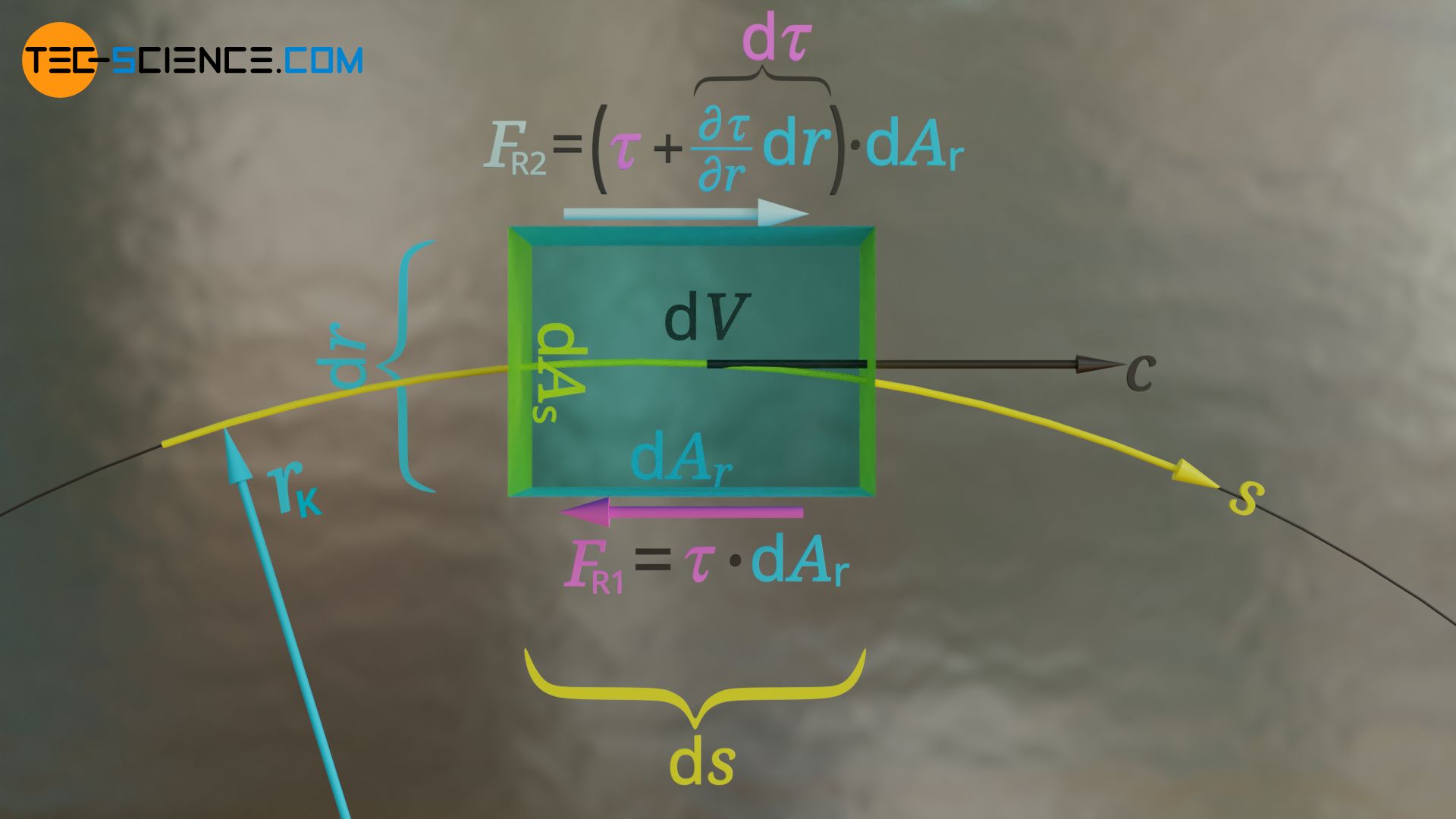
Beachte, dass die seitlichen wirkenden Kräfte in unterschiedliche Richtungen zeigen. Gehen wir davon aus, dass die Strömungsgeschwindigkeit in radialer Richtung zunimmt, dann strömt das umgebende Fluid an der rechten Seite (in Strömungsrichtung betrachtet) mit geringerer Geschwindigkeit als das Fluidelement. Das Fluidelement wird sozusagen abgebremst und die Kraft ist dementsprechend entgegen der Strömungsrichtung gerichtet. Auf der gegenüberliegenden linken Seite strömt das umgebende Fluid hingegen schneller als das Fluidelement. Das umgebende Fluid versucht sozusagen das Fluidelement „mitzureißen“ und die Kraft wirkt somit in Strömungsrichtung.

Drückt man an dieser Stelle die in den oberen Gleichungen auftretenden Scherspannungen durch das Newtonsche Reibungsgesetz gemäß Gleichung (\ref{n}) aus, dann erhält man für die seitlich wirkenden Schubkräfte (Reibungskräfte) folgende Beziehung:

\begin{align}
&\underline{F_{R1} = \eta \cdot \frac{\partial c}{\partial r} \cdot \text{d}A_r} \\[5px]
\end{align}

\begin{align}
F_{R2} &= \left(\eta \cdot \frac{\partial c}{\partial r}+ \frac{\partial}{\partial r}\left(\eta \cdot \frac{\partial c}{\partial r}\right) \text{d}r\right)\cdot \text{d}A_r \\[5px]
&= \left(\eta \cdot \frac{\partial c}{\partial r}+ \eta \cdot \frac{\partial}{\partial r}\left(\frac{\partial c}{\partial r}\right) \text{d}r\right)\cdot \text{d}A_r \\[5px]
\end{align}

\begin{align}
&\underline{F_{R2}= \eta \left(\frac{\partial c}{\partial r}+ \frac{\partial^2 c}{\partial r^2}~\text{d}r\right) \cdot \text{d}A_r} \\[5px]
\end{align}

Somit sind nun alle Reibungskräfte auf das Fluidelement vollständig beschrieben. Beachte, dass senkrecht zur betrachteten Horizontalebene (d.h. auf die Ober- und Unterseite des Fluidelements) keine Reibungskräfte wirken, da bei einer ebenen Strömung kein Geschwindigkeitsgradient in vertikaler Richtung existiert (räumlich konstante Geschwindigkeit). Und wenn kein Geschwindigkeitsgradient vorhanden ist, dann ist gemäß des Newtonschen Reibungsgesetzes auch keine Reibung vorhanden. Dies wird auch anschaulich klar, denn wenn in vertikaler Richtung die Geschwindigkeit der Fluidschichten jeweils identisch ist, dann bewegen sich diese auch nicht relativ zueinander und erzeugen somit keine Reibungskräfte bzw. verursachen keinen Impulsaustausch.

Die effektiv wirkende Reibungskraft auf das Fluidelement F_R ergibt sich schließlich aus der Differenz beider entgegenwirkender Kräfte:

\begin{align}
\require{cancel}
F_{R} &= F_{R2} – F_{R1} \\[5px]
&= \eta \left(\frac{\partial c}{\partial r}+ \frac{\partial^2 c}{\partial r^2}~\text{d}r\right) \cdot \text{d}A_r – \eta \cdot \frac{\partial c}{\partial r} \cdot \text{d}A_r\\[5px]
&= \cancel{\eta \cdot \frac{\partial c}{\partial r}\cdot \text{d}A_r}+\eta \frac{\partial^2 c}{\partial r^2}~\underbrace{\text{d}r \cdot \text{d}A_r}_{\text{d}V}-\cancel{ \eta \cdot \frac{\partial c}{\partial r} \cdot \text{d}A_r}\\[5px]
\end{align}

\begin{align}
&\boxed{F_R= \eta \frac{\partial^2 c}{\partial r^2}~\text{d}V} ~~~~~\text{effektiv wirkende Reibungskraft}\\[5px]
\end{align}

Kräftebilanz

Die Summe der am Fluidelement angreifenden Kräfte, bestehend aus stirnseitig wirkender Druckkraft F_p und seitlich wirkender Reibungskraft F_R, entspricht schließlich der beschleunigenden Tangentialkraft gemäß Gleichung (\ref{t}):

\begin{align}
\require{cancel}
&F_{t} = F_{R} + F_{p} \\[5px]
&\cancel{\text{d}V} \cdot \rho \cdot \left( \frac{\partial c}{\partial t} + c\frac{\partial c}{\partial s}\right) = \eta \frac{\partial^2 c}{\partial r^2}~\cancel{\text{d}V} – \frac{\partial p}{\partial s}\cdot \cancel{\text{d}V} \\[5px]
&\frac{\partial c}{\partial t} + c\frac{\partial c}{\partial s}= \underbrace{\frac{\eta}{\rho}}_{\nu} \frac{\partial^2 c}{\partial r^2} – \frac{1}{\rho}\frac{\partial p}{\partial s} \\[5px]
&\boxed{\frac{\partial c}{\partial t} + c\frac{\partial c}{\partial s}=\nu \frac{\partial^2 c}{\partial r^2} – \frac{1}{\rho}\frac{\partial p}{\partial s}} ~~~~~\text{Stromliniengleichung für Horizontalebene}\\[5px]
\end{align}

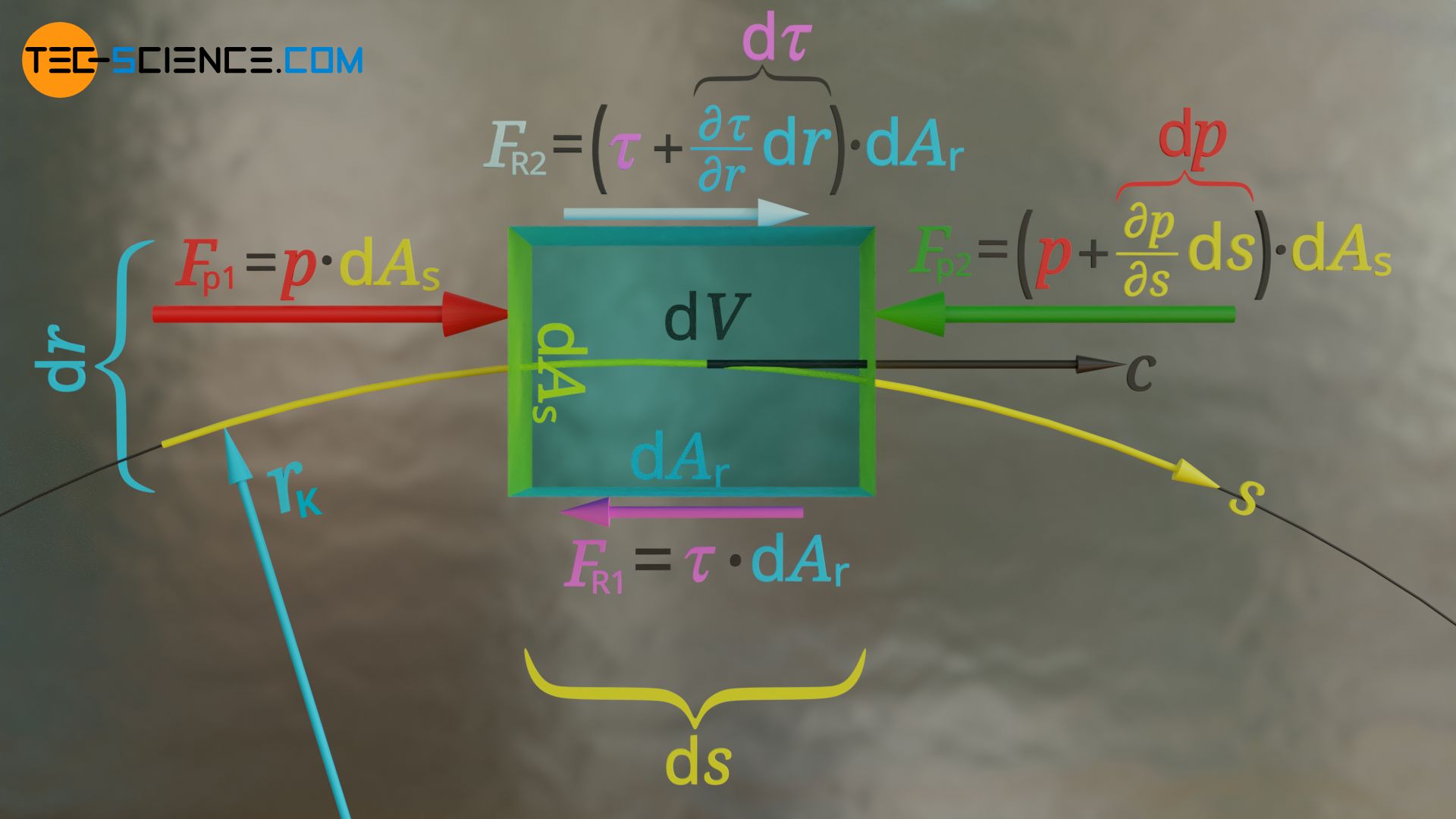
Bei der Herleitung der Stromliniengleichung wurde ausgenutzt, dass der Quotient aus dynamischer Viskosität und Dichte, der kinematischen Viskosität ν (Griechischer Kleibuchstabe Nu) entspricht. Beachte, dass diese Gleichung nur für eine ebene Strömung gilt, bei der die Gewichtskraft senkrecht zur Strömungsebene wirkt (horizontale Ebene).

Wird hingegen eine Strömung in vertikaler Ebene betrachtet, dann muss zusätzlich jene Komponente der Gewichtskraft die in Stromlinienrichtung zeigt, in der Kräftebilanz mitberücksichtigt werden. In der Stromliniengleichung tritt dann ein zusätzlicher Term auf.

\begin{align}
\label{euler}
&\boxed{\frac{\partial c}{\partial t} + c\frac{\partial c}{\partial s}=\nu \frac{\partial^2 c}{\partial r^2} – \frac{1}{\rho}\frac{\partial p}{\partial s}-g\frac{\partial z}{\partial s}} ~~~~~\text{Stromliniengleichung für Vertikalebene}\\[5px]
\end{align}

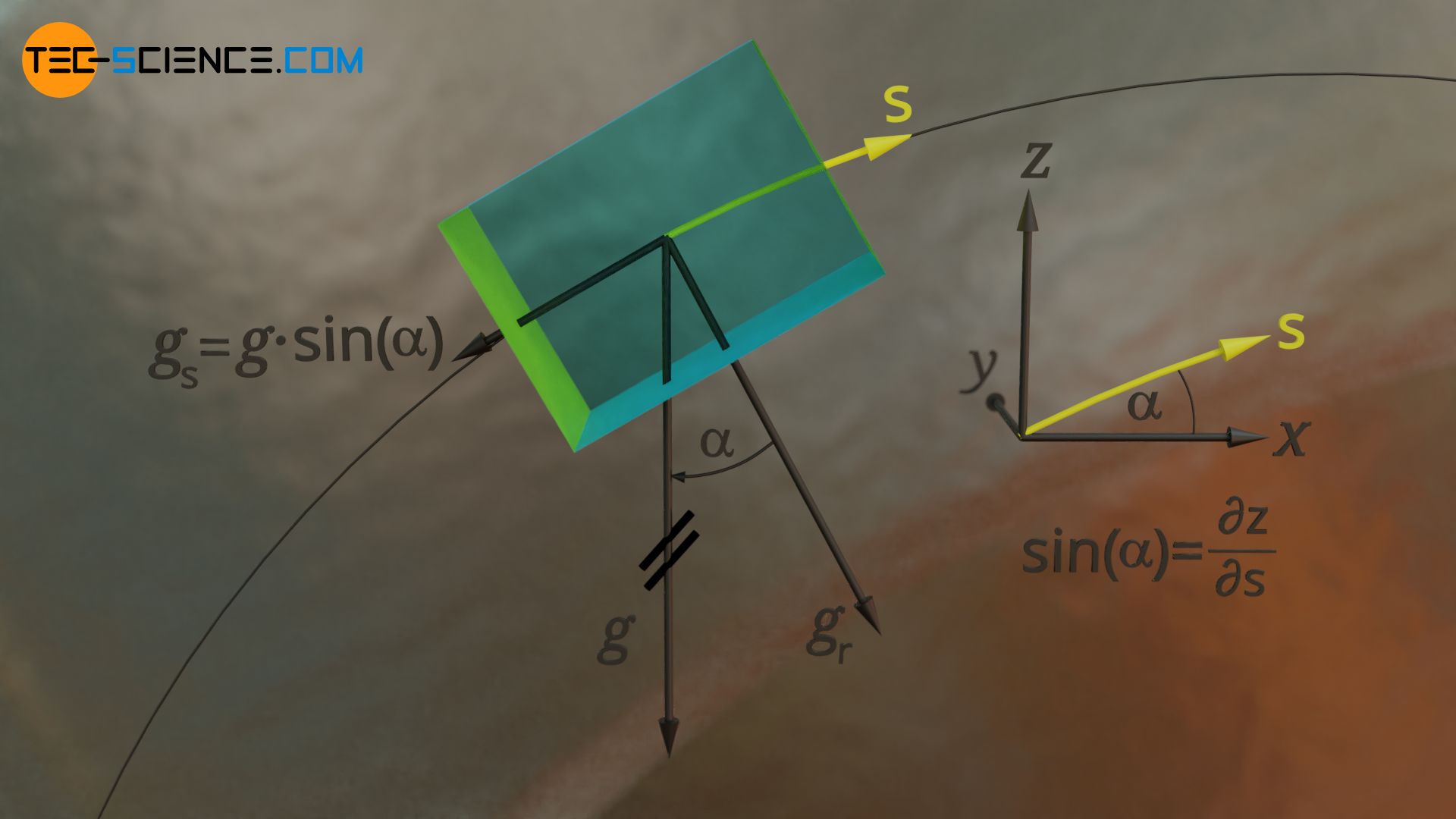
Der Ausdruck ∂z/∂s entspricht letztlich dem Sinus des Winkel zwischen vertikaler Achse (z-Richtung) und der Richtung der Stromlinie (∂z/∂s=sin(α)). Den oberen Ausdruck könnte man deshalb auch schreiben als g⋅sin(α). Dabei wird deutlich, dass dieser Ausdruck gerade der Gewichtskraftkomponente in Stromlinienrichtung entspricht.

Für eine horizontale Strömungsebene hingegen gibt es offensichtlich keine Gewichtskraftkomponente in Stromlinienrichtung, weshalb dieser Ausdruck dann verschwindet. Beide Gleichungen vereinfachen sich zudem, wenn eine stationäre Strömung betrachtet wird, bei der sich die Geschwindigkeiten definitionsgemäß zeitliche nicht mehr ändern. Die partielle zeitliche Ableitung der Geschwindigkeit ist damit null und somit gilt: ∂c/∂t=0 (keine lokale Beschleunigung, sondern nur konvektive Beschleunigung)!

Gleichung (\ref{euler}) ist letztlich eine Spezialfall der Euler-Gleichung, die um den reibungsbedingten Term der Viskosität erweitert wurde.

Bewegungsgleichung eines Fluidelements senkrecht zur Stromlinie

Im diesem Abschnitt betrachten wir das Fluidelement und die wirkenden Kräfte senkrecht zur Stromlinie. Der Einfachheit halber gehen wir dabei von einer stationären Strömung aus. Die gekrümmte Stromlinie lässt sich als Abschnitt einer Kreisbahn mit dem Krümmungsradius r_K ansehen. Für das Zustandekommen dieser Kreisbahn müssen die in radiale Richtung wirkende Kräfte in Summe eine entsprechende Zentripetalkraft F_z erzeugen. Der Betrag dieser aufzubringenden Zentripetalkraft ist abhängig von der Strömungsgeschwindigkeit c dem Krümmungsradius r_K und der Masse des Fluidelements dm:

\begin{align}
&\boxed{F_z = \frac{\text{d}m \cdot c^2}{r_K}} ~~~~\text{aufzubringende Zentripetalkraft} \\[5px]
\end{align}

Vernachlässigen wir an dieser Stelle Reibungskräfte an den Stirnflächen des Fluidelements, dann kann die Zentripetalkraft nur eine Ursache haben: Die Druckkräfte auf den seitlichen Flächen des Fluidelements müssen unterschiedlich groß sein, sodass eine Zentripetalkraft entgegen der radialen Richtung entsteht. Über die Breite des Fluidelements muss der Druck in radialer Richtung also zunehmen. Von welchen Größen dieser radiale Druckgradient ∂p/∂r abhängig ist, wird im Folgenden gezeigt.

Der Druck nimmt quer zu den Stromlinien in radialer Richtung zu!

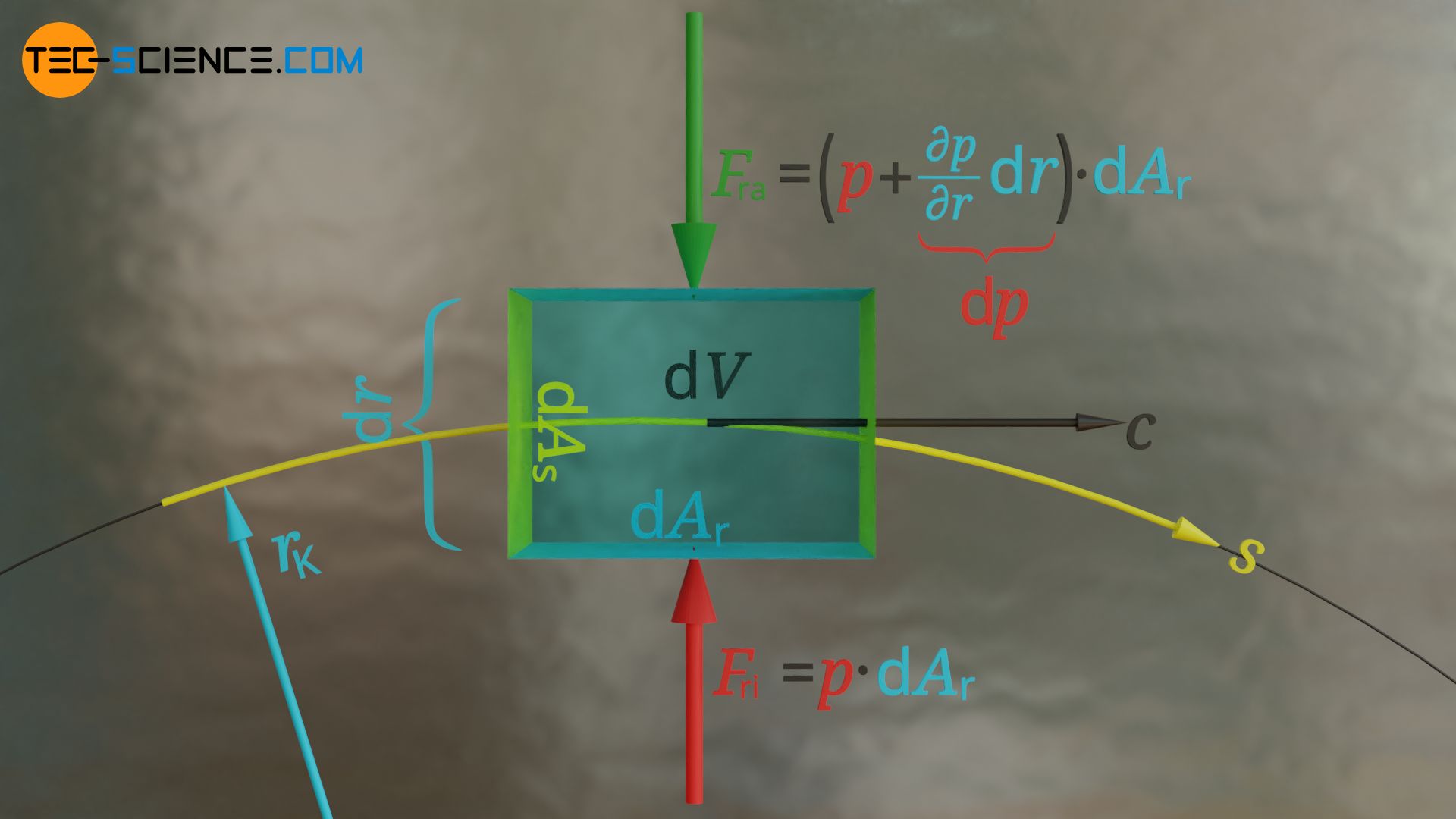
Wirkt an der „Innenseite“ des Fluidelements ein Druck p (Innenseite bzgl. der Kurve), dann ergibt sich bei gegebenem Druckgradienten ∂p/∂r>0 über die Breite dr hinweg an der „Außenseite“ ein um ∂p/∂r⋅dr geringerer Druck. Für die Druckkräfte in radialer Richtung gilt somit:

\begin{align}
& \underline{F_{ri} = p \cdot \text{d}A_r} \\[5px]
& \underline{F_{ra} = \left(p+\frac{\partial p}{\partial r}\cdot \text{d}r \right) \cdot \text{d}A_r} \\[5px]
\end{align}

Der Betrag der effektiv wirkenden Druckkraft in radialer Richtung F_r ergibt sich schließlich aus der Differenz beider Kräfte:

\begin{align}
\require{cancel}
F_r &= F_{ra} – F_{ri} \\[5px]
&= \left(p+\frac{\partial p}{\partial r}\cdot \text{d}r \right) \cdot \text{d}A_r – p \cdot \text{d}A_r \\[5px]
&= \cancel{p \cdot \text{d}A_r} + \frac{\partial p}{\partial r}\cdot \underbrace{\text{d}r \cdot \text{d}A_r}_{\text{d}V}- \cancel{p \cdot \text{d}A_r}\\[5px]
\end{align}

\begin{align}
\boxed{F_r = \frac{\partial p}{\partial r}\cdot \text{d}V}~~~~~\text{effektiv wirkende Radialkraft} \\[5px]
\end{align}

Diese Druckkraft in radialer Richtung ist letztlich die Ursache der Zentripetalkraft. Gleichsetzen beider Gleichungen liefert schließlich folgenden Zusammenhang zwischen der Strömung des Fluids und dem hieraus resultierenden Druckgradienten in radialer Richtung:

\begin{align}
&F_r = F_z \\[5px]
&\frac{\partial p}{\partial r}\cdot \text{d}V = \frac{\text{d}m \cdot c^2}{r_K} \\[5px]
&\frac{\partial p}{\partial r}= \frac{\overbrace{\frac{\text{d}m}{\text{d}V}}^{\rho} \cdot c^2}{r_K} \\[5px]
&\boxed{\frac{\partial p}{\partial r}= \frac{\rho \cdot c^2}{r_K}} \\[5px]
\end{align}

Der Druckgradient in radialer Richtung ist umso größer, je höher die Strömungsgeschwindigkeit ist und je dichter das Fluid ist, sowie je kleiner der Krümmungsradius der Stromlinie ist.

Obere Gleichung zeigt aber auch, dass für große Krümmungsradien der radiale Druckgradient immer kleiner wird. Bei geradlinigen Stromlinien mit letztlich einem unendlich großen Krümmungsradius, ist der Druckgradient unendlich klein. In anderen Worten: Bei geradlinigen Stromlinien existiert kein Druckgradient in radialer Richtung.

Druckmessungen in Rohren sollten deshalb auch immer stets an geradlinigen Rohrabschnitten mit entsprechend geradlinigen Stromlinien vorgenommen werden. Der gemessene Druck ist in diesen Fällen unabhängig von der Platzierung des Druckmessers am Rohrumfang. Bei Druckmessungen an Rohrwinkel hingegen variiert der Druck je nach Abstand zum Krümmungsmittelpunkt und damit je nach Platzierung am Umfang des Rohrs.