Stromlinien, Bahnlinien, Streichlinien oder der Zeitlinien dienen der Veranschaulichung von Strömungen.
Bahnlinien (Bahnkurven)
Bahnlinien sind Strömungswege, die die Fluidteilchen beim Strömen nehmen. Diese Strömungspfade werden auch Bahnkurven genannt. Sichtbar machen kann man Bahnlinien, wenn man leichte Partikel in das Fluid einbringt, die nahezu trägheitslos dem Fluid folgen. Die untere Abbildung zeigt hierzu schematisch die Bahnkurven in einer laminaren und einer turbulenten Strömung.

Zur Sichtbarmachung der Bahnkurven in Windkanälen nutzt man meist Glycerin, das zum Verdampfen gebracht wird. Es entsteht ein weißlicher Nebel („Partynebel“), der der strömenden Luft beigesetzt wird. Bei strömenden Flüssigkeiten, kann man dem Fluid Farbstoffe (z.B. Tinte) zusetzen, um die Bahnlinien sichtbar zu machen.

Bahnlinien (Bahnkurven) sind gedachte Strömungspfade, auf denen sich masselose Partikel im Fluide bewegen würden!
Man könnte an dieser Stelle vorschnell den Schluss ziehen, dass sich mit einer Bahnlinie auch immer die Strömungsrichtung visualisieren lässt. Dies ist aber nur einem speziellen Fall möglich, nämlich wenn sich die Strömung zeitlich nicht ändert. Man spricht in diesem Fall auch von einer stationären Strömung.
Eine Strömung ist immer dann stationär, wenn Teilchen, die in Gedanken an einer bestimmten Stelle in das Fluid eingebracht werden, sich immer auf derselben Bahnlinie bewegen. Ein Beispiel für eine näherungsweise stationäre Strömung, wäre das Strömung von Wasser in Mitten eines kleinen, flachen Bachs. Egal zu welchem Zeitpunkt man bspw. ein Papierschiff in die Strömung gibt (Punkt A in der Abbildung), würde dieses immer dieselbe Bahnkurve verfolgen.
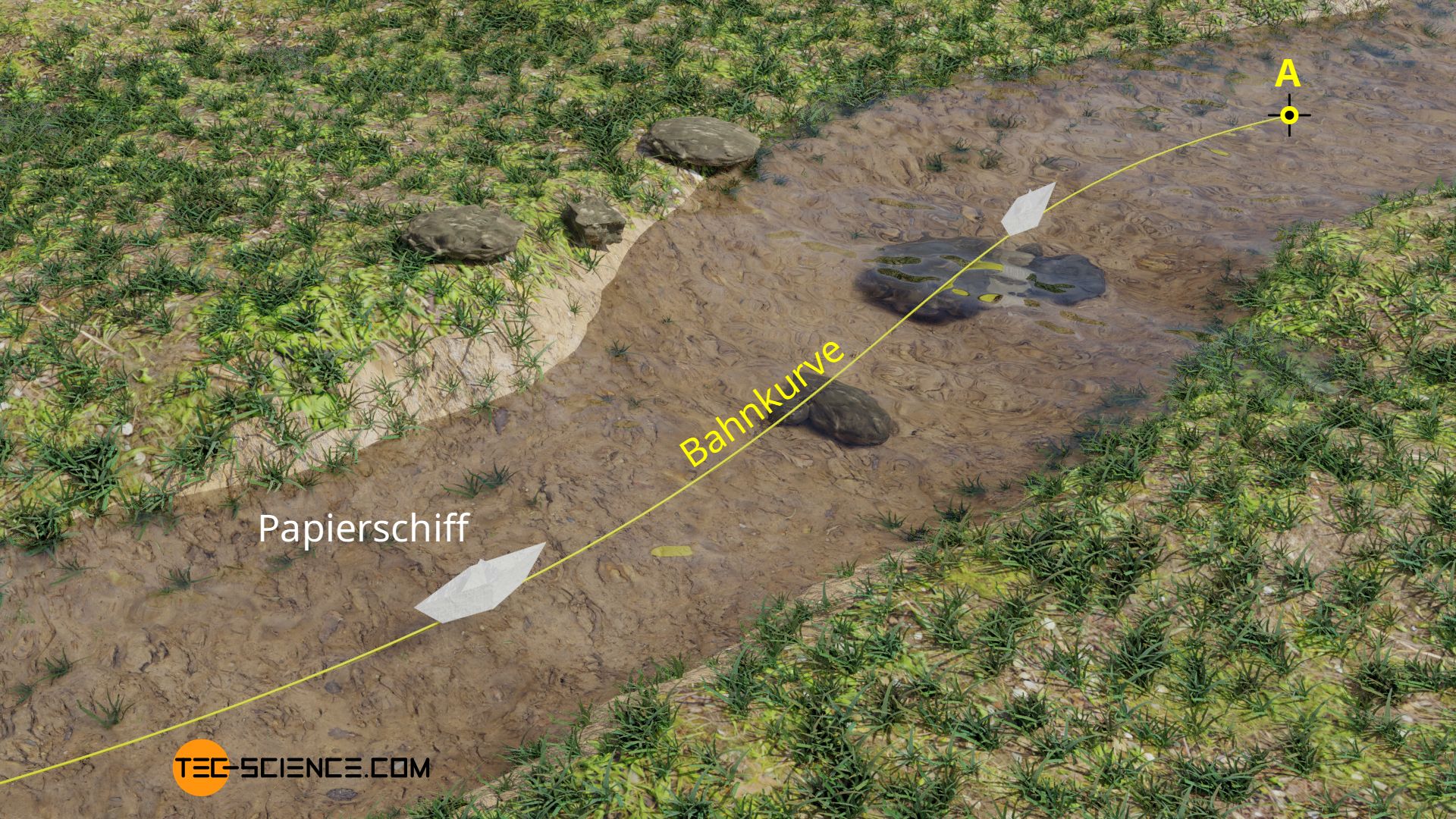
Bei einer stationären Strömung bleibt die Geschwindigkeit der Strömung in jedem Punkt zeitlich konstant, d.h. ausgehend eines bestimmten Punktes verfolgt ein Fluidteilchen stets dieselbe Bahnlinie!
Ändert sich eine Strömung hingegen zeitlich, dann würde sich ein Teilchen, das an einer bestimmten Stelle später in der Fluid eingebracht wird, auf einer anderen Bahnlinie bewegen. Man spricht in diesem Fall von einer instationären Strömung. Ein sehr gutes Beispiel für eine instationäre Strömung ist Wind an einem stürmischen Tag. Lässt man zwei Federn zu unterschiedlichen Zeitpunkten an demselben Punkt los (Punkt A in der Abbildung), dann werden sie unterschiedliche Bahnlinien vollziehen, da sich die Geschwindigkeit der Strömung permanent ändert.

Bei einer instationären Strömung ändert sich die Geschwindigkeit der Strömung, d.h. ausgehend eines bestimmten Punktes verfolgt ein Fluidteilchen immer andere Bahnlinien!
Stromlinien
Es zeigt sich also bei genauer Betrachtung, dass nur für den stationären Fall eine Bahnlinie auch die (konstanten) Geschwindigkeitsverhältnisse wiedergeben kann. Die Richtung der Strömungsgeschwindigkeit entspricht in diesem Fall der Tangente an die Bahnlinie. Eine solche Geschwindigkeitslinie wird dann auch als Stromlinie bezeichnet. Mehrere parallele Stromlinien in Form einer Röhre, bilden eine sogenannte Stromröhre.
Stromlinien sind gedachte Linien, die in tangentialer Richtung die Geschwindigkeitsrichtung des strömenden Fluids zu einem bestimmten Zeitpunkt wiedergeben. Nur für den stationären Fall sind Stromlinien mit den Bahnlinien identisch.
Unterschied zwischen Stromlinie und Bahnlinie
Bei einer instationären Strömung, kann aus einer vorliegenden Bahnkurve grundsätzlich nicht mehr auf die Geschwindigkeit der Strömung zu einem bestimmten Zeitpunkt geschlossen werden. Die untere Abbildung zeigt hierzu nochmals die Bahnkurven der beiden Federn, die zu unterschiedlichen Zeitpunkten losgelassen werden.
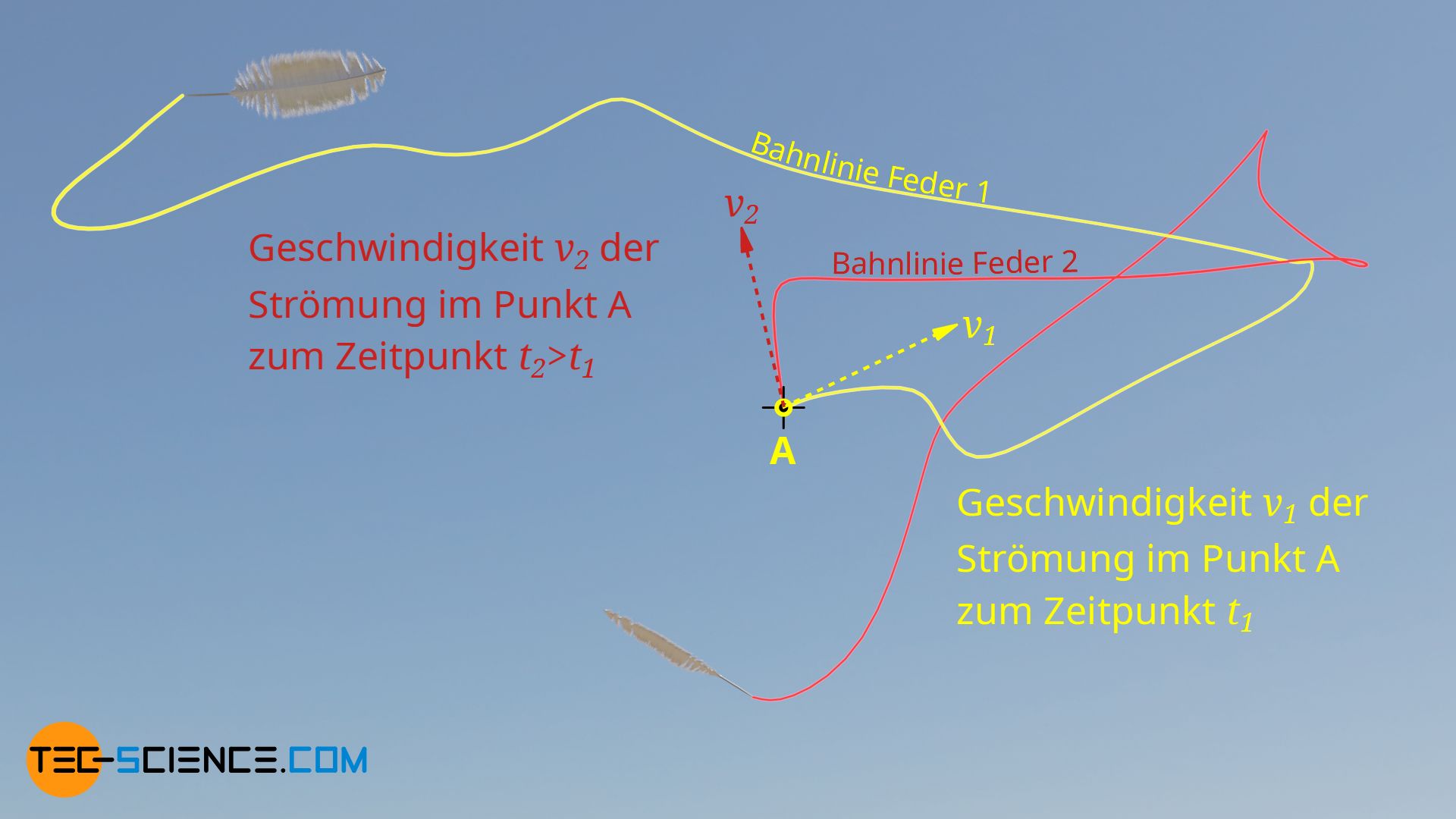
Während beim Loslassen der Feder 1 zu einem Zeitpunkt t1 die Geschwindigkeit der Strömung im Punkt A nach rechts oben zeigt (v1), zeigt sie zu einem späteren Zeitpunkt t2 – beim Loslassen der Feder 2 – nach links oben (v2). Zu diesem Zeitpunkt t2 ist die Strömungsgeschwindigkeit also nicht mehr tangential zur Bahnkurve der Feder 1. Bahnkurven geben also nicht das Geschwindigkeitsfeld einer instationären Strömung wieder. Bahnkurven und Stromlinien unterscheiden sich folglich.
Im Falle der turbulenten Luft könnte man das Geschwindigkeitsfeld bspw. durch viele kleine Fahnen sichtbar machen. Diese Fahnen geben zu einem bestimmten Zeitpunkt für ihren jeweiligen Ort die aktuelle Strömungsrichtung wieder. Zeichnet man dann Linien ein, die jeweils parallel zu den Fahnen liegen (Geschwindigkeitsrichtung), dann erhielte man auf diese Weise Stromlinien.
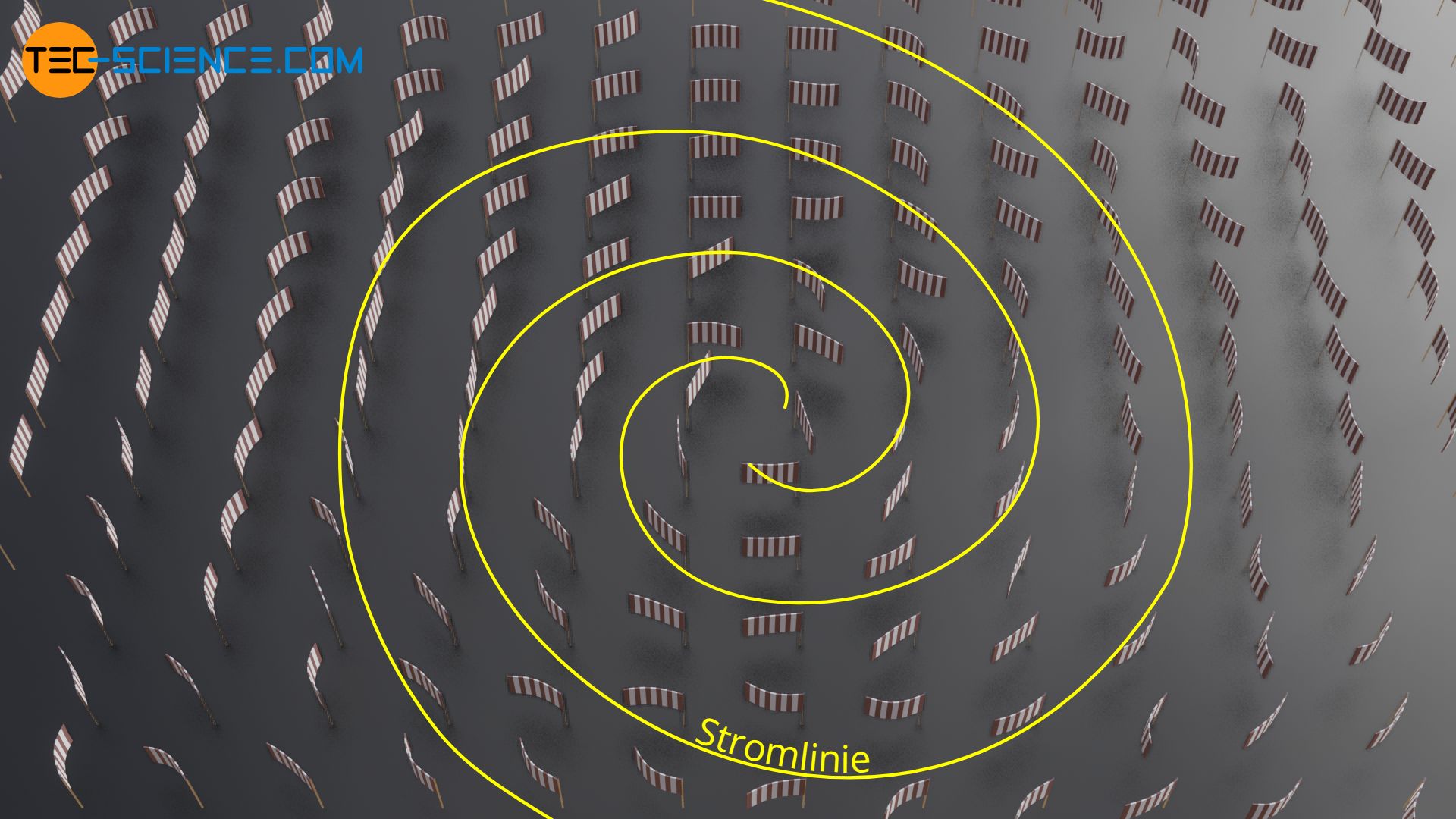
In der Praxis es die Bestimmung der Stromlinien für instationäre Strömungen also mit einem relativ großen Aufwand verbunden. In vielen praktischen Fällen hat man es aber ohnehin mit stationären Strömungen zu tun, sodass in diesen Fällen keine Unterscheidung zwischen Bahnlinie und Stromlinie erforderlich ist. Anhand der einfach sichtbar zu machenden Bahnlinien (mit bspw. dem angesprochenen Nebel oder einer eingefärbten Flüssigkeit) erhält man somit auf unkomplizierte Weise auch eine Aussage über das Geschwindigkeitsfeld der stationären Strömung.
Stromliniendichte als Maß für den Betrag der Strömungsgeschwindigkeit
Stromlinien veranschaulichen Geschwindigkeitsfelder auf die analoge Weise wie Feldlinien Kraftfelder veranschaulichen. Dementsprechend können Stromlinienbilder auch noch vor dem Hintergrund Stromliniendichte interpretiert werden. Die untere Abbildung zeigt hierzu die Stromlinien im einem sich verengenden Rohr.
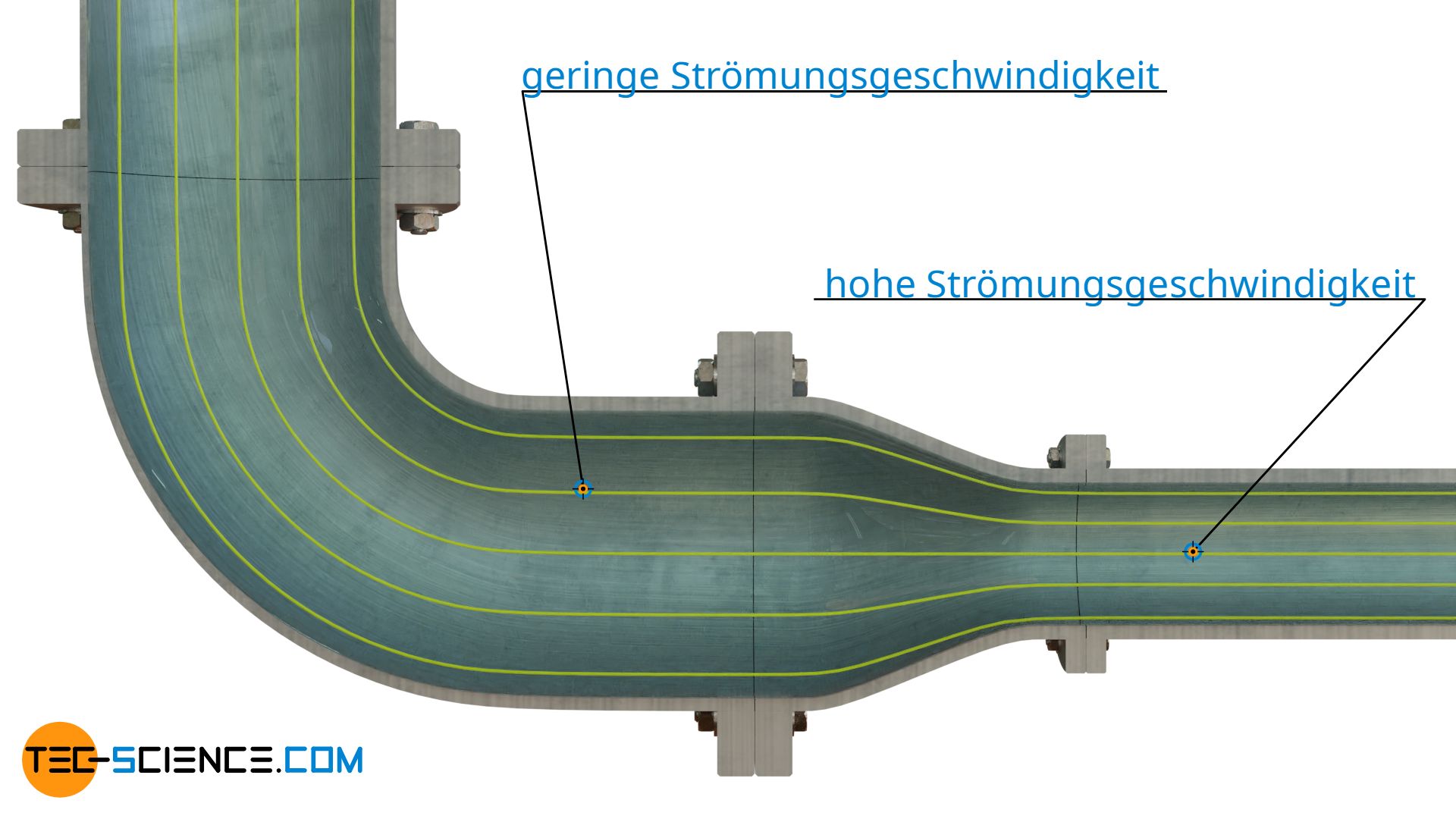
Aufgrund des engeren Querschnitts tritt das Wasser dort mit höherer Geschwindigkeit hindurch als im vergrößerten Teil, da durch beide Abschnitte innerhalb derselben Zeit weiterhin dieselbe Masse hindurch bewegt werden muss (Massenerhaltung). Man kann an diesem Beispiel erkennen, dass die Dichte der Stromlinien somit ein Maß für die Geschwindigkeit der Strömung ist. Dies gilt zumindest für Unterschallströmungen. Im Überschallbereich tritt bei einer Geschwindigkeitszunahme eine Verringerung der Stromliniendichte auf.
Im Unterschallbereich bedeutet eine Verengung der Stromlinien (hohe Stromliniendichte) eine Erhöhung der Strömungsgeschwindigkeit und im Überschallbereich eine Verringerung der Strömungsgeschwindigkeit!
Des Weiteren gilt für Stromlinien, dass sich diese nicht kreuzen oder abknicken können. In einem Punkt ist die Strömungsgeschwindigkeit immer eindeutig festgelegt und kann nicht zwei Richtungen aufweisen, wie dies in einem Kreuzungspunkt der Fall wäre. Dies gilt auch für einen Knickpunkt, in dem die Richtung nicht mehr eindeutig definiert wäre.
Stromlinien knicken nicht ab und kreuzen sich nicht!
Druckgradient senkrecht zu gekrümmten Stromlinien
Das untere Stromlinienbild zeigt, dass sich die Fluidteilchen beim strömen durch den Rohrwinkel auf gekrümmten Bahnlinien (Stromlinien) bewegen. Aufgrund der Trägheit ist ein Fluidteilchen aber grundsätzlich bestrebt sich geradlinig fortzubewegen. Der gekrümmte Verlauf muss deshalb durch Aufbringen einer entsprechenden Zentripetalkraft erzwungen werden. Dies geschieht durch einen nach außen hin zunehmenden Druck quer zu den Stromlinien. Die Fluidteilchen werden durch den größeren Druck an der Außenseite damit nach hinnen gedrückt und bewegen sich somit auf gekrümmten Bahnen. Der Druckanstieg quer zur Strömungsrichtung ist dabei umso größer …
- je höher die Strömungsgeschwindigkeit und
- umso geringer der Krümmungsradius und
- je höher die Dichte des Fluids ist.
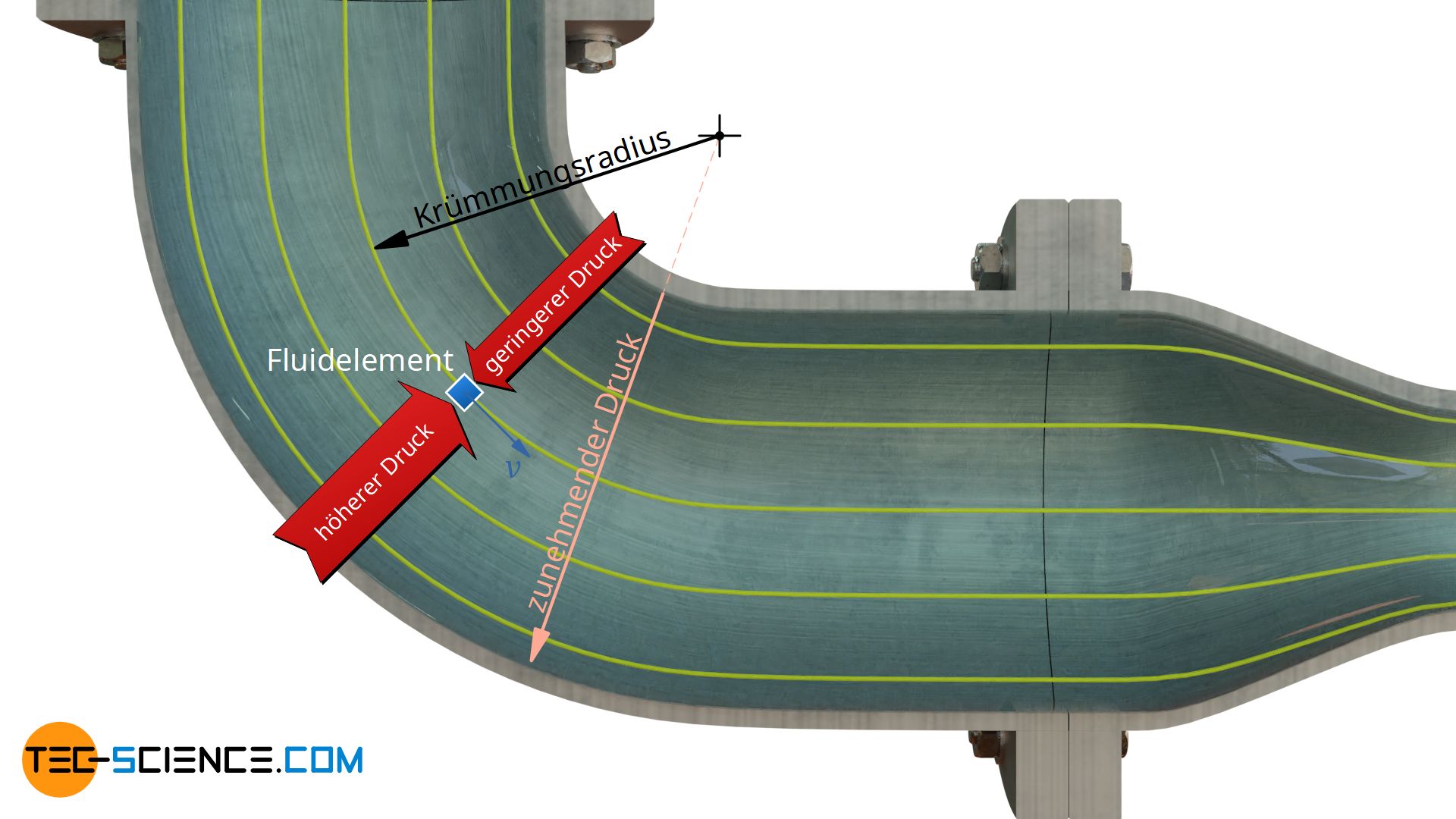
Umgekehrt bedeutet dies, dass je weniger stark die Stromlinien gekrümmt sind, desto geringer der Druckgradient quer zur Strömung ist. Für parallel verlaufende Stromlinien ist der Krümmungsradius letztlich unendlich groß und damit der Druckgradient unendlich klein. Dies bedeutet also, dass bei parallel verlaufenden Stromlinien kein Druckänderung quer zur Strömungsrichtung zu verzeichnen ist. Bei geradlinig verlaufenden Stromlinien muss schließlich auch keine Zentripetalkraft aufgebracht werden. Mehr Informationen zu Stromlinien sowie eine Herleitung zum Druckgradienten bei gekrümmten Stromlinien finden Sie im Artikel Bewegungsgleichung eines Fluids auf einer Stromlinie.
Bei gekrümmten Stromlinien nimmt der Druck quer zur Stromlinie von innen nach außen zu. Bei geradlinigen Stromlinien tritt kein Druckgradient quer zur Strömung auf!
Druckmessungen in Rohren sollten deshalb auch nicht an gekrümmten Rohrabschnitten durchgeführt werden. Denn je nach Lage des Messpunktes am Umfang (unterschiedliche Krümmungsradien), würde man unterschiedliche Messergebnisse erhalten. Druckmessungen sind deshalb nur an geraden Abschnitten sinnvoll, wo der Druck über die Querschnittsfläche der Strömung konstant ist und somit unabhängig der Lage des Messpunktes am Rohrumfang ist.
Streichlinien
Es wurde bereits erläutert, dass bei instationären oder turbulenten Strömungen, zeitlich nacheinander eingebrachte Partikel (an stets demselben Ort jeweils unterschiedliche Bahnkurven beschreiben. Verbindet man zu einem bestimmten Zeitpunkt alle nacheinander eingebrachten Partikel miteinander, dann bildet sich eine sogenannte Streichlinie.
Als Streichlinie bezeichnet man die Verbindungslinie von in Gedanken nacheinander eingebrachte Partikel in ein strömendes Fluid!
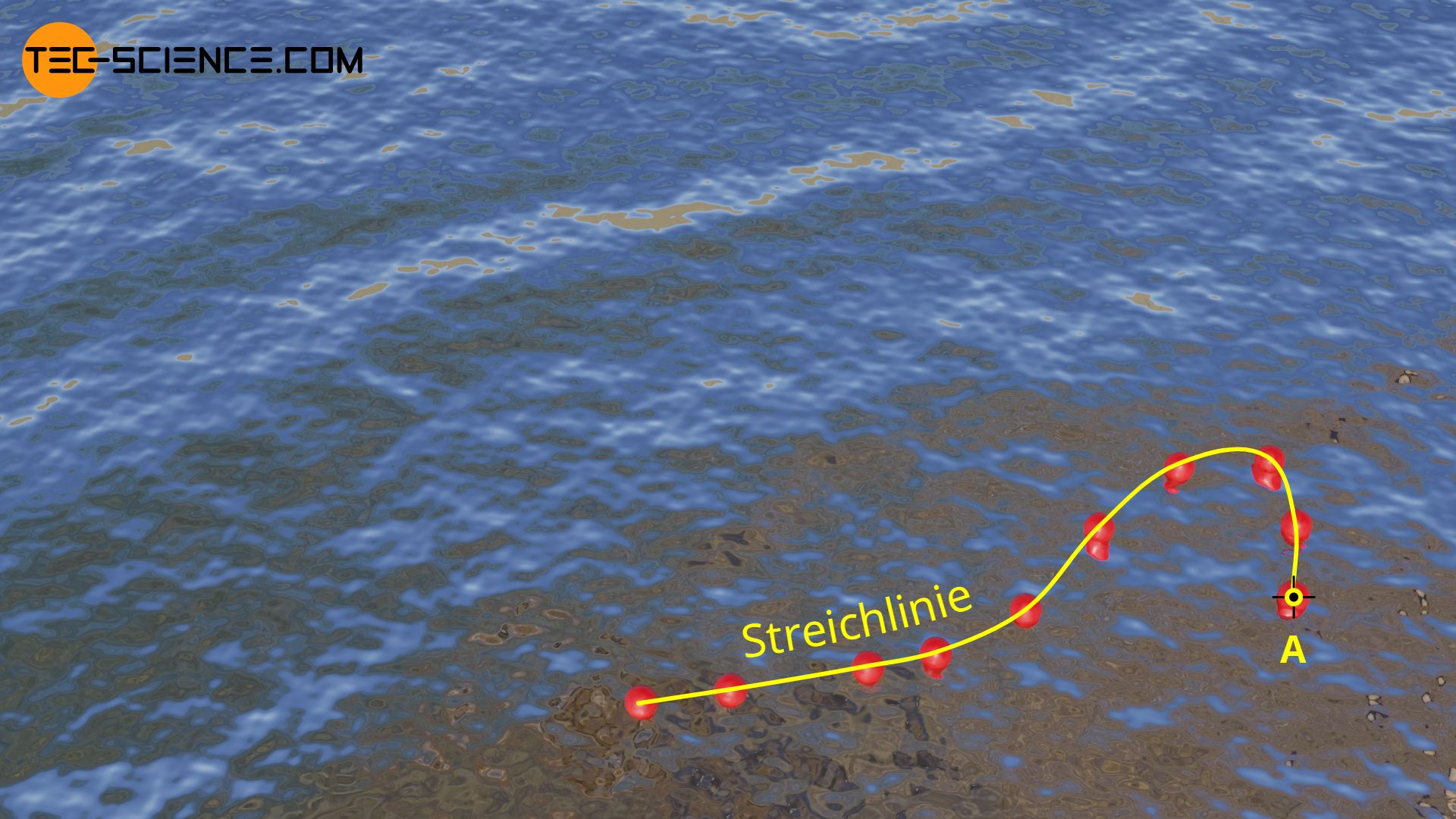
Im Falle eines instationär strömenden Gewässers, kann man sich die Streichlinien wie folgt vorstellen. Hierzu stelle man sich Kugeln aus Plastik vor, die über eine imaginäre Schnur miteinander verbunden sind. Diese Kugeln werden nun zeitlich nacheinander an immer derselben Position ins Wasser gebracht (Punkt A in der oberen Abbildung). Die imaginäre Schnur beschreibt dann die Streichlinie. Im Fall einer stationären Strömung sind Streichlinien wiederum identisch mit den Bahnkurven bzw. Stromlinien.
Zeitlinien
Das zeitliche Verhalten einer Strömung (insbesondere einer turbulenten Strömung) kann man auch mit sogenannten Zeitlinien sichtbar machen. Unter einer Zeitlinie kann man sich eingebrachte (masselose) Partikel in einem Fluid vorstellen, die diesmal aber nicht nacheinander am selben Ort eingebracht werden, sondern gleichzeitig an verschiedenen Orten. Die Verbindungslinie dieser eingebrachten Partikel bestimmt zu einem beliebig weiteren Zeitpunkt die Zeitlinie.







