The specific latent heat of fusion (enthalpy of fusion) is the amount of heat required to melt a solid substance!
Process of melting
If a solid is heated more and more, then at some point the melting point is reached. At this point, the state of matter changes and the solid finally begins to melt. During melting, no further increase in temperature is observed for pure substances, despite the continued supply of heat energy. During melting, the energy obviously no longer benefits the increase of the vibrational energy of the molecules, which would otherwise mean an increase in temperature (see also article Temperature and particle motion).

During melting, the transferred energy leads to an increase in the internal energy in terms of changed binding energies between the molecules in the solid and liquid state. The intermolecular bonds in the solid state are being broken by the added heat energy, thus allowing the transition to the liquid state. In the liquid state, the molecules are less strongly bound to each other due to the lower binding forces. In this way, the molecules are no longer bound to a specific location. That is why liquids do not have a solid form.

During melting, energy must be added to break the intermolecular bonds. In the case of pure substances, the temperature of the solid remains constant until the process of melting is completed!
More detailed information on this can also be found in the article Why does the temperature remain constant during a change of state (phase transition)?
The question arises as to how much heat must be added in order to completely melt a certain amount of a solid. The heat required for this is also referred to as the heat of fusion or enthalpy of fusion. This heat of fusion does not include the amount of heat required to heat the solid to the melting point. The heat of fusion therefore only includes the heat energy to be added during melting if the solid has already been heated to melting temperature.
The heat of fusion (enthalpy of fusion) is the heat energy to be added to a solid at its melting point in order to completely melt a certain amount of the substance!
Since the heat of fusion added during melting is not directly noticeable in an increase in temperature, but can nevertheless be found in the molten substance in the form of internal energy, the heat of fusion is also referred to as latent heat. The term “latent” comes from Latin and means “to be hidden” or “not to appear directly”.
Experimental determination of the heat of fusion
Experimental setup
Using frozen water (ice) as an example, the heat of fusion required to melt a certain amount of ice will be determined experimentally in the following. For this purpose, ice from the refrigerator is placed in an electrically heated vessel. The vessel should be thermally insulated so that the melting of the ice is due solely to the power output of the heater (which can be easily determined) and not to the heat from the warmer surroundings, which would normally cause the ice to melt. Through a small hole at the bottom of the vessel, the melted water is collected on a balance. In this way the melting process over time is observed.

The added heat of fusion can be determined via the electrical power of the heater, which is completely converted into heat. The heat energy Qf (= latent heat of fusion) added at a power P is obtained by the operating time t of the heater according to the following formula:
\begin{align}
\label{q}
Q_\text{f} = P \cdot t \\[5px]
\end{align}
Observation
First, the ice is heated to melting temperature with the heater. When the ice begins to melt, the experiment can be started at any time. To do this, the balance is reset to zero and the time measurement is started. The ice gradually melts and the melted mass is displayed on the balance. At regular time intervals, the displayed mass of the balance is recorded. At each time t, the added heat of fusion Qf up to that point can be determined using formula (\ref{q}). In this way one obtains a statement which amount of heat led to the melting of which mass mf.
Evaluation
If one plots the melted mass as a function of the added heat, then a proportional relationship becomes apparent. This means that in order to melt twice the amount of ice, twice the amount of heat must be added. The evaluation of the experimental data shows that about 35 kJ of heat are necessary to melt 100 g of water. With a supplied heat energy of about 70 KJ, twice the ice mass of 200 g has then finally melted.
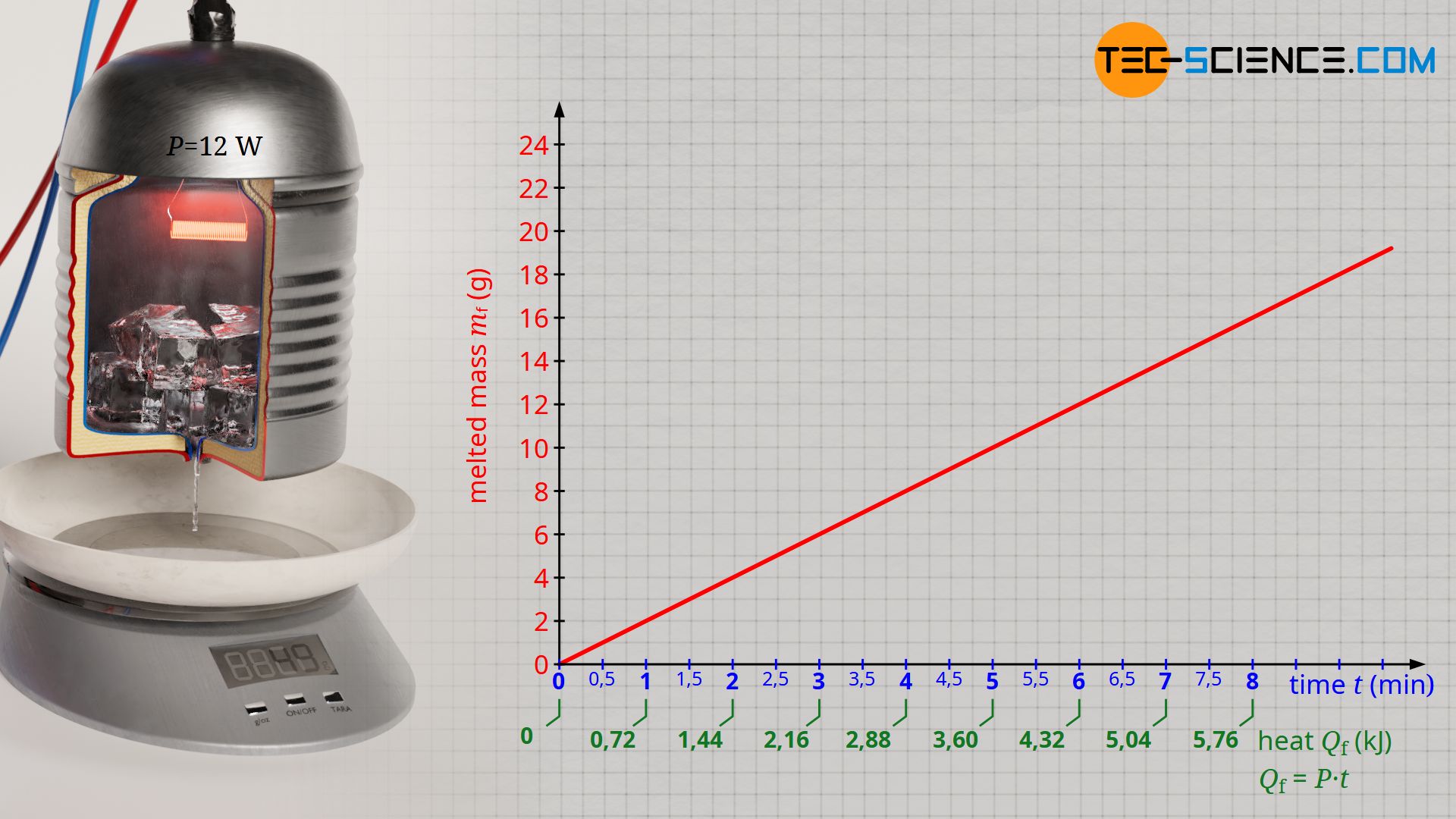
Especially with regard to the comparability of the heats of fusion of different solids, it therefore makes sense to always relate the heats of fusion Qf to a standardized amount of mass to be melted (e.g. 1 kilogram or 1 gram). This constant ratio between the heat of fusion and the mass mf to be melted is called specific heat of fusion or specific enthalpy of fusion qf:
\begin{align}
&\boxed{q_\text{f} = \frac{Q_\text{f}}{m_\text{f}}}~~~[q_\text{f}]=\frac{\text{J}}{\text{kg}}~~~~~\text{specific heat of fusion} \\[5px]
\end{align}
From the experiment, a specific heat of fusion of around qf = 350 kJ/kg is finally obtained for ice. This means that 350 kJ of heat is required to melt 1 kilogram of ice. However, with the experimentally determined heat of fusion using the described experimental setup, it must be noted that the heat emitted by the heater does not completely benefit the melting of the ice. Some of the heat is also used to heat the vessel and is thus transferred to the surroundings. Therefore, a lower amount of heat is used for the melting of the ice than calculated with formula (\ref{q}). The literature value for the specific heat of fusion of ice is therefore somewhat lower with qf = 334 kJ/kg.

Specific heat of fusion is the heat of fusion to be added per unit mass of a solid to be melted!
In the case of ice, the latent heat to be added for melting is 334 kJ per kilogram, which is about the same as the amount of heat that would be needed to bring the water to a boil from room temperature. A great deal of heat must therefore be used for melting. This explains, for example, why ice cubes are ideal for cooling drinks.
Conclusion
The specific heat of fusion qf describes the relationship between the mass to be melted mf and the heat of fusion to be added for this purpose Qf:
\begin{align}
&\boxed{Q_\text{f} = q_\text{f} \cdot m_\text{f}} ~~~\text{heat of fusion} \\[5px]
\end{align}
Specific heat of fusion of selected substances
If the experiment described above were to be carried out with other solids instead of ice (e.g. metals that are being molten), it would be shown that these substances melt at different rates. As a result, more or less heat energy is required to melt a given mass of the respective substance. The specific latent heat of fusion is therefore dependent on the substance.
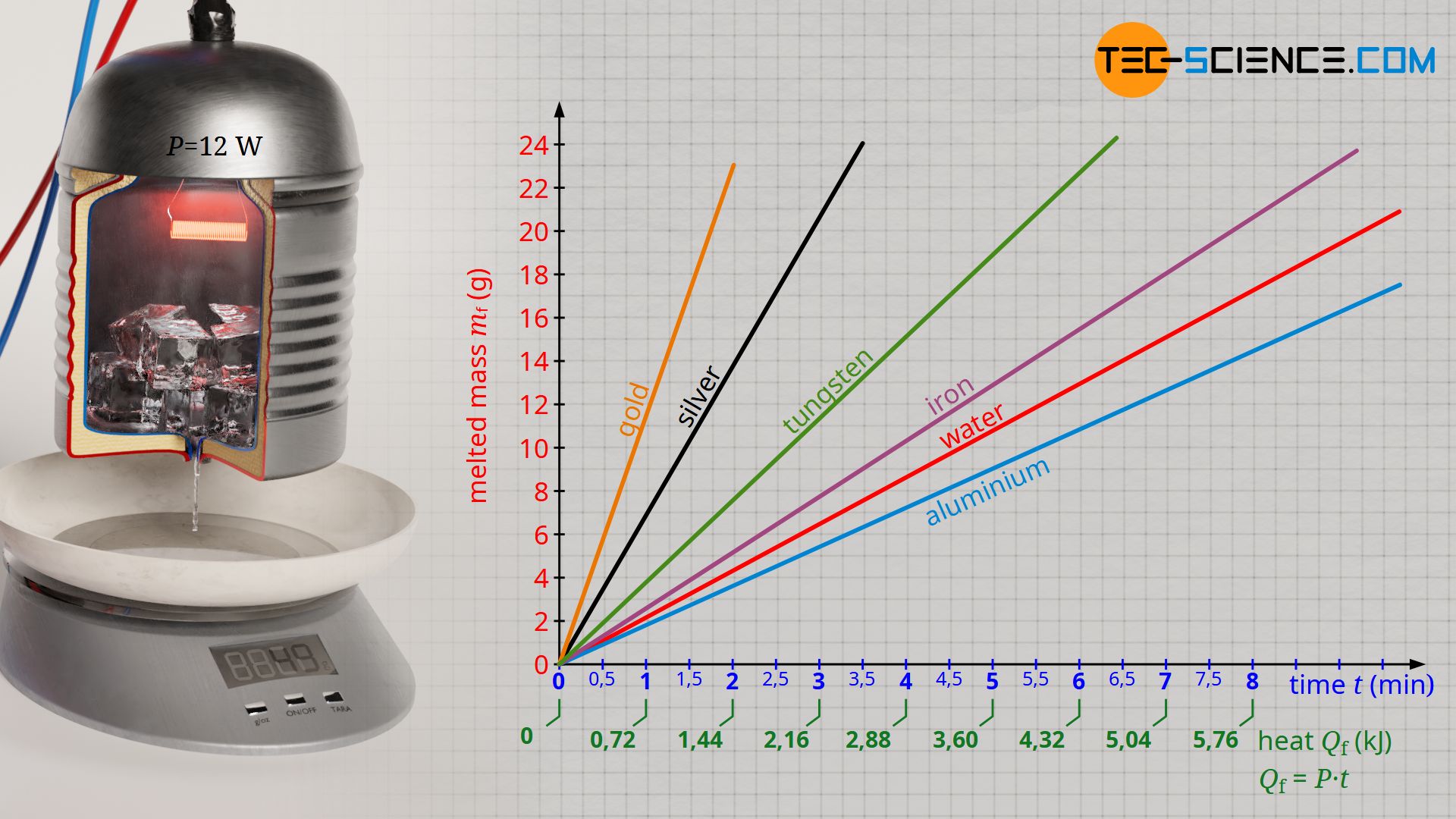
The greater the specific heat of fusion of a substance, the more heat is required to melt a certain mass. Solids with large specific heats of fusion therefore do not melt as quickly. The table below shows the specific heats of fusion of selected substances.
| Substance | Melting temperature in the unit °C | Specific heat of fusion in the unit kJ/kg |
|---|---|---|
| Aluminium | 660 | 398 |
| Lead | 328 | 25 |
| Iron | 1538 | 268 |
| Mercury | -39 | 12 |
| Silver | 962 | 105 |
| Water | 0 | 334 |
| Tungsten | 3422 | 191 |
| Tin | 232 | 59 |
| Gold | 1064 | 63 |
Note: The relatively high specific heat of fusion of aluminum is, among other things, a reason why the production of aluminum, especially the melting down, is very energy-intensive and thus expensive!






