Die Maxwell-Boltzmann-Verteilung der Geschwindigkeit von idealen Gasen kann aus der barometrischen Höhenformel hergeleitet werden.
Einleitung
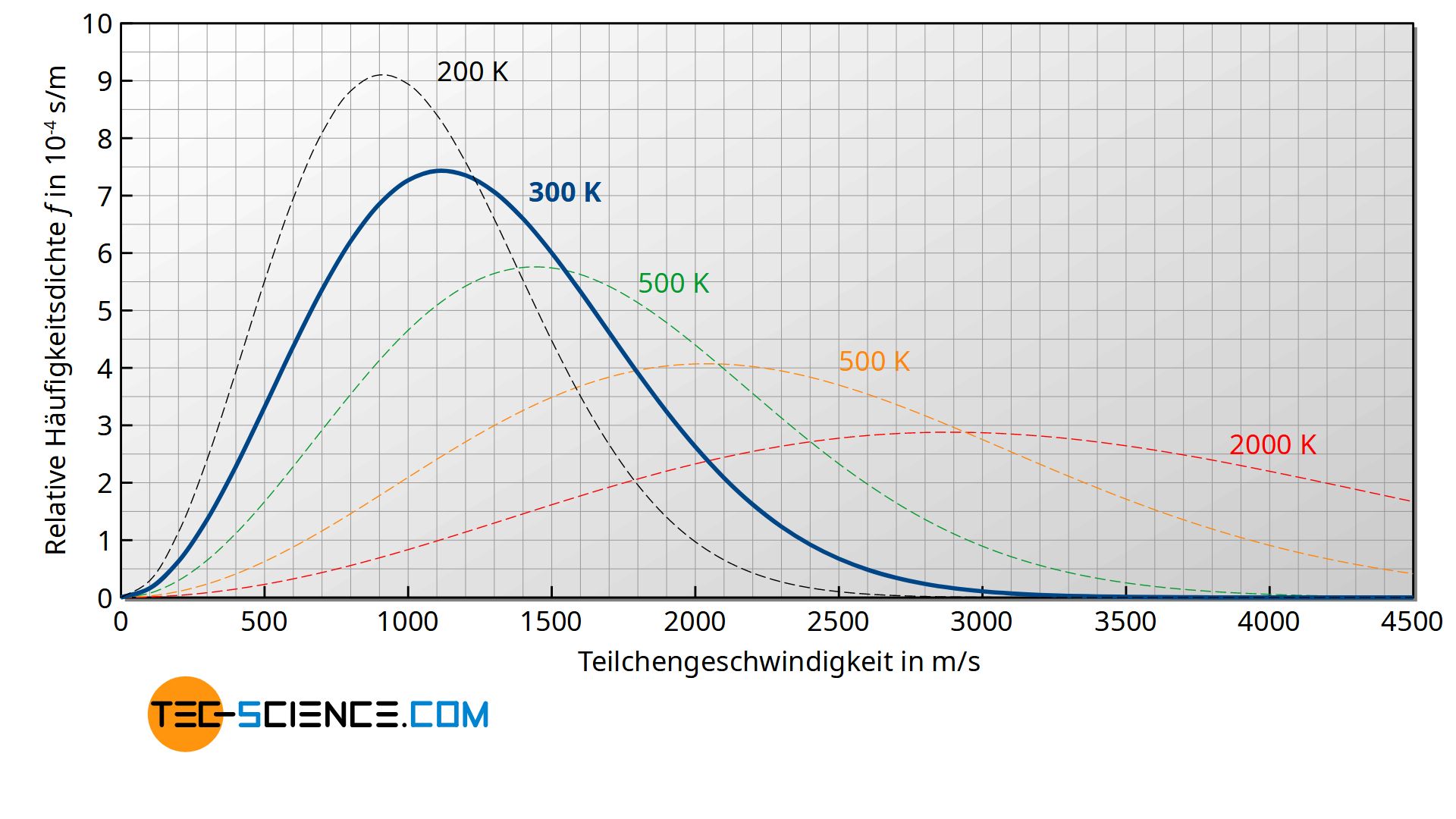
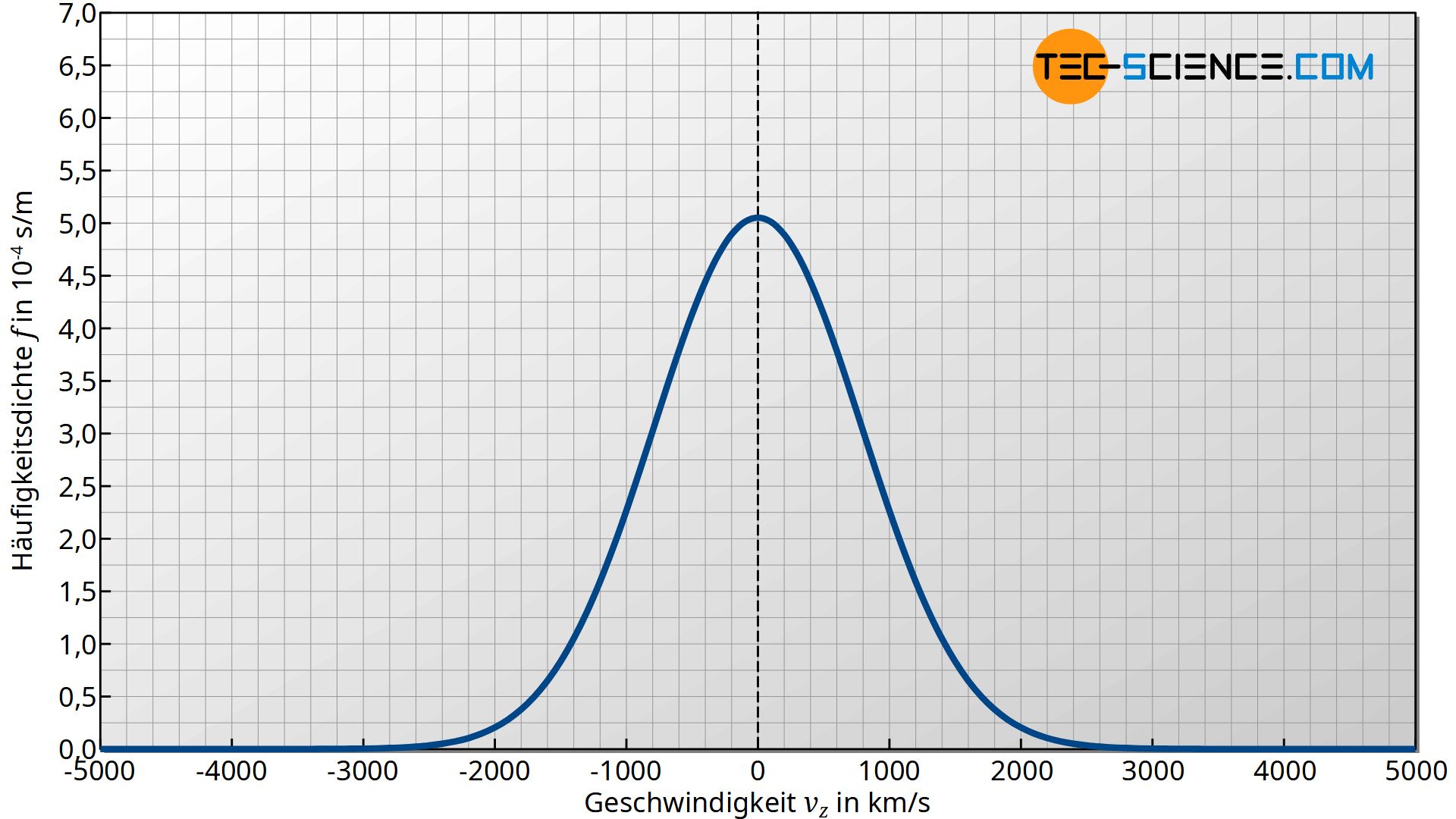
Für ideale Gase wurde im Artikel Maxwell-Boltzmann-Verteilung die Verteilungsfunktion f(v) der Geschwindigkeiten bereits ausführlich erläutert. Die untere Abbildung zeigt hierzu nochmals für verschiedene Temperaturen die jeweiligen Kurvenverläufe.
\begin{align}
\label{p}
&\boxed{ f(v) = \left( \sqrt{\frac{m}{2 \pi k_B T}} \right)^{3} \cdot 4 \pi v^2 \cdot \exp{\left(- \frac{m \cdot v^2}{2 k_B \cdot T} \right)} } ~~~\text{Maxwell-Boltzmann-Verteilung} \\[5px]
\end{align}
In diesem Artikel soll diese Verteilungsfunktion hergeleitet werden.
Barometrische Höhenformel
Die barometrische Höhenformel beschreibt den Verlauf des atmosphärischen Luftdrucks p bzw. der Luftdichte ϱ in Abhängigkeit der Höhe z über einem Bezugsniveau (z.B. Meereshöhe):
\begin{align}
\label{bar}
&\boxed{p(z) = p_0 \cdot \exp{\left(-\dfrac{\rho_0 g z}{p_0}\right)}} ~~~\text{barometrische Höhenformel} \\[5px]
\end{align}
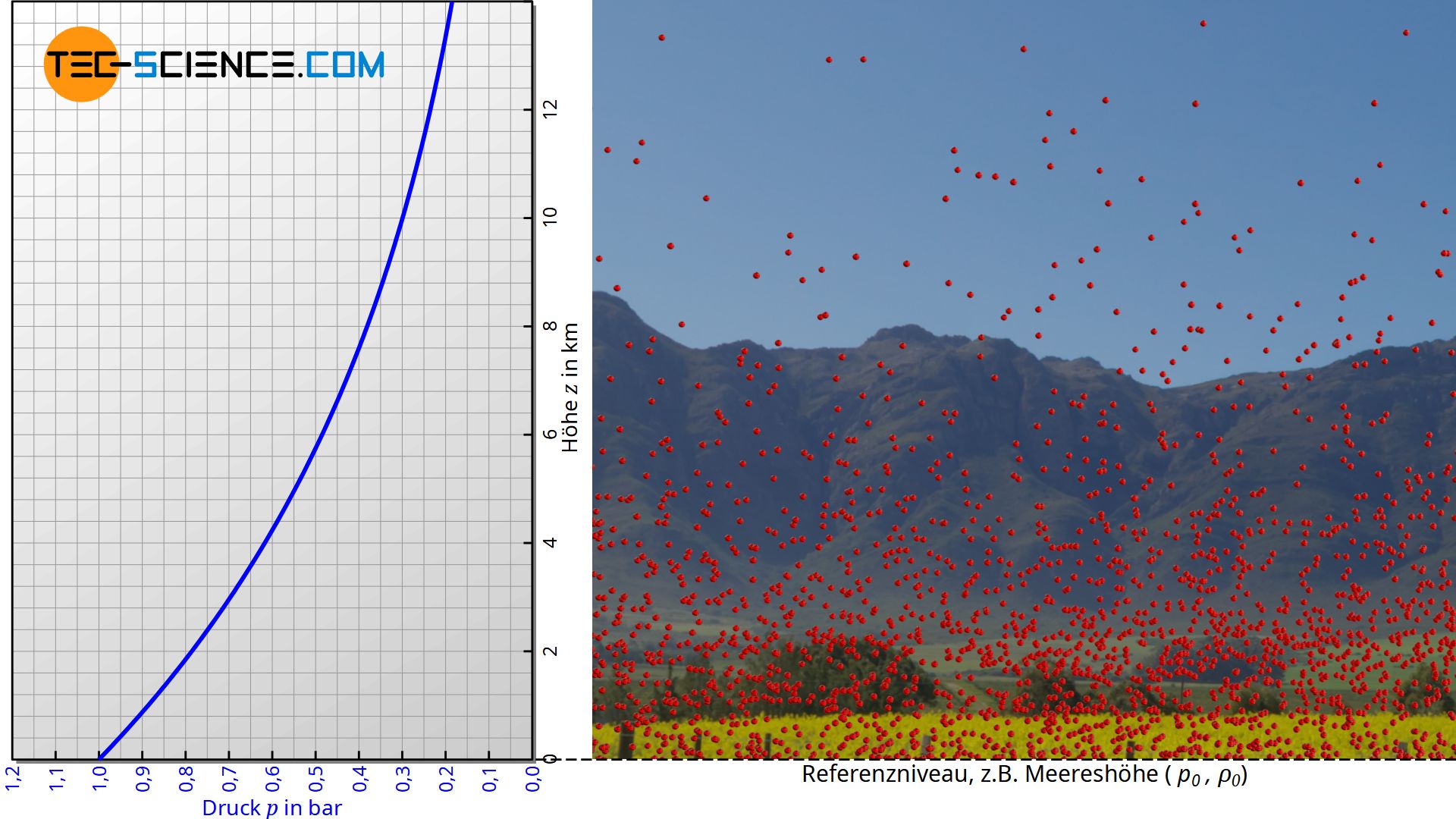
Die barometrische Höhenformel bleibt grundsätzlich nicht auf Luft beschränkt. Sie kann für jedes (ideale) Gas angewendet werden, welches einem Gravitationsfeld ausgesetzt ist. Die ideale Gasgleichung liefert hierzu in Abhängigkeit der Teilchenanzahl N folgenden Zusammenhang zwischen dem Druck p, dem Volumen V und der Temperatur T (kB ist die Boltzmann-Konstante):
\begin{align}
&p V = N k_B T \\[5px]
\end{align}
Die Gesamtmasse des betrachteten Gases mgas (welches das Volumen V einnimmt) lässt sich aus dem Produkt von Teilchenmasse m und Teilchenanzahl N ermitteln (mgas=N⋅m). Somit ergibt sich die Teilchenanzahl aus dem Quotienten von Gasmasse und Teilchenmasse (N=mgas/m). Wird dies in der idealen Gasgleichung berücksichtigt, dann folgt für die Gasdichte ϱ=mgas/V:
\begin{align}
&p V = \frac{m_{gas}}{m} \cdot k_B T \\[5px]
&p = \frac{m_{gas}}{V} \cdot \frac{k_B T}{m} \\[5px]
\label{density}
&\boxed{p = \rho \cdot \frac{k_B T}{m}} ~~~\text{bzw.}~~~\boxed{p_0 = \rho_0 \cdot \frac{k_B T}{m}} \\[5px]
\end{align}
In Gleichung (\ref{density}) bezeichnet ϱ0 die Gasdichte auf dem Referenzniveau und ϱ die zu einem beliebigen Druck p gehörende Dichte. Wird Gleichung (\ref{density}) nun in die barometrische Höhenformel (\ref{bar}) eingesetzt, dann ergibt sich folgender Zusammenhang zwischen der Dichte auf dem Referenzniveau ϱ0 und der Dichte ϱin einer beliebigen Höhe z:
\begin{align}
\require{cancel}
&p(z) = p_0 \cdot \exp{\left(-\dfrac{\rho_0 g z}{p_0}\right)} \\[5px]
&\rho(z) \cdot \bcancel{\frac{k_B T}{m}}= \rho_0 \cdot \bcancel{\frac{k_B T}{m}} \cdot \exp{\left(-\dfrac{\bcancel{\rho_0} g z}{ \bcancel{\rho_0} \cdot \frac{k_B T}{m} }\right)} \\[5px]
\label{rho}
&\rho(z)= \rho_0 \cdot \exp{\left(-\dfrac{m g z}{k_BT}\right)} \\[5px]
\end{align}
Da sich die Masse m in Gleichung (\ref{rho}) auf ein einzelnen Teilchen bezieht, lässt sich der Ausdruck m⋅g⋅z als potentielle Energie Wpot (Lageenergie) eines Teilchen auf der Höhe z interpretieren:
\begin{align}
\label{rhoz}
&\rho(W_{pot})= \rho_0 \cdot \exp{\left(-\dfrac{W_{pot}}{k_BT}\right)} \\[5px]
\end{align}
An dieser Stelle stellt sich zunächst die Frage wie die einzelnen Teilchen überhaupt zu ihreren potentiellen Energie kommen. Hierzu stelle man sich zunächst die Gasteilchen am absoluten Nullpunkt vor. Aufgrund der fehlenden Wärmebewegung werden sich dann alle Gasteilchen unter dem Gravitationseinfluss am Boden sammeln (Referenzniveau).
Nun erhöht man durch Wärmezufuhr in Gedanken langsam die Temperatur, sodass die Teilchen sich immer heftiger bewegen und früher oder später zusammenstoßen. Durch die permanent stattfindenden Stöße katapultieren sich die einzelnen Teilchen im Prinzip gegenseitig immer höher. Energetisch ist dies aber nichts anderes als ein Zuführen von kinetischer Energie auf Referenzniveau die anschließend in potentielle Energie umgewandelt wird. Die Teilchen gelangen also aufgrund ihrere kinetischen Energie am Boden (zugeführt durch die Wärme) in die Höhe.
Modellvorstellung
Man kann sich hierzu folgendes Modell vorstellen. Man geben viele Kügelchen in eine vertikale Röhre, die auf einer Platte steht. Die Platte wird durch einen Motor in Vibration versetzt. Die Kugeln werden sich je nach Stärke der Vibration mehr oder weniger stark bewegen, so wie sich die Gasteilchen je nach Temperatur mehr oder weniger stark bewegen. Die Kugeln werden durch diese Bewegung in die Luft katapultiert, so wie sich auch die Gasteilchen in der Realität gegenseitig in die Höhe befördern.

Man wird dabei aber feststellen, dass sich keine gleichmäßige Verteilung der Kugeln über die Rohrlänge hinweg ergibt, wie auch bei einem realen Gas. Dies liegt daran, dass nicht allen Kugeln dieselbe kinetische Energie am Boden zugeführt wird. Die Kugeln stoßen schließlich untereinander zusammen. Einige werden hierdurch abgebremst und andere wiederum beschleunigt. Wird bspw. eine nach oben fliegende Kugel durch eine eine schnellere Kugel angestoßen, dann wird sich die kinetische Energie der gestoßenen Kugel erhöhen. Sie ist damit in der Lage eine größere Höhe zu erreichen. Wird sie dabei zufällig durch eine weitere Kugel angestoßen, dann wird sich nochmals deutlich höher fliegen können. Für einige wenige Kugeln könnte dies vielleicht ein oder zwei weitere Male passieren. Ein solcher idealer Katapulteffekt wird aber nur auf wenige Kugeln beschränkt bleiben. Deshalb finden sich mit zunehmender Höhe auch immer weniger Kugeln wieder.
Mit zunehmender Höhe wird die Kugeldichte („Anzahl an Kugeln pro Volumen“) also abnehmen, da es immer unwahrscheinlicher wird, dass eine Kugel am Boden zufällig eine so hohe kinetische Energie mitbekommt, um diese Höhe zu erreichen (ob dabei auf dem Weg nach oben noch Stoßprozesse mit anderen Kugeln stattfinden oder nicht spielt aus energetischer Sicht keine Rolle). Dabei ist zu beachten, dass es prinzipiell nicht möglich ist einer ganz bestimmten Höhe eine konkrete Kugelanzahl zuzuordnen. So wird man bspw. auf einer vorgegebenen Höhe von exakt 10 cm keine einzige Kugel finden, da keine Kugel bis auf die „letzte“ Nachkommastelle eine exakte Höhe von 10 cm erreichen wird (evtl. nur 10,0003 cm oder 9,9998 cm).
Für eine konkrete Kugelanzahl muss man also die Höhe in kleine Intervalle Δz einteilen und die darin vorkommenden Kugeln ermitteln. Als Beispiel werden 1000 Kugeln betrachtet. Jede Kugel hat eine Masse von 10 g. Werden nun in einer Höhe zwischen 10 cm und 11 cm im statistischen Mittel jeweils 5 Kugeln registriert, dann haben offensichtlich 0,5% der gesamten Kugeln eine potentielle Energie zwischen 10 mJ und 11 mJ (die Teilchen kommen auf dieser Höhe also zum Stillstand und die ehemals kinetische Energie auf Bodenhöhe wurde vollständig in Lageenergie umgewandelt). Auf Referenzniveau betrachtet, besitzen energetisch gesehen somit 0,5 % der Kugeln eine kinetische Energie zwischen 10 mJ und 11 mJ. Die Wahrscheinlichkeit, dass eine zufällig herausgegriffene Kugel eine Bewegungsenergie zwischen 10 mJ und 11 mJ aufweist beträgt somit ebenfalls 0,5 %. Die Häufigkeit mit der bestimmte Energien vorhanden sind lässt sich also auch als Wahrscheinlichkeit interpretieren!
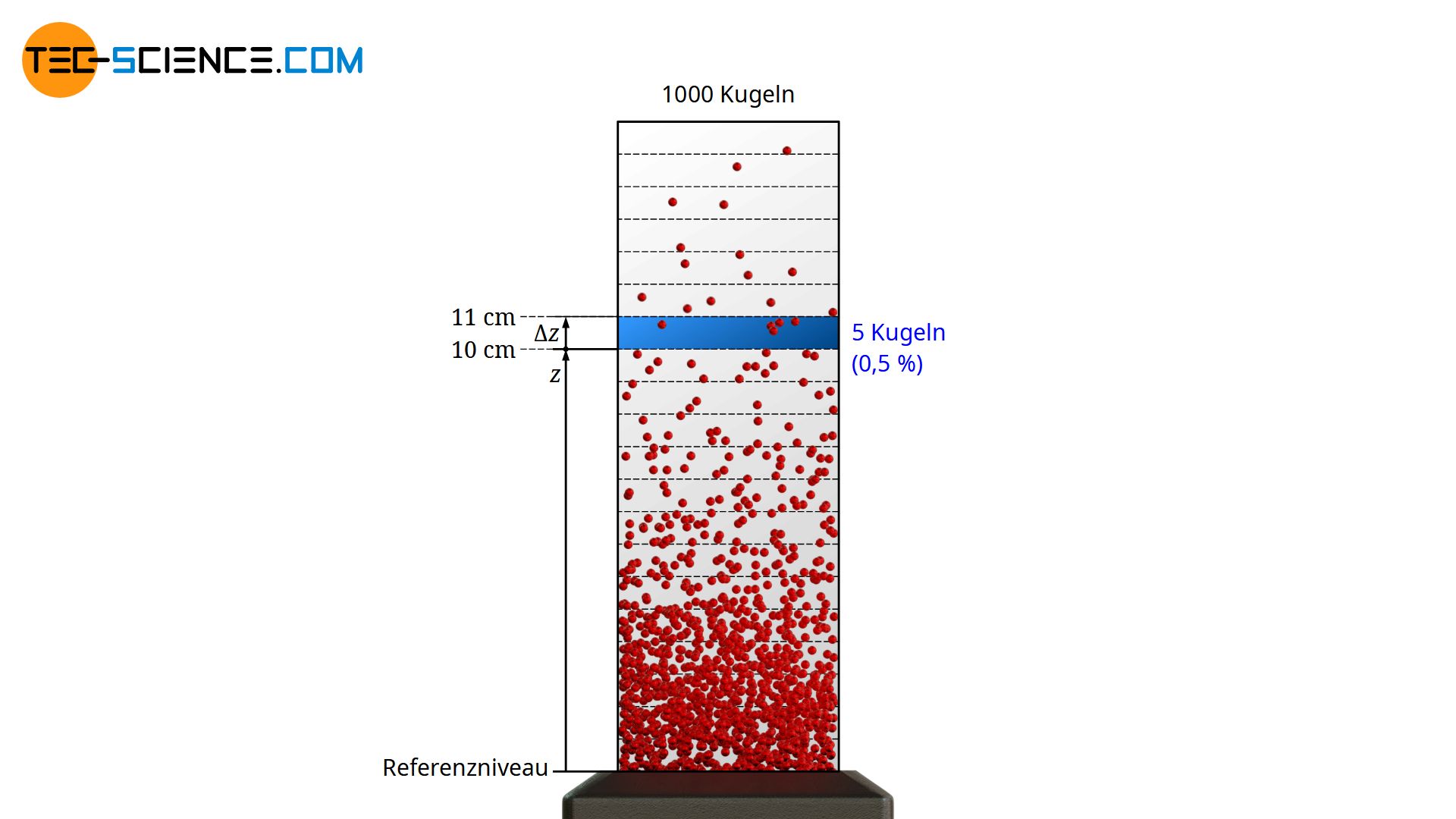
Die Häufigkeit mit der Kugeln innerhalb eines bestimmten Höhenbereichs angetroffen werden, entspricht der Wahrscheinlichkeit mit der bestimmte kinetische Energiebereiche auf Referenzniveau vorhanden sind!
Anstelle des betrachteten Höhenbereichs von Δz = 1 cm, hätte man auch eine Intervallbreite von Δz = 2 cm wählen können (siehe Abbildung unten). In diesem Fall betrachtet man dann Kugeln, die sich in einer Höhe zwischen 10 cm und 12 cm befinden. Die Wahrscheinlichkeit wäre groß, dass man darin dann die doppelte Anzahl an Kugeln wiederfindet. Denn schließlich betrachtet man nun ja auch ein doppelt so großen Raumbereich. Dieses Proportionalität gilt strenggenommen nur für (unendlich) kleine Intervallbreiten, da sich mit der Höhe auch die Kugeldichte ändert. Diese Beispiel verdeutlicht aber, dass für die Ermittlung der Häufigkeit nicht nur die Kugeldichte auf einer bestimmten Höhe relevant ist, sondern auch die Intervallbreite innerhalb deren untersucht wird!
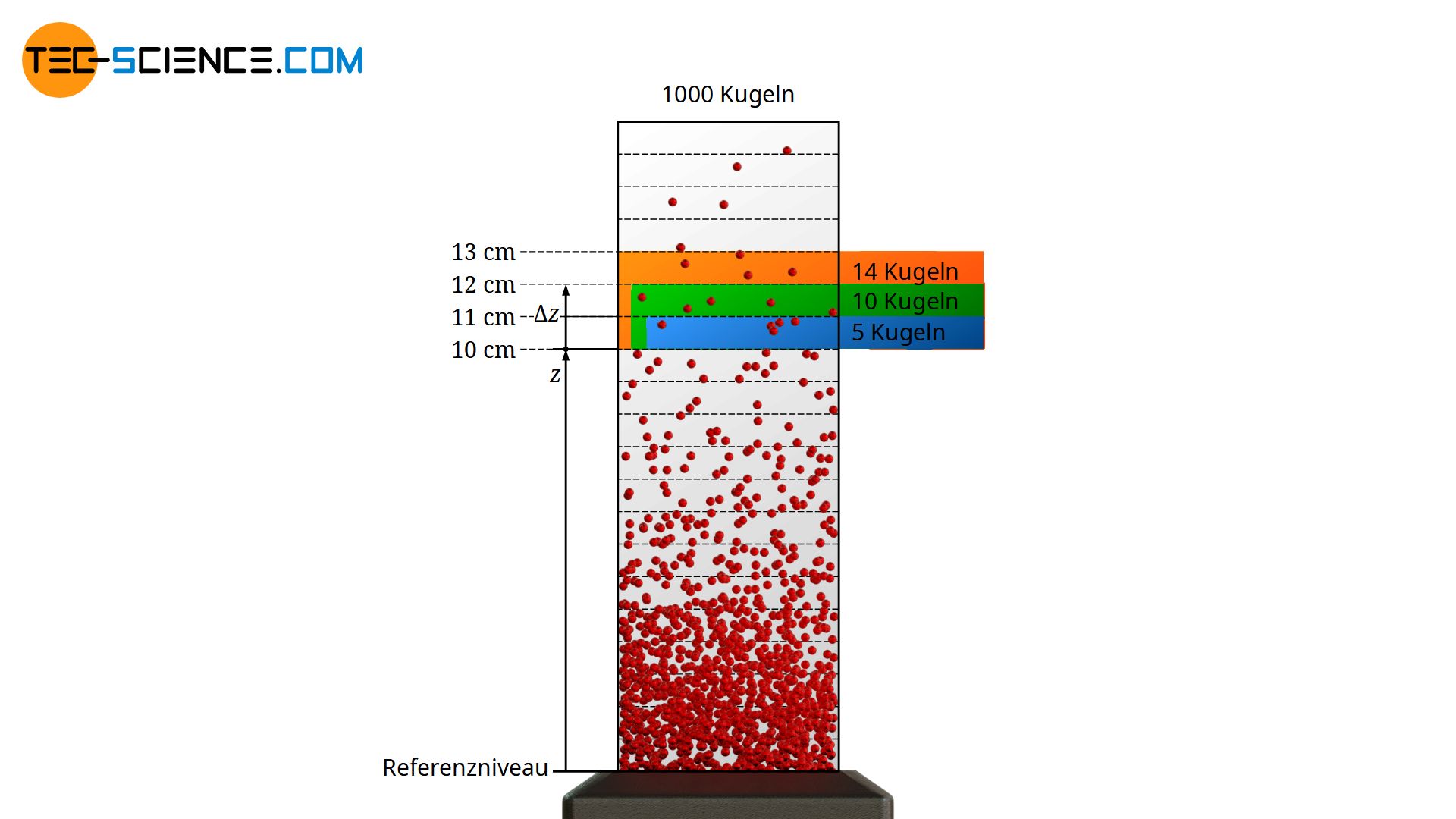
Die Kugeldichte in Kombination mit dem Höhenintervall, welches man auf einer bestimmen Höhe zulässt, ist ein Maß für die Häufigkeit bzw. Wahrscheinlichkeit mit der die entsprechenden kinetische Energieintervalle auf Referenzniveau vorhanden sind!
Was bedeutet „Kugeldichte in Kombination mit dem Höhenintervall“ nun konkret? Wie bereits erläutert, ergibt sich für kleine Intervallbreiten ein proportionaler Zusammenhang zu der darin liegenden Anzahl an Kugeln (meist in Prozent als sogenannte relative Häufigkeit oder eben als Wahrscheinlichkeit angegeben):
\begin{align}
&\text{Häufigkeit} ~\sim \text{„Intervallbreite“} \\[5px]
\end{align}
Zudem ist die Kugeldichte ohnehin proportional zur Kugelanzahl, denn eine zweifach so große Dichte mein schließlich per Definition eine zweifach so hohe Kugelanzahl (pro Volumen):
\begin{align}
&\text{Häufigkeit} ~\sim \text{„Kugeldichte“} \\[5px]
\end{align}
Die Häufigkeit mit der die Kugeln auf einer bestimmten Höhe z und innerhalb eines bestimmten Intervalls verteilt sind, ist somit proportional zum Produkt aus vorhandener Kugeldichte und im Vorfeld festgelegter Intervallbreite:
\begin{align}
\label{hau}
&\boxed{\text{Häufigkeit} ~\sim \text{„Kugeldichte“} \times \text{„Intervallbreite“} } \\[5px]
\end{align}
Diese Modellvorstellung der Kugeln zeigt, dass man anhand der Kugeldichte in den verschiedenen Höhen sowie der zugelassenen Intervallbreite, auf die Verteilung der kinetischen Energien auf Referenzniveau schließen kann. Hieraus lässt sich dann die Geschwindigkeitsverteilung ermitteln. Da für das Erreichen einer bestimmten Höhe nur die Geschwindigkeitskomponente in z-Richtung relevant ist, beziehen sich die kinetischen Energien nur auf die Geschwindigkeiten die mit der z-Richtung verknüpft sind:
\begin{align}
\label{wpot}
&W_{pot}=W_{kin,z}=\frac{1}{2}mv_z^2 \\[5px]
\end{align}
Übertragung der Modellvorstellung auf Gase
Das oben beschriebene Kugelmodell lässt sich nun auf Gasteilchen im Schwerefeld der Erde übertragen und damit auf die barometrische Höhenformel. Die Gasdichte nimmt mit zunehmender Höhe also deshalb ab, da offensichtlich immer weniger Teilchen ausreichend hohe kinetische Energien am Boden besaßen, um auf die entsprechende Höhe zu gelangen.
Die Stoffdichte auf einer bestimmten Höhe ist ein Maß für die Häufigkeit mit der bestimmte Geschwindigkeiten auf Referenzniveau vorhanden ist!
Wird hierzu Gleichung (\ref{wpot}) in Gleichung (\ref{rhoz}) eingesetzt, so ergibt sich folgender Zusammenhang:
\begin{align}
&\rho(W_{pot})= \rho_0 \cdot \exp{\left(-\dfrac{W_{pot}}{k_BT}\right)} ~~~\text{mit}~~~ W_{pot}=W_{kin,z}=\tfrac{1}{2}mv_z^2~~~\text{folgt:}\\[5px]
\label{rhov}
&\boxed{\rho(v_z)= \rho_0 \cdot \exp{\left(-\dfrac{mv_z^2}{2k_BT}\right)}} \\[5px]
\end{align}
Auf die selbe Weise wie die Dichte eines Gases im Schwerefeld der Erde gemäß der Barometrischen Höhenformel (\ref{bar}) mit zunehmender Höhe exponentiell abnimmt, nimmt gemäß Gleichung (\ref{rhov}) die Häufigkeit bestimmter Geschwindigkeitsanteile exponentiell mit dem Quadrat der Geschwindigkeit ab:
\begin{align}
&\text{Häufigkeit} \sim \underbrace{\exp{\left(-\dfrac{mv_z^2}{2k_BT}\right)}}_{\text{Boltzmann-Faktor}} \\[5px]
\end{align}
Dieser Faktor, der die exponentielle Abnahme der Häufigkeit mit zunehmender Geschwindigkeit beschreibt (allgemeiner: zunehmender Energie), wird auch als Boltzmann-Faktor bezeichnet und spielt in der statistischen Physik eine zentrale Rolle!
Wie das Beispiel der Kugeln verdeutlichte, muss für eine konkrete Häufigkeit immer auch eine gewisse Intervallbreite zugelassen werden. Auf dieselbe Weise wie man bei einer exakt vorgegeben Höhe keine einzige Kugel wiederfinden würde, würde man nun kein einziges Teilchen mit einer exakt vorgeschriebenen Geschwindigkeit finden. Man kann somit nur danach fragen wie viele Teilchen eine Geschwindigkeit innerhalb eines gewissen Bereichs Δvz aufweisen. Solange dieses Geschwindigkeitsintervall Δvz hinreichen klein gewählt wird, ergibt sich ein proportionaler Zusammenhang zur Häufigkeit. Denn lässt man ein doppelt so großes Intervall zu, dann kommen potentiell auch doppelt so viele Teilchen infrage, die nun innerhalb dieses Intervalls liegen können.
\begin{align}
&\text{Häufigkeit} \sim \Delta v_z \\[5px]
\end{align}
Insgesamt ist die Häufigkeit (Wahrscheinlichkeit) mit der ein bestimmter Geschwindigkeitsbereich vorhanden ist somit proportional zum Boltzmann-Faktor exp(-mvz2/2kBT) und zur betrachteten Intervallbreite Δvz:
\begin{align}
&\text{Häufigkeit} \sim \underbrace{\exp{\left(-\dfrac{mv_z^2}{2k_BT}\right)}}_{\text{Boltzmann-Faktor}} \cdot \underbrace{~~~\Delta v_z~~~}_{\text{Intervallbreite}} \\[5px]
\end{align}
Um nun eine konkrete Formel zur Berechnung der Häufigkeit zu erhalten, kann rein formal ein Proportionalitätsfaktor f0 eingeführt werden, sodass folgende Gleichung gilt, die die Häufigkeit einer Geschwindigkeit im Bereich zwischen vz und vz+Δvz beschreibt:
\begin{align}
\label{z}
&\boxed{\text{Häufigkeit} = \underbrace{f_0 \cdot \exp{\left(-\dfrac{mv_z^2}{2k_BT}\right)}}_{\text{Häufigkeitsdichte}} \cdot \underbrace{\Delta v_z}_{\text{Geschwindigkeitsintervall}}} \\[5px]
\end{align}
Die untere Abbildung zeigt anschaulich welche Geschwindigkeitsvektoren in Frage kommen, wenn eine Geschwindigkeit vz und ein entsprechendes Intervall Δz vorgegeben wird. Alle Vektorpfeile deren Spitzen innerhalb des grün markieren Bereichs und damit mit ihren z-Komponenten zwischen vz und vz+Δz liegen, würden für die Bestimmung der Häufigkeit berücksichtigt.
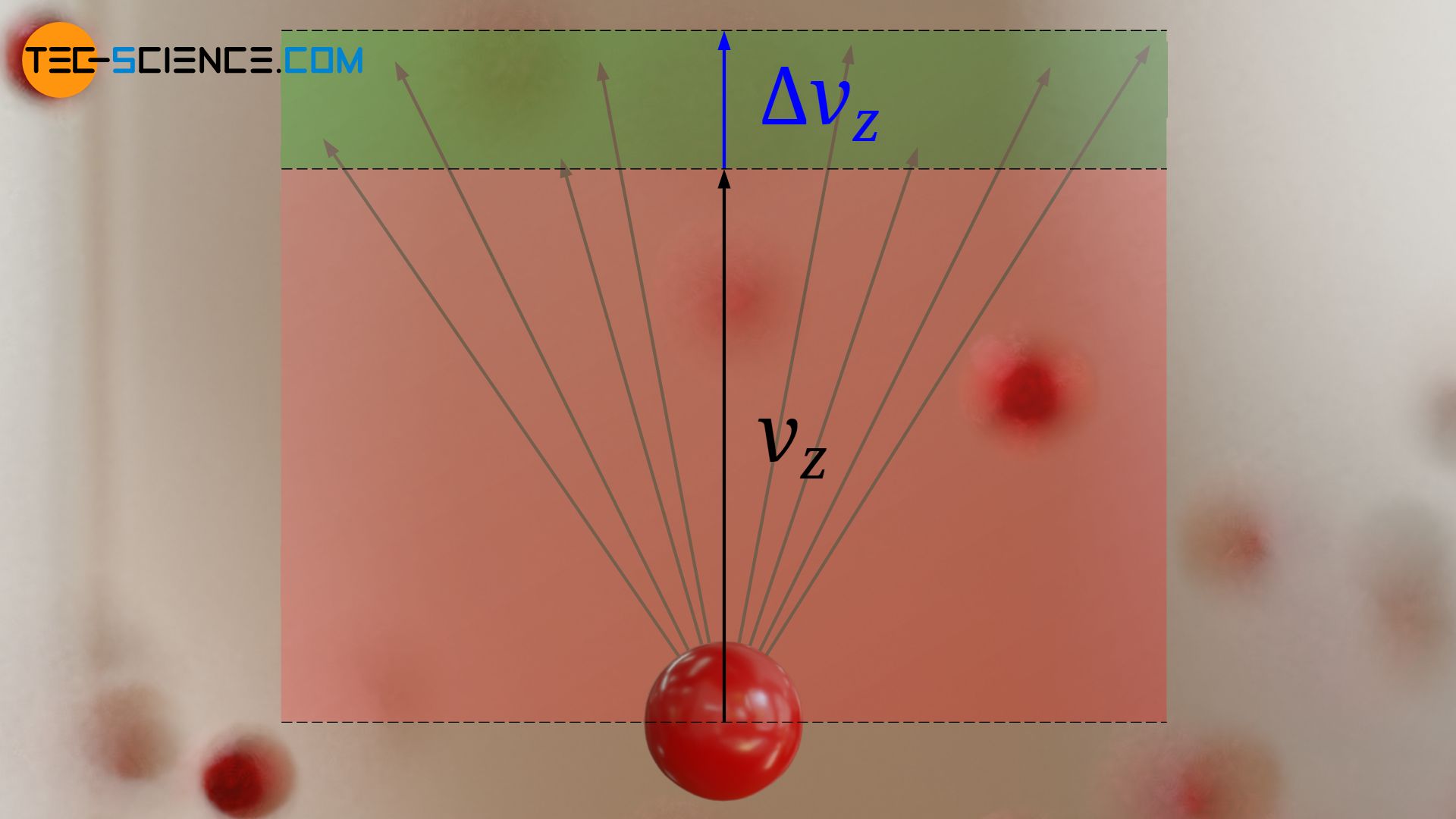
Die untere Abbildung zeigt den qualitativen Verlauf des Ausdrucks f0⋅exp(-mvz2/2kBT) wie er in der oberen Gleichung auftritt. Dieser Ausdruck entspricht im übertragenen Sinne der Teilchendichte bzw. Kugeldichte in der anschaulichen Vorstellung. Diese Funktion stellt in diesem Fall ein Maß für die Häufigkeit dar mit der bestimmte Geschwindigkeiten vz vorhanden sind und wird deshalb Häufigkeitsdichtefunktion oder Wahrscheinlichkeitsdichtefunktion genannt. Der Begriff „Dichte“ meint dabei die Häufigkeit bzw. Wahrscheinlichkeit einer Geschwindigkeit bezogen auf das entsprechende Geschwindigkeitsintervall:
\begin{align}
\label{norm}
&\text{Häufigkeitdichte} f(v_z) = \frac{\text{Häufigkeit}}{\text{Geschwindigkeitsintervall}} = f_0 \cdot \exp{\left(-\dfrac{mv_z^2}{2k_BT}\right)} \\[5px]
\end{align}
Normierung der Funktion
Nun gilt es schließlich noch den eingeführten Proportionalitätsfaktor in der Häufigkeitsdichtefunktion zu bestimmen. Diesen erhält man über eine sogenannte Normierung der Funktion. Auf diese Normierung wird im folgenden näher eingegangen.
Soll Gleichung (\ref{z}) wie gefordert eine Häufigkeit (=Wahrscheinlichkeit!) darstellen mit der ein bestimmter Geschwindigkeitsbereich zwischen vz und vz+Δvz vorhanden ist, dann muss letztlich die Summe der Häufigkeiten über alle möglichen Geschwindigkeitsbereiche hinweg 100 % ergeben. Denn summiert man schließlich alle vorkommenden Häufigkeiten (Wahrscheinlichkeiten) im Geschwindigkeitsbereich zwischen -∞ und +∞, dann wird man letztlich alle Teilchen zu 100 % erwischen (Wahrscheinlichkeit = 1), denn irgendeine Geschwindigkeit muss ein Teilchen schließlich haben. Beachte, dass die Teilchen eben nicht nur eine positive Geschwindigkeitskomponenten in z-Richtung aufweisen können, sondern auch eine negative!
Die Berechnung der Gesamthäufigkeit, wenn über alle Geschwindigkeiten im Bereich zwischen plus und minus unendlich summiert wird, lässt sich mathematisch wie folgt darstellen:
\begin{align}
&\text{Gesamthäufigkeit} = \sum_{-\infty}^{+\infty} f_0 \cdot \exp{\left(-\dfrac{mv_z^2}{2k_BT}\right)} \cdot \Delta v_z \overset{!}{=} 1 \\[5px]
\end{align}
Mathematisch entspricht dieses Aufsummieren dem Integrieren, wenn anstelle der endlichen Geschwindigkeitsintervalle Δvz infinitesimale Geschwindigkeitsbereiche dvz betrachtet werden. Mit der Bedingung, dass das Ergebnis 1 sein muss, kann der Proportionalitätsfaktor f0 schließlich bestimmt werden:
\begin{align}
&\text{Gesamthäufigkeit} = \int_{-\infty}^{+\infty} \underbrace{f_0 \cdot \exp{\left(-\dfrac{mv_z^2}{2k_BT}\right)}}_{\text{Häufigkeitsdichtefunktion}} \cdot \text{d}v_z = \underline{f_0 \cdot \sqrt{\frac{2\pi k_B T}{m}} \overset{!}{=} 1} \\[5px]
&\boxed{f_0 = \sqrt{\frac{m}{2\pi k_B T}} }
\end{align}
Anschaulich entspricht die Bestimmung des Integrals der Fläche unter dem Graphen der Häufigkeitsdichtefunktion. Diese Fläche wurde letztlich auf 1 normiert. Damit wird offensichtlich deutlich, dass die Fläche unter der Kurve der Dichtefunktion die Dimension einer Häufigkeit bzw. Wahrscheinlichkeit besitzt!
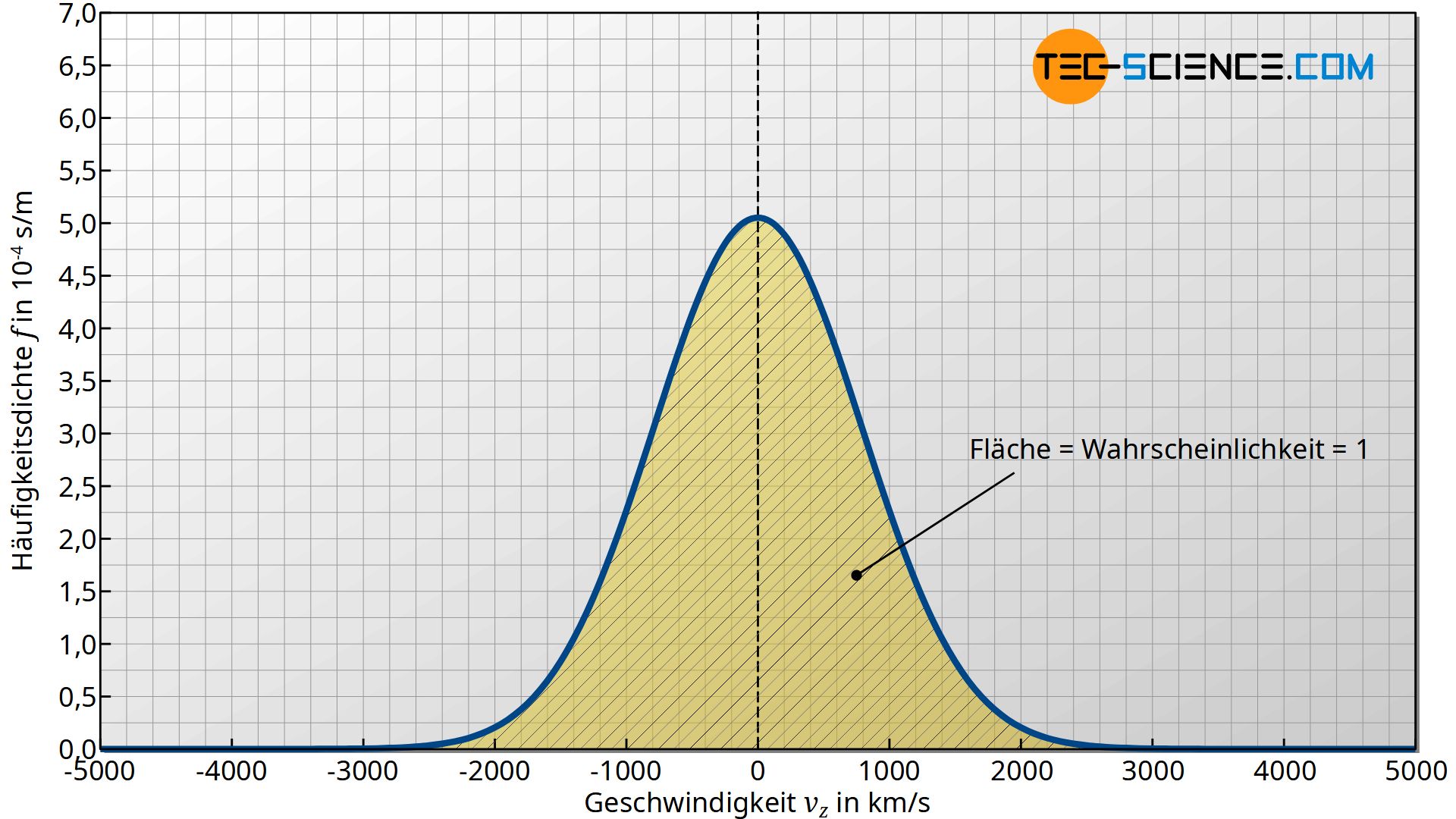
Mit dem Faktor f0 ist die Gleichung zur Berechnung der Häufigkeit nun also normiert, d.h. auf den Wert 1 festgelegt, wenn über alle Geschwindigkeiten integriert wird! Damit gilt für die Häufigkeit einer Geschwindigkeit im Bereich zwischen vz und vz+dvz die nachfolgende Gleichung:
\begin{align}
\label{dic}
&\boxed{\text{Häufigkeit} = \underbrace{\sqrt{\frac{m}{2\pi k_B T}} \cdot \exp{\left(-\dfrac{mv_z^2}{2k_BT}\right)}}_{\text{Häufigkeitsdichte } f(v_z)} \cdot \underbrace{~~~\text{d}v_z~~~}_{\text{Geschwindigkeitsintervall}}} \\[5px]
\end{align}
Beachte, dass anstelle makroskopischer Geschwindigkeitsbereiche Δvz nun infinitesimale Geschwindigkeitsintervalle dvz betrachtet werden.
Für die Häufigkeitsdichte bzw. Wahrscheinlichkeitsdichte gilt gemäß Gleichung (\ref{norm}) schließlich folgende Funktion f:
\begin{align}
\label{f}
&\boxed{f(v_z) =\sqrt{\frac{m}{2\pi k_B T}} \cdot \exp{\left(-\dfrac{mv_z^2}{2k_BT}\right)} } ~~~\text{Häufigkeitsdichtefunktion}
\end{align}
Für die Berechnung einer konkreten Häufigkeit F mit der eine Geschwindigkeit im Bereich zwischen vz1 und vz2 vorkommt, muss die Häufigkeitsdichtefunktion f(vz) innerhalb dieser Grenzen integriert werden:
\begin{align}
& \boxed{\text{Häufigkeit } F=\int_{v_{z1}}^{v_{z2}} f(v_z) ~~ \text{d} v_z} \\[5px]
\end{align}
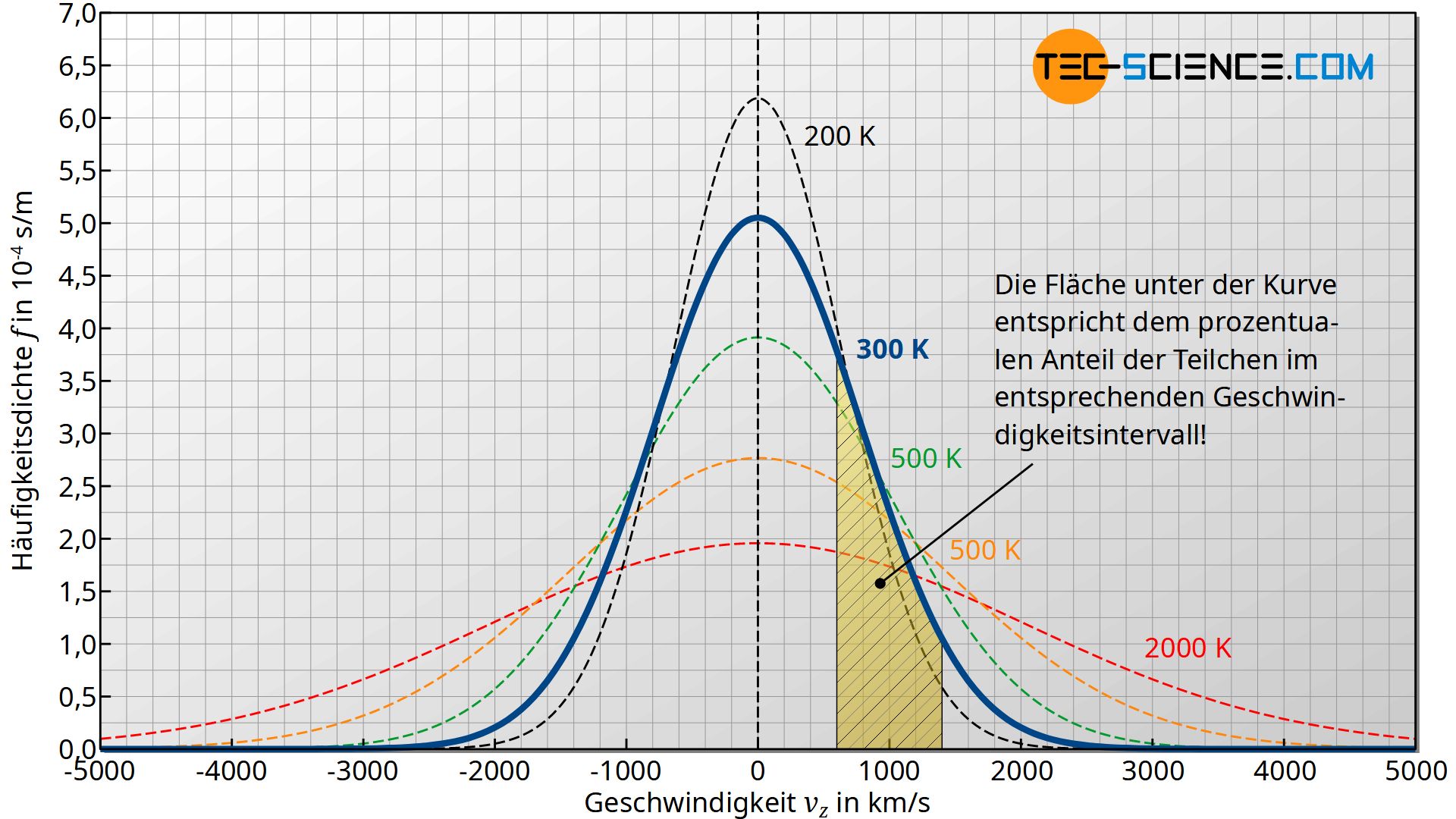
Die untere Abbildung zeigt den Verlauf der Häufigkeitsdichte f(vz) in Abhängigkeit der Geschwindigkeit vz für verschiedene Temperaturen. Beachte, dass dabei die Fläche unter der Kurve als Integral der Dichtefunktion die Häufigkeit bzw. Wahrscheinlichkeit darstellt mit der der entsprechende Geschwindigkeitsbereich vorhanden ist!
Erweiterung auf der Dichtefunktion auf drei Dimensionen
Die bisherige Betrachtung der Geschwindigkeitsverteilung beschränkte sich lediglich auf die Geschwindigkeit der Teilchen in z-Richtung. Wesentlich interessanter ist jedoch die Verteilung der Geschwindigkeit insgesamt, d.h. der Geschwindigkeitsbeträge. Hierzu muss die Häufigkeitsdichtefunktion (\ref{f}) auf drei Dimensionen erweitert werden.
Im Folgenden wird ein ideales Gas betrachtet, das sich in alle drei Raumrichtungen gleichermaßen verhält. Dies bedeutet, dass die Gasteilchen keine Richtung aufweisen in der sie bevorzugt fliegen, insbesondere wird hierzu der Einfluss der Gravitation vernachlässigt! Ein solches Gas ohne Vozugsrichtung der Teilchen, das sich deshalb in alle Richtungen gleich verhält, wird auch als isotropes Gas bezeichnet.
Der Geschwindigkeitsvektor
Im Allgemeinen haben Gasteilchen Geschwindigkeitsanteile in allen drei Raumrichtungen (vx, vy und vz). Der Geschwindigkeitsvektor v eines Gasteilchens lässt sich durch diese drei Komponenten darstellen:
\begin{align}
\vec{v} &= \begin{pmatrix}
v_{x} \\
v_{y} \\
v_{z}
\end{pmatrix}
\end{align}
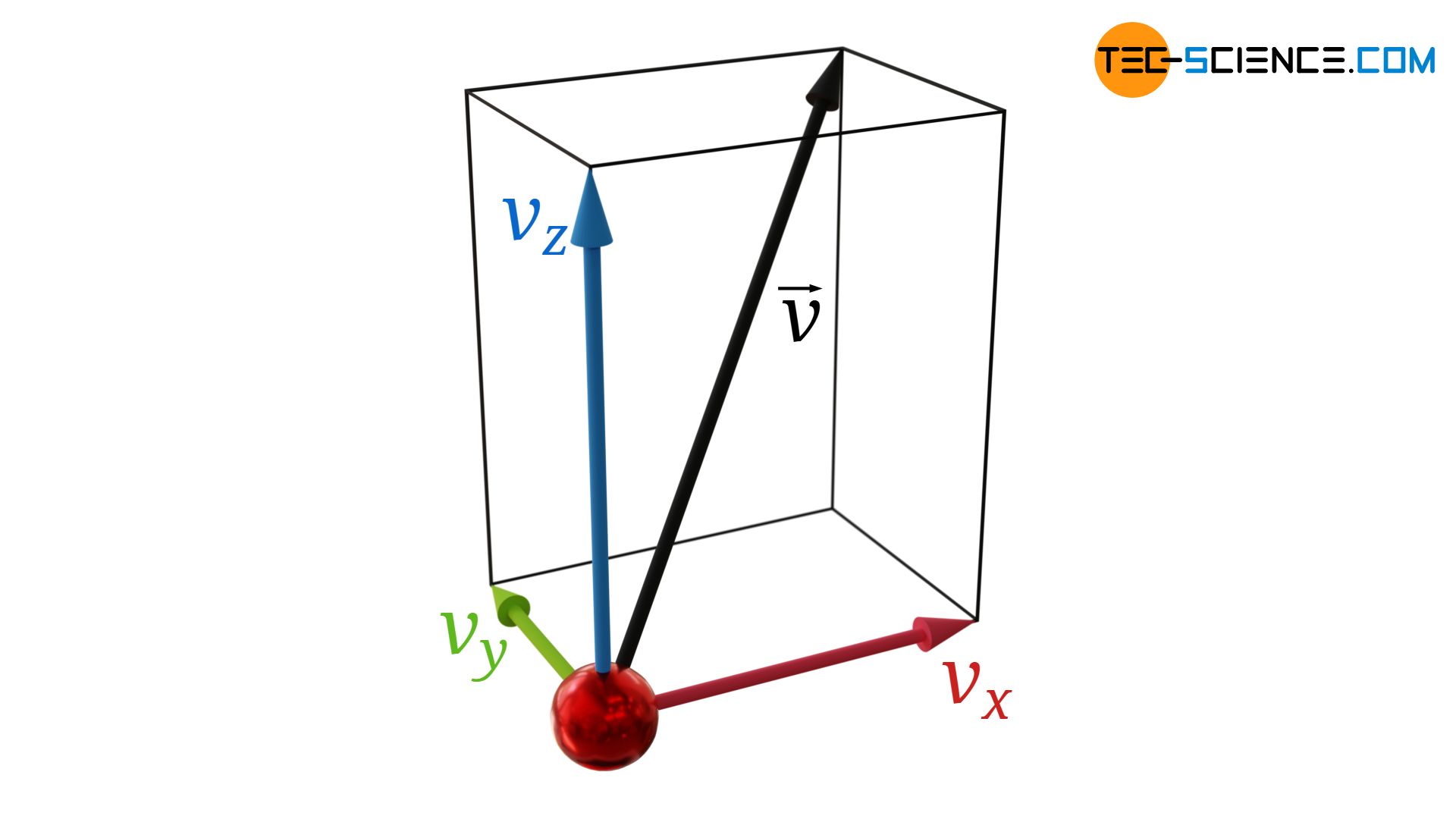
Für den Betrag der Geschwindigkeit |v| bzw. für das Quadrat des Geschwindigkeitsbetrages |v|² gilt:
\begin{align}
&|\vec{v}| = \sqrt{v_x^2+v_y^2+v_z^2} \\[5px]
\label{v22}
&|\vec{v}|^2 = v_x^2+v_y^2+v_z^2\\[5px]
\end{align}
Beachte, dass beim Quadrieren eines Geschwindigkeitsbetrages (wie in Gleichung (\ref{v22}) geschehen) auch auf die Betragsstriche verzichtet werden kann. Dies führt zum selben Ergebnis:
\begin{align}
&\vec{v}^2 = \begin{pmatrix}
v_{x} \\
v_{y} \\
v_{z}
\end{pmatrix}
\begin{pmatrix}
v_{x} \\
v_{y} \\
v_{z}
\end{pmatrix} = v_x^2+v_y^2+v_z^2 = |\vec{v}|^2 \\[5px]
\label{v2}
&\boxed{\vec{v}^2 = v_x^2+v_y^2+v_z^2}
\end{align}
Das Quadrat eines Vektors ist also eine rein skalare Größe. Durch das Quadrieren eines Vektors geht somit die Richtungsinformation eines Vektors verloren. Diese Tatsache wird später noch wichtig!
Häufigkeit des Auftretens eines Geschwindigkeitsvektors
Gleichung (\ref{dic}) beschreibt die Häufigkeit mit der eine Geschwindigkeitskomponente in z-Richtung innerhalb eines Intervalls vz und vz+dvz vorhanden ist. Da es sich wie vorausgesetzt um ein isotropes Gas handelt gilt diese Häufigkeitsverteilung für jede Geschwindigkeitskomponente i=x,y,z gleichermaßen:
\begin{align}
\label{dicc}
&\text{Häufigkeit }(v_i) = \sqrt{\frac{m}{2\pi k_B T}} \cdot \exp{\left(-\dfrac{mv_i^2}{2k_BT}\right)} \cdot \text{d}v_i ~~~~~\text{für } i=x,y,z\\[5px]
\end{align}
Für die Geschwindigkeitsverteilung stellt sich nun die Frage wie häufig ein bestimmter Geschwindigkeitsvektor v mit gegebenen Komponenten vx, vy und vz innerhalb der jeweils vorgegebenen Geschwindigkeitsintervalle dvx, dvy und dvz vorkommt.
Ein einfaches Beispiel zeigt hierzu die prinzipielle Vorgehensweise. In diesem Zusammenhang ist es für das Verständnis sinnvoller die Häufigkeit des Auftretens einer Geschwindigkeit besser als Wahrscheinlichkeit für das Auftreten zu interpretieren. Als Beispiel nehmen wir nun an, dass unter allen Teilchen die x-Komponente eines vorgegebenen Geschwindigkeitsbereichs mit einer Wahrscheinlichkeit von 10 % (0,1) auftritt und die y-Komponente mit einer Wahrscheinlichkeit von 5 % (0,05) sowie die z-Komponente mit einer Wahrscheinlichkeit von 20 % (0,2). Die Gesamtwahrscheinlichkeit, dass ein Teilchen alle drei vorgegebenen Geschwindigkeitsbereiche zur selben Zeit aufweist, ergibt sich dann aus dem Produkt der Einzelwahrscheinlichkeiten. In diesem Fall beträgt die Gesamtwahrscheinlichkeit 0,1 % (0,001 = 0,1 × 0,05 × 0,2).
Für die Gesamtwahrscheinlichkeit bzw. die Häufigkeit des Auftretens eines Geschwindigkeitsvektors v (innerhalb der Intervalle dvx, dvy und dvz) muss Gleichung (\ref{dicc}) somit für alle drei Geschwindigkeitskomponenten i=x,y,z multipliziert werden:
\begin{align}
&\text{Häufigkeit}(\vec{v}) =\text{Häufigkeit}(v_x) \cdot \text{Häufigkeit}(v_y) \cdot \text{Häufigkeit}(v_z) \\[5px]
&\text{Häufigkeit }\vec{v} = \left(\sqrt{\frac{m}{2\pi k_B T}}\right)^3 \cdot \exp{\left(-\dfrac{m(v_x^2+v_y^2+v_z^2)}{2k_BT}\right)} \cdot \text{d}v_x \cdot \text{d}v_x \cdot \text{d}v_x \\[5px]
\end{align}
Beachte, dass bei der Multiplikation von Exponentialfunktionen die einzelnen Exponenten addiert werden können. Deshalb tritt im Exponent nun die Summe aus den quadrierten Geschwindigkeitskomponenten auf! Gemäß Gleichung (\ref{v2}) entspricht diese Summe dem Quadrat des Geschwindigkeitsvektors, sodass gilt:
\begin{align}
&\text{Häufigkeit}(\vec{v}) = \left(\sqrt{\frac{m}{2\pi k_B T}}\right)^3 \cdot \exp{\left(-\dfrac{m\vec{v}^2}{2k_BT}\right)} \cdot \text{d}v_x \cdot \text{d}v_x \cdot \text{d}v_x \\[5px]
\end{align}
Häufigkeit des Auftretens eines Geschwindigkeitsbetrags
Die Aussage der oberen Gleichung ist nun folgende. Gibt man einen Geschwindigkeitsvektor v vor und für jede Geschwindigkeitskomponente einen gewissen Bereich dvi innerhalb dessen die einzelnen Komponenten variieren können, dann lässt sich durch die oberen Gleichung die Häufigkeit (Wahrscheinlichkeit) ermitteln mit der all die infrage kommenden Geschwindigkeitsvektoren vorhanden sind. Die Spitzen der Geschwindigkeitsvektoren auf die sich die Angabe der Häufigkeit bezieht, liegen alle innerhalb des „Volumens“ das durch dvx, dvy und dvz aufgespannt wird.
Die Gleichung zeigt aber auch, dass der vektorielle Charakter der Geschwindigkeit auf der rechten Seite der Gleichung verloren geht. Es taucht nur das Quadrat des Geschwindigkeitsvektors auf und dies ist wie bereits erwähnt eine skalare Größe! Alle Geschwindigkeitsvektoren die denselben Betrag haben, treten somit mit derselben Häufigkeit auf (da für all diese Vektoren v² denselben Wert hat).
Dies ist auch gut so, denn letztlich wird ja vorausgesetzt, dass die Richtung der Geschwindigkeit für die Häufigkeitsverteilung keine Rolle spielen darf! Schließlich wurde ein isotropes Gas angenommen, bei dem die Wahrscheinlichkeiten für das Auftreten bestimmter Geschwindigkeiten richtungsunabhängig sein sollen! Für die Häufigkeitsverteilung ist die Richtung der Geschwindigkeit also gar nicht entscheidend sondern nur der Geschwindigkeitsbetrag!
Auf den Vektorpfeil kann in der oberen Gleichung also verzichtet werden, sodass mit v nur der Geschwindigkeitsbetrag eines Teilchens gemeint ist:
\begin{align}
\label{g}
&\text{Häufigkeit }v = \underbrace{\left(\sqrt{\frac{m}{2\pi k_B T}}\right)^3 \cdot \exp{\left(-\dfrac{mv^2}{2k_BT}\right)}}_{\text{Häufigkeitsdichte}} \cdot \underbrace{\text{d}v_x \cdot \text{d}v_x \cdot \text{d}v_x}_{\text{dreidimensionales Geschwindigkeitsintervall}} \\[5px]
\end{align}
Anstelle für die einzelnen Geschwindigkeitskomponenten jeweils Intervalle von dvx, dvy und dvz vorzugeben, wäre es sinnvolle für den Geschwindigkeitsbetrag ein einzelnes Intervall dv vorzugeben. Hierfür muss ein Zusammenhang zwischen diesen einzelnen Intervallen gefunden werden.
Hierzu wird Gleichung (\ref{g}) graphisch interpretiert. Wird ein Geschwindigkeitsbetrag v vorgegeben und jeweils Intervalle dvx, dvy und dvz zugelassen, innerhalb deren die Komponenten aller möglichen Geschwindigkeitsvektoren mit demselben Betrag v variieren können, dann ergibt sich ein dreidimensionales Kugelschalenvolumen (mit Volumen ist dabei ein Geschwindigkeitsraum gemeint). Die Dicke dieser Kugelschale entspricht dem gesuchten Intervall dv innerhalb dessen der vorgegebene Geschwindigkeitsbetrag v variieren kann.
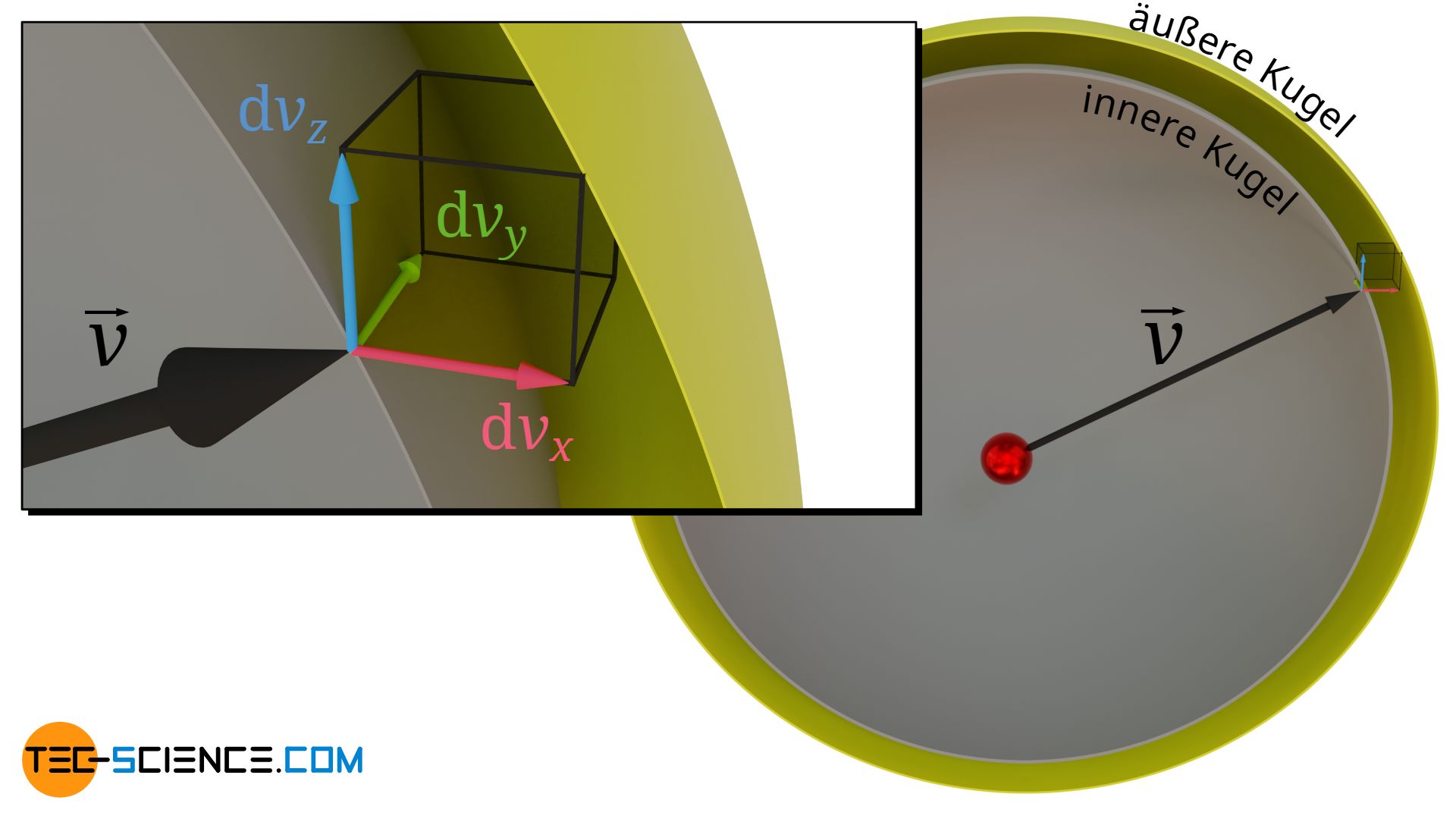
Man kann also die Bedeutung des dreidimensionalen Volumenintervalls in Gleichung (\ref{g}) (beschrieben durch dvx, dvy und dvz) durch ein Kugelschalenvolumen mit dem Radius v und der Dicke dv ersetzt denken. Begrenzt wird die Kugelschale durch zwei konzentrische Kugeln. Aufgrund des infinitesimalen Abstandes beider Kugeln kann das Kugelvolumen (im Geschwindigkeitsraum!) aus dem Produkt von Kugeloberfläche 4π⋅v² und dem Abstand dv der Kugelschalen zueinander bestimmt werden:
\begin{align}
&\text{Dreidimensionales Geschwindigkeitsintervall} = 4\pi v^2 \cdot \text{d}v \\[5px]
\end{align}
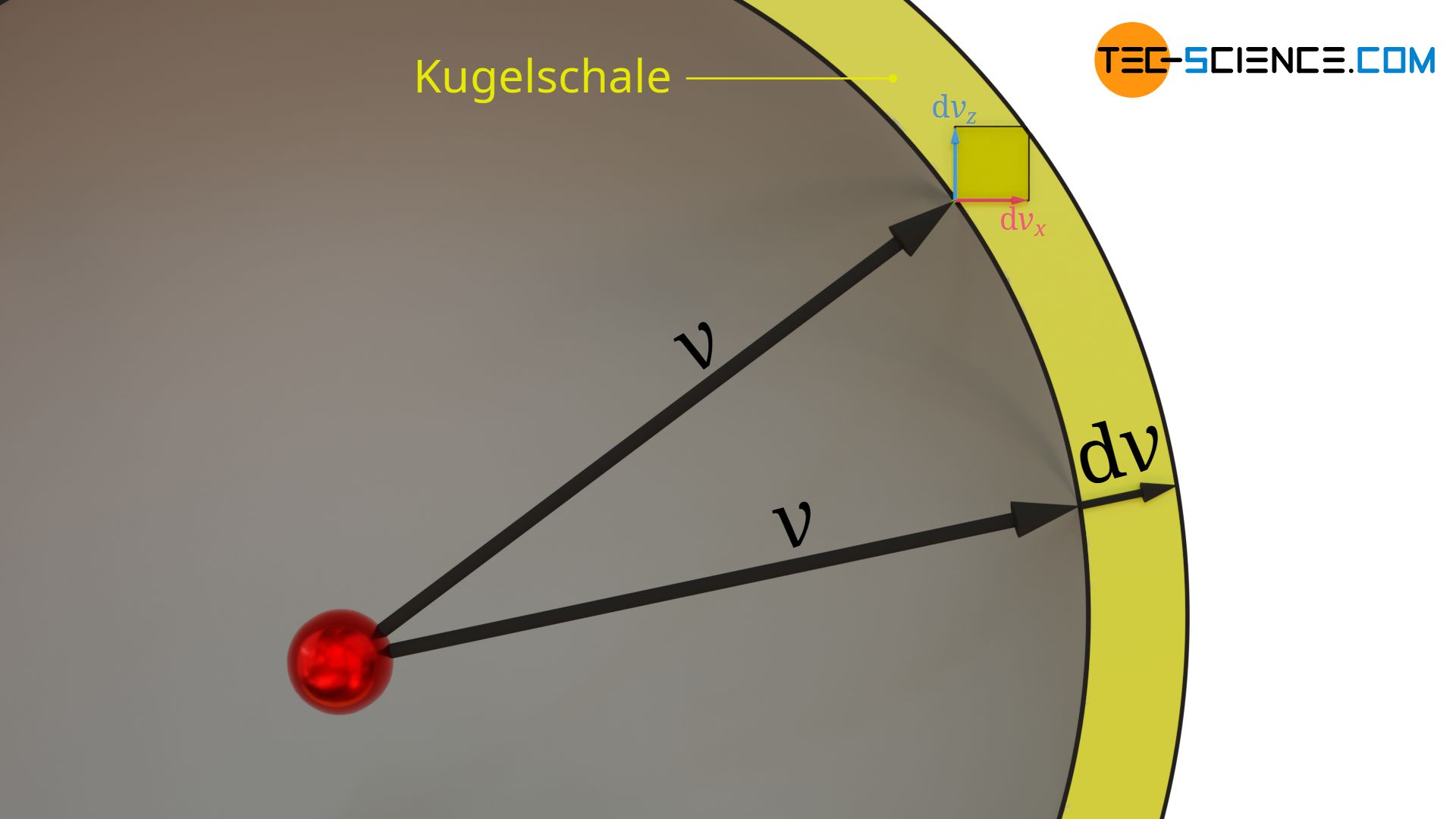
Wird dieses dreidimensionale Geschwindigkeitsintervall in Gleichung (\ref{g}) eingesetzt, dann folgt hieraus:
\begin{align}
&\text{Häufigkeit} =\left(\sqrt{\frac{m}{2\pi k_B T}}\right)^3 \cdot \exp{\left(-\dfrac{mv^2}{2k_BT}\right)} \cdot \overbrace{\text{d}v_x \cdot \text{d}v_x \cdot \text{d}v_x}^{4\pi v^2 \cdot \text{d}v } \\[5px]
&\boxed{\text{Häufigkeit} = \underbrace{\left(\sqrt{\frac{m}{2\pi k_B T}}\right)^3 \cdot 4\pi v^2 \cdot \exp{\left(-\dfrac{mv^2}{2k_BT}\right)}}_{\text{Häufigkeitsdichte }f(v)} \cdot \underbrace{\text{d}v}_{\text{Geschwindigkeitsintervall}}} \\[5px]
\end{align}
Diese Gleichung beschreibt nun die gesuchte Häufigkeit bzw. Wahrscheinlichkeit mit der ein bestimmter Geschwindigkeitsbetrag v innerhalb des Intervalls dv vorhanden ist. Wie bereits für Gleichung (\ref{z}) erläutert, so lässt sich auch an dieser Stelle wieder eine Dichtefunktion f(v) definieren, die bezogen auf das Geschwindigkeitsintervall dv ein Maß für die Häufigkeit einer vorhandenen Geschwindigkeit darstellt. Diese Verteilungsfunktion wird schließlich Maxwell-Boltzmann-Verteilung genannt:
\begin{align}
\label{max}
&\boxed{f(v) = \left(\sqrt{\frac{m}{2\pi k_B T}}\right)^3 \cdot 4\pi v^2 \cdot \exp{\left(-\dfrac{mv^2}{2k_BT}\right)}}~~~~~\text{Maxwell-Boltzmann-Verteilung} \\[5px]
\end{align}
Für die Berechnung einer konkreten Häufigkeit F mit der eine Geschwindigkeit im Bereich zwischen v1 und v2 vorkommt, muss die Häufigkeitsdichtefunktion f(v) innerhalb dieser Grenzen integriert werden:
\begin{align}
& \boxed{\text{Häufigkeit } F=\int_{v_{1}}^{v_{2}} f(v) ~~ \text{d} v} \\[5px]
\end{align}
Die untere Abbildung zeigt hierzu nochmals den Verlauf der Maxwell-Boltzmann-Verteilung f(v) in Abhängigkeit der Geschwindigkeit v für verschiedene Temperaturen. Beachte, dass auch dabei wieder die Fläche unter der Kurve (als Integral der Dichtefunktion) die Häufigkeit bzw. Wahrscheinlichkeit darstellt mit der der entsprechende Geschwindigkeitsbereich vorhanden ist!
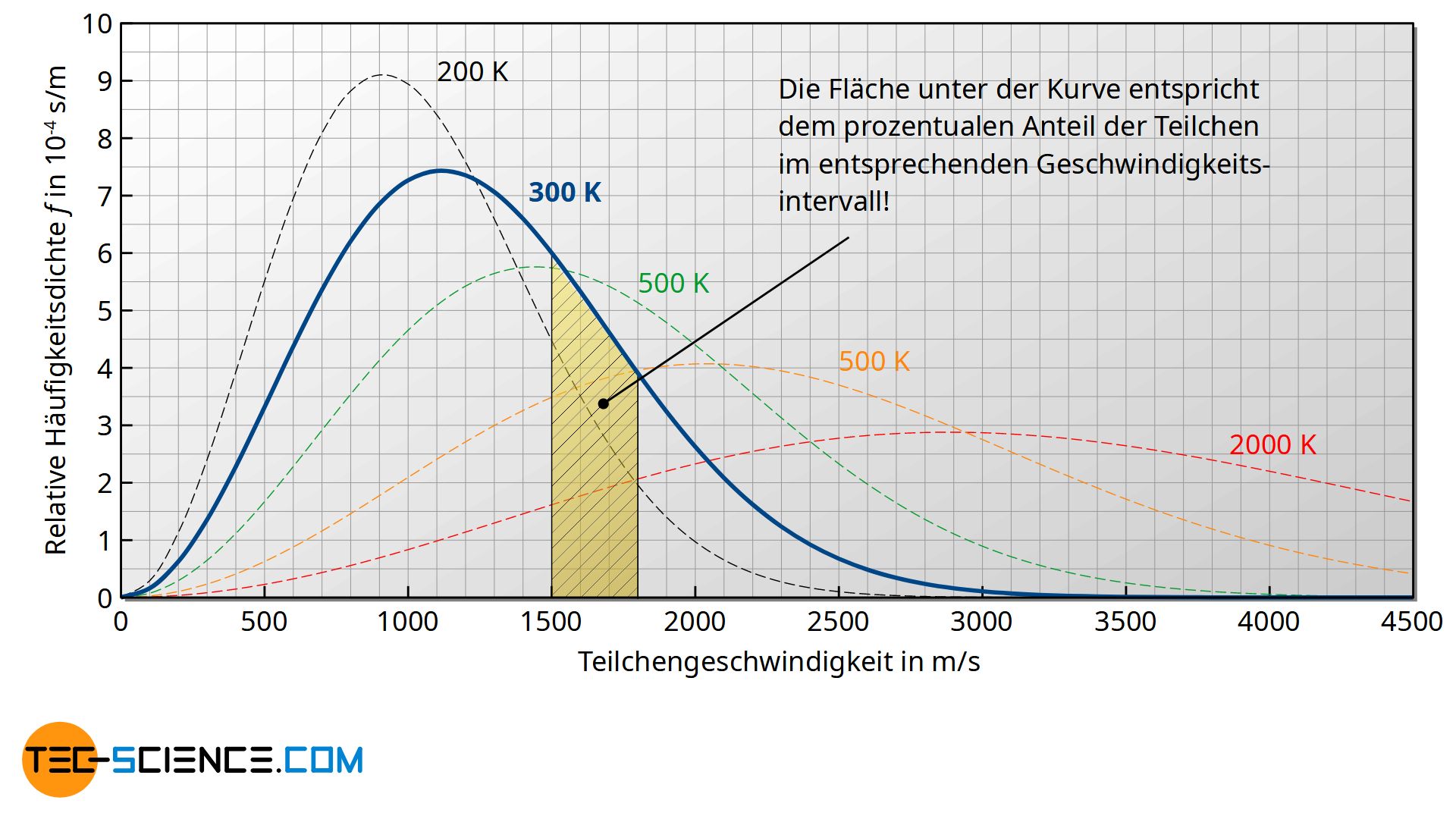
Ausführlichere Erläuterungen zur Aussage dieser Verteilungsfunktion sind im Artikel „Maxwell-Boltzmann-Verteilung“ wiederzufinden.
Der scheinbare Widerspruch
Vergleicht man die Maxwell-Boltzmann-Verteilung mit der Verteilung der einzelnen Geschwindigkeitskomponenten, so zeigt sich auf den ersten Blick ein scheinbarer Widerspruch. Wie kann die Häufigkeitsdichte der einzelnen Komponenten bei v=0 ein Maximum haben, während in der Maxwell-Boltzmann-Verteilung bei v=0 einen Minimum vorliegt (genauer gesagt, die Häufigkeitsdichte null ist). Sollte bei einer hohen Wahrscheinlichkeit, dass die einzelnen Geschwindigkeitskomponenten null sind, nicht auch die Wahrscheinlichkeit für einen Geschwindigkeitsbetrag von null recht hoch sein?
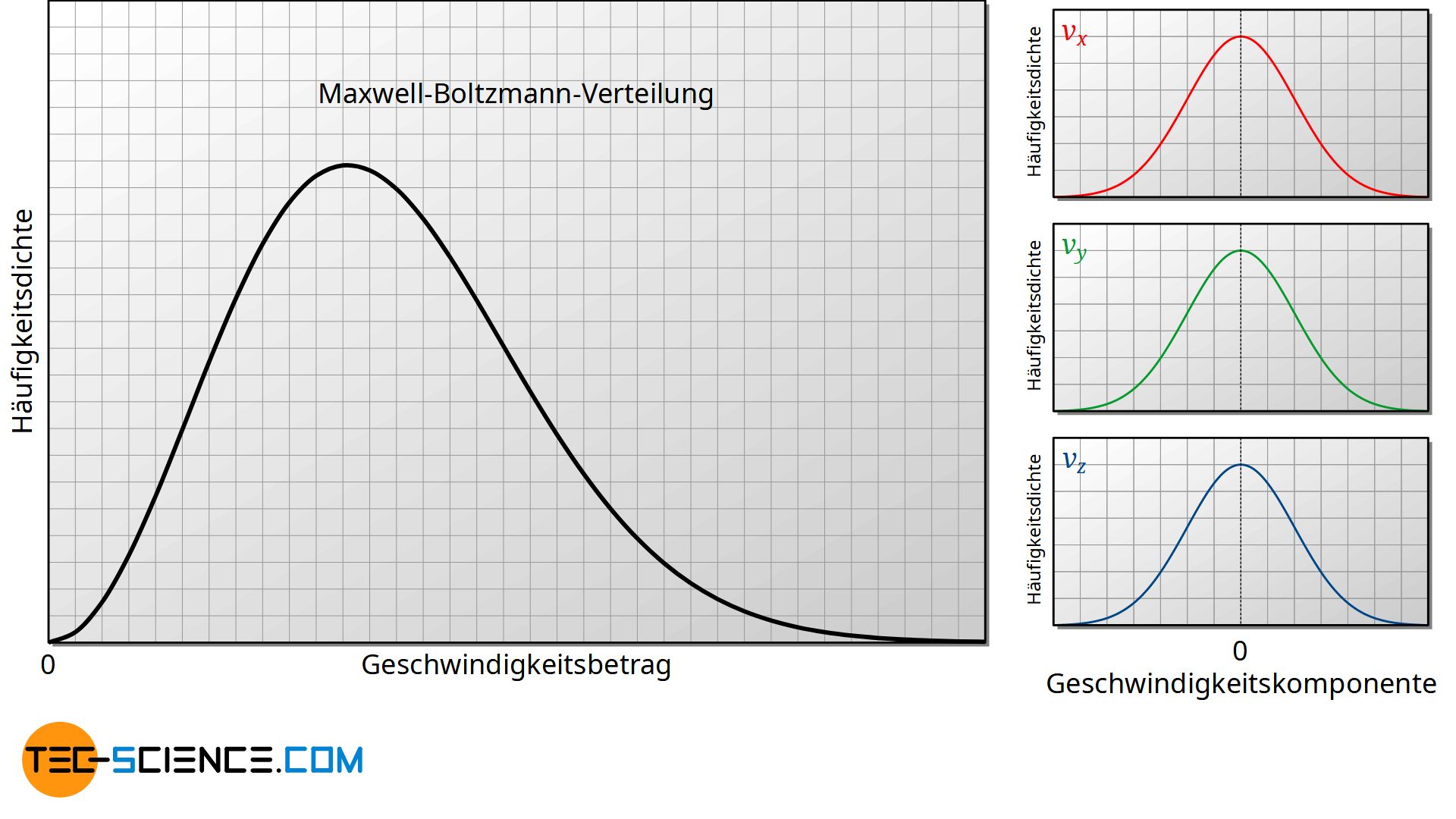
An dieser Stelle gilt es die Diagramme richtig zu interpretieren. Die Diagramme zeigen eben nicht die Häufigkeit bzw. Wahrscheinlichkeit sondern die Häufigkeitsdichte bzw. Wahrscheinlichkeitsdichte. Für eine Interpretation ob eine Geschwindigkeitskomponente selten oder häufig vorkommt, muss auch das entsprechende Geschwindigkeitsintervall betrachtet werden (d.h. die Fläche unter der Kurve!).
Mit folgendem zweidimensionalen Beispiel soll dies verdeutlicht und der scheinbare Widerspruch aufgelöst werden. Betrachtet wird einmal ein relativ geringer Geschwindigkeitbetrag v (siehe Abbildung links) und einer relative hoher Geschwindigkeitsbetrag v (siehe Abbildung rechts). Für beide Fälle wird ein gleich großes Geschwindigkeitsintervall dv vorgeben, innerhalb dessen der Geschwindigkeitsbetrag variieren kann. Dieses Intervall ist graphisch durch eine Kugelschale um den Geschwindigkeitsvektor v dargestellt.
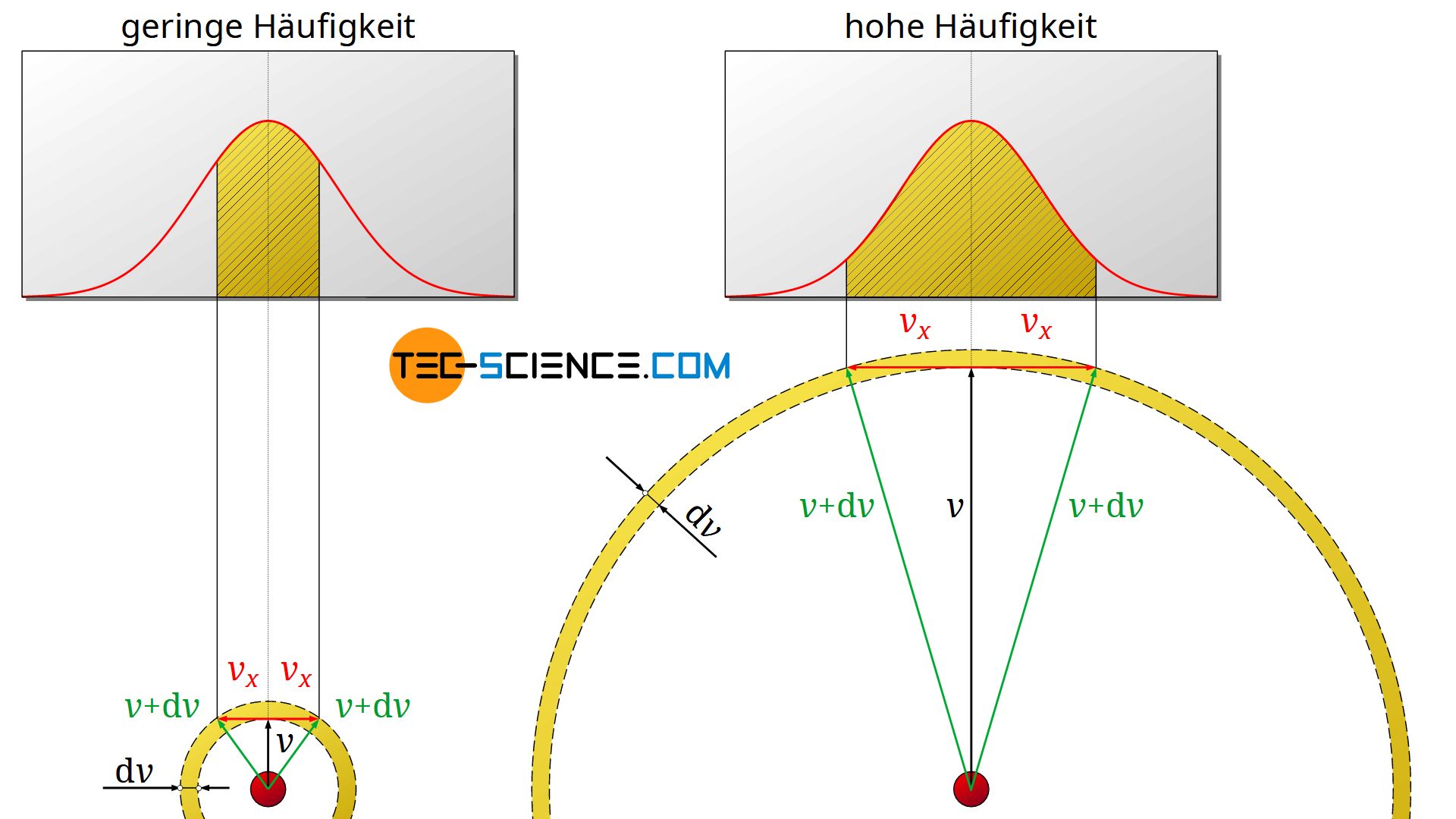
In welchem Geschwindigkeitsbereich finden sich nun mehr Teilchen wieder; in jenem mit dem geringen Geschwindigkeitsbetrag (linke Seite der Abbildung) oder in dem mit dem höheren Geschwindigkeitsbetrag (rechte Seite der Abbildung)?
Gemäß der Argumentation mit der Häufigkeitsverteilung der einzelnen Geschwindigkeitskomponenten würde man wahrscheinlich schlussfolgern, dass geringe Geschwindigkeitskomponenten wahrscheinlicher sind als große. Demnach müsste es doch auch mehr Teilchen mit geringeren Geschwindigkeiten geben als Teilchen mit höheren Geschwindigkeiten (bei dieser Argumentation wird die Häufigkeitsdichte fälschlicherweise mit einer Häufigkeit gleichgesetzt).
Schaut man sich aber die graphische Darstellung der beiden Fälle an, so zeigt sich das Gegenteil. Damit die vorgegebenen Geschwindigkeitsbeträge v innerhalb der zulässigen Bereiche dv liegen, können die x-Komponenten vx bis zu einem gewissen Grad variieren. Graphisch betrachtet wäre ein Geschwindigkeitsvektor v+dv, dessen Pfeilspitze sich auf der äußeren Kugelschale befindet, gerade noch zulässig (als grüner Pfeil dargestellt). Die zugehörige Geschwindigkeitkomponente vx ist mit einem roten Pfeil dargestellt.
Wie der Vergleich zeigt, kann bei einer großen Geschwindigkeit v die x-Komponente offensichtlich in einem deutlich größeren Bereich variieren, ohne dabei den vorgegebenen Geschwindigkeitsbereich dv zu überschreiten. Es kommen somit deutlich mehr x-Komponenten in Frage. Wie häufig diese konkret vorkommen, zeigt die die Häufigkeitsverteilung der Geschwindigkeitskomponenten. Dabei muss jedoch die Fläche unter der Kurve betrachtet werden und eben nicht der Betrag der Häufigkeitsdichte an sich (Beachte, dass die Fläche unter der Kurve die konkrete Häufigkeit angibt)! Man muss also die Diagramme richtig interpretieren und darf vor allem die Häufigkeitsdichte nicht mit einer Häufigkeit gleichsetzen!
In diesem Fall ist somit der größere Geschwindigkeitsbetrag v deutlich häufiger vorhanden (da die infrage kommenden x-Komponenten häufiger vertreten sind) als der kleinere Geschwindigkeitsbetrag. Mathematisch betrachtet ist dies auf den quadratischen Einfluss der Geschwindigkeit (der durch die „Kugelschale“ 4π⋅v² zustande kommt) in der Maxwell-Boltzmann-Verteilungsfunktion zurückzuführen!
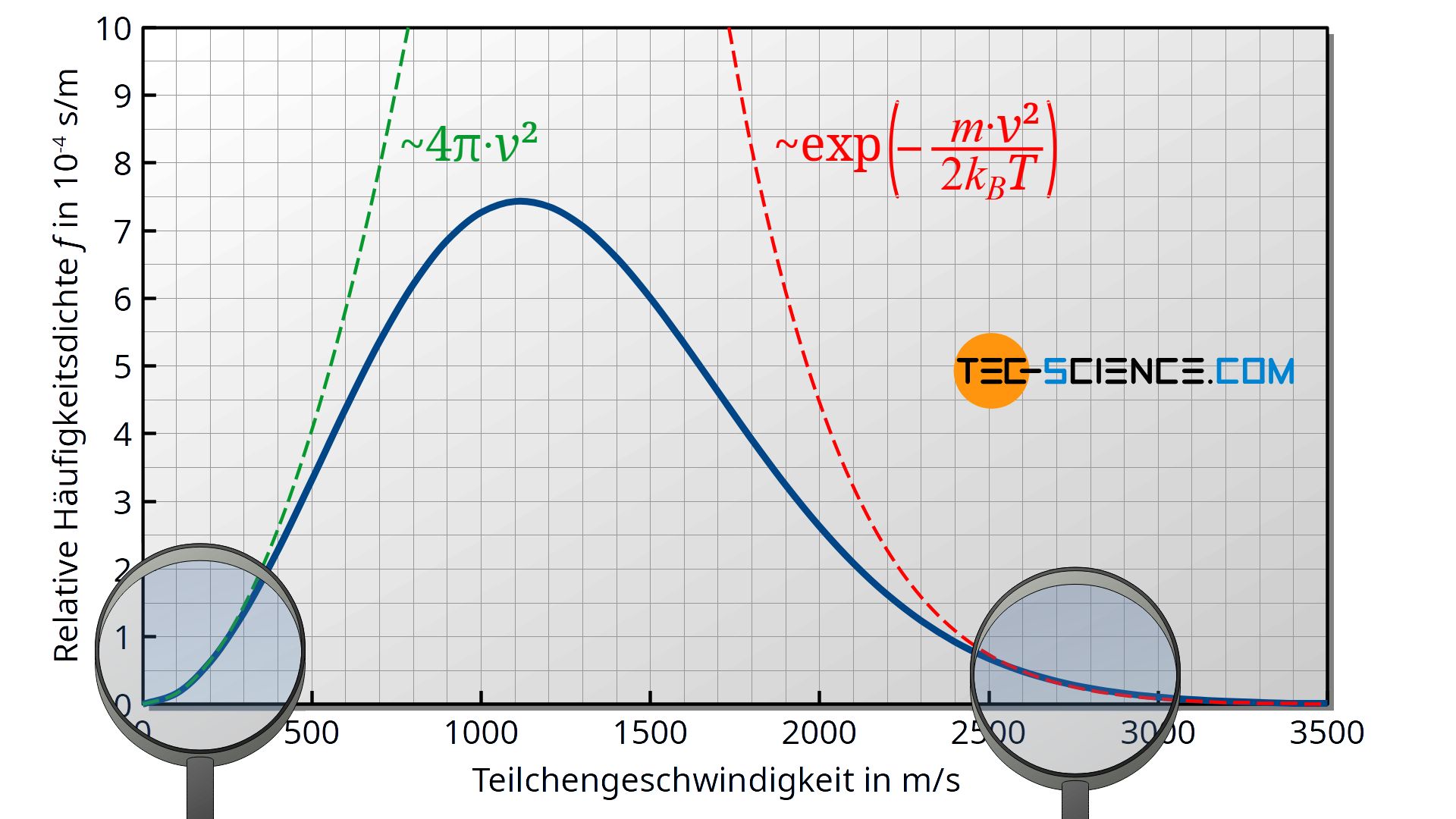
Nun wird auch klar, weshalb ein extrem geringer Geschwindigkeitsbetrag von v≈0 gemäß der Maxwell-Boltzmann-Verteilung nahezu nicht vorhanden ist. Denn dies würde bedeuten, dass die Geschwindigkeitskomponenten ebenfalls nur in einem extrem kleinen Bereich variieren dürften. Die Häufigkeit, dass ein so schmaler Geschwindigkeitsbereich vorhanden ist, ist extrem gering (extrem schmale Fläche unter der Häufigkeitsdichtefunktion der Komponenten).
An dieser Stelle stellt sich dann die Frage, weshalb dann die Maxwell-Boltzmann-Verteilung überhaupt wieder abflacht, wenn – wie argumentiert – größere Geschwindigkeiten doch häufiger vorhanden ein sollten als geringere. Diese Argumentation gilt natürlich nur bis zu einem gewissen Grad. Denn wie die Häufigkeitsverteilung der einzelnen Komponenten ja auch zeigt, nimmt die Häufigkeitsdichte mit zunehmender Geschwindigkeit ab. D.h. allzu hohe Geschwindigkeiten sind aufgrund der begrenzen Häufigkeit ohnehin nicht stark vertreten. Mathematisch schlägt an dieser Stelle die Exponentialfunktion in der Maxwell-Boltzmann-Verteilungsfunktion zu (siehe rot gestrichelte Linie in der Abbildung oben)!