Gleichverteilungssatz (Äquipartitionstheorem)

Der Gleichverteilungssatz besagt, dass sich die Bewegungsenergie der Gasteilchen auf alle drei Raumrichtungen gleichermaßen aufteilt!

Gleichverteilungssatz (Äquipartitionstheorem)

Im Artikel Druck und Temperatur wurde folgenden Gleichung zur Berechnung des Druck p in idealen Gase hergeleitet:

\begin{align}
\label{druck}
& \boxed{p = 2 \cdot \frac{N}{V} \cdot \overline{W_{kin,x}}} \\[5px]
\end{align}

Darin bezeichnet N die Teilchenanzahl, die sich in einem betrachteten Gasvolumen V befindet (z.B. in einem Zylinder). W_kin,x beschreibt die mittlere kinetische Energie mit der die Teilchen auf eine Grenzfläche prallen und hierdurch den Druck p ausüben (z.B. auf einen Kolben). Dabei bezieht sich die Bewegungsenergie nur auf jene Geschwindigkeitskomponenten mit denen die Teilchen auch tatsächlich auf die Grenzfläche prallen (hier: die Geschwindigkeitskomponenten entlang der x-Richtung). Senkrecht zur Fläche gerichtete Geschwindigkeitskomponenten (in y- und z-Richtung) führen bei der Kollision nicht zu einem Impulsübertrag auf den Kolben und sind daher für das Zustandekommen des Drucks auf den Kolben nicht relevant.

Der in Gleichung (\ref{druck}) angegebene Druck bezieht sich zunächst also nur auf jenen Druck der in x-Richtung gemessen wird. Für die anderen Raumrichtungen kann ganz analog ein Druck definiert werden, der mit den Bewegungsenergien in entlang der entsprechenden Richtungen verknüpft ist:

\begin{align}
\label{pi}
& p_i = 2 \cdot \frac{N}{V} \cdot \overline{W_{kin,i}} ~~~~~\text{mit }i=x,y,z \\[5px]
\end{align}

Die Praxis zeigt jedoch dass der Druck in Gasen stets in alle Raumrichtungen gleichermaßen vorhanden ist, auch wenn scheinbar nur die Geschwindigkeit der Teilchen in x-Richtung geändert wird. Um dies zu überprüfen kann der mit einem Kolben verschlossene Zylinder mit drei Druckmessern versehen werden. Diese werden jeweils rechtwinklig zueinander am Zylinder angebracht, sodass der Druck den das Gas in die verschiedenen Raumrichtungen ausübt getrennt gemessen werden kann. Und tatsächlich wird man zunächst feststellen, dass der Druck in alle drei Raumrichtungen identisch ist.

Nun wird das Gas im Zylinder komprimiert, indem der Kolben schlagartig in den Zylinder geschoben wird. Der sich bewegende Kolben trifft dabei im Gas mit großer Wucht auf die entgegenkommenden Gasteilchen. Auf mikroskopischer Ebene gleicht dieser Vorgang dem Schlagen eines entgegenkommenden Tennisballes mit einem Tennisschläger. Die Gasteilchen bekommen durch den sich bewegenden Kolben einen zusätzlichen Impuls in (negative) x-Richtung und werden schneller. Damit steigt auch die mittlere kinetische Energie die mit dieser Bewegungsrichtung verknüpft ist, d.h. die Bewegungsenergie in x-Richtung (damit lässt sich im Übrigen auch die Temperaturzunahme während einer Verdichtung erklären).

Demzufolge sollte sich durch die Kompression nur der Druck in x-Richtung vergrößern und die Drücke in y- und z-Richtung unberührt bleiben. Dies wird man in der Praxis aber nicht feststellen! Die Erfahrung zeigt, dass auch bei einem solchen Kompressionsvorgang der Druck in alle Raumrichtungen gleichermaßen ansteigen wird. Gemäß Gleichung (\ref{pi}) muss somit auch die kinetische Energie entlang der drei Raumrichtungen gleichermaßen angestiegen sein. Offensichtlich muss die zugeführte Energie durch den Verdichtungsvorgang auf alle drei Raumrichtungen gleichermaßen aufgeteilt worden sein. Dies bezeichnet man auch als Gleichverteilungssatz oder Äquipartitionstheorem.

Der Gleichverteilungssatz (Äquipartitionstheorem) im Zusammenhang mit idealen Gasen besagt, dass sich die Bewegungsenergie der Teilchen (bzw. des Gases) auf alle drei Raumrichtungen gleichermaßen aufteilt und somit auch der Druck in alle Raumrichtungen identisch ist!

Der Gleichverteilungssatz ist letztlich eine direkte Folge der ungeordneten, statistischen Bewegung der Teilchen. Diese „chaotische“ Bewegung der Teilchen führt dazu, dass ständig Stoßprozesse ausgeübt werden bei denen sich die Teilchen anschließend in unterschiedliche Richtungen weiterbewegen. Auf diese Weise werden die ursprünglich geordneten Bewegungen rasch zu ungeordneten Bewegungen bei denen keine Richtung mehr bevorzugt wird und somit eine Gleichverteilung stattfindet.

Der Gleichverteilungssatz bleibt grundsätzlich nicht nur auf die translatorische Bewegung beschränkt sondern gilt für jede Energieform auf atomarer Ebene. Im nächsten Abschnitt wird hierauf näher eingegangen.

Aufteilung der Energie auf Freiheitsgrade

Im Artikel „Druck und Temperatur“ wurde gezeigt, dass die mittlere kinetische Energie eines Teilchens Wkin (nun nicht mehr nur auf eine Richtung beschränkt sondern als Gesamtbewegungsenergie eines Teilchens zu verstehen!) wie folgt mit der thermodynamischen Temperatur T verknüpft ist:

\begin{align}
\label{kin}
& \boxed{\overline{W_{kin}} = \frac{3}{2} k_B \cdot T} \\[5px]
\end{align}

Für die gesamte Energie des idealen Gases mit insgesamt N Teilchen gilt somit folgende innere Energie:

\begin{align}
\label{u}
& \boxed{U = \frac{3}{2} N k_B T} \\[5px]
\end{align}

Translation

Die drei Raumrichtungen in denen sich die Teilchen eines idealen Gases bewegen können stehen letztlich für die Möglichkeiten die das Gas hat Energie zu speichern. Ein Teilchen kann sozusagen seine Energie sowohl in die Bewegung in x-Richtung stecken als auch in die Bewegung in y-Richtung oder z-Richtung. Man spricht bei diesen Möglichkeiten Energie zu speichern auch von Freiheitsgraden.

Als Freiheitsgrade bezeichnet man in der Thermodynamik die Anzahl an prinzipiellen Möglichkeiten auf atomarer Ebene Energie zu speichern!

Ein Teilchen eines idealen Gases besitzt somit insgesamt drei Freiheitsgrade; nämlich für jede Raumrichtung eine Möglichkeit Energie in Form einer translatorischen Bewegung zu speichern. Auf jeden Freiheitsgrad f, d.h. auf jede Raumrichtung entfällt gemäß dem Gleichverteilungssatz für ein Teilchen dabei eine Energie von ½⋅k_B⋅T bzw. auf das gesamte Gas eine (innere) Energie von ½⋅N⋅k_B⋅T pro Freiheitsgrad.

\begin{align}
\label{frei}
&\boxed{W = \frac{f}{2} k_BT} ~~\text{Energie eines Teilchens}\\[5px]
\label{inn}
&\boxed{U = \frac{f}{2}Nk_BT} ~~\text{innere Energie des Gases}\\[5px]
\end{align}

Rotation

Während bei einatomigen Gasen nur drei Freiheitsgrade in Form der drei Raumrichtungen für die translatorische Bewegung vorhanden sind, können bei zweiatomigen Moleküle (bzw. etwas allgemeiner:lineare Moleküle) auch Rotationsbewegungen auftreten. Dabei ergeben sich dann theoretisch drei weitere Möglichkeiten Energie zu speichern: in Form der Rotation um die x-Achse, der y-Achse und die z-Achse. Theoretisch erhält man in diesem Fall somit insgesamt f = 6 Freiheitsgrade.

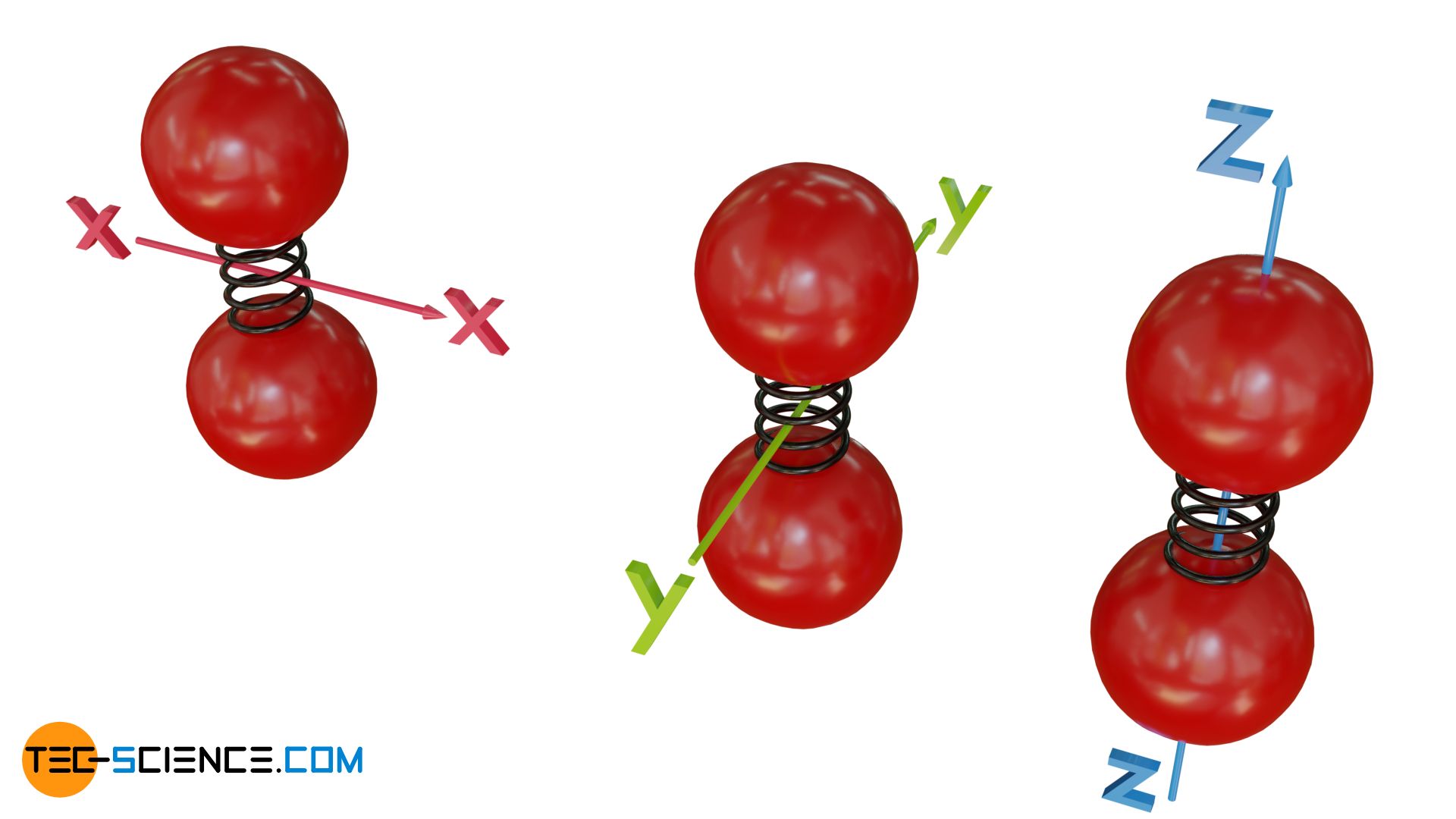
Tatsächlich wird man auch dabei eine Gleichverteilung zwischen diesen einzelnen Möglichkeiten Energie zu speichern feststellen, unabhängig davon ob es sich um eine translatorische oder rotatorische Bewegung handelt! Gibt man den Teilchen eines zweiatomigen Gases in Gedanken zunächst nur eine translatorische Bewegung in eine Richtung mit, dann werden die Moleküle sich durch Stoßprozesse von selbst in Rotation versetzen. Aufgrund der ungeordneten Bewegung wird sich die ursprünglich rein translatorische Energie allmählich auch in Rotationsenergie umwandeln und sich auf alle Freiheitsgrade gleichermaßen verteilen. Die translatorische Energie in x-Richtung wird dann bspw. dieselbe sein wie die Rotationsenergie um die y-Achse.

Der Gleicherverteilungssatz besagt, dass sich die Gesamtenergie auf jeden Freiheitsgrad gleichermaßen aufteilt!

Beachte, dass die Temperatur ausschließlich durch die translatorische Bewegungsenergie der Teilchen bestimmt ist, unabhängig davon ob die Moleküle rotieren oder nicht! Somit wird bei einer bestimmten Temperatur immer dieselbe Energiemenge auf die translatorische Bewegung entfallen, welche durch Gleichung (\ref{kin}) bestimmt ist. Gemäß dem Gleichverteilungssatz, muss somit aber auch dieselbe Energiemenge in der Rotationsbewegung stecken, sofern die Moleküle auch rotieren können! Deshalb gilt auch für jeden Freiheitsgrad einer Rotationsbewegung Gleichung (\ref{frei}). Analog gilt dies für Gleichung (\ref{inn}). Ein zweiatomiges Gas mit insgesamt 6 Freiheitsgraden enthält bei derselben Temperatur somit die doppelte (innere) Energie im Vergleich zu einem einatomigen Gas mit nur 3 Freiheitsgrade (gleiche Teilchenanzahl vorausgesetzt).

Beachte, dass aus quantenmechanischen Gründen nicht immer alle theoretisch in Frage kommenden Freiheitsgrade auch tatsächlich bedient werden können. So ist bspw. bei molekularem Wasserstoff eine sehr hohe Energie notwendig, damit das Wasserstoffmolekül um die Molekülachse rotiert (Rotation um die z-Achse in der oberen Abbildung). Bei „normalen“ Temperaturen reicht die im Gas gespeicherte Energie in der Regel nicht aus, um das Molekül um diese Achse rotieren zu lassen. Somit ist die Nutzung dieser Rotationsenergie vorerst nur theoretischer Natur. Man spricht auch von einem sogenannten „eingefrorenen“ Freiheitsgrad, da dieser nur bei hohen thermischen Energien bzw. Temperaturen tatsächlich vorhanden ist. Das Wasserstoffmolekül wie auch viele andere zweiatomige Moleküle besitzen somit nur effektiv 5 Freiheitsgrade.

Anmerkung: In vielen Fällen werden die Atome als Massepunkte angenommen, so auch die einzelnen Atome von linearen Molekülen. In diesem Fall kann dann um die Molekülachse ohnehin keinerlei Energie gespeichert werden, da effektiv keine Masse in Rotation ist (kein Trägheitsmoment)! Ein solches zweiatomiges Atom hat dann in dieser Modellvorstellung ohnehin nur zwei Freiheitsgrade für die Rotation! Deshalb wird in den meisten Fällen auch von zwei Freiheitsgraden für die Rotation gesprochen und nicht von drei. Die Betrachtung als Massepunkte ist auch insofern sinnvoll als dass man ansonsten auch bei einatomigen Gasteilchen von vorne herein hätte Rotationsenergien berücksichtigen müssen (schließlich können kugelförmige Atome auch rotieren und damit Energie speichern). Zudem zeigt die Praxis, dass für die Rotationsbewegung zweiatomiger Moleküle in den meisten Fällen ohnehin nur effektiv zwei Freiheitsgrade vorhanden sind.

Schwingung

Zweiatomige Moleküle (hantelförmig)

Bei zweiatomigen Molekülen muss beachtet werden, dass im Allgemeinen auch Bindungsenergien zwischen den Teilchen vorhanden sind, die ähnlich einer elastischen Feder wirken. Aufgrund dieser elastischen Bindungskräfte kann das Molekül entlang der Verbindungsachse auch schwingen. Man könnte nun meinen, dass es sich dabei um nur einen Freiheitsgrad handelt. Tatsächlich beinhalten Schwingungen aber sowohl potentielle Energien als auch Bewegungsenergien. Deshalb entfallen auf mögliche Schwingungsrichtungen immer zwei Freiheitsgrade.

Dreiatomige lineare Moleküle

Dreiatomige lineare Moleküle können bspw. auf vier unterschiedliche Arten schwingen, sodass sich für diese vier Schwingungsfreiheitsgrade (auch Schwingungsmoden genannt) effektiv acht Freiheitsgrade ergeben.

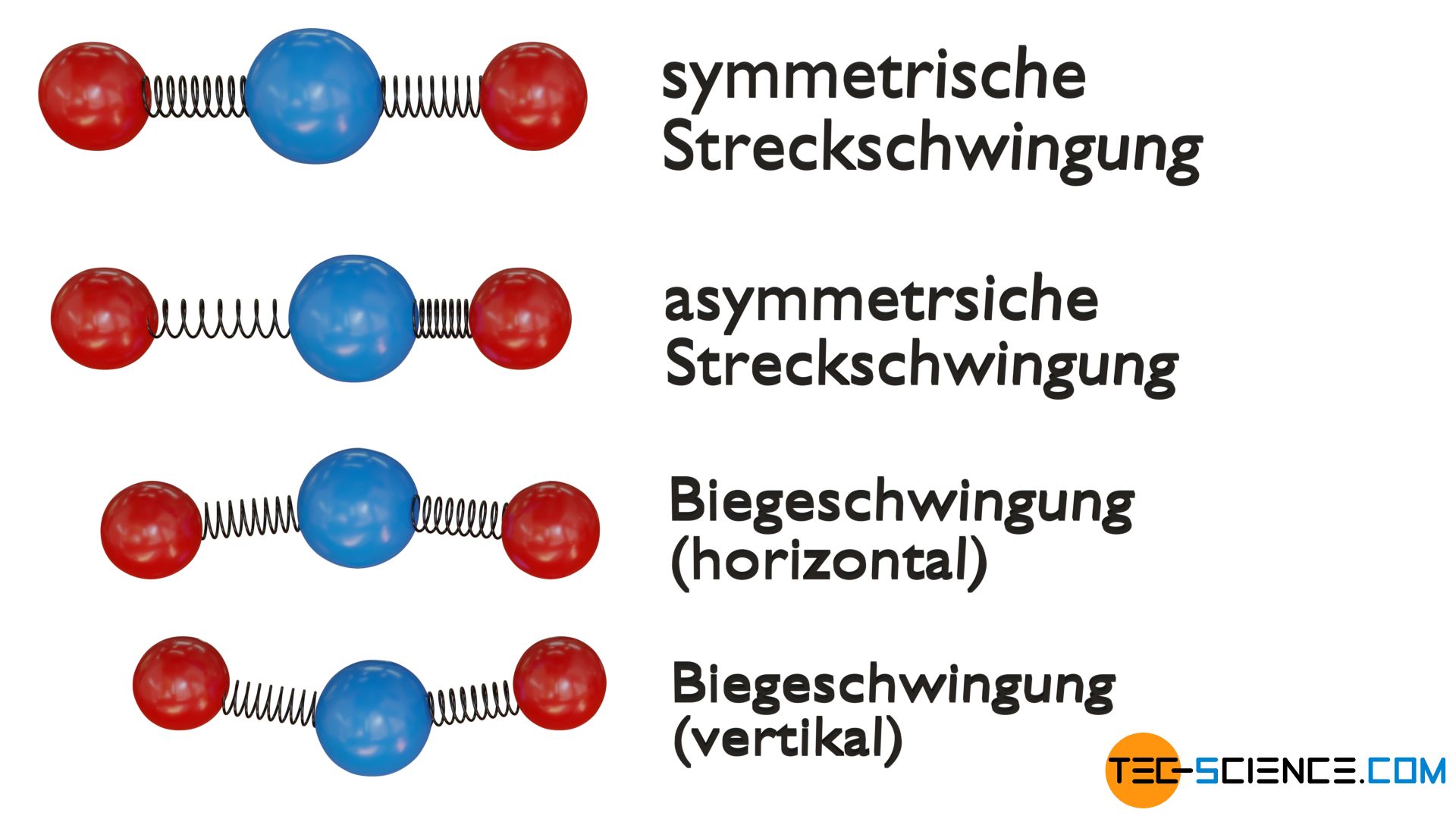
Eine Schwingungsmode ergibt sich aus der symmetrischen Streckschwingung der beiden äußeren Atome (rot) entlang der Molekülachse um das zentral gelegene Atom (blau). Als weitere Möglichkeit kann das Molekül auch eine asymmetrische Streckschwingung ausführen, indem alle drei Atome entlang der Molekülachse schwingen. Die Schwingungen entlang der Molekülachse werden auch als Valenzschwingungen bezeichnet.

Die dritte und vierte Schwingungsmode ergibt sich hingegen aus einer sogenannten Deformationsschwingung (auch Biegeschwingung oder Scherschwingung genannt), bei der die Atome eine Art Scherbewegung ausführen. Dabei wird unterschieden, in welcher Ebene (vertikal oder horizontal) die Deformationsschwingung stattfindet.

Dreiatomige nicht-lineare Moleküle

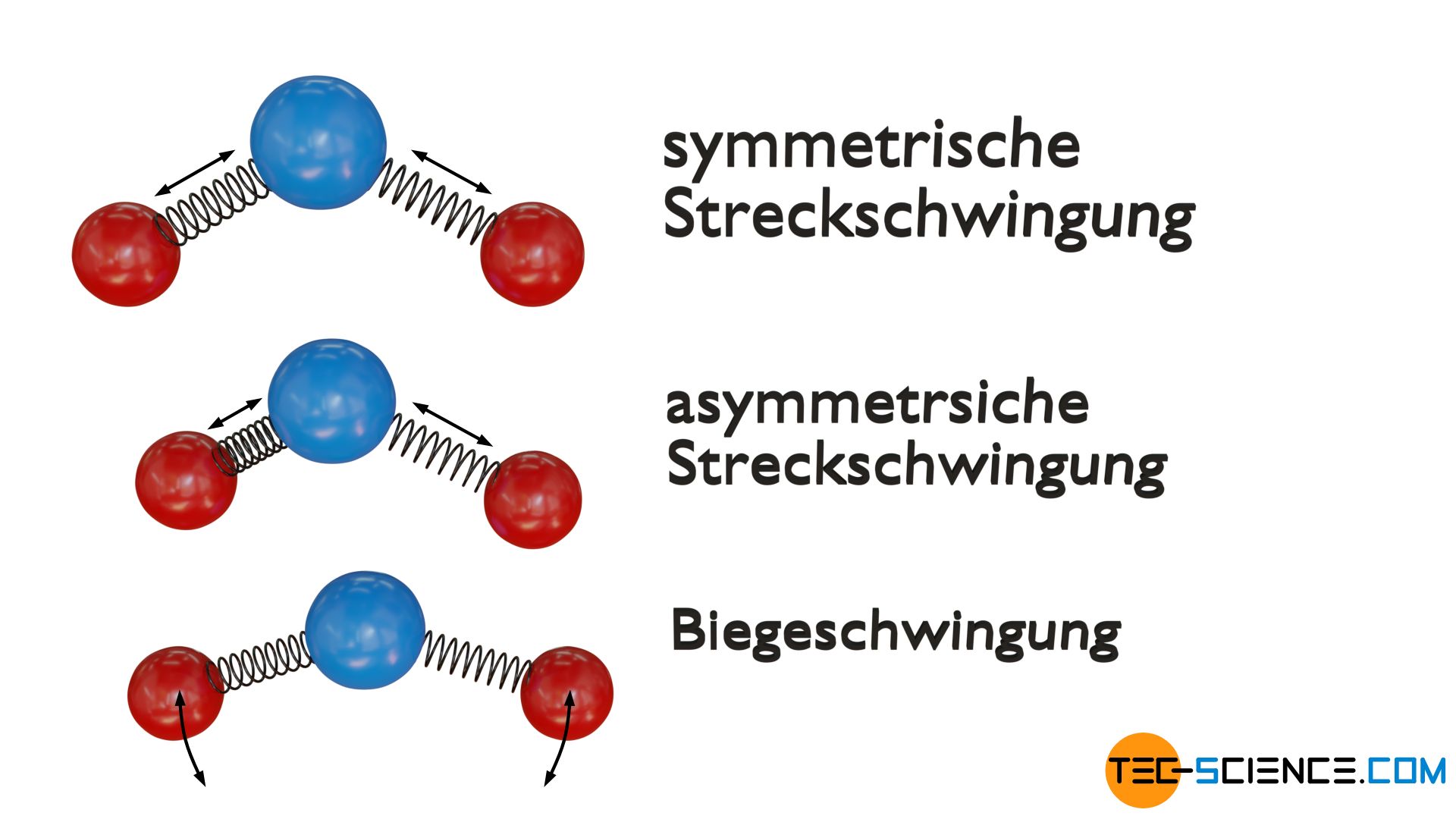
Für dreiatomige nicht-lineare Moleküle gibt es im Allgemeinen drei Schwingungsfreiheitsgrade. Zum einen ergibt sich wieder eine symmetrische Streckschwigung, bei der die äußeren Atome (rot) entlang der Valenzbindung symmetrisch schwingen. Zum anderen existiert wiederum eine asymmetrische Streckschwingung, bei der die Atome phasenverschoben oszillieren. Bei der dritten Schwingungsmode handelt es sich wieder um eine Biegeschwingung, bei der die äußeren Atome innerhalb der Molekülebene in einer Art Scherbewegung schwingen (d.h. der Bindungswinkel schwingt um eine Ruhelage).

Bestimmung der Schwingungsmoden

Um die Position eines Atoms innerhalb eines Moleküls eindeutig festzulegen benötigt man drei Raumkoordinaten (x-, y- und z-Koordinate). Ein Molekül mit n Atomen benötigt somit insgesamt 3⋅n Koordinaten, durch die es dann zu einem bestimmten Zeitpunkt eindeutig festgelegt ist. Diese Anzahl der Raumparameter entspricht der Gesamtzahl der Freiheitsgrade f_ges, die ein Molekül prinzipiell hat:

\begin{align}
&\boxed{f_{ges} = 3 n} \\[5px]
\end{align}

Diese Gesamtfreiheitsgrade können auf die Translation (f_trans), die Rotation (f_rot) und die Schwingung (f_sch) aufgeteilt werden:

\begin{align}
&f_{ges} = 3 n = f_{trans} + f_{rot} + f_{sch} \\[5px]
\end{align}

Ist die Anzahl der Translationsfreiheitsgrade und die Anzahl der Rotationsfreiheitsgrade bekannt, dann können folglich die Freiheitsgrade der Schwingung (Schwingungsmoden) wie folgt bestimmt werden:

\begin{align}
\label{xx}
&\boxed{f_{sch} = 3 n – f_{trans} – f_{rot}} \\[5px]
\end{align}

Zusammenfassung

Beachtet werden muss, dass für die Anzahl der Freiheitsgrade f, die im Zusammenhang mit der innere Energie relevant sind, nicht die Gesamtfreiheitsgrade f_ges wesentlich sind, da für die Beschreibung der Energie die Freiheitsgrade der Schwingung doppelt gezählt werden müssen!

Teilt man die Freiheitsgrade auf die translatorische Bewegung (f_trans), die rotatorische Bewegung (f_rot) und die Schwingungsbewegung (f_sch) auf, dann gilt für die Gesamtzahl der für die innere Energie relevanten Freiheitsgrade f:

\begin{align}
\label{yy}
&\boxed{f = f_{trans} + f_{rot} + 2 \cdot f_{sch}} \\[5px]
\end{align}

Wird an dieser Stelle Gleichung (\ref{xx}) in Gleichung (\ref{yy}) eingesetzt, dann können die „energetischen“ Freiheitsgrade f auch über die Anzahl der Atome n eines Moleküls ermittelt werden:

\begin{align}
&f = f_{trans} + f_{rot} +2 \cdot \overbrace{ \left(3 n – f_{trans} – f_{rot} \right)}^{f_{sch} } \\[5px]
&\boxed{f =6n- f_{trans} – f_{rot}} \\[5px]
\end{align}

Die untere Tabelle zeigt für ein-, zwei- und dreiatomige Moleküle die Anzahl der jeweiligen Freiheitsgrade.

Teilchenart	Translation ftrans	Rotation frot	Schwingung fsch	Gesamt f
einatomig	3	0	0 (x 2)	3
zweiatomig	3	2	1 (x 2)	7
dreiatomig (nicht-linear)	3	3	3 (x 2)	12
dreiatomig (linear)	3	2	4 (x 2)	13