Erfahre in diesem Artikel mehr über die experimentelle Ermittlung der Geschwindigkeitsverteilung der Moleküle in Gasen.
Einleitung
Wie im Kapitel „Temperatur und Teilchenbewegung“ bereits erläutert stellt die Temperatur eines Gases ein Maß für die Bewegungsenergie der darin enthaltenen Teilchen dar. Selbst bei konstanter Temperatur besitzen allerdings nicht alle Teilchen in einem Gase dieselbe Geschwindigkeit. Denn schließlich finden in einem Gas auf atomarer Ebene ständig Stoßprozesse zwischen den Teilchen statt. Einige Teilchen werden durch den Stoß abgebremst und andere hierdurch wiederum beschleunigt. Es finden sich in einem Gas somit Teilchen mit unterschiedlich hohen Geschwindigkeiten wieder.
Es stellt sich natürlich Frage, wie sich Geschwindigkeiten der Gasteilchen experimentell bestimmen lassen, um dann eine Aussage über die genauere Geschwindigkeitsverteilung in einem Gas zu machen. Im Folgenden sollen hierzu ein Experimente näher erläutert und dessen Ergebnis diskutiert werden.

Versuchsaufbau
Um die Geschwindigkeit von Teilchen eines Gases zu messen, wird ein Stoff in einem Ofen zunächst verdampft und auf konstante Temperatur erhitzt. Durch ein Loch können die Gasteilchen aus dem Ofen in unterschiedliche Richtungen entweichen. Anschließend wird mit Hilfe von zwei Blenden (als Kollimator bezeichnet) dann ein scharf begrenzter Teilchenstrahl erzeugt. In diesem Gasstrahl bewegen sich die Teilchen zwar in einem gemeinsame Richtung, jedoch mit unterschiedlichen Geschwindigkeiten.

Die Geschwindigkeitsverteilung der Teilchen im Gasstrahl ist repräsentativ für die Geschwindigkeitsverteilung des gesamten Gases, auch wenn durch die Blenden Teilchen mit unterschiedlichen Ausbreitungsrichtungen ausgeblendet wurden. Denn letztlich gibt es keine Richtung in die die Teilchen sich im Gas bevorzugt bewegen. Deshalb ist die Geschwindigkeitsverteilung in jeder Richtung repräsentativ für das gesamte Gas.

Der Teilchenstrahl wird nun auf eine rotierende Trommel gerichtet. Am Umfang dieser Trommel sind mehrere Nuten in axialer Richtung spiralförmig eingefräst (analog zu den Gewindegängen von Schrauben). Nur Teilchen deren Geschwindigkeiten in einem gewissen Bereich liegen, gelangen bei gegebener Drehzahl durch die geschlitzte Trommel. Zu schnelle Teilchen werden innerhalb der Nut auf die linke Wandseite prallen. Im Falle von zu langsamen Teilchen werden diese innerhalb Nut mit der rechten Wandseite kollidieren.

Die zu filternde Geschwindigkeit kann durch die Drehzahl der Trommel gesteuert werden. Ist die Drehzahl hoch, denn gelangen auch nur Teilchen mit höherer Geschwindigkeit durch die Anordnung. Bei geringer Drehzahl werden hingegen nur Teilchen mit geringer Geschwindigkeit die Anordnung passieren. Diese Anordnung der geschlitzten Trommel dient somit als Geschwindigkeitsfilter. Damit die zu messenden Gasteilchen nicht durch Stöße mit Luftmoleküle in ihrer Geschwindigkeit beeinflusst werden, muss sich die gesamte Anordnung in einem Vakuum befinden.
Um nun die Verteilung der unterschiedlichen Geschwindigkeiten zu erhalten, muss bei verschiedenen Drehzahlen die jeweilige Teilchenanzahl ermittelt werden, die durch den Geschwindigkeitsfilter gelangt. Dies wird mit einem Teilchendetektor realisiert, der die Auftreffhäufigkeit misst.

Beachte: Aufgrund der endlichen Abmessung der Schlitze kann die Geschwindigkeit der Teilchen, die durch die Anordnung gelangen, in gewissen Grenzen variieren. Man kann also nicht die exakten Geschwindigkeiten der Gasteilchen messen sondern nur Geschwindigkeitsbereiche analysieren. Dies ist aber für die Darstellung einer Geschwindigkeitsverteilung völlig ausreichend, wie später noch gezeigt wird.
Aufgrund der Messmethode können nur Geschwindigkeitsbereiche einer konkreten Teilchenzahl zugeordnet werden!
Versuchsdurchführung
Ein Gas enthält in der Regel unzählig viele Teilchen. Um die Geschwindigkeitsverteilung besser zu veranschaulichen, soll im Folgenden deshalb von einer Anzahl von 1000 Gasteilchen ausgegangen werden. Als Gas wird dabei Helium angenommen, bei einer Temperatur von 0 °C. Die zu untersuchenden Geschwindigkeitsintervalle betragen jeweils 500 m/s. In diesem Fall ergäbe sich typischerweise folgendes statistisches Bild nach der erläuterten Messmethode:
- 68 Teilchen besäßen eine Geschwindigkeit im Bereich zwischen 0 m/s und 500 m/s,
- 309 Teilchen befänden sich im Geschwindigkeitsbereich zwischen 500 m/s und 1000 m/s,
- 358 Teilchen würde man im Intervall zwischen 1000 m/s und 1500 m/s messen,
- 195 Teilchen besäßen eine Geschwindigkeit im Bereich zwischen 1500 m/s und 2000 m/s,
- 59 Teilchen befänden sich im Geschwindigkeitsbereich zwischen 2000 m/s und 2500 m/s,
- 10 Teilchen hätten eine Geschwindigkeit im Bereich zwischen 2500 m/s und 3000 m/s,
- 1 Teilchen würde eine Geschwindigkeit größer 3000 m/s aufweisen.
Versuchsauswertung
Histogramm der Geschwindigkeitsverteilung
Die anschauliche Darstellung der oben genannten Messung kann in einem Diagramm erfolgen, das auf der horizontalen Achse die Geschwindigkeit und auf der vertikalen Achse die Teilchenanzahl auflistet. In einer solchen Geschwindigkeitsverteilung gibt also die Höhe eines Balkens die Teilchenanzahl wieder, deren Geschwindigkeiten innerhalb der entsprechenden Breite des Balkens liegen.
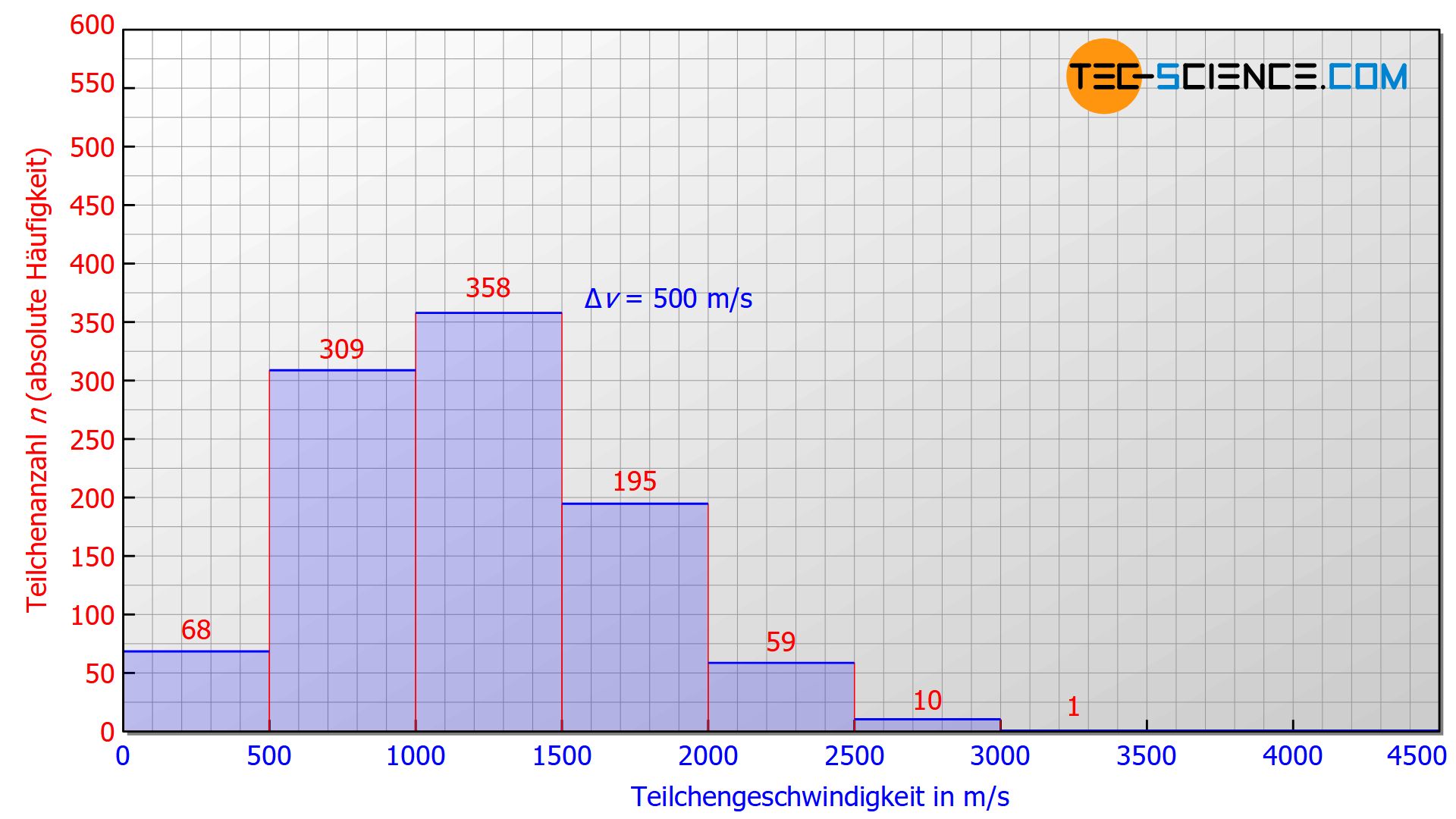
Eine solche Darstellung der Häufigkeitsverteilung innerhalb von sogenannter Klassen* bezeichnet man auch als Histogramm.
*) Als Klassen dienen im vorliegenden Fall die jeweiligen Geschwindigkeitsbereiche.
Das abgebildete Histogramm gibt zwar sehr übersichtlich einen Einblick in die Geschwindigkeitsverteilung, es fehlt jedoch eine Verallgemeinerung auf beliebige Geschwindigkeitsbereiche. So ist es mit dieser Diagrammform beispielsweise nicht möglich auf die Anzahl der Moleküle im Geschwindigkeitsbereich zwischen 1300 m/s und 1600 m/s zu schließen. Auf dem Histogramm aufbauend wird deshalb eine andere Darstellungsform genutzt. Auf diese wird im nächsten Abschnitt näher eingegangen.
Abhängigkeit des Histogramms von der Intervallbreite
Für eine sinnvolle bzw. allgemeinere Darstellung der Geschwindigkeitsverteilung muss beachtet werden, dass es prinzipiell unmöglich ist einer bestimmten Geschwindigkeit direkt eine konkrete Teilchenzahl zuzuordnen. Denn schließlich wird die beobachtete Geschwindigkeit eines Teilchens niemals bis auf die letzte Nachkommastelle mit dem vorgegebenen Wert übereinstimmen. Man würde schließlich kein einziges Teilchen finden, das diese vorgegeben Geschwindigkeit exakt aufweist. Auch aufgrund der bereits erläuterten Messmethodik kann ohnehin nicht auf die exakte Geschwindigkeit der Gasteilchen geschlossen werden, sondern nur auf Geschwindigkeitsbereiche (bedingt durch die endliche Größe der Schlitze).
Man könnte für eine feinere Auflösung der Geschwindigkeitsverteilung im Experiment die Schlitze in den Scheiben verkleinern. Somit würde man den zu filternden Geschwindigkeitsbereich ebenfalls verringern. Dies gibt dann einen detaillierteren Aufschluss darüber, wie viele Moleküle sich in einem bestimmten Geschwindigkeitsbereich bewegen. Die untere Abbildung zeigt hierzu das Histogramm bei einem zu untersuchenden Geschwindigkeitsintervall von Δv = 250 m/s und Δv = 125 m/s.
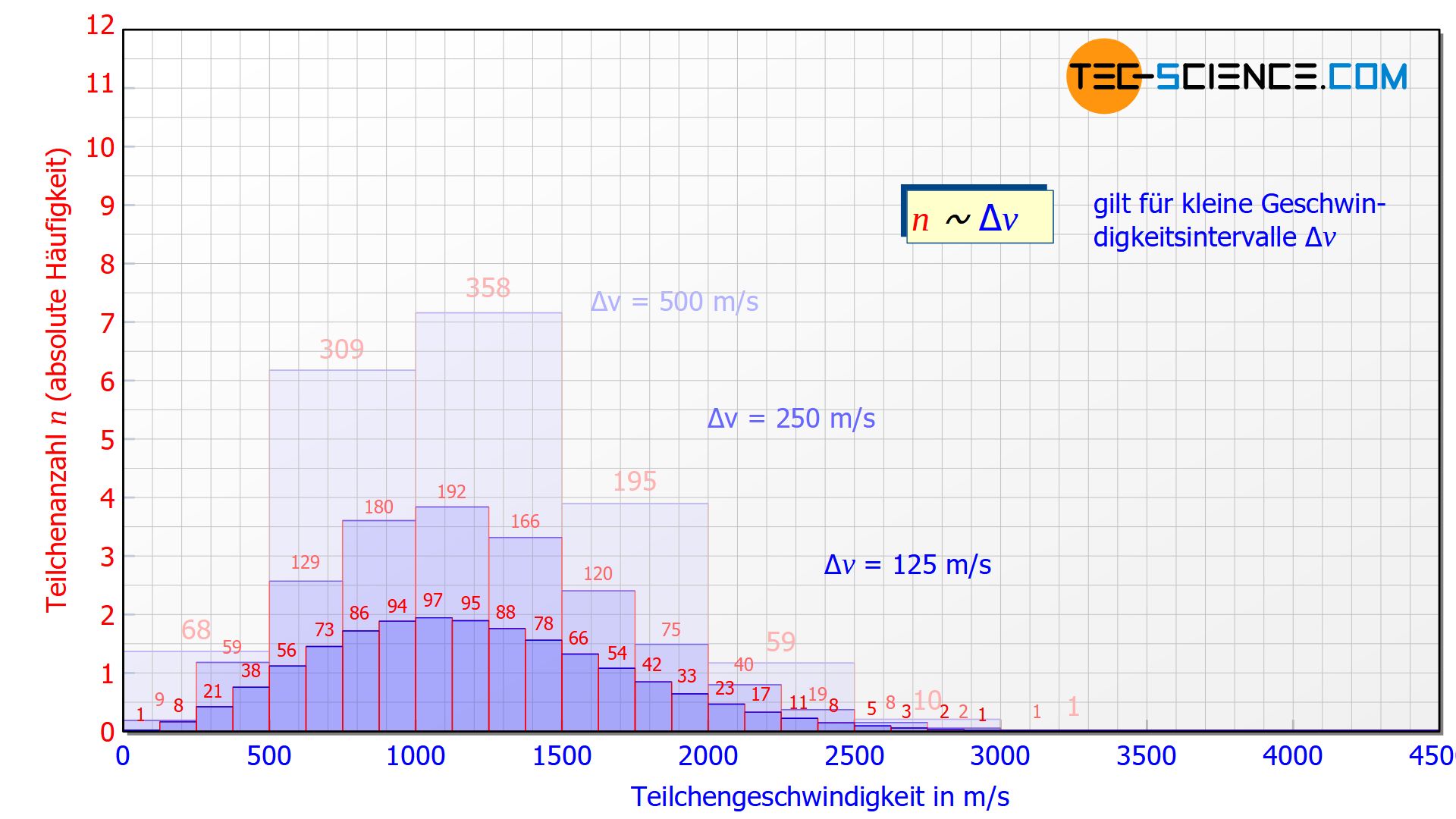
Je feiner das Geschwindigkeitsintervall gewählt wird, desto „flacher“ ist der Diagrammverlauf, da die Teilchen auf immer kleine Geschwindigkeitsbereiche aufgeteilt werden. Für kleine Geschwindigkeitsbereiche ergibt sich dabei ein proportionaler Zusammenhang zwischen der gewählten Intervallbreite Δv und der darin befindlichen Teilchenanzahl n:
\begin{align}
&n \sim \Delta v ~~~~~~~~~\text{(gilt nur für kleine Geschwindigkeitintervalle)}\\[5px]
\end{align}
Die Höhe des ursprünglichen Balkens wird also mit jeder Halbierung des Geschwindigkeitsintervalls somit um die Hälfte kleiner. Dies wird auch anschaulich klar, denn bei einer Halbierung des Intervalls, wird im statistischen Mittel die Hälfte der Teilchen im ursprünglichen Intervall eine höhere Geschwindigkeit haben und die andere Hälfte eine geringere Geschwindigkeit.
Für kleine Intervallbreiten, ist die darin befindliche Teilchenanzahl („Höhe des Balkens“) proportional zur Intervallbreite („Breite des Balkens“)!
Absoulte Häufigkeitsverteilung
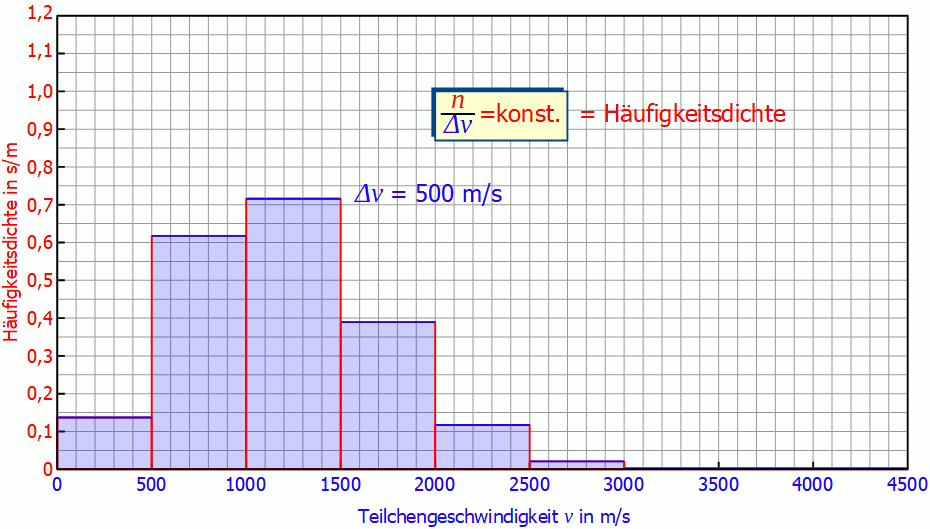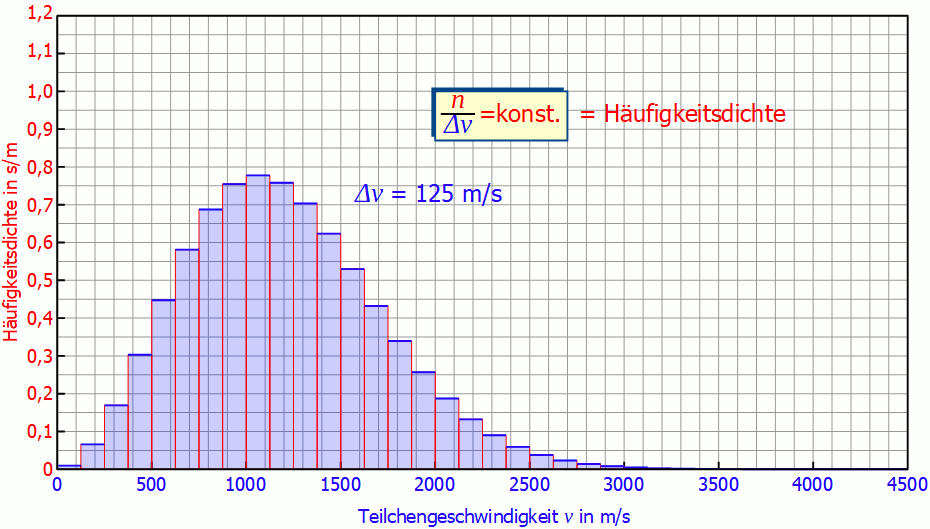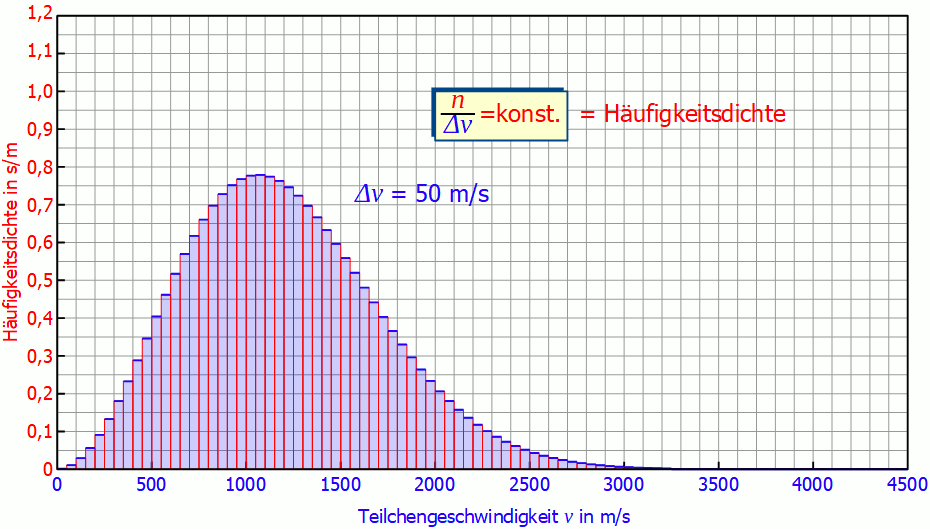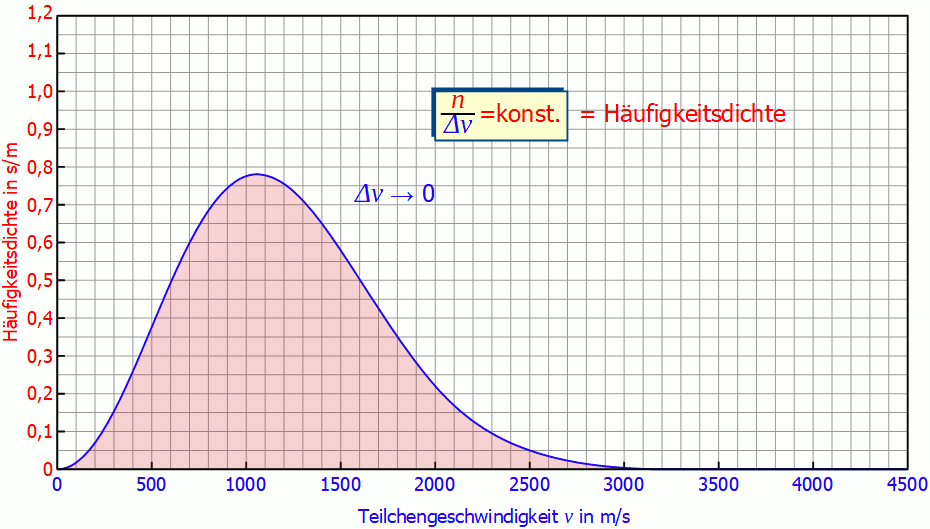
Für eine allgemeine Darstellung der Geschwindigkeitsverteilung kann man nun genau diese Tatsache nutzen, dass Intervallbreite und darin befindliche Teilchenanzahl proportional zueinander sind. Denn damit ist der Quotient aus Teilchenanzahl und Intervallbreite konstant und nicht mehr vom gewählten Intervall selbst abhängig:
\begin{align}
&\frac{n}{\Delta v } = \text{konstant} ~~~~\text{(Häufigkeitsdichte)}\\[5px]
\end{align}
Aus diesem Grund wird auf der vertikalen Achse nicht mehr die Teilchenanzahl sondern der Quotient aus Teilchenanzahl und Intervallbreite aufgetragen. Diese Größe wird auch (absolute) Häufigkeitsdichte genannt (Einheit: s/m). Die untere Animation zeigt hierzu die Auswirkungen einer immer kleineren Intervallbreite auf die Häufigkeitsverteilung. Es wird deutlich, dass sich für kleine Intervallbreiten die Diagramme mehr und mehr angleichen. Für unendlich kleine Intervallbreiten erhält man dann schließlich einen kontinuierlichen Kurvenverlauf, der unabhängig der Intervallbreite ist!
Man muss also gar nicht die exakten Geschwindigkeiten der einzelnen Gasteilchen messen, es genügt ein hinreichend kleines Geschwindigkeitsintervall um die Geschwindigkeitsverteilung zu ermitteln.
In einem solchen Diagramm der Häufigkeitsverteilung entspricht nicht mehr die Höhe des Graphen der Teilchenanzahl sondern der Flächeninhalt! In der unteren Abbildung entspräche die rot markierte Fläche einer Anzahl von 185 Teilchen, die eine Geschwindigkeit zwischen 1300 m/s und 1600 m/s besitzen. Die Fläche unterhalb der gesamten Kurve im Geschwindigkeitsbereich zwischen 0 bis ∞ entspräche schließlich 1000 Teilchen, da im Hinblick auf die Geschwindigkeit somit die Gesamtheit aller Teilchen erfasst werden würde.
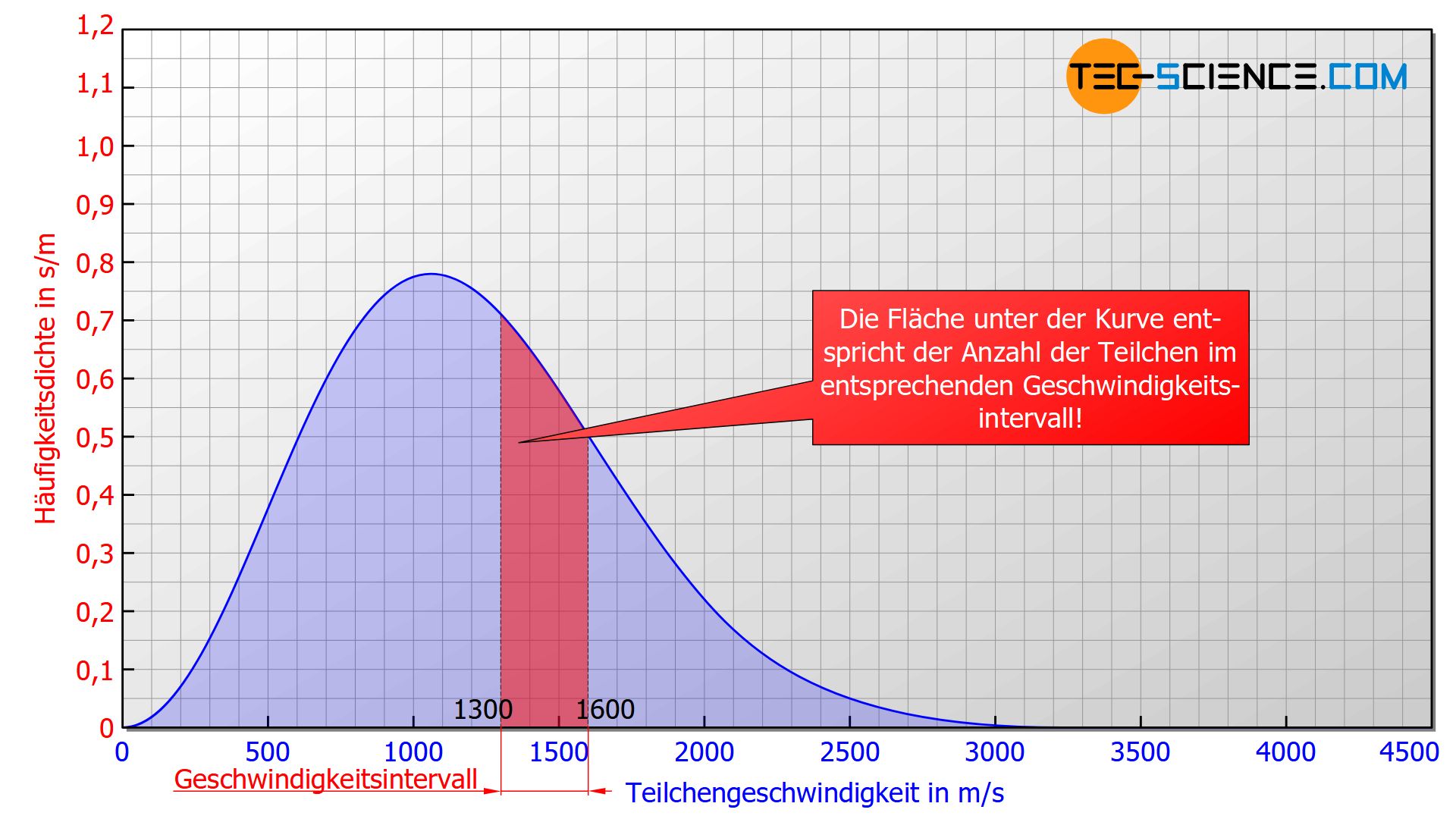
Die Fläche unter der Häufigkeitsverteilung entspricht der Anzahl der Teilchen im entsprechenden Geschwindigkeitsbereich!
Beachte, dass der Begriff Dichte im Zusammenhang mit der Häufigkeitsdichte nicht auf ein Volumen oder eine Fläche bezogen sondern ist auf die Geschwindigkeit. Eine Häufigkeitsdichte von bspw. 5 s/m bedeutet anschaulich, dass sich um diesen Bereich herum pro 1 m/s Geschwindigkeitsintervall 5 Teilchen befinden. Beachtet werden muss bei dieser Aussage natürlich, dass sich die Häufigkeitsdichte mit der Geschwindigkeit ändert. Deshalb gilt diese Aussage nur für Geschwindigkeitsbereiche die nahe um diesen Punkt herum liegen.
Relative Häufigkeitsverteilung
Die Darstellung der Häufigkeitsverteilung in der oberen Abbildung gilt in dieser Form nur für eine Anzahl von insgesamt 1000 Teilchen. Der qualitative Verlauf wäre aber auch selbst für 1 Millionen Teilchen derselbe. Das Diagramm wäre lediglich in der Höhe gestreckt. Für eine allgemeine Darstellung der Geschwindigkeitsverteilung ist es deshalb wenig praktikable die absolute Anzahl der Teilchen aufzutragen.
Viel mehr wird die Häufigkeitsverteilung in Prozent angegeben, um unabhängig von der Gesamtheit der Teilchen zu sein. Man spricht dann nicht mehr von der absoluten Häufigkeitsverteilung sondern von der relativen Häufigkeitsverteilung. Die Größe auf der vertikalen Achse wird schließlich relative Häufigkeitsdichte genannt.
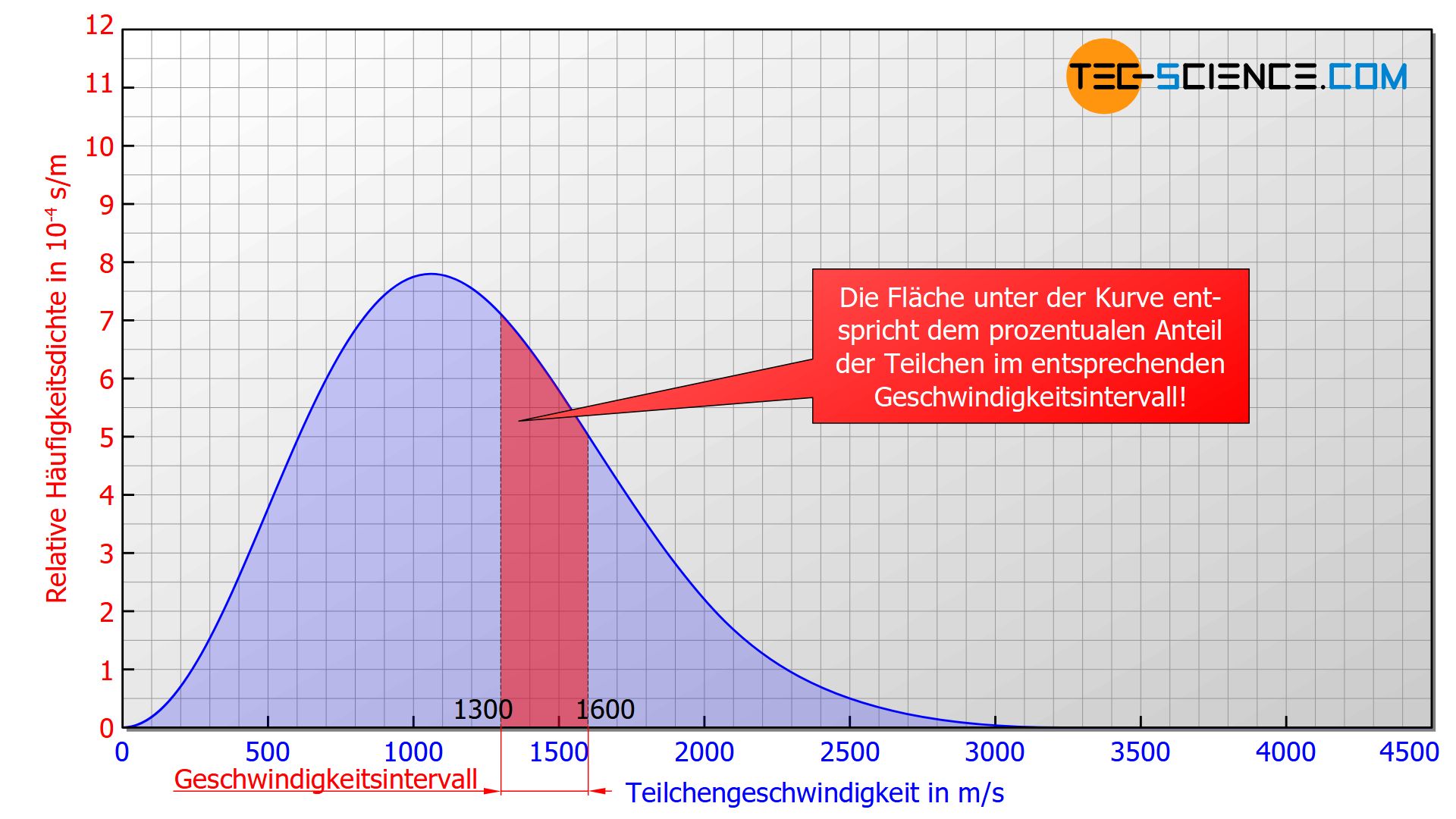
In einer solchen Diagrammform entspricht dann der Flächeninhalt unterhalb der Kurve dem prozentualen Anteil der Teilchen im entsprechenden Geschwindigkeitsbereich (relative Häufigkeit). In der oberen Abbildung wären dies 18,5 % der Teilchen, die eine Geschwindigkeit zwischen 1300 m/s und 1600 m/s besitzen. Die Fläche unterhalb der gesamten Kurve im Geschwindigkeitsbereich zwischen 0 bis ∞ entspräche schließlich 1 (≙ 100 %), da im Hinblick auf die Geschwindigkeit somit die Gesamtheit aller Teilchen erfasst werden würde.
Die Fläche unter der Kurve entspricht dem prozentualen Anteil der Teilchen im entsprechenden Geschwindigkeitsbereich!
Einfluss der Temperatur auf die Geschwindigkeitsverteilung
Die untere Abbildung zeigt den Einfluss der Temperatur auf die Geschwindigkeitsverteilung. Für höhere Temperaturen wird die Geschwindigkeitsverteilung in der Länge gestreckt und in der Höhe gestaucht. Es ergibt sich somit eine breitere Geschwindigkeitsverteilung mit höheren Geschwindigkeitsanteilen.
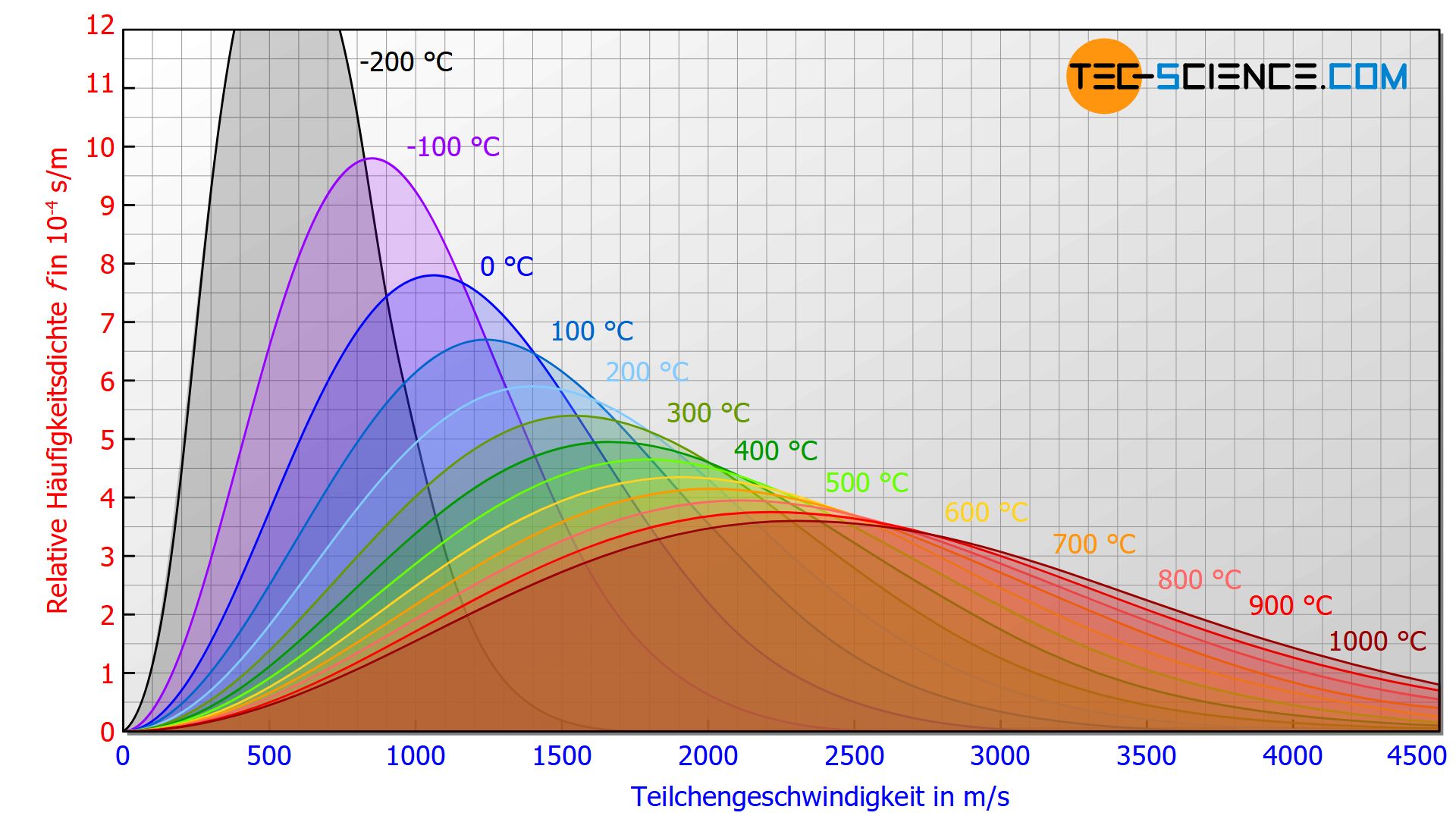
Mit steigender Temperatur nimmt der Anteil an Teilchen mit höheren Geschwindigkeiten zu!
Diese Tatsache deckt sich mit der bereits im Artikel Temperatur und Teilchenbewegung gemachten Aussage, dass die Temperatur eines Stoffes ein Maß für die Bewegungsenergie der darin enthaltenen Teilchen ist. Je höher die Temperatur, desto mehr Energie haben die Teilchen und umso schneller bewegen sich diese folglich. Im Gegensatz zur Temperatur hat der Gasdruck hingegen keinen Einfluss auf die Geschwindigkeitsverteilung (zumindest für ein ideales Gas).
Die Geschwindigkeitsverteilung eines idealen Gases ist unabhängig vom Gasdruck!
Die Physiker James Clerk Maxwell und Ludwig Boltzmann versuchten mit statistischen Methoden eine solche Geschwindigkeitsverteilung auf Grundlage der kinetischen Gastheorie herzuleiten. Im Jahre 1860 gelang es den beiden Physikern auch schließlich. Deshalb wird eine solche Geschwindigkeitsverteilung wie oben abgebildet auch als Maxwell-Boltzmann-Verteilung bezeichnet. Im Artikel Maxwell-Boltzmann-Verteilung wird hierauf näher eingegangen.