Energetische Betrachtung des Hagen-Poiseuille-Gesetzes

Das Hagen-Poiseuille-Gesetz zur Beschreibung des parabolischen Geschwindigkeitsprofils gilt aus energetischen Gründen nur für lange Rohr.

Zusammenfassung der Gesetzmäßigkeiten

Wie im Artikel zum Hagen-Poiseuille-Gesetz ausführlich hergeleitet, lässt sich die Hagen-Poiseuille-Strömung mit dem typischen parabolischen Geschwindigkeitsprofil durch folgende Gleichungen beschreiben.

\begin{align}
\label{vrr}
&\boxed{v(r)=v_\text{max} \cdot \left[1-\left(\frac{r}{R}\right)^2\right]} \\[5px]
\label{max}
&\boxed{v_{\text{max}}= -\frac{R^2}{4\eta} \frac{\text{d} p}{\text{d}x} } \\[5px]
\label{pv}
& \boxed{\frac{\text{d}p}{\text{d}x} = \frac{\Delta p}{ \Delta L}} \\[5px]
\label{loss}
& \boxed{\Delta p_V = \frac{8\eta \cdot \Delta L}{R^2} \cdot c} ~~~\text{Druckverlust} \\[5px]
\label{vmax}
& \boxed{c = \frac{1}{2} \cdot v_\text{max}} \\[5px]
\end{align}

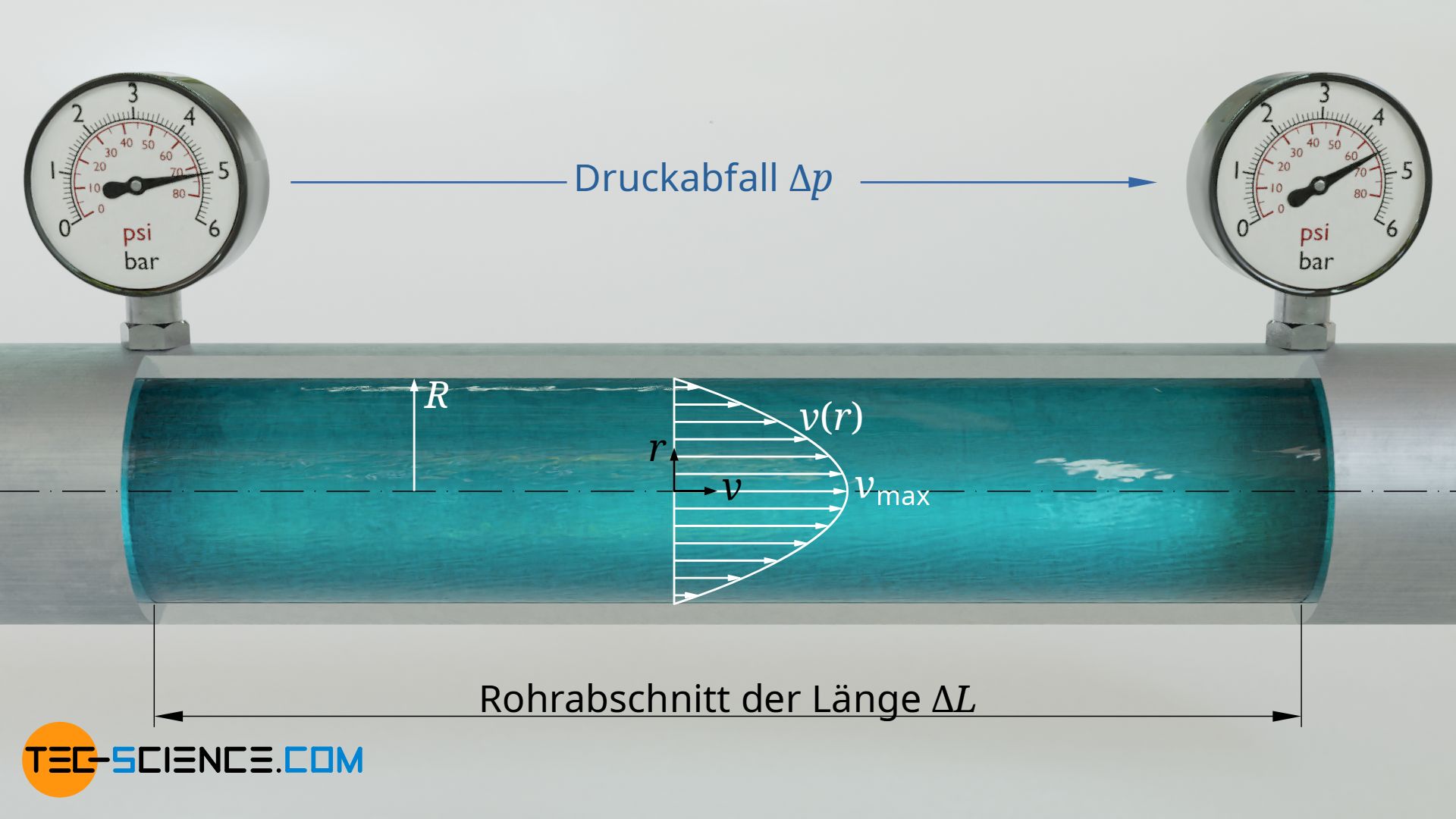
Darin bezeichnet ΔL die Länge des Rohrabschnitts und R den Innenradius. v(r) ist die Geschwindigkeit des Fluids im Abstand r zur Rohrachse und η die Viskosität des strömenden Fluids. Der Druckgradient dp/dx ist der Antrieb für die Rohrströmung und entspricht der Druckänderung pro Längeneinheit. Der Druckgradient bestimmt sich aus der Druckänderung Δp entlang des Rohres. Die mittlere Strömungsgeschwindigkeit c entspricht bei der Hagen-Poiseuille-Strömung gerade der Hälfte der maximalen Strömungsgeschwindigkeit v_max in der Mitte des Rohres.

Anlaufstrecke (Ausbilden des laminaren Strömungsprofils)

Der Druckgradient dp/dx in der oberen Gleichung ist zum Ausgleich der Reibungsverluste erforderlich. Hierdurch wird das Fluid am Strömen gehalten. Eine Strömung ist aber nicht „einfach da“, sondern sie muss erzeugt werden. In anderen Worten: Das Fluid muss erst einmal auf das Strömungsprofil beschleunigt werden. Die im Artikel zum Hagen-Poiseuille-Gesetz erläuterten und hergeleiteten Zusammenhänge gelten also strenggenommen nur für Rohrabschnitte, in denen sich die Strömung bereits vollständig ausgebildet hat. So auch die oberen Gleichungen.

Im Folgenden möchten wir deshalb etwas näher auf den gesamten Strömungsprozess eingehen. Wir stellen uns hierzu einen großen Tank vor, der vollständig mit einem Fluid gefüllt ist. Am Boden des Tanks ist seitlich ein horizontales Rohr angeschlossen, über das das Fluid ins Freie strömt. Der Tank sei so groß, dass der Flüssigkeitsspiegel beim Ausströmen des Fluids nicht merklich sinkt. Das Fluid ruht sozusagen im Tank; wird aber offensichtlich durch das Rohr ins Freie beschleunigt.

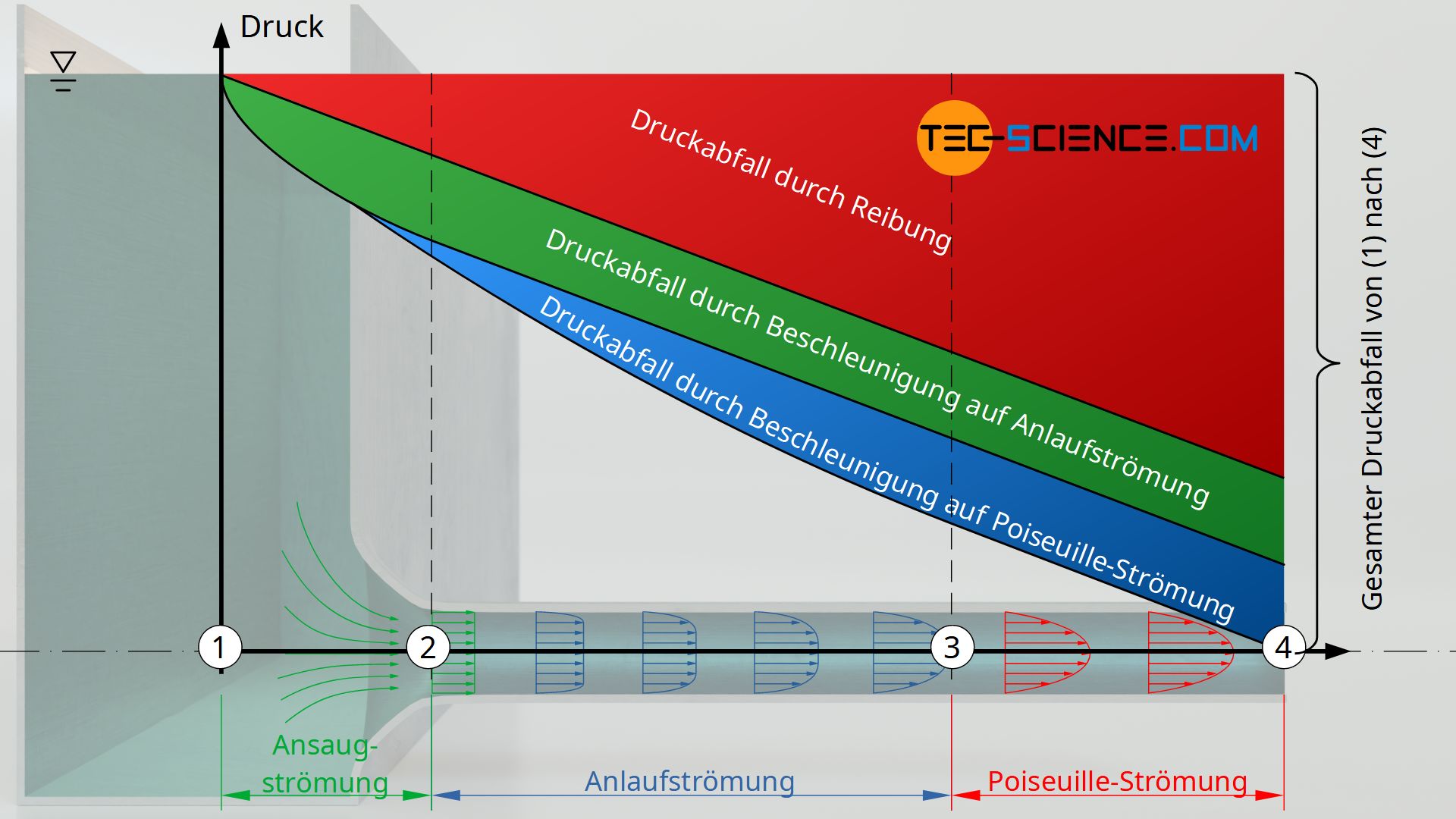
Die Strecke die das Fluid im Rohr zurücklegt bis sich das parabelförmige Strömungsprofil vollständig ausgebildet hat, wird auch als Anlaufstrecke bezeichnet. Die Strömung in diesem Bereich wird Anlaufströmung genannt. Die untere Abbildung zeigt hierzu schematisch die Geschwindigkeitsverteilung an verschiedenen Stellen im Rohr. Der Strömungsprozess kann dabei in drei Teile unterteilt werden:

• Beschleunigung auf die konstante Einlaufgeschwindigkeit und
• anschließendes Beschleunigen auf das parabolische Geschwindigkeitsprofil,
• sowie die permanent zu kompensierende Reibung.

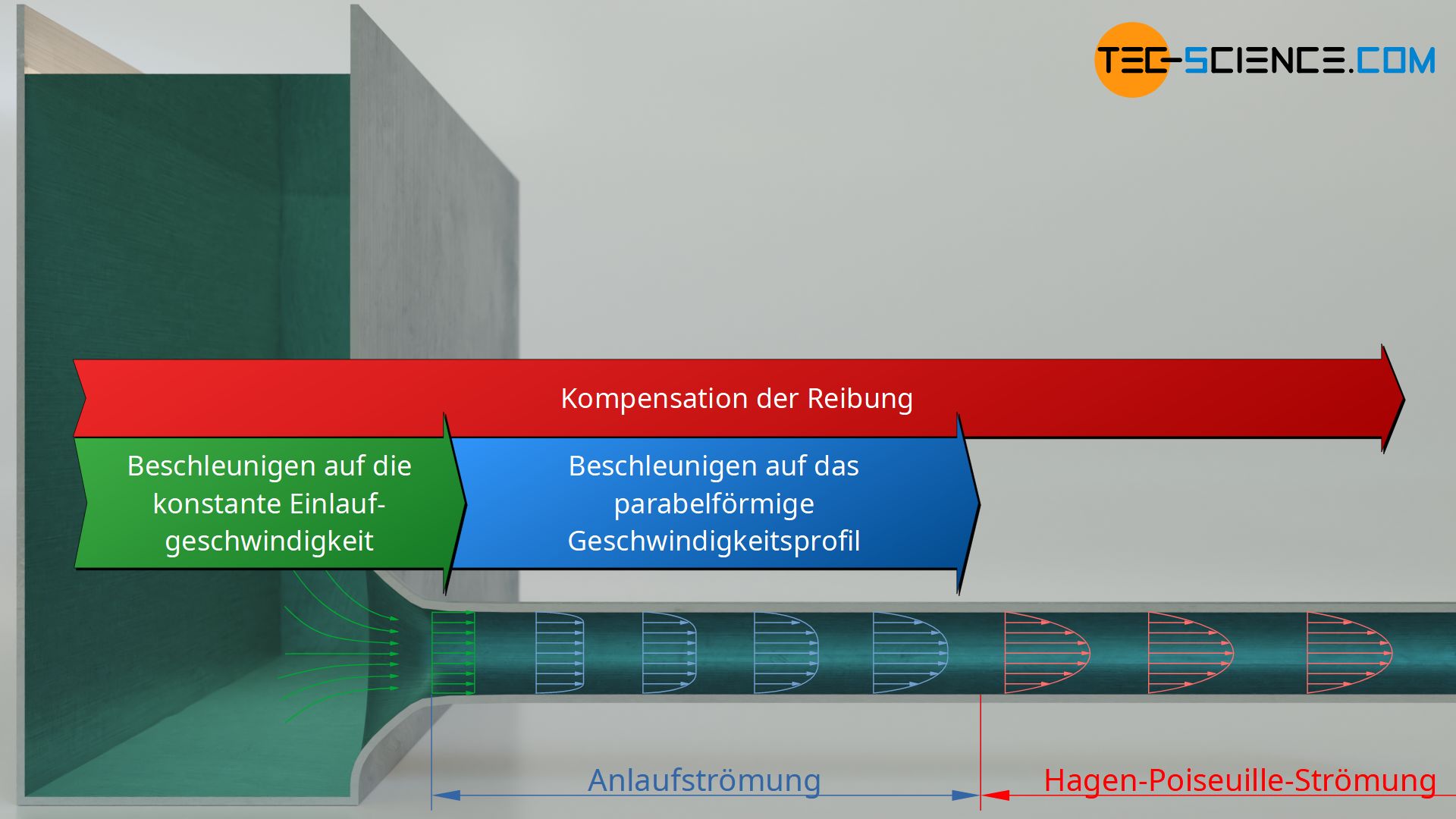
Alle drei Vorgänge sind mit einem entsprechenden Energieaufwand und somit mit einem Druckabfall verbunden. Hierauf soll im Folgenden näher eingegangen werden.

Beschleunigung auf die konstante Einlaufgeschwindigkeit

Das Fluid wird im Tank auf der Höhe der Rohrachse zunächst bis zum Einlauf hin beschleunigt (Ansaugströmung). Es tritt mit nahezu konstanter Geschwindigkeit c in den stromlinienförmig ausgerundeten Einlauf ein. Die Abrundung ist in der Praxis entscheidend, da bei scharfkantigen Übergängen das Strömungsprofil aufgrund der sogenannten vena contracta sonst eingeschnürt werden würde, was eine Verringerung des Durchflusses zur Folge hätte (speziell hierzu mehr im Artikel Ausströmen von Flüssigkeiten).

Wenn im ruhenden Fluid auf Höhe der Rohrachse der Druck p₁ herrscht, dann wird ein Teil dieses Drucks also für das Beschleunigen auf die konstante Einlaufgeschwindigkeit c genutzt. Gemäß der Energiegleichung nach Bernoulli führt dies am Einlauf zur Verringerung des (statischen) Druck auf einen Wert p₁. Für den Betrag des Druckverlusts Δp_b1 aufgrund dieses Beschleunigungsvorgangs gilt somit:

\begin{align}
&p_2 = p_1 – \frac{\rho}{2} c^2 \\[5px]
\label{p}
&\Delta p_{b1} =p_1-p_2= \frac{\rho}{2} c^2 \\[5px]
\end{align}

Beschleunigung auf das parabolische Geschwindigkeitsprofil

Nachdem das Fluid bis zum Einlauf hin auf die konstante Einlaufgeschwindigkeit c beschleunigt wurde, beginnt nun innerhalb der Anlaufstrecke die Reibung zwischen Fluid und Rohrwand wirksam zu werden (dieser Übergang von der Ansaugströmung zur Anlaufströmung ist fließend). Das Fluid haftet dort regelrecht an der Wand, sodass die Strömungsgeschwindigkeit an der Wand Null ist (Haftbedingung). Aufgrund der Viskosität werden die weiter innen liegenden Fluidschichten entlang der Anlaufstrecke mehr und mehr abgebremst.

Trotz der Verringerung der Geschwindigkeit in den Randbereichen, muss aber nach wie vor derselbe Massenstrom durch die Rohrleitung strömen (Kontiniutätsbedingung). Während also die Strömungsgeschwindigkeit zum Rand hin abnimmt, muss die Geschwindigkeit in der Kernströmung im Vergleich zur Einlaufgeschwindigkeit zunehmen. Häufig wird die Kernströmung in der Anlaufstrecke als einen Bereich mit konstanter Geschwindigkeit betrachtet. Zum Rand hin fällt die Geschwindigkeit dann quadratisch auf Null ab. Ab einer bestimmten Länge, hat sich schließlich ein kontinuierliches parabelförmiges Profil eingestellt. Dies kennzeichnet das Ende der Anlaufstrecke.

Man könnte nun vorschnell der Meinung sein, dass das Ausbilden des parabolischen Geschwindigkeitsprofils keine zusätzliche Energie erfordert, denn schließlich verliert das Fluid aufgrund der Kontinuitätsbedingung im Randbereich im selben Maße Geschwindigkeit wie es in der Rohrmitte hinzu gewinnt. Dies mag vielleicht für die Geschwindigkeit gelten, aber nicht für die kinetische Energie. Die kinetische Energie hängt quadratisch mit der Geschwindigkeit zusammen. Zudem ist das Geschwindigkeitsprofil selbst parabelförmig, sodass die höheren Geschwindigkeitsanteile in der Mitte der Strömung deutlich mehr Einfluss auf die kinetische Energie haben.

Der Verlust an kinetischer Energie im Randbereich wiegt nicht die benötigte kinetische Energie zur Beschleunigung des Fluids in der Kernströmung auf. Für das Ausbilden des parabolsichen Strömungsprofils ausgehend der Einlaufströmung ist also zusätzlich Energie erforderlich. Diese zusätzliche Energie entspricht nochmals dem Betrag der kinetischen Energie der Einlaufströmung. Man erhält also analog zur Gleichung (\ref{p}) nochmals einen Druckverlust Δp_b2 aufgrund der benötigten Energie zur Ausbildung des Strömungsprofils. Tatsächlich ist diese benötigte Energie identisch mit Gleichung (\ref{p}) (wird im letzten Abschnitt gezeigt):

\begin{align}
\label{pp}
&\Delta p_{b2} = \frac{\rho}{2} c^2 \\[5px]
\end{align}

Insgesamt entfällt also auf den Beschleunigungsvorgang des Fluids folgender Druckverlust:

\begin{align}
&\Delta p_{b} =\Delta p_{b1} + \Delta p_{b1} \\[5px]
\label{ppp}
&\boxed{\Delta p_{b} = \rho c^2} ~~~~~\text{Korrektionsglied} \\[5px]
\end{align}

Für den Gesamtdruckverlust kommen natürlich noch die eigentlichen Reibungsverluste gemäß Gleichung (\ref{loss}) hinzu (beachte, dass dieser Term auch in der Anlaufstrecke vorhanden ist, denn unabhängig davon ob sich das Strömungsprofil ausgebildet hat oder nicht, wirken Reibungskräfte, die durch diesen Term beschrieben werden):

\begin{align}
&\Delta p = \Delta p_b + \Delta p_V \\[5px]
&\boxed{\Delta p = \frac{8\eta \cdot L}{R^2} \cdot c + \rho c^2} \\[5px]
\end{align}

Diskussion

Man sieht also, dass beim Druckverlust über eine Rohrleitung im Allgemeinen auch die kinetischen Energien während der Beschleunigungsphase zu berücksichtigen sind. Man erkennt aber auch, dass für große Rohrlängen L bei gleichzeitig kleinen Rohrradien R, der Term zur Beschreibung der Reibungsverluste groß wird gegenüber dem Term, der zur Beschreibung der Beschleunigungsarbeit dient.

Tatsächlich erkannte Poiseuille zunächst nicht die Notwendigkeit die Druckverluste aufgrund der Beschleunigungsvorgänge zu berücksichtigen. Die Folge waren falsche Vorhersagen des Volumenstroms, vor allem bei kurzen Rohren. Erst als Hagen seine Gleichungen durch den Term (\ref{ppp}) korrigierte, übereinstimmten die theoretischen Vorhersagen mit der Praxis. Dieser Beschleunigungsterm wird deshalb auch als Korrektionsglied bezeichnet.

Wäre das Rohr im Übrigen nicht horizontal angeordnet, sondern würde eine Höhendifferenz Δh überwinden, dann müsste man dem Fluid zusätzlich auch noch potentielle Energie zuführen (Lageenergie). Dies wäre mit einem weiteren Druckverlust verbunden (Δp_h=ϱ⋅g⋅Δh)! Mehr zu diesem Thema im Artikel Bernoulli-Gleichung.

Mindest-Verhältnis von Rohrlänge zur Rohrdurchmesser

Beschleunigungsarbeit (mikroskopische Betrachtung der Rohrströmung)

Im Folgenden soll die Hagen-Poiseuille-Strömung unter energetischen Gesichtspunkten näher betrachtet werden. In einem Rohrabschnitt der Länge ΔL soll hierzu die kinetische Energie der Strömung auf mikroskopischer Ebene bestimmt werden. Wir betrachten dazu einen Hohlzylinder mit dem Radius r und mit der Dicke dr. Die Höhe dieses Zylinders entspricht der Länge ΔL des Rohrabschnitts. Die Masse dieses Hohlzylinders bestimmt sich wie folgt:

\begin{align}
\label{dm}
&\text{d}m = \overbrace{\underbrace{2\pi r \cdot \text{d}r}_{\text{d}A} \cdot \Delta L}^{\text{d}V}\cdot \rho \\[5px]
\end{align}

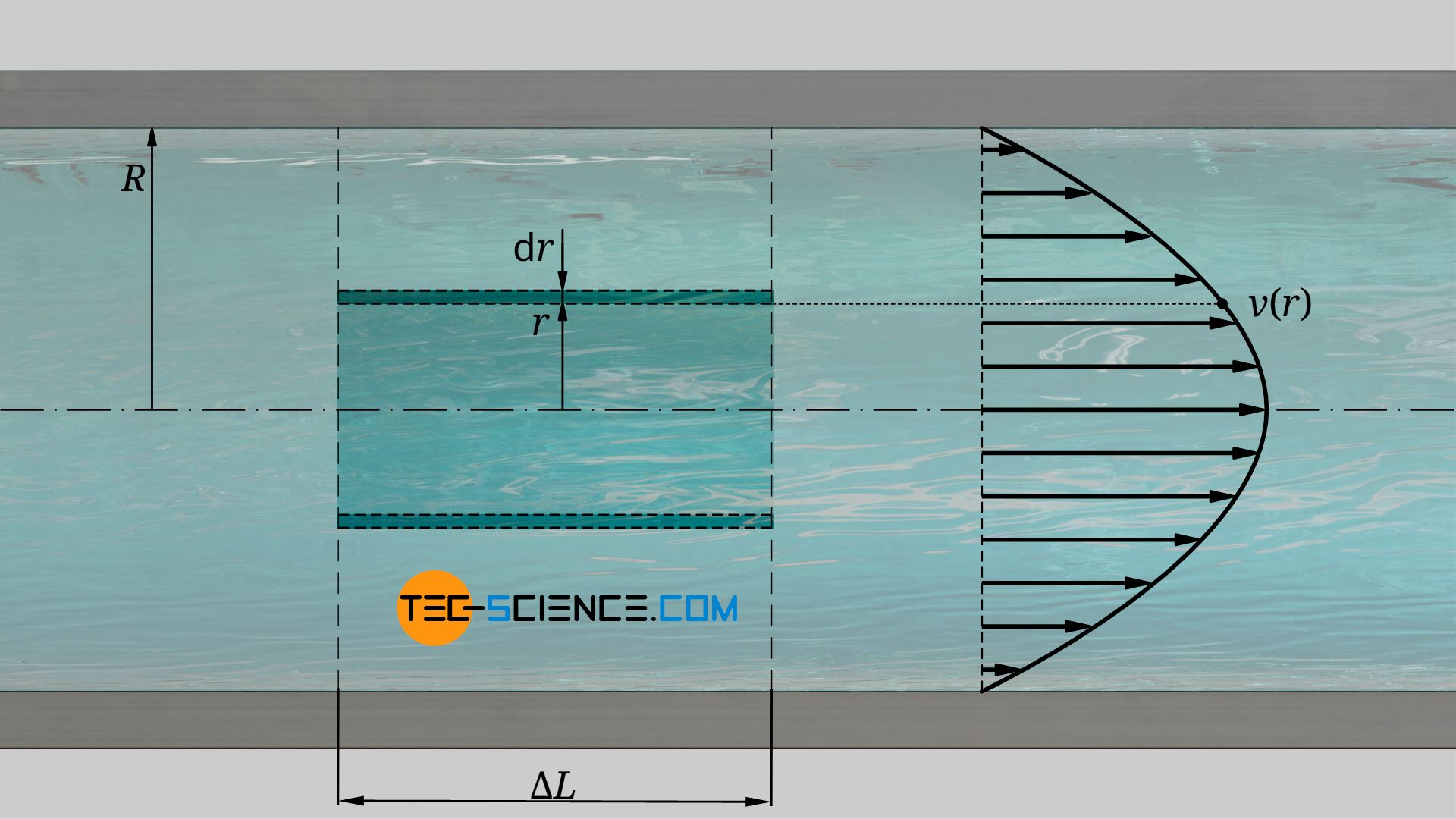
Die Geschwindigkeit dieser Masse im Abstand r ist durch Gleichung (\ref{vrr}) gegeben, sodass für die kinetische Energie dW_kin gilt:

\begin{align}
\text{d}W_\text{kin} &= \frac{1}{2} \text{d}m \cdot v^2(r) \\[5px]
&= \frac{1}{2} \overbrace{2\pi r \cdot \text{d}r \cdot \Delta L \cdot \rho}^{\text{d}m} \cdot v^2(r) \\[5px]
&= \pi r \rho \Delta L \cdot v^2(r) \cdot \text{d}r \\[5px]
&= \pi r \rho \Delta L \cdot v_\text{max}^2 \cdot \left[1-\left(\frac{r}{R}\right)^2\right]^2 \cdot \text{d}r \\[5px]
&= \pi \rho \Delta L \cdot v_\text{max}^2 \cdot \left(r-\frac{2r^3}{R^2} +\frac{r^5}{R^4} \right) \cdot \text{d}r \\[5px]
\end{align}

Die kinetische Energie W_kin im gesamten Rohrabschnitt erhält man schließlich durch Integration dieser Gleichung innerhalb der Grenzen von r=0 bis r=R:

\begin{align}
W_\text{kin} &= \int \text{d} P_\text{kin} = \pi\rho \Delta L ~v_\text{max}^2 \cdot \int \limits_0^R \left(r-\frac{2r^3}{R^2} +\frac{r^5}{R^4} \right) \cdot \text{d}r \\[5px]
&= \pi\rho\Delta L~v_\text{max}^2 \cdot \left\vert \frac{r^2}{2}-\frac{r^4}{2R^2} +\frac{r^6}{6R^4}\right\vert_0^R \\[5px]
&= \pi\rho \Delta L~ v_\text{max}^2 \cdot \left( \frac{R^2}{2}-\frac{R^4}{2R^2} +\frac{R^6}{6R^4} \right) \\[5px]
&= \pi\rho \Delta L~ v_\text{max}^2 \cdot \frac{R^2}{6} \\[5px]
\end{align}

Durch Umstellen dieser Gleichung, kann man die kinetische Energie auch in Abhängigkeit der mittleren Strömungsgeschwindigkeit c ausdrücken:

\begin{align}
W_\text{kin} &= \pi\rho \Delta L~ v_\text{max}^2 \cdot \frac{R^2}{6} \\[5px]
&= \pi\rho \Delta L~ v_\text{max} \cdot \underbrace{\frac{v_\text{max}}{2}}_{c} \cdot \frac{R^2}{3} \\[5px]
&= \pi\rho c \Delta L~ v_\text{max} \cdot \frac{R^2}{3} \\[5px]
\end{align}

Setzt man für die maximale Geschwindigkeit die Beziehung gemäß Gleichung (\ref{max}) ein, dann kann die die kinetische Energie wie folgt anhand des Druckgradienten ermittelt werden (an dieser Stelle soll nur der Betrag des Druckgradienten berücksichtigt werden, ohne Vorzeichen):

\begin{align}
W_\text{kin} &= \pi\rho c \Delta L \cdot \overbrace{\frac{R^2}{4\eta} \frac{\text{d} p}{\text{d}x}}^{v_\text{max}} \cdot \frac{R^2}{3} \\[5px]
W_\text{kin} &=\frac{ \pi\rho c \Delta L R^4}{12\eta} \frac{\text{d} p}{\text{d}x} \\[5px]
\end{align}

Bei einem Rohrabschnitt der Länge ΔL und der Druckdifferenz Δp ist der Druckgradient gemäß Gleichung (\ref{pv}) gegeben, sodass die kinetische Energie wie folgt anhand der Druckdifferenz bestimmt ist:

\begin{align}
&W_\text{kin} =\frac{ \pi\rho c \Delta L R^4}{12\eta} \frac{\Delta p}{\Delta L} \\[5px]
\label{x}
&\boxed{W_\text{kin} =\frac{\pi\rho c R^4 \Delta p}{12 \eta}} \\[5px]
\end{align}

Diese kinetische Energie der Strömung entspricht letztlich der zur Beschleunigung des Fluids erforderlichen Arbeit.

Verschiebearbeit (makroskopische Betrachtung der Rohrströmung)

Das Strömen des Fluids kommt dadurch zustande, dass dieses aufgrund der Druckdifferenz zwischen Rohranfang und Rohrende durch die Rohrleitung gedrückt wird. Um dieses Verschieben des Fluids durch den Rohrabschnitt zu ermöglichen, ist eine bestimmte Kraft und damit Arbeit erforderlich, die sogenannte Verschiebearbeit. Um diese zu ermitteln, betrachten wir das Fluid nun nicht mehr auf mikroskopischer Ebene, sondern auf makroskopischer Ebene.

Die zur Verschiebung erforderliche Kraft ergibt sich aus der Differenz der Drücke zwischen Rohranfang und Rohrende sowie der Querschnittsfläche des Rohrs:

\begin{align}
F = \Delta p \cdot A = \Delta p \cdot \pi R^2 \\[5px]
\end{align}

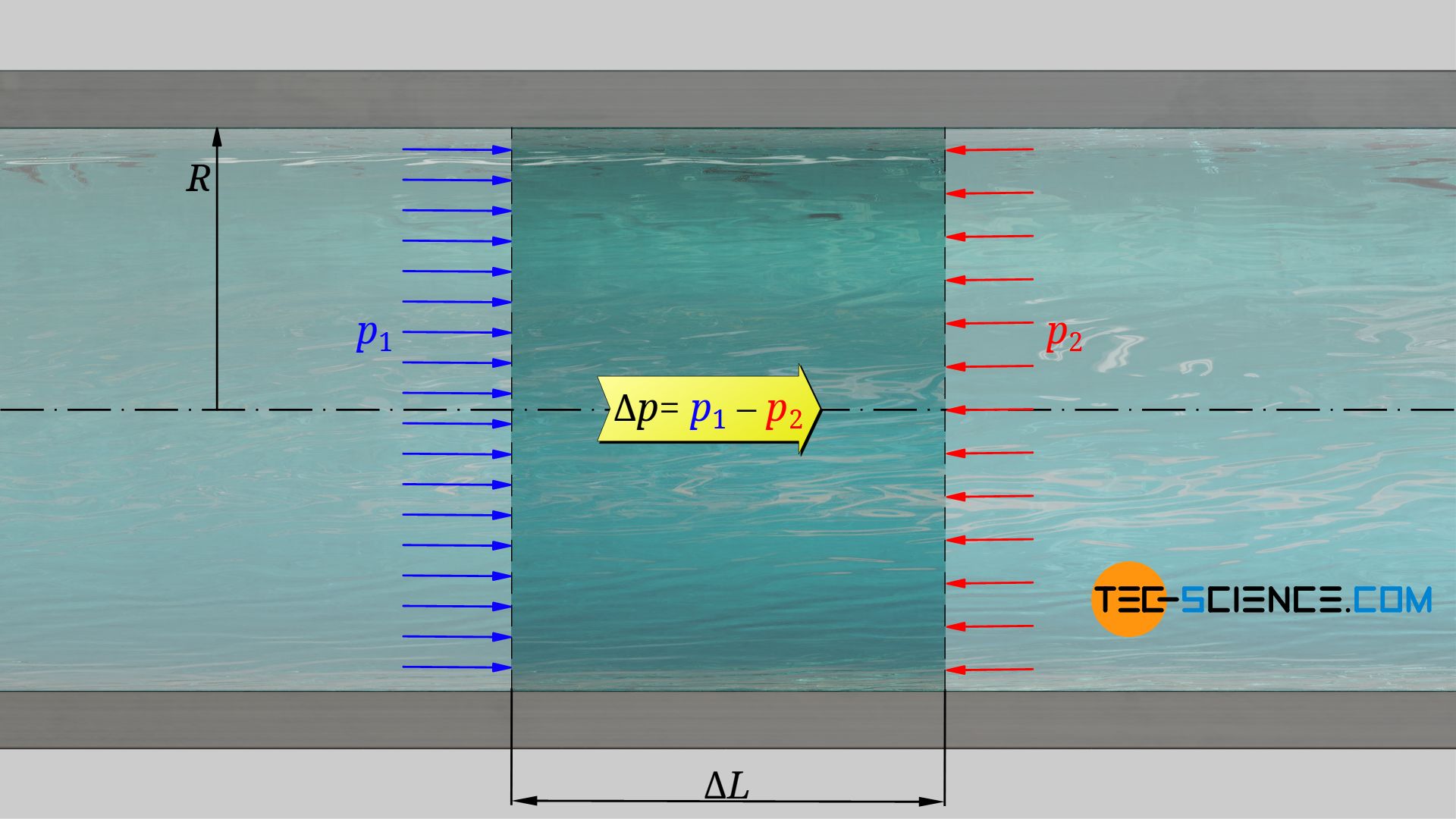
Die zugeführte Arbeit beim Strömen des Fluids über den gesamten Rohrabschnitt ΔL bestimmt sich somit wie folgt:

\begin{align}
&W_V = F \cdot \Delta L \\[5px]
\label{y}
&\boxed{W_V = \Delta p \cdot \pi R^2 \Delta L} ~~~~~\text{zugeführte Verschiebearbeit}\\[5px]
\end{align}

Mindestverhältnis zwischen Rohrlänge und Rohrdurchmesser

Man kann das Mindestverhältnis zwischen Rohrlänge und Rohrdurchmesser zur Gültigkeit des Hagen-Poiseuille-Gesetz nun durch folgende Überlegung abschätzen. Die zugeführte Verschiebearbeit wird zum Einen zur Verrichtung der Beschleunigungsarbeit genutzt und zum Anderen zum Aufbringen der Reibungsarbeit. Da Reibung stets vorhanden ist, kann die Beschleunigungsarbeit bzw. die kinetische Energie nach Gleichung (\ref{x}) nicht größer sein als die zugeführte Verschiebearbeit gemäß Gleichung (\ref{y}). Somit muss folgende Bedingung erfüllt sein:

\begin{align}
\require{cancel}
W_V & >W_{\text{kin}} \\[5px]
\cancel{\Delta p} \cdot \cancel{\pi} R^2 \Delta L & > \frac{\cancel{\pi} \rho c R^4 \cancel{\Delta p}}{12 \eta}\\[5px]
\Delta L & > \frac{ \rho c R^2 }{12 \eta}\\[5px]
\Delta L & > \frac{ \rho c ~2R }{\eta}\cdot \frac{2R}{48}\\[5px]
\Delta L & > \color{red}{\frac{ \rho ~c ~D }{\eta}}\cdot \frac{D}{48}\\[5px]
\end{align}

Der rot markierte Term (bestehend aus Dichte, Strömungsgeschwindigkeit, Rohrdurchmesser und Viskosität) entspricht der sogenannten Reynold-Zahl. Das mindestens erforderliche Länge-Durchmesser-Verhältnis des Rohres ist also abhängig von der Reynoldszahl der Strömung und wie folgt gegeben:

\begin{align}
& \Delta L > \color{red}{Re}\cdot \frac{D}{48}\\[5px]
&\boxed{\frac{\Delta L}{D} > \frac{Re}{48}} \\[5px]
\end{align}

Das Länge-Durchmesser-Verhältnis eines Rohres sollte größer sein als ein Achtundvierzigstel der Reynoldszahl, damit das Hagen–Poiseuille-Gesetz gültig ist!

Weiter eingeschränkt werden muss diese Aussage im Hinblick auf turbulente Strömungen. Dort gilt das Hagen-Poiseuille-Gesetz grundsätzlich nicht. Die Praxis zeigt, dass turbulente Rohrströmungen ab Reynoldszahlen größer 2300 zu erwarten sind. In einem solchen Grenzfall beträgt das Länge-Durchmesser-Verhältnis rund 50, d.h. das Rohr müsste etwa 50 mal so lange sein wie sein Durchmesser, damit sich ein parabolisches Geschwindigkeitsprofil gemäß des Hagen–Poiseuille-Gesetzes einstellt.

Kinetische Leistung der konstanten Einlaufströmung im Vergleich zum parabolischen Geschwindigkeitsprofil

Den Beweis, dass das Ausbilden des parabelförmigen Geschwindigkeitsprofils nochmals dieselbe Energie erfordert wie das Ausbilden der konstanten Einlaufströmung aus dem sie resultiert, wollen wir in diesem Abschnitt erbringen. Hierzu berechnen wir jeweils kinetische Leistung, mit der das Fluid durch den Querschnitt des Rohres strömt (kinetische Energie pro Zeiteinheit).

Im Abstand r zur Rohrachse betrachten wir eine Ringfläche mit der Dicke dr. Innerhalb der Zeit dt strömt dann das Fluid mit der Geschwindigkeit v(r)durch die Ringfläche dA=2π⋅r⋅dr. Das Fluid legt dabei die Strecke dl=v(r)⋅dt zurück. Für die durchströmte Masse dm durch die Ringfläche gilt dann:

\begin{align}
& \text{d}m = \text{d}V \cdot \rho = \text{d}A\cdot \text{d}l \cdot \rho=2\pi r\cdot\text{d}r \cdot v(r)\cdot \text{d}t \cdot \rho\\[5px]
\end{align}

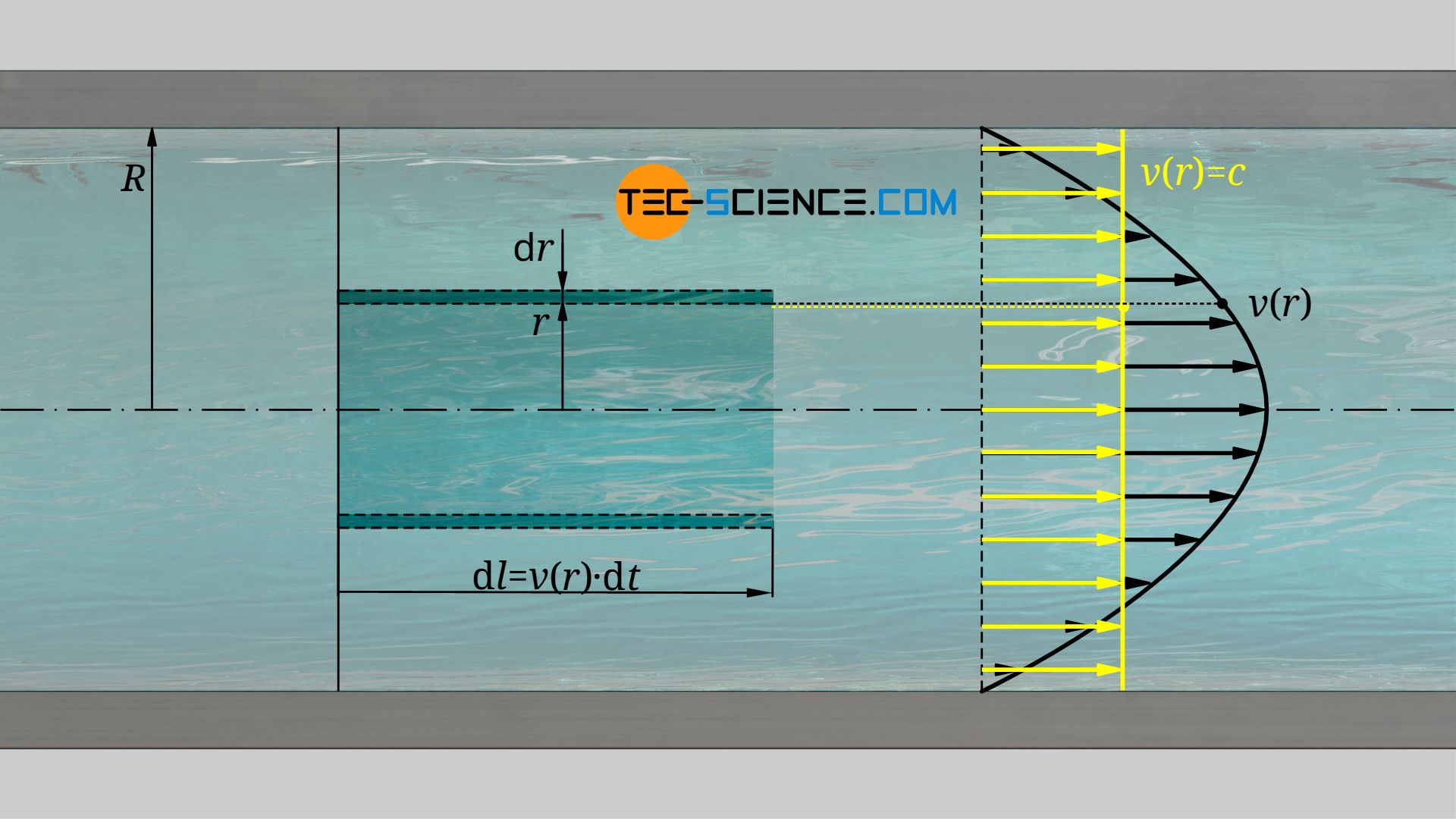
Innerhalb der Zeit dt strömt somit folgende Energiemenge dW_kin, was wiederum einer bestimmten Leistung dP_kin entspricht:

\begin{align}
& W_\text{kin}= \frac{1}{2} \text{d}m~ v^2(r)= \pi\rho r\cdot v^3(r)\cdot \text{d}r ~\text{d}t \\[5px]
& \text{d}P_\text{kin}=\frac{W_\text{kin}}{\text{d}t} = \pi\rho r\cdot v^3(r)\cdot \text{d}r\\[5px]
\end{align}

Die kinetische Leistung durch den gesamten Rohrquerschnitt erhält man schließlich durch die Integration der oberen Gleichung im Bereich zwischen r=0 und r=R:

\begin{align}
& \underline{P_\text{kin}=\pi\rho ~\int\limits_0^R r\cdot v^3(r)\cdot \text{d}r}\\[5px]
\end{align}

Am Einlauf ist die Geschwindigkeit über den gesamten Querschnitt konstant, d.h. keine Funktion des Radius. Aufgrund der Kontinuitätsbedingung entspricht die Geschwindigkeit letztlich der mittleren Strömungsgeschwindigkeit c der Hagen-Poiseuille-Strömung. Bei einem über den gesamten Querschnitt konstanten Geschwindigkeitsprofil mit v(r)=c gilt für die Strömungsleistung also:

\begin{align}
& P_\text{kin,1}=\pi\rho~c^3~\int\limits_0^R r \cdot \text{d}r =\pi\rho~\left\vert \frac{1}{2}r^2 \right\vert_0^R \\[5px]
& \boxed{P_\text{kin,1}=\frac{1}{2}\pi\rho~R^2~c^3} \\[5px]
\end{align}

Diese Leistung entspricht der Strömungsleistung unmittelbar am Einlauf, d.h. direkt vor der Anlaufstrecke. Nun bestimmen wir die Strömungsleistung mit dem parabolischen Strömungsprofil, d.h. die Strömungsleistung nach der Anlaufstrecke. Die Geschwindigkeit ist in diesem Fall eine Funktion des Radius gemäß Gleichung (\ref{vrr}), was zur folgender Leistung führt:

\begin{align}
P_\text{kin,2}&=\pi\rho~~\int\limits_0^R r~\overbrace{v^3_\text{max} \cdot \left[1-\left(\frac{r}{R}\right)^2\right]^3}^{v^3(r)}~ \cdot \text{d}r \\[5px]
&=\pi\rho~v^3_\text{max} ~\int\limits_0^R \left(r-\frac{3r^3}{R^2}+\frac{3r^5}{R^4} -\frac{r^7}{R^6} \right) \cdot \text{d}r \\[5px]
&=\pi\rho~v^3_\text{max}\left\vert \frac{r^2}{2}-\frac{3r^4}{4R^2}+\frac{3r^6}{6R^4} -\frac{r^8}{8R^6} \right\vert_0^R \\[5px]
&=\frac{1}{8}\pi\rho~R^2~v^3_\text{max} \\[5px]
\end{align}

Da die maximale Geschwindigkeit v_max gemäß Gleichung (\ref{vmax}) soppelt so groß ist wie die mittlere Strömungsgeschwindigkeit c, ergibt sich folgende Strömungsleistung:

\begin{align}
&P_\text{kin,2}=\frac{1}{8}\pi\rho~R^2~(2c)^3\\[5px]
& \boxed{P_\text{kin,2}=\pi\rho~R^2~c^3} \\[5px]
\end{align}

Die Strömungsleistung nach dem Ausbilden des parabelförmigen Geschwindigkeitsprofils ist also doppelt so groß wie davor. Offensichtlich muss man also zum Ausbilden des parabolischen Geschwindigkeitsprofils nochmals dieselbe Arbeit (pro Zeiteinheit) in die Strömung stecken wie zuvor nötig war, um die konstante Einlaufgeschwindigkeit zu erhalten.

Salopp formuliert, bildet sich bei kurzen Rohren also deshalb kein parabelförmiges Geschwindigkeitsprofil aus, weil die Energie die hierfür nötig wäre, innerhalb der relativ kurzen Strömungszeit nicht aufgebracht werden kann. Deshalb steigt mit zunehmender Geschwindigkeit (Reynolds-Zahl) auch die mindestens erforderliche Rohrlänge.