The Van der Waals equation describes the relationship between pressure, volume and temperature for real gases.
Ideal gas law
In thermodynamic processes, gases are often considered as ideal gases for simplicity. Depending on the gas mass enclosed in a certain volume, this gas generates a certain pressure as a function of the temperature. The relationship between gas mass m, gas volume V, gas temperature T and the resulting gas pressure p is described by the so-called ideal gas law (in which Rm denotes the universal gas constant, which is independent of the type of gas):
\begin{align}
\label{ideal}
&\boxed{p \cdot V = n \cdot R_\text{m} \cdot T} ~~~~~\text{ideal gas law}\\[5px]
\end{align}
Ideal gases are based on the assumption that the gas molecules are point masses, i.e. they have no spatial expansion. However, the molecules in real gases have a certain volume (size) that must be taken into account. Furthermore, in the conception of ideal gases, it is assumed that no attractive forces act between the molecules. In reality, however, the gas particles influence each other through their mutual attraction.
Both the size of the gas molecules and their mutual attraction make a modification of the ideal gas law necessary when it comes to the description of real gases. This finally results in the so-called Van der Waals equation, which is described in more detail below.
Taking into account the attractive force of the molecules
We consider a real gas confined in a container. The gas molecules exert a small attraction on each other. At a sufficiently large distance from the wall, the gas molecules are “surrounded” by neighboring molecules. Since, on time average, the attractive force exerted by the molecules is symmetrical in all directions, such a particle experiences no resultant force. Of course, the same argumentation is valid for any other particle as long as it is not near the wall.
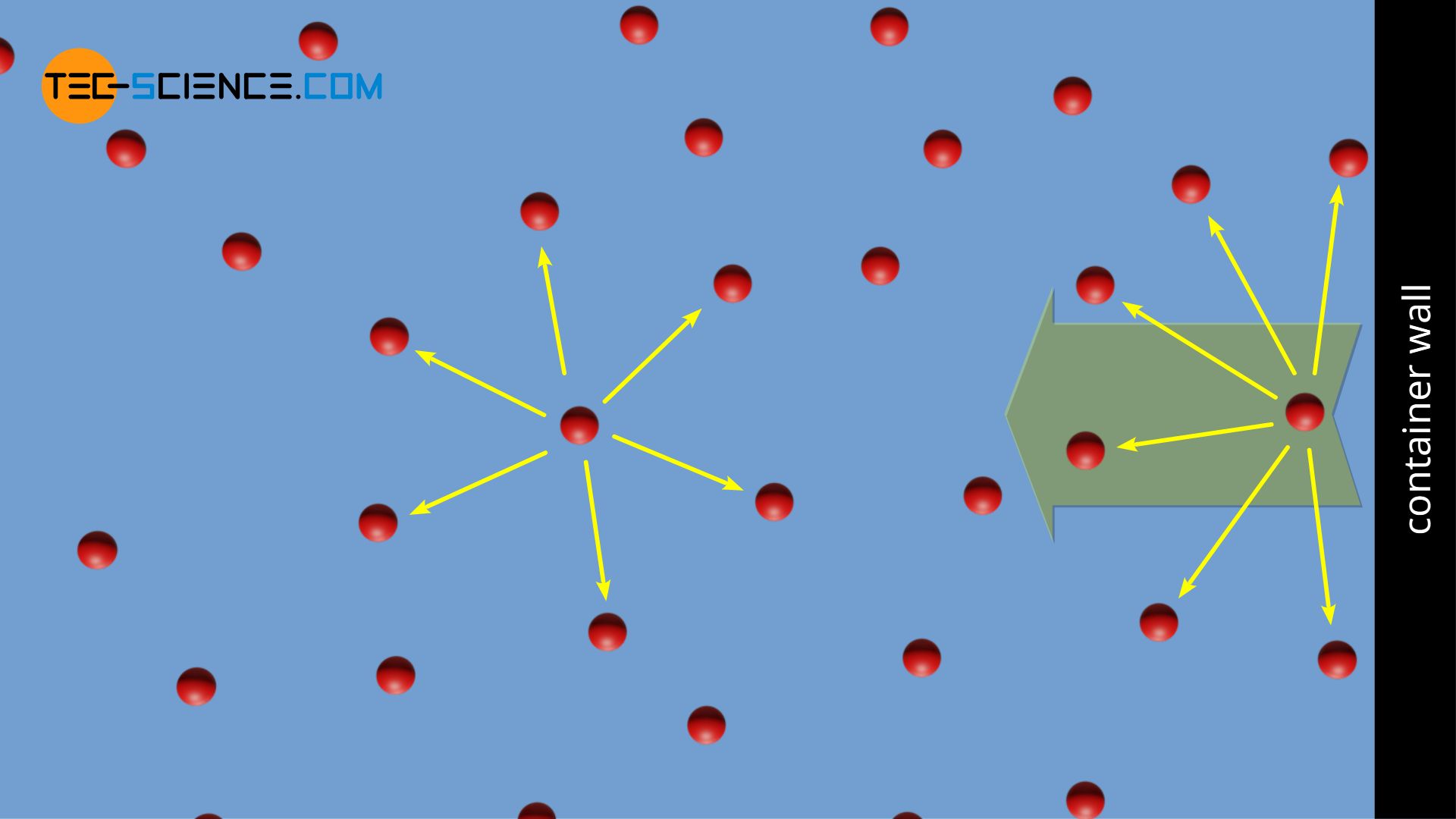
However, the situation is different if a gas molecule is near the wall. For such a molecule, there are more particles away from the wall. Thus, this molecule experiences a resultant force which is directed away from the wall. Therefore, if a gas molecule flies towards the container wall, it is slowed down somewhat by the resultant force. The impulse during the collision with the wall is thus reduced. However, this impulse accounts for the measurable pressure in a gas (see article Pressure in gases), which is reduced by the deceleration of the molecules just before they hit the wall.
Taking into account the mutual attraction of the molecules, the measurable pressure p in a gas is therefore lower by an amount Δp than if the gas were considered an ideal gas (pressure pideal):
resp.
\begin{align}
\label{pi}
& p < p_\text{ideal} ~~~\Rightarrow~~~ \underline{p_\text{ideal} = p + \Delta p} \\[5px]
\end{align}
The phenomenon that for an ideal gas the pressure pideal is greater by an amount Δp than if this gas were considered as a real gas (pressure p) is mainly determined by the volumetric particle density n/V (n denotes the amount of substance). This pressure difference Δp, is also called internal pressure. Empirical studies show that the internal pressure Δp is proportional to the square of the particle density (n/V)²:
\begin{align}
\label{dp}
& \Delta p \sim \left(\frac{n}{V}\right)^2 ~~~\Rightarrow~~~ \boxed{\Delta p = a \cdot \left(\frac{n}{V}\right)^2} ~\text{internal pressure}\\[5px]
\end{align}
For the mathematical description of the internal pressure, a proportionality constant “a” is introduced, which depends on the gas type and is determined from experiments. All in all, it can thus be stated that the pressure pideal of a gas considered as ideal is higher by the value a⋅(n/V)² than the pressure of the real gas. If equation (\ref{dp}) is put into equation (\ref{pi}), the following relationship between the ideal gas pressure and the real gas pressure is evident:
\begin{align}
\label{pp}
& \boxed{p_\text{ideal} = p + a \cdot \left(\frac{n}{V}\right)^2} \\[5px]
\end{align}
Taking into account the volume of the molecules
For an ideal gas, whose molecules can be assumed as (infinitesimally small) mass points, in principle the entire geometrical gas volume V is available for their motion. For real gases, however, the volume of the molecules (spatial dimension of the molecules) must be taken into account. Thus, the individual gas molecules effectively have less volume available for their motion where they can freely move.
The center of mass of a molecule can obviously approach the container wall (or any other boundary surface) only to a minimum distance, which corresponds to the radius of the real gas molecule. The white hatched areas in the figure below therefore represent excluded volumes into which the centers of mass of the molecules cannot move. This reduces the volume available for the movement of the molecules.
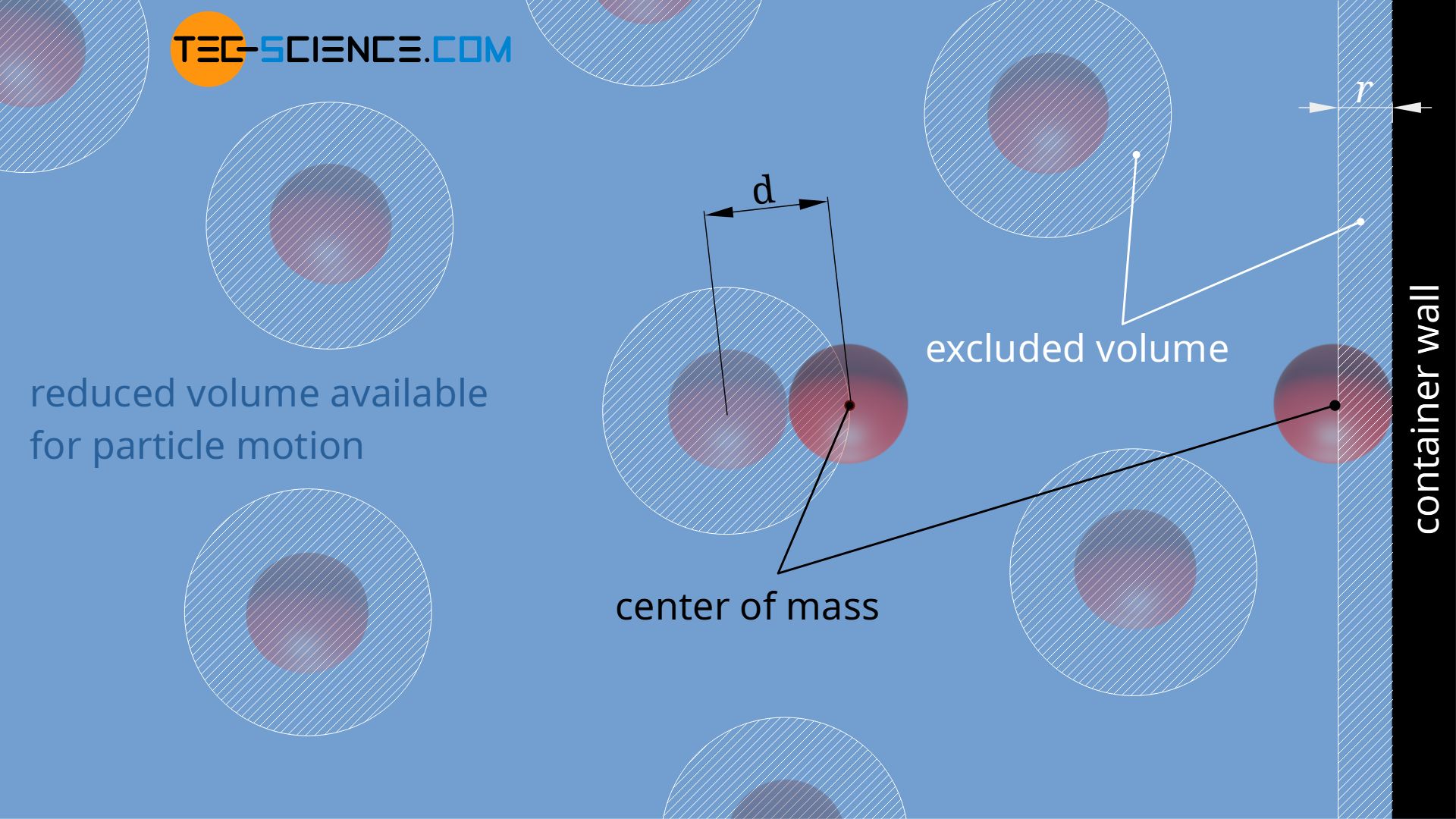
However, excluded volumes are formed not only near the container wall, but also around the molecules. The centers of mass of two molecules can approach each other up to the molecule diameter d at the most. If a molecules falls below this distance, a collision would occur. Therefore, the available volume for the molecules is further limited by the excluded volumes around the centers of mass of the molecules.
If the macroscopically measurable volume is denoted by V and the reduction of the volume due to the excluded volumes is denoted by ΔV, the effective gas volume Veff, within which the molecules can move freely, is obtained as follows:
\begin{align}
\label{ve}
& V_\text{eff} = V – \Delta V \\[5px]
\end{align}
The excluded volume at the container wall can be neglected compared to the excluded volumes around the molecules due to the vast number of molecules. Therefore, the reduced volume ΔV is determined only by the excluded volumes around the gas particles. Thus, the more molecules a gas contains, the larger the reduced volume become, i.e. the reduction in volume ΔV is proportional to the amount of substance n:
\begin{align}
\label{dv}
& \Delta V \sim n ~~~\Rightarrow~~~ \boxed{\Delta V = b \cdot n} ~\text{excluded volume} \\[5px]
\end{align}
Here, too, a proportionality constant “b” has been introduced to describe the available volume to the molecules quantitatively; this constant also depends on the type of gas and must be determined experimentally. If equation (\ref{dv}) is put into equation (\ref{ve}), the following relationship between the geometrically measurable volume V and the effectively available volume Veff is evident:
\begin{align}
\label{veff}
& \boxed{V_\text{eff}= V – b \cdot n} \\[5px]
\end{align}
The reduction of the volume available to the molecules has the opposite effect on the pressure as the consideration of the attractive force between the molecules. In an ideal gas, a reduction of the available volume would correspond to a compression, which leads to an increase of the pressure. Unlike the mutual attraction between the molecules, the excluded volume therefore leads to an increase of the pressure in real gases compared to ideal gases. However, both effects do not cancel each other out, since both follow different laws (see volume-pressure diagram below)!
Van der Waals equation
At this point, one can now use the ideal gas law (\ref{ideal}) to account for both the excluded volume and the internal pressure. It is first considered that in a real gas obviously not the entire geometric gas volume is available for the gas molecules, but only the effectively available volume Veff:
\begin{align}
&\color{red}{p_\text{ideal}} \cdot \color{blue}{V_\text{eff}} = n \cdot R_\text{m} \cdot T \\[5px]
\end{align}

In a next step, we put in the relations valid for the real gas according to equation (\ref{pp}) and equation (\ref{veff}):
\begin{align}
&\boxed{\color{red}{\left[p+a \cdot \left(\frac{n}{V}\right)^2\right]} \cdot \color{blue}{\left(V- b \cdot n \right)} = n \cdot R_\text{m} \cdot T} ~~~\text{Van der Waals equation} \\[5px]
\end{align}
This equation is finally called the Van der Waals equation and describes the behavior of real gases taking into account the volume of the molecules and their mutual attraction. Note that neglecting the internal pressure (a=0) and the excluded volume (b=0), the Van der Waals equation becomes the ideal gas law! Also for high temperatures or low pressures, the values obtained from the Van der Waals equation approach more and more the values from the ideal gas law.
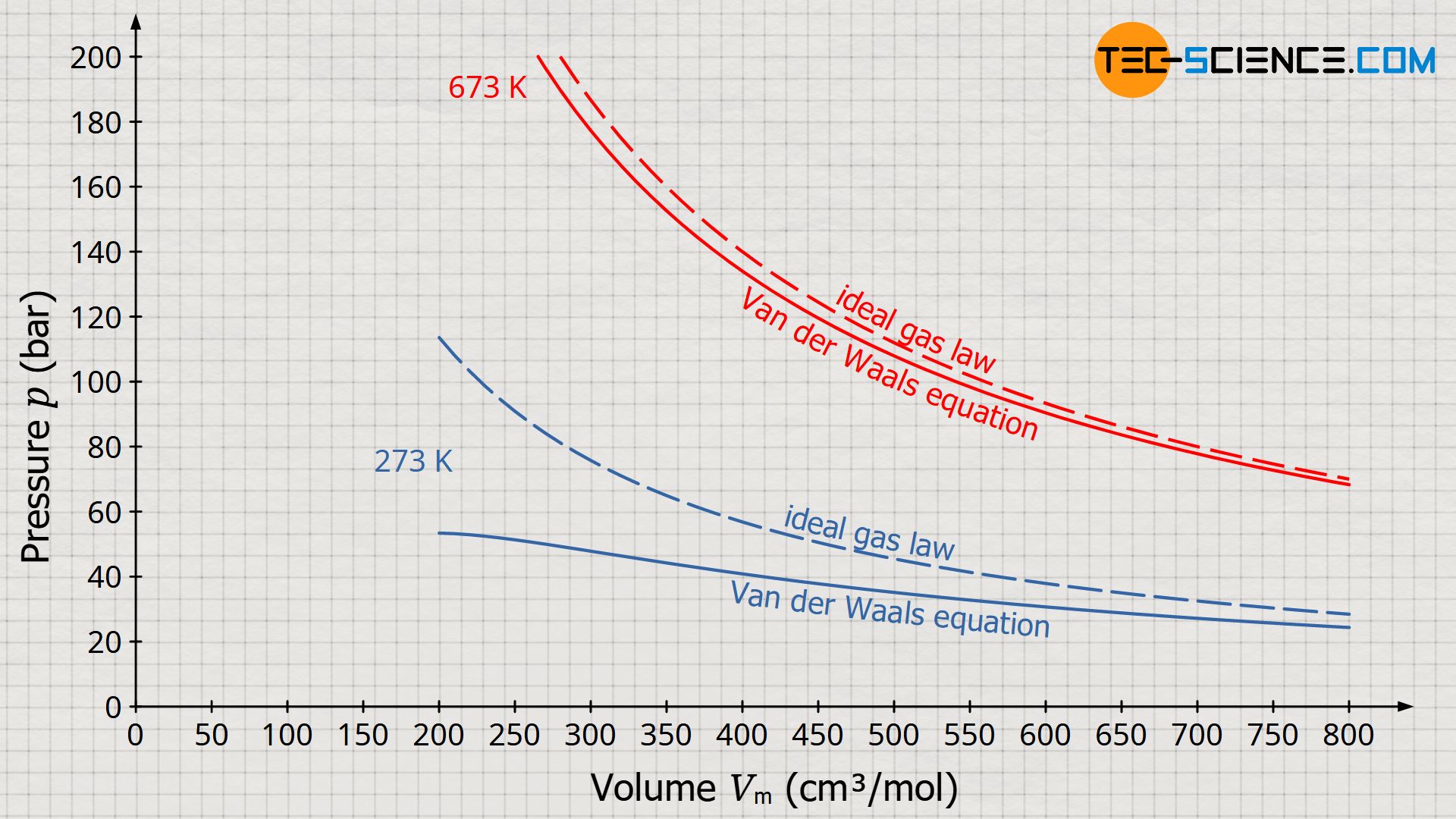
The Van der Waals equation is a modification of the ideal gas law and takes into account both the volume of the gas molecules and the attractive forces acting between them!
The Van der Waals equation can also be expressed using the molar volume Vm=V/n (quotient of geometric volume V and amount of substance n as “volume per unit mole”):
\begin{align}
&\boxed{\color{red}{\left(p+\frac{a}{V_\text{m}^2}\right)} \cdot \color{blue}{\left(V_\text{m} – b\right)} = R_\text{m} \cdot T} ~~~\text{where}~~~\boxed{V_\text{m}=\frac{V}{n}}~~\text{molar volume} \\[5px]
\end{align}
The table below shows for selected gases the experimentally determined values for the internal pressure “a” and the excluded volume “b”. Note that these quantities are generally not constants, but depend on pressure and temperature. They are therefore only approximate values. Especially at high pressures, where the gas molecules are compressed to a very small volume, there are strong deviations from the constants given below.
If, for example, the pressure becomes so great that the molar volume Vm becomes smaller than the excluded volume b, the Van der Waals equation obviously fails, since the left-hand side of the equation then becomes negative; the right-hand side, however, always remains positive. However, experiments show that the molar volume of real gases can indeed be smaller than the excluded volume, since the gas molecules are not, as assumed, rigid spheres which can no longer be compressed further when they are “touching” each other.
| Type of gas | Internal pressure a (10-3 J⋅m³/mol²) | Excluded volume b (10-6 m³/mol) |
|---|---|---|
| Ammonia (NH3) | 424 | 37 |
| Argon (Ar) | 136 | 32 |
| Chlorine (Cl2) | 655 | 56 |
| Helium (He) | 3.45 | 24 |
| Carbon dioxide (CO2) | 365 | 43 |
| Air | 136 | 37 |
| Methane (CH4) | 230 | 43 |
| Neon (Ne) | 21 | 17 |
| Propane (C3H8) | 93 | 90 |
| Oxygen (O2) | 138 | 32 |
| Nitrogen (N2) | 141 | 39 |
| Water (H2O) | 553 | 30 |
| Hydrogen(H2) | 25 | 27 |
With the help of the Van der Waals equations, not only can more precise statements be made about the behavior of real gases, but this equation also provides an explanation of why gases liquefy at high pressures. The article Explanation of liquefaction using the Van-der-Waals-equation discusses this in more detail.