Isochoric process in a closed system

In this article, learn more about the calculation of pressure, temperature, work and heat in an isochoric process in a closed system.

A change of state of a gas in which the volume does not change is also called an isochoric process. This means that the same volume applies to all the states through which the gas passes between the initial and final state.

How to achieve an isochoric process

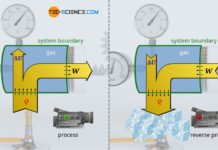
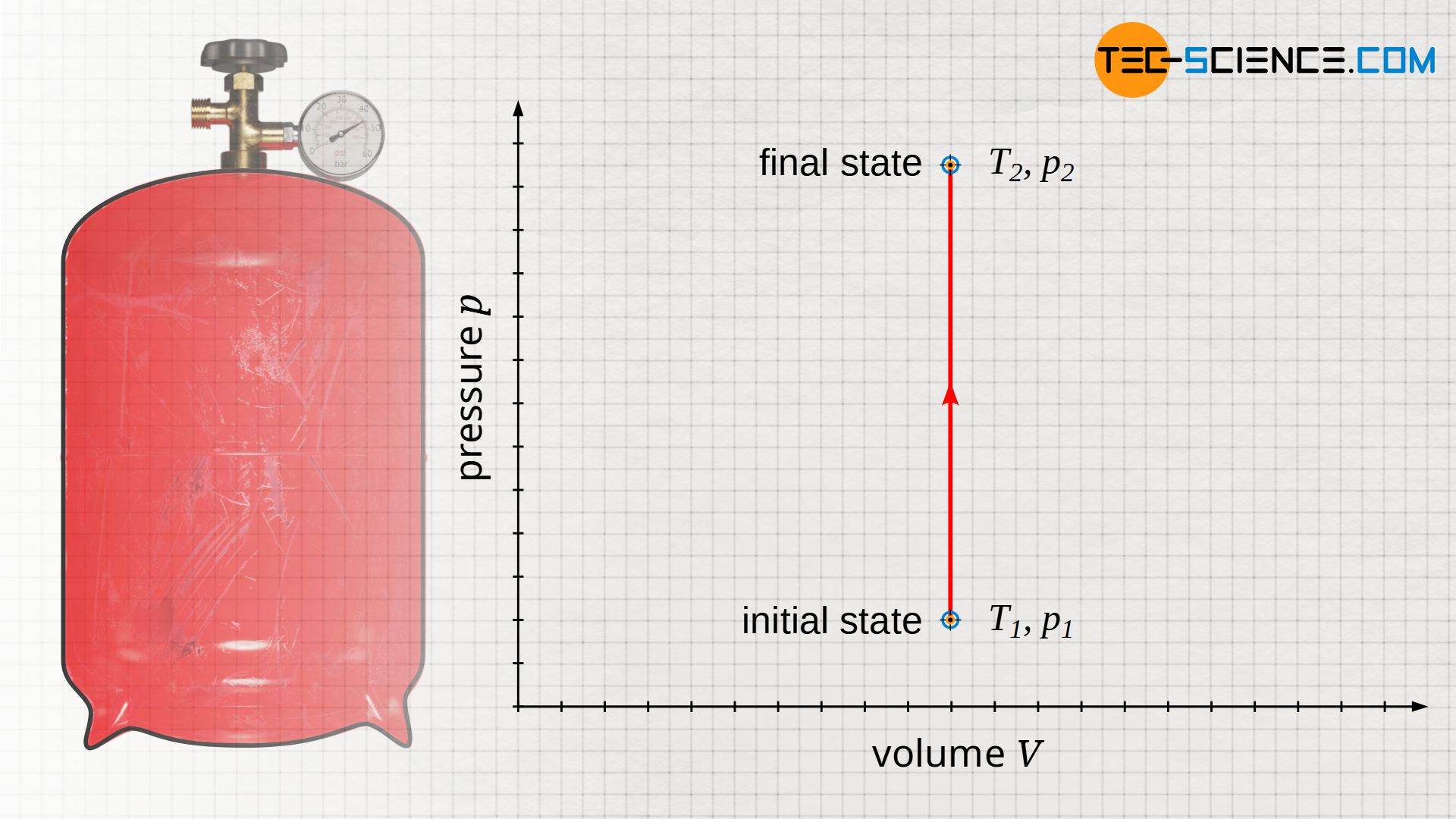
An isochoric change of state in a closed system can be found, for example, in a sealed gas cylinder filled with air, which heats up in summer due to solar radiation. The gas volume is given by the geometric dimensions of the bottle. Neglecting the small thermal expansion of the bottle, the bottle volume and thus the gas volume remains constant during heating. The change in state of the gas therefore takes place at constant volume.

Illustration in the volume-pressure diagram

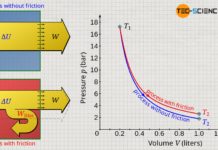
If heat is now absorbed by the gas due to solar radiation, the gas temperature will rise from T₁ to T₂. This is also associated with an increase in pressure from p₁ to p₂. If this isochoric process is illustrated in a volume-pressure diagram, a vertical line results from the initial pressure p₁ to the final pressure p₂ at constant volume V.

Relationship between pressure and temperature (law of Amontons)

In an isochoric process, the pressure increases proportionally with the temperature. However, this statement only applies if the temperature is given in the unit Kelvin. A doubling of the temperature in an isochoric heating thus also means a doubling of the gas pressure. This proportionality is equivalent to the statement that pressure and temperature always have a constant ratio. This phenomenon is also referred to as Amontons’ law:

\begin{align}
&p \sim T ~\Rightarrow~ {p \over T} = \text{constant}
\end{align}

Any two states within an isochoric process are consequently linked by the constant quotient of pressure and temperature:

\begin{align}
\label{1}
\boxed{ {p_1 \over T_1} = {p_2 \over T_2} } ~\text{law of Amontons}
\end{align}

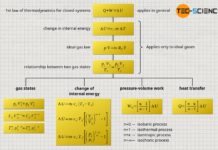
Calculation of the change in internal energy

For ideal gases, the change in internal energy ΔU results independent of the thermodynamic process only on the basis of the temperature change ΔT=T₂-T₁:

\begin{align}
\label{2}
\boxed{ \Delta U = c_\text{v} ~ m ~ \left(T_2-T_1 \right)} = c_\text{v} ~ m ~ T_1 \left({T_2 \over T_1}-1 \right) = c_\text{v} ~ m ~ T_1 \left({p_2 \over p_1}-1 \right)
\end{align}

In this equation c_v denotes the specific heat capacity and m the mass of the gas. The change in internal energy can also be determined by the initial and final pressure. For this purpose, equation (\ref{1}) must be used in equation (\ref{2}). In doing so, T₁ is first factored out in equation (\ref{2}), so that the quotient of the temperatures T₂/T₁ results. According to equation (\ref{1}), the ratio of the temperatures also corresponds to the ratio of the pressures (T₂/T₁=p₂/p₁).

Calculation of the pressure-volume work

Since the gas volume does not change during the isochoric process (ΔV=0), no pressure-volume work is done by the gas or on the gas (W_v=0). This is also evident from the pressure-volume diagram. Due to the vertical p(V)-line, there is no area under the curve and thus no volume-pressure work (note that the area under the p(V)-curve – if it exists – represents the pressure-volume work).

\begin{align}
\label{3}
\boxed{ W_\text{v} = 0}
\end{align}

Calculation of the transferred heat

Finally, the first law of thermodynamics can be used to calculate the heat absorbed by the gas or released by the gas during an isochoric process.

\begin{align}
\boxed{W_\text{v} + Q = \Delta U} ~~~ \text{first law of thermodynamics}  \\[5px]
\end{align}

Since no (pressure-volume) work is done in an isochoric process (W_v=0), the heat Q corresponds to the change of the internal energy ΔU. This is also clear, because into what other form should the transferred heat be converted, when apparently not into mechanical work? Thus, the heat supplied to the gas or released by the gas can only result in a change of the internal energy. The heat in an isochoric process is therefore determined in the same way as the change of the internal energy:

\begin{align}
&Q = \Delta U – \underbrace{W_\text{v}}_{=0} = \Delta U \\[5px]
&\boxed{Q = \Delta U}= c_\text{v} \cdot m \cdot \Delta T = c_\text{v} ~ m ~ T_1 \left({p_2 \over p_1}-1 \right)
\end{align}