Blackbody radiation (cavity radiation) is the thermal radiation of a blackbody, i.e. a body that absorbs all incident radiation.
Blackbody
When white light hits an opaque object, a certain part of that light is always absorbed and the rest is reflected. Depending on which wavelengths are absorbed, the reflected light consists of certain wavelengths. These reflected wavelengths determine the perceived color of the object.
A green leaf absorbs almost all wavelengths except the green wavelength range between 500 nm and 550 nm. Thus, the reflected light contains exactly the wavelength range that gives us the green color impression.

If, on the other hand, an object absorbs all incident wavelengths of visible light, then obviously no visible radiation is reflected. The object appears black to us under normal conditions. A black object therefore does not emit any visible radiation. An object that absorbs all incident radiation is therefore also called a blackbody (or black body). A perfect black body, however, only exists in the ideal conception. In reality, every object will always reflect a part of the incident radiation. That’s why even black objects often show slight shading. For this reason, the charcoal shown in the figure below also shows slight shading on the left hand side.

A blackbody is an idealized object that absorbs all incident electromagnetic radiation!
Thermal radiation
One could now jump to the conclusion that a blackbody does not emit any electromagnetic radiation. From an energetic point of view, however, this conclusion is quickly disproved. Electromagnetic radiation is always connected with radiant energy, depending on the wavelength. If this energy is absorbed by an object, then the absorbed energy cannot simply disappear. The absorbed radiant energy becomes noticeable in a temperature increase of the object (increase of the internal energy)!
As long as a black body is irradiated and absorbs energy, its temperature would have to rise steadily. Experience shows, however, that objects placed in the sun and thus irradiated do not heat up permanently. It does not matter whether it is an ideal or a real black body. As long as the radiation is only partially absorbed, the temperature should rise steadily due to the permanently absorbed radiant energy.

In reality, however, one notices that the temperature of irradiated objects does not rise permanently. At some point a thermal equilibrium will be established. This also applies to black painted objects, which can be regarded as ideal black bodies in very good approximation. Objects that absorb radiant energy must therefore also somehow release energy again. Otherwise the forming of a thermal equilibrium could not be explained.
One could now think that an object placed in the sun is cooled by the surrounding air by convection or by thermal conduction with the ground. These heat transfers will certainly take place and contribute to the thermal equilibrium, but there must be another mechanism. This becomes apparent when one looks at an object in a vacuum. Thermal convection and conduction require particles that transport the thermal energy. In a vacuum, however, there are no particles, so that these heat transfers cannot take place. And yet one will notice that even irradiated bodies in a vacuum sooner or later come into a thermal equilibrium.
An everyday example is the earth. The earth is irradiated by the sun in the vacuum of space and absorbs part of the solar radiation. Obviously, there is no permanent heating of the earth. The earth is in a stable thermal equilibrium, which leads to an average surface temperature of about 15 °C. This thermal equilibrium in a vacuum can only be explained by the fact that the earth itself emits energy through electromagnetic radiation.
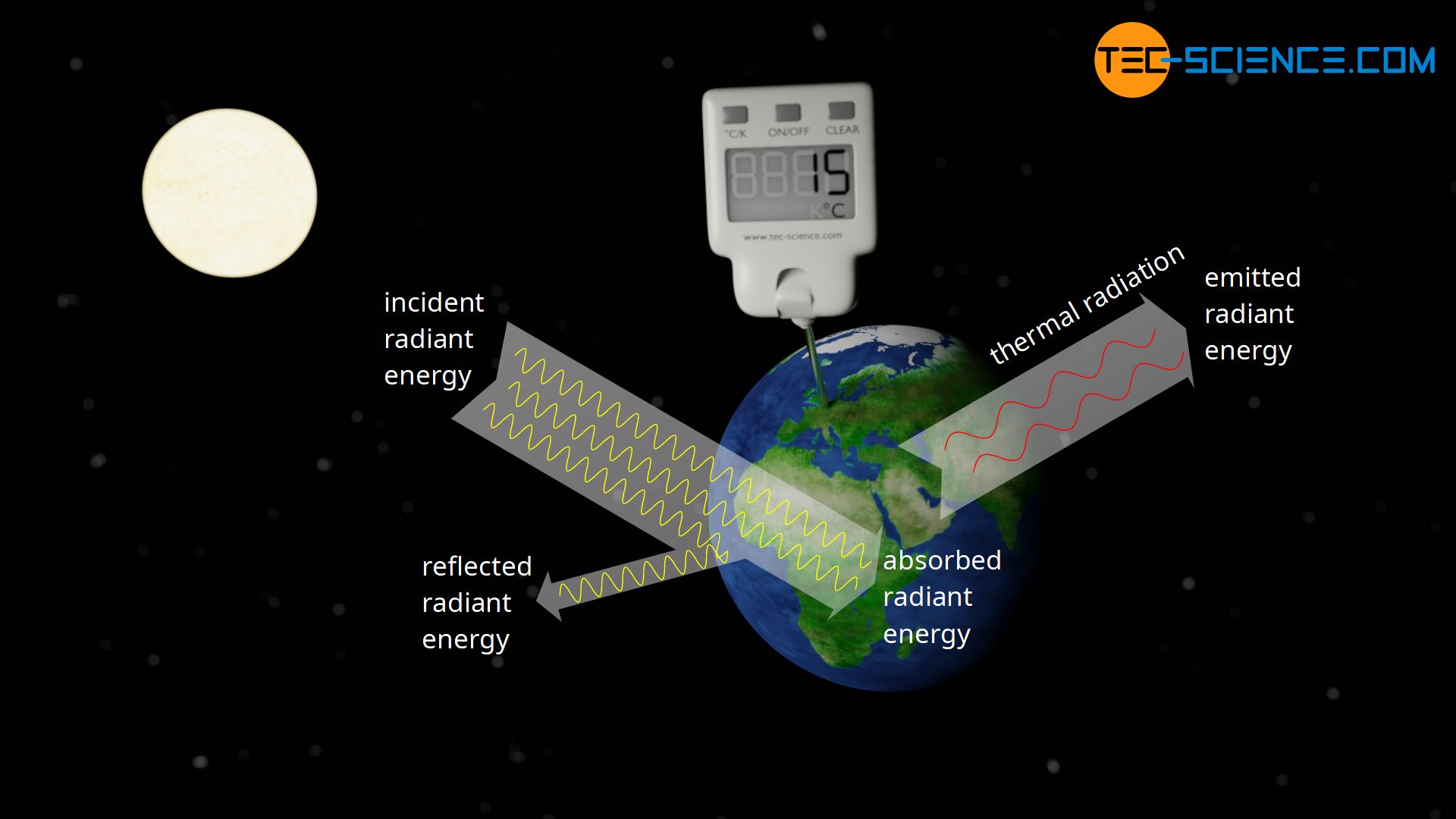
This radiation emitted by a body in thermal equilibrium is also referred to as thermal radiation. Thermal radiation occurs with all objects, not only those in vacuum! With very strongly heated objects as for example a glowing bar of metal, this thermal radiation can not only be felt very clearly, but can also be seen by the glowing reddish color!

In incandescent light bulbs, this thermal radiation is technically used to emit visible light. In fact, most of the thermal radiation in this case is emitted in the infrared wavelength range. In this wavelength range we cannot see the radiation, but we can still perceive it. We perceive the infrared radiation through our skin in the form of heat.
The emitted wavelength spectrum depends strongly on the temperature of the body. At low current and therefore low temperature, the filament is slightly reddish. At high current and therefore high temperature, the filament glows intensively yellowish. This spectral distribution of the wavelength as a function of temperature is discussed in more detail in the section on blackbody radiation.

Thermal radiation is the radiation emitted by a body in thermal equilibrium due to its temperature!
Note: Thermal radiation in the narrower sense is often referred to only as invisible radiation in the infrared range. In the broadest sense (and also in this article), the term thermal radiation refers to the entire emitted wavelength range of a body due to its temperature, i.e. the entire energetic radiation!
The generation of the thermal radiation can be explained by the oscillation of the atoms. In principle, every accelerated movement of charged particles leads to the generation of electromagnetic waves, i.e. radiation. The higher the temperature, the stronger and faster the particles vibrate and the more radiation is emitted (higher intensity). Only at absolute zero are there no atomic motions and the body does not emit any thermal radiation.
Thermal radiation comes from oscillations of the atoms!
Remark on the term blackbody
As already explained, an ideal black body must also emit thermal radiation. Otherwise it could not be explained why a complete absorption of radiant energy leads to a thermal equilibrium at some point! Even if by definition a blackbody absorbs all incident radiation, it still emits radiation. This is not reflected radiation, but radiation which the body emits “from inside” due to the oscillation of the atoms. See also the article Stefan-Boltzmann law.
Note that the definition of a blackbody is simply that all incident radiation is absorbed and not that it cannot emit any radiation itself! It can do this very well, but under ambient conditions this emitted radiation lies in the non-visible wavelength range (infrared radiation). The object therefore initially appears black to the eye, which is why it is called a black-body.
Only if the temperature is increased very strongly and the body starts to glow, radiation in the visible wavelength range is emitted. Even if the body now has a color depending on the temperature (“annealing colors”), this object is still called a blackbody by definition, since all incident radiation is still absorbed. So a blackbody does not necessarily have to be black! An impressive example is the sun. In fact, the sun is an almost perfect black body. Only due to the enormous temperature of 5778 K it appears incandescent in the sky.
The definition of a blackbody is not that it appears black under all circumstances, but that it absorbs all incident radiation! Depending on the temperature, even a supposedly black object emits visible radiation and “glows” in different colors!
Blackbody radiation
If an object is not heated too much, the thermal radiation emitted is in the infrared wavelength range. This infrared radiation is invisible to the human eye, which is why a blackbody actually appears black! With a thermal imaging camera, however, this thermal radiation can be made “visible”. One can then draw conclusions about the temperature from this.
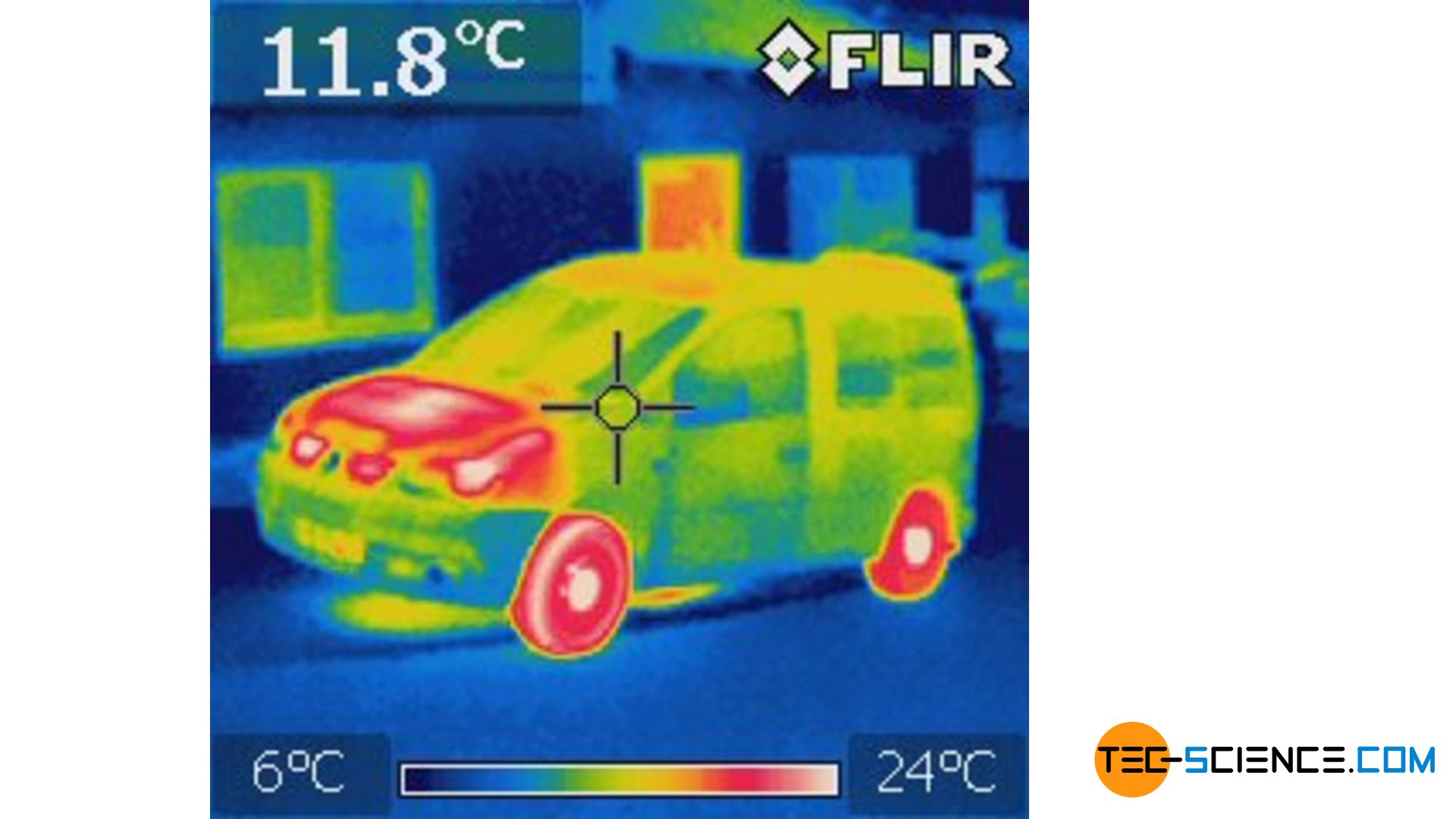
The emitted thermal radiation, however, changes its wavelength range with temperature. At sufficiently high temperatures, the emitted wavelength spectrum shifts into the visible range and even beyond (i.e. in the ultraviolet range). Even a supposedly “black” body then begins to “glow” in color. This glow is not reflected radiation but self-emitted radiation from “inside”!
This is where the blackbody comes into play. In order to examine the emitted radiation spectrum of an object, it is necessary that only the thermal radiation emitted by the body itself is actually measured and not the reflected radiation by other radiation sources. Therefore, the body to be examined must not reflect any radiation but must absorb all incident radiation. To examine the wavelength spectrum of thermal radiation (also known as spectral distribution), one needs a blackbody!
A blackbody is particularly suitable for the investigation of the spectral distribution of thermal radiation, since the radiation does not contain any reflecting parts of interference sources!
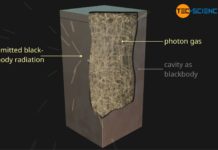
The thermal radiation of a blackbody is also called blackbody radiation.
The emitted thermal radiation of a black body is called blackbody radiation!
Realization of blackbodies in practice (cavity radiation)
In practice, a blackbody can be realized relatively easily in a very good approximation. For this purpose only a hole is drilled into a hollow object. If radiation enters the cavity through the hole, it is reflected several times by the walls. With each reflection a certain part of the radiation is always absorbed. After several reflections, the radiation is almost completely absorbed. Consequently, no more radiation exits through the hole (at least not the incident radiation). All incident radiation is “swallowed” by the cavity and the hole therefore appears black. The cavity can therefore be regarded as a blackbody in a very good approximation.

The figure above shows an upside-down flowerpot with a hole and an empty beverage can. Due to the absorbed incident radiation, the interiors appear black through the openings. Even with the beverage can made of highly reflective aluminium, almost no visible radiation gets to the outside! Even reflective materials such as metals can thus become a black hollow body in very good approximation. For this reason, blackbody radiation is often referred to as cavity radiation.

Note that the term black body actually refers only to the cavity or hole and not to the object itself! Because the body itself usually has a color, which is caused by reflections of the incident light. So the outside of the object is by no means a black body!
Even if no visible light is emitted from the cavity at first and therefore appears black, radiation in terms of thermal radiation is emitted due to the oscillation of the atoms. With a thermal imaging camera, this initially invisible blackbody radiation can be made visible in the form of infrared radiation (white areas in the illustration below).

Spectral distribution of blackbody radiation (Planck spectrum)
With cavity radiation, the emitted wavelength spectrum of different materials can now be examined at different temperatures. Due to the thermal resistance even at relatively high temperatures, it makes sense to use metals. Holes are then drilled into the hollow metal blocks. Through the holes the blackbody radiation can finally pass to the outside and the spectral distribution of the blackbody radiation can be determined with a detector. The temperature can be changed relatively easily by heating the metal blocks and the resulting effects on the spectral distribution can be examined.

The animation below shows the principle of cavity radiation, in which radiation enters through a hole, but no longer exits it due to absorption processes.
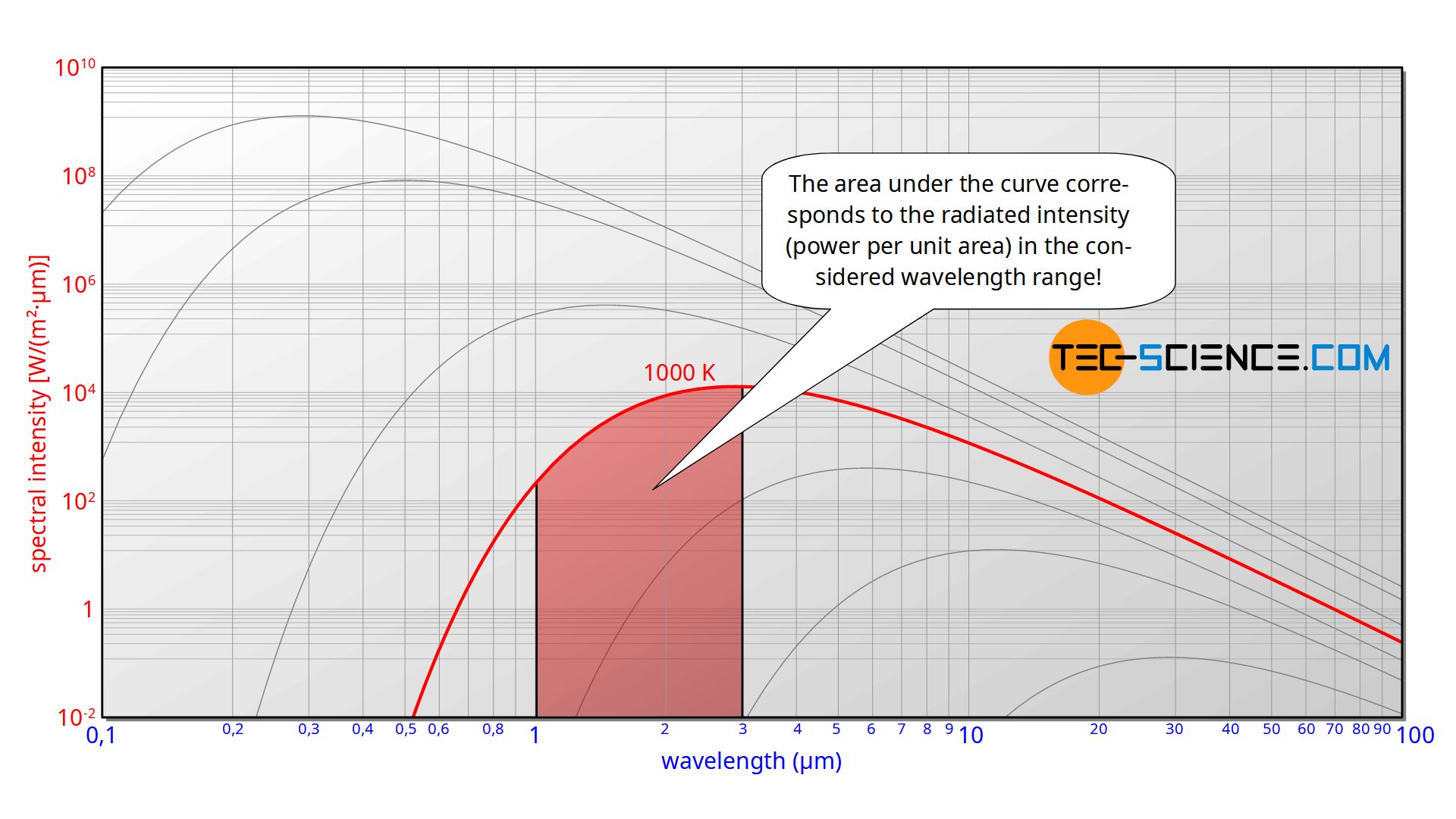
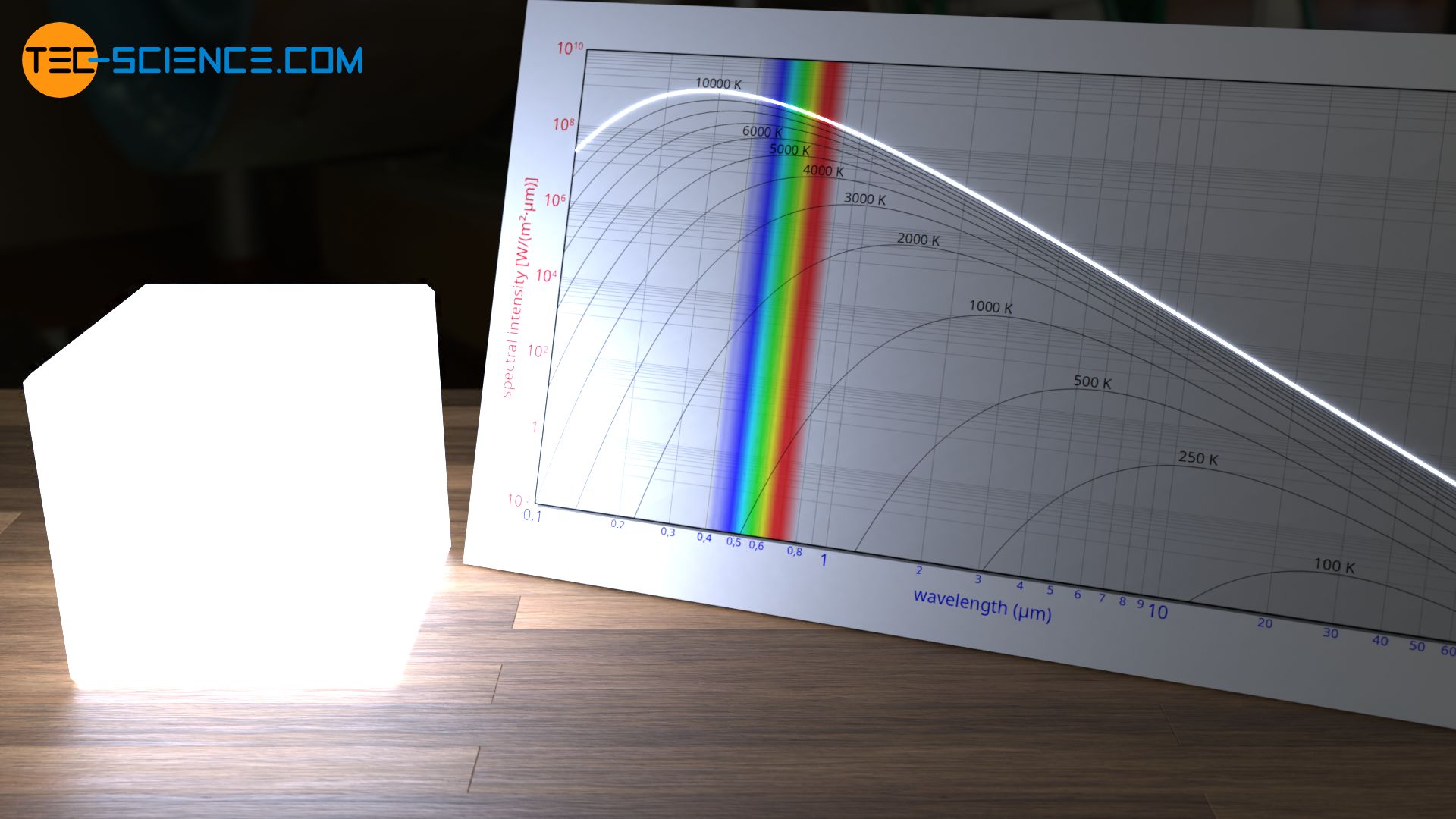
The evaluation of the experiment takes place with a diagram in which the so-called spectral intensity is plotted over the wavelength. In simplified terms, such a diagram indicates which wavelength is radiated with which intensity (radiant power per unit area). Usually a double logarithmic division is used in order to be able to cover a large wavelength range at the different temperatures.
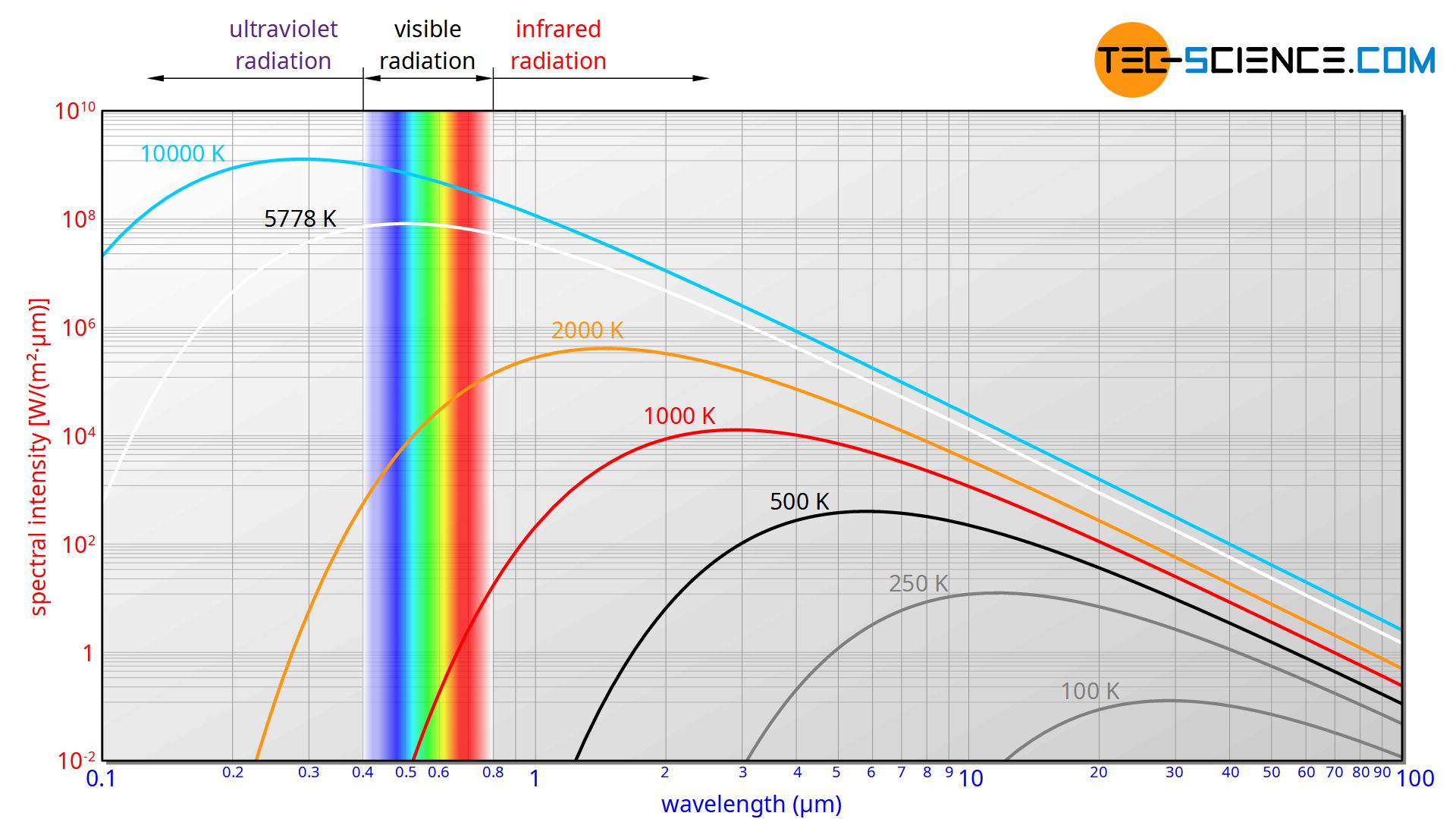
In the physical sense, the term intensity refers to the radiant power per unit area (surface power density), i.e. the radiant energy emitted per unit area and per unit time. In this case, area means the area of the opening to the cavity, since this opening acts as a source of radiation and thus as the actual black body. The intensity plotted in the diagram is related to the wavelength itself, since the intensity can always only be measured within a wavelength range and cannot be determined for an exact wavelength. This intensity per wavelength is therefore also referred to as spectral intensity. In such a diagram, the area under the curve corresponds to the intensity with which the radiation is perceived in the corresponding wavelength range. The area under the entire curve thus corresponds to the total radiated intensity.
The experiment shows that the emitted wavelength spectrum depends only on the temperature and not on the material. The cavity radiation of an aluminium block thus has the same spectral distribution as a steel or brass block.
The wavelength spectrum of blackbody radiation depends only on the temperature and not on the material!
A more detailed examination of the wavelength spectrum shows that the maximum spectral intensity shifts with increasing temperature to ever shorter wavelengths. At relatively low temperatures the maximum lies in the infrared range and the radiation is not visible to our eyes. However, with increasing temperature the spectrum shifts into the visible range. The hole or blackbody now begins to glow due to the visibly emitted radiation.
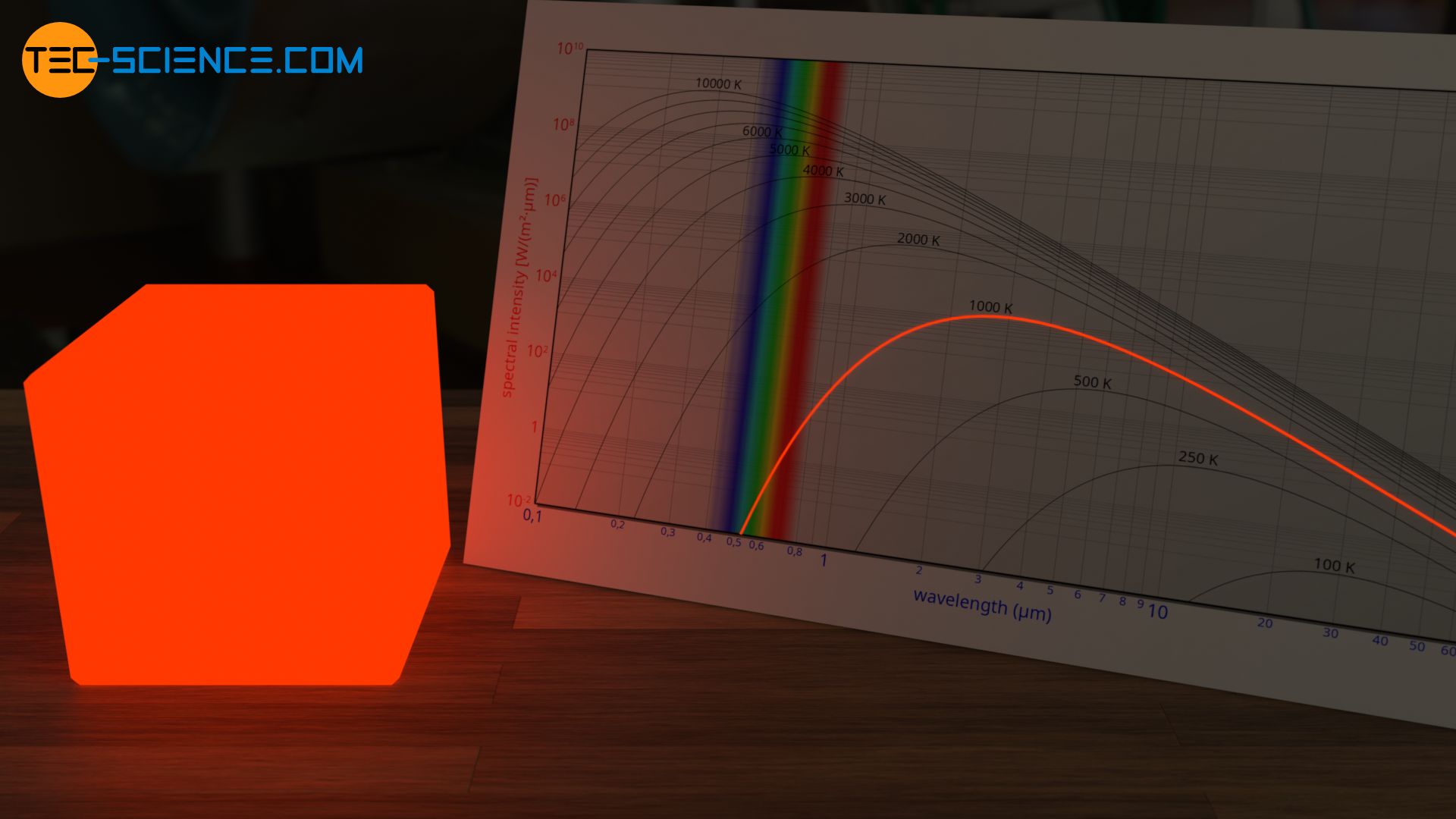
From approx. 1000 K it is a slightly reddish glow, as known from glowing metal. The figure below shows the glow of a heating element of a baking oven. The temperature is about 800 °C.

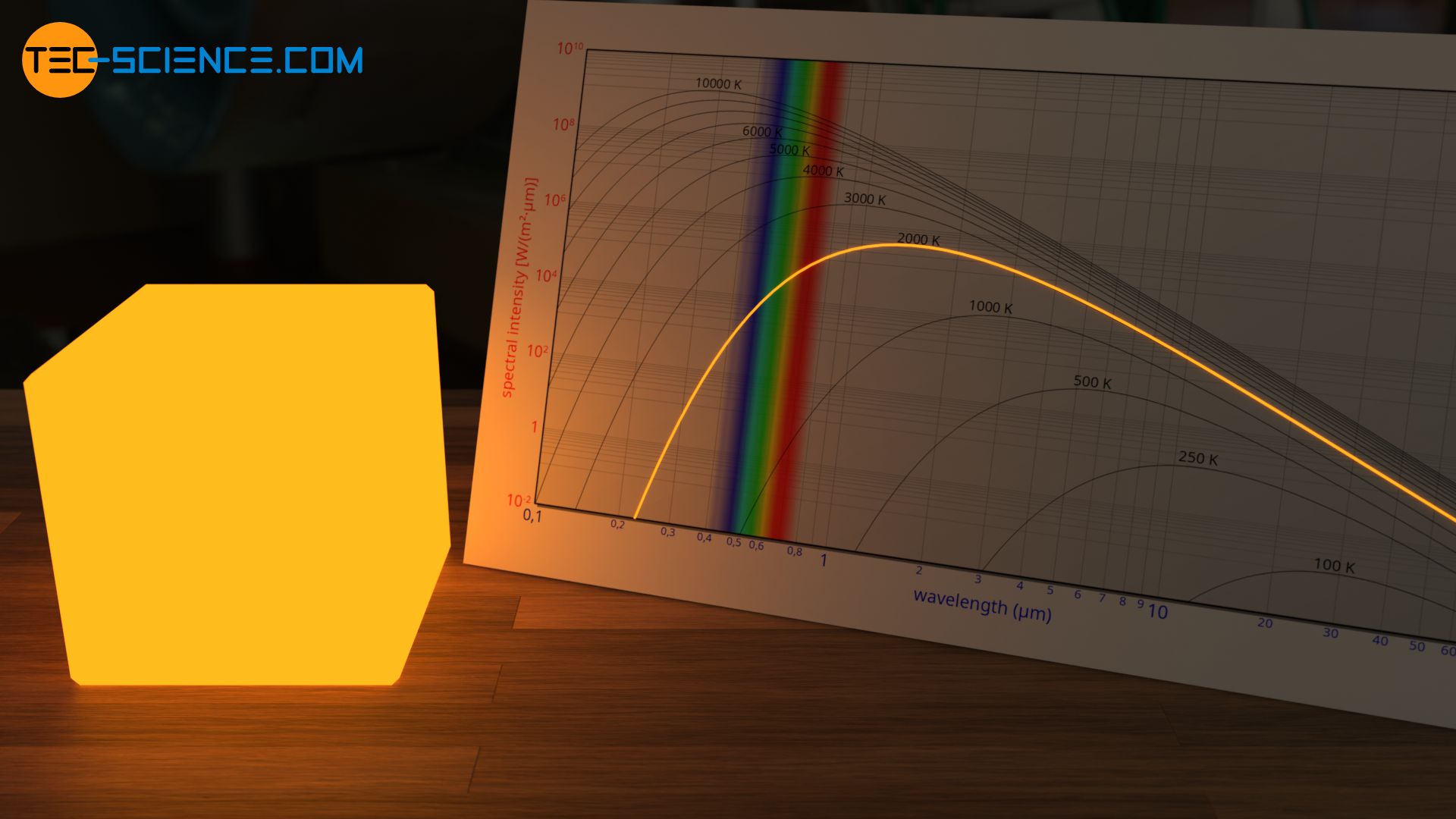
At 2000 K, the proportion of the yellow wavelength range in the spectrum has increased. The body tends to radiate yellowish. However, since the emitted intensity is relatively high in the entire visible range, all color receptors in our eyes are “overexposed”. In this case, all receptors are excited almost identically and the yellowish radiation usually appears white to our eye (see also article Color vision).
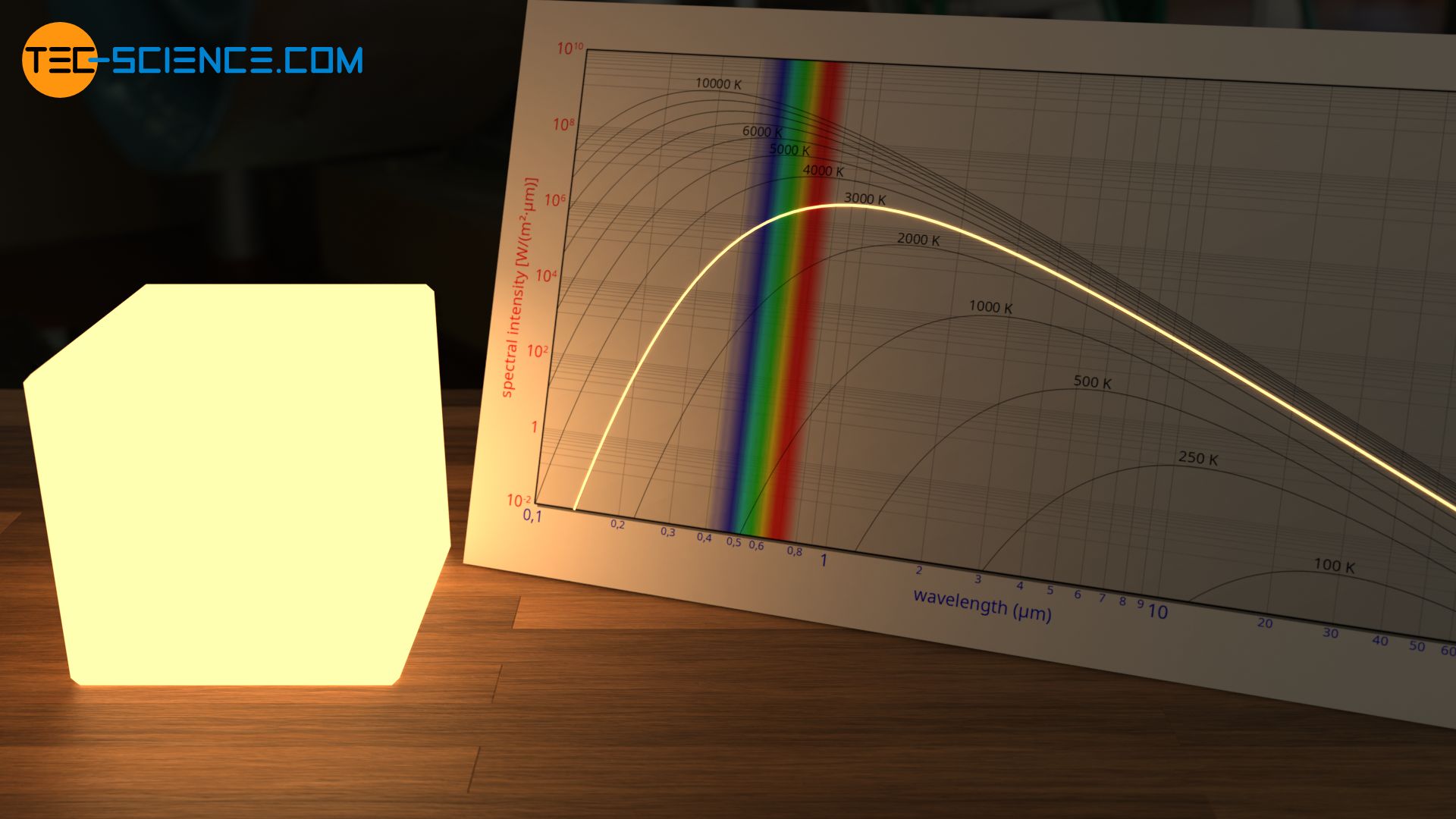
The white color of the electric arc during welding with temperatures of over 3000 K can also be explained by the overexposure of the color receptors in our eyes. In fact, the emitted spectrum is rather a yellowish wavelength spectrum. This yellowish color can only be perceived as such if the intensity is greatly reduced, e.g. if it is observed indirectly as scattered light on a white sheet of paper.

In addition, the spectral distribution shows that at such high temperatures of over 3000 K more ultraviolet radiation (UV radiation) is emitted. This explains the protective equipment required for welding, which not only protects the eyes but also the arms. Without covered arms one would get a “sunburn” by the UV radiation otherwise!
At even higher temperatures of about 6000 K, almost all visible wavelengths with the same intensity are present in the radiated spectrum. This radiation is therefore a white “color”. This also explains the white solar radiation, since the sun as an almost perfect blackbody has a surface temperature of 5778 K! The sun also radiates UV radiation to a not inconsiderable extent. Fortunately, however, a large part of this UV radiation is absorbed by the earth’s atmosphere.
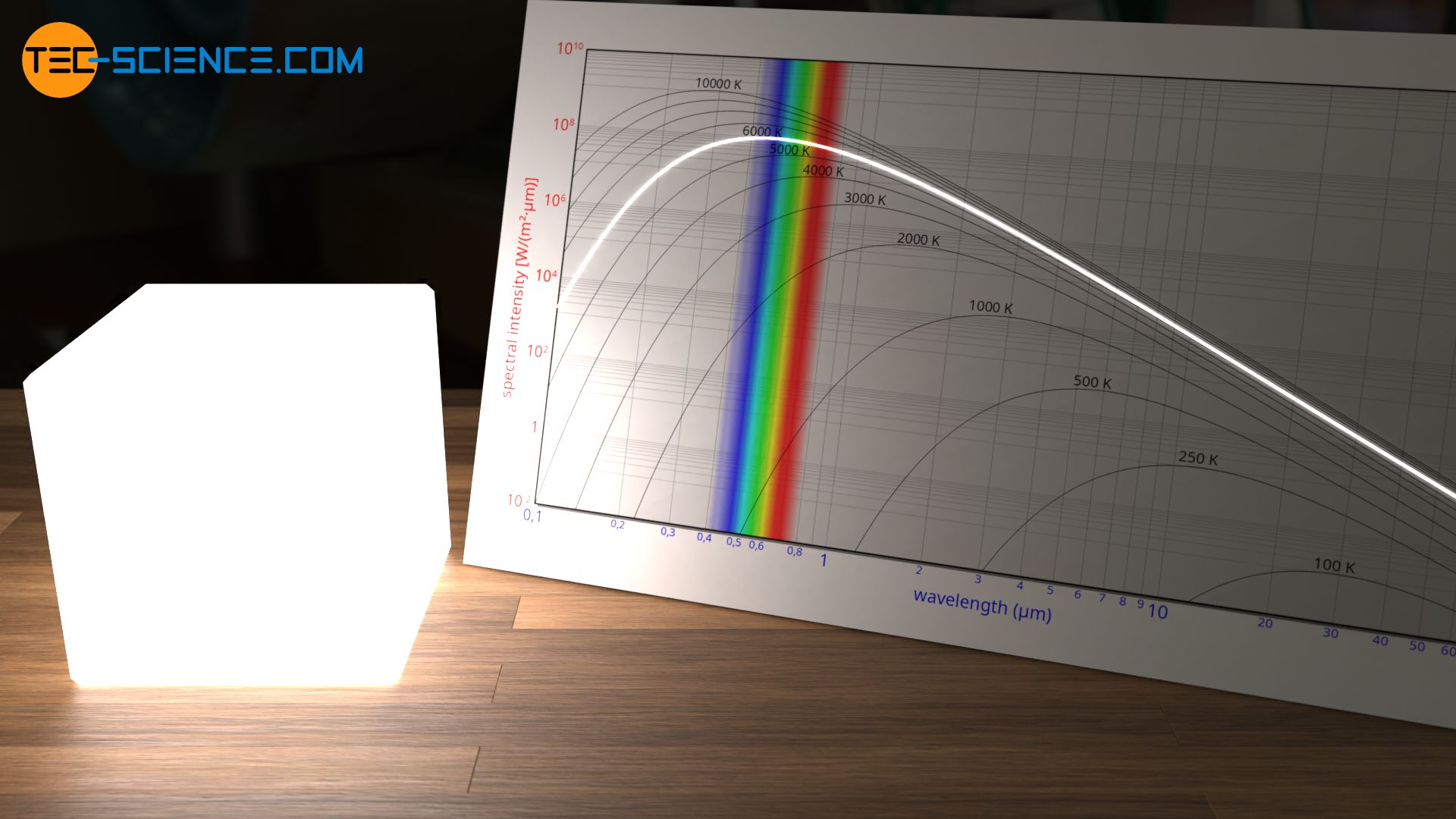

Significantly higher temperatures than our sun have so-called blue giants. Some of these astronomical objects have 50 times the mass of the sun. The surface temperatures can reach several 10,000 Kelvin. At these temperatures the blue wavelength range is more present in the radiated spectrum than the reddish parts. The light of such blue giants therefore appears bluish, which is the reason why such stars are called blue giants.
The mathematical description of blackbody radiation is discussed in the article Planck’s law of blackbody radiation.