The Stefan-Boltzmann law states that the radiant power of an object in thermal equilibrium is proportional to the fourth power of temperature and directly proportional to its surface!
Introduction
In the article Blackbody radiation it has already been explained in detail why every object emits radiation above absolute zero. This radiation is also called thermal radiation. Thermal radiation is caused by the motions of atoms that emit electromagnetic waves, i.e. radiation.
Thermal radiation can not only be proven by the fact that it is able to heat other objects, as one could derive from the term thermal radiation. At sufficiently high temperatures, the radiated wavelength spectrum shifts into the visible range and can thus be observed directly by the human eye. The reddish annealing of a heated metal rod during forging is, for example, the result of such a visible thermal radiation.

The visible glow of the filament of a light bulb at over 3000 °C is also a typical example which can be traced back to the phenomenon of thermal radiation. More than 90 % of the energy is radiated in the non-visible infrared range and can therefore only be perceived as heat. The remaining part, however, is in the visible wavelength spectrum and can be directly observed as a yellowish glow (a small part is also radiated as ultraviolet light).

Radiant power
As a heat lamp or a glowing steel block clearly shows, emitting radiation is obviously associated with emitting energy. How much radiant energy ΔQ an object emits per unit time Δt, i.e. how high its radiant power Φ is, depends mainly on the temperature T, but also on the area of the surface A as well as on the radiative property of the body (the so-called emissivity ε
\begin{align}
&\boxed{\Phi = \frac{\Delta Q}{\Delta t}}=\Phi(T,A,\varepsilon) \\[5px]
\end{align}
Note that the radiant power (also called radiant flux) does not only refer to the thermal energy in the infrared spectrum or to the radiated energy in the visible wavelength range, but to the energy related to the entire wavelength spectrum, i.e. to the entire energetic radiation!
If, for example, an incandescent light bulb is operated at low current, the temperature of the filament is correspondingly low. The light bulb does not only glow less but it also does not heat up as much. Overall, the radiant power is relatively low at low temperatures. With a large current, on the other hand, the filament heats up strongly and the temperature is correspondingly high. It then not only glows intensely yellow but also radiates infrared radiation to a high degree, which is clearly noticeable as heat. The higher the temperature of a body, the higher the radiant power is!

Note: The fact that the filament is weakly reddish at low temperature and bright yellow at high temperature is due to the wavelength spectrum emitted, which shifts to the yellowish range with increasing temperature (more information on this in the article Blackbody radiation).
In addition to the temperature, the area of the surface of the radiating body also influences the radiant flux. The larger the surface, the more atoms can vibrate and emit radiation. Note that radiation emitted by the atoms inside the body is directly reabsorbed by the surrounding atoms. Thus only the atoms on the surface are relevant for the radiation of the electromagnetic waves. If the surface is twice as large, the radiant power should therefore be twice as high.
More detailed studies by the physicists Josef Stefan and Ludwig Boltzmann at the end of the 19th century showed that the radiant power is actually directly proportional to the surface area of the emitting object. The influence of temperature on radiant power, on the other hand, is far greater. It increases with the fourth power of the absolute temperature. A doubling of the temperature from e.g. 1000 K to 2000 K thus increases the radiant power by a factor of 16! For an ideal thermal radiator, a so-called blackbody, the radiant power Φideal results as a function of temperature T and surface area A as follows:
\begin{align}
&\Phi_{ideal} \sim A \cdot T^4 \\[5px]
&\boxed{\Phi_{ideal} = \sigma \cdot A \cdot T^4} ~~~~~ \sigma = 5,670 \cdot 10^{-8} \frac{\text{W}}{\text{m²K}^4} \\[5px]
\end{align}
The Stefan-Boltzmann law states that the radiant power of an object in thermal equilibrium is proportional to the fourth power of temperature and directly proportional to its surface area!
The proportionality factor σ is called the Stefan-Boltzmann constant and is a universal constant, i.e. it does not depend on the material of the radiating object as long as the body absorbs all incident radiation and can therefore be regarded as a blackbody.
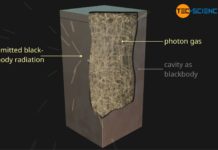
A black-body is an ideal thermal radiator that absorbs all incident radiation and therefore radiates at maximum power!
Why a black body is not only a perfect absorber of radiation but also a perfect emitter of radiation will be explained later.
If the radiant power Φ of the black body is related to its surface area A, then one also speaks of the so-called intensity I (surface power density). The intensity indicates the strength of the radiant power per unit area. The intensity of black-body radiation depends only on temperature:
\begin{align}
&I=\frac{\Phi}{A} = \frac{\sigma \cdot A \cdot T^4}{A} = \sigma \cdot T^4\\[5px]
&\boxed{I = \sigma \cdot T^4 } \\[5px]
\end{align}
The Stefan-Boltzmann law can be derived from Planck’s law or from a thermodynamic approach. You can read more about this in the linked articles.
Kirchhoff’s law of thermal radiation
In the following a blackbody is considered, which is irradiated by a heat lamp. By definition, the blackbody will absorb all incident radiation. The absorbed energy leads to an increase in temperature and the blackbody begins to emit more and more radiation. Finally, over time, a thermal equilibrium will be reached in which the temperature no longer rises. In thermodynamic equilibrium, the radiant energy emitted within a certain time (emitted radiant power Φe) must therefore be the same as the absorbed radiant energy (absorbed radiant power Φa):
\begin{align}
\label{kirch}
&\boxed{\Phi_a \overset{!}{=} \Phi_e} \\[5px]
\end{align}
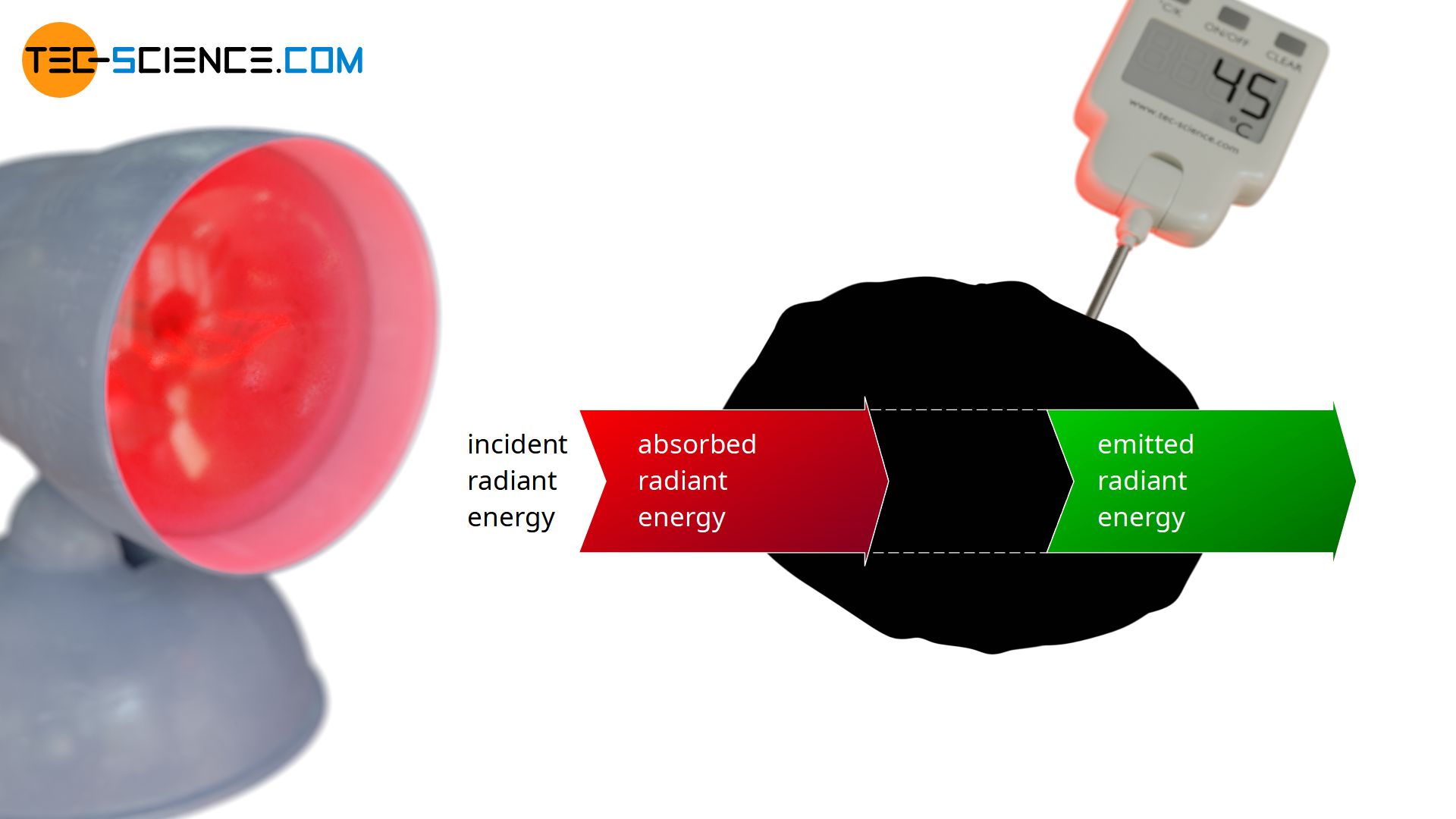
This radiation equilibrium between emitted radiation and absorbed radiation basically applies to every body in thermal equilibrium, including non-ideal black bodies that do not radiate at maximum power. After all, a constant temperature and thus a thermal equilibrium will be reached for every object after a certain time, in which emission and absorption must take place to the same extent. This law is also called Kirchhoff’s law of radiation.
Kirchhoff’s law of radiation states that in thermal equilibrium of a radiating body, emission and absorption take place to the same extent!
In the same way as the emitted radiant power increases with the fourth power of the temperature, the absorbed radiant power must also increase with the fourth power of the temperature. Otherwise there would be no thermal equilibrium. The law with which an ideal blackbody emits radiation according to the Stefan-Boltzmann law must therefore also apply to the absorbed radiation in thermal equilibrium!
\begin{align}
&\boxed{\Phi_{a,ideal} = \Phi_{e,ideal} = \sigma \cdot A \cdot T^4} \\[5px]
\end{align}
Real bodies
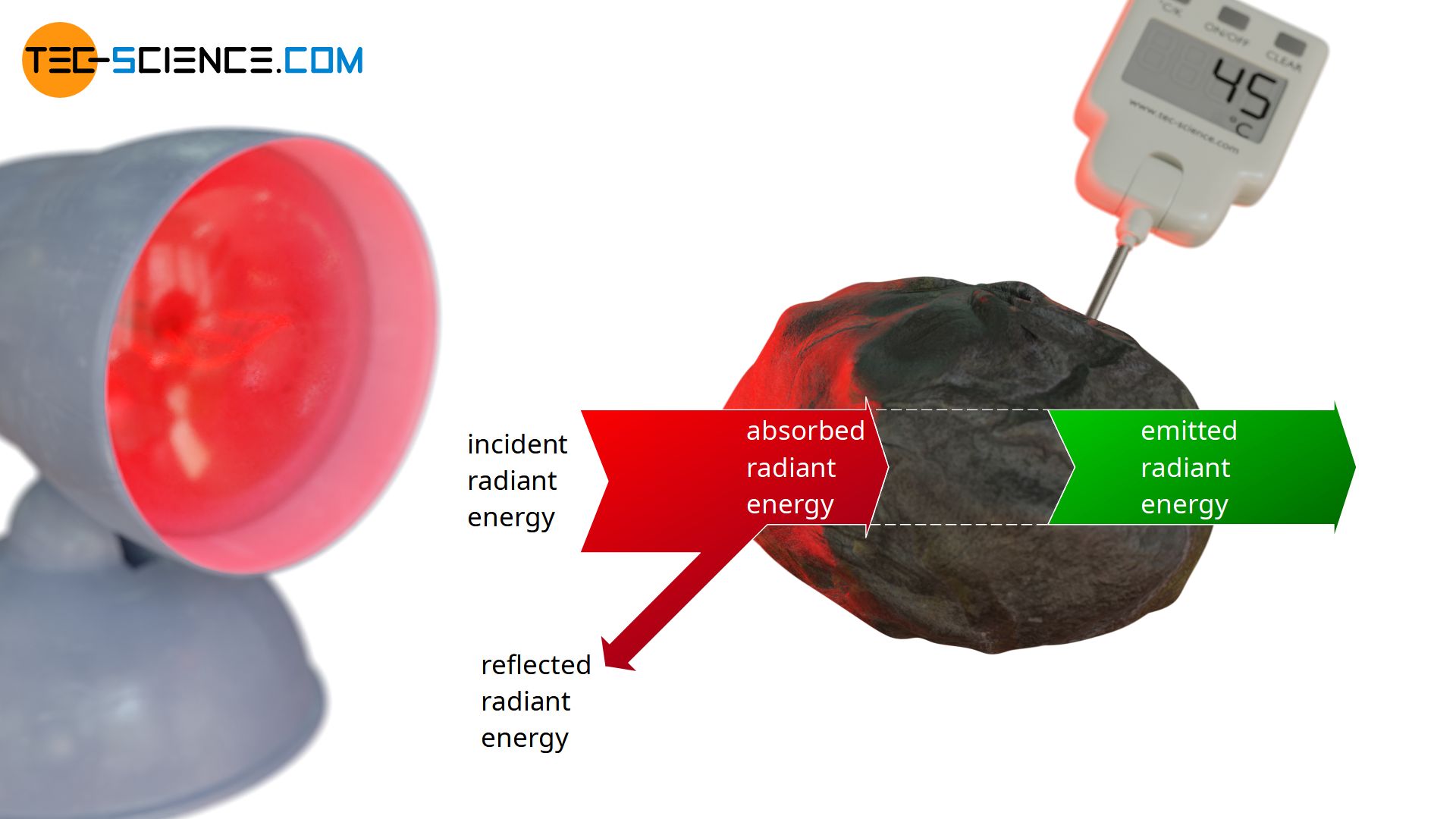
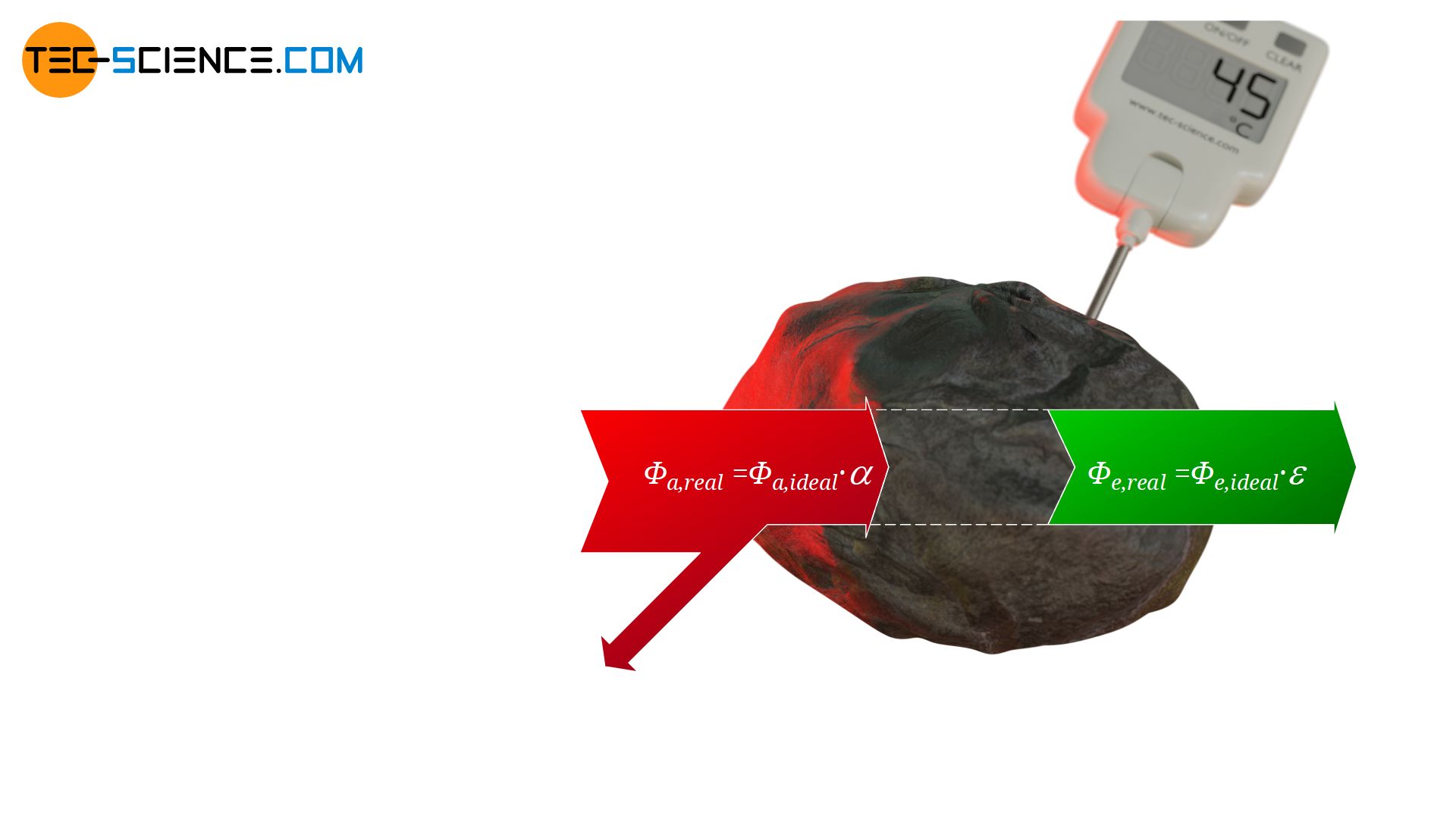
This situation can now be transferred to real objects, which are not perfect black bodies. With real objects a certain part of the radiation is always reflected and not completely absorbed like with black bodies. The absorbed radiant power of a real body will therefore be a factor α<1 less than that of an ideal black body. This factor α, which describes the absorbed part of the incident radiation and thus indicates the absorbed radiant power in comparison to an ideal black body, is also referred to as absorptivity α.
\begin{align}
&\boxed{\Phi_{a,real} = \alpha \cdot \Phi_{a,ideal} } ~~~~~\alpha<1 \\[5px]
&\Phi_{a,real} = \alpha \cdot \sigma \cdot A \cdot T^4 \\[5px]
\end{align}
Absorptivity α is the absorbed radiation portion of an incident radiation, i.e. the absorbed radiant energy of a real body compared to an ideal blackbody!
According to Kirchhoff’s law of radiation, the emitted radiant power in thermal equilibrium is just as high as the absorbed radiant power. A real body that has a lower absorption power than an ideal black body will therefore also have a lower emission power to the same extent!
The emission power of a real body in thermal equilibrium is as much lower as the absorption power!
However, this also means that a body that absorbs to the maximum also emits to the maximum. A blackbody is therefore not only an ideal absorber of radiation but also a perfect emitter of radiation!
A blackbody is an ideal thermal radiator with the maximum possible radiant power!
In purely formal terms, the emission power of a real body can also be expressed with a factor which then indicates the ratio of the emitted radiation of the real body compared to an ideal black body! This factor is referred to as emissivity ε.
\begin{align}
&\boxed{\Phi_{e,real} = \varepsilon \cdot \Phi_{e,ideal} } ~~~~~\varepsilon<1 \\[5px]
&\Phi_{e,real} = \varepsilon \cdot \sigma \cdot A \cdot T^4 \\[5px]
\end{align}
An emissivity of e.g. ε=0.9 means that the considered object has 90 % of the radiant power of an ideal thermal radiator (perfect black body). Many non-metallic objects have an emissivity of more than 90 % and can therefore be regarded as blackbodies in very good approximation with respect to their emitted radiation. The emissivity for an ideal blackbody is ε=1.
The emissivity represents the ratio of the radiation actually emitted by a real body to that of an ideal thermal radiator, a perfect blackbody!
Although the absorptivity and the emissivity are formally differentiated, in thermal equilibrium this distinction is obsolete, since both quantities have the same value according to Kirchhoff’s law of radiation (\ref{kirch}):
\begin{align}
\require{cancel}
&\Phi_{e,real} \overset{!}{=} \Phi_{e,real} \\[5px]
&\alpha \cdot \bcancel{\sigma \cdot A \cdot T^4} = \varepsilon \cdot \bcancel{\sigma \cdot A \cdot T^4} \\[5px]
&\boxed{\alpha = \varepsilon} \\[5px]
\end{align}
In thermal equilibrium, the absorptivity is equal to the emissivity!
Remark
Real bodies which have a constantly lower (spectral) emission power in the entire radiated wavelength spectrum compared to an ideal black body are also called gray bodies. Gray bodies therefore have an absorptivity or emissivity that is not dependent on the wavelength.
In some cases, however, a body will also absorb or emit radiation to different degrees depending on the wavelength. The absorptivity or emissivity then depends on the wavelength. Such bodies are called selective absorbers or selective radiators.