Das Stefan-Boltzmann-Gesetz besagt, dass die Strahlungsleistung eines Gegenstandes im thermischen Gleichgewicht proportional zur vierten Potenz der Temperatur und direkt proportional zu dessen Oberfläche ist!
Einleitung
Im Artikel Schwarzkörperstrahlung wurde bereits ausführlich erläutert, warum jeder Körper oberhalb des absoluten Nullpunktes Strahlung emittiert. Diese Strahlung wird auch als Wärmestrahlung, Temperaturstrahlung oder thermische Strahlung bezeichnet. Die Temperaturstrahlung kommt aufgrund der Schwingungen der Atome zustande, die dabei elektromagnetische Wellen aussenden, also Strahlung.
Die Wärmestrahlung lässt sich nicht nur durch dadurch nachweisen, dass sie in der Lage ist andere Gegenstände zu erwärmen, wie man aus dem Begriff der Wärmestrahlung ableiten könnte. Bei ausreichend hohen Temperaturen verschiebt sich das abgestrahlte Wellenlängenspektrum in den sichtbaren Bereich und kann hierdurch direkt beobachtet werden. Das rötliche Glühen eines erhitzten Stahls beim Schmieden ist bspw. die Folge einer solchen sichtbar gewordenen Temperaturstrahlung.

Auch das sichtbare Leuchten der Glühwendel einer Glühbirne bei über 3000 °C ist ebenfalls ein typisches Beispiel welches auf das Phänomen der Temperaturstrahlung zurückzuführen ist. Über 90 % der Strahlungsenergie wird dabei im nicht-sichtbaren Infrarotbereich abgestrahlt und ist somit tatsächlich nur als Wärme wahrzunehmen. Der restliche Anteil entfällt aber auf das sichtbare Wellenlängenspektrum und ist als gelbliches Glühen direkt beobachtbar (ein geringer Teil wird auch im ultravioletten Wellenlängenbereich abgestrahlt).

Strahlungsleistung
Wie eine Wärmelampe oder ein glühender Stahlblock deutlich zeigt, ist das Emittieren von Strahlung offensichtlich mit einem Aussenden von Energie verbunden. Wie viel Strahlungsenergie ΔQ pro Zeit Δt ein Gegenstand dabei aussendet, d.h. wie hoch seine Strahlungsleistung Φ ist, hängt hauptsächlich von der Temperatur T ab, aber auch von der Größe der Oberfläche A sowie von der Strahlungseigenschaft des Körpers (dem sogenannten Emissionsgrad ε).
\begin{align}
&\boxed{\Phi = \frac{\Delta Q}{\Delta t}}=\Phi(T,A,\varepsilon) \\[5px]
\end{align}
Beachte, dass sich die Strahlungsleistung nicht nur auf die Wärmeenergie im Infrarotbereich bezieht oder auf die abgestrahlte Energie im sichtbaren Wellenlängenbereich, sondern auf die Energie im gesamten Wellenlängenspektrum, also auf die gesamte energetische Strahlung!
Wird zum Beispiel eine Glühlampe bei geringem elektrischem Strom betrieben, so ist die Temperatur der Glühwendel entsprechend gering. Die Lampe leuchtet hierdurch nicht nur schwächer sondern sie erwärmt sich auch nicht so stark. Insgesamt ist bei niedrigen Temperaturen die Strahlungsleistung also relativ gering. Bei großem Strom hingegen erwärmt sich die Glühwendel stark und die Temperatur ist entsprechend hoch. Sie leuchtet dann nicht nur intensiv gelb sondern strahlt auch im hohen Maße Infrarotstrahlung ab, die deutlich als Wärme spürbar ist. Je höher die Temperatur eines Körpers also ist, desto höher ist offensichtlich die abgegebene Strahlungsleistung!

Anmerkung: Dass die Glühwendel bei geringer Temperatur schwach rötlich strahlt und bei hoher Temperatur in einem intensiven Gelb, ist dem abgestrahlten Wellenlängenspektrum geschuldet, das sich mit zunehmender Temperatur in den gelblichen Bereich verschiebt (mehr Informationen hierzu im Artikel Schwarzkörperstrahlung).
Neben der Temperatur beeinflusst aber auch die Größe der Oberfläche des strahlenden Körpers die abgegebene Strahlungsleistung. Denn je größer die Oberfläche, desto mehr Atome können dort schwingen und Strahlung nach außen abgeben. Beachte, dass Strahlung, die die Atome im Inneren des Körpers abgeben, von den umgebenden Atomen direkt wieder absorbiert wird und deshalb nicht nach außen tritt. Somit sind nur die Atome an der Oberfläche für die Abstrahlung der elektromagnetischen Wellen relevant. Bei doppelter Oberflächengröße sollte deshalb auch die Strahlungsleistung doppelt so hoch sein.
Genauere Untersuchungen der Physiker Josef Stefan und Ludwig Boltzmann Ende des 19. Jahrhunderts zeigten, dass die Strahlungsleistung tatsächlich direkt proportional zur Oberfläche des Körpers ist. Der Einfluss der Temperatur auf die Strahlungsleistung ist hingegen weitaus größer. Sie nimmt mit der vierten Potenz der absoluten Temperatur zu. Eine Verdopplung der Temperatur von bspw. 1000 K auf 2000 K erhöht die Strahlungsleistung somit um das 16-fache! Für einen idealen Temperaturstrahler, einem sogenannten Schwarzen Körper, ergibt sich die Strahlungsleistung Φideal in Abhängigkeit der Temperatur T und der Fläche A somit wie folgt:
\begin{align}
&\Phi_{ideal} \sim A \cdot T^4 \\[5px]
&\boxed{\Phi_{ideal} = \sigma \cdot A \cdot T^4} ~~~~~ \sigma = 5,670 \cdot 10^{-8} \frac{\text{W}}{\text{m²K}^4} \\[5px]
\end{align}
Das Stefan-Boltzmann-Gesetz besagt, dass die Strahlungsleistung eines Gegenstandes im thermischen Gleichgewicht proportional zur vierten Potenz der Temperatur und direkt proportional zu dessen Oberfläche ist!
Der Proportionalitätsfaktor σ wird Stefan-Boltzmann-Konstante genannt und ist eine Naturkonstante, d.h. insbesondere nicht vom Material des strahlenden Gegenstandes abhängig, solange der Körper alle auftreffende Strahlung absorbiert und deshalb als Schwarzer Körper betrachtet werden kann.
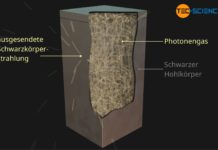
Als Schwarzer Körper wird ein idealer Temperaturstrahler bezeichnet, der alle auftreffende Strahlung absorbiert und deshalb mit maximaler Leistung strahlt!
Weshalb ein Schwarzer Körper nicht nur ein perfekter Absorber von Strahlung sondern immer auch ein perfekter Emitter von Strahlung ist, wird im Abschnitt Reale Körper näher erläutert.
Wird die Strahlungsleistung Φ des Schwarzen Körpers auf dessen Fläche A bezogen, dann spricht man auch von der sogenannten Strahlungsintensität I (Flächenleistungsdichte). Die Intensität gibt die Stärke der Strahlungsleistung pro Flächeneinheit an. Die Intensität der Wärmestrahlung ist bei einem Schwarzer Körper nur von Temperatur abhängig:
\begin{align}
&I=\frac{\Phi}{A} = \frac{\sigma \cdot A \cdot T^4}{A} = \sigma \cdot T^4\\[5px]
&\boxed{I = \sigma \cdot T^4 } \\[5px]
\end{align}
Anmerkung: Das Stefan-Boltzmann-Gesetz kann aus dem Planck’sch Strahlungsgesetz oder aus einer thermodynamischen Betrachtungsweise hergeleitet werden. In den entsprechenden Artikeln erfahren Sie mehr darüber.
Kirchhoffsches Strahlungsgesetz
Im Folgenden wird ein Schwarzer Körper betrachtet, der von einem Strahler bestrahlt wird. Definitionsgemäß wird der Schwarze Körper alle einfallende Strahlung absorbieren. Die absorbierte Energie führt zur Erhöhung der Temperatur und der Schwarze Körper beginnt verstärkt Strahlung abzugeben. Schließlich wird sich mit der Zeit ein thermisches Gleichgewicht einstellen, in dem die Temperatur nicht mehr weiter ansteigt. Im thermodynamischen Gleichgewicht muss somit die innerhalb einer gewissen Zeit emittiert Strahlungsenergie (Emissionsleistung Φe) gleich groß sein wie die absorbierte Strahlungsenergie (Absorptionsleistung Φa):
\begin{align}
\label{kirch}
&\boxed{\Phi_a \overset{!}{=} \Phi_e} \\[5px]
\end{align}
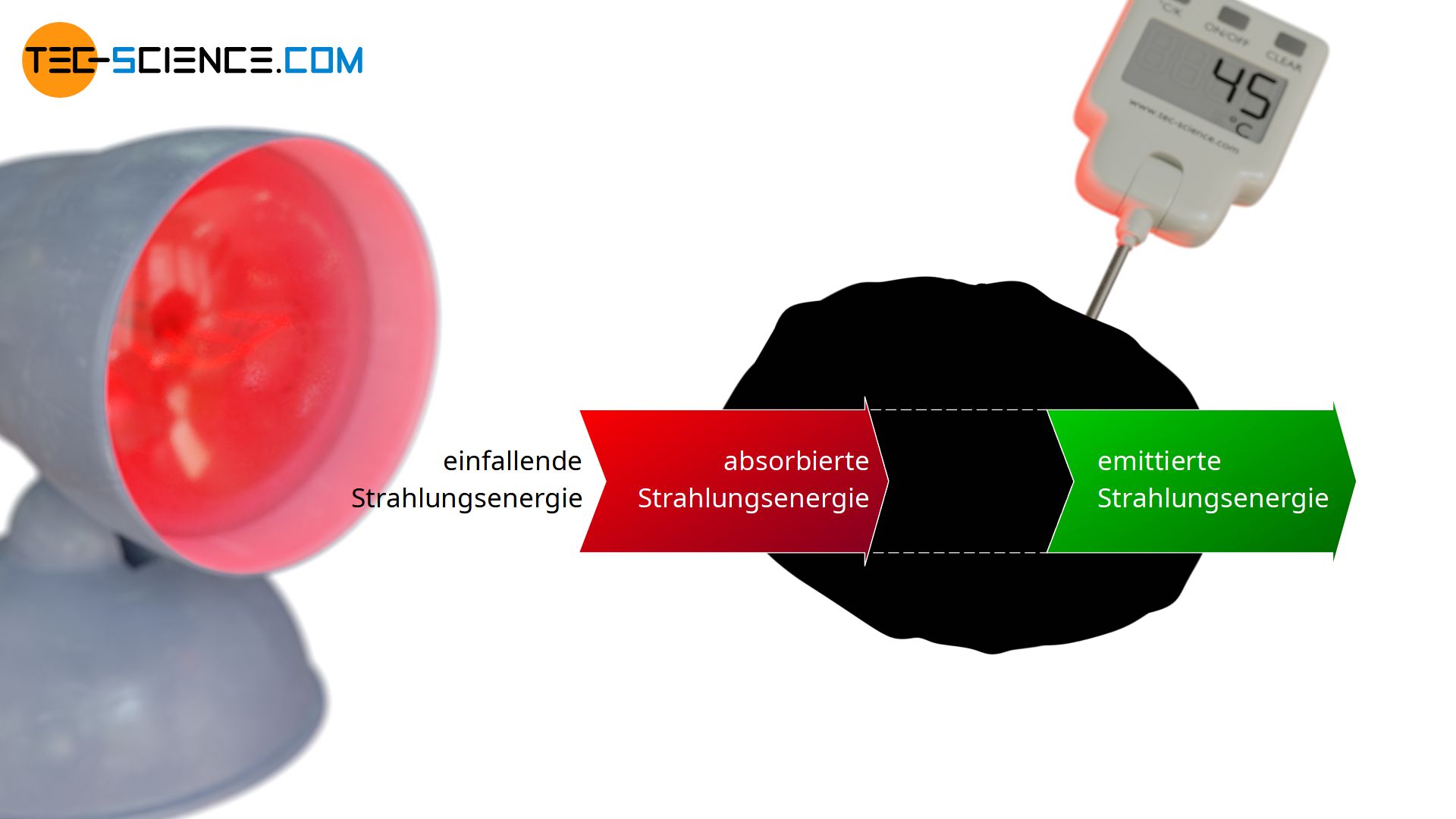
Dieses Strahlungsgleichgewicht zwischen emittierter Strahlung und absorbierter Strahlung gilt grundsätzlich für jeden Körper im thermischen Gleichgewicht, also auch für nicht-ideale Schwarze Körper, welche nicht mit maximaler Leistung strahlen. Denn schließlich wird sich bei jedem Körper nach einer gewissen Zeit eine konstante Temperatur und somit ein thermodynamisches Gleichgewicht einstellen, in dem Emission und Absorption im selben Maße ablaufen müssen. Diese Gesetzmäßigkeit wird auch als Kirchhoffsches Strahlungsgesetz bezeichnet.
Als Kirchhoffsches Strahlungsgesetz bezeichnet man die Tatsache, dass im thermischen Gleichgewicht eines strahlenden Körpers, die Emissionsleistung gleich der Absorptionsleistung ist!
Auf dieselbe Weise wie die Emissionsleistung mit der vierten Potenz der Temperatur steigt, muss somit auch die Absorptionsleistung mit der vierten Potenz der Temperatur steigen. Ansonsten gäbe es kein thermisches Gleichgewicht. Die Gesetzmäßigkeit mit der ein idealer Schwarzer Körper gemäß des Stefan-Boltzmann-Gesetztes Strahlung emittiert, muss im thermischen Gleichgewicht also auch für die absorbierte Strahlung gelten!
\begin{align}
&\boxed{\Phi_{a,ideal} = \Phi_{e,ideal} = \sigma \cdot A \cdot T^4} \\[5px]
\end{align}
Reale Körper
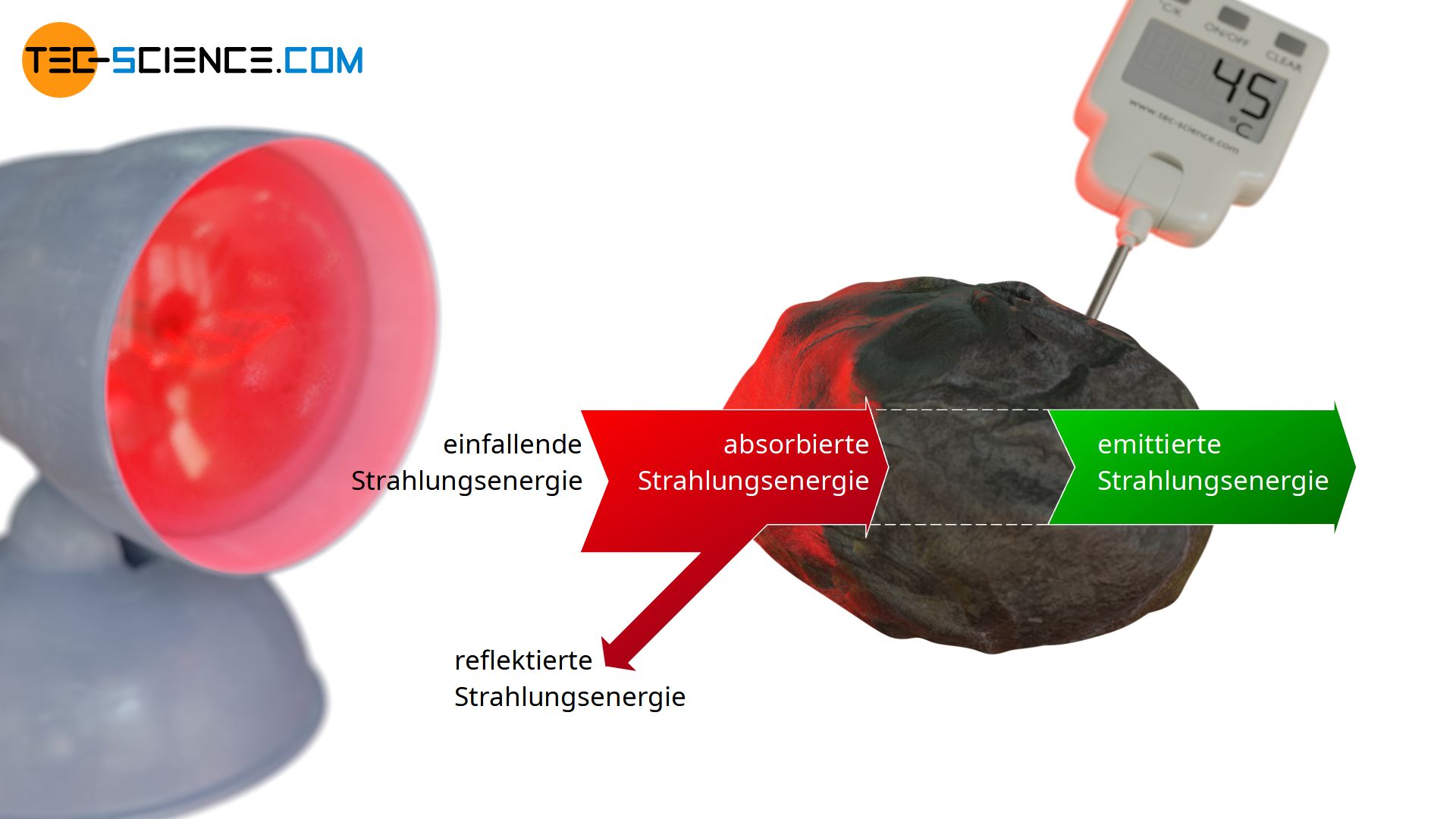
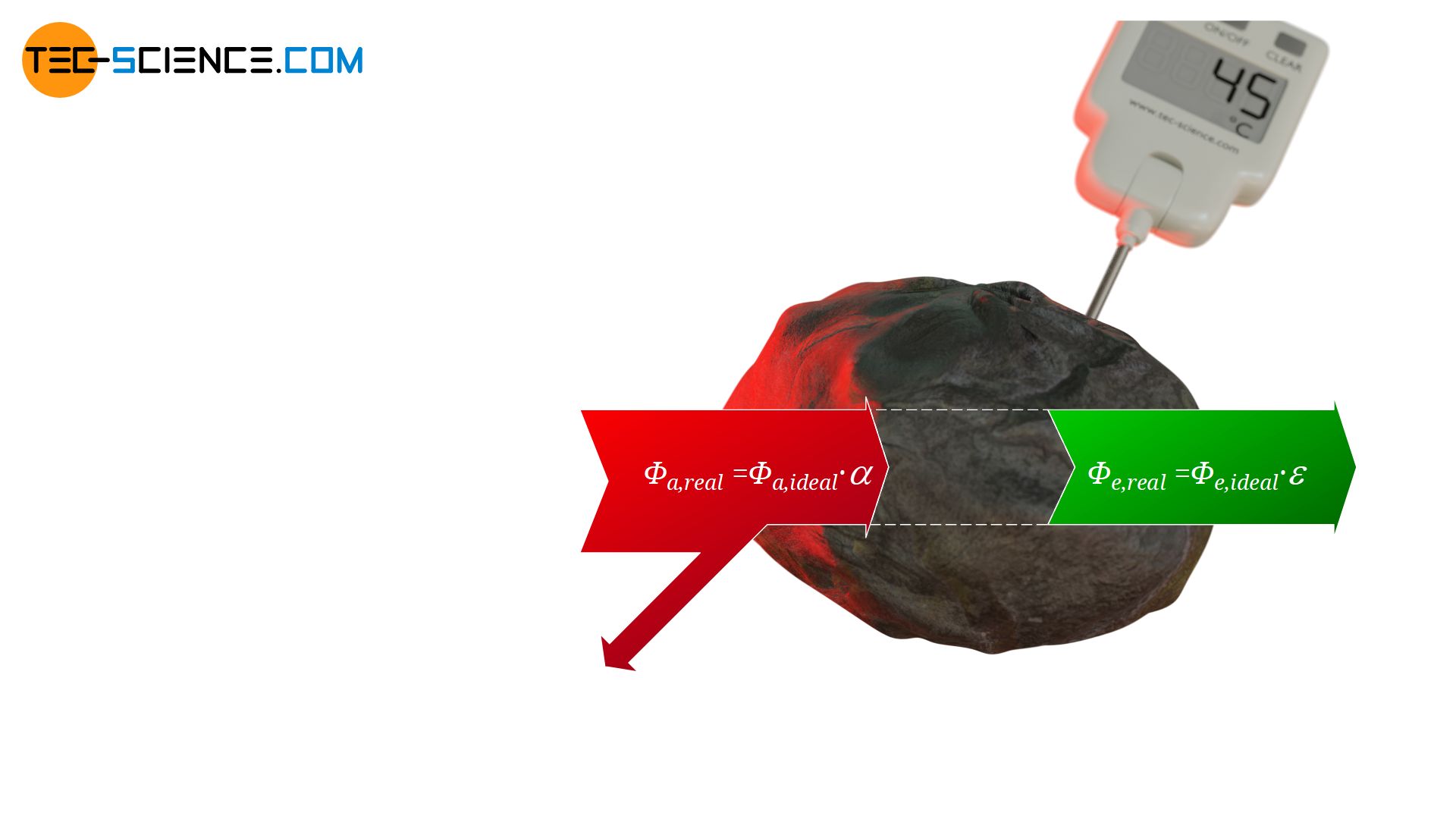
Man kann diese Situation nun auch auf reale Körper übertragen, die eben keine perfekte Schwarze Körper sind. Bei realen Gegenständen wird immer ein gewisser Teil der Strahlung reflektiert und nicht wie bei Schwarzen Körpern vollständig absorbiert. Die absorbierte Strahlungsleistung eines realen Körpers wird also um einen Faktor α<1 geringer sein als die eines idealen Schwarzen Körpers. Dieser Faktor α, der den absorbierten Anteil der auftreffenden Strahlung beschreibt und somit die Absorptionsleistung im Vergleich zu einem idealen Schwarzen Körper angibt, wird auch als Absorptionsgrad α bezeichnet.
\begin{align}
&\boxed{\Phi_{a,real} = \alpha \cdot \Phi_{a,ideal} } ~~~~~\alpha<1 \\[5px]
&\Phi_{a,real} = \alpha \cdot \sigma \cdot A \cdot T^4 \\[5px]
\end{align}
Als Absorptionsgrad α bezeichnet man den absorbierten Strahlungsanteil einer auftreffenden Strahlung, d.h. die Absorptionsleistung des Körpers im Vergleich zu einem idealen Schwarzen Körper!
Gemäß des Kirchhoffschen Strahlungsgesetzes ist im thermischen Gleichgewicht die Emissionsleistung genauso groß wie die Absorptionsleistung. Ein realer Körper der eine geringere Absorptionsleistung als ein idealer Schwarzer Körper hat, wird somit auch eine im selben Maße geringere Emissionsleistung haben!
Die Emissionsleistung eines realen Körpers ist im thermischen Gleichgewicht im selben Maße geringer wie die Absorptionsleistung!
Dies bedeutet aber auch: Ein Körper der maximal absorbiert, emittiert auch maximal. Ein Schwarzer Körper ist also nicht nur ein idealer Absorber von Strahlung sondern eben auch ein perfekter Emitter von Strahlung!
Ein Schwarzer Körper ist ein idealer Wärmestrahler mit der maximal möglichen Strahlungsleistung!
Rein formal kann man die Emissionsleistung eines realen Körpers ebenfalls mit einem Faktor versehen, der dann das Verhältnis der emittierten Strahlung des realen Körpers im Vergleich zu einem idealen Schwarzen Strahler angibt! Dieser Faktor wird dann Emissionsgrad ε genannt.
\begin{align}
&\boxed{\Phi_{e,real} = \varepsilon \cdot \Phi_{e,ideal} } ~~~~~\varepsilon<1 \\[5px]
&\Phi_{e,real} = \varepsilon \cdot \sigma \cdot A \cdot T^4 \\[5px]
\end{align}
Ein Emissionsgrad von bspw. ε=0,9 bedeutet anschaulich, dass der betrachtete Gegenstand 90 % der Strahlungsleistung eines idealen Temperaturstrahlers besitzt. Viele nicht-metallische Gegenstände besitzen einen Emissionsgrad über 90 % und können bezüglich ihrer abgegebenen Strahlung daher in sehr guter Näherung als Schwarze Körper betrachtet werden. Für einen perfekten Schwarzen Körper gilt ε=1.
Der Emissionsgrad gibt das Verhältnis der tatsächlich abgegebenen Strahlung eines realen Körpers im Vergleich zu einem idealen Wärmestrahler wieder, einem Schwarzen Körper!
Zwar wird der Absorptionsgrad und der Emissionsgrad formal unterschieden, im thermischen Gleichgewicht ist diese Unterscheidung aber hinfällig, da beide Werte gemäß des Kirchhoffschen Strahlungsgesetzes (\ref{kirch}) identisch sind:
\begin{align}
\require{cancel}
&\Phi_{e,real} \overset{!}{=} \Phi_{e,real} \\[5px]
&\alpha \cdot \bcancel{\sigma \cdot A \cdot T^4} = \varepsilon \cdot \bcancel{\sigma \cdot A \cdot T^4} \\[5px]
&\boxed{\alpha = \varepsilon} \\[5px]
\end{align}
Im thermischen Gleichgewicht ist der Absorptionsgrad gleich dem Emissionsgrad!
Anmerkung
Reale Körper die im gesamten abgestrahlten Wellenlängenspektrum eine konstant geringere (spektrale) Emissionsleistung aufweisen im Vergleich zu einem idealen Schwarzen Körper, werden auch als graue Körper bzw. graue Strahler bezeichnet. Graue Körper haben also einen Absorptionsgrad bzw. Emissionsgrad, der nicht von der Wellenlänge abhängig ist.
In machen Fällen wird ein Körper aber auch je nach Wellenlänge unterschiedlich stark Strahlung absorbieren bzw. emittieren. Der Absorptionsgrad bzw. der Emissionsgrad ist dann von der Wellenlänge abhängig. Solche Körper werden als selektive Absorber bzw. als selektive Strahler bezeichnet.