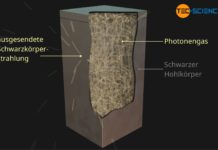
Als Schwarzkörperstrahlung oder Hohlraumstrahlung versteht man die Wärmestrahlung eines Schwarzen Körpers, d.h. die ausgesendete Strahlung Körpers, der alle Strahlung absorbiert.
Schwarzer Körper
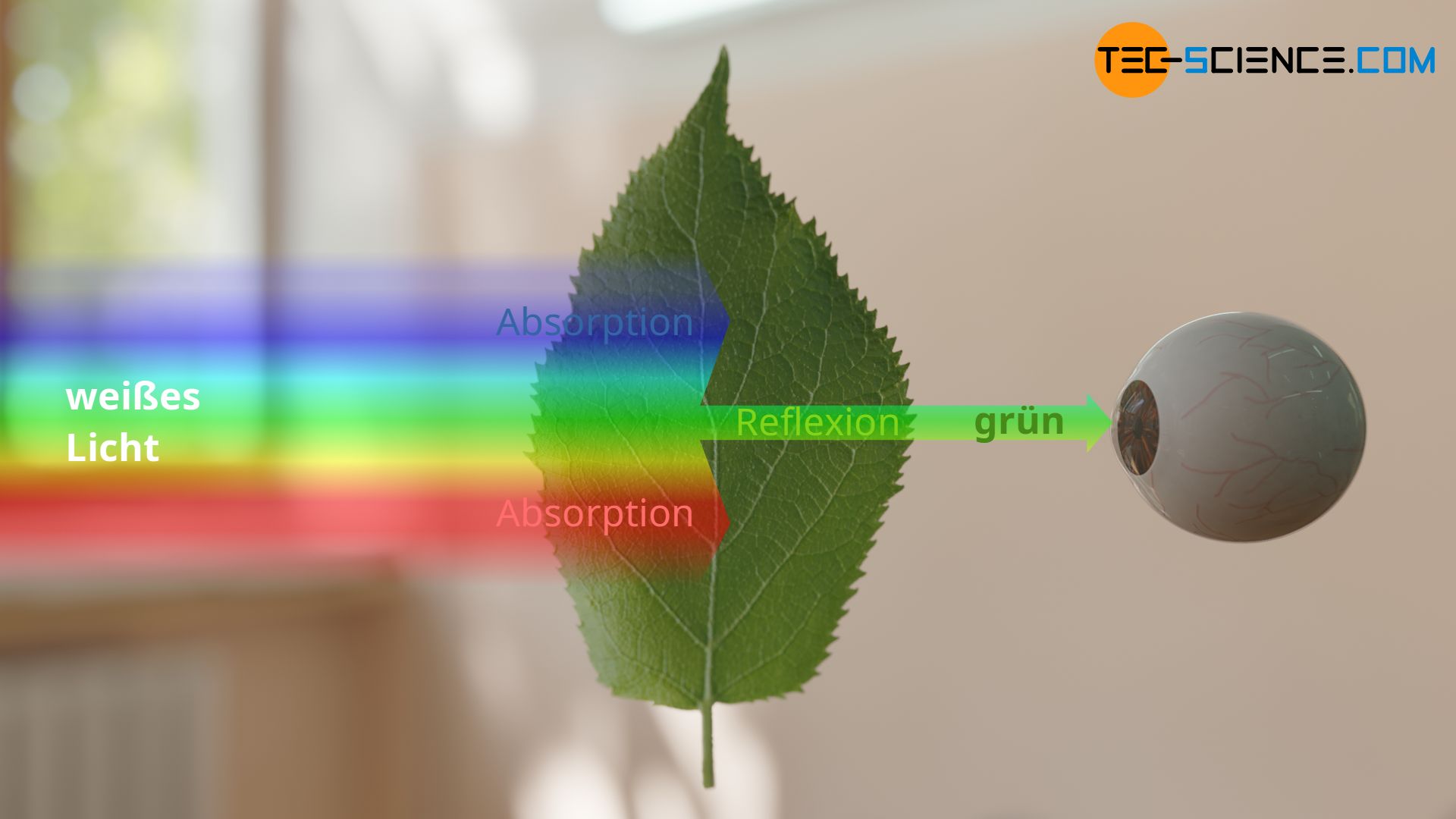
Trifft weißes Licht auf einen opaken Gegenstand, dann wird immer ein gewisser Teil absorbiert und der Rest reflektiert. Je nachdem welche Wellenlängen absorbiert werden, besteht das reflektierte Licht aus bestimmten Wellenlängen. Diese reflektierten Wellenlängen bestimmten die wahrgenommene Farbe des Gegenstandes.
Bei einem grünen Blatt werden fast alle Wellenlängen absorbiert, bis auf den grünen Wellenlängenbereich zwischen 500 nm und 550 nm. Somit beinhaltet das reflektierte Licht genau jenen Wellenlängenbereich, der uns den grünen Farbeindruck vermittelt.
Absorbiert ein Gegenstand hingegen alle auftreffenden Wellenlängen im sichtbaren Bereich, dann wird auch keine sichtbare Strahlung reflektiert. Der Gegenstand erscheint unter normalen Bedingungen deshalb schwarz. Von einem schwarzen Gegenstand geht also keine sichtbare Strahlung aus. Ein Gegenstand, der alle auftreffende Strahlung absorbiert wird deshalb auch als Schwarzer Körper bezeichnet. Einen perfekten Schwarzen Körper gibt es allerdings nur in der Idealvorstellung. In der Realität wird jeder Körper immer einen Teil der auftreffenden Strahlung auch reflektieren. Deshalb sieht man selbst bei schwarzen Gegenständen häufig noch Schattierungen. Das untere Bild zeigt hierzu illustrativ schwarze Kohle. Man kann auf der lichteinfallenden Seite leichte Schattierungen erkennen.

Ein Schwarzer Körper ist ein idealisierter Gegenstand, der alle auftreffende elektromagnetische Strahlung absorbiert!
Wärmestrahlung
Man könnten nun meinen, dass von einem Schwarzen Körper keinerlei elektromagnetische Strahlung ausgeht. Denn schließlich ist er schwarz und sendet keine sichtbare Strahlung aus. Aus energetischer Sicht ist diese Vermutung allerdings sehr schnell wiederlegt. Denn elektromagnetische Strahlung ist immer mit einer bestimmten Strahlungsenergie verbunden. Je höher die Frequenz der Strahlung, desto energiereicher. Wird nun Strahlungsenergie von einem Gegenstand absorbiert, dann kann die aufgenommene Energie ja nicht einfach verschwinden. Vielmehr macht sich die absorbierte Strahlungsenergie in einer Temperaturerhöhung des Gegenstandes bemerkbar (Erhöhung der inneren Energie)!
Solange ein Schwarzer Körper also bestrahlt wird und Energie absorbiert, müsste seine Temperatur stetig ansteigen. Die Erfahrung zeigt aber, dass bspw. Gegenstände die in die Sonne gelegt und damit bestrahlt werden, sich nicht permanent aufheizen. Dabei spielt es keine Rolle, ob es sich um einen idealen oder um einen realen Schwarzen Körper handelt. Solange auch nur teilweise die Strahlung absorbiert wird, sollte die Temperatur aufgrund der permanent aufgenommenen Strahlungsenergie stetig ansteigen.

In der Realität stellt man aber fest, dass die Temperatur von bestrahlten Gegenständen nicht permanent ansteigt. Irgendwann wird sich ein thermodynamisches Gleichgewicht einstellen. Dies gilt auch für schwarz angemalte Gegenstände, die in sehr guter Näherung als ideale Schwarze Körper betrachtet werden können. Körper die Strahlungsenergie absorbieren, müssen folglich auch irgendwie Energie wieder abgegeben. Anders könnte das thermische Gleichgewicht nicht erklärt werden.
Man könnte nun meinen, dass ein in die Sonne gelegter Gegenstand durch die umgebende Luft per Wärmeströmung (Konvektion) gekühlt wird. Denkbar wäre auch ein Wärmetransport durch Wärmeleitung mit dem Boden. Diese Wärmetransportvorgänge werden sicherlich auch stattfinden und einen Beitrag zum thermischen Gleichgewicht leisten. Es muss aber noch ein anderer Mechanismus vorhanden sein. Dies wird deutlich, wenn man einen Gegenstand im Vakuum betrachtet. Wärmeströmung und Wärmeleitung erfordern Materieteilchen, die die Wärmeenergie transportieren. Im Vakuum gibt es allerdings keine Teilchen, sodass diese Wärmetransportvorgänge nicht stattfinden können. Und dennoch wird man feststellen, dass auch bestrahlte Körper im Vakuum früher oder später in ein thermisches Gleichgewicht kommen.
Als alltägliches Beispiel sei hierzu die Erde genannt. Sie wird im Vakuum des Weltalls von der Sonne bestrahlt und absorbiert somit einen Teil der Sonnenstrahlung. Offensichtlich findet aber dabei kein permanentes Aufheizen der Erde statt. Die Erde befindet sich in einem relativ stabilen thermischen Gleichgewicht, welches zu einer mittleren Oberflächentemperatur von rund 15 °C führt. Dieses thermische Gleichgewicht im Vakuum lässt sich nur dadurch erklären, dass die Erde selbst Energie durch elektromagnetische Strahlung abgibt.
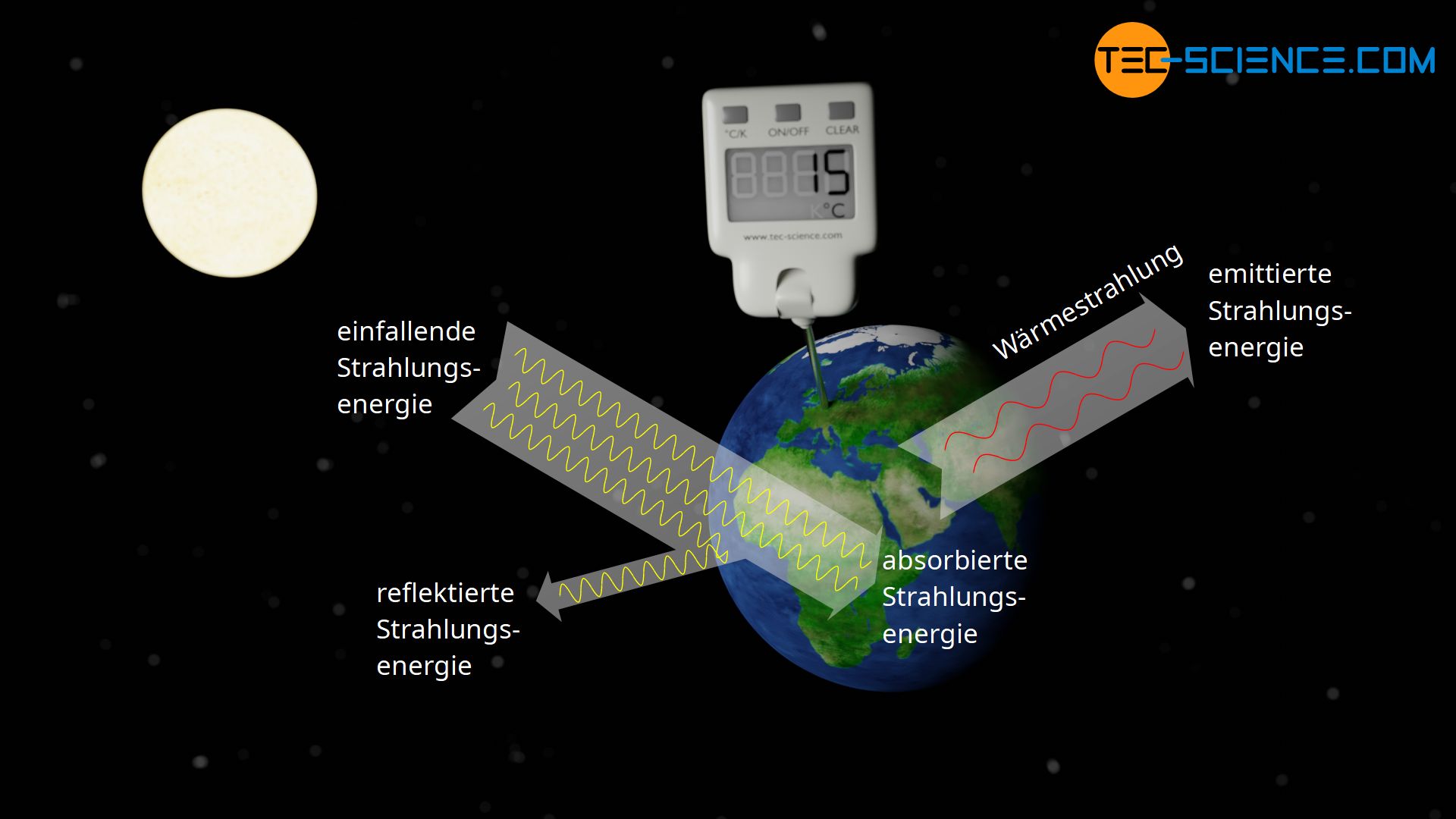
Man bezeichnet diese abgegebene Strahlung eines Körpers im thermischen Gleichgewicht aufgrund seiner Temperatur auch als Wärmestrahlung, thermische Strahlung oder Temperaturstrahlung. Sie tritt bei allen Gegenständen auf, nicht nur bei solchen die sich im Vakuum befinden! Bei sehr stark aufgeheizten Gegenständen wie bspw. einem glühenden Stück Metall, kann man diese Wärmestrahlung nicht nur sehr deutlich spüren sondern anhand der glühenden rötlichen Farbe auch tatsächlich sehen!

In Glühbirnen wird diese thermische Strahlung technisch genutzt, um sichtbares Licht zu emittieren. Tatsächlich wird der meiste Teil der thermischen Strahlung in diesem Fall jedoch im Infrarotbereich emittiert. In diesem Wellenlängenbereich können wir die Strahlung zwar nicht direkt sehen, aber wir können sie dennoch wahrnehmen. Wir nehmen die Infrarotstrahlung nämlich durch unsere Haut in Form eines Wärmeempfindens wahr. Deshalb wird die thermische Strahlung eben auch als Wärmestrahlung bezeichnet.
Das abgestrahlte Wellenlängenspektrum hängt stark von der Temperatur des Körpers ab. Bei geringem Strom und damit geringer Temperatur strahlt der Glühfaden schwach rötlich. Bei großem Strom und somit großer Temperatur strahlt der Glühfaden dann intensiv gelblich. Auf diese spektrale Verteilung in Abhängigkeit der Temperatur wird im späteren Abschnitt Schwarzkörperstrahlung näher eingegangen.

Als Wärmestrahlung, thermische Strahlung oder Temperaturstrahlung bezeichnet man die im thermischen Gleichgewicht abgegebene Strahlung eines Körpers aufgrund seiner Temperatur!
Anmerkung: Häufig wird als Wärmestrahlung im engeren Sinne nur die nicht-sichtbare Strahlung im Infrarot-Bereich bezeichnet. Im weitesten Sinne (und so auch in diesem Artikel) bezieht sich der Begriff der Wärmestrahlung auf den gesamten abgestrahlten Wellenlängenbereich eines Körpers aufgrund seiner Temperatur, d.h. auf die gesamte energetisch abgegebene Strahlung!
Das Zustandekommen der thermischen Strahlung kann durch die Schwingung der Atome erklärt werden. Grundsätzlich führt jede beschleunigte Bewegung von elektrisch geladenen Teilchen zur Erzeugung von elektromagnetischen Wellen, also Strahlung. Je höher die Temperatur desto stärker und schneller schwingen die Teilchen und umso mehr Strahlung wird abgegeben (höhere Intensität). Lediglich im absoluten Nullpunkt sind keine Atomschwingungen vorhanden und der Körper emittiert keine Wärmestrahlung.
Die Wärmestrahlung kommt durch Schwingungen der Atome zustande!
Anmerkung zum Begriff des Schwarzen Körpers
Wie bereits erläutert, muss auch ein idealer Schwarzer Körper je nach Temperatur eine bestimmte Wärmestrahlung emittieren. Ansonsten könnte eben nicht erklärt werden, weshalb es bei vollständiger Absorption von Strahlungsenergie dennoch irgendwann zu einem thermischen Gleichgewicht kommt! Auch wenn also ein Schwarzer Körper definitionsgemäß alle auftreffende Strahlung absorbiert, so gibt dieser dennoch Strahlung ab. Es handelt sich dabei eben nicht um reflektierte Strahlung, sondern um Strahlung, die der Körper aufgrund der Schwingung der Atome „selbst“ emittiert. Siehe hierzu auch den Artikel Stefan-Boltzmann-Gesetz.
Beachte, dass die Definition eines Schwarzen Körpers also lediglich darin besteht, dass alle auftreffende Strahlung absorbiert wird und nicht darin, dass dieser selbst keine Strahlung emittieren könnte! Dies kann er sehr wohl, nur liegt diese ausgesendete Strahlung bei Umgebungsbedingungen im nicht-sichtbaren Wellenlängenbereich (Infrarot-Strahlung). Der Gegenstand erscheint für unser Auge deshalb zunächst schwarz, weshalb es zur Bezeichnung Schwarzer Körper kommt.
Lediglich wenn die Temperatur sehr stark erhöht wird und der Körper zu glühen anfängt, wird Strahlung im sichtbaren Bereich ausgesendet. Auch wenn der Körper nun je nach Temperatur eine Farbe besitzt („Glühfarben“), bezeichnet man diesen Gegenstand definitionsgemäß nach wie vor als Schwarzen Körper, da weiterhin alle auftreffende Strahlung absorbiert wird. Ein Schwarzer Körper muss also tatsächlich nicht zwangsläufig schwarz sein! Ein eindrucksvolles Beispiel ist die Sonne. Tatsächlich handelt es sich bei der Sonne um einen fast perfekten Schwarzen Körper. lediglich aufgrund der enormen Temperatur von 5778 K erscheint er weißglühend am Himmel.
Die Definition eines Schwarzer Körpers ist nicht, dass dieser unter allen Umständen schwarz erscheint, sondern dass er alle auftreffende Strahlung absorbiert! Je nach Temperatur sendet auch ein vermeintlich schwarzer Gegenstand sichtbare Strahlung aus und „glüht“ somit in verschiedenen Farben!
Schwarzkörperstrahlung
Sofern ein Gegenstand nicht allzu stark erhitzt wird, liegt die von einem Körper abgegebene Wärmestrahlung im infraroten Wellenlängenbereich. Diese Infrarotstrahlung ist für unser Auge unsichtbar, weshalb ein Schwarzer Körper zunächst tatsächlich schwarz erscheint! Mit einer Wärmebildkamera kann diese Wärmestrahlung aber „sichtbar“ gemacht werden. Man kann hieraus dann Rückschlüsse auf die Temperatur ziehen.
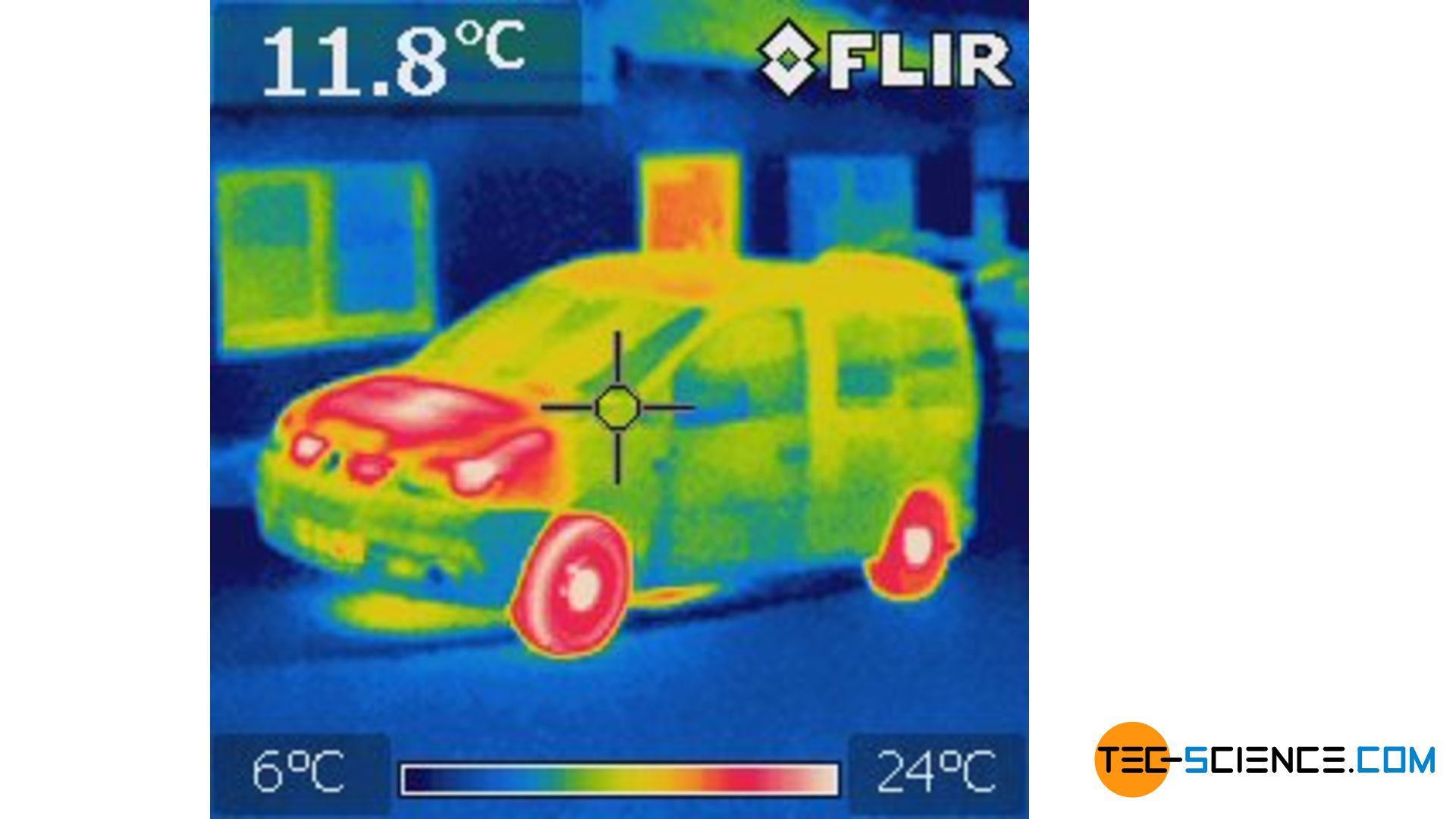
Die abgegebene Wärmestrahlung ändert ihren Wellenlängenbereich jedoch mit der Temperatur. Bei ausreichend hohen Temperaturen verschiebt sich das emittierte Wellenlängenspektrum in den sichtbaren Bereich und sogar darüber hinaus (d.h. in der Ultraviolett-Bereich). Auch ein vermeintlich „schwarzer“ Körper beginnt dann farblich zu „glühen“. Es handelt sich bei diesem Glühen eben nicht um reflektierte Strahlung sondern um selbst emittierte Strahlung „von innen“ heraus!
An dieser Stelle kommt nun auch der Schwarze Körper ins Spiel. Zur Untersuchung des emittierten Strahlungspektrums eines Gegenstandes (auch als spektrale Verteilung bezeichnet) ist es notwendig, dass auch tatsächlich nur die vom Körper selbst emittierte Wärmestrahlung gemessen wird und nicht die von anderen Strahlungsquellen reflektierten Anteile. Deshalb darf der zu untersuchende Körper keine Strahlung reflektieren sondern muss alle auftreffende Strahlung absorbieren. Man benötigt also einen Schwarzen Körper!
Ein Schwarzer Körper eignet sich zur Untersuchung der spektralen Verteilung der ausgesendeten Wärmestrahlung besonders, da die Strahlung keine reflektierenden Anteile von Störquellen enthält!
Die thermische Strahlung eines Schwarzen Körpers wird auch als Schwarzkörperstrahlung bezeichnet.
Als Schwarzkörperstrahlung wird die emittierte Wärmestrahlung eines Schwarzen Körpers bezeichnet!
Realisierung Schwarzer Körper in der Praxis (Hohlraumstrahlung)
In der Praxis kann ein Schwarzer Körper in sehr guter Näherung relativ einfach realisiert werden. Hierzu wird lediglich ein Loch in einen hohlen Gegenstand gebohrt. Trifft nun Strahlung in das Loch, dann wird diese im Inneren mehrfach an den Wänden reflektiert. Bei jeder Reflexion wird immer auch ein gewisser Teil der Strahlung absorbiert. Nach mehreren Reflexionen ist die eingetretene Strahlung somit nahezu vollständig absorbiert. Es tritt folglich keine Strahlung mehr durch das Loch wieder aus (zumindest nicht die einfallende Strahlung). Der Hohlraum „verschluckt“ praktisch alle einfallende Strahlung und das Loch erscheint deshalb schwarz. Der Hohlraum kann somit in sehr guter Näherung als Schwarzer Körper betrachtet werden.

Die obere Abbildung zeigt hierzu einen auf den Kopf gestellten Blumentopf mit Bodenöffnung sowie eine leere, geöffnete Getränkedose. Aufgrund der absorbierten einfallenden Strahlung erscheinen die Innenräume durch die Öffnungen jeweils schwarz. Selbst bei der Getränkedose aus hoch-reflektierendem Aluminium, dringt so gut wie keine sichtbare Strahlung mehr nach außen! Selbst reflektierende Materialen wie Metalle können also durch ein Loch in sehr guter Näherung zu einem Schwarzen Hohlkörper werden. Aus diesem Grund bezeichnet man die Schwarzkörperstrahlung oft auch als Hohlkörperstrahlung.

Beachte, dass sich der Begriff des Schwarzen Körpers tatsächlich nur auf den Hohlraum bzw. das Loch bezieht und nicht auf den Gegenstand an sich! Der Körper selbst hat in der Regel eine sichtbare Farbe. Die Außenseite des Gegenstandes stellt also keineswegs einen Schwarzen Körper dar!
Auch wenn kein sichtbares Licht aus dem Hohlraum emittiert wird, so tritt aufgrund des Schwingens der Atome dennoch Strahlung in Form von Wärmestrahlung aus. Mit einer Wärmebildkamera kann diese zunächst nicht sichtbare Schwarzkörperstrahlung in Form von Infrarotstrahlung sichtbar gemacht werden (weiße Bereiche in der unteren Illustration).

Spektrale Verteilung der Intensität der Schwarzkörperstrahlung (Planck-Sepktrum)
Mithilfe der Hohlraumstrahlung kann nun das emittierte Wellenlängenspektrum von unterschiedlichen Materialien bei verschiedenen Temperaturen untersucht werden. Aufgrund der thermischen Beständigkeit ist es an dieser Stelle sinnvoll Materialien aus Metall zu verwenden. In die hohlen Metallblöcke werden dann Löcher gebohrt. Durch die Löcher kann die Schwarzkörperstrahlung schließlich nach außen dringen und die spektrale Verteilung der Schwarzkörperstrahlung mit einem Detektor bestimmt werden. Die Temperatur kann dabei relativ einfach durch Erwärmung der Metallblöcke verändert werden und die sich hieraus ergebenden Auswirkungen auf die spektrale Verteilung untersucht werden.

Die untere Animation zeigt hierzu nochmals das Prinzip der Hohlraumstrahlung, bei der Strahlung durch ein Loch einfällt, aber durch Absorptionsprozesse nicht mehr aus diesem austritt.
Die Auswertung des Experiments erfolgt in einem Diagramm, in dem die sogenannte spektrale Intensität über die Wellenlänge aufgetragen wird. Ein solches Diagramm gibt vereinfacht gesagt an, welche Wellenlänge mit welcher Intensität abgestrahlt wird. Meist wird dabei eine doppelt-logarithmische Einteilung verwendet, um bei den verschiedenen Temperaturen einen möglichst großen Wellenlängenbereich abdecken zu können.
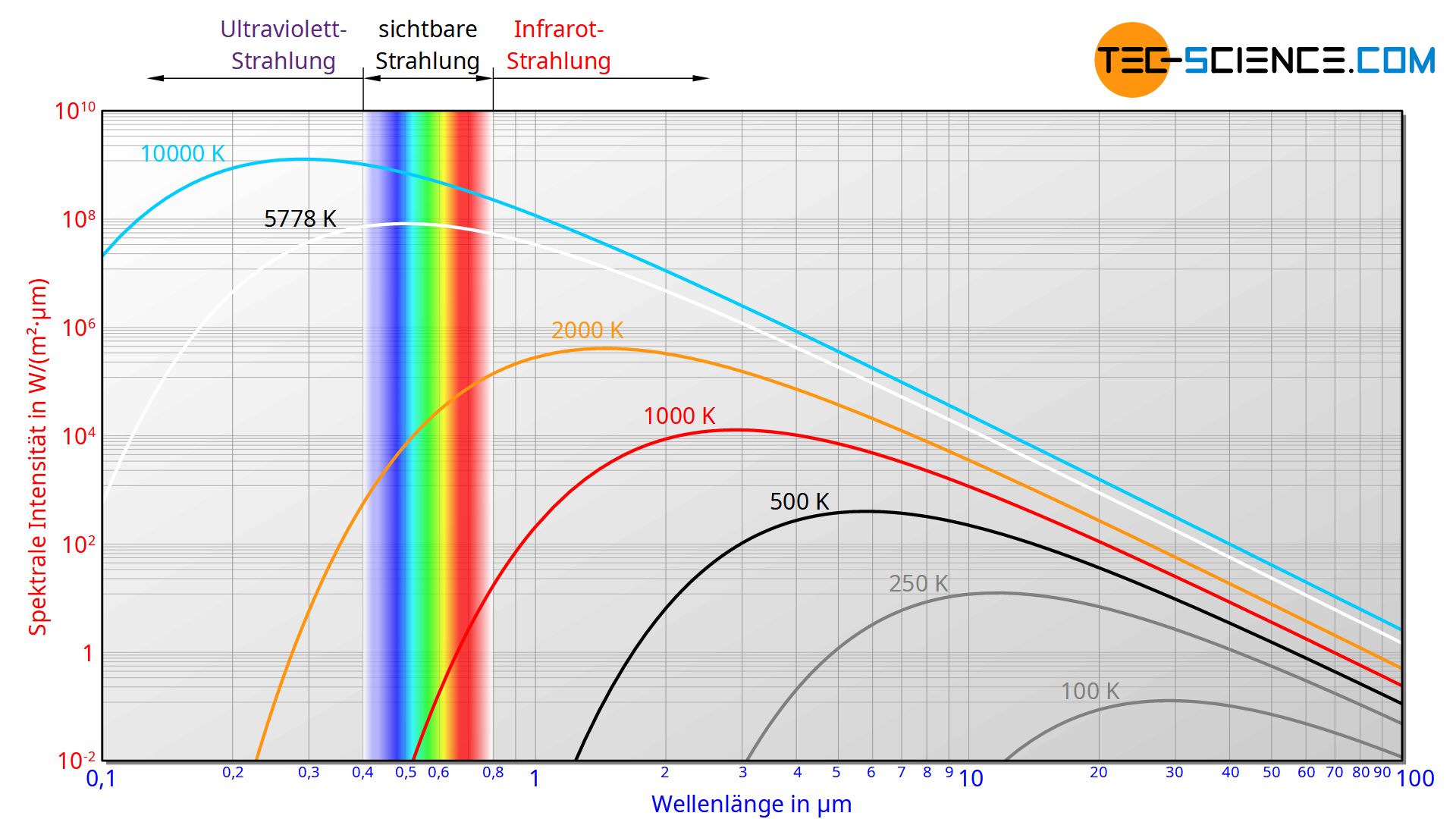
Bei dem Begriff der Intensität handelt es sich im physikalischen Sinne um eine Strahlungsleistung pro Flächeneinheit (Flächenleistungsdichte), d.h. um die pro Flächeneinheit emittierte Strahlungsenergie pro Zeit. Mit Fläche ist in diesem Fall die Fläche der Öffnung zum Hohlraum gemeint, da diese Öffnung sozusagen als Strahlungsquelle und damit als eigentlicher schwarzer Körper fungiert. Die Intensität wird für die Auftragung im Diagramm zudem auf die Wellenlänge selbst bezogen. Dies ist deshalb nötig, weil die Intensität immer nur innerhalb eines Wellenlängenbereichs gemessen werden kann und nicht für eine exakte Wellenlänge bestimmt werden kann. Diese Intensität pro Wellenlänge wird deshalb auch als spektrale Intensität bezeichnet. In einem solchen Diagramm entspricht die Fläche unter der Kurve der Intensität mit der die Strahlung im entsprechenden Wellenlängenintervall wahrgenommen wird. Die Fläche unter der gesamten Kurve entspricht somit der insgesamt abgestrahlten Intensität.
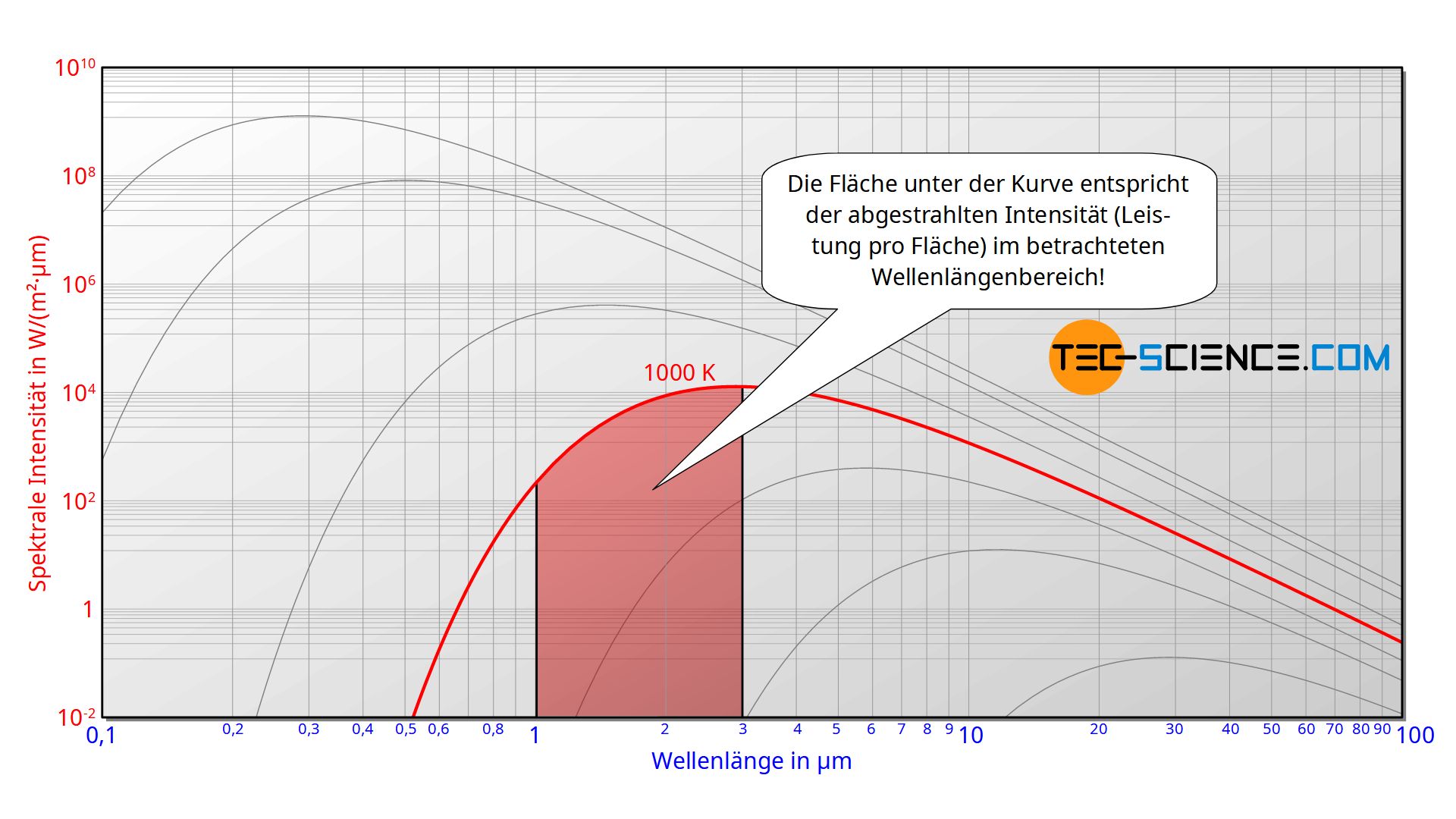
Man stellt im Experiment nun fest, dass das abgestrahlte Wellenlängenspektrum nur von der Temperatur abhängig ist und nicht vom Material. Die Hohlraumstrahlung eines Aluminiumblock weist somit dieselbe spektrale Intensitätsverteilung auf wie ein Block aus Stahl oder Messing.
Das Wellenlängespektrum einer Schwarzkörperstrahlung ist nur von der Temperatur abhängig und nicht vom Material!
Die genauere Untersuchung des Wellenlängenspektrums zeigt, dass sich das Maximum der spektralen Intensität mit zunehmender Temperatur zu immer geringeren Wellenlängen verschiebt. Bei relativ niedrigen Temperaturen liegt das Maximum im Infrarotbereich und die Strahlung ist für unser Auge nicht sichtbar. Mit zunehmender Temperatur verschiebt sich das Wellenlängenspektrum allerdings in den sichtbaren Bereich. Das Loch bzw. der Schwarze Körper beginnt nun aufgrund der sichtbar emittierten Strahlung zu leuchten.
Ab ca. 1000 K handelt es sich dabei um ein leicht rötliches leuchten. Man kennt dies bspw. von glühendem Metall. Die untere Abbildung zeigt hierzu das Glühen eines Heizelementes eines Backofens. Die Temperatur liegt dabei im Bereich von etwa 800 °C.

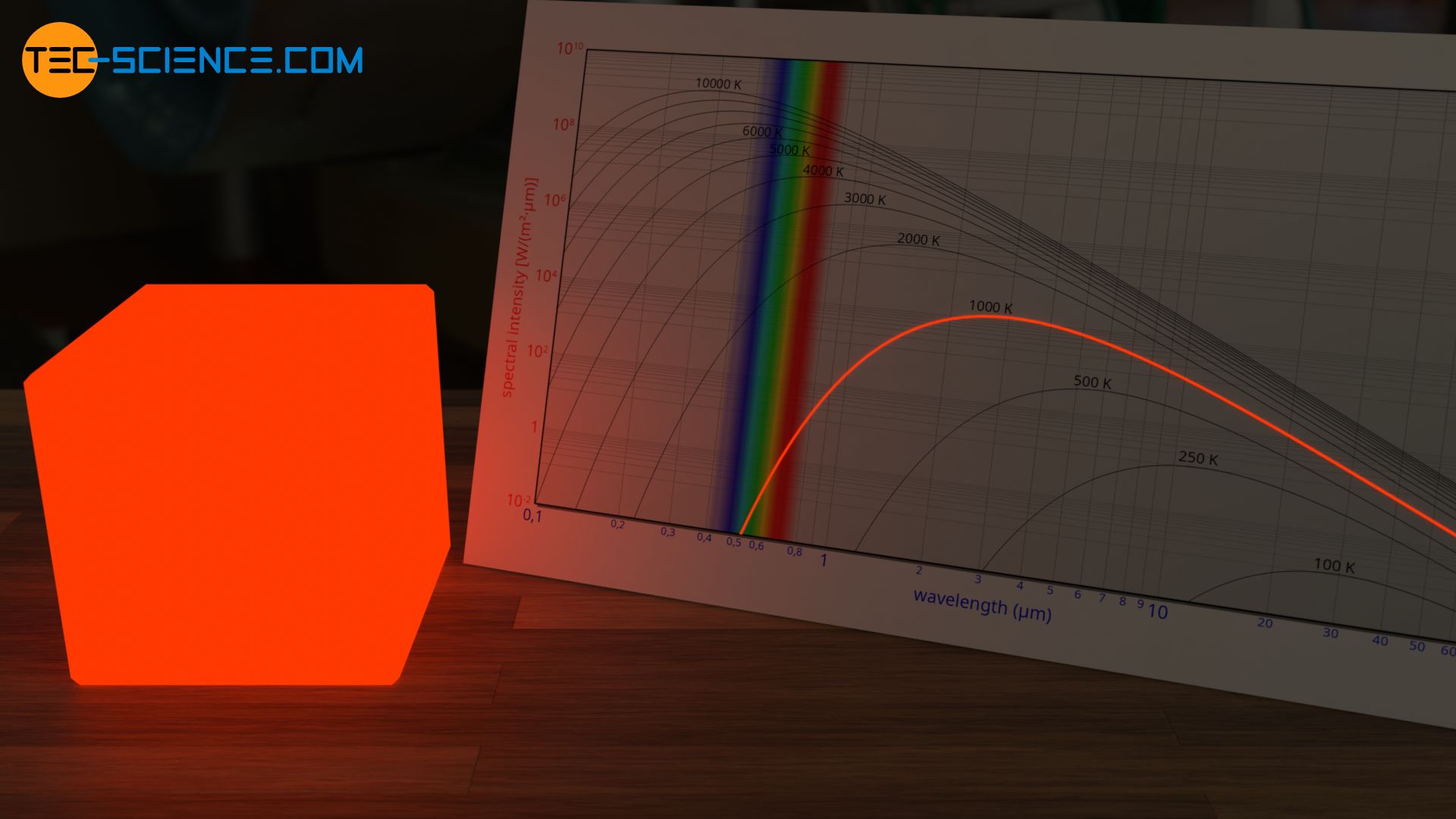
Bei 2000 K treten im Wellenlängenspektrum vermehrt Anteile im gelben Wellenlängenbereich auf. Der Körper strahl folglich eher gelblich. Die abgestrahlte Intensität ist im sichtbaren Bereich jedoch relativ hoch. Es werden dann praktisch alle Farbrezeptoren in unserem Auge „überbelichtet“. In diesem Fall werden alle Rezeptoren nahezu identisch angeregt. Die gelbliche Strahlung bei einer solch hohen Temperatur erscheint für unser Auge deshalb meist weiß (siehe auch Artikel Farbwahrnehmung).
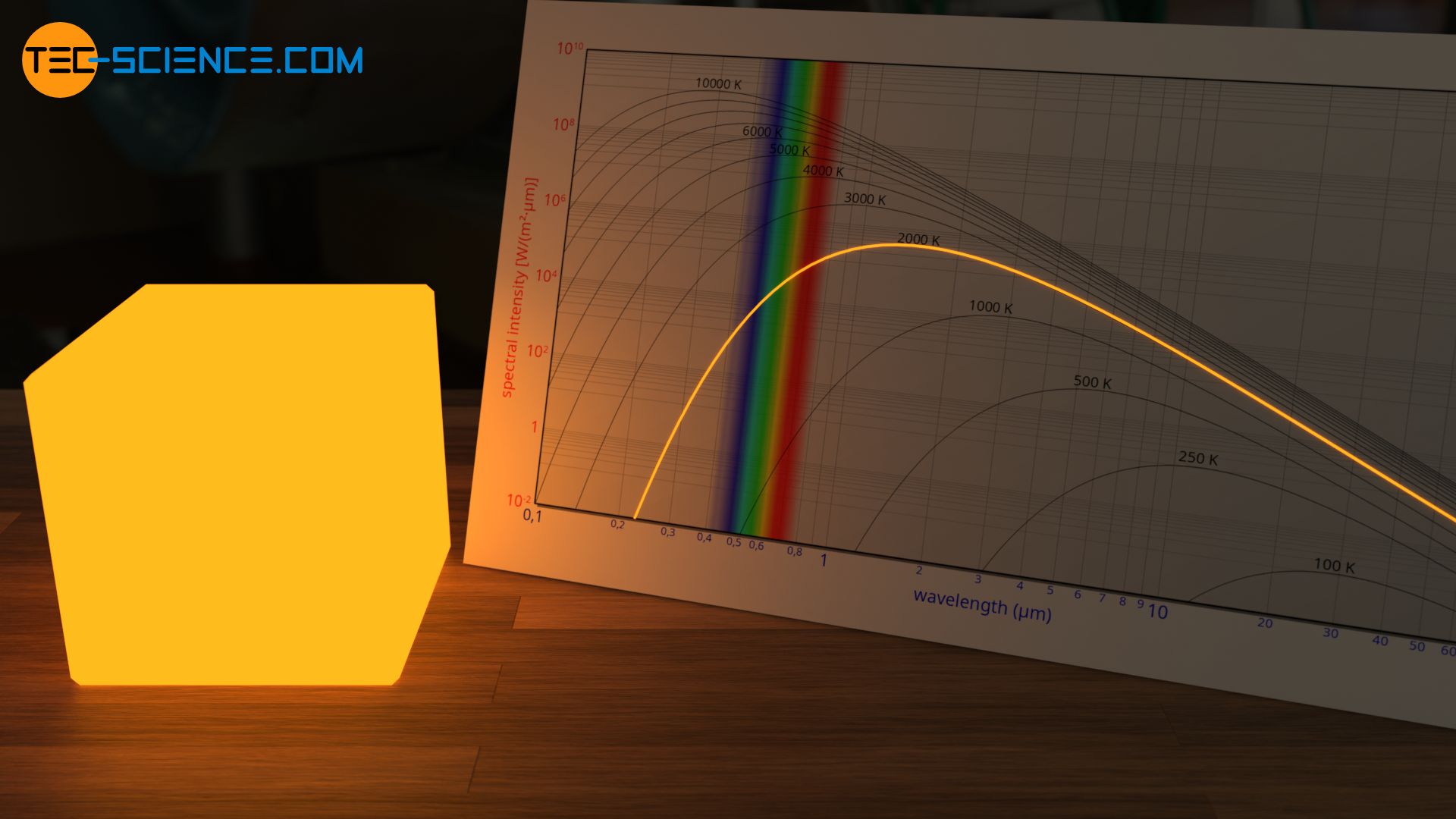
Auch die weiße Farbe des Lichtbogens beim Schweißen mit Temperaturen von über 3000 K lässt sich mit der Überblendung der Farbrezeptoren in unserem Auge erklären. Tatsächlich handelt es sich bei dem abgestrahlten Spektrum jedoch eher um eine gelbliches Wellenlängenspektrum. Diese gelbliche Farbe kann als solche nur wahrgenommen werden, wenn die Intensität stark verringert wird, z.B. wenn sie indirekt als Streulicht auf einem weißen Blatt Papier beobachtet wird.

Darüber hinaus zeigt sich anhand der spektralen Verteilung, dass bei solch hohen Temperaturen von über 3000 K vermehrt Ultraviolett-Strahlung emittiert wird. Dies erklärt die erforderliche Schutzausrüstung beim Schweißen, um die Augen und die Arme zu schützen. Ohne bedeckte Arme würde man durch die UV-Strahlung ansonsten einen „Sonnenbrand“ bekommen!
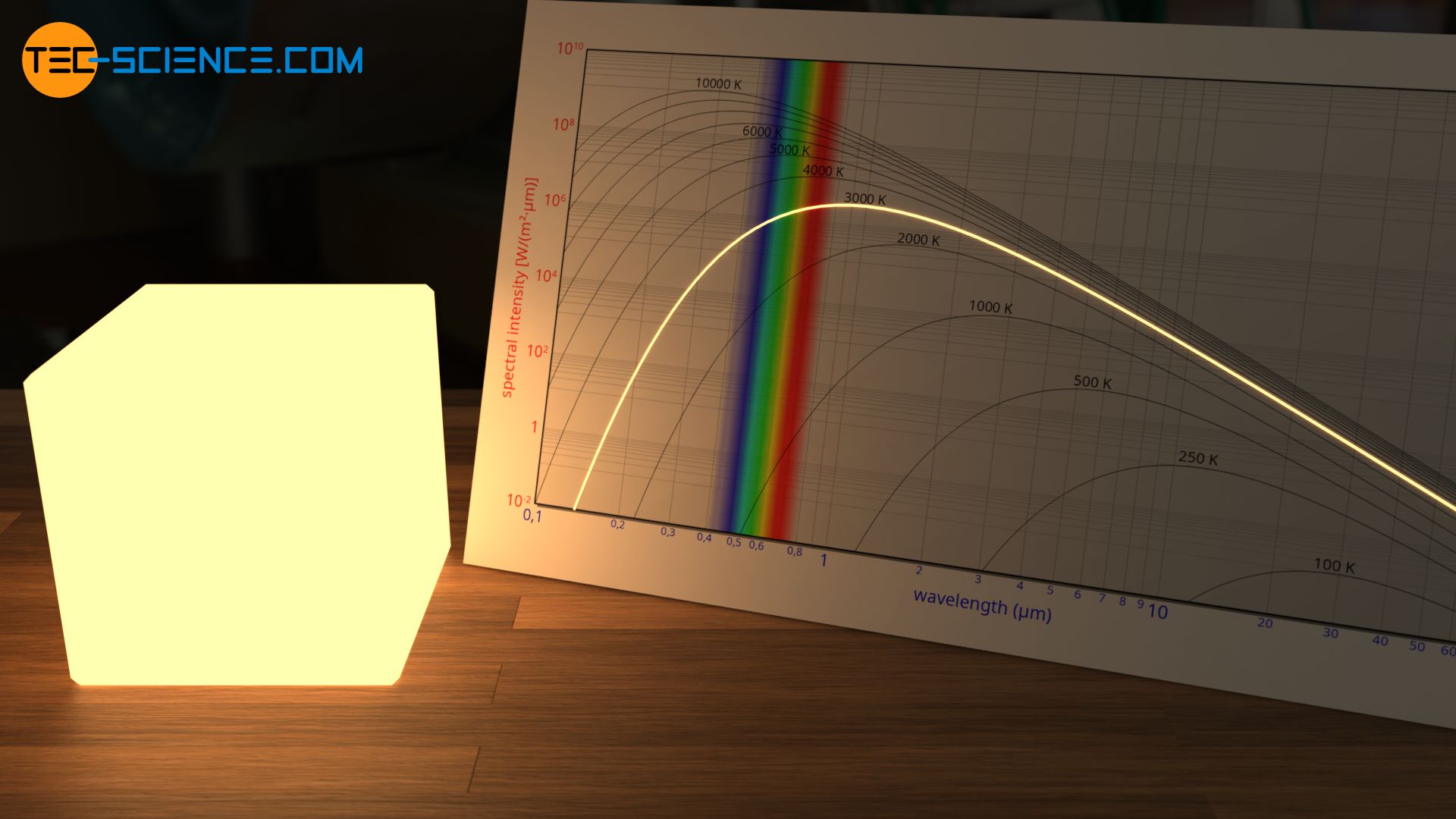
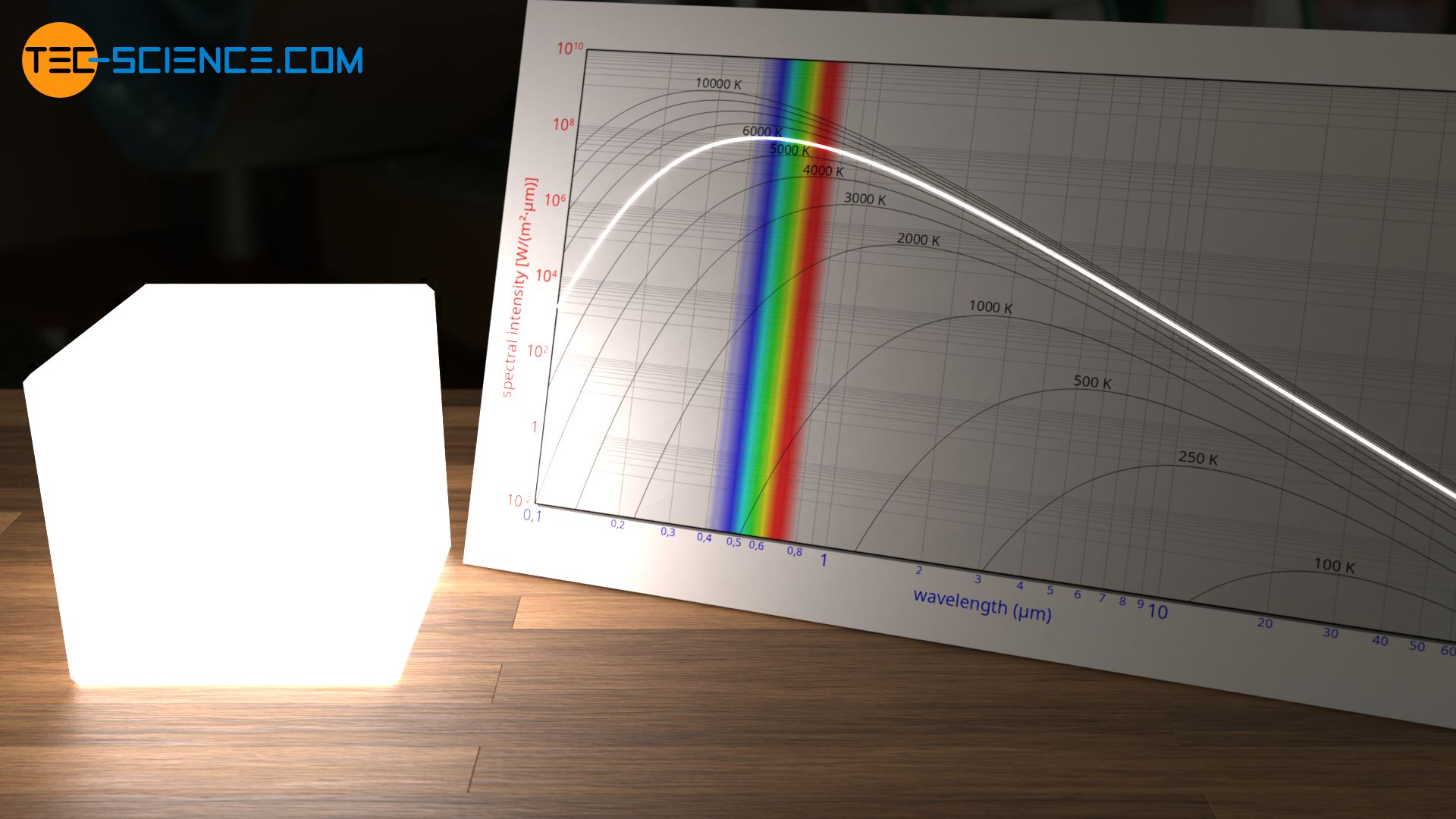
Bei noch größeren Temperaturen von etwa 6000 K sind im abgestrahlten Wellenlängenspektrum nahezu alle sichtbaren Wellenlängenanteile mit gleicher Intensität vertreten. Bei dieser Strahlung handelt es sich also um eine weiße „Farbe“. Dies erklärt auch die weiße Sonnenstrahlung, da die Sonne als nahezu perfekter Schwarze Körper eine Oberflächentemperatur von 5778 K aufweist! Dabei strahlt die Sonne auch in nicht unerheblichem Maße UV-Strahlung ab. Zum Glück wird jedoch ein Großteil dieser UV-Strahlung durch die Erdatmosphäre absorbiert.

Deutlich höhere Temperaturen als unsere Sonne haben bspw. sogenannte Blaue Riesen. Diese astronomischen Gebilde haben teilweise das 50-fache der Sonnenmasse. Die Oberflächentemperaturen können dabei mehrere 10.000 Kelvin betragen. Bei diesen Temperaturen sind im abgestrahlten Spektrum die blauen Wellenlängenanteile stärker vertreten als die rötlichen Anteile. Das Licht solcher Blauer Riesen erscheint deshalb bläulich, was letztlich auch Namensgeber dieser Sternenart ist.
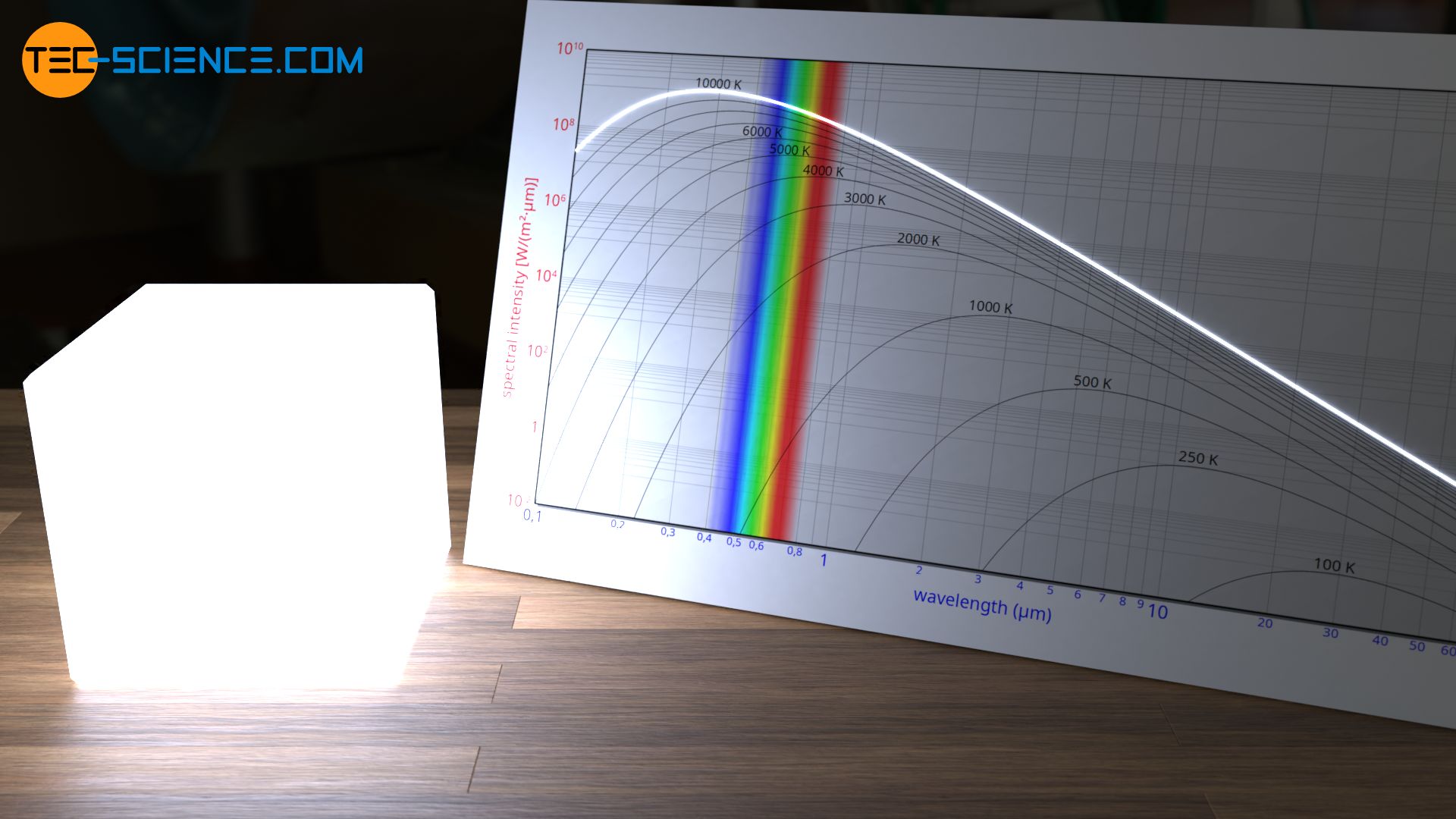
Die mathematische Beschreibung der Schwarzkörperstrahlung wird im Artikel Planck’sches Strahlungsgesetz näher behandelt.