In addition to the hydrodynamic boundary layer, the thermal boundary layer and the concentration boundary layer also have a decisive influence on the entire heat and mass transport in a flow.
Temperature boundary layer (thermal boundary layer)
In the article Hydrodynamic boundary layer, the course of the velocity profile in laminar and turbulent flows has already been explained in detail using the example of a plate. However, the plate generally influences not only the flow velocity but also the temperature of the flow, provided that the temperature of the fluid differs from that of the plate. Let us therefore consider the following isothermally heated plate with the temperature T0. The temperature of the freestream is T∞.
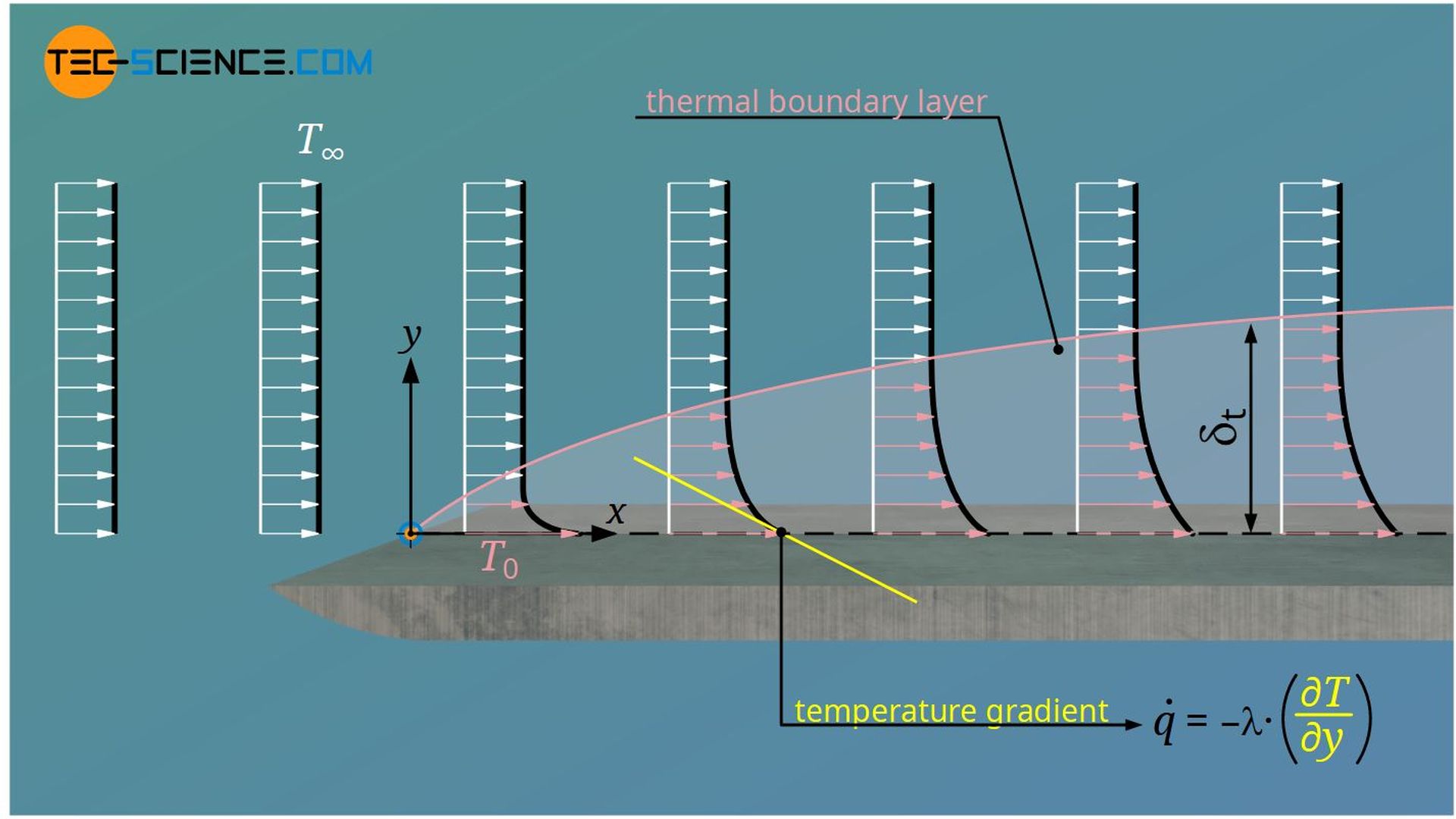
The temperature of the fluid directly at the wall ist T0, because the fluid adheres to the plate due to the no-slip condition. The temperature then decreases perpendicular to the main flow direction until the temperature T∞ of the freestream is reached. Analogous to the velocity boundary layer, a temperature boundary layer can thus be defined, which is also called a thermal boundary layer.
The boundary area up to which the difference between local temperature and temperature of the freestream has reached 99 % of the temperature difference between the plate and freestream is also called thermal boundary layer.
The thermal boundary layer also gradually grows, as the heat penetrates more and more into the fluid and thus heats the fluid layers over time. The thermal boundary layer is thus defined by the fact that temperature gradients exists and thus transport of heat takes place.
At the same time, however, the heat transport has an effect on the flow, since the temperature decisively determines the viscosity of the fluid. For example, the fluid starts to flow faster due to the decreasing viscosity caused by an increase in temperature. This, in turn, has an effect on the heat transfer and thus on the flow itself. The thermal and hydrodynamic boundary layer therefore influence each other. The thickness of both boundary layers generally differ from each other!
Concentration boundary layer (substance boundary layer)
When two or more fluids are mixed, mass transport is not only caused by convection currents, but also by differences in concentration. The associated mass transport by diffusion is treated in the same way as heat transport by conduction (see article Fick’s laws of diffusion). Instead of a thermal conductivity and a temperature gradient, there is now a diffusion coefficient D and a concentration gradient ∂c/∂y. The heat flux \(\dot q\) corresponds to a diffusion flux \(\dot n\) (= amount of substance per unit area per unit time).
| heat transport | mass transport | momentum transport | |
|---|---|---|---|
| law of | Fourier | Fick | Newton |
| \begin{align} \notag &\boxed{\dot q = – \lambda ~\frac{\partial T}{\partial y}} \end{align} | \begin{align} \notag &\boxed{\dot n = – D~ \frac{\partial c}{\partial y}} \end{align} | \begin{align} \notag &\boxed{\tau = \eta~ \frac{\partial v}{\partial y}} \left(= \dot p_a\right) \end{align} | |
| drive | temperature gradient | concentration gradient | velocity gradient |
| characteristic quantity | thermal conductivity | diffusion coefficient | viscosity |
| flux | heat flux | diffusion flux | momentum flux |
At this point an analogy to the transport of momentum can also be drawn. In fact, shear stresses τ also have the dimension of a flux (analogous to the heat flux or diffusion flux). By definition, a force is a change of momentum per unit time (\(F=\frac{\Delta p}{\Delta t}=\dot p\)) and thus represents a momentum flow rate. If one relates this momentum flow rate to an area, as in the case of shear stresses, one can also speak of a momentum flux (=\(\dot p_a\)).
An analogy between all three cases is also evident with regard to the gradients. The drive for the momentum flow is a velocity gradient, just like a temperature gradient is the drive for a heat flow or a concentration gradient is the drive for a mass transport. In the same way as the thermal boundary layer and the velocity boundary layer, a concentration boundary layer can be defined for mass transfer by diffusion:
The boundary area up to which the difference between local concentration and concentration of the freestream has reached 99 % of the concentration difference between the plate and freestream is also called concentration boundary layer.
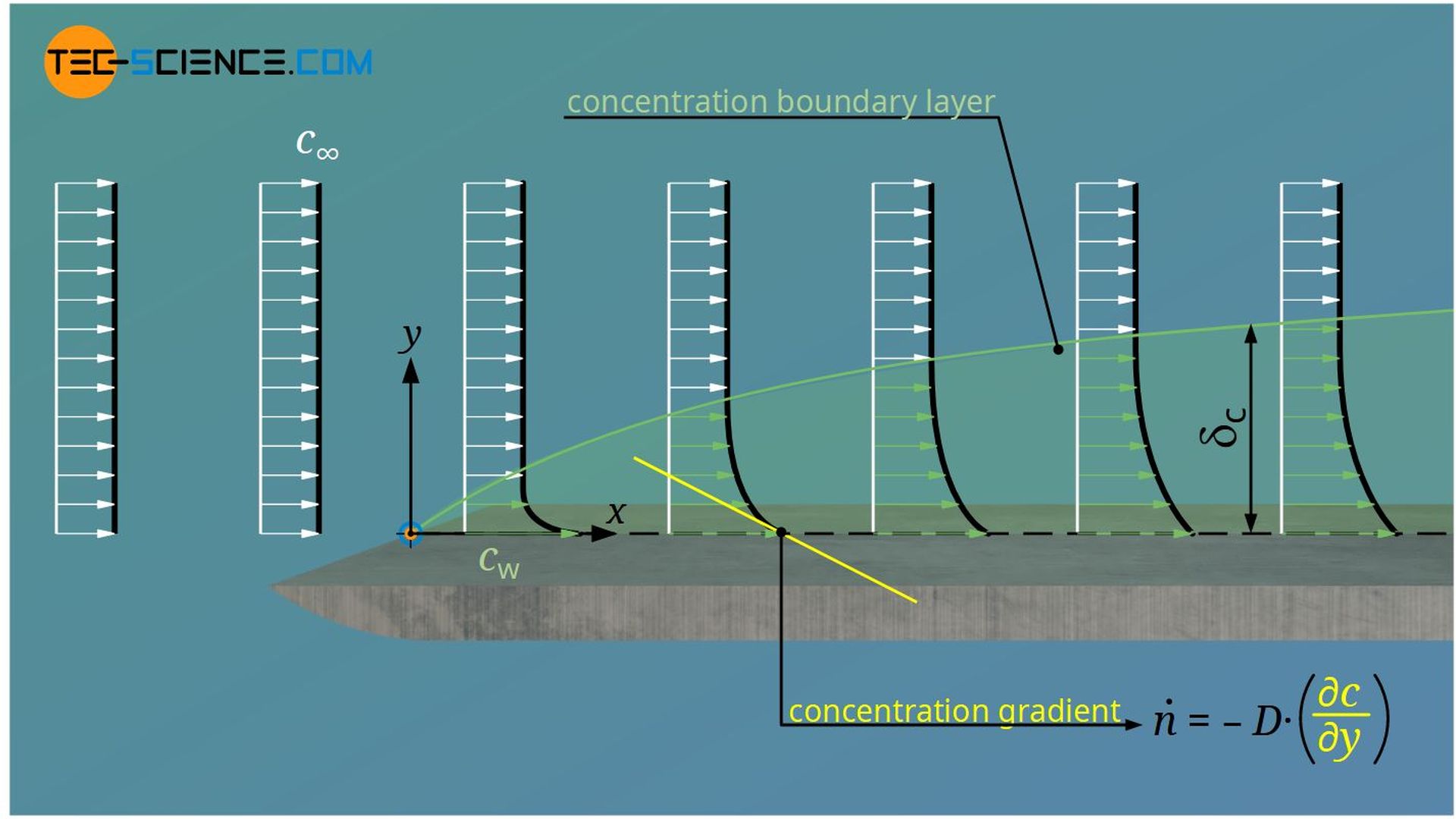
A closer look reveals that the concentration boundary layer does not exist independently of the hydrodynamic or thermal boundary layer. On the one hand, especially for gases, the diffusion coefficient is very strongly dependent on the temperature, so that the thermal boundary layer has a direct influence on mass transport. On the other hand, the flow in the hydrodynamic boundary layer takes away the diffused particles. If this removal takes place relatively quickly, a large concentration gradient is formed. This in turn results in increased mass transport. Thus, the velocity boundary layer also directly influences the concentration boundary layer.
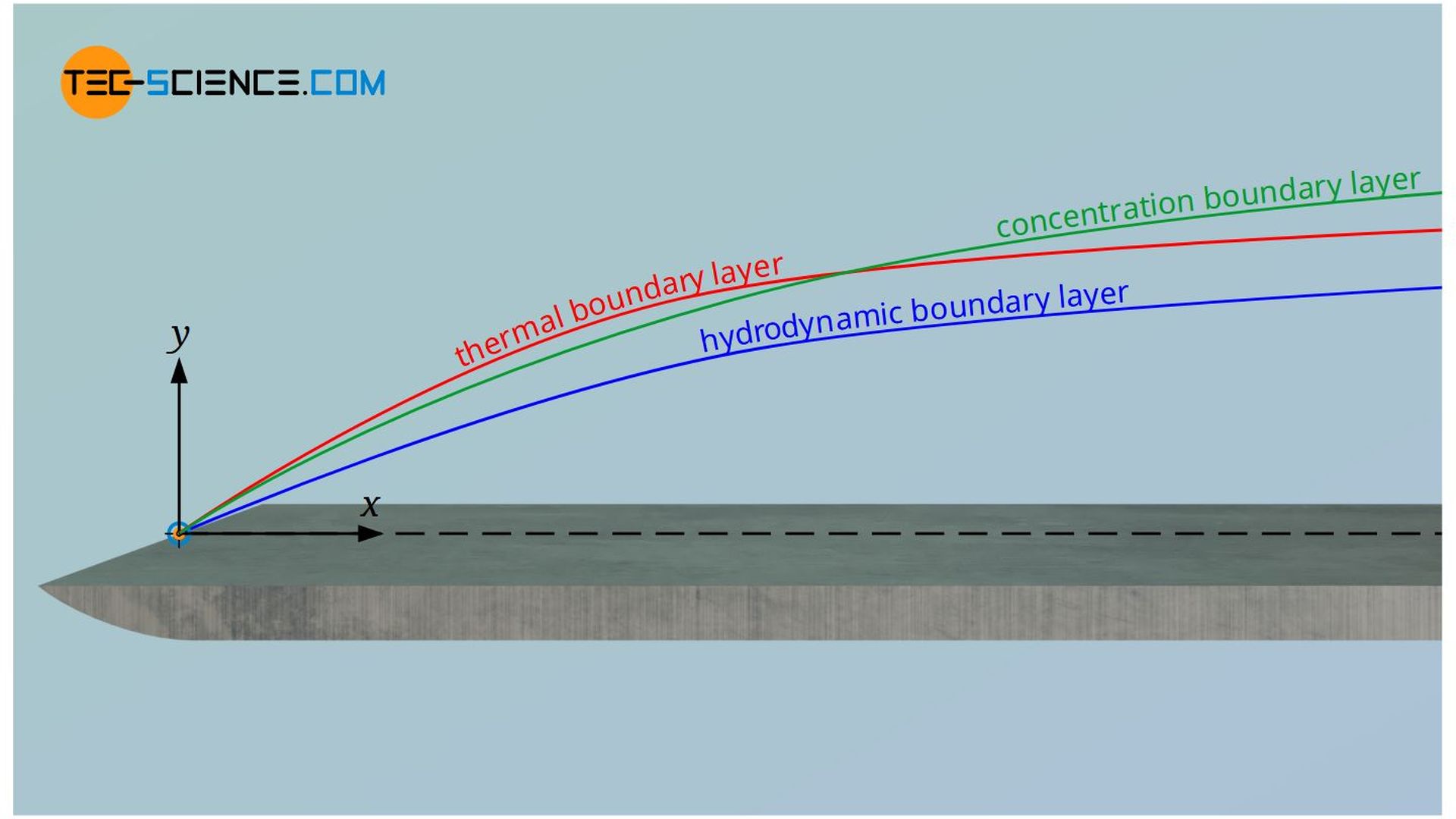
The conclusion is that all three boundary layers always influence each other and cannot be considered independently of each other. This leads directly to the dimensionless numbers, which relate two boundary layers to each other. These are discussed in more detail in the following section.






