Learn more about calculating the final temperature of several objects with different temperatures in this article.
Heating of several objects
In practice, when heating or cooling objects, one usually has to deal with several materials that are heated or cooled simultaneously. Such simultaneous heating can be seen, for example, when heating a sausage in a pot of water. The heat output by the hotplate heats both the pot and the water at the same time, as well as the sausage inside. The surrounding air is also partially heated by convection currents, but this will be neglected in the following.

The question arises as to how much total heat energy must be transferred in order to change the temperature of this system consisting of several objects by a certain amount.
Derivation of the relationship between heat and temperature change
To derive the relationship between heat and temperature change, it is assumed that the considered objects of the system have a common initial temperature. In addition, it is assumed that a common temperature is again established after heating. In this case, each object obviously experiences the same temperature change.
Based on the respective heat capacities C of the objects, the absorbed heat Q with a given temperature change ΔT can be determined for each object:
\begin{align}
\label{qq}
&\boxed{Q = C \cdot \Delta T} \\[5px]
\end{align}
The sum of all amounts of heat transferred to the individual objects corresponds to the total heat transferred, which is to be provided by the hotplate in the example above. In principle, this statement can be extended to any number of objects to be heated:
\begin{align}
\label{q}
Q_\text{tot} &= Q_1+Q_2+Q_3+… \\[5px]
&= C_1 \cdot \Delta T + C_2 \cdot \Delta T + C_3 \cdot \Delta T +… \\[5px]
& = \underbrace{(C_1+C_2+C_3+…)}_{C_\text{tot}} \cdot \Delta T \\[5px]
& = C_\text{tot} \cdot \Delta T \\[5px]
\end{align}
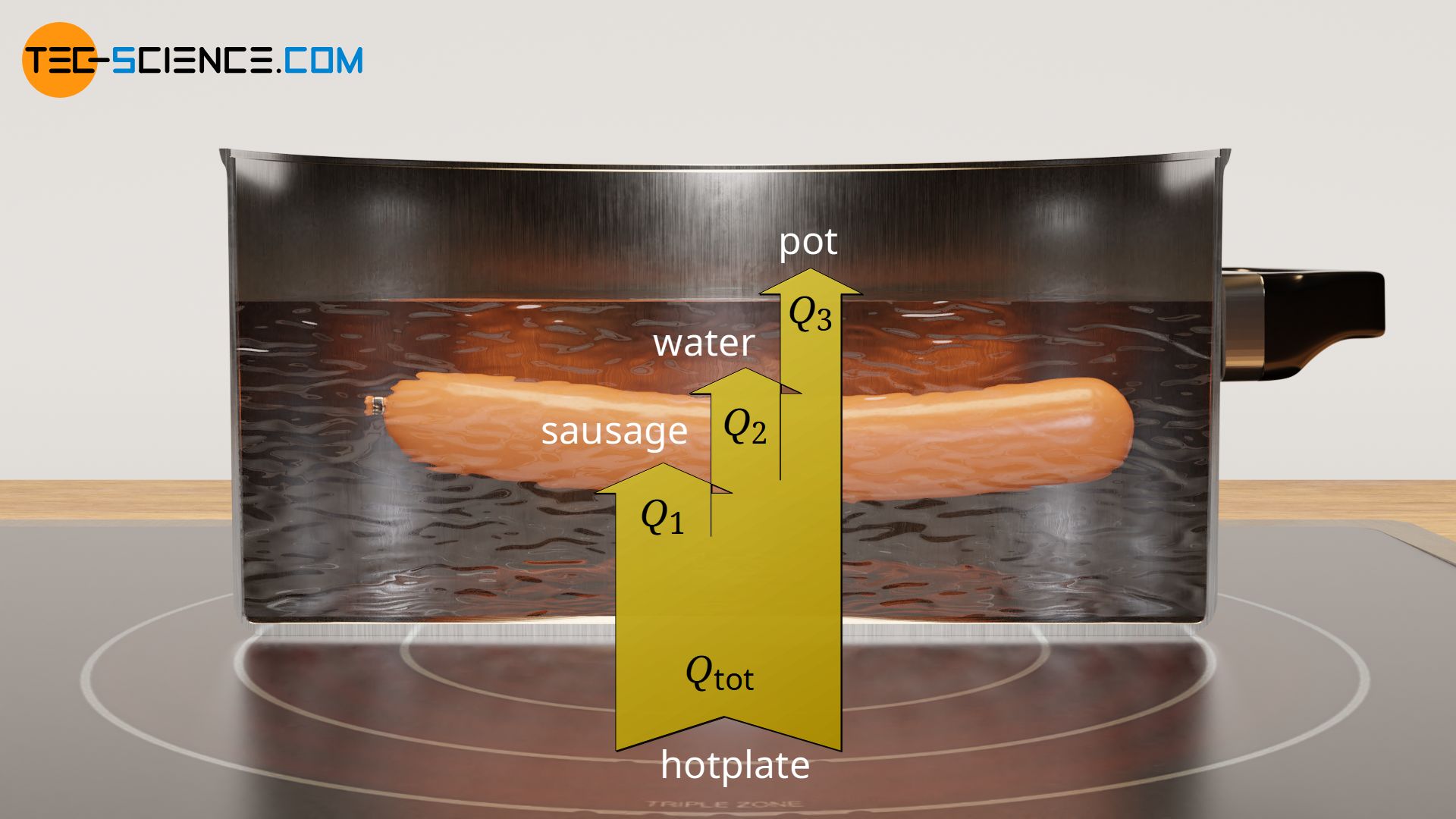
It turns out that the total heat capacity Ctot of a system consisting of several objects, can be determined from the sum of the individual heat capacities C of the respective objects. This total heat capacity can then be used to determine the total heat energy Qtot required for a given temperature change ΔT:
\begin{align}
\label{1}
&\boxed{Q_\text{tot} = C_\text{tot} \cdot \Delta T} \\[5px]
\notag
&~~\text{where} ~~~ \\[5px]
\label{0}
&\boxed{C_\text{tot}=C_1+C_2+C_3+…} \\[5px]
\end{align}
The heat capacity of a system consisting of several objects can be determined from the sum of the heat capacities of the individual objects!
Note that the derived relationship according to formula (\ref{1}) is not only valid for a heating, but also for cooling. In this case, ΔT denotes the decrease in temperature and Qtot the total heat to be dissipated.
Determination of heat capacities
The derived relationship is of course not only valid for a system consisting of several individual objects, but also applies to an object composed of different materials. In this case, the individual heat capacities correspond to the heat capacities of the materials used. The heat capacities C of the individual objects or materials can be determined from the specific heat capacities c and the respective masses m in the case of homogeneous substances (see article Heat capacity of objects):
\begin{align}
\label{2}
&\boxed{C = c \cdot m} ~~~\text{applies only to a homogeneous substance} \\[5px]
\end{align}
Remarks
In the above example, the various objects will usually heat up to different degrees for the operation of the hotplate. It can be assumed that the pot heats up first, then the water and finally the sausage. Thus, during the heating process, there will be different temperatures. However, sooner or later a common temperature will be reached after the hotplate is switched off.
The pot, which is usually warmer, will transfer some of the heat previously supplied by the hotplate to the water after the hotplate is switched off, and this in turn will then be transferred to the sausage. Thus, there is only a kind of redistribution of the total heat already supplied (note, that heat losses to the surroundings are neglected). But sooner or later, when a common temperature has been reached (thermodynamic equilibrium), all objects have experienced the same temperature change and equation (\ref{1}) is still valid. It must be presupposed of course that at the beginning water, sausage and pot have the same temperature!
If, on the other hand, the different objects have different temperatures at the beginning or if there is no common final temperature and thus no uniform temperature change, then the amount of heat must be determined explicitly for each object on the basis of its individual temperature change and its heat capacity and then summed up (see also the article Final temperature of mixtures).






