Centrifugal forces in the belt of a belt drive

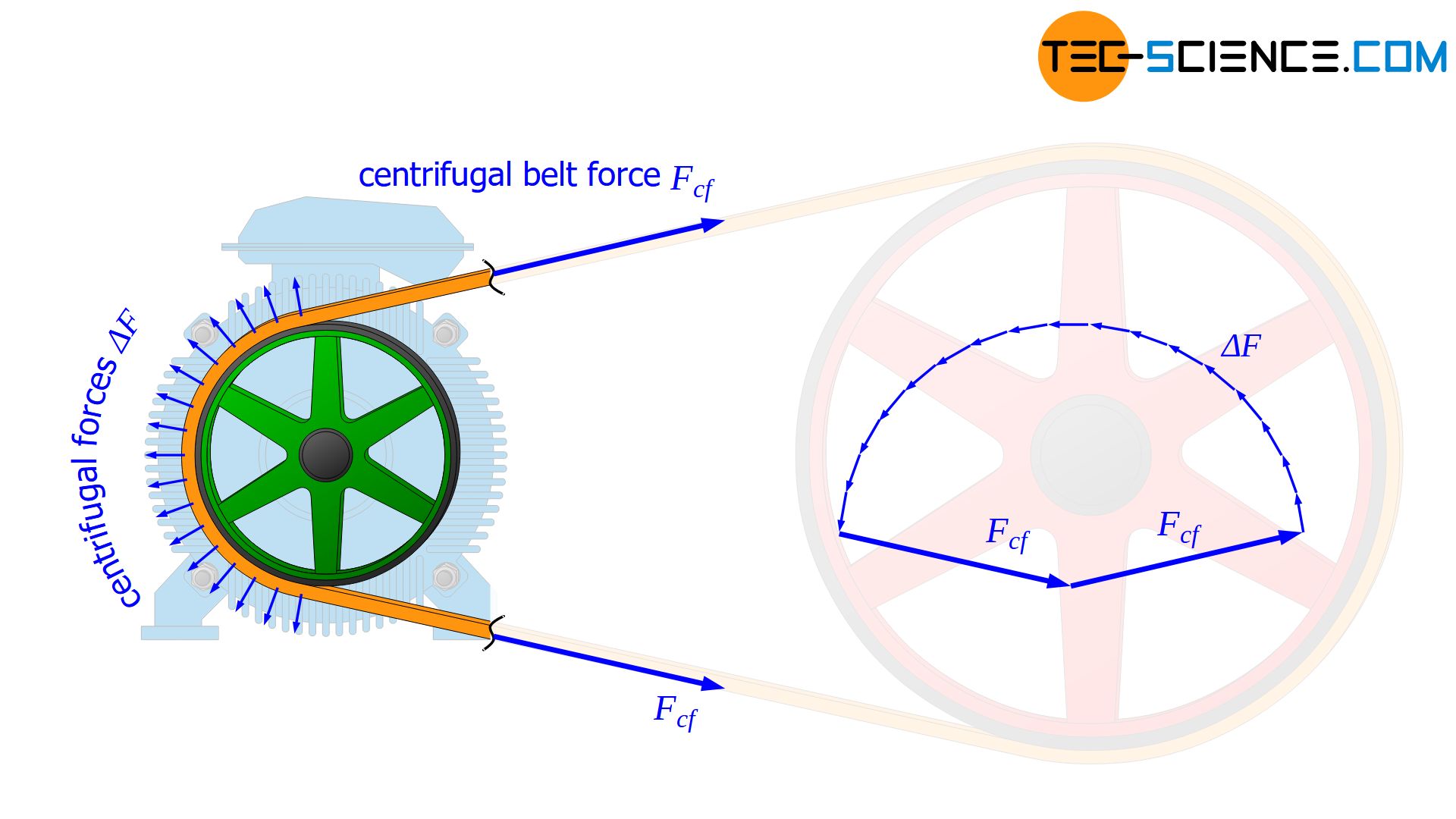
At high speeds, the centrifugal forces acting on the belt reduce the contact pressure and thus the maximum transmittable circumferential force.

Formation of centrifugal forces

With a belt drive in a resting state, only the pretensioning force F_p acts in the belt. This force is the same for all belt sections, i.e. in both spans of the belt. Only under load different belt forces act and a tight side with the belt force F_t and a slack side with the belt force F_s is formed (see article Power transmission of a belt drive). If the belt drive comes to a standstill under load or if only low speeds are used, the belt forces at constant torque can be regarded as almost independent of the belt speed.

At higher belt speeds, however, considerable centrifugal forces act on the belt sections which run around the pulleys. These centrifugal forces are trying to pull the belt outwards and lift it off the pulley. However, this would mean a reduction in the contact pressure and thus a reduction in the frictional force between belt and pulley. With large circumferential forces to be transmitted, slippage could then occur.

To avoid this, the belt must also be tensioned by the amount of the centrifugal effect acting during operation (centrifugal belt force). This can be achieved, for example, through a higher overall preload force, or belt tensioning systems must be used.

The centrifugal forces are generated when the belt revolves around the pulley. They are tempted to lift the belt off the pulley. This must be counteracted with an additional preload by the amount of the centrifugal effect!

Influence of the centrifugal forces on the belt forces

Centrifugal forces are only generated at the wrap, i.e. when the belt rotates around the pulleys. There they are each directed radially away from the pulleys. Although no centrifugal forces act on the straight span sections of the belt, the belt tension there is influenced by the centrifugal forces. If the deflection of the slack side is neglected, then the centrifugal forces are directed symmetrically to the center line of pulleys. The centrifugal effect generated at the bended belt sections thus act outwards along that center line.

The centrifugal forces act as if someone were pulling the belt outwards. This then also becomes noticeable in the straight belt sections as an additional force to be applied by the belt (otherwise the contact pressure would drop). Due to the symmetrical pulling effect of the centrifugal forces, it is also clear that this has the same effect on both belt spans! As the total force in the tight side increases, so does the total force in the slack side.

Due to the centrifugal forces, the forces in tight side and the slack side increase equally!

Influence of the centrifugal forces on circumferential force

The tight side force F_t and slack side force F_s acting in the quasi-static state must increase at high speeds by the amount F_cf  in order to compensate for the centrifugal effect. However, the additionally acting centrifugal forces do not influence the transmitted circumferential force F_c at all (at least as long as the load of the belt under the centrifugal effect does not become too high and the belt is damaged):

\begin{align}
\label{umfang}
&F_c = \underbrace{\left(F_t + F_{cf}\right)}_{\text{total force at the tight side}} – \underbrace{\left(F_s + F_{cf}\right)}_{\text{total force at the slack side}} = F_t + F_{cf}- F_s – F_s = F_t – F_s \\[5px]
\label{nutzkraft}
&\boxed{F_c = F_t – F_s} \\[5px]
\end{align}

The centrifugal forces have no direct influence on the transmitted circumferential force!

Note that the terms tight side force and slack side force often only refer the forces F_t and F_s relevant for the actual power transmission according to equation (\ref{nutzkraft}) (i.e. forces in the quasi-static state). Centrifugal forces are often listed separately for the aforementioned reason that they have no influence on the transmitted circumferential force, although both forces (“static belt force+centrifugal force”) act together in the span and cannot be physically separated either, since they always act as a resulting sum of forces.

Calculation of the centrifugal belt force

The centrifugal belt force F_cf acting in the belt due to centrifugal effects, will be determined at a given belt speed v in the following section. Note that the term centrifugal belt force F_cf does not mean the centrifugal force itself, but rather to the force additionally acting in the belt by the centrifugal effect (this corresponds to the force by which the belt must be additionally tensioned at rest in order to completely compensate for the centrifugal forces)!

For the derivation of the centrifugal belt force it is sufficient to take a closer look at the load-free operation, i.e. the rotating belt without transmitting a circumferential force, since to due equation (\ref{umfang}) centrifugal forces do not influence the circumferential force and vice versa the circumferential force does not influence centrifugal forces.

If, for reasons of simplicity, only an “idling” belt is considered, then the only force acting in this belt is the required centrifugal belt force. This force ultimately holds the belt together. At constant belt speed the centrifugal belt force must be the same at any point of the belt for equilibrium reasons (otherwise a cut-off section of the belt would be accelerating). This applies in particular to the curved belt sections that run over the pulleys.

If such a belt section is considered more closely at the angle dφ, then the centrifugal force dF acting on this section must be balanced with the centrifugal belt forces F_cf. The vectorial sum of forces thus geometrically forms a closed triangle. The following relationship between the centrifugal force dF and belt force F_cf can then be established by the infinitesimal arc angle dφ:

\begin{align}
&\text{d} \varphi = \frac{\text{d}F}{F_{cf}} \\[5px]
\label{FF}
&\underline{F_{cf}= \frac{\text{d}F}{\text{d}\varphi}} \\[5px]
\end{align}

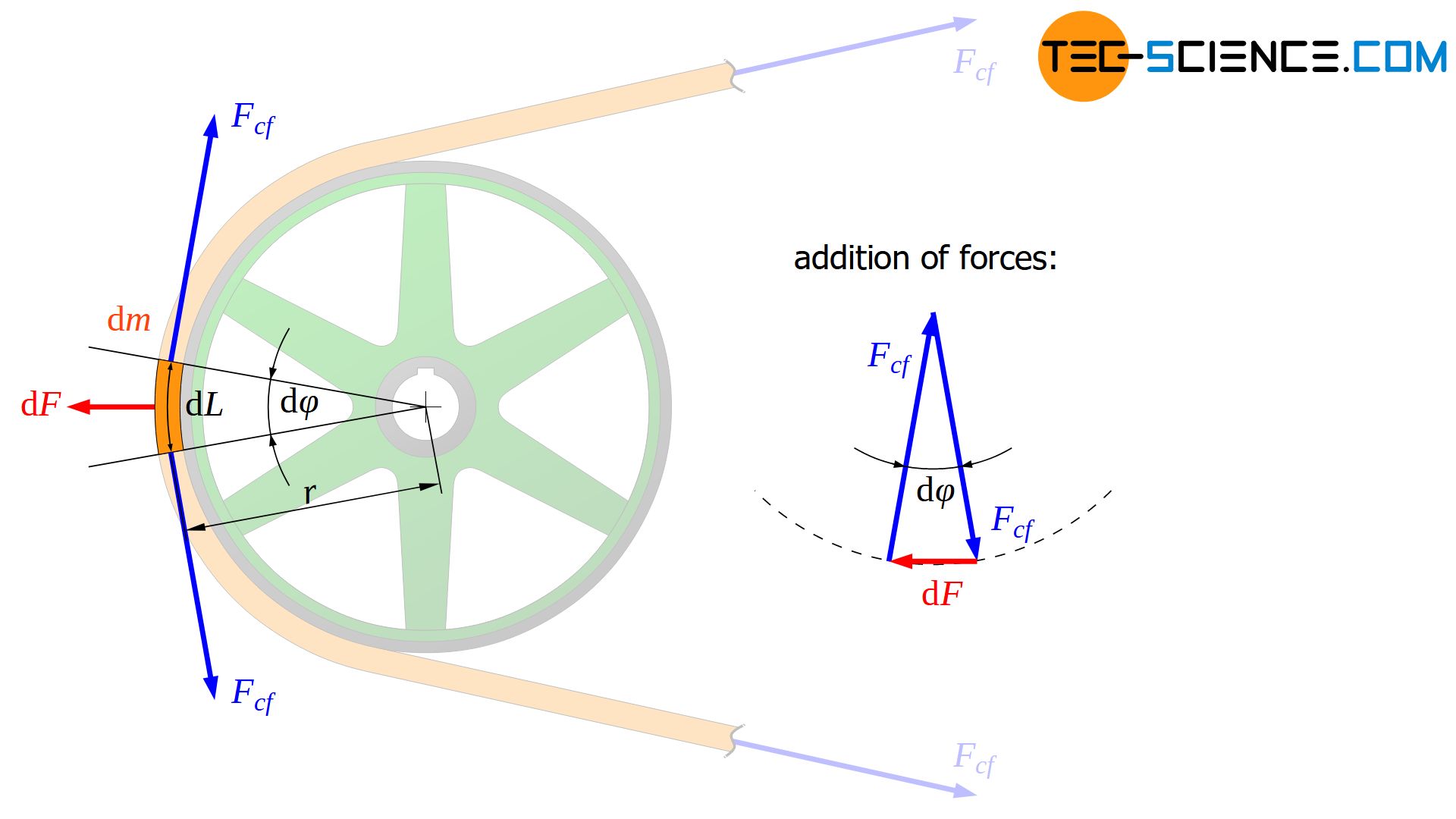
The centrifugal force dF acting on the considered belt section with a mass dm results from the pulley radius r and the rotational speed v as follows:

\begin{align}
&\text{d}F = \text{d}m \cdot \frac{v^2}{r} \\[5px]
\end{align}

The mass dm of the considered belt section depends on the angular section dφ. The larger the angle, the larger the mass dm. If the total mass m of the belt is referred to its total length L (“mass per unit length”) and denoted by m’

\begin{align}
&m’ = \frac{m}{L} ~~~\text{“mass per unit length”},
\end{align}

then the (arc) length dL of the considered belt section and thus its mass dm =m’⋅dL can be determined by the arc angle dφ:

\begin{align}
\text{d} \varphi  &= \frac{\text{d}L}{r}  \\[5px]
\text{d}L &= r \cdot \text{d} \varphi \\[5px]
\rightarrow \underline{\text{d} m} &= m’ \cdot \text{d}L = \underline{m’ \cdot r \cdot \text{d}\varphi}  \\[5px]
\end{align}

For the centrifugal force dF acting on the considered belt section at the angle dφ thus applies:

\begin{align}
\label{dF}
&\underline{\text{d}F} = \text{d}m \cdot \frac{v^2}{r} = m’ \cdot r \cdot \text{d}\varphi \cdot \frac{v^2}{r} = \underline{m’ \cdot \text{d}\varphi \cdot v^2} \\[5px]
\end{align}

If this equation (\ref{dF}) is now applied to equation (\ref{FF}), the required dependence of the centrifugal belt forces F_cf on the belt speed v is obtained:

\begin{align}
&F_{cf}= \frac{\text{d}F}{\text{d}\varphi} = \frac{m’ \cdot \text{d}\varphi \cdot v^2}{\text{d}\varphi} = m’ \cdot v^2  \\[5px]
&\boxed{F_{cf}= m’ \cdot v^2}  \\[5px]
\end{align}

The belt force F_cf caused by the centrifugal effect is therefore only dependent on the specific mass m’ and the square of the belt speed v. Neither the pulley diameter nor the wrap angle influence the centrifugal belt force! In order to completely compensate the centrifugal effect during operation, the belt must be additionally pre-tensioned by the amount of this centrifugal belt force!

The additional force required in the belt to compensate for the centrifugal forces that occur (centrifugal belt force) depends only on the speed and the specific mass of the belt! Neither the pulley diameter nor the wrap angle have any influence on this!