Basics of power transmission in belt drives

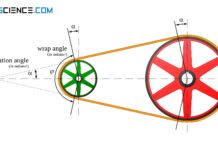
The basis of power transmission in the belt drive is the belt friction equation according to Euler and Eytelwein (rope friction equation).

Forces acting on a fixed pulley

In the article How does a belt drive work? it has already been explained that the power transmission of belt drives is due to frictional forces between belt and pulley (exception: toothed belt). This section will discuss the physical principles in more detail.

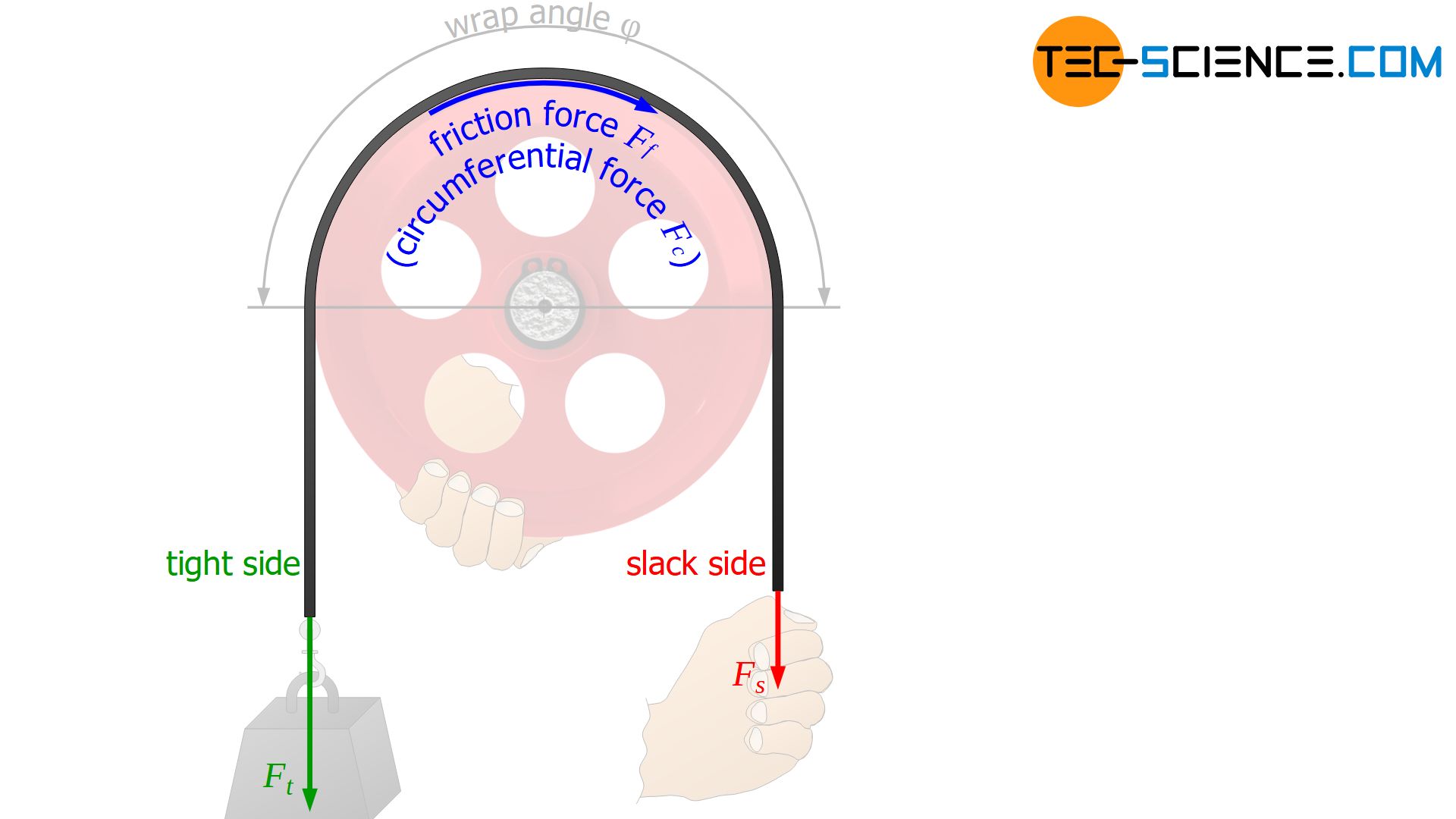
In order to better understand the forces acting on a belt drive, a fixed pulley is first considered, around which an open belt is placed. Imagine a person holding the pulley locked at its circumference.

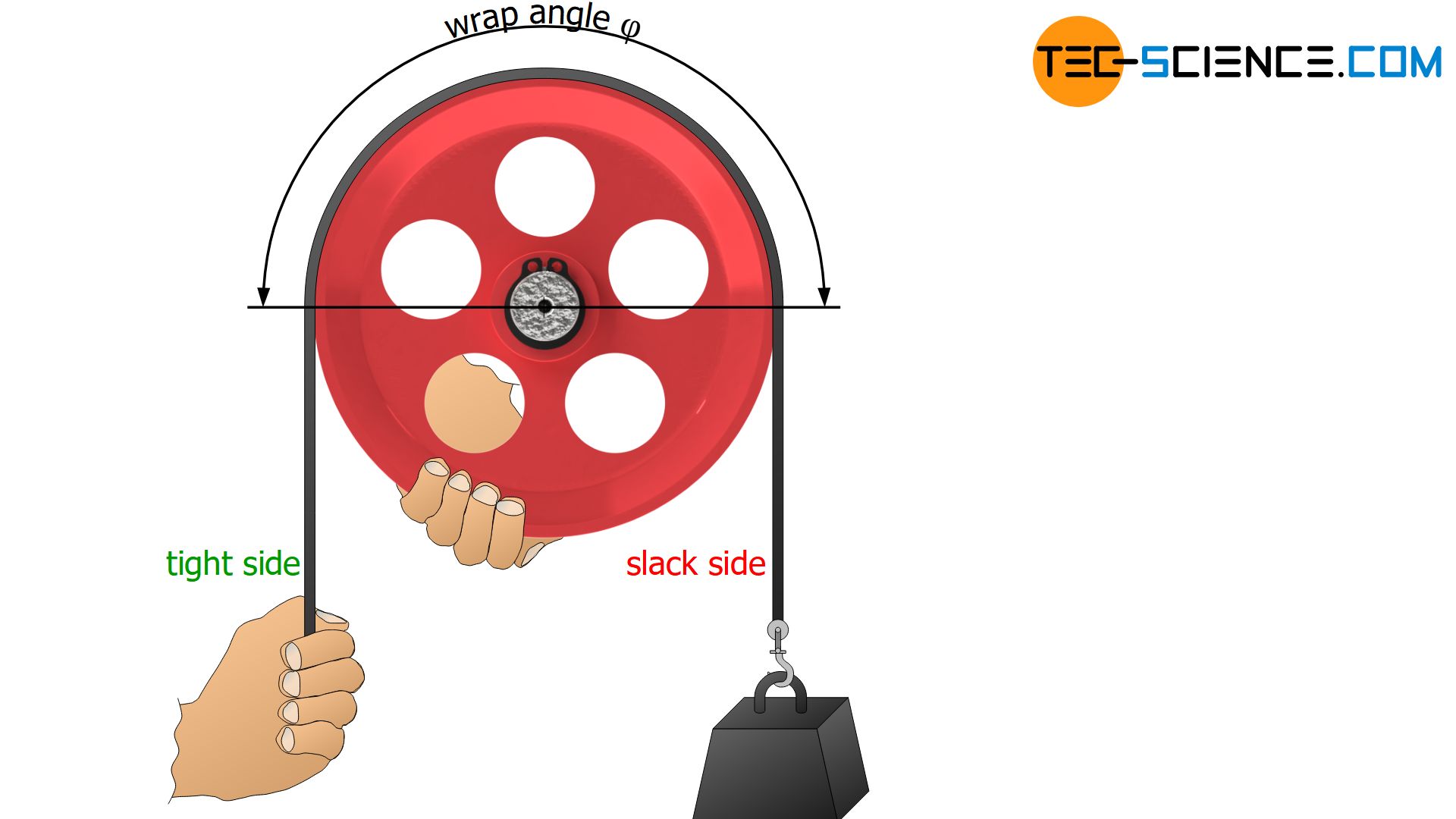
At one end of the belt a certain holding force F_s is applied (“slack side force”). In principle, such a holding force can also simply be a suspended load. At the other end of the belt, a person pulls with increasing force until the point is reached where the belt has not yet slipped over the fixed pulley. In this state, the maximum possible tensile force F_t,max is acting (“tight side force). A supposedly stronger pulling would cause the static friction to be overcome and the belt to slip over the pulley. However, then it would no longer be the static friction that would be active but the significantly lower sliding friction, which in turn would result in a reduced tensile force.

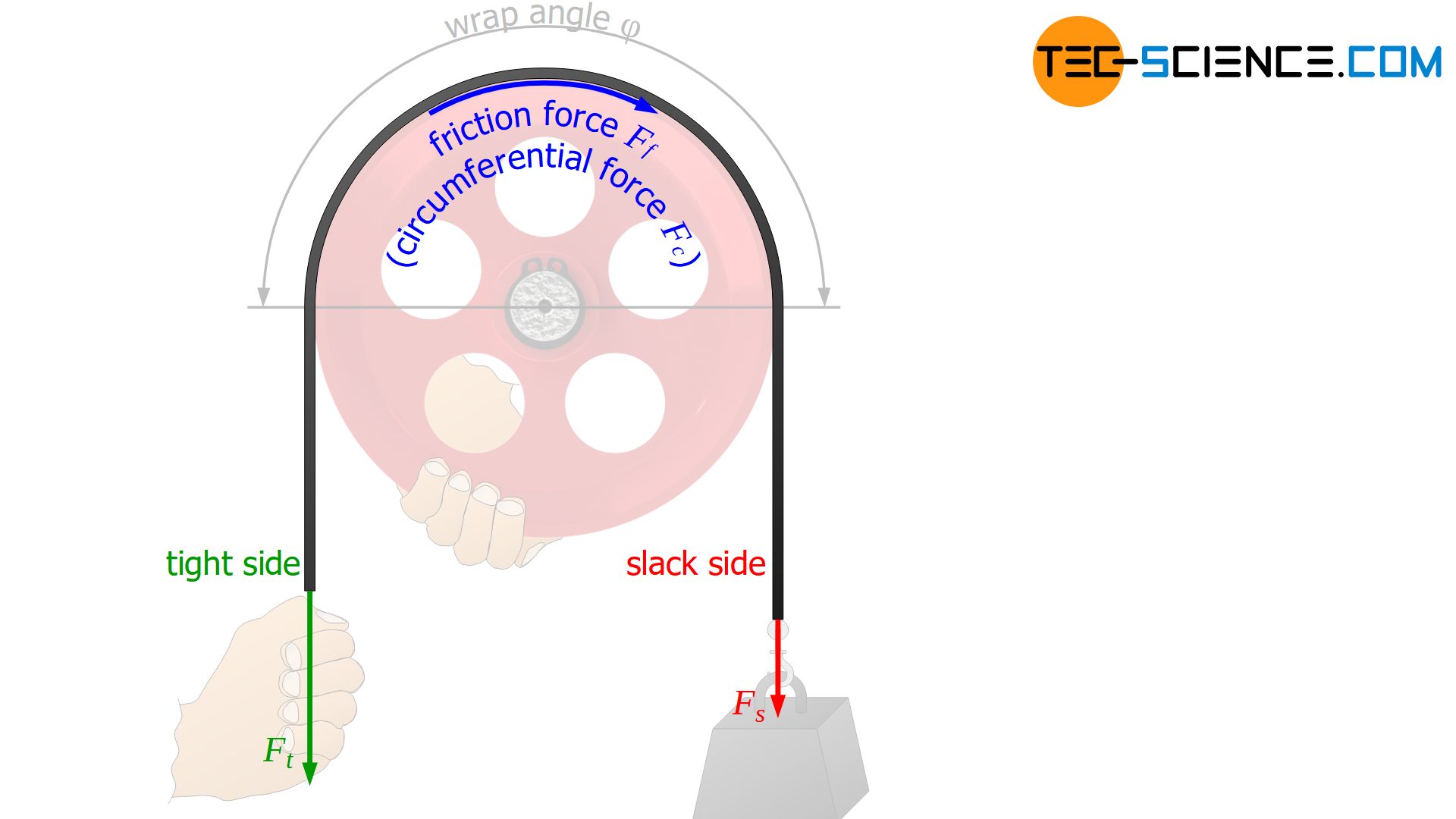
In the limiting case of static equilibrium (i.e. immediately before the belt slips), not only the holding force must be applied to the tight side, but it can also be pulled as much as the maximum frictional force can ever be. The sum of slack side force F_s and maximum frictional force F_f,max thus corresponds to the maximum possible tight side force F_t,max in static equilibrium:

\begin{align}
&F_{t,max} =F_s + F_{f,max} \\[5px]
\label{zugkraft}
&\boxed{F_{f,max} =F_{t,max} – F_s} \\[5px]
\end{align}

Belt friction equation

In the 18th century, the scientists Euler and Eytelwein were dealing with the forces acting at the ends of a rope that were wrapped around round objects (e.g. ship’s rope around a bollard). In the static limit case, the physicists were able to establish a correlation between the holding force on the one side (“slack side force” F_s) and the maximum possible pulling force on the other side (“tight side force” F_t,max).

This correlation is made on the one hand by the friction coefficient µand on the other hand by the wrap angle φ, because at a given holding force both parameters influence the maximum possible pulling force to the same extent:

• The greater the coefficient of friction, the greater the friction itself and the greater the maximum pulling force
• the greater the wrap angle, the greater the friction and the greater the maximum pulling force

Mathematically, Euler and Eytelwein’s considerations led to the following belt friction equation:

\begin{align}
\label{eytelwein}
&\boxed{F_{t,max} =F_s \cdot e^{\mu \cdot \varphi}} ~~~\text{belt friction equation}\\[5px]
\end{align}

The Euler-Eytelweins belt friction equation is only valid in static limit cases, i.e. when the maximum possible pulling force and thus the maximum possible friction acts before the belt begins to slip!

Released pulley

Finally, the belt friction equation can be applied to the belt drive. According to this equation, with a given force on the slack side F_s, the maximum force F_t,max = F_s⋅e^µφ can be applied on the tight side without the belt slipping from the fixed pulley.

With the maximum frictional force F_f,max acting in this state, the belt tries to set the still fixed pulley in rotation. This force is also felt by the person holding the pulley at its circumference. The friction force thus acts as the circumferential force with which the pulley tries to rotate.

If the pulley is released in this state, it is consequently driven with this circumferential force or with the maximum possible friction force F_f,max. According to the equation (\ref{zugkraft}) this corresponds to the difference of the forces F_t and F_s:

\begin{align}
&F_{f,max} = F_{t,max} – F_s \\[5px]
\end{align}

The maximum possible pulling force F_t,max is clearly related to the slack side force F_s by the belt friction equation (\ref{eytelwein}), so that for the pulley driving frictional force finally applies:

\begin{align}
\label{reibungskraft}
&\boxed{F_{t,max} =F_s \cdot \left(e^{\mu \cdot \varphi} -1 \right)} ~~~\text{maximum possible (driving) frictional force} \\[5px]
\end{align}

This equation describes the maximum effective friction force F_f,max with which the pulley can be driven at a given slack side force F_s without the belt slipping.

Interpretation

Equation (\ref{reibungskraft}) clearly states that a force must be present at the slack side if a driving frictional force is to come about between belt and pulley! If there is no slack side force (F_s=0), the friction coefficient and the wrap angle can be as high as one could ever imagine, the friction force still becomes zero and the pulley cannot be driven.

The necessary presence of a slack side force for power transmission can also be explained in this example directly out of experience. If one imagines that the load on slack side of the belt is missing, then one would simply pull the rope loosely over the pulley without effort when pulling (and thus without force-transmitting friction). The person holding the pulley at its circumference would hardly perceive any circumferential force.

In this case, the necessary contact force between belt and pulley is missing in order to be able to generate a high frictional force and thus circumferential force. This contact force can only be achieved by the load on the slack side! Only in this way can high frictional forces act and high forces be transmitted.

Applying this situation to belt drives, an absence of a slack side force would ultimately mean that the belt is without tension and cannot press against the pulleys to provide the necessary frictional force for power transmission. Therefore, a force on the slack side of the belt (belt tension) is absolutely necessary if a certain power transmission is to be ensured.

For power transmission, a force must be present on the slack side so that the belt tension is maintained and the belt is pressed against the pulleys!

Minimum force on the slack side

The minimum value of slack side force required for a given tight side force can also be determined from the belt friction equation. It is now assumed that the force on the tight side is fixed with F_t. The question then is what minimum force F_s,min must be applied on the slack side so that the belt does not yet slip over the pulley with the given tight side force F_t (Note that the tight side force always corresponds to the “active” pulling force and the slack side force always to the “passive” holding force). Thus equation (\ref{eytelwein}) becomes:

\begin{align}
&F_{t} =F_{s,min} \cdot e^{\mu \cdot \varphi}  \\[5px]
\label{minimal}
&\boxed{F_{s,min} =F_{t} \cdot \frac{1}{e^{\mu \cdot \varphi}}} ~~~\text{minimum slack side force to be applied} \\[5px]
\end{align}

By equation (\ref{minimal}) now the same facts can be deduced. If a force on the tight side of the belt is to be transmitted, a minimum force F_s,min must inevitably be present on the slack side of the belt, otherwise slipping would occur due to lack of belt tension! At this minimum force, the maximum driving frictional force acts (since the lowest possible force is held against the pulling direction). This maximum frictional force is determined analogously to the equation (\ref{zugkraft}):

\begin{align}
& F_{f,max} = F_{t} – F_{s,min} = F_t – F_t \cdot \frac{1}{e^{\mu \cdot \varphi}} \\[5px]
\label{123}
&\boxed{F_{f,max} =F_t \cdot \left(1-\frac{1}{e^{\mu \cdot \varphi}} \right)} ~~~\text{maximum possible (driving) frictional force} \\[5px]
\end{align}

Overload protection

With the belt friction equation the overload protection of the belt drives can also be explained. For this purpose, the example of a rope winch presented in the previous article is considered again. If, for example, the output pulley can hardly set the winch in motion due to a high load, the tensile force on the tight side of the belt increases enormously as the motor continues to try to turn the input pulley and move the belt with it. The belt is thus very strongly stretched on the tight side. The input pulley pushes the belt to the slack side, so to speak. As a result, the belt tension on the slack side decreases, which according to the equation (\ref{reibungskraft}) leads directly to a decrease in the maximum possible frictional force and finally causes the input pulley to slip from a critical point. Such a “sliding” of the belt over the pulley is also called slippage.