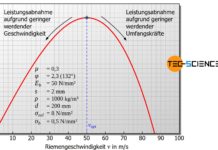
Bei hohen Drehzahlen nimmt durch die angreifenden Fliehkräfte am Riemen die Anpresskraft und damit die maximal übertragbare Umfangskraft ab.
Erzeugung der Fliehkräfte
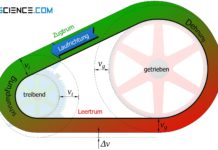
Bei antriebslosem Riementrieb wirkt im Ruhezustand nur die Vorspannkraft FV im Riemen. Sie ist in den gesamten Riemenabschnitten, d.h. in den beiden Trumen gleich groß. Lediglich unter Last wirken unterschiedliche Riemenkräfte und es bildet sich ein Zugtrum mit der Riemenkraft FZ und ein Leertrum in dem die Kraft FL wirkt aus (siehe Artikel Kraftübertragung am Riementrieb). Steht der Riementrieb dabei Still oder werden nur geringe Geschwindigkeiten gefahren, dann können die Trumkräfte bei konstantem Drehmoment als nahezu unabhängig von der Riemengeschwindigkeit betrachtet werden.
Bei größeren Riemengeschwindigkeiten wirken jedoch beachtliche Fliehkräfte (Zentrifugalkräfte) auf die entsprechenden Riemenabschnitte welche um die Riemenscheiben laufen. Diese Zentrifugalkärfe sind dabei versucht den Riemen nach außen zu ziehen und diesen praktisch von der Scheibe abzuheben. Dies würde dann jedoch ein Absinken der Anpresskraft und damit eine Abnahme der Reibungskraft zwischen Riemen und Scheibe bedeuten. Bei großen zu übertragenden Umfangskräften könnte es dann zum Gleitschlupf kommen.
Um dies zu vermeiden, müssen die Riemen zusätzlich um den Betrag der im Betrieb wirkenden Fliehkraftwirkung gespannt werden (auch Riemenfliehkraft genannt). Dies kann bspw. über eine größere Vorspannkraft erreicht werden, oder es müssen Spannsysteme verwendet werden. Fakt jedoch ist, dass diese größeren Kräfte letztlich durch den Riemen aufgebracht werden müssen.
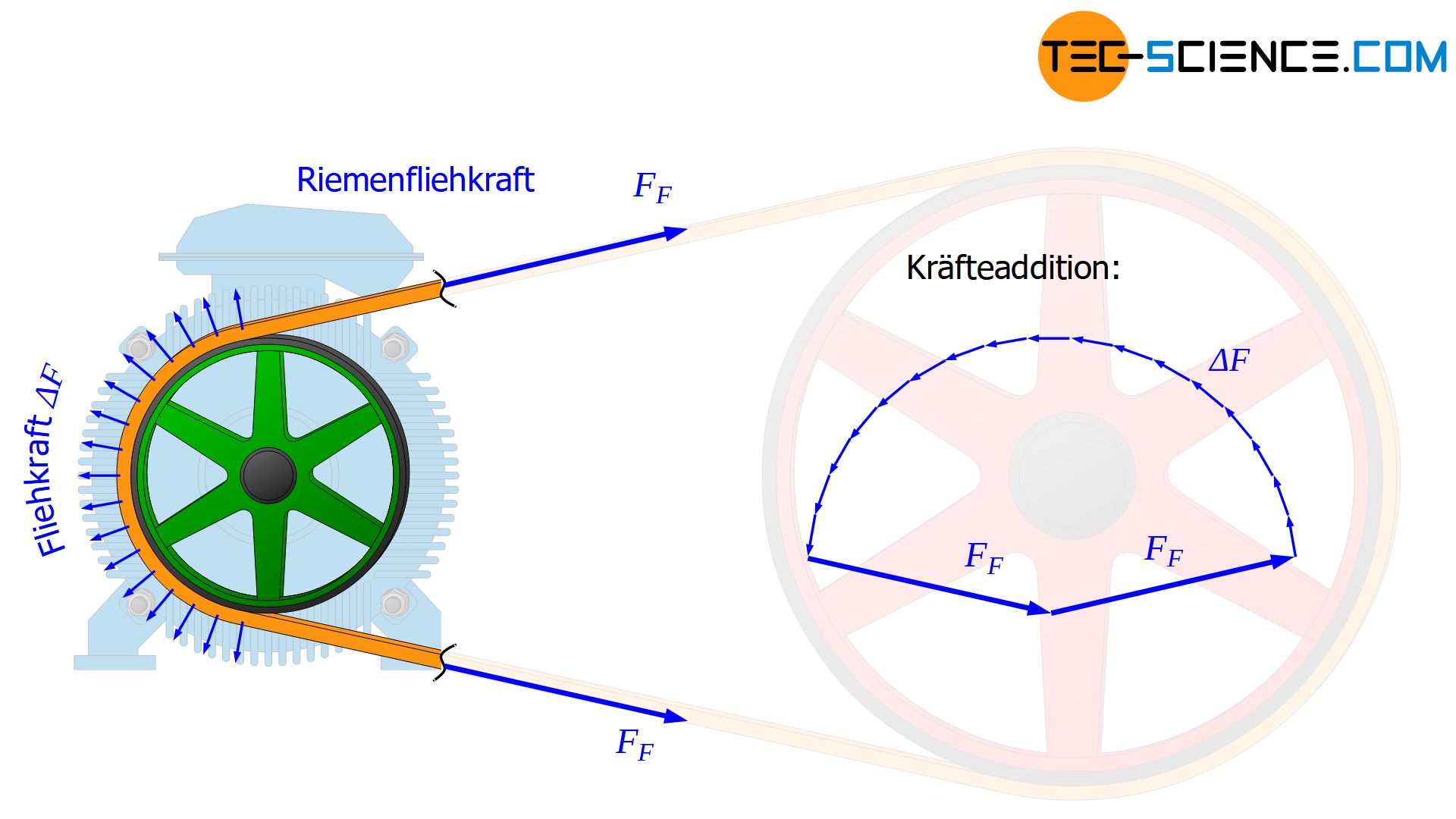
Die Fliehkräfte werden beim Umlaufen des Riemens um die Riemenscheibe erzeugt. Sie sind versucht den Riemen von der Riemenscheibe abzuheben. Dem muss mit einer zusätzlichen Vorspannung um den Betrag der Fliehkraft entgegengewirkt werden!
Einfluss der Fliehkraft auf die Trumkräfte
Die Fliehkräfte werden grundsätzlich nur an der Umschlingung erzeugt, d.h. beim Umlauf des Riemens um die Scheiben. Sie sind dort jeweils radial von den Riemenscheiben weg gerichtet. An den geraden Trumabschnitten wirken selbst zwar keine Fliehkräfte, jedoch wird die dortige Riemenspannung durch die Fliehkräfte beeinflusst. Wird die Durchhängung des Riemens im Leertrum vernachlässigt, dann sind die Fliehkräfte symmetrisch zur Verbindungsline der beiden Scheibenachsen gerichtet. Die jeweils an den gekrümmten Riemenabschnitten resultierende Fliehkraftwirkung wirkt damit entlang dieser Verbindungslinie nach außen.
Die Fliehkräfte wirken also so, als würde jemand den Riemen nach außen ziehen. Dies macht sich dann eben auch in den geraden Riemenabschnitten als eine zusätzlich vom Riemen aufzubringende Kraft bemerkbar (ansonsten würde es zum besagten Abfallen der Anpresskraft kommen). Aufgrund der symmetrischen Zugwirkung der Fliehkräfte wird auch deutlich, dass diese auf beide Trume gleichermaßen wirkt! Im selben Maße wie also die Gesamtkraft im Zugtrum ansteigt, nimmt auch die Gesamtkraft im Leertrum zu.
Durch die Fliehkräfte nehmen die Kräfte im Zug- und Leertrum gleichermaßen zu!
Einfluss der Fliehkraft auf die Umfangskraft
Die im quasi-statischen Zustand wirkende Zugtrumskraft FZ und Leertrumskraft FL müssen bei hohen Geschwindigkeiten um den Betrag FF ansteigen, um die Fliehkraftwirkung zu kompensieren. Die zusätzlich wirkenden Fliehkräfte beeinflussen die übertragene Umfangskraft FU dabei allerdings nicht (zumindest solange die Belastung des Riemens unter der Fliehkraftwirkung nicht zu groß wird und der Riemen Schaden nimmt):
\begin{align}
\label{umfang}
&F_U = \underbrace{\left(F_Z + F_F \right)}_{\text{Gesamtkraft im Zugtrum}} – \underbrace{\left(F_L + F_F \right)}_{\text{Gesamtkraft im Leertrum}} = F_Z + F_F – F_L – F_L = F_Z – F_L \\[5px]
\label{nutzkraft}
&\boxed{F_U = F_Z – F_L} \\[5px]
\end{align}
Die Fliehkräfte haben keinen direkten Einfluss auf die übertragene Umfangskraft!
Beachte, dass mit den Begriffen Zugtrumkraft und Leertrumkraft häufig nur die für die eigentliche Kraftübertragung relevanten Trumkräfte FZ und FL nach Gleichung (\ref{nutzkraft}) gemeint sind (d.h. die Kräfte im quasi-statischen Zustand). Fliehkräfte werden aus dem besagten Grund, dass diese keinen Einfluss auf die übertragende Umfangskraft haben, häufig separat aufgezählt, obgleich beide Kräfte („Trumkraft+Fliehkraft“) gemeinsam im Trum wirken und physikalisch auch nicht getrennt werden können, da sie stets als resultierende Kräftesumme wirken.
Berechnung der Riemenfliehkraft
Die durch die Fliehkräfte zusätzlich wirkende Riemenfliehkraft FF soll im Folgenden bei gegebener Riemengeschwindigkeit v ermittelt werden. Beachte, dass mit dem Begriff der Riemenfliehkraft FF nicht die Fliehkraft an sich gemeint ist sondern die durch Fliehkräfte zusätzlich im Riemen wirkende Kraft (dies entspricht jener Kraft um die der Riemen im Ruhezustand zusätzlich gespannt werden muss, um die Fliehkraftwirkung vollständig zu kompensieren)!
Für die Herleitung der Riemenfliehkraft genügt es völlig den lastfreien Leerlaufbetrieb näher zu betrachten, d.h. den rotierenden Riemen ohne dass dabei eine Umfangskraft übertragen wird, da nach Gleichung (\ref{umfang}) die Fliehkräfte ohnehin nicht die Umfangskraft und umgekehrt die Umfangskraft nicht die Fliehkräfte beeinflussen.
Wird der Einfachheithalber also nur ein „leer“ laufender Riemen betrachtet, dann ist die einzige Kraft die in diesem Riemen wirkt die gesuchte Riemenfliehkraft. Diese Kraft hält den Riemen letztlich zusammen. Bei konstanter Riemengeschwindigkeit muss aus Gründen des Kräftegleichgewichts die Riemenfliehkraft an jeder Stelle des Riemens gleich groß sein (ansonsten würde ein freigeschnittener Riemenabschnitt in eine Richtung beschleunigt werden). Dies gilt insbesondere auch für die gekrümmten Riemenabschnitte die über die Scheiben laufen.
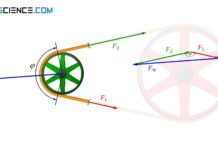
Wird ein solcher Riemenabschnitt unter dem Winkel dφ näher betrachtet, dann muss als mitbewegter Beobachter die an diesem Abschnitt angreifende Fliehkraft dF mit den Riemenfliehkräften FF im Gleichgewicht stehen. Die vektorielle Kräfteaddition bildet geometrisch somit ein geschlossene Kräftedreieck. Über den als infinitesimal angenommenen Bogenwinkel dφ kann dann folgender Zusammenhang zwischen der Fliehkraft dF und der Riemenfliehkraft FF hergestellt werden:
\begin{align}
&\text{d} \varphi = \frac{\text{d}F}{F_F} \\[5px]
\label{FF}
&\underline{F_F = \frac{\text{d}F}{\text{d}\varphi}} \\[5px]
\end{align}
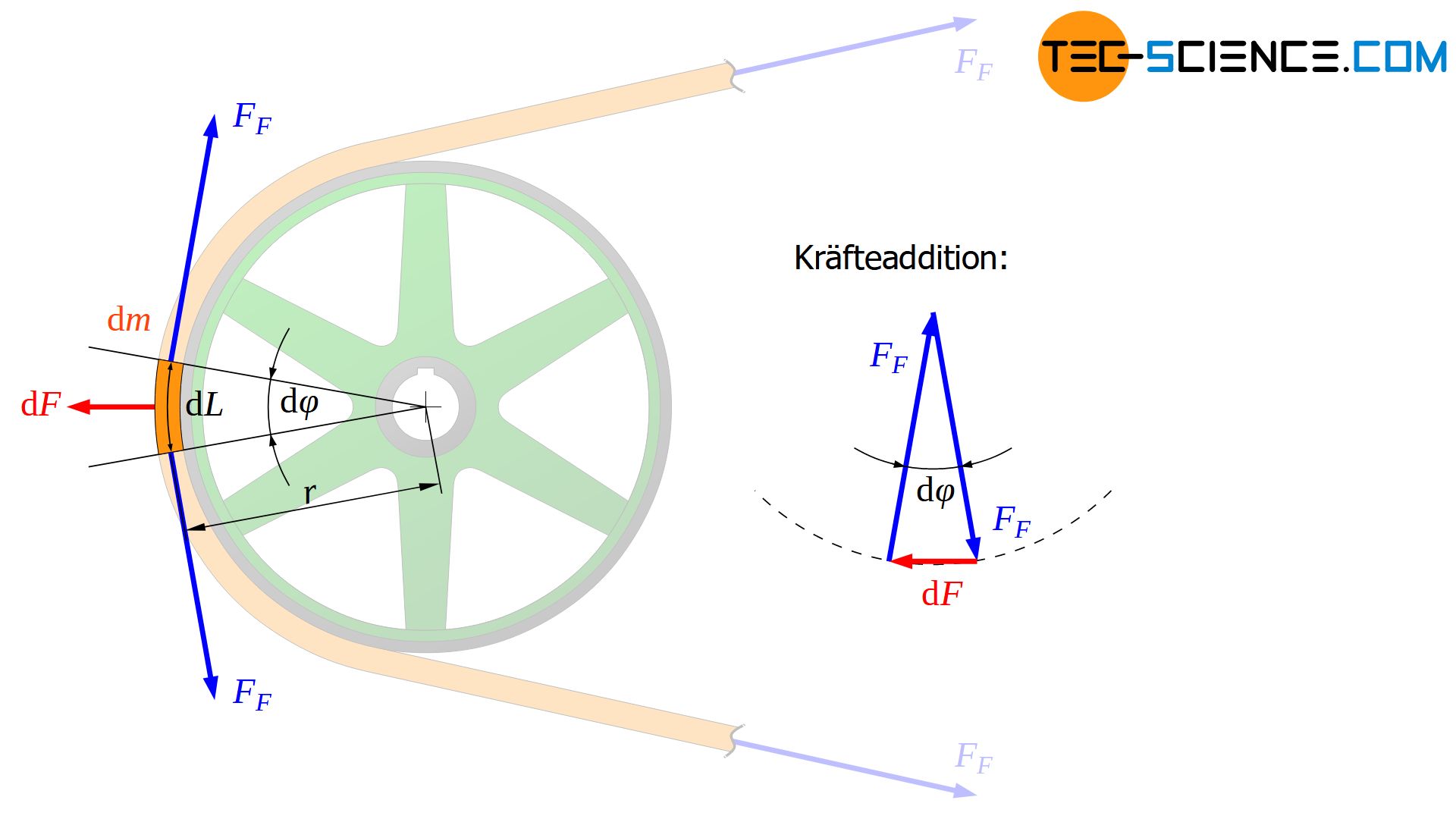
Die am betrachteten Riemenabschnitt der Masse dm wirkende Fliehkraft dF ergibt sich aus dem Scheibenradius r und der Umlaufgeschwindigkeit v wie folgt:
\begin{align}
&\text{d}F = \text{d}m \cdot \frac{v^2}{r} \\[5px]
\end{align}
Die Masse dm des betrachteten Riemenabschnitts hängt vom gewählten Winkelausschnitt dφ ab. Je größer der Winkel, desto größer die Masse dm. Wird die Gesamtmasse m des Riemens auf dessen Gesamtlänge L bezogen („Längengewicht“) und mit m‘ bezeichnet
\begin{align}
&m‘ = \frac{m}{L} ~~~\text{„Kilogramm pro Meter“},
\end{align}
dann kann über den Bogenwinkel dφ die (Bogen-)Länge dL des betrachteten Riemenabschnitts und damit dessen Masse dm=m’⋅dL bestimmt werden:
\begin{align}
\text{d} \varphi &= \frac{\text{d}L}{r} \\[5px]
\text{d}L &= r \cdot \text{d} \varphi \\[5px]
\rightarrow \underline{\text{d} m} &= m‘ \cdot \text{d}L = \underline{m‘ \cdot r \cdot \text{d}\varphi} \\[5px]
\end{align}
Für die Fliehkraft dF des unter dem Winkel dφ betrachteten Riemenabschnitts gilt somit:
\begin{align}
\label{dF}
&\underline{\text{d}F} = \text{d}m \cdot \frac{v^2}{r} = m‘ \cdot r \cdot \text{d}\varphi \cdot \frac{v^2}{r} = \underline{m‘ \cdot \text{d}\varphi \cdot v^2} \\[5px]
\end{align}
Wird diese Gleichung (\ref{dF}) nun in Gleichung (\ref{FF}) eingesetzt, so erhält man die gesuchte Abhängigkeit der Riemenfliehkraft FF von der Riemengeschwindigkeit v:
\begin{align}
&F_F = \frac{\text{d}F}{\text{d}\varphi} = \frac{m‘ \cdot \text{d}\varphi \cdot v^2}{\text{d}\varphi} = m‘ \cdot v^2 \\[5px]
&\boxed{F_F = m‘ \cdot v^2} \\[5px]
\end{align}
Die durch die Fliehkraftwirkung hervorgerufene Riemenkraft FF ist somit nur vom spezifischen Längengewicht m‘ und vom Quadrat der Riemengeschwindigkeit v abhängig. Weder der Scheibendurchmesser noch der Umschlingungswinkel beeinflussen die Riemenfliehkraft! Um die Fliehkraftwirkung im Betrieb also vollständig zu kompensieren muss der Riemen im Ruhezustand um den Betrag dieser Riemenfliehkraft zusätzlich gespannt werden!
Die zusätzlich notwendige Kraft im Riemen zur Kompensation der auftretenden Fliehkräfte (Riemenfliehkraft) ist nur von der Geschwindigkeit und dem Längengewicht des Riemens abhängig! Weder der Scheibendurchmesser noch der Umschlingungswinkel haben hierauf Einfluss!