In this article, learn more about the power transmission in belt drives and the necessary pretensioning force.
Circumferential force in the belt
In belt drives, forces are transmitted from the input pulley to the belt and then from the belt back to the output pulley. The force to be transmitted from one pulley to the other is also referred to as the effective force or circumferential force Fc. The amount of force Fc applied to the circumference of the input pulley depends on the torque Mi or the power Pi and the speed ni as well as the diameter di of the driving pulley:
\begin{align}
&M_i = F_c \cdot \frac{d_i}{2} ~~~~~\text{and} ~~~~~ P_i = 2 \pi M_i n_i\\[5px]
\label{umfang}
&\boxed{F_c = \frac{2 M_i}{d_i} = \frac{P_i}{\pi d_i n_i}} \\[5px]
\end{align}
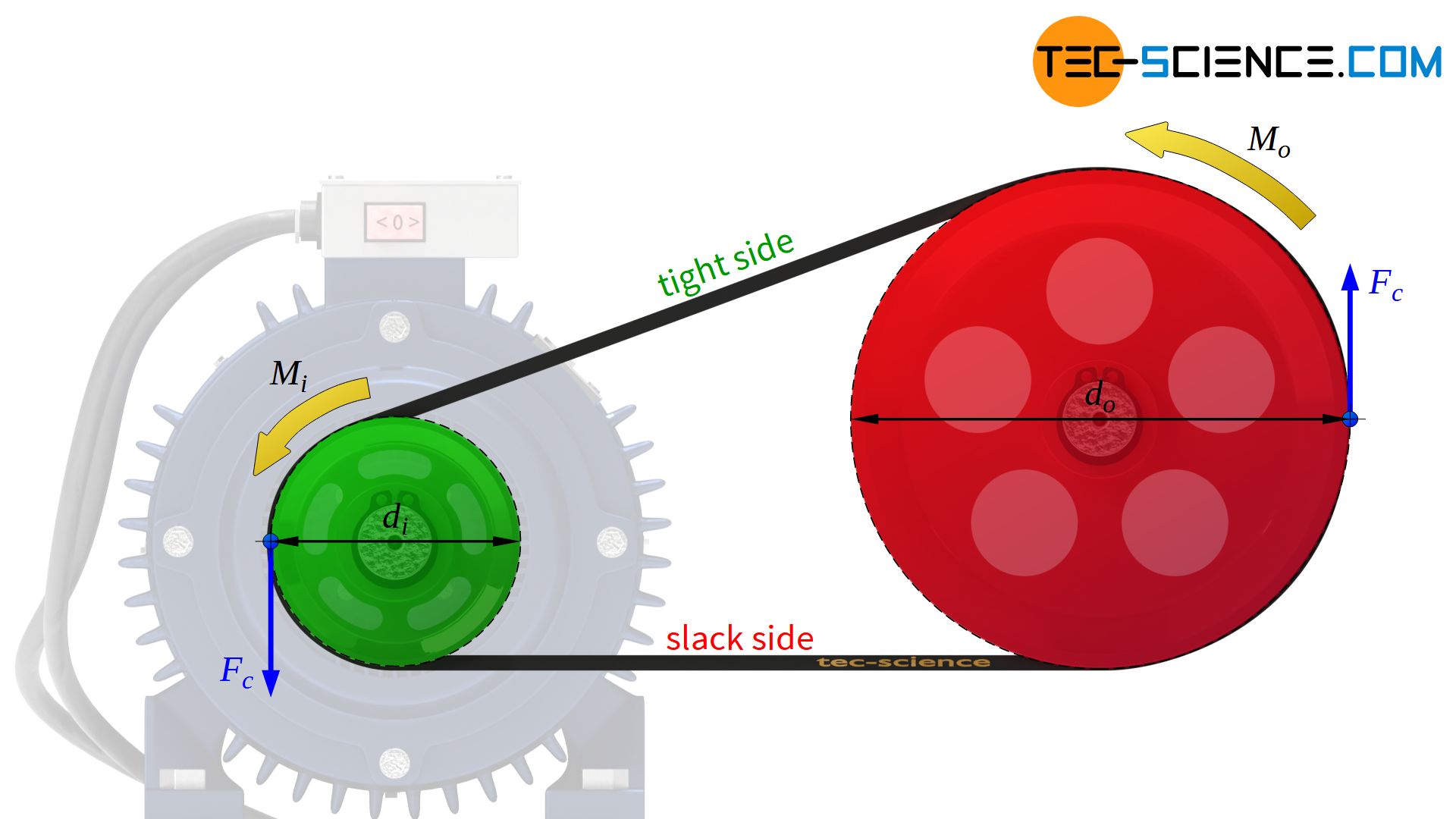
This circumferential force Fc causes different forces on the two belt sections and a tight side and a slack side will form. The balance of forces on a pulley generally shows that the difference between the tight side force Ft and the slack side force Fs corresponds to the transmitting circumferential force Fc:
\begin{align}
\label{fu}
&\boxed{F_c = F_t – F_s} \\[5px]
\end{align}
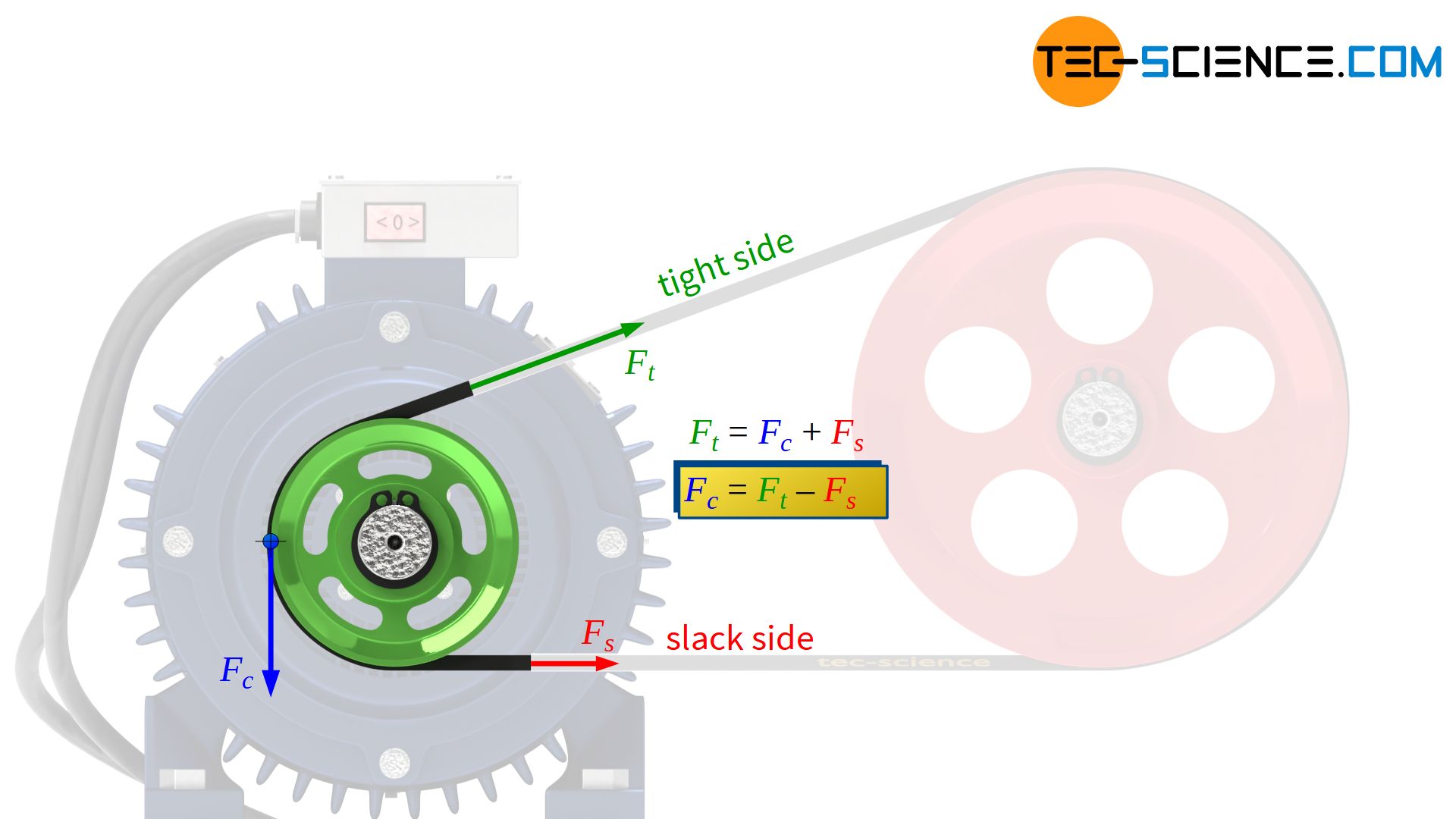
The decisive factor for the transmission of power in belt drives is the circumferential force (also called effective force), which results from the difference between the tight side force and the slack side force of the belt!
At the pulley with the diameter do driven by the belt this effectively circumferential force Fc leads to a changed torque Mo (see also the section transmission ratio):
\begin{align}
&\boxed{M_o = F_c \cdot \frac{d_o}{2}} \\[5px]
\end{align}
The circumferential force is generated at the input pulley by the torque acting there and the effective diameter of the pulley. At the output pulley, the circumferential force causes a change in torque in accordance with the effective diameter of the output pulley.
The circumferential force is transmitted at the interface between belt and pulley by frictional forces. These maximum possible frictional forces must be sufficiently high to ensure that the circumferential force can be transmitted safely. If the maximum possible frictional force is lower than the circumferential force to be transmitted, then obviously there is not enough “adhesion” to be able to transfer the circumferential force from the pulley to the belt or from the belt to the pulley according to the equation (\ref{umfang}). The pulley or belt slips (sliding slip) and the full circumferential force is no longer transmitted.
The circumferential force is transmitted by frictional forces between pulley and belt!
Maximum transmittable circumferential force
In the article Basics of power transmission it was shown with the belt friction equation that the maximum frictional force Ff,max between belt and pulley at a given tight side force Ft or slack side force Fs can be determined with the formulae listed below. These maximum frictional forces therefore also represent the limit for the maximum transmittable circumferential forces Fc,max:
\begin{align}
\label{leertrum}
& F_{f,max} = \boxed{F_{c,max} = F_s \cdot \left(e^{\mu \cdot \varphi} -1 \right)} \ge F_c \\[5px]
\end{align}
or
\begin{align}
\label{zugtrum}
&F_{f,max} = \boxed{F_{c,max} =F_t \cdot \left(1-\frac{1}{e^{\mu \cdot \varphi}} \right)} \ge F_c \\[5px]
\end{align}
Gain
In the context of the circumferential force, the so-called gain k describes the percentage of the existing tight side force Ft that could be used to transmit the maximum circumferential force Fc,max (limiting case to slippage). According to equation (\ref{zugtrum}) the gain corresponds to the term (1-1/eµφ):
\begin{align}
&k = \frac{F_{cmax}}{F_t} = 1-\frac{1}{e^{\mu \cdot \varphi}} \\[5px]
\label{ausbeute}
&\boxed{k =1-\frac{1}{e^{\mu \cdot \varphi}} } \\[5px]
\end{align}
A gain of e.g. k = 0.6 means that a maximum of 60% of the tight side force can be used as circumferential force for power transmission. In this case, the remaining 40 % is required for maintaining the belt’s tension on the slack side (slack side force).
The gain indicates what percentage of the tight side force can be used as the maximum circumferential force; the rest is accounted for by the slack side force to maintain the belt tension!
Note that the circumferential force is transmitted by frictional forces and their formation always requires a certain pressure of the belt on the pulley. This means that there must always be an acting force on the slack side of the belt to ensure the belt tension and with it the contact pressure. The slack side must therefore not be force-free at all (see also the article Basics of power transmission)!
The relationship between a given tight side force Ft and the maximum possible circumferential force Fc,max is thus established by using the gain k as follows:
\begin{align}
&\boxed{F_{c,max} = F_t \cdot k } \\[5px]
\end{align}
According to the equation (\ref{ausbeute}), the gain depends only on the wrap angle and the coefficient of friction. While the coefficient of friction applies equally to both pulleys, the wrap angle of the smaller pulley is usually smaller. Thus, the smaller pulley (often the driving pulley) is decisive for the gain or the entire power transmission!
The smallest wrap angle of the pulleys is always decisive for power transmission!
However, based on the equation (\ref{ausbeute}) it can also be seen that the greater the coefficient of friction, the less influence the wrap angle has on the gain. The relatively small change in the wrap angle under load (due to the sagging of the slack side of the belt) therefore plays a subordinate role for large coefficients of friction in practice.
Elastic slippage
Due to the elasticity of the belt, elongation processes occur in the belt during rotation around the pulleys. These stretching processes are due to the increase (or decrease) in the belt tension at the transition from the slack side to the tight side (or vice versa) – the belt stretches according to the force acting on the pulley.
This results in relative motions between belt and pulley (called slastic slip). It is therefore not a static friction between belt and pulley but rather a sliding friction! Therefore, when applying the above equations, the sliding coefficient of friction should also be used instead of the static coefficient of friction.
The coefficient of sliding friction is decisive for power transmission!
However, it must be noted that the sliding friction depends on the (elongation) speed. Thus, the coefficient of sliding friction is also influenced by the belt speed!
Pre-load tension (initial tension of the belt)
The equations (\ref{leertrum}) and (\ref{zugtrum}) reflect the maximum possible, transmittable circumferential forces Fc,max depending on the slack side force Fs or tight side force Ft. These equations must therefore be interpreted at the limit to slippage. In principle, however, belt drives are not driven at the limit to slippage, but well below it.
The maximum possible circumferential force according to equation (\ref{leertrum}) or equation (\ref{zugtrum}) is therefore not fully utilized to transmit forces from the belt to the pulley and vice versa. However, the equations show that an increase in the slack side force or tight side force leads to an increase in the maximum frictional force.
This can be clearly explained by an increase in the contact pressure of the belt on the pulley, which increases the maximum frictional force. By increasing the belt forces, safety against slippage can be increased or larger circumferential forces can be transmitted.
The tension in the two spans of the belt (slack side and tight side) is influenced by the pre-tensioning of the belt (initial tension). The stronger the belt is already under tension in the load-free state by the so-called pre-load, the higher the belt tension will be during operation under load. Since higher belt tensions mean higher frictional forces, higher circumferential forces can be transmitted.
Preload without taking centrifugal forces into account
In principle, it must be borne in mind that the belt forces arising during operation depend on the circumferential force to be transmitted. In the load-free idle state, only the pre-load Fp in the belt initially acts. If a circumferential force Fc is introduced by the torque of the input pulley, the belt force in the tight side increases to Ft and the slack side force decreases to the same extent to Fs.
Due to the equilibrium of forces (more precisely: equilibrium of torques), the difference between the tight side force and the slack side force corresponds to the circumferential force to be transmitted. This means that the tight side force increases by just half the circumferential force and the slack side force decreases by half the circumferential force:
\begin{align}
&\boxed{F_t = F_p + \tfrac{F_c}{2}} \\[5px]
\label{F_L}
&\boxed{F_s = F_p – \tfrac{F_c}{2}} \\[5px]
&F_t – F_s = \left(F_p+\tfrac{F_c}{2} \right) – \left(F_p – \tfrac{F_c}{2} \right) = F_p + \tfrac{F_c}{2} – F_p + \tfrac{F_c}{2} = F_c \\[5px]
\end{align}
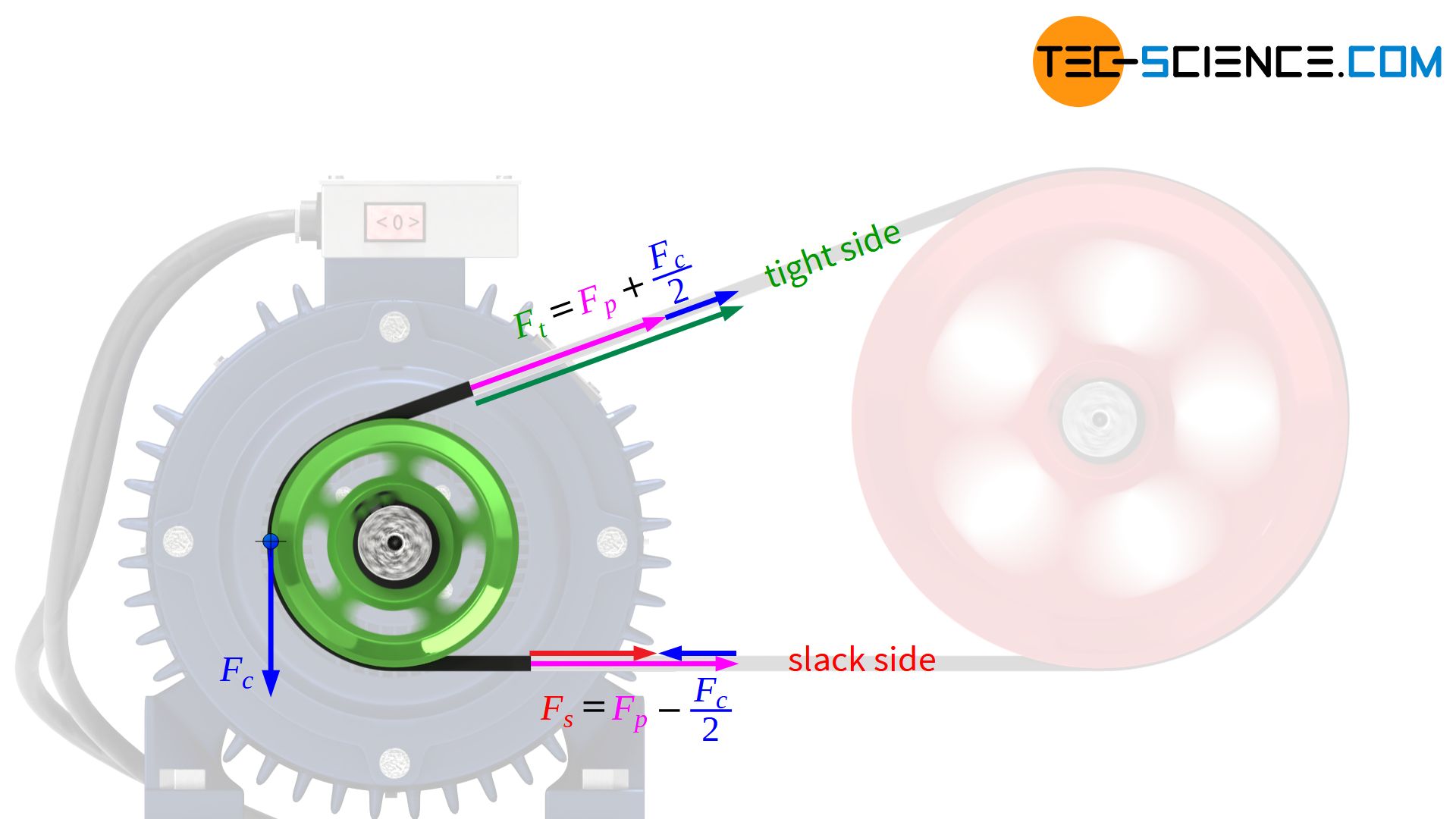
In accordance with the equation (\ref{leertrum}), the slack side force must under no circumstances drop to zero under load, as otherwise the belt tension would be lost. There would be no contact pressure between belt and pulley and there would be no friction that would be capable of transmitting circumferential forces.
The preload Fp in equation (\ref{F_L}) must therefore be chosen in such a way that the slack side force Fs does not fall below a critical value during operation, i.e. when the circumferential force Fc is transmitted. This critical case is reached when the slack side force has decreased to such an extent that the circumferential force Fc can just be transmitted with the maximum possible circumferential force according to the equation (\ref{leertrum}) [Fc,max=Fc]. The slack side force must therefore not fall below the following value:
\begin{align}
&F_{c} = F_{c,max} = F_{s,min} \cdot \left(e^{\mu \cdot \varphi} -1 \right) \\[5px]
& F_{s,min} = F_{c} \cdot \frac{1}{e^{\mu \cdot \varphi} -1} \\[5px]
\end{align}
With this slack side force Fs,min, which must be present at least to be able to transmit the given circumferential force Fc, the minimum preload Fp,min can then also be determined according to equation (\ref{F_L}):
\begin{align}
\label{F_V}
& F_{s,min} = F_{p,min} – \tfrac{F_c}{2} \\[5px]
& F_{p,min} = F_{L,min} + \tfrac{F_U}{2} \\[5px]
& F_{p,min} = F_{c} \cdot \frac{1}{e^{\mu \cdot \varphi} -1} + \tfrac{F_c}{2} \\[5px]
& F_{p,min} = F_{c} \cdot \left( \frac{1}{e^{\mu \cdot \varphi} -1} + \frac{1}{2} \right) \\[5px]
& \underline{F_{p,min} = F_{c} \cdot \frac{e^{\mu \cdot \varphi}+1}{2 \left(e^{\mu \cdot \varphi} -1 \right) }} ~~~\text{without taking centrifugal forces into account} \\[5px]
\end{align}
Preload with taking centrifugal forces into account
In the previous section, centrifugal forces have not yet been taken into account, but at high belt speeds v they lead to a reduction in contact pressure and thus to a reduction in frictional force. In such a case, the required circumferential force can no longer be transmitted. To compensate for this effect, the belt must be additionally preloaded by the amount of the centrifugal effect Fcf=m’⋅v² (with m’ as specific weight – “mass per unit belt length”):
\begin{align}
& F_{p,total,min} = F_{p,min} + F_cf \\[5px]
& \boxed{F_{p,total,min} = F_{c} \cdot \frac{e^{\mu \cdot \varphi}+1}{2 \left(e^{\mu \cdot \varphi} -1 \right)} + m’ \cdot v^2} ~~~\text{taking centrifugal forces into account} \\[5px]
\end{align}
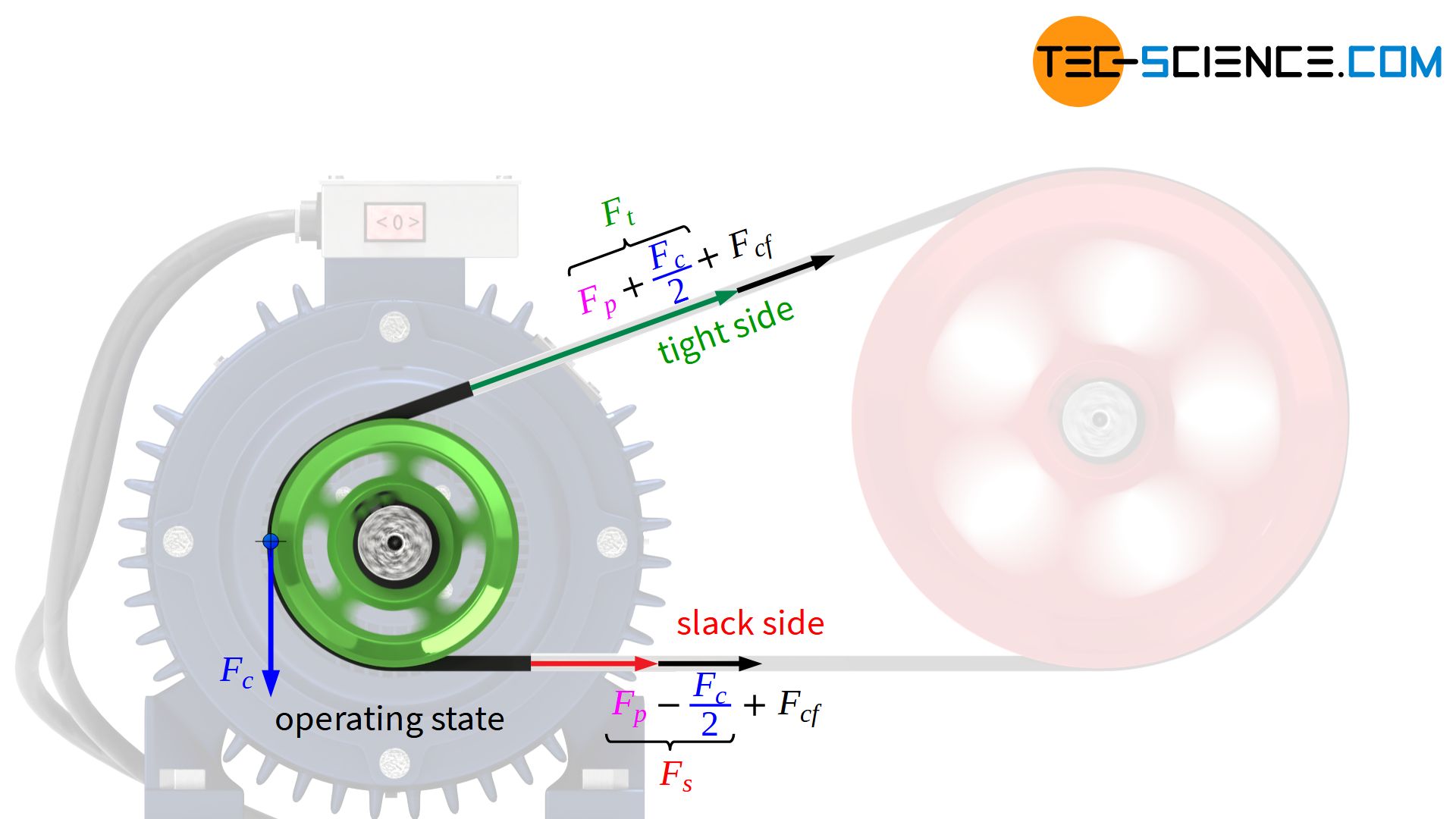
Since the centrifugal force during operation is compensated by the additional preload Fcf, only the preload Fp remains as the relevant effect for contact pressure, which is therefore also referred to as dynamic preload. In contrast, the total (static) preload Fp,total also takes into account the centrifugal force to be compensated, which only acts as an additional contact force at rest. In a separate article, the concept of the belt centrifugal force is explained in more detail and the derivation of the corresponding formula is shown.
Preload measuring
The sections above showed, that the higher the circumferential force to be transmitted and the higher the belt speed, the greater the total preload must be. However, excessive pre-tensioning forces should be avoided, as this not only leads to high bearing loads but also increases belt wear. In addition, only small circumferential forces can be transmitted with high pretensioning forces, as otherwise there is a risk that the belt will tear under the high tension.
In practice, the preload force of the belt can be measured and adjusted accordingly by vibration tests. For this the belt span is picked like the string of a guitar. The frequency at which the belt span now oscillates is called natural frequency f. In the same way that the oscillation frequency (pitch) of a guitar is determined by the tension of the string, the natural frequency of the oscillating string is also directly related to the pre-load tension.
The higher the tension of the belt, i.e. the higher the preload, the higher its natural frequency. The frequency of the oscillating belt span is finally measured with the aid of an optical measuring device. In addition to the preload Fp,total, the span length l and the specific weight m’ (“mass per meter belt length”) influence the natural frequency, but these variables are generally known in advance. The following formula can then be used to determine the preload from the measured natural frequency:
\begin{align}
&F_{p,total} = 4 \cdot f^2 \cdot m’ \cdot l^2 \\[5px]
\end{align}
Or at a desired preload, the natural frequency to be set applies:
\begin{align}
& \boxed{f = \sqrt{\frac{F_{p,total}}{4 \cdot m’ \cdot l^2}} } \\[5px]
\end{align}