Dauerfestigkeitsschaubilder nach Haigh oder Smith geben die maximal ertragbare Spannungsamplitude in Abhängigkeit der Mittelspannung wieder.
Dauerfestigkeitsschaubilder
Das Wöhlerdiagramm eignet sich zwar für die Auswertung von Dauerschwingversuchen, für den Konstrukteur ist dieses Diagramm jedoch oft wenig aufschlussreich. So gilt eine Kurve im Wöhlerdiagramm grundsätzlich nur für eine bestimmte Mittelspannung. Bei dynamisch beanspruchten Bauteilen ändert sich in der Praxis jedoch häufig die Mittelspannung, was wiederum die Schwingfestigkeit beeinflusst. Um auch den Einfluss der Mittelspannung auf die Schwingfestigkeit abzubilden, müssten viele weitere Kurven für die unterschiedlichsten Mittelspannungen in das Wöhlerdiagramm aufgenommen werden. Hierunter würde die Übersichtlichkeit stark leiden.
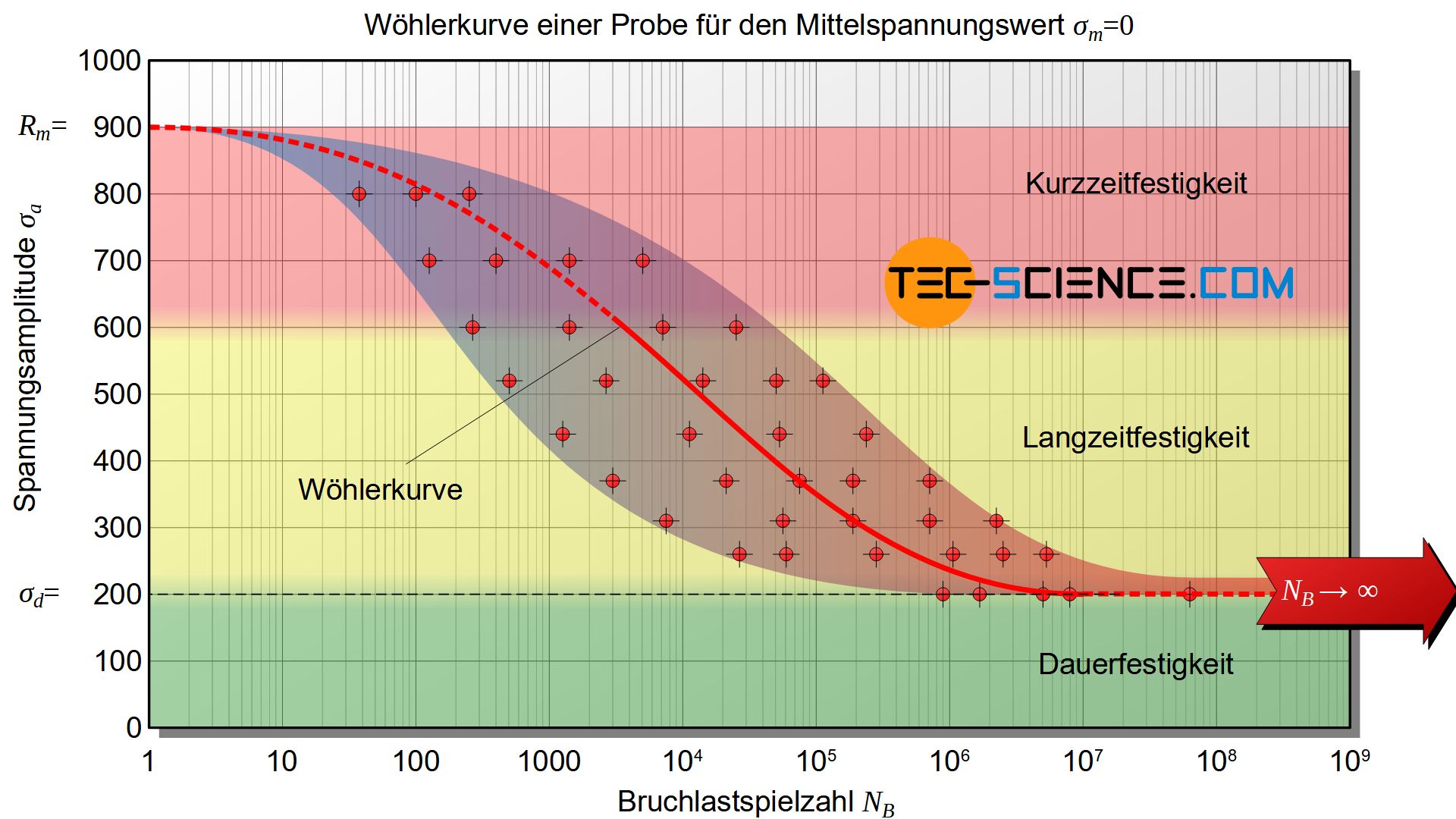
Aus diesem Grund nutzt man für die Darstellung der Schwingfestigkeit spezielle Schaubilder, die den Einfluss der Mittelspannung übersichtlicher abbilden. Die bedeutendsten Diagrammformen sind die nach Haigh und die nach Smith. Wird in solchen Diagrammen die Dauerfestigkeit als Maßgabe zugrunde gelegt, so spricht man von Dauerfestigkeitsschaubilder bzw. Dauerfestigkeitsdiagrammen. Wird hingegen eine bestimmte zu ertragende Lastspielzahl als Grundlage gesetzt, so spricht man von Zeitfestigkeitsschaubilder. Oft werden Dauerfestigkeits- und Zeitfestigkeitskurven auch in einem gemeinsamen Schwingfestigkeitsdiagramm abgebildet.
Dauerfestigkeitsschaubilder nach Haigh (Haigh-Diagramm)
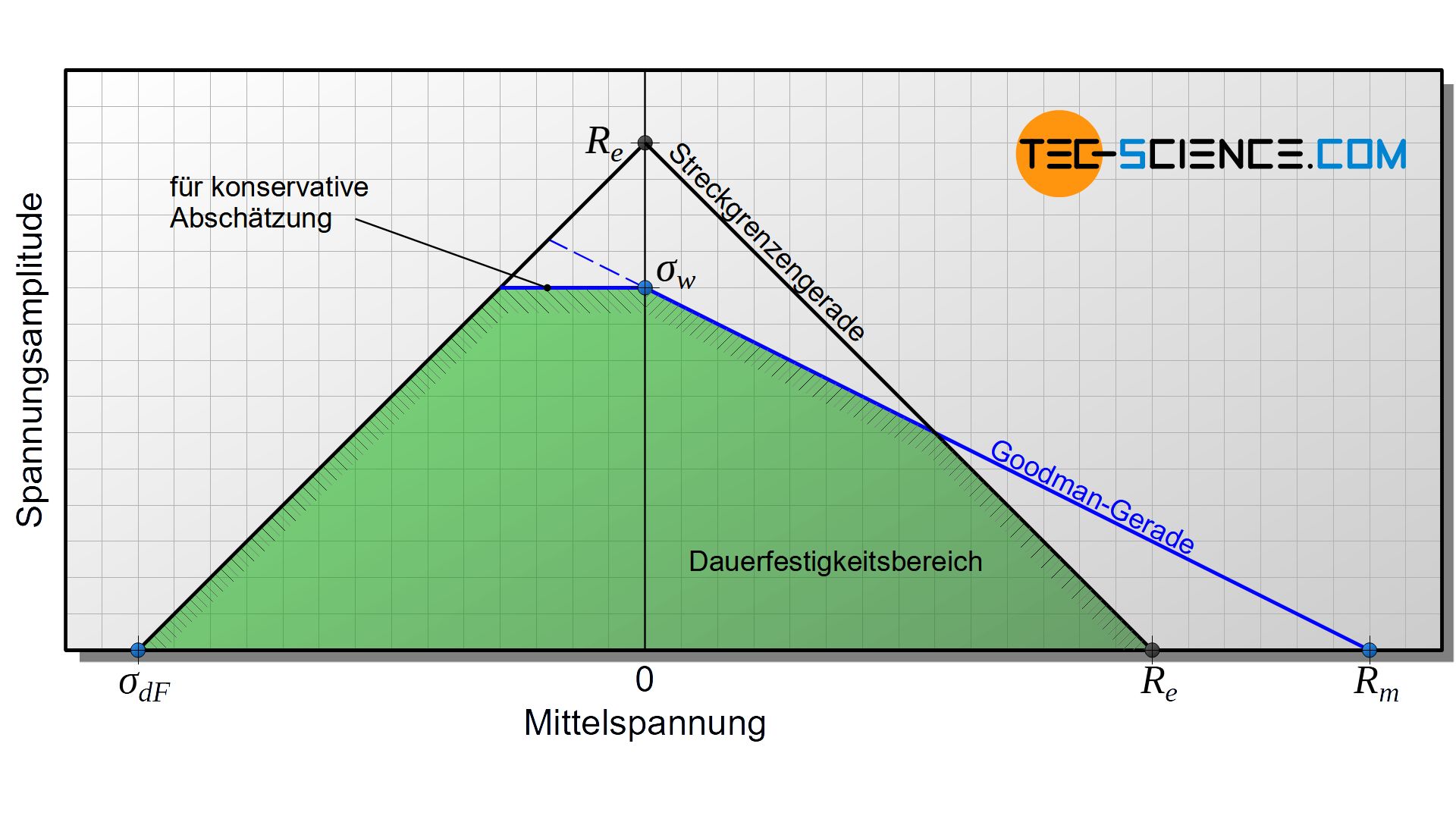
In Dauerfestigkeitsschaubilder nach Haigh wird die ertragbare Spannungsamplitude direkt über der Mittelspannung aufgetragen. Der Schnittpunkt der Kurve mit der vertikalen Achse entspricht gerade der Wechselfestigkeit \(\sigma_w\), da die Mittelspannung dort null ist (Spannungsverhältnis \(R=-1\)). Der Kurvenschnittpunkt mit der horizontalen Achse lässt sich hingegen als Zugfestigkeit \(R_m\) interpretieren, da dort die Probe theoretisch ohne eine vorhandene Spannungsamplitude brechen würde, d.h. alleinig aufgrund der aufgebrachten Mittelspannung (Spannungsverhältnis \(R=1\)).
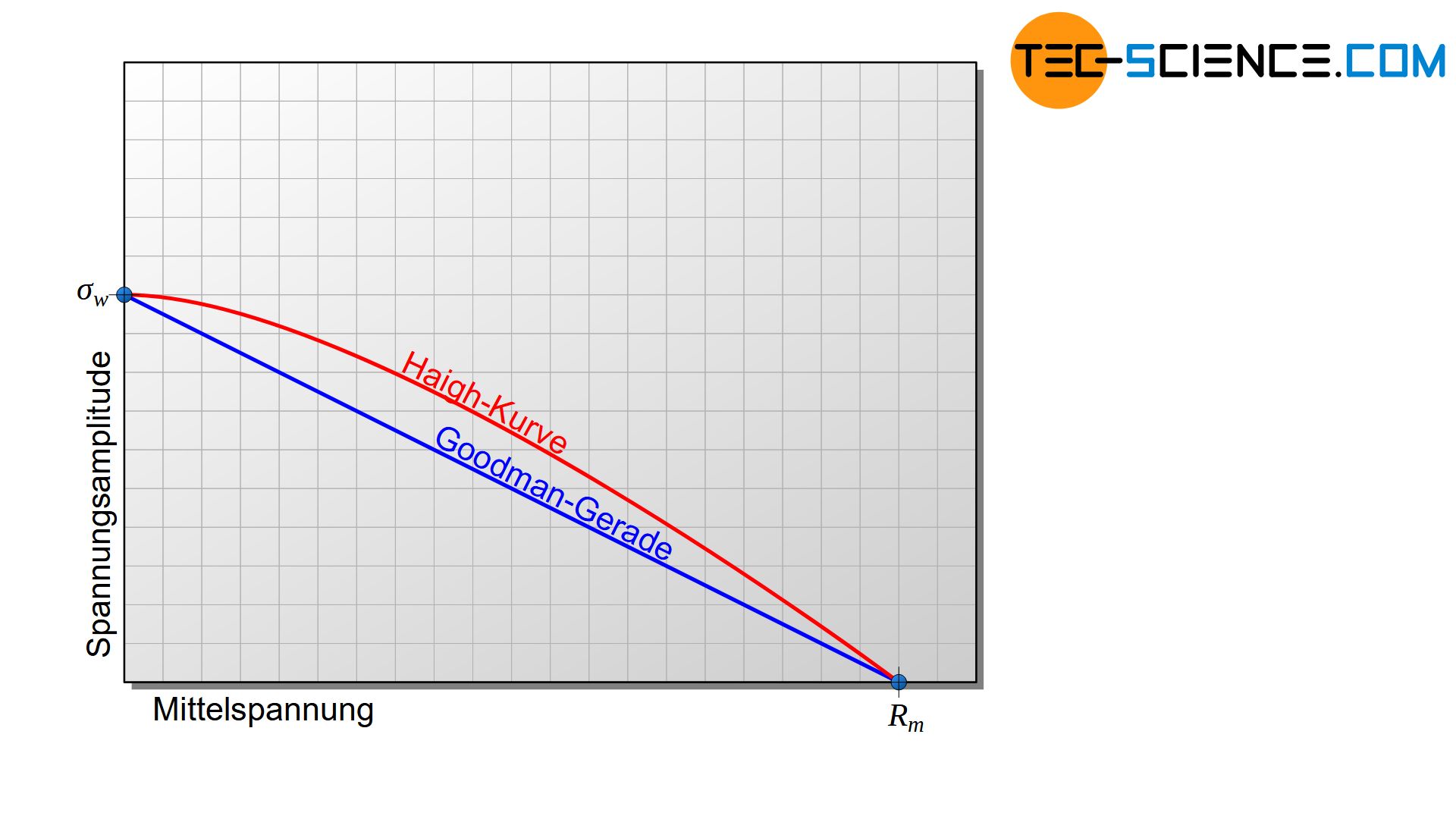
Zwischen diesen beiden Achsen-Schnittpunkten verläuft die Haigh-Kurve („Dauerfestigkeitskurve“). Unterhalb der Dauerfestigkeitskurve liegen die zulässigen Spannungsamplituden für eine gegebene Mittelspannung. Zur vereinfachten Konstruktion des Diagramms nähert man die eigentliche Haigh-Kurve durch ein Gerade an, die sogenannte Goodman-Gerade. Aufgrund dieser Geradennäherung ergibt sich eine Art natürlicher Sicherheitsfaktor, da Goodman-Gerade unter der Haigh-Kurve verlauft. Die tatsächlich ertragbaren Spannungsamplituden fallen somit etwas größer aus als die Goodman-Gerade vorgibt.
Vor allem bei hohen Mittelspannungen ist die Haigh-Kurve bzw. Goodman-Gerade jedoch nur von theoretischer Bedeutung, da in diesem Bereich die Streckgrenze bereits überschritten wird und es somit zu unzulässigen plastischen Verformungen kommt. Die praktische Grenze verläuft deshalb auch nicht bis zur Zugfestigkeit \(R_m\), sondern vielmehr immer nur bis zur Streckgrenze \(R_e\) (bzw. bis zur Dehngrenze \(R_{p0,2}\)).
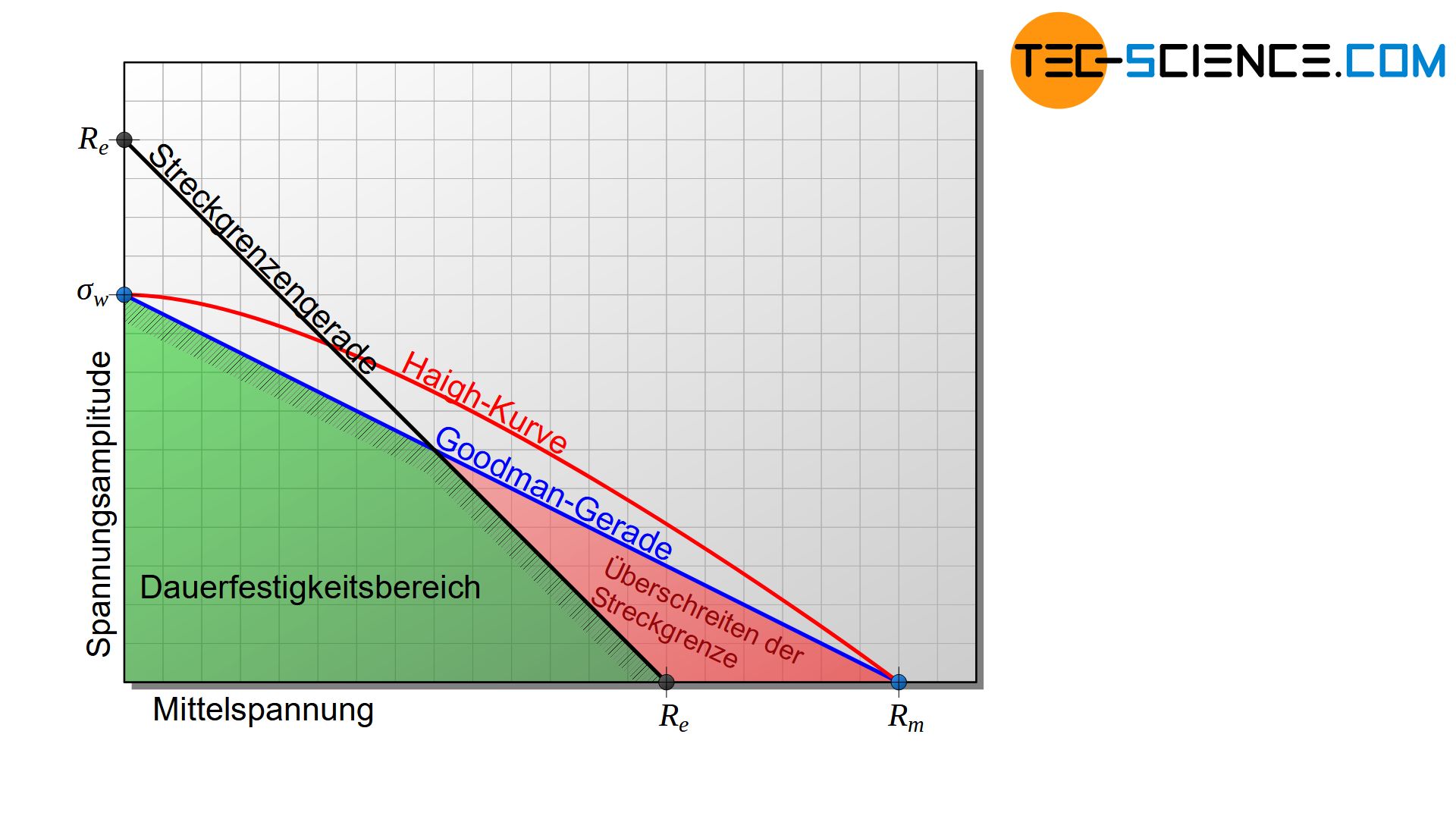
Grundsätzlich darf die Summe aus Mittelspannung und Spannungsamplitude den Wert der Streckgrenze zu keinem Zeitpunkt überschreiten. Im selben Maße wie die Mittelspannung ausgehend des aufgetragenen Streckgrenzenwertes verringert wird, kann theoretisch die Spannungsamplitude erhöht werden. Aus diesem Grund ergibt sich als zusätzliche Begrenzung eine unter 45° liegende Gerade, die auch als Streckgrenzengerade bezeichnet wird.
Auf diese Weise erhält man im Diagramm zwei Geraden, die den technisch nutzbaren Dauerfestigkeitsbereich begrenzen. Für die Erstellung eines vereinfachten Dauerfestigkeitsdiagramm nach Haigh genügt in der Praxis also lediglich die Kenntnis über die Wechselfestigkeit \(\sigma_w\), die Zugfestigkeit \(R_m\) und die Streckgrenze \(R_e\) (bzw. Dehngrenze \(R_{p0,2}\)).
Erstellen des Haigh-Diagramms
Das Dauerfestigkeitsschaubild nach Haigh erhält man also durch Einzeichnen der Goodman-Geraden vom Punkt der Wechselfestigkeit \(\sigma_w\) auf der y-Achse bis zum Punkt der Zugfestigkeit \(R_m\) auf der x-Achse. Anschließend wird der Wert der Streckgrenze auf beiden Achsen markiert und mit einer Geraden verbunden (Streckgrenzengerade). Goodman-Gerade und Streckgrenzengerade markieren nun den Bereich der Dauerfestigkeit.
Um das Ablesen der Dauerfestigkeit für ein gegebenes Spannungsverhältnis \(R\) zu erleichtern, werden oft ausgewählte Spannungsverhältnisse in das Diagramm mit eingetragen. Für jede Mittelspannung kann im Haigh-Diagramm nun die zulässige Spannungsamplitude für einen dauerfesten Betrieb des entsprechenden Werkstoffes abgelesen werden.
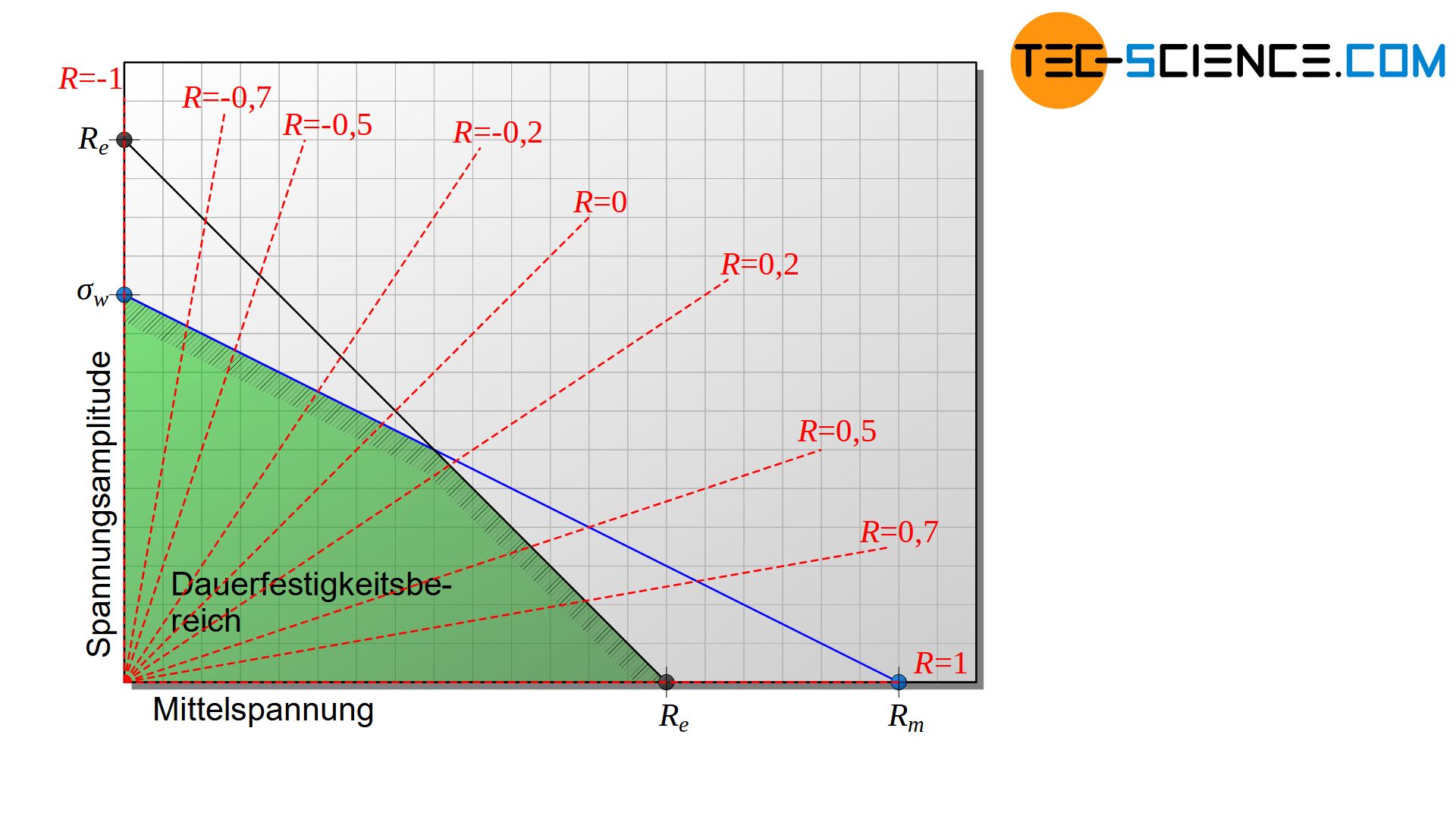
Erweiterung des Haigh-Diagramms auf den Druckbereich
Grundsätzlich kann das Haigh-Diagramm auch auf negative Mittelspannungswerte erweitert werden und so die Dauerfestigkeit auch im Druckbereich abgebildet werden. Zur Erweiterung wird dann als Grenzwert für die Mittelspannung die Quetschgrenze \(\sigma_{dF}\) zugrunde gelegt. Dieser Wert wird analog zum Zugbereich auf beiden Achsen eingetragen und anschließend durch eine Gerade miteinander verbunden. Die Verlängerung der Goodman-Geraden begrenzt schließlich den noch offenen Bereich. Ob diese Verlängerung der Goodman-Geraden jedoch immer zulässig ist, muss gesondert geprüft werden! Für eine konservative Abschätzung kann dieser Linienabschnitt auch in erster Näherung als horizontale angenommen werden.
Beachte, dass durch Effekte der Rissschließung im Druckbereich tendenziell jedoch meist größere Spannungsamplituden ertragen werden können als im Zugbereich. Besonders ausgeprägt ist dieser Effekt bei Lamellengraphitguss, da die Graphitlamellen durch ihre Kerbwirkung nur relativ geringe Zugspannungen zulassen. Druckspannungen nimmt Lamellengraphitguss hingegen sehr viel besser auf.
Dauerfestigkeitsschaubilder nach Smith (Smith-Diagramm)
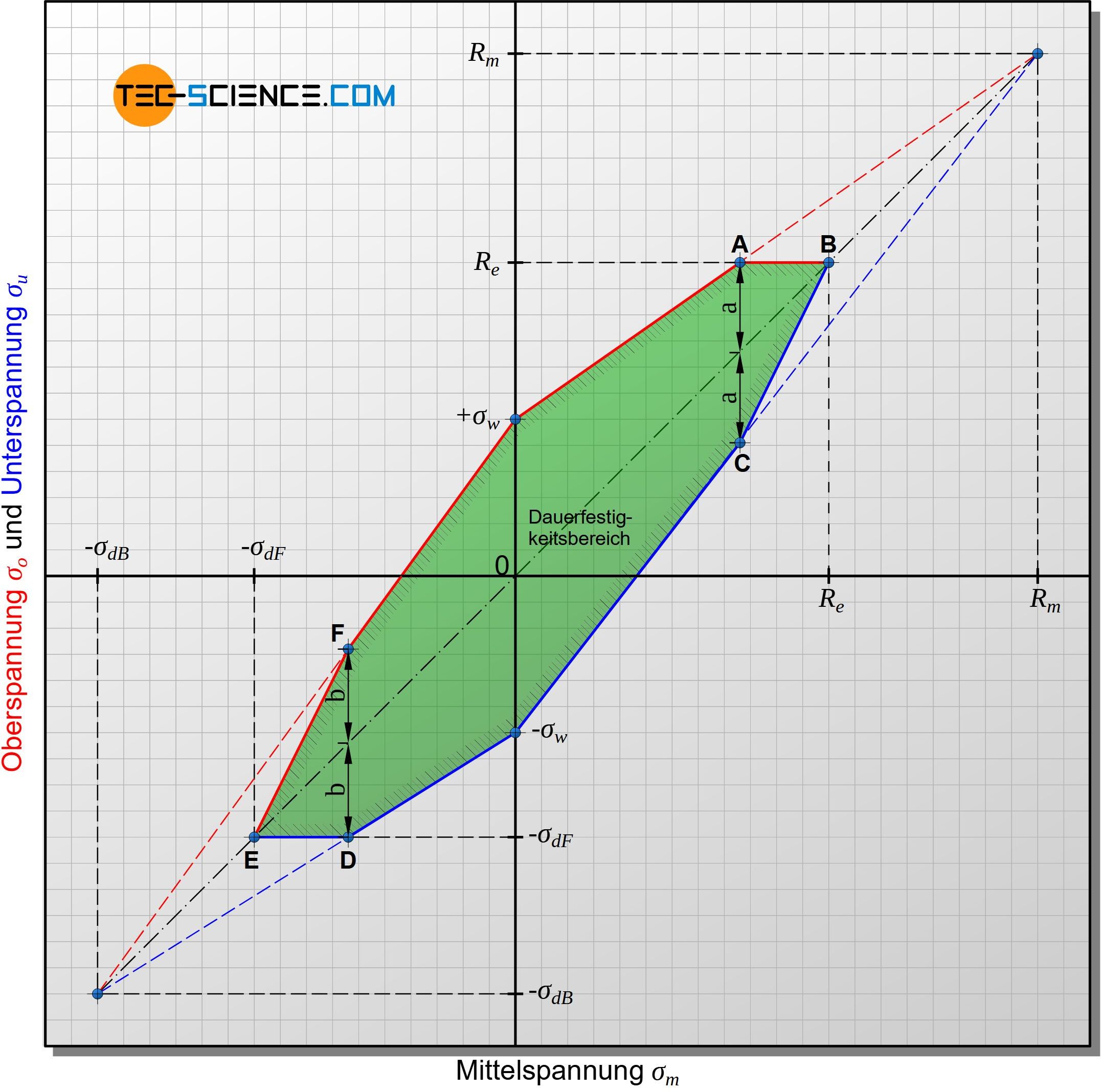
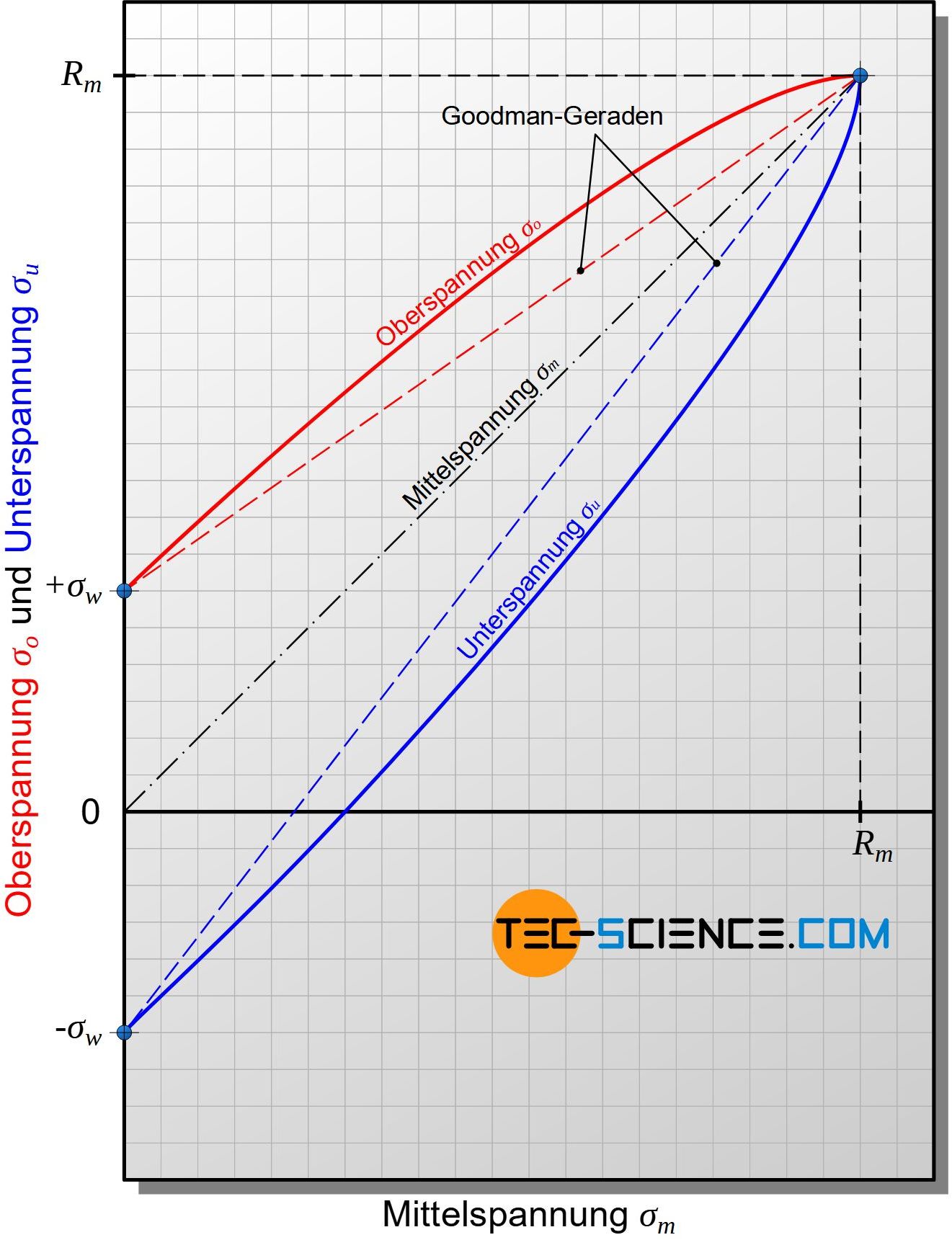
Neben dem weit verbreiteten Dauerfestigkeitsdiagramm nach Haigh, kann die Dauerfestigkeit auch nach Smith veranschaulicht werden. In einem solchen Smith-Diagramm wird nicht mehr die Spannungsamplitude, sondern die Unterspannung \(\sigma_u\) und die Oberspannung \(\sigma_o\) über der Mittelspannung \(\sigma_m\) aufgetragen. Aus grundsätzlichen Überlegungen heraus ergeben sich wieder bestimmte Fixpunkte.
Erstellen des Smith-Diagramms
Bei einer Mittelspannung von \(\sigma_m=0\) erhält man gerade die Wechselfestigkeit \(\sigma_w\) des Materials, sodass der Wert der Oberspannung folglich bei \(+\sigma_w\) und die Unterspannung bei \(-\sigma_w\) liegt. Ein weiterer Fixpunkt ergibt sich, wenn die Mittelspannung gerade den Wert der Zugfestigkeit erreicht (\(\sigma_m=R_m\)). In diesem Fall kann der Werkstoff keine Spannungsamplitude mehr ertragen, da ansonsten die Zugfestigkeit überschritten werden würde. Ober- und Unterspannung entsprechen folglich ebenfalls dem Wert der Zugfestigkeit. Somit müssen die Kurvenverläufe für die Ober- und Unterspannung ausgehend den Punkten der Wechselfestigkeit auf diesen Punkt zulaufen.
Für eine vereinfachende Darstellungen können die Ober- und Unterspannungskurven wieder als Goodman-Geraden angenähert werden. Ebenfalls ergibt sich aus praktischen Gründen wieder eine zusätzliche Begrenzung, da das bisherige Diagramm nur das Bruchkriterium berücksichtigt. In der Regel sind aber unzulässige Verformungen maßgebend, die bei Spannungen oberhalb der Streckgrenze auftreten. Deshalb verlaufen die Goodman-Geraden nur bis maximal zum Wert der Streckgrenze. Dies gilt sowohl für die Oberspannung (Punkt A) als auch für die Mittelspannung (Punkt B), da natürlich auch die Mittelspannung nicht größer werden darf als die Streckgrenze.
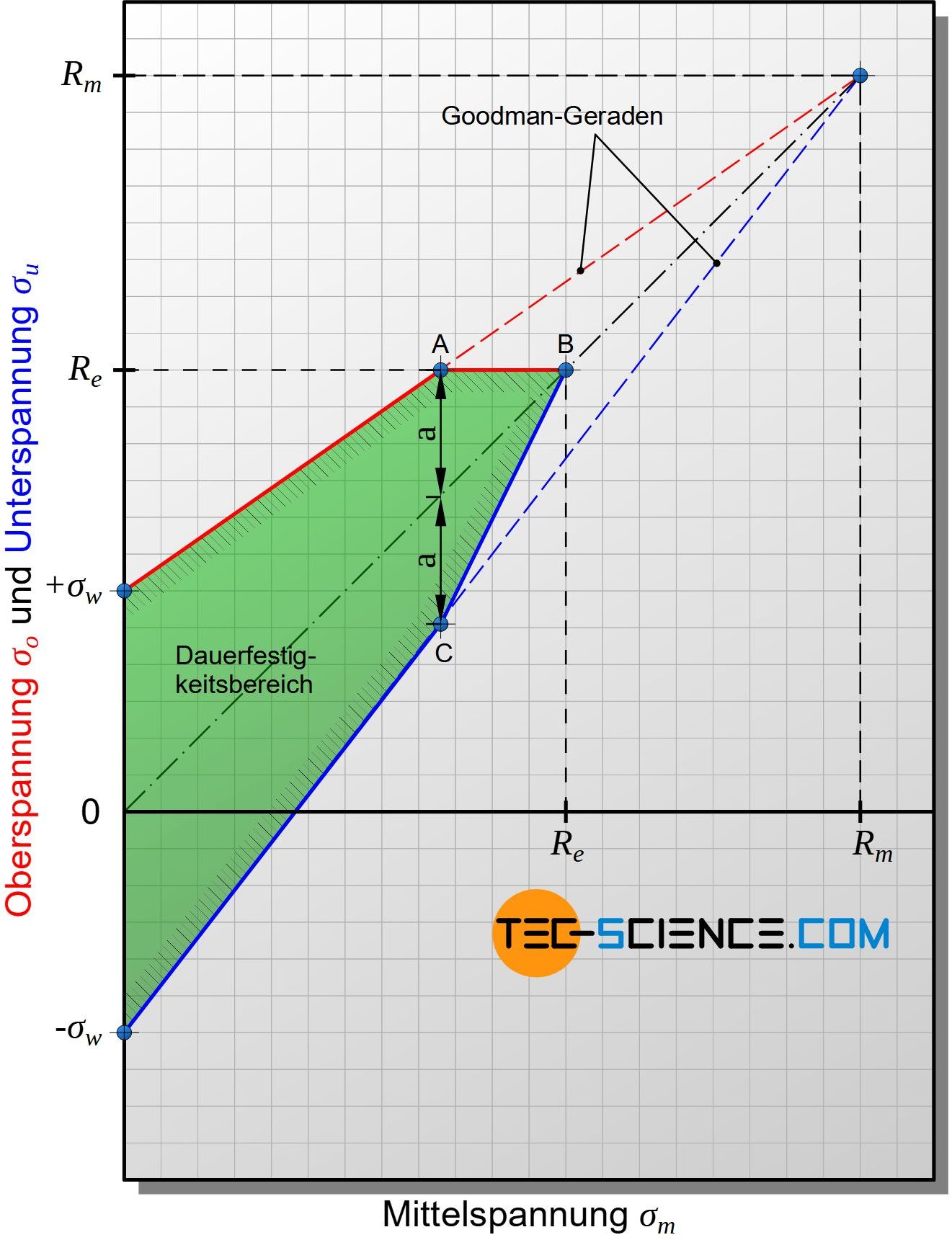
Ab Erreichen der Streckgrenze im Punkt A setzt sich die Oberspannungslinie somit als horizontale Gerade fort. Dies führt jedoch zu einer entsprechenden Anpassung der Unterspannungswerte, da die Spannungsausschläge zur Ober- und Unterspannung symmetrisch zur Mittelspannung liegen müssen. Um diese Anpassung vorzunehmen, wird der Abstand des Punktes A zur Mittelspannungslinie symmetrisch nach unten abgetragen und man erreicht wieder die Goodman-Gerade der Unterspannung (Punkt C). Die beiden Goodman-Geraden und der Linienzug der Punkte A, B, C begrenzen nun den technisch relevanten Dauerfestigkeitsbereich.
Im Smith-Diagramm kann nun für jede Mittelspannung die zulässige Ober- und Unterspannung für einen dauerfesten Einsatz des entsprechenden Werkstoffes direkt abgelesen werden. Anhand der unter 45° liegenden Hilfsgeraden kann zusätzlich die Spannungsamplitude als Abstand zur Goodman-Geraden relativ ermittelt werden.
Weitere Informationen zum Erstellen des Smith-Diagramms finden Sie auch unter ingenieurkurse.de.
Erweiterung des Smith-Diagramms auf den Druckbereich
Eine Erweiterung des Smith-Diagramms auf negative Mittelspannungswerte (Druckbereich) ist ohne weiteres möglich. Anstelle der Begrenzung der Oberspannung durch die Streckgrenze kommt nun die Quetschgrenze \(\sigma_{dF}\) zur Begrenzung der Unterspannung zum Einsatz (Punkt D). Ebenfalls ist die Mittelspannung durch die Quetschgrenze limitiert (Punkt E). Die in diesem Bereich notwendige symmetrische Verteilung der Unter- und Oberspannungswerte um die Mittelspannung herum, erhält man wiederum durch Spiegeln des Punktes D um die Mittelspannungslinie (Punkt F).