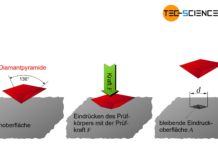
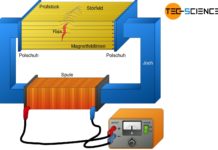
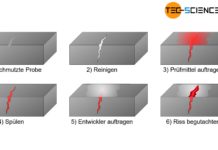
Beim Druckversuch wird eine Werkstoffprobe unter Druckbeanspruchung bis zum Bruch oder Anriss belastet!
Die Prüfung von Werkstoffen unter Druckbeanspruchung wird im sogenannten Druckversuch vorgenommen. Dabei kommen genormte Rundproben zum Einsatz, die im Gegensatz zu Zugproben wesentlich dicker sind. Die Probenhöhe beträgt maximal das Doppelte des Probendurchmessers, um ein Abknicken der Probe im Versuch zu verhindern. Die Probe wird zur Prüfung zwischen zwei Druckplatten eingespannt und unter zunehmender Kraft gestaucht. Die Druckprüfung erfolgt bei spröden Proben bis zum Bruch und bei duktilen Werkstoffen bis zum Erscheinen eines ersten Anrisses.
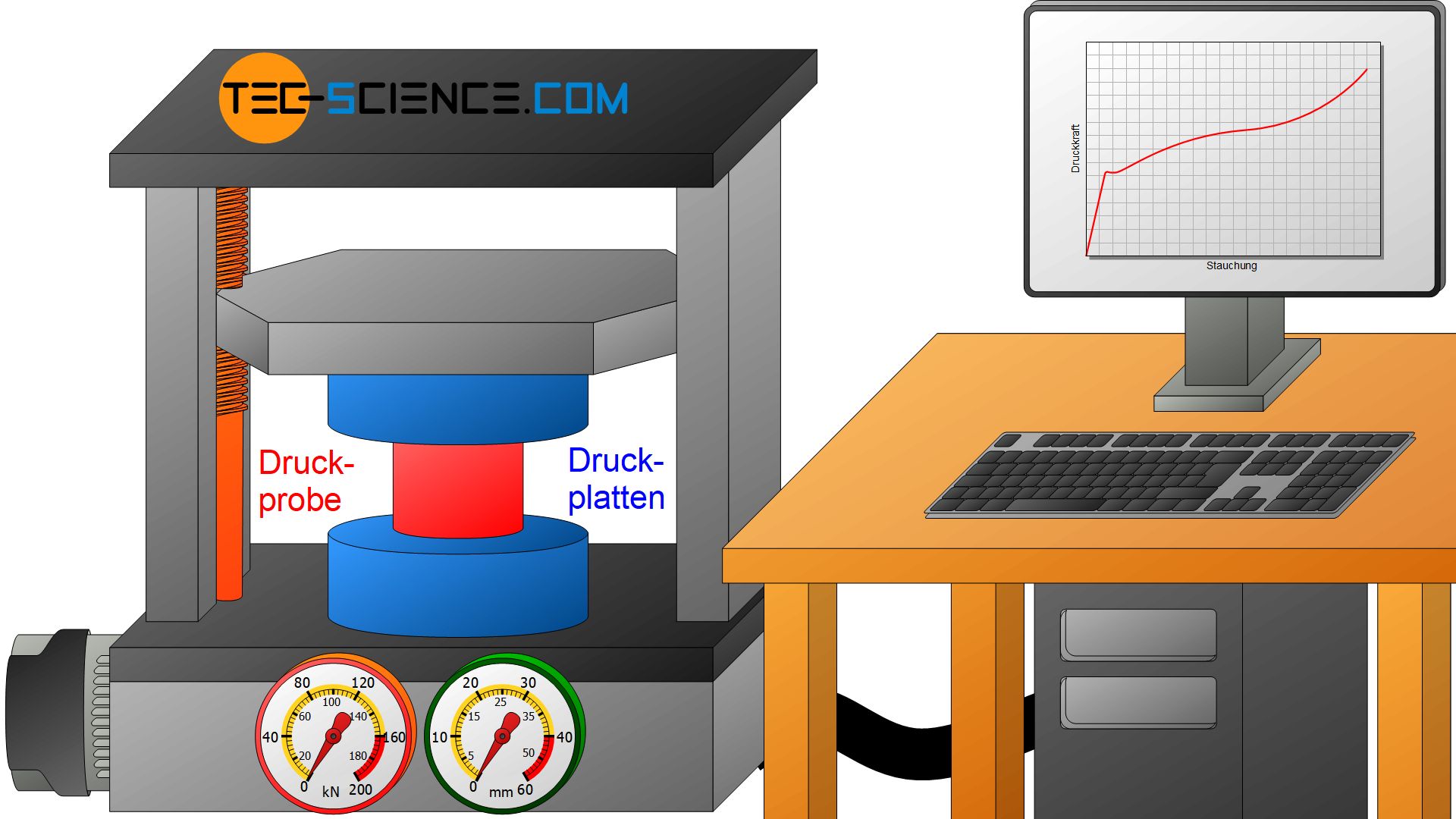
Beim Druckversuch wird eine genormte Werkstoffprobe unter Druckbeanspruchung bis zum Bruch oder bis zum Erscheinen eines ersten Anrisses belastet und die Kraft in Abhängigkeit der Probenstauchung aufgezeichnet!
Die während des Versuches aufgenommene Kraft-Weg-Kurve (geometrieabhängig) wird anschließend ein geometrieunabhängiges Druckspannung-Stauchungs-Diagramm überführt. Zur Bestimmung der technischen Druckspannung \(\sigma_d\) wird die Druckkraft \(F_d\) analog zur Zugspannung und ungeachtet des tatsächlich vorhandenen Querschnitts stets auf die Anfangsquerschnittsfläche \(S_0\) bezogen:
\begin{align}
\label{technische_druckspannung}
&\boxed{\sigma_d = \frac{F_d}{S_0}}~~~~~[\sigma]=\frac{\text{N}}{\text{mm²}} &&\text{technische Druckspannung} \\[5px]
\end{align}
Auf die analoge Weise zur Dehnung erhält man die Probenstauchung \(\epsilon_d\) indem man die Verkürzung der Probe \(\Delta h\) auf die Ausgangshöhe \(h_0\) bezieht (meist in Prozent angegeben):
\begin{align}
\label{stauchung}
&\boxed{\epsilon_d= \frac{\Delta h}{h_0} \cdot 100 \text{%}}~~~~~[\epsilon_d]=\text{%} ~~~~~\text{Stauchung} \\[5px]
\end{align}
Das abgebildete Druckspannung-Stauchungs-Diagramm zeigt den typischen Kurvenverlauf einer spröden Druckprobe (Gusseisen) und einer duktilen Probe (Stahl) sowie den Spannungsverlauf einer duktilen Probe mit niedriger Festigkeit (Zink). Beachtet werden muss an dieser Stelle wieder, dass dabei die Druckspannung stets anhand der Ausgangsquerschnittsfläche ermittelt wird und nicht der tatsächliche Querschnitt zugrunde gelegt wird.
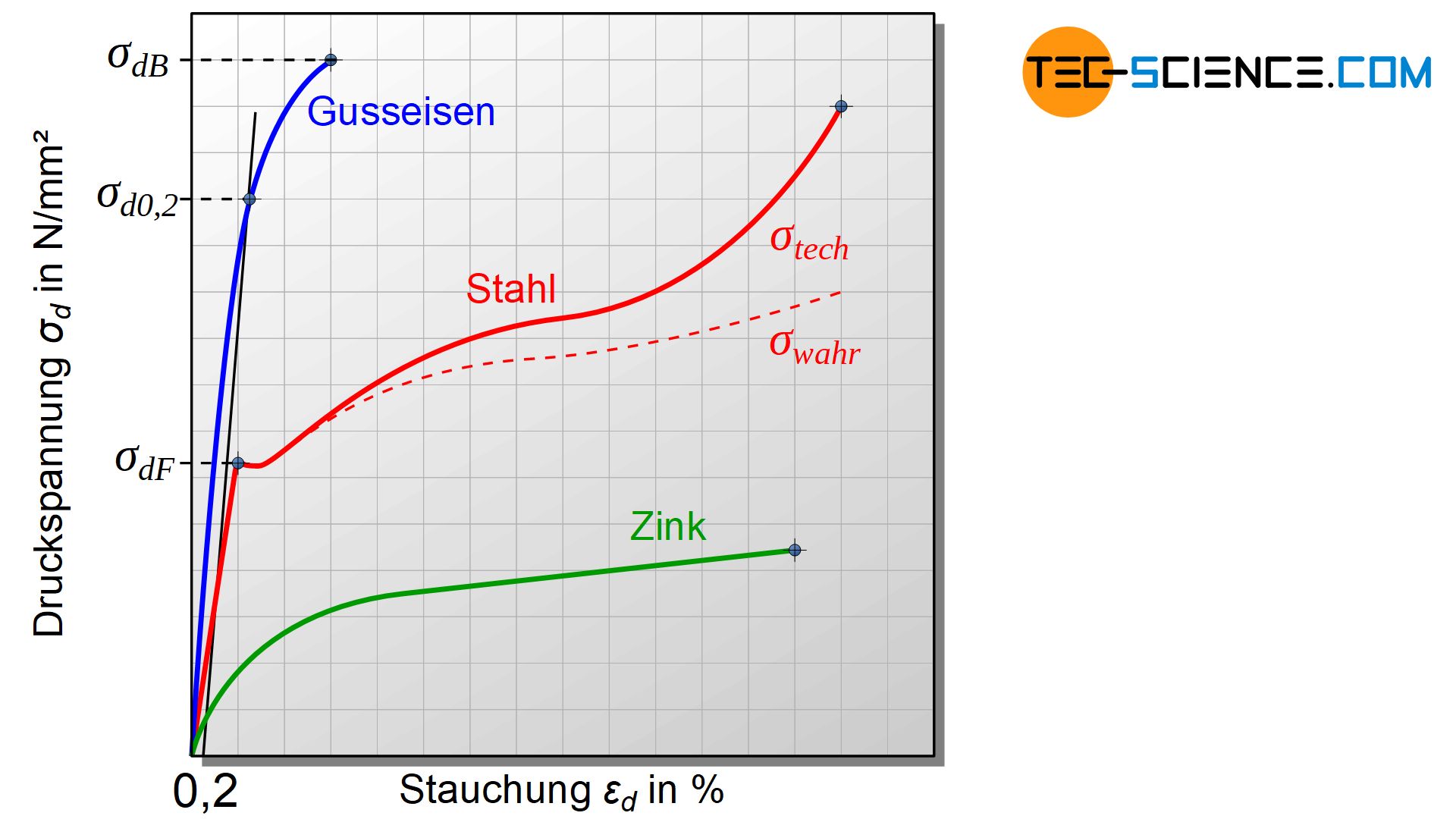
Durch Ausbauchungseffekte während des Versuchs vergrößert sich in Wahrheit die Querschnittsfläche und die wahre Druckspannung im Inneren ist geringer als die technische Druckspannung. Die wahre Druckspannungskurve verläuft deshalb unterhalb der technischen Spannungskurve.
Gemäß dem Druckspannung-Dehnungs-Diagramm lässt sich das Werkstoffverhalten unter Druck in unterschiedliche Bereiche untergliedern. Wird eine Druckprobe nur relativ gering auf Druck beansprucht, so wird die Verformung nach Wegnahme der Spannung wieder vollständig zurückgehen. Dieser elastische Bereich ist im Diagramm anhand des nahezu geraden Kurvenverlaufes zu erkennen.
Bei hoher Spannung wird hingegen die Elastizitätsgrenze überschritten und es bleibt eine dauerhafte Verformung auch nach Wegnahme der Kraft erhalten (plastischer Bereich). Bei einigen Werkstoffen ist diese Grenze im Diagramm sehr deutlich anhand des unstetigen Übergangs vom geradlinigen Verlauf in eine nunmehr gekrümmte Kurve zu erkennen.
Die Grenzspannung bei der eine Probe im Druckversuch gerade noch ohne bleibende Verformungen gequetscht wird, wird auch als Quetschgrenze \(\sigma_{dF}\) (Druck-Fließgrenze) bezeichnet. Die Quetschgrenze ist als Analogie zur Streckgrenze bei einer Zugbeanspruchung zu betrachten.
Als Quetschgrenze (Druckfließgrenze) bezeichnet man die maximal ertragbare Druckspannung ohne dass sich der Werkstoff bleibend verformt (Elastizitätsgrenze)!
Voraussetzung für die Bestimmung der Quetschgrenze ist, dass sich im Diagramm eine deutliche Gerade mit einem entsprechend unstetigen Übergang in den plastischen Bereich finden lässt (z.B. bei vielen Stählen). Einige Werkstoffe zeigen im Diagramm jedoch keine Gerade sondern einen stetigen Übergang in den plastischen Bereich (z.B. bei Grauguss). Für diese Werkstoffe werden in Analogie zu den Dehngrenzen des Zugversuchs die entsprechenden Stauchgrenzen ausgewiesen. Besondere Bedeutung hat auch dabei wieder die 0,2%-Grenze. Diese 0,2%-Stauchgrenze \(\sigma_{d0,2}\) ist als jene Druckspannung zu interpretieren ist, bei der eine Stauchung von 0,2 % nach Entlastung der Probe zurückbleibt.
Bei Werkstoffen die keine ausgeprägte Quetschgrenze aufweisen, wird als Ersatz eine entsprechende Stauchgrenze angegeben, die die Druckspannung bei einer festgelegten bleibenden Dehnung angibt!
Durch die hohen Reibungskräfte zwischen Probenoberseite und Druckstempel bzw. zwischen Probenunterseite und Unterlage erfolgt die Stauchung grundsätzlich nicht gleichmäßig über die Probenhöhe hinweg. Vielmehr haftet die Probe an den Kontaktstellung und lässt dort keine Verformung zu, während der Mittelteil der Probe zur Seite wegfließen kann. Es kommt somit je nach Duktilität der Probe zu einer mehr oder weniger stark ausgeprägten Ausbauchung während des Druckversuchs.
Anders als im Zugversuch bei dem ein Gleichmaßdehnungsbereich existiert, gibt es im Druckversuch also kein analoges Gegenstück wie etwa einen Gleichmaßstauchungsbereich! Die Zone der Verformungsbehinderung durch Reibung nimmt ausgehend der Pressflächen zur Probenmitte hin ab. Es entstehen im Werkstoffinneren kegelförmige Verformungsbehinderungszonen, die auch als Druckkegel bezeichnet werden.
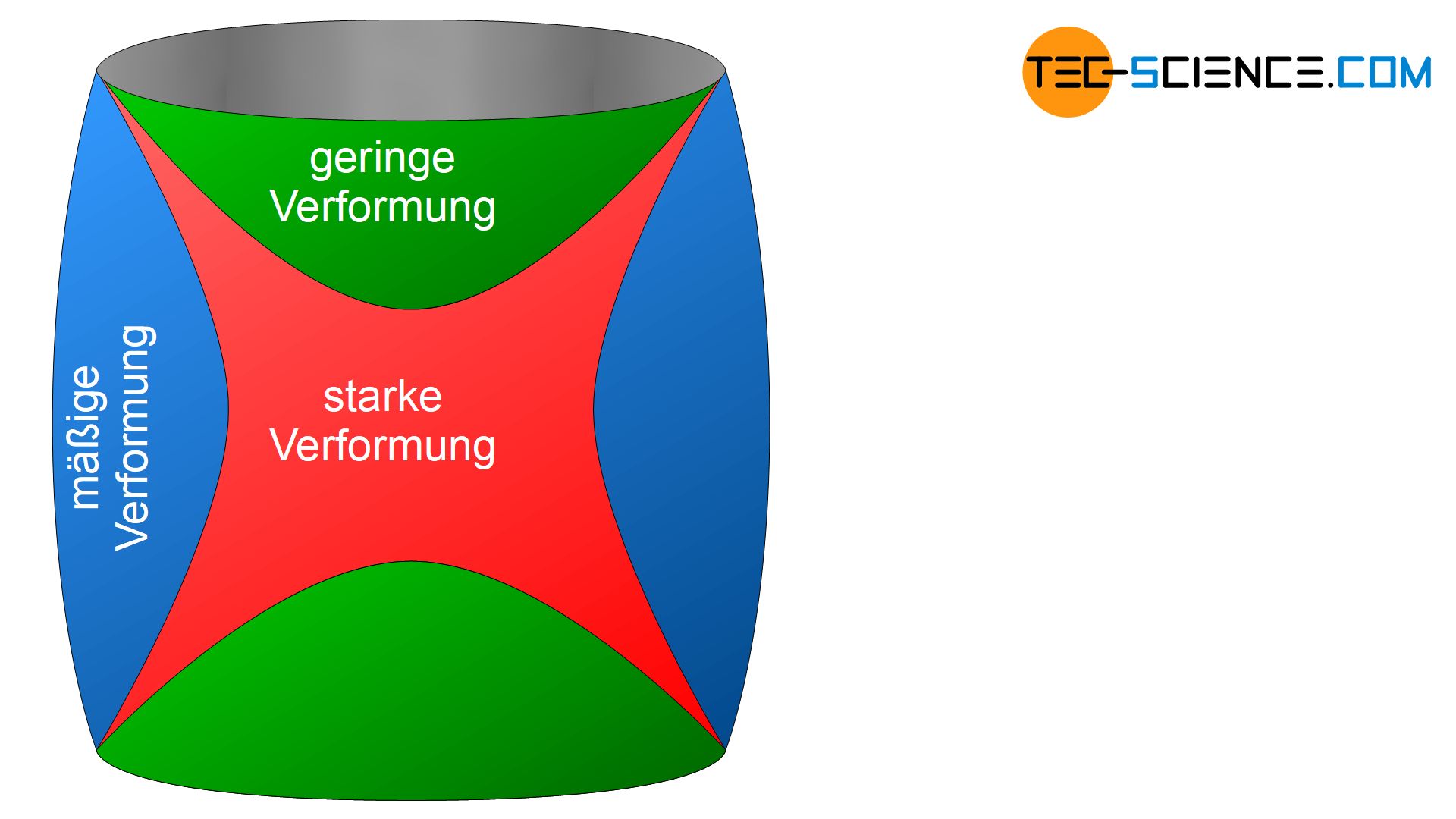
Durch die Ausbauchung der Probe werden die Randfasern der Probe stark gelängt und es kommt in diesen Randbereichen zu einer Zugbeanspruchung. Diese können so groß werden, dass der Werkstoff entlang der Beanspruchungsrichtung aufreißt. Der entstehende Anriss wird bei duktilen Werkstoffen oft als Versagenskriterium herangezogen.
Bei spröden Werkstoffen schieben sich die nahezu unverformten Druckkegel wie Keile in das umgebende Material und sorgen im Mittelteil der Probe für sehr hohe Schubspannungen. Da die größten Schubspannungen in einem Winkel von 45° zur Druckbeanspruchungsrichtung auftreten, brechen spröden Proben meist entlang dieser Richtung.
Das Einsetzen eines Anrisses bei duktilen Werkstoffen oder der plötzliche Bruch bei spröden Proben wird durch die sogenannte Druckfestigkeit \(\sigma_{dB}\) charakterisiert. Diese Größe ist in Analogie zur Zugfestigkeit des Zugversuchs zu betrachten.

Als Druckfestigkeit bezeichnet man die maximal ertragbare Druckspannung bevor schließlich der Bruch einsetzt!
Darüber hinaus lässt sich im Druckversuch als Verformungskenngröße die bleibende Stauchung nach dem Bruch ermitteln, die sogenannte Bruchstauchung \(\epsilon_{dB}\). Diese Kenngröße entspricht im Zugversuch der Bruchdehnung. Ferner kann in Analogie zur Brucheinschnürung einer Zugprobe die Bruchausbauchung \(\Psi\) als Verhältnis von Querschnittsänderung und Anfangsquerschnitt der Druckprobe ermittelt werden.
Zusammenfassend ist eine tabellarische Gegenüberstellung über die charakteristischen Größen des Zugversuchs und des Druckversuchs gegeben:
| Kenngröße | Zugversuch | Druckversuch |
| Nennspannung | Zugspannung \(\sigma\) | Druckspannung \(\sigma_{d}\) |
| Relative Längenänderung | Dehnung \(\epsilon\) | Stauchung \(\epsilon_{d}\) |
| Fließgrenze | Streckgrenze \(R_e\) | Quetschgrenze \(\sigma_{dF}\) |
| Alternative Grenzwerte | 0,2%-Dehngrenze \(R_{p0,2}\) | 0,2%-Stauchgrenze \(\sigma_{d0,2}\) |
| Versagenskenngröße | Zugfestigkeit \(R_m\) | Druckfestigkeit \(\sigma_{dB}\) |
| Relative bleibende Längenänderung | Bruchdehnung \(A\) | Bruchstauchung \(\epsilon_{dB}\) |
| Relative bleibende Querschnittsänderung | Brucheinschnürung \(Z\) | Bruchausbauchung \(\Psi\) |