Heizdrahtverfahren zur Bestimmung der Wärmeleitfähigkeit (THW)

Beim Heizdrahtverfahren (Transient Hot Wire, THW) bestimmt man die Wärmeleitfähigkeit über die zeitliche Temperaturerhöhung einer Probe in einem gewissen Abstand zu einem Heizdraht.

Aufbau

Beim Heizdrahtverfahren bestimmt man die Wärmeleitfähigkeit anhand der zeitlichen Erhöhung der Temperatur eines Stoffes, wenn dieser durch einen dünnen Heizdraht erwärmt wird. Der Heizdraht befindet sich dabei direkt in der Probe. Besonders einfach lassen sich damit gasförmige und flüssige Stoffe untersuchen, da der Heizdraht in diesen Fällen relativ einfach in die Fluide eingetaucht werden kann. Die Messapparatur bzw. der zu untersuchende Stoff kann durch äußere Temperierung auch auf verschiedene Temperaturen gebracht werden. Auf diese Weise kann man die Wärmeleitfähigkeit in Abhängigkeit der Temperatur untersuchen.

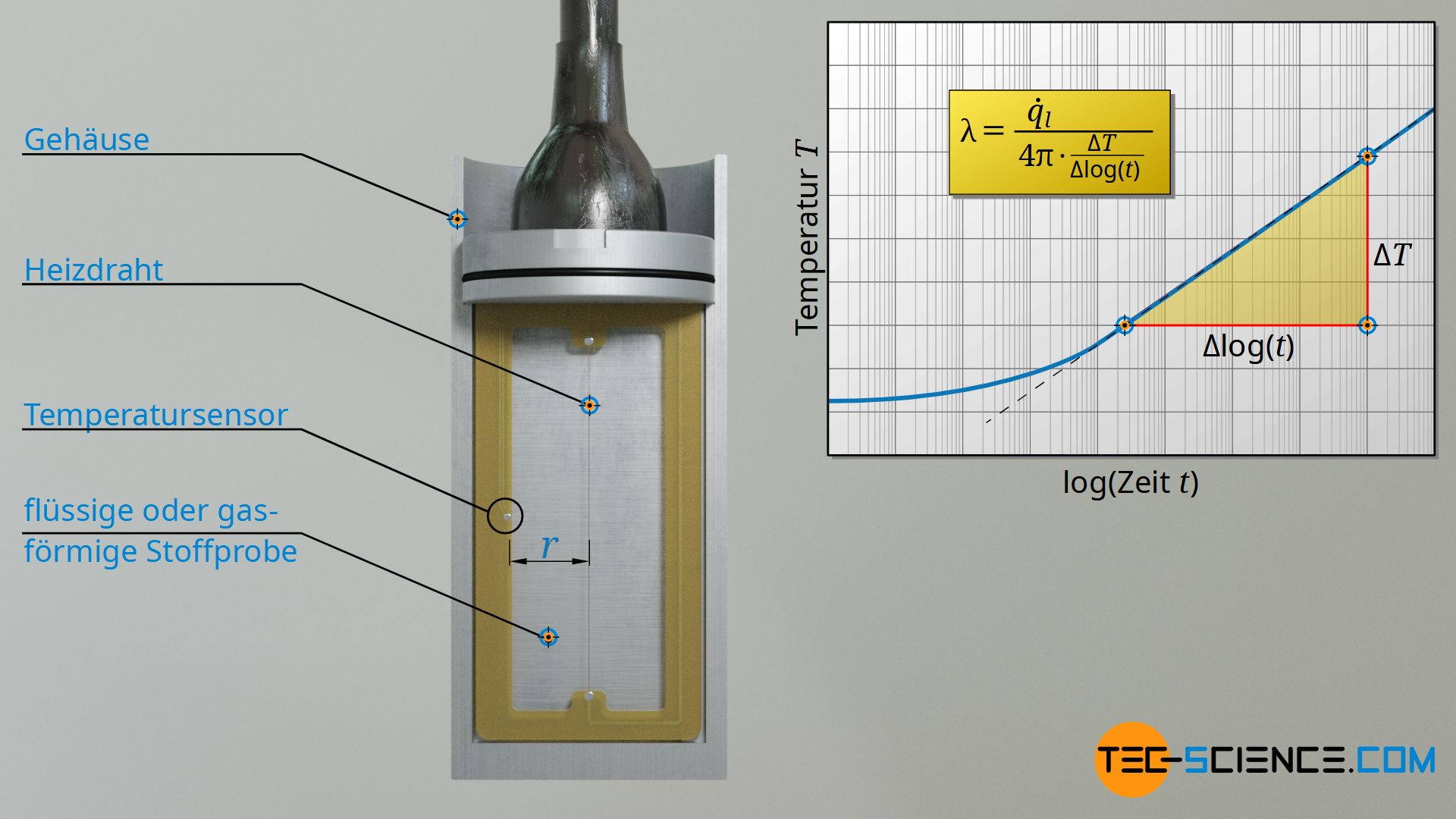
Mathematische Beschreibung

Um aus der beobachteten Temperaturerhöhung die Wärmeleitfähigkeit ermitteln zu können, muss dieser Vorgang zunächst mathematische beschrieben werden. Aus der Wärmeleitungsgleichung erhält man für eine linienförmige Wärmequelle (Draht) folgende Gleichung, mit der man die Temperatur T in einem Abstand r zur Wärmequelle zu einem bestimmten Zeitpunkt termitteln kann:

\begin{align}
\label{t}
& \boxed{T(r,t) = \frac{\dot q_l}{4 \pi \cdot \lambda} \cdot \left[\ln \left( \frac{4\cdot a \cdot t}{r^2}\right) -\gamma\right]} \\[5px]
\end{align}

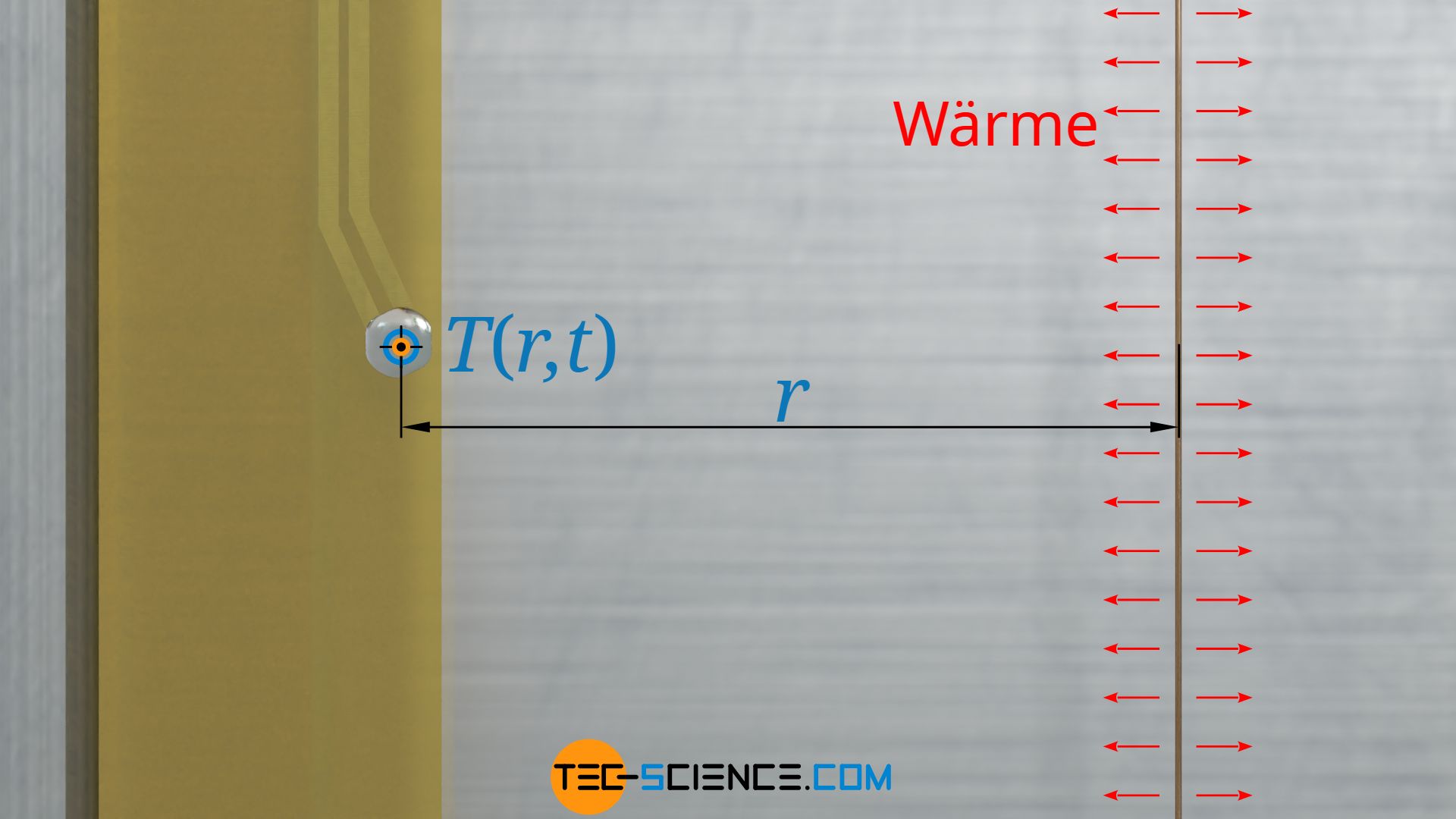
Darin bezeichnet q*_l die spezifische Wärmeleistung der linienförmigen Wärmequelle (Wärmeleistung pro Längeneinheit) und λ die Wärmeleitfähigkeit des umgebenden Mediums und a die entsprechende Temperaturleitfähigkeit. \gamma entspricht der Eulerschen Konstante mit einem Wert von 0,57721. Letzterer Ausdruck kommt durch eine angenäherte Reihenentwicklung zustande, die nur für den Fall gültig ist, falls der Ausdruck r²/(4⋅a⋅t) sehr viel kleiner 1 ist. Dies ist insbesondere dann erfüllt, wenn kleine Abstände r zum Heizdraht betrachtet werden oder/und die Zeiten t relativ groß gewählt werden.

Praktische Durchführung

Zwar gibt es gemäß der unten aufgeführten Gleichung (\ref{d}) einen eindeutigen Zusammenhang zwischen der Wärmeleitfähigkeit und der Temperaturleitfähigkeit, jedoch steht die Temperaturleitfähigkeit in Gleichung (\ref{t}) im Argument der Logarithmusfunktion, sodass sich selbst mit dieser eingesetzten Beziehung die obere Gleichung nicht direkt nach der Wärmeleitfähigkeit auflösen lässt.

\begin{align}
\label{d}
& \boxed{\lambda = a \cdot \rho \cdot c_p} \\[5px]
\end{align}

Man misst bei gegebenem Abstand r deshalb nicht die Temperatur zu einem bestimmten Zeitpunkt, sondern die Temperaturdifferenz zwischen zwei Zeitpunkten. Auf diese Weise spielt weder der Abstand r, noch die Temperaturleitfähigkeit a eine Rolle:

\begin{align}
\require{cancel}
\Delta T &= T(r,t_2) – T(r,t_1) \\[5px]
\Delta T & = \frac{\dot q_l}{4 \pi \cdot \lambda} \cdot \left[\ln \left( \frac{4\cdot a \cdot t_2}{r^2}\right)-\gamma \right] – \frac{\dot q_l }{4 \pi \cdot \lambda} \cdot \left[\ln \left( \frac{4\cdot a \cdot t_1}{ r^2}\right)-\gamma\right] \\[5px]
\Delta T & =\frac{\dot q_l }{4 \pi \cdot \lambda} \cdot \left[\ln \left( \frac{4\cdot a \cdot t_2}{ r^2}\right) – \bcancel{\gamma}~ – \ln \left( \frac{4\cdot a \cdot t_1}{r^2}\right) +\bcancel{\gamma} \right] \\[5px]
\Delta T & =\frac{\dot q_l }{4 \pi \cdot \lambda} \cdot \left[\ln \left( \frac{4\cdot a \cdot t_2}{r^2}\right) – \ln \left( \frac{4\cdot a \cdot t_1}{ r^2}\right) \right] \\[5px]
\Delta T & =\frac{\dot q_l }{4 \pi \cdot \lambda} \cdot \ln \left( \frac{\frac{4\cdot a \cdot t_2}{ r^2} }{ \frac{4\cdot a \cdot t_1}{r^2} } \right) \\[5px]
\Delta T & =\frac{\dot q_l }{4 \pi \cdot \lambda} \cdot \ln \left(\frac{t_2}{t_1}\right) \\[5px]
\end{align}

\begin{align}
\label{l}
&\boxed{\lambda =\frac{\dot q_l }{4 \pi \cdot \Delta T } \cdot \ln \left(\frac{t_2}{t_1}\right)} \\[5px]
\end{align}

Zur Bestimmung der Wärmeleitfähigkeit λ muss man bei gegebener spezifischer Heizleistung q*_l also lediglich die Temperaturänderung ΔT zwischen zwei Zeitpunkten t₁ und t₂ bestimmen. Beachte, dass für die Gültigkeit dieser Formel der Abstand r zum Heizdraht relativ klein zu wählen ist und die Zeitmessung nicht direkt mit Einschalten des Heizdrahtes begonnen werden sollte, sondern erst einige Zeit später.

Auswertung der Messung

In der Praxis bestimmt man die Wärmeleitfähigkeit nicht nur anhand von zwei Messungen, sondern man nimmt zunächst die zeitliche Temperaturänderung auf. Diesen Verlauf stellt man anschließend in einem logarithmischen Zeit-Temperatur-Schaubild graphisch dar. Aus der Geradensteigung lässt sich dann die Wärmeleitfähigkeit bestimmen. Die Messdauer beträgt in der Regel nur wenige Sekunden, wobei Temperaturänderungen von bereits unter 1 °C für eine verlässliche Auswertung genügen. Innerhalb einer solchen kurzen Messzeit, werden Konvektionsströme in Fluide praktisch vernachlässigbar. Die untere Abbildung zeigt hierzu schematisch den Verlauf der Temperatur in Abhängigkeit der logarithmierten Zeit.

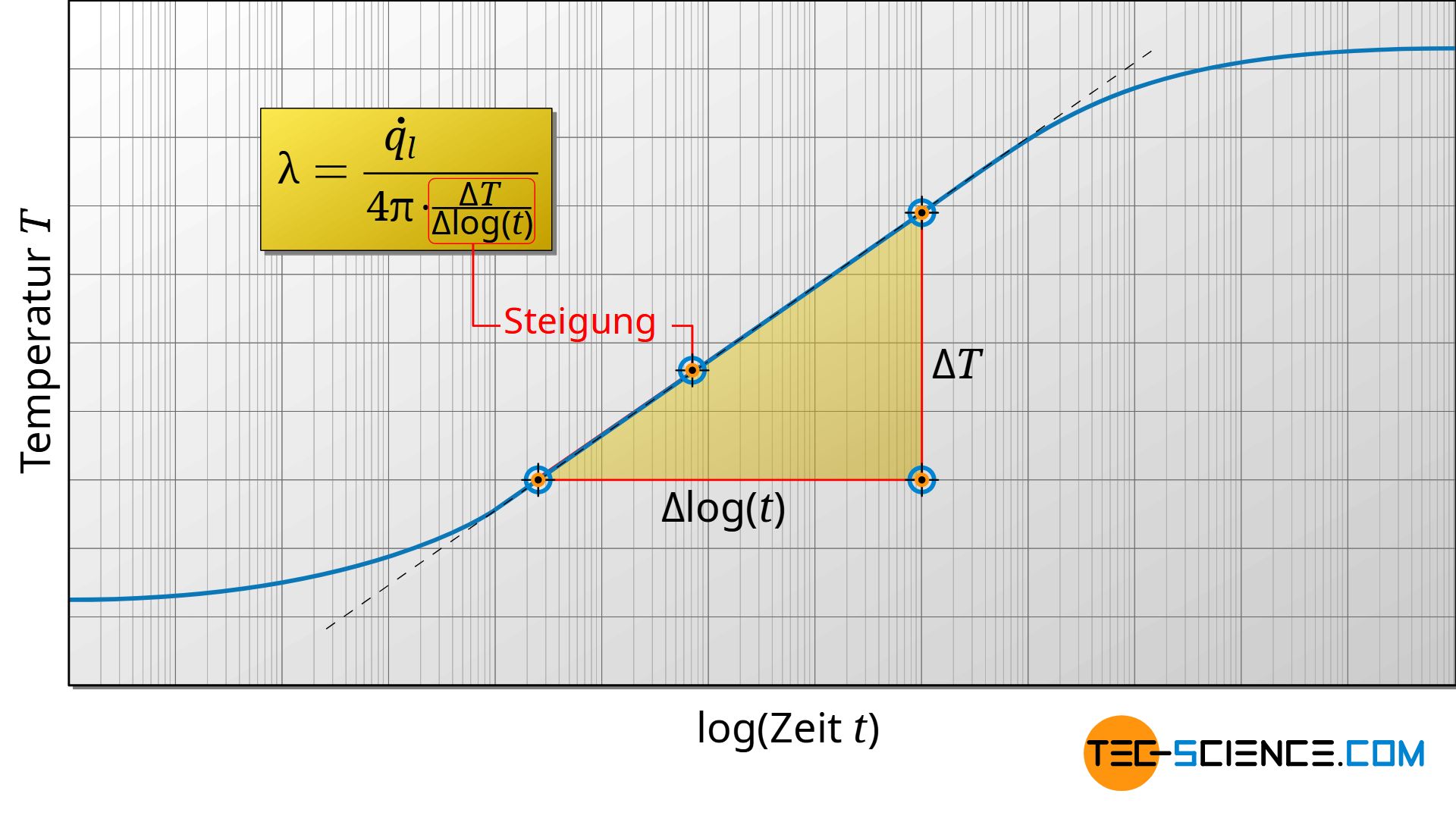
Beachte, dass die hergeleiteten Formeln nur im linearen Bereich des Diagramms gelten. Dies ist der bereits erwähnten Forderung geschuldet, dass für die Anwendbarkeit der Formeln die Zeiten ausreichen groß sein müssen. Auch muss beachtet werden, dass sich der Heizdraht in der Praxis erst selbst erwärmen muss, bevor dieser die eigentliche Probe erwärmen kann. Aus diesem Grund entsteht zu Beginn der Messwerterfassung eine Nicht-Linearität zwischen Temperaturänderung und logarithmierter Zeit. Erst nach einer gewissen Zeitdauer ist die Linearität vorhanden. Bei zu großen Zeiten verschwindet diese Linearität jedoch auch wieder. Dies ist dann der Fall, wenn die Wärme sozusagen durch das Material gedrungen ist und sie sich anschließend nur noch insgesamt erwärmt.

Die im Diagramm gezeigte lineare Abhängigkeit erhält man auf mathematische Weise durch Umstellen von Gleichung (\ref{l}):

\begin{align}
&\lambda =\frac{\dot q_l }{4 \pi \cdot \Delta T } \cdot \ln \left(\frac{t_2}{t_1}\right) \\[5px]
&\Delta T=\frac{\dot q_l }{4 \pi \cdot \lambda} \cdot \left[\ln(t_2)-\ln(t_1) \right] \\[5px]
&\Delta T=\frac{\dot q_l }{4 \pi \cdot \lambda} \cdot \Delta \ln(t) \\[5px]
\end{align}

Folglich bestimmt sich die Wärmeleitfähigkeit λ wie folgt anhand der Geradensteigung im linearen Bereich des Graphen:

\begin{align}
&\frac{\Delta T}{ \Delta \ln(t) }=\frac{\dot q_l }{4 \pi \cdot \lambda} = \text{Steigung im } T(\ln(t))\text{-Diagramm}\\[5px]
&\boxed{\lambda=\frac{\dot q_l}{4\pi \cdot \text{Steigung}}} \\[5px]
\end{align}

Einsatzbereiche

Typischerweise wird das Heizdrahtverfahren für Gase und Flüssigkeiten verwendet, deren Wärmeleitfähigkeiten zwischen 0,1 und 50 W/(mK) liegen. Bei zu großen Wärmeleitfähigkeiten erhält man im Diagramm oft keinen ausgeprägten linearen Abschnitt, sodass keine Auswertung möglich ist.