Ausströmen von Flüssigkeiten (Torricelli’s Theorem)

Das Torricelli Theorem besagt, dass die Ausflussgeschwindigkeit einer Flüssigkeit aus einem Behälter, einem freien Fall gleicht.

Ausflussgeschwindigkeit

Herleitung

Man kann die Geschwindigkeit mit der eine Flüssigkeit in einem Gefäß aufgrund des hydrostatischen Drucks durch eine Öffnung ausströmt relativ einfach ermitteln. Hierzu betrachten wir ein Gefäß, das mit Wasser gefüllt ist. In Bodennähe ist ein Auslass angebracht, der nach oben zeigt. Folglich strömt das Wasser mit einer uns noch unbekannten Geschwindigkeit nach oben aus. In diesem Fall gilt es nun folgende Frage zu beantworten: Mit welcher maximalen Geschwindigkeit kann das Wasser überhaupt ausströmen, damit der Energieerhaltungssatz nicht verletzt ist?

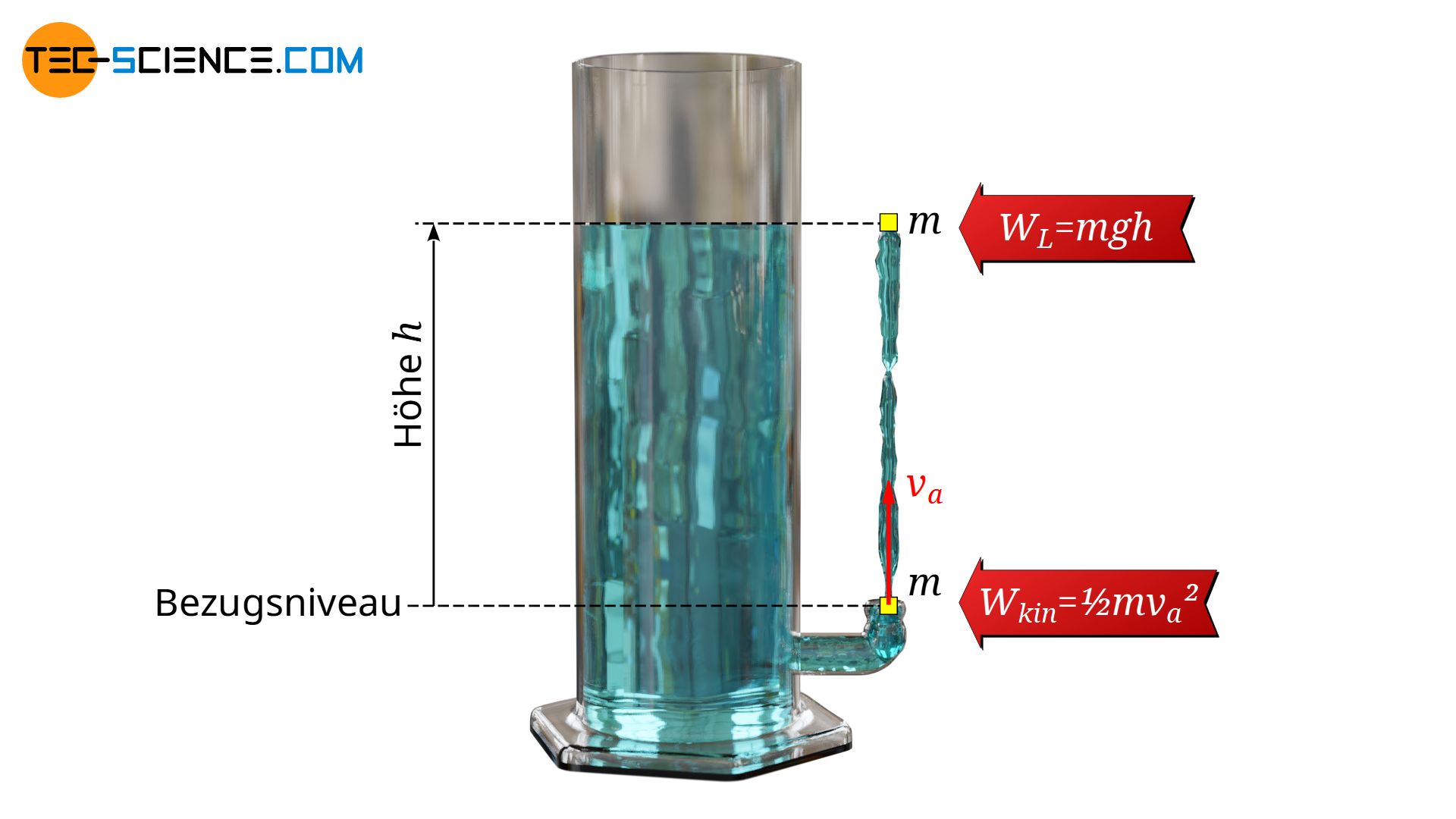
Die auf diese Frage Antwort lautet: Das Wasser kann maximal so stark ausströmen, dass der Strahl nicht höher als bis zur ursprünglichen Wasseroberfläche kommt (unter Vernachlässigung von Reibung). Denn wäre dies so, dann könnte man mit diesem Strahl ein höher gelegenes Gefäß befüllen. Nach demselben Prinzip könnte man nun ein weiters, noch höher gelegenes Gefäß füllen. Das Wasser würde sich praktisch von selbst immer weiter nach oben befördern. Dies widerspräche aber dem Energieerhaltungssatz. Umgekehrt würde Energie vernichtet werden, wenn Wasser nur eine geringere Höhe als die ursprüngliche Wasseroberfläche erreicht.

Folglich ist aus energetischer Sicht klar, dass sich die kinetische Energie eines Wasserteilchens (W_kin=½⋅m⋅v_a²) maximal vollständig in Lageenergie umwandeln kann (W_L=m⋅g⋅h). Dabei entspricht die Höhe h gerade der Höhe der Wasseroberfläche über der Öffnung (bzw. der Tiefe der Öffnung unterhalb der Wasseroberfläche) und m der Masse eines Wasserteilchens. Für die Ausflussgeschwindigkeit v gilt folglich:

\begin{align}
\require{cancel}
W_{L} &= W_{kin} \\[5px]
\bcancel{m} \cdot g \cdot h &= \frac{1}{2} \cdot \bcancel{m} \cdot v_a^2 \\[5px]
\end{align}

\begin{align}
\label{tl}
&\boxed{v_a=\sqrt{2gh}} \\[5px]
\end{align}

Beachte, dass diese Formel nur unter der Bedingung gilt, dass die Flüssigkeit frei ausströmen kann. Sollte sich beim Ausströmen ein Gegendruck aufbauen, gilt diese Formel nicht mehr, da die Flüssigkeit dann am Ausströmen gehindert wird. Dies wird bspw. dann der Fall sein, wenn die ausströmende Flüssigkeit über einen Schlauch in einen geschlossenen Behälter geleitet wird. Durch das Ansteigen des Flüssigkeitsspiegels in dem geschlossenen Behälter, wird dann die darin befindliche Luft komprimiert und es baut sich ein Gegendruck auf. Die Ausflussgeschwindigkeit ist dann geringer als Gleichung (\ref{tl}) suggeriert.

Interpretation der Formel

Wie man anhand der Gleichung sieht, hängt die Geschwindigkeit mit der eine Flüssigkeit aus einem Behälter mit Loch ausströmt, nur vom Höhenunterschied zwischen Öffnung und Flüssigkeitsoberfläche ab. Es spielt für die Ausflussgeschwindigkeit (die unmittelbar auf die Öffnung bezogen ist) auch keine Rolle, ob die Öffnung nach oben, nach unten oder zur Seite zeigt.

Ebenfalls zeigt Gleichung (\ref{tl}), dass die Ausfließgeschwindigkeit nicht von der Dichte der Flüssigkeit abhängt! Demzufolge ist es unter Vernachlässigung der Reibung also völlig egal, welche Flüssigkeit sich im Behälter befindet. Dies erscheint zunächst paradox, da der hydrostatische Druck in einer dichteren Flüssigkeit größer ist. Demzufolge könnte man meinen, dass eine dichtere Flüssigkeit dann auch mit einem größeren Druck durch die Öffnung gepresst wird und deshalb eine größere Höhe erreicht. Dass der Druck größer ist, ist soweit völlig richtig, aber genau hierdurch erreicht die „schwerere“ Flüssigkeit ja auch schließlich dieselbe Höhe!

Diese Interpretation macht auch deutlich, dass Gleichung (\ref{tl}) nur gültig ist, wenn die Sinkgeschwindigkeit der Flüssigkeitsoberfläche vernachlässigbar klein gegenüber der Austrittsgeschwindigkeit ist. Ansonsten hätte ein Teilchen an der Wasseroberfläche nicht nur Lageenergie, sondern auch bereits kinetische Energie. Dies müsste dann ebenfalls in die Energiebilanz mit einfließen (später mehr dazu).

Torricellis Theorem

Die Herleitung der Ausfließgeschwindigkeit lässt aber noch eine andere interessante Interpretation zu. Hierzu betrachten wir nicht den Ausströmprozess außerhalb des Gefäßes, sondern die Vorgänge innerhalb. Wasser strömt dabei von der Oberfläche nach unten und fließt dann aus der Öffnung. Wir betrachten also in der Höhe h über der Öffnung (Bezugsniveau) eine kleine Flüssigkeitsmenge der Masse m. Dieser Masse lässt sich folglich die Lageenergie W_L=m⋅g⋅h zuordnen. Auf dem Weg zur Öffnung wandelt sich diese Lageenergie in kinetische Energie um. Beim Ausströmen aus der Öffnung hat sich die Lageenergie vollständig in kinetische Energie W_kin=½⋅m⋅v_a². Gleichsetzen der Energien und auflösen liefert schließlich dasselbe Ergebnis wie Gleichung (\ref{tl}).

In der vorliegenden Betrachtungsweise nimmt man also offensichtlich an, dass eine betrachtete Wassermasse an der Oberfläche einen freien Fall bis zur Öffnung vollführt. Auch wenn die Wasserteilchen tatsächlich keinen freien Fall vollziehen, so ist dies aus einem energetischen Standpunkt heraus betrachtet dennoch dasselbe. Denn mit jedem Ausströmen einer bestimmten Masse aus der Öffnung, muss im selben Maße Wasser nach unten sinken, d.h. nach unten fallen.

Man kann sich einen solchen kontinuierlichen Prozess auch als diskontinuierlichen Vorgang gedacht vorstellen. Hierzu stelle man sich vor, man verschließt die Öffnung mit einem Finger. Für eine kurze Zeit öffnet man den Auslass, sodass plötzlich eine kleine Wassermenge ausströmt. Der Wasserspiegel sinkt hierdurch schlagartig ab. Er fällt sozusagen für eine kurze Strecke im freien Fall nach unten. Man kann sich deshalb das Absinken der Flüssigkeitsoberfläche beim Ausströmen des Wassers aus der Öffnung als viele kleine freie Fälle gedacht vorstellen.

Der gedachte freie Fall einer Flüssigkeitsmenge beim Ausströmen aus einer Öffnung wird auch als Torricelli’s Theorem bezeichnet.

Kommunizierende Röhren

Mit der Formel für die Ausströmgeschwindigkeit lässt sich auch unmittelbar erklären, warum sich ein gemeinsamer Flüssigkeitsstand einstellt, wenn man unterschiedlich gefüllte Gefäße miteinander verbindet. Dies bezeichnet man auch als Prinzip der kommunizierenden Röhren.

Jenes Gefäß mit dem geringeren Flüssigkeitsstand kann dabei als Öffnung des anderen Gefäßes betrachtet werden. Durch diese Öffnung strömt das Wasser gemäß Gleichung (\ref{tl}) mit der Geschwindigkeit v_a aus dem einen Gefäß heraus bzw. in das andere Gefäß ein. Solange also ein Höhenunterschied in den Wasserpegel besteht, strömt Wasser nach oben. Erst wenn kein Höhenunterschied mehr vorliegt, strömt das Wasser auch nicht mehr aus bzw. ein, da die Strömungsgeschwindigkeit dann null beträgt. In diesem Fall haben sich dann identische Wasserspiegel eingestellt.

Entleerungszeit

Beim Ausfließen einer Flüssigkeit aus einem Behälter stellt sich häufig die Frage, wie lange das vollständige Entleeren insgesamt dauert. Im Alltag tritt ein solcher Fall bspw. beim Entleeren einer wassergefüllten Badewanne ein. Im Folgenden möchten wir deshalb für einfache geometrische Behälter solche Entleerungszeiten ermitteln. Vereinfachend nehmen wir dabei an, dass die Höhe der Austrittsöffnung (Öffnungsdurchmesser) klein gegenüber der Füllstandshöhe ist.

Wie schnell ein Behälter entleert ist, hängt unter anderem davon wie schnell die Flüssigkeit ausströmt. Eine hohe Ausflussgeschwindigkeit bedeutet schließlich viel ausströmende Masse pro Zeit. Die Ausflussgeschwindigkeit ist gemäß Gleichung (\ref{tl}) aber von der Füllstandshöhe h abhängig. Zu Beginn, wenn der Flüssigkeitsstand hoch ist, strömt folglich viel Flüssigkeit aus dem Behälter. Somit sinkt der Füllstandspegel zunächst relativ schnell. Mit sinkendem Füllstand nimmt jedoch die Ausflussgeschwindigkeit immer mehr ab, und der Behälter entleert sich immer langsamer.

Bedeutung für den Alltag und die Technik

Eine wichtige Erkenntnis kann man an dieser Stelle bereits ziehen. Ein Behälter lässt sich umso schneller entleeren, je höher der Flüssigkeitsstand gehalten werden kann. Dies ist auch der Grund weshalb sich eine Badewanne schneller entleert, wenn man darin sitzen bleibt. Denn dadurch verdrängt man das umgebende Wasser und der Füllstand befindet sich länger auf einem höheren Niveau als wenn man aus der Badewanne steigt.

Auf die Technik übertragen bedeutet dies, dass man Gefäße die sich schnell von selbst entleeren müssen, eher in Höhe bauen sollte als in die Breite. Eine einfache Alternative hierzu ist es den Ausfluss mit einem Schlauch einfach so tief wie möglich zu legen. Je tiefer der Schlauch gelegt wird, desto schneller strömt das Wasser aus und umso geringere Entleerungszeiten entstehen.

Kontinuitätsgleichung (Massenerhaltung)

Die Bestimmung der Entleerungszeit ist im Allgemeinen gar nicht so einfach, da diese auch von der Form des Gefäßes abhängig ist. In der technischen Praxis hat man es aber meistens mit Gefäßen zu tun, deren Querschnitt konstant ist. D.h. die Flüssigkeitsoberfläche bleibt auch beim Absinken des Flüssigkeitsspiegels stets konstant. Man denke zum Beispiel an Regentonnen oder an Getränketanks in der Nahrungsmittelindustrie. Auch bei einer Badewanne ändert sich die Querschnittsfläche bzw. die Wasseroberfläche kaum über die Höhe (außer gegen Ende, wenn das Wasser fast komplett abgeflossen ist).

Im Folgenden betrachten wir deshalb ein Behälter dessen Querschnitts A stets konstant bleibt. Am Boden des Behälters strömt die darin befindliche Flüssigkeit über ein Loch mit dem Querschnitt A_a aus. Zunächst müssen wir einen Zusammenhang finden zwischen der Ausflussgeschwindigkeit der Flüssigkeit aus dem Behälter und der Sinkgeschwindigkeit des Füllstandes im Behälter. Dies geschieht durch die simple Bedingung, dass die Masse die durch die Öffnung ausströmt, exakt jener Masse entspricht, um die der Behälterinhalt abnimmt (Massenerhaltung). Für inkompressible Stoffe ist dies gleichbedeutend mit der Aussage, dass sich das Flüssigkeitsvolumen im Behälter genau um den Betrag des ausströmenden Volumens verringert.

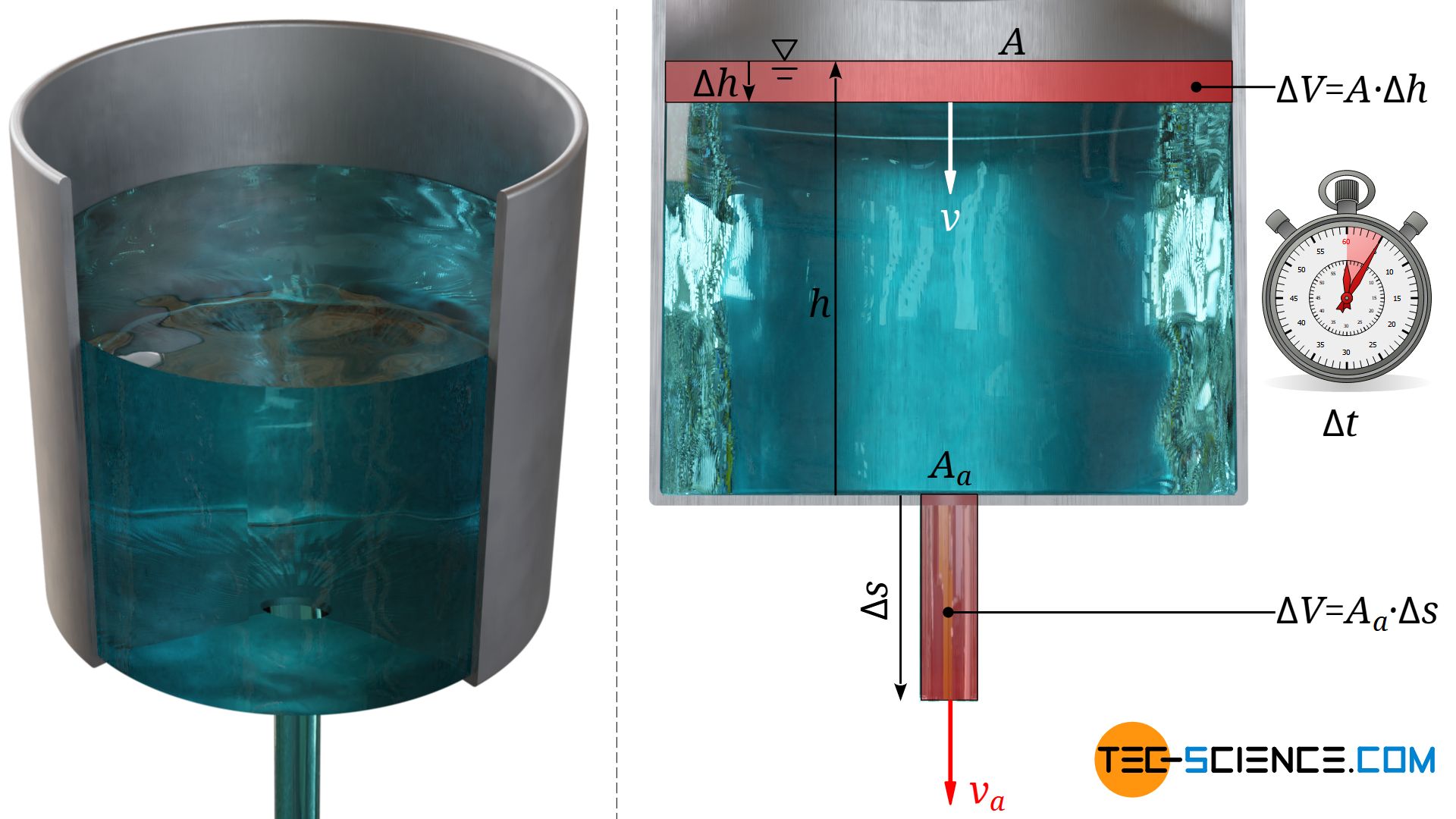
Hierzu betrachten wir bei einer beliebigen Füllstandshöhe h einen sehr kleinen Zeitabschnitt Δt. Die Flüssigkeit ströme dabei mit der konstanten Geschwindigkeit v_a aus der Öffnung und lege somit die Strecke Δs=v_a⋅Δt zurück. In Kombination mit dem Öffnungsquerschnitt A_a kann hieraus das austretende Flüssigkeitsvolumen ΔV ermittelt werden:

\begin{align}
\label{v1}
& \Delta V = \Delta s \cdot A_a = v_a \cdot \Delta t \cdot A_a \\[5px]
\end{align}

Die austretende Flüssigkeit führt dazu, dass der Flüssigkeitsspiegel sinkt. Innerhalb des betrachteten Zeitabschnitts Δt sei die Sinkgeschwindigkeit konstant und betrage v. Somit sinkt der Füllstand innerhalb dieser Zeit um Δh=v⋅Δt. Das Flüssigkeitsvolumen im Behälter nimmt somit analog zur oberen Gleichung um einen Betrag ΔV ab:

\begin{align}
\label{v2}
& \Delta V = \Delta h \cdot A = v \cdot \Delta t \cdot A \\[5px]
\end{align}

Aufgrund der bereits angesprochenen Massenerhaltung entspricht bei inkompressiblen Flüssigkeiten das ausgelaufene Flüssigkeitsvolumen nach Gleichung (\ref{v1}) dem abgenommenen Flüssigkeitsvolumen im Behälter gemäß Gleichung (\ref{v2}). Beide Gleichungen können also gleichgesetzt werden und man erhält auf diese Weise eine Beziehung zwischen der Ausflussgeschwindigkeit v_a aus dem Behälter und der Sinkgeschwindigkeit v im Behälter:

\begin{align}
\require{cancel}
& v \cdot \bcancel{\Delta t} \cdot A = v_a \cdot \bcancel{\Delta t} \cdot A_a \\[5px]
\label{k}
& \boxed{v = \frac{A_a}{A} \cdot v_a} ~~~~~\text{Kontinuitätsgleichung für inkompressible Stoffe} \\[5px]
\end{align}

Gleichung (\ref{k}) wird auch als Kontinuitätsgleichung bezeichnet und beschreibt letztlich nichts anderes als die Massenerhaltung. Konkret bedeutet dies: eine Flüssigkeit muss umso schneller strömen, je kleiner der Querschnitt wird, da innerhalb derselben Zeit dieselbe Masse hindurch befördert werden muss. Man kann den Behälter letztlich als Rohrsystem betrachten, dessen Querschnitt sich von A auf A_a verjüngt.

An dieser Stelle wird auch nochmals deutlich, weshalb die Annahme eines über die Behälterhöhe konstanten Behälterquerschnittes A im Folgenden vieles vereinfacht. Denn hierdurch stehen Sink- und Ausströmgeschwindigkeit unabhängig der Füllstandshöhe immer im selben Verhältnis, welches nur vom Verhältnis der Querschnittsflächen abhängig ist.

Torricellis Theorem

Nachdem der Zusammenhang zwischen Sink- und Ausströmgeschwindigkeit geklärt ist, muss die Abhängigkeit der Ausströmgeschwindigkeit von der Füllstandshöhe gefunden werden. An dieser Stelle hilft Torricelli’s Theorem in Form von Gleichung (\ref{tl}), das direkt in Gleichung (\ref{k}) eingesetzt werden kann:

\begin{align}
\label{vv}
& \boxed {v = \frac{A_a}{A} \cdot \sqrt{2gh}} ~~~\text{Sinkgeschwindigkeit des Füllstandes} \\[5px]
\end{align}

An dieser Stelle zeigt sich in mathematischer Form was bereits qualitativ erläutert wurde. Die Sinkgeschwindigkeit hängt vom Füllstand ab, was wiederum Auswirkungen auf den Füllstand selbst hat und somit wieder die Sinkgeschwindigkeit beeinflusst. Die Sinkgeschwindigkeit des Füllstandes ist dabei aber nichts anderes als die Änderungsrate der Füllstandshöhe. D.h. die Sinkgeschwindigkeit entspricht der Änderung der Füllstandshöhe dh pro Zeit dt. Dabei drückt das negative Vorzeichen aus, dass sich der Füllstand bei positiver Sinkgeschwindigkeit verringert.

\begin{align}
& \boxed {v = – \frac{\text{d}h}{\text{d}t}} \\[5px]
\end{align}

Kombiniert man beide Gleichungen, so erhält man schließlich folgende Differentialgleichung, die es zu lösen gilt:

\begin{align}
& -{\frac{\text{d}h}{\text{d}t} = \frac{A_a}{A} \cdot \sqrt{2gh}} \\[5px]
\end{align}

Lösen der Differentialgleichung

Um die Rechnungen übersichtlicher zu gestalten, werden die konstanten Größen in der Differentialgleichung zunächst zu einer gemeinsamen Konstanten K zusammengefasst:

\begin{align}
& \boxed{-\frac{\text{d}h}{\text{d}t} = K \cdot \sqrt{h}} ~~~\text{mit } \boxed{K=\sqrt{2g} \cdot \frac{A_a}{A}}=\text{konstant} \\[5px]
\end{align}

Um die Differentialgleichung zu lösen, sind die veränderlichen Größen zu trennen (hier: die Variablen h und t). D.h. alle Größen die mit der Variablen h zu tun haben kommen auf die eine Seite der Gleichung und alle Größen die mit der Variablen t zu tun haben auf die andere Seite der Gleichung. Auf welcher Seite die Konstante K steht, ist dabei prinzipiell egal, schließlich hängt sie ja von keinen der beiden Variablen ab.

\begin{align}
& -\frac{\text{d}h}{ \sqrt{h}} = K \cdot \text{d}t \\[5px]
\end{align}

Beide Seiten der Gleichung kann man nun unabhängig voneinander integrieren. Die Integrationsgrenzen ergeben sich dabei aus folgender Überlegung. Zum Zeitpunkt 0 habe der Füllstand die Höhe H und zu einem beliebig anderen Zeitpunkt t die Höhe h.

\begin{align}
& -\int\limits_H^h \frac{\text{d}h}{ \sqrt{h}} = \int\limits_0^t K \cdot \text{d}t \\[5px]
& -\left[2\sqrt{h}\right]_H^h = K \cdot \left[ t \right]_0^t \\[5px]
& -2\left(\sqrt{h}-\sqrt{H}\right) = K \cdot t \\[5px]
& t = \frac{2}{K} \left(\sqrt{H}-\sqrt{h}\right)\\[5px]
\end{align}

Der Vollständigkeit halber wird die Konstante K noch in die obere Gleichung eingesetzt. Für die Zeitdauer t, die man benötigt um einen Behälter ausgehend der Füllstandshöhe H bis auf die Höhe h zu entleeren gilt also:

\begin{align}
& t = \frac{2}{ \underbrace{\sqrt{2g} \cdot \tfrac{A_a}{A}}_{=K} } \left(\sqrt{H}-\sqrt{h}\right)\\[5px]
\label{gl}
& \boxed{t = \frac{A}{A_a} \sqrt{\frac{2}{g}} \left(\sqrt{H}-\sqrt{h}\right)} \\[5px]
\end{align}

Für das vollständige Entleeren gilt h=0 und für die Entleerungsdauer t_e damit:

\begin{align}
&t_e = \frac{A}{A_a} \sqrt{\frac{2}{g}} \sqrt{H}\\[5px]
& \boxed{t_e = \frac{A}{A_a} \sqrt{\frac{2H}{g}}} ~~~\text{Entleerungsdauer} \\[5px]
\end{align}

Anmerkung

Es wurde zu Beginn erläutert, dass sich ein hoher Behälter bei gleichem Füllvolumen schneller entleert als ein breiterer. Die Formel zur Berechnung der Entleerungsdauer schein dabei vordergründig im Widerspruch zu stehen. Denn gemäß dieser Gleichung nimmt die Entleerungsdauer zu, wenn der Füllstand höher ist.

Dies ist natürlich kein Widerspruch, denn bei gleichem Füllvolumen nimmt die Querschnittsfläche des Behälters im selben Maße ab wie die Füllhöhe zunimmt. Bei einer Halbierung der Querschnittsfläche bspw. nimmt die Füllstandshöhe um das Doppelte zu. Die Füllstandshöhe geht aber nicht in vollem Umfang in die Entleerungsdauer ein, sondern mit der Quadratwurzel. Bei einer Verdopplung des Füllstandes entspräche dies einem Faktor von 1,4 (=√2). In Kombination mit der Halbierung der Querschnittsfläche, verkürzt sich somit die Entleerungsdauer insgesamt um den Faktor 0,7 (=√2⋅0,5).

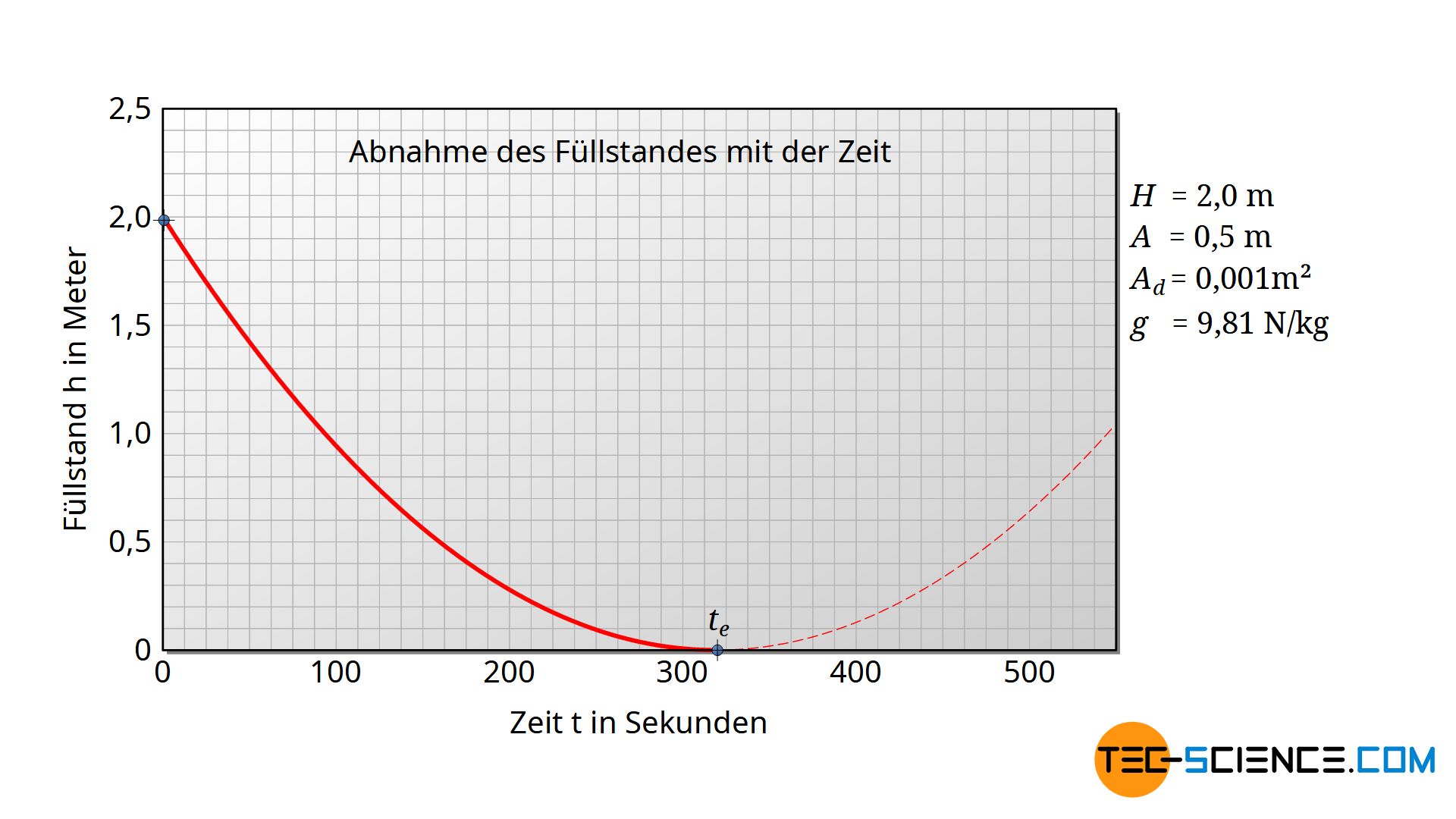
Darstellung der Abnahme des Füllstandes mit der Zeit

Möchte man die Abnahme des Füllstandes in Abhängigkeit der Zeit darstellen, dann muss man Gleichung (\ref{gl}) lediglich nach der Höhe h umstellen:

\begin{align}
t &= \frac{A}{A_a} \sqrt{\frac{2}{g}} \left(\sqrt{H}-\sqrt{h}\right) \\[5px]
\frac{A_a}{A} \sqrt{\frac{g}{2}} \cdot t &= \sqrt{H}-\sqrt{h} \\[5px]
\sqrt{h} &= \sqrt{H} – \frac{A_a}{A} \sqrt{\frac{g}{2}} \cdot t \\[5px]
h &= \left(\sqrt{H} – \frac{A_a}{A} \sqrt{\frac{g}{2}} \cdot t \right)^2 \\[5px]
\end{align}

\begin{align}
&\boxed{h(t) = \left(\sqrt{H} – \frac{A_a}{A} \sqrt{\frac{g}{2}} \cdot t \right)^2} \\[5px]
\end{align}

Der Füllstand nimmt also quadratisch mit der Zeit ab. Der Scheitelpunkt der Parabel entspricht dabei dem Zeitpunkt, bei dem der Behälter vollständig entleert ist.

Ausfließender Volumenstrom

Gemäß Gleichung (\ref{vv}) kann man zu jeder Füllstandshöhe h die entsprechende Ausströmgeschwindigkeit v berechnen. Auf diese Weise lässt sich auch eine Aussage über den austretenden Volumenstrom V* gewinnen. Als Volumenstrom bezeichnet man dabei das innerhalb einer bestimmten Zeit Δt austretende Flüssigkeitsvolumen ΔV:

\begin{align}
&\boxed{\dot V = \frac{\Delta V}{\Delta t}} ~~~\left[\dot V \right] = \frac{\text{m³}}{\text{s}}~~~\text{Volumenstrom} \\[5px]
\end{align}

Den austretenden Volumenstrom V* kann man gemäß dieser Definition direkt durch Umstellen von Gleichung (\ref{v1}) bestimmen:

\begin{align}
& \Delta V = A_a \cdot v_a \cdot \Delta t \\[5px]
\label{vd}
& \frac{ \Delta V }{\Delta t} = \boxed{\dot V = A_a \cdot v_a} \\[5px]
\end{align}

Schließlich kann nun die Ausströmgeschwindigkeit nach Gleichung (\ref{tl}) genutzt werden, um den austretenden Volumenstrom (Ausflussrate) in Abhängigkeit der Höhe zu bestimmen:

\begin{align}
\label{dV}
& \boxed{\dot V = A_a \cdot \sqrt{2gh} } \\[5px]
\end{align}

Einfluss der Sinkgeschwindigkeit auf die Ausflussgeschwindigkeit

Es wurde bereits angedeutet, dass die hergeleiteten Formeln nur gelten, solange die Sinkgeschwindigkeit vernachlässigbar klein gegenüber der Ausströmgeschwindigkeit ist. Gerade bei großen Öffnungen kann aber sehr viel Flüssigkeit ausströmen. Der Füllstand sinkt dann relativ schnell. Wird das Ausströmen vor dem Hintergrund des Torricelli Theorems betrachtet, dann handelt es sich dabei nicht mehr nur um einfachen freien Fall, sondern um einen freien Fall mit einer Anfangsgeschwindigkeit. Die Anfangsgeschwindigkeit entspricht der Sinkgeschwindigkeit v des Flüssigkeitsspiegels zum aktuellen Zeitpunkt.

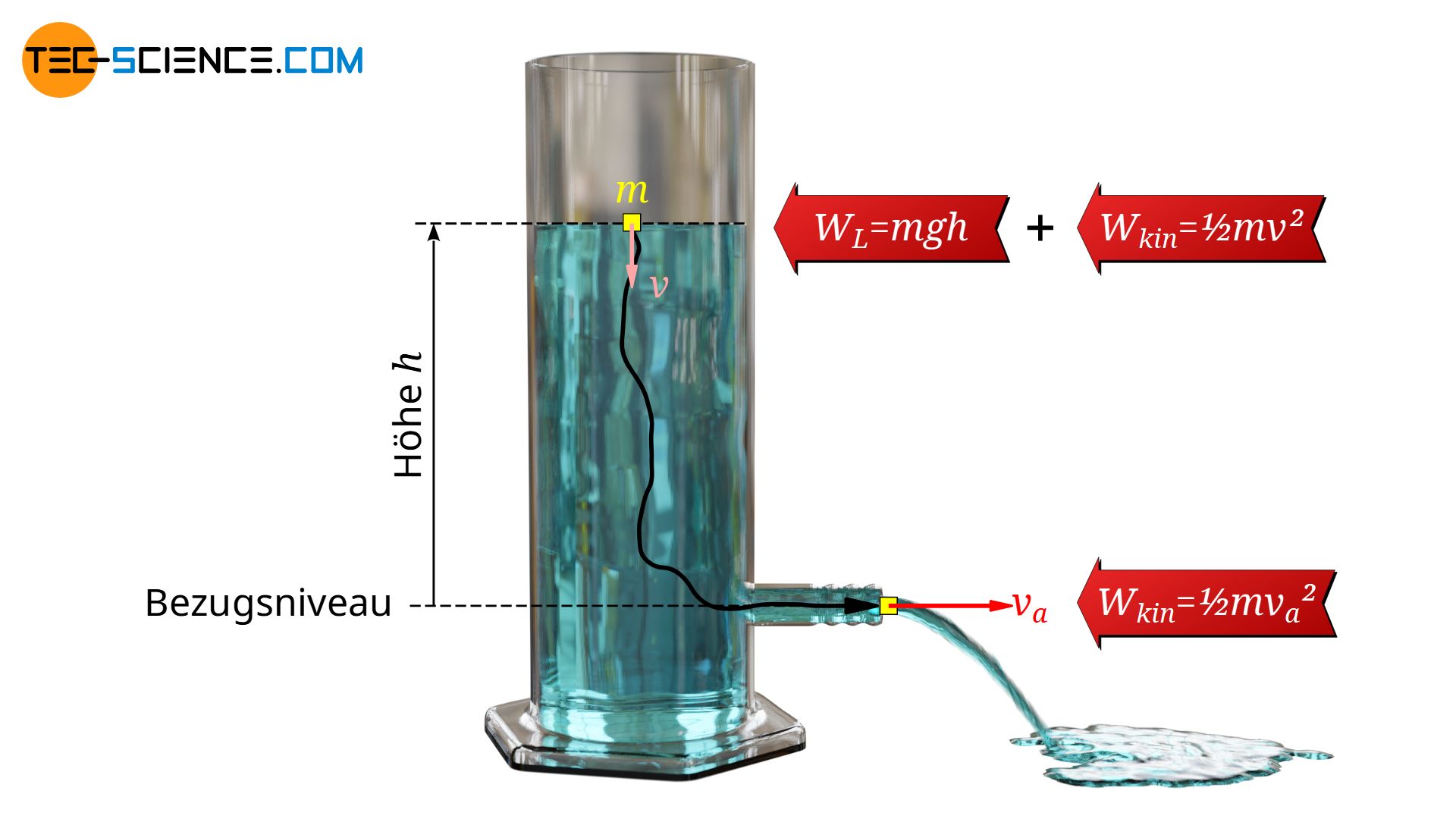
Energetisch betrachtet, hat ein betrachtete Flüssigkeitsmenge an der Oberfläche somit nicht nur Lageenergie (m⋅g⋅h) sondern auch kinetische Energie (½⋅m⋅v²). In diesem allgemeinen Fall ergibt sich für die Ausströmgeschwindigkeit v_a folgende Formel:

\begin{align}
\require{cancel}
& \bcancel{m} \cdot g \cdot h + \frac{1}{2} \cdot \bcancel{m} \cdot v^2 = \frac{1}{2} \cdot \bcancel{m} \cdot v_a^2 \\[5px]
\end{align}

\begin{align}
&\boxed{v_a=\sqrt{v^2+2gh}} \\[5px]
\end{align}

Die Ausströmgeschwindigkeit ist bei schnellem Absinken der Flüssigkeitsoberfläche größer im Vergleich zu geringen Sinkgeschwindigkeiten. Die ausströmende Flüssigkeit bezieht sozusagen zusätzliche kinetische Energie aus dem Absinkvorgang. Nach wie vor gilt dabei natürlich die Kontinuitätsgleichung nach Gleichung (\ref{k}). Somit stehen Sinkgeschwindigkeit v und Ausströmgeschwindigkeit v_a nun wie folgt in Zusammenhang:

\begin{align}
& v = \frac{A_a}{A} \cdot v_a \\[5px]
& v = \frac{A_a}{A} \cdot \sqrt{v^2+2gh} \\[5px]
\end{align}

Diese Gleichung nach der Sinkgeschwindigkeit v aufgelöst, ergibt:

\begin{align}
& \boxed{v = \color{red}{\tfrac{1}{\sqrt{ 1- \left(\tfrac{A_a}{A}\right)^2 }}} \cdot \frac{A_a}{A} \cdot \sqrt{2gh} } \\[5px]
\end{align}

Vergleicht man diese Formel mit der Formel (\ref{vv}) (welche unter Vernachlässigung der Sinkgeschwindigkeit gegenüber der Ausströmgeschwindigkeit erhalten wurde), dann unterscheiden sich beide Formeln nur durch den rot markierten Term. Dieser Geometrieterm ist letztlich nur durch das Verhältnis der Querschnittsflächen von Öffnung und Behälter bestimmt. Die untere Abbildung zeigt den Verlauf dieses Terms in Abhängigkeit vom Querschnittsverhältnis. Ist der Öffnungsquerschnitt kleiner als 10 % des Behälterquerschnitts, dann beträgt dieser Faktor nur noch 1,005. Der Einfluss der Sinkgeschwindigkeit bleibt unterhalb eines Querschnittsverhältnisses von 0,1 also vernachlässigbar! Dies dürfte für viele praktische Fälle gelten.

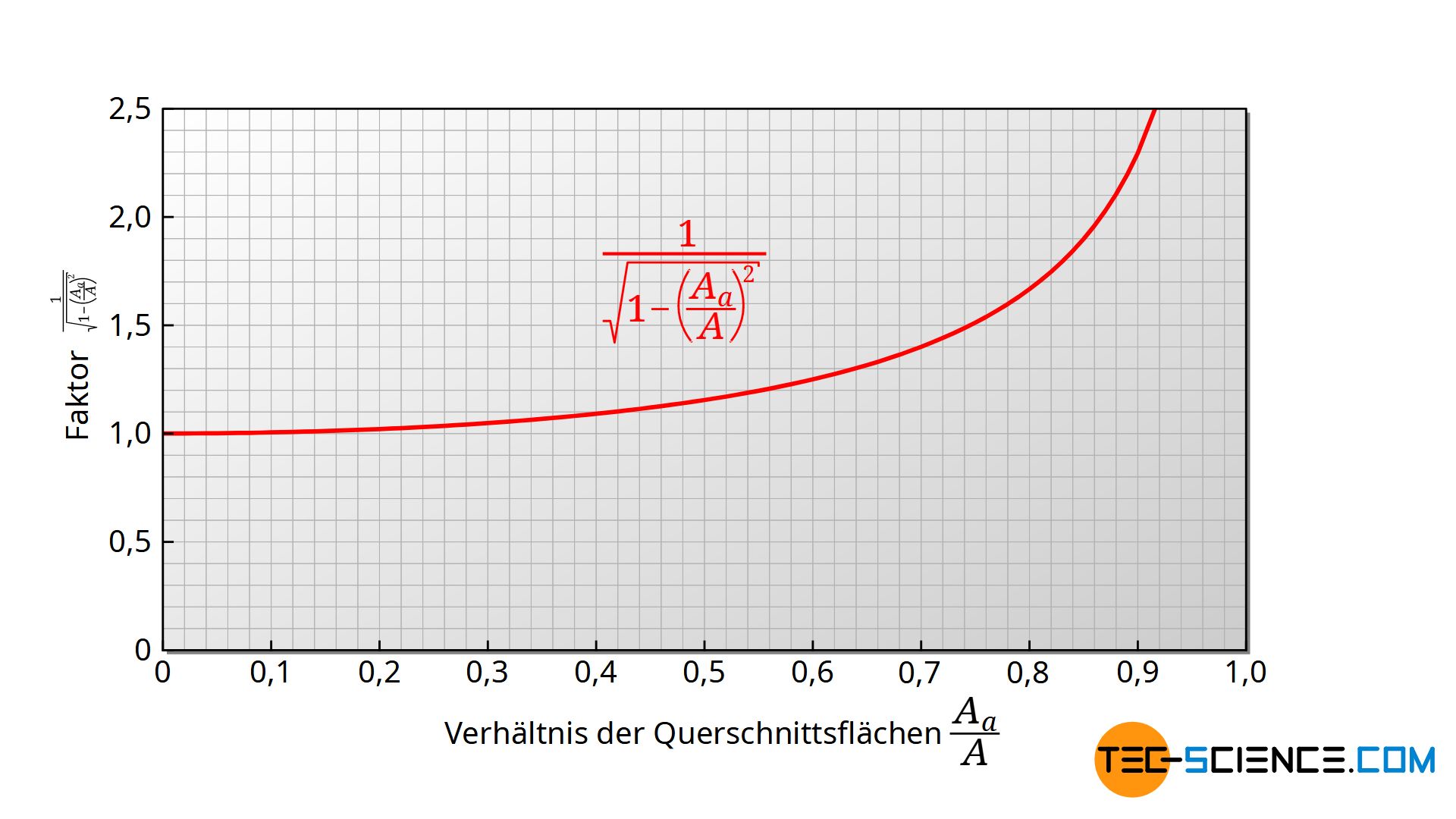
Für Fälle, bei denen dies nicht gilt, muss dieser Faktor berücksichtigt werden. Dementsprechend wirkt sich dies auf die Ausströmgeschwindigkeit v_a, die Entleerungsdauer t und auf die Ausflussrate V* aus (rot markiert ist jeweils der zusätzlich auftretende Term im Vergleich zur Vernachlässigung der Sinkgeschwindigkeit):

\begin{align}
& \boxed{v_a = \color{red}{\tfrac{1}{\sqrt{1-\left(\tfrac{A_a}{A}\right)^2}}} \cdot \sqrt{2gh} } \\[5px]
\end{align}

\begin{align}
& \boxed{\dot V = \color{red}{\tfrac{1}{\sqrt{1-\left(\tfrac{A_a}{A}\right)^2}}} \cdot A_a \cdot \sqrt{2gh} } \\[5px]
\end{align}

\begin{align}
& \boxed{t = \color{red}{\sqrt{1-\left(\tfrac{A_a}{A}\right)^2}} \cdot \frac{A}{A_a} \sqrt{\frac{2}{g}} \left(\sqrt{H}-\sqrt{h}\right)} \\[5px]
\end{align}

Ausfluss durch große Öffnungen

Bisher wurde angenommen, dass die Abmessung der Öffnung klein gegenüber der Füllstandshöhe ist. Diese Annahme ist vor allem bei seitlichen Ausströmvorgängen vorteilhaft. Somit hat man über die gesamte Öffnungshöhe hinweg einen (nahezu) konstanten Druck und deshalb eine nahezu konstante Ausströmgeschwindigkeit. Ist hingegen die Öffnungshöhe relativ groß, dann ergibt sich an der Oberkante ein geringerer hydrostatischer Druck als an der Unterkante. Folglich unterscheiden sich auch die Ausströmgeschwindigkeiten über die Öffnungshöhe hinweg.

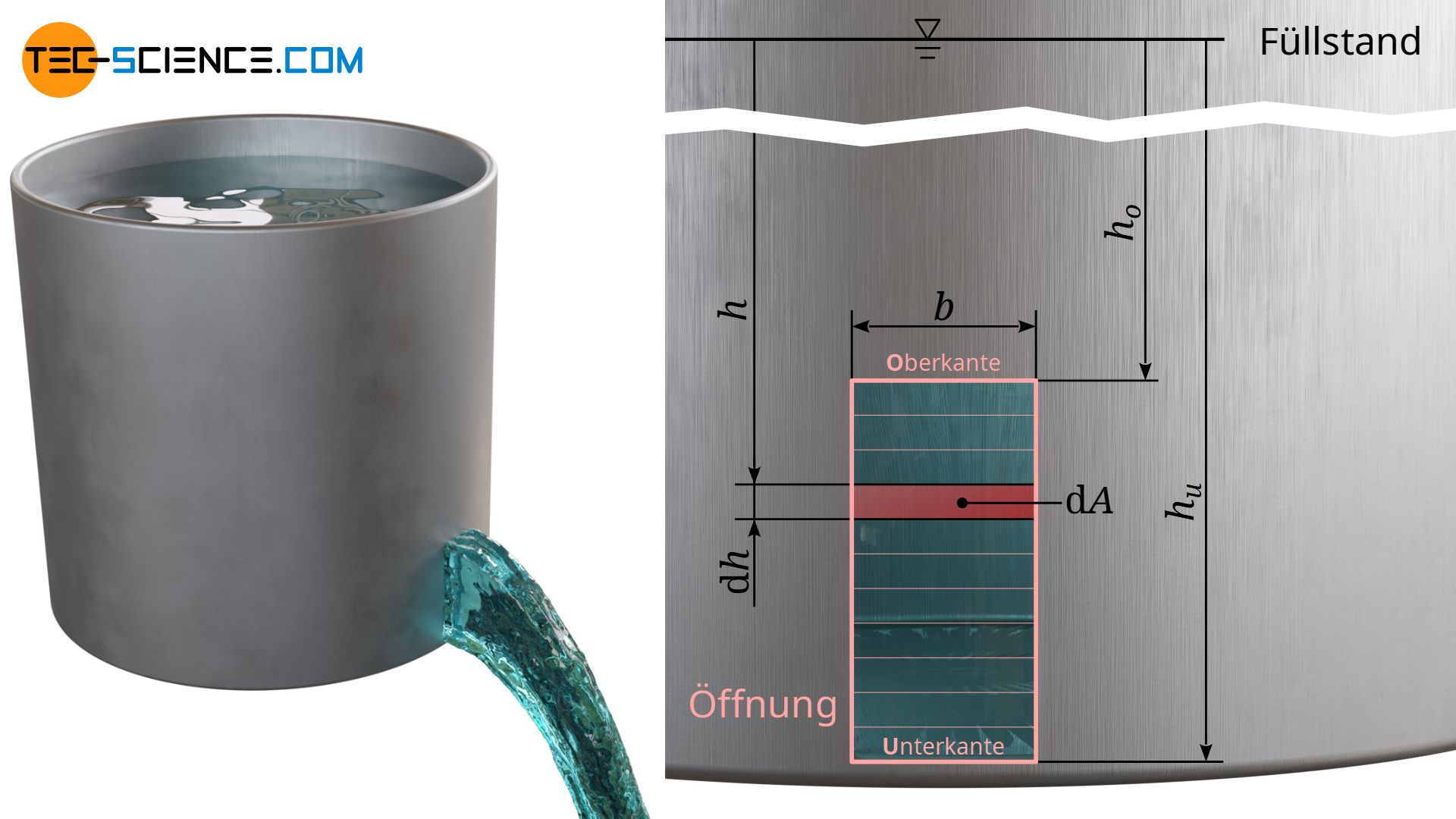
Der Einfachheit halber wird ein rechteckförmiger Öffnungsquerschnitt an der Seite eines Behälters betrachtet (siehe Abbildung oben). Man sich die Öffnung als aus vielen kleinen „Schlitzen“ aufgebaut vorstellen. Die Querschnittsfläche dA_a eines solchen Schlitzes ergibt sich aus dem Produkt von Schlitzbreite b und Schlitzhöhe dh. Durch jeden Schlitz in der Tiefe h lässt sich der entsprechende Volumenstrom dV* gemäß Gleichung (\ref{dV}) berechnen:

\begin{align}
& \text{d} \dot V = \text{d}A_a \cdot \sqrt{2gh} = b \cdot \text{d} h \cdot \sqrt{2gh} \\[5px]
& \text{d} \dot V = b \cdot \sqrt{2gh} \cdot \text{d}h \\[5px]
\end{align}

Gemäß des festgelegten Koordinatensystems ist diese Gleichung innerhalb der Grenzen von h_o (Oberkante Öffnung) und h_u (Unterkante Öffnung) zu integrieren und liefert damit den insgesamt vorhandenen Volumenstrom V* durch die Öffnung:

\begin{align}
\dot V &= \int\limits_{h_o}^{h_u} b \cdot \sqrt{2gh} \cdot \text{d}h \\[5px]
&= \sqrt{2g} \cdot b \int\limits_{h_o}^{h_u} \sqrt{h} \cdot \text{d}h \\[5px]
&= \sqrt{2g} \cdot b \int\limits_{h_o}^{h_u} h^{\frac{1}{2}} \cdot \text{d}h \\[5px]
&= \tfrac{2}{3} \sqrt{2g} \cdot b \cdot |h^{\frac{3}{2}}| _{h_o}^{h_u} \\[5px]
&= \tfrac{2}{3} \sqrt{2g} \cdot b \cdot \left(h_u^{\frac{3}{2}} – h_o^{\frac{3}{2}} \right) \\[5px]
\end{align}

\begin{align}
&\boxed{\dot V = \tfrac{2}{3} \sqrt{2g} \cdot b \cdot \left(\sqrt{h_u^3} – \sqrt{h_o^3} \right)} \\[5px]
\end{align}

Beachte, dass sich die angegebenen Tiefen h_u und h_o nicht auf den Behälterboden beziehen, sondern auf die Flüssigkeitsoberfläche!

Reale Ausströmvorgänge

Ausflussbeiwert

Vergleicht man die theoretischen Vorhersagen über das Ausflussverhalten eines Behälters mit der Praxis, so zeigen sich teilweise sehr große Unterschiede. Der Behälter entleert sich in der Realität meist deutlich langsamer.

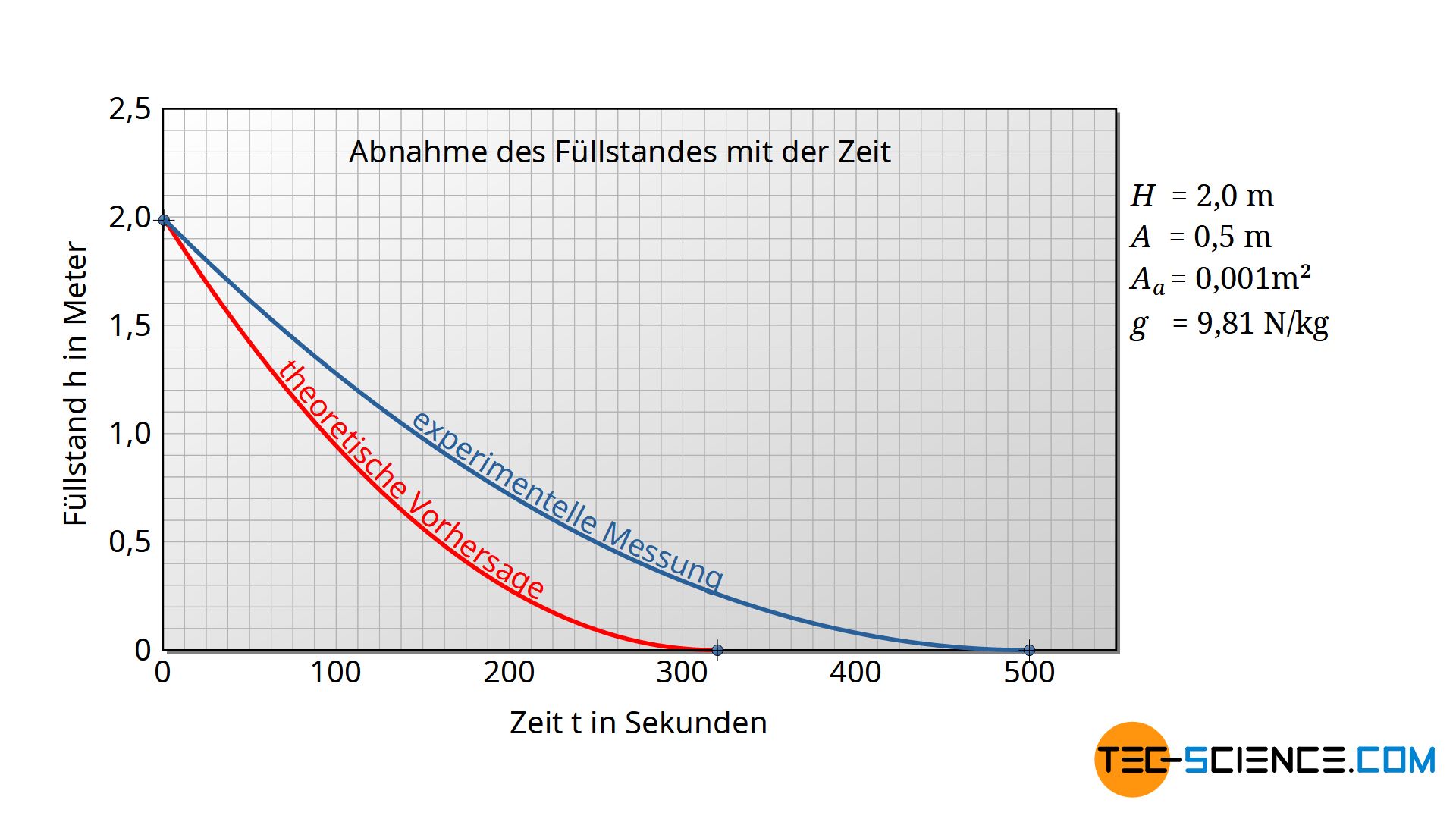
Der austretende Volumenstrom gemäß Gleichung (\ref{dV}) ist also in der Praxis geringer. Die Verringerung des idealen Volumenstroms kann mit einem sogenannten Ausflussbeiwert µ<1 berücksichtigt werden (manchmal auch als Abflussziffer bezeichnet):

\begin{align}
& \dot V_{\text{real}} = \mu \cdot V_{\text{ideal}} \\[5px]
\label{t}
& \boxed{\dot V_\text{real} = \mu \cdot A_a \sqrt{2gh} ~} ~~~\text{mit } \mu<1 ~~~\text{als Ausflussbeiwert}\\[5px]
\end{align}

Der Ausflussbeiwert gibt den Faktor an um den sich der reale Ausflussstrom im Vergleich zum idealen Volumenstrom in der Praxis verringert! Einfluss auf den Ausflussbeiwert haben maßgeblich zwei Phänomene, auf die im Folgenden näher eingegangen wird.

Viskosität (innere Reibung)

Beim Abfließen durch eine Öffnung treten innerhalb der Flüssigkeit Strömungen auf. Dies bedeutet, dass sich einzelne Flüssigkeitsschichten schneller bewegen als andere. Vor allem in der Nähe des Ausflusses ist dies der Fall, wo die zur Öffnung hinströmende Flüssigkeit an den umgebenden Schichten abschert und somit reibt. Diese Reibung der Flüssigkeitsschichten ist den Bindungskräfte zwischen den Schichten bzw. den Teilchen geschuldet. Dies sind entweder Van-der-Waals-Kräfte, Dipol-Dipol-Kräfte oder Wasserstoff-Brücken-Bindungen.

Um eine Flüssigkeitsschicht gegen eine andere zu verschieben, muss man folglich diese Bindungskräfte überwinden und eine entsprechende Kraft aufbringen. Flüssigkeitsschichten werden deshalb durch diese Bindungskräfte am Abscheren voneinander gehindert, analog zu Reibungskräften in der Mechanik. Man spricht deshalb bei Flüssigkeiten auch von innerer Reibung. Je stärker die Bindungskräfte sind, desto größer ist die innere Reibung beim Verschieben der Flüssigkeitsschichten. Beschrieben wird die Stärke der inneren Reibung durch die Zähigkeit bzw. Viskosität der Flüssigkeit.

Geschwindigkeitsbeiwert

Die Viskosität ist der Grund dafür, dass eine Flüssigkeit in der Realität mit einer geringeren Geschwindigkeit durch einen Ausfluss strömt als idealerweise angenommen. Berücksichtigt werden kann die Abnahme der Ausflussgeschwindigkeit durch einen sogenannten Geschwindigkeitsbeiwert φ<1 in Gleichung (\ref{tl}):

\begin{align}
&v_\text{a,real} = \varphi \cdot v_\text{a,ideal} \\[5px]
\label{vvv}
& \boxed {v_\text{a,real} = \varphi \cdot \sqrt{2gh}} ~~~\text{mit } \varphi<1 ~~~\text{als Geschwindigkeitsbeiwert} \\[5px]
\end{align}

Experimentelle Bestimmung des Geschwindigkeitsbeiwerts

Für horizontale Ausflüsse lässt sich der Geschwindigkeitsbeiwert aus der Bahnkurve des austretenden Flüssigkeitsstrahls ermitteln. Der Strahl wird dabei als horizontaler Wurf betrachtet. Unter Vernachlässigung der Luftreibung behält der austretende Strahl in horizontaler Richtung konstant die Ausflussgeschwindigkeit v_a,real bei. Somit legt der Strahl innerhalb einer Zeit t die folgende Strecke x zurück:

\begin{align}
&x = v_{\text{a,real}} \cdot t \\[5px]
\end{align}

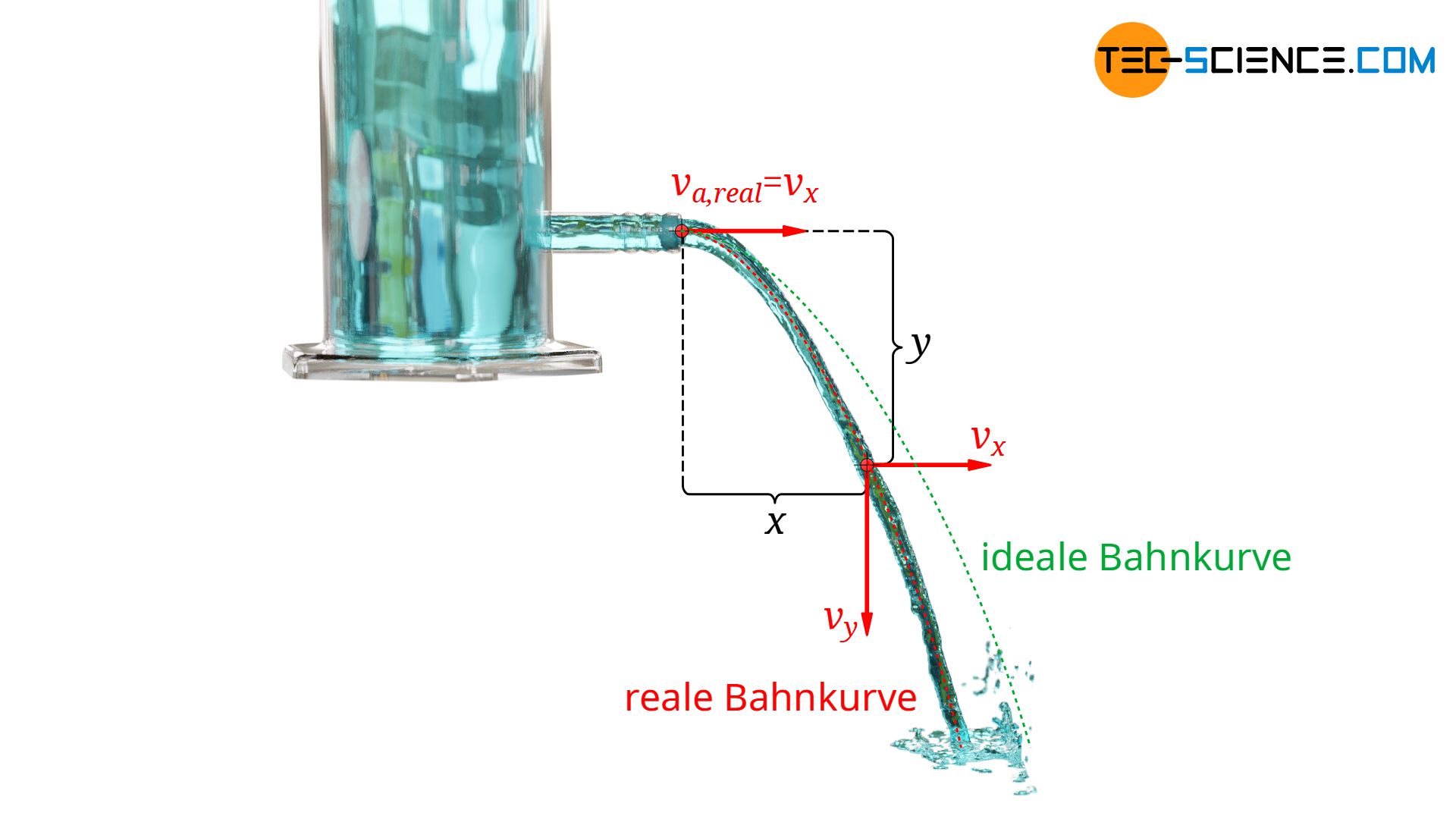
Innerhalb der Zeit t verursacht die Schwerkraft eine beschleunigte Bewegung des Strahls nach unten (freier Fall). Für die Fallstrecke y in vertikaler Richtung gilt die unten angegeben Formel. Diese wird anschließend nach der Zeit t umgestellt und in obere Gleichung eingesetzt und nach der Austrittsgeschwindigkeit v_a,real aufgelöst.

\begin{align}
&y = \frac{1}{2} \cdot g \cdot t^2 ~~~~\Rightarrow ~~~~t = \sqrt{\frac{2y}{g}} \\[5px]
& x = v_{\text{a,real}} \cdot t = v_{\text{a,real}} \cdot \sqrt{\frac{2y}{g}} \\[5px]
& \underline{v_{\text{a,real}} = x \cdot \sqrt{\frac{g}{2y}}} \\[5px]
\end{align}

Diese Gleichung ist nun mit Gleichung (\ref{vvv}) gleichzusetzen und nach dem gesuchten Geschwindigkeitsbeiwert φ aufzulösen:

\begin{align}
& \varphi \cdot \sqrt{2gh} = x \cdot \sqrt{\frac{g}{2y}} \\[5px]
& \boxed{\varphi = \frac{x}{2 \sqrt{hy}}} \\[5px]
\end{align}

Zur experimentellen Untersuchung der Geschwindigkeitsbeiwerte muss also lediglich ein Punkt der Bahnkurve (beschrieben durch x und y) bei zugehöriger Füllstandshöhe ermittelt werden. Versuche an solchen Bahnkurven zeigen, dass für niedrig-viskose Flüssigkeiten wie bspw. Wasser die Geschwindigkeitsbeiwerte in der Größenordnung von 0,95 und höher liegen.

Die geringen Geschwindigkeitsabnahmen können also nicht alleinig für die relativ großen Abweichungen zwischen dem theoretischen Volumenstrom und dem tatsächlich beobachteten Volumenstrom verantwortlich sein. Ein weitaus größeres Phänomen muss hierauf Einfluss haben, auf das wir im nächsten Abschnitt näher eingehen.

Stromlinienverengung

Stromlinien

Die Praxis zeigt, dass die Lage und die Form des Ausflusses maßgeblich für die Abweichungen im Volumenstrom verantwortlich sind. Besonders deutlich wird der Einfluss bei scharfkantigen Übergängen zwischen Behälter und Ausflussöffnung. Ein einfaches Loch in einem Behälter stellt ein solcher scharfkantiger Übergang dar. Die untere Abbildung zeigt hierzu einen Behälter, bei dem der Ausfluss durch ein rundes Loch am Boden erfolgt. Die Strömungswege sind dabei durch sogenannte Stromlinien sichtbar gemacht (weiße Linien in der unteren Abbildung). Solche Stromlinien sind gedankliche Wege, auf denen sich masselose Partikel bewegen würden, wenn man sie ins Fluid gibt.

Stromlinien sind Bahnkurven, die masselose Partikel beim Strömen mit dem Fluid nehmen würden!

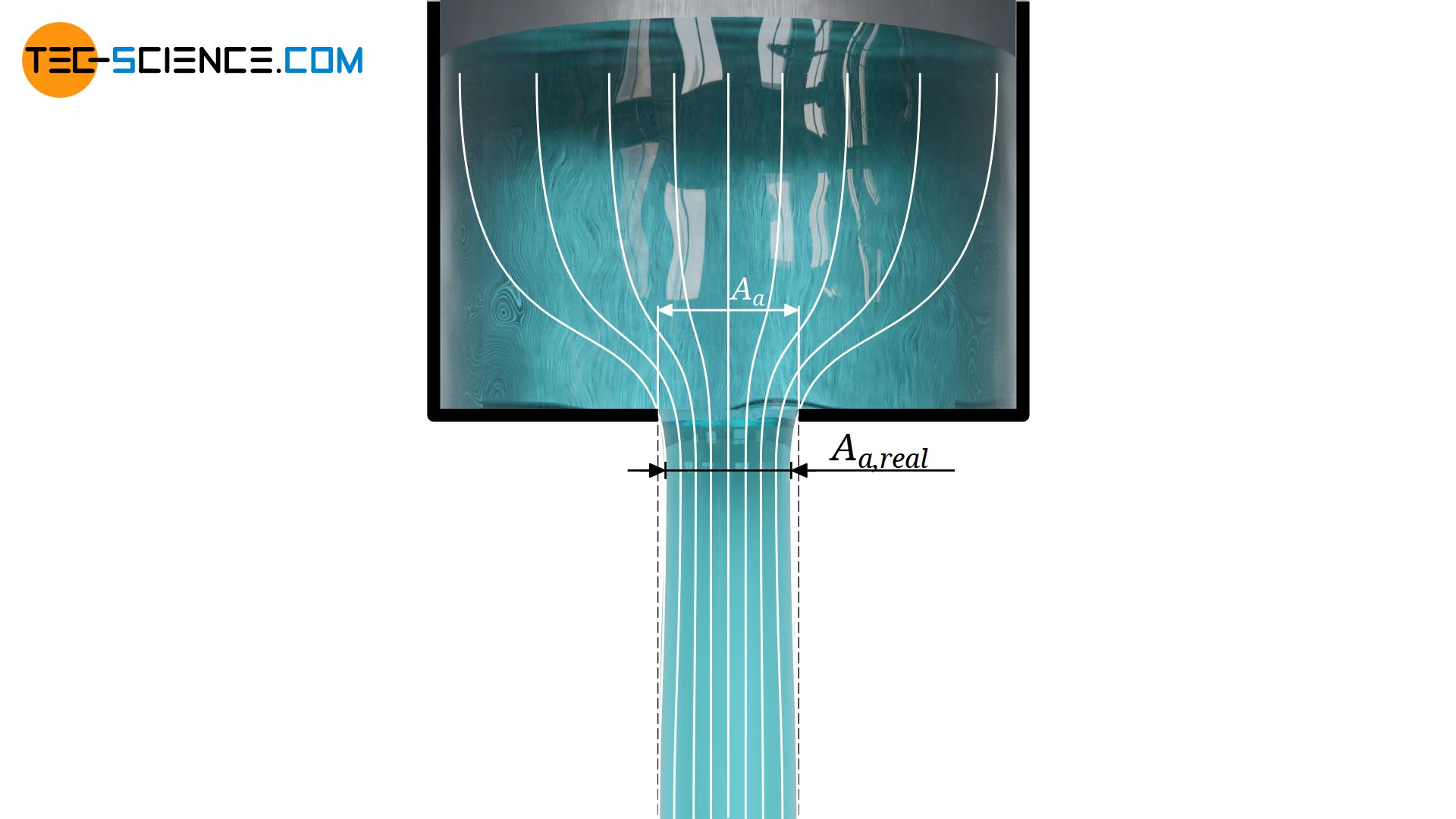
Die sichtbar gemachten Stromlinien liefern schließlich auch die Antwort auf die Frage, warum in der Praxis ein geringerer Volumenstrom zu verzeichnen ist als das bisherige Modell vorhersagt. In der Praxis tritt nämlich die ausströmende Flüssigkeit nicht im vollen Maße senkrecht durch den Querschnitt, sondern die Öffnung wird zum Großteil seitlich angeströmt. Die Strömungswege (Stromlinien) können aus physikalischer Sicht nicht rechtwinklig abknicken. Hierzu müsste das Fluid schließlich masselos sein, um den wirkenden Strömungskräften trägheitslos folgen zu können.

Kontraktionsbeiwert

Der austretende Strahlquerschnitt ist in der Praxis somit geringer als der Querschnitt der Öffnung. Dieser Querschnitt, in dem die Stromlinien tatsächlich parallel nach unten verlaufen, befindet sich stromabwärts der Öffnung. Dies ist der eigentliche Austrittsquerschnitt A_a,real den man zugrunde legen müsste. Dieser Querschnitt wird auch als effektiver Austrittsquerschnitt bezeichnet. Das Phänomen der Verengung von Stromlinien und der hieraus resultierenden Abnahme des Strahlquerschnitts ist auch als vena contracta bekannt.

Als vena contracta bezeichnet man die Verengung der Stromlinien an Querschnittsänderungen, d.h. das Einschnüren des Strahlquerschnitts unterhalb des tatsächlichen Rohrquerschnitts.

Die Abnahme des Strahlquerschnitts wird durch den sogenannten Kontraktionsbeiwert Ψ berücksichtigt. Er gibt das Verhältnis von tatsächlichem Strahlquerschnitt A_a,real zum Öffnungsquerschnitt A_a des Ausflusses an:

\begin{align}
& \boxed {A_\text{a,real} = \Psi \cdot A_\text{a} } ~~~\text{mit } \Psi<1 ~~~\text{als Kontraktionsbeiwert} \\[5px]
\end{align}

Zusammenhang zwischen Ausflussbeiwert, Kontraktionsbeiwert und Geschwindigkeitsbeiwert

Sowohl das Phänomen der Geschwindigkeitsabnahme als auch der weitaus größere Effekt der Stromlinienverengung beeinflussen den Volumenstrom in der Praxis. Werden für den Volumenstrom nach Gleichung (\ref{vd}) die realen Werte zugrunde gelegt, dann zeigt sich folgender Zusammenhang, zwischen dem Ausflussbeiwert µ, Kontraktionsbeiwert Ψ und Geschwindigkeitsbeiwert φ:

\begin{align}
\dot V_\text{a,real} &= A_\text{a,real} \cdot v_\text{a,real} \\[5px]
&= \underbrace{\Psi A_a}_{ A_\text{a,real} } \cdot \underbrace{ \varphi v_a}_{ v_\text{a,real} } \\[5px]
&= \Psi \varphi \cdot A_a v_a ~~~\text{mit }~~~ v_a=\sqrt{2gh} ~~~\text{folgt:}\\[5px]
\label{u}
& = \underbrace{\Psi \varphi}_{=\mu} \cdot A_a \sqrt{2gh} \\[5px]
\end{align}

\begin{align}
& \boxed{\dot V_\text{a,real} = \mu \cdot A_a \sqrt{2gh}} ~~~\text{mit}~~~ \boxed{\mu=\Psi \varphi} \\[5px]
\end{align}

Vergleicht man Gleichung (\ref{u}) mit Gleichung (\ref{t}), dann zeigt sich, dass der Ausflussbeiwert µ letztlich nichts anderes ist als das Produkt von Kontraktionsbeiwert Ψ und Geschwindigkeitsbeiwert φ. Da der Geschwindigkeitsbeiwert für praxisübliche Fluide meist vernachlässigbar gegenüber dem Kontraktionsbeiwert ist, wird der Ausflussbeiwert maßgeblich durch die vena contracta bestimmt. In der Praxis interessiert man sich aber ohnehin meist nur für den Ausflussbeiwert, sodass man den Geschwindigkeitsbeiwert und den Kontraktionsbeiwert nicht extra ermittelt.

Experimentelle Bestimmung des Ausflussbeiwerts

Der Ausflussbeiwert beeinflusst unmittelbar die Zeitdauer, die zum Entleeren eines Behälters nötig ist. Der Ausflussbeiwert geht deshalb direkt in Gleichung (\ref{gl}) ein und verlängert die Entleerungsdauer entsprechend:

\begin{align}
& \boxed{t = \frac{1}{\mu} \cdot \frac{A}{A_a} \sqrt{\frac{2}{g}} \left(\sqrt{H}-\sqrt{h}\right)} \\[5px]
\end{align}

In der Praxis muss man also lediglich die Zeitdauer t ermitteln, innerhalb deren der Füllstand ausgehend der Höhe H auf die Höhe h abgenommen hat. Umstellen der oberen Gleichung liefert dann den Ausflussbeiwert:

\begin{align}
& \boxed{\mu = \frac{1}{t} \cdot \frac{A}{A_a} \sqrt{\frac{2}{g}} \left(\sqrt{H}-\sqrt{h}\right)} \\[5px]
\end{align}

Einfluss der Form der Öffnung auf den Ausflussbeiwert

Runde Öffnungen

Für den oben gezeigten Fall eines runden Lochs in einem Behälter, liegt der Ausflussbeiwert für Wasser in der Größenordnung von etwa µ=0,65. Wünschenswert ist in der Praxis meist ein hoher Ausflussbeiwert, um mit der Ausflussrate möglichst nahe an den idealen Volumenstrom heran zu kommen. Dies erfordert eine entsprechende Anpassung der Öffnungsform.

Da der Ausflussbeiwert maßgeblich durch die vena contracta bestimmt ist, muss man die Verengung der Stromlinien so gering wie möglich halten. Dies erreicht man durch Anpassen der Geometrie der Öffnung. Eine einfache Möglichkeit ist es Rohrstutzen zu verwenden. Die Flüssigkeit strömt dann nicht sofort aus, sondern wird davor durch ein kurzes Rohrstück hindurch geleitet. Dies sorgt dafür, dass sich die Stromlinien wieder parallel anordnen und den gesamten Querschnitt einnehmen können.

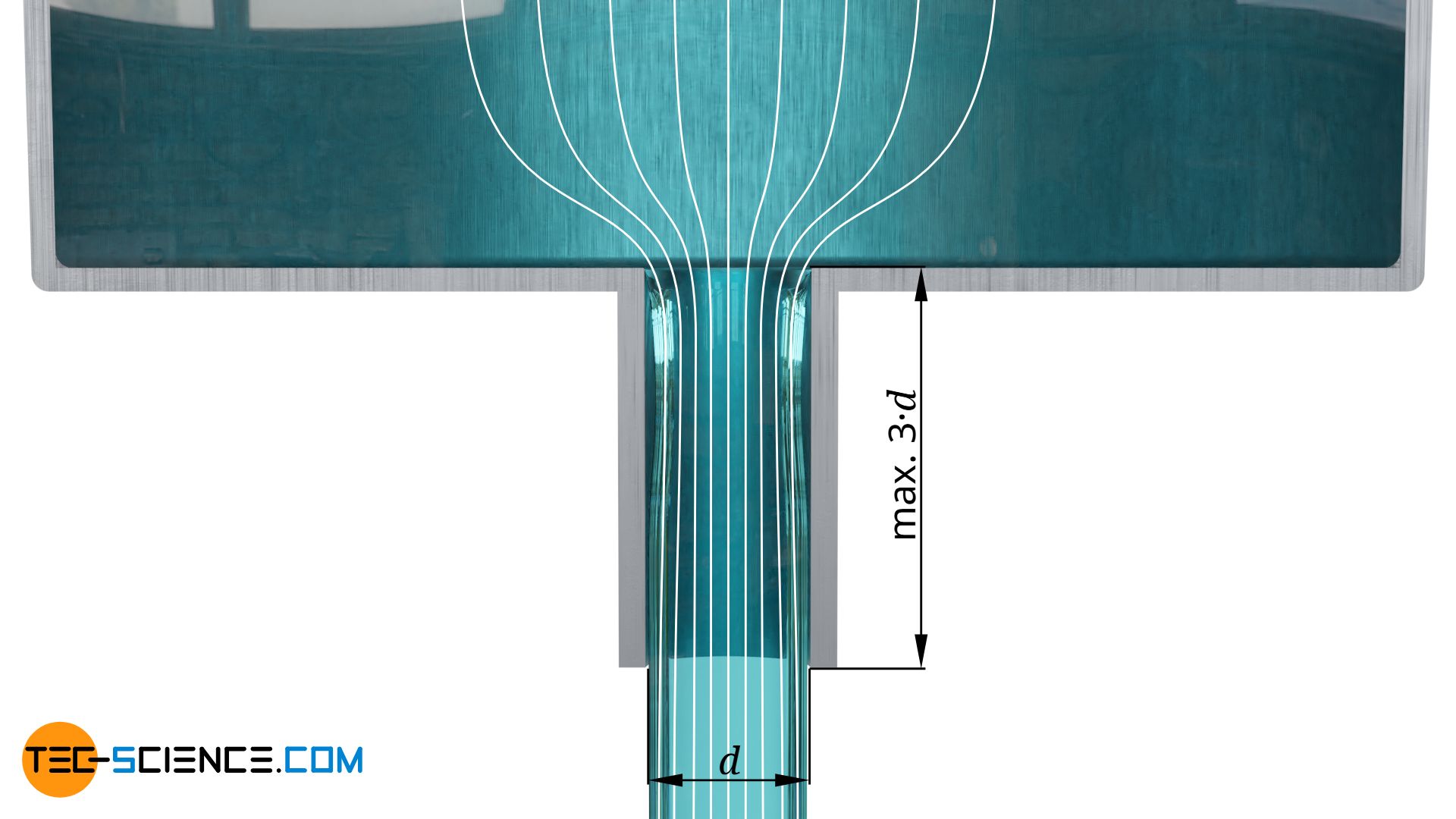
Um einen wirksamen Effekt zu erzielen sollten Ausflussstutzen etwa 2 bis maximal 3-mal so lange sein wie ihr Durchmesser. In diesem Rahmen sind in der Praxis dann Steigerungen der Ausflussrate um etwa 25 % gegenüber der direkten Ausströmung an scharfkantigen Öffnungen möglich. Aus Gründen erhöhter Rohrreibung sollte man die Rohrstutzen so kurz wie möglich halten.

Nochmalige Steigerung der Ausflussrate lässt sich durch ausrunden der Kanten erzielen (möglichst „stromlinienförmig“), sodass die Stromlinien weich um diese Kanten geführt werden. Ausflussbeiwerte über 0,9 und höher sind auf diese Weise möglich.

Im Gegensatz dazu, kann man den Ausfluss aber auch deutlich ungünstiger gestalten als mit einem bloßen Loch. Zum Beispiel, dann wenn ein kurzer Rohrstutzen nicht aus dem Behälter ragt, sondern in diesen hinein. Dann vollziehen die Stromlinien sehr starke Änderungen beim Ausströmen mit einer entsprechend ausgeprägteren vena contracta. Eine solche ungünstige Anordnung eines Rohrstutzens wird auch als Borda’sche Öffnung bezeichnet. Die Ausflussbeiwerte liegen dabei in der Größenordnung um 0,53.

Rechteckige Öffnungen

Bisher wurde stillschweigend von runden Öffnungen ausgegangen. Vor allem aber wenn Flüssigkeiten seitlich ausströmen, beeinflusst die Querschnittsgeometrie den Ausflussbeiwert sehr stark. Bei rechteckförmigen Öffnungen ist es dabei immer ungünstig, wenn Flüssigkeit seitlich in die Öffnung einströmt, da die Stromlinien sehr starke Richtungsänderungen zeigen. Deshalb sollte die Öffnungshöhe so gering wie möglich gehalten werden und mehr in die Breite gehen als in die Höhe.

Bei quadratischen Öffnungen bei denen die Öffnungshöhe der Öffnungsbreite entspricht, liegt der Abflussbeiwert in Größenordnung von etwa 0,58. Ist die Öffnungshöhe hingegen doppelt so groß wie die Öffnungsbreite sinkt der Abflussbeiwert auf ca. 0,44. Beträgt die Öffnungshöhe nur die Hälfte der Öffnungsbreite, dann steigt der Ausflussbeiwert auf 0,64. Die Öffnungshöhe kann zwar gegenüber der Öffnungsbreite weiter verringert werden, jedoch erreicht man hierdurch maximal einen Abflussbeiwert von 0,67. Mehr Informationen zur Bestimmung der Ausflussbeiwerte finden Sie auch auf bauformeln.de.