Die Arbeit, die zur Aufrechterhaltung der Strömung entgegen der unterschiedlichen statischen Drücke zwischen Ein- und Ausgang eines offenen Systems erforderlich ist, wird als Verschiebearbeit bezeichnet!
Einleitung
Viele thermodynamische Vorgänge laufen in offenen Systemen ab. Im Gegensatz zu geschlossenen Systemen, findet bei offenen Systemen nicht nur ein Energieumsatz in Form von Wärme oder Arbeit statt sondern auch ein Masseaustausch mit der Umgebung. Dies ist zum Beispiel bei Pumpen, Verdichtern, Flugzeugtriebwerken oder Gasturbinen der Fall. Bei diesen Maschinen tritt von der einen Seite Masse in das System ein und auf der einen Seite wieder aus.
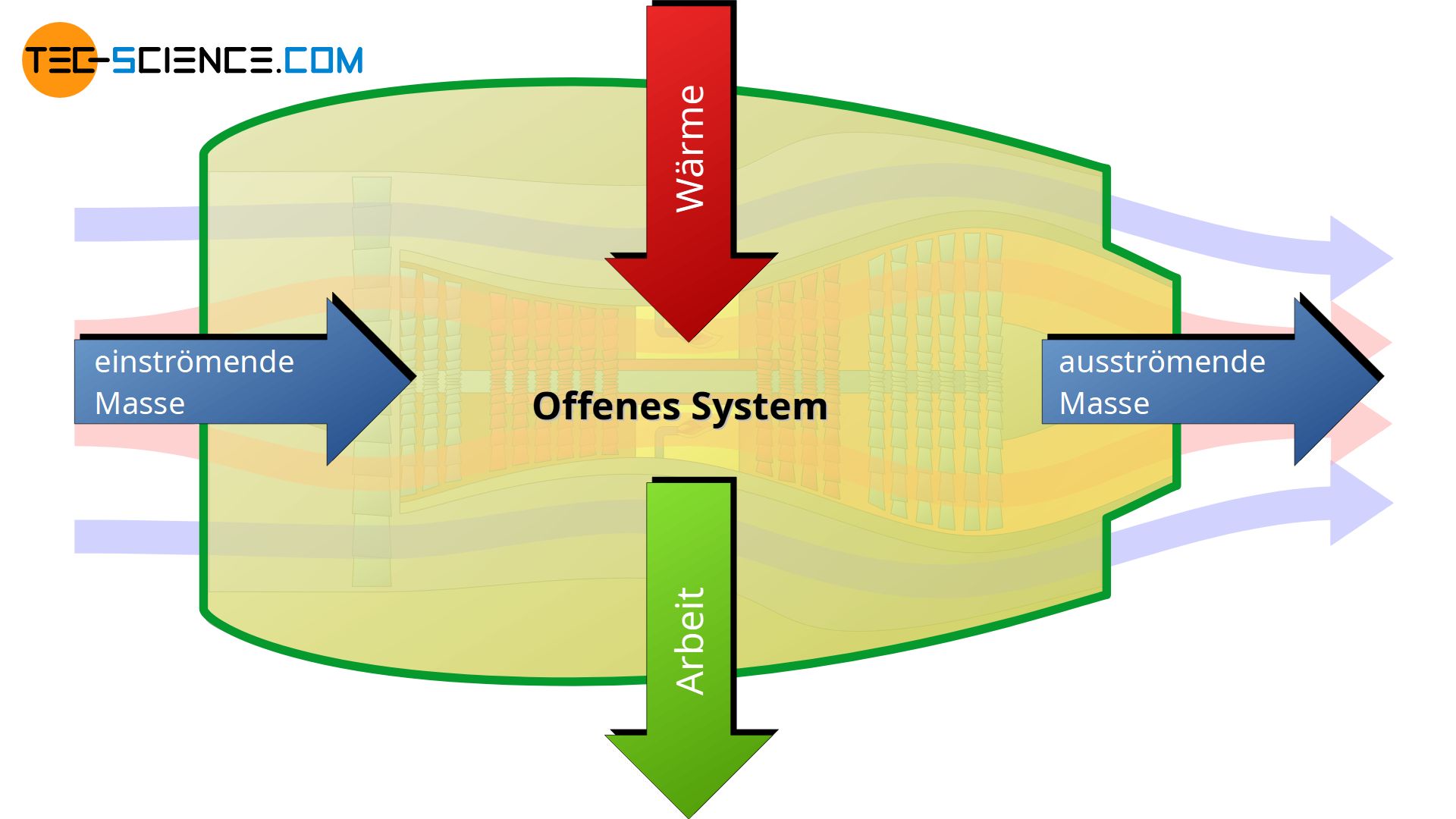
Dieses Durchschieben der Masse durch ein offenes System ist mit einem bestimmten Aufwand an Energie verbunden. Dies soll im Folgenden am Beispiel einer Wasserpumpe verdeutlicht werden. Zunächst betrachten wir den Fall ohne Pumpe, bei dem Wasser aus einem Becken durch eine horizontale Rohrleitung strömt. In diesem Fall tritt das Wasser ohne größeren Druck mit relativ langsamer Geschwindigkeit aus der Rohrleitung aus.

Nun wird eine Pumpe in die Rohrleitung eingebaut. Ähnlich einer Schiffsschraube, sitzt in der Pumpe ein rotierendes Laufrad, Impeller genannt (siehe hierzu auch den Artikel Kreiselpumpen). Dieses Laufrad setzt das Wasser im vorderen Teil der Pumpe bzw. der Rohrleitung unter hohen Druck. Somit strömt das Wasser insgesamt schneller durch die Rohrleitung und erhöht den Massenstrom, sodass mehr Wasser in derselben Zeit gefördert werden kann als ohne Pumpe.

Die Wasserpumpe stellt folglich ein typisch offenes System dar, in das Masse am Pumpeneingang bei relativ geringem Druck einströmt am Pumpenausgang wieder mit erhöhtem Druck ausgeschoben wird. Unter vereinfachten, reibungsfreien Bedingungen soll im Folgenden nun der Fragestellung nachgegangen werden, welche Arbeit die Pumpe aufwenden muss, um eine bestimmte Wassermasse zu fördern. Hierzu werden im Folgenden die energetischen Vorgänge am Eingang und am Ausgang der Pumpe näher betrachtet.

Einschiebearbeit an der Saugseite
Unmittelbar vor dem Eingang in die Pumpe steht das Wasser unter einem bestimmten Druck p1. Dieser Druck kommt in diesem Fall zum einen durch den hydrostatischen Druck der Wassersäule im Becken zustand und zum anderen durch den auf der Wasseroberfläche lastende Umgebungsdruck der Luft. Beide Einflussgrößen drücken das Wasser an der sogenannten Saugseite in die Pumpe.
Achtung: Nicht die Pumpe saugt das Wasser durch einen Unterdruck an wie, man fälschlicherweise aus dem Begriff Saugseite ableiten könnte, sondern der Umgebungsdruck und hydrostatischer Druck drücken das Wasser in die Pumpe! Denn selbst wenn die Pumpe am Eingang ein Vakuum erzeugen würde, könnte ohne Umgebungsdruck und hydrostatischer Druck kein Wasser in die Pumpe geschoben werden (siehe hierzu auch den Artikel Wie funktioniert das Trinken mit einem Trinkhalm?).

Anhand des wirkenden Drucks p1 und der Querschnittsfläche A1 des Pumpeneingangs kann nun die Kraft F1 bestimmt werden mit der das Wasser von der Umgebung in die Pumpe hineingedrückt wird:
\begin{align}
\label{7481}
&F_1 = p_1 \cdot A_1
\end{align}
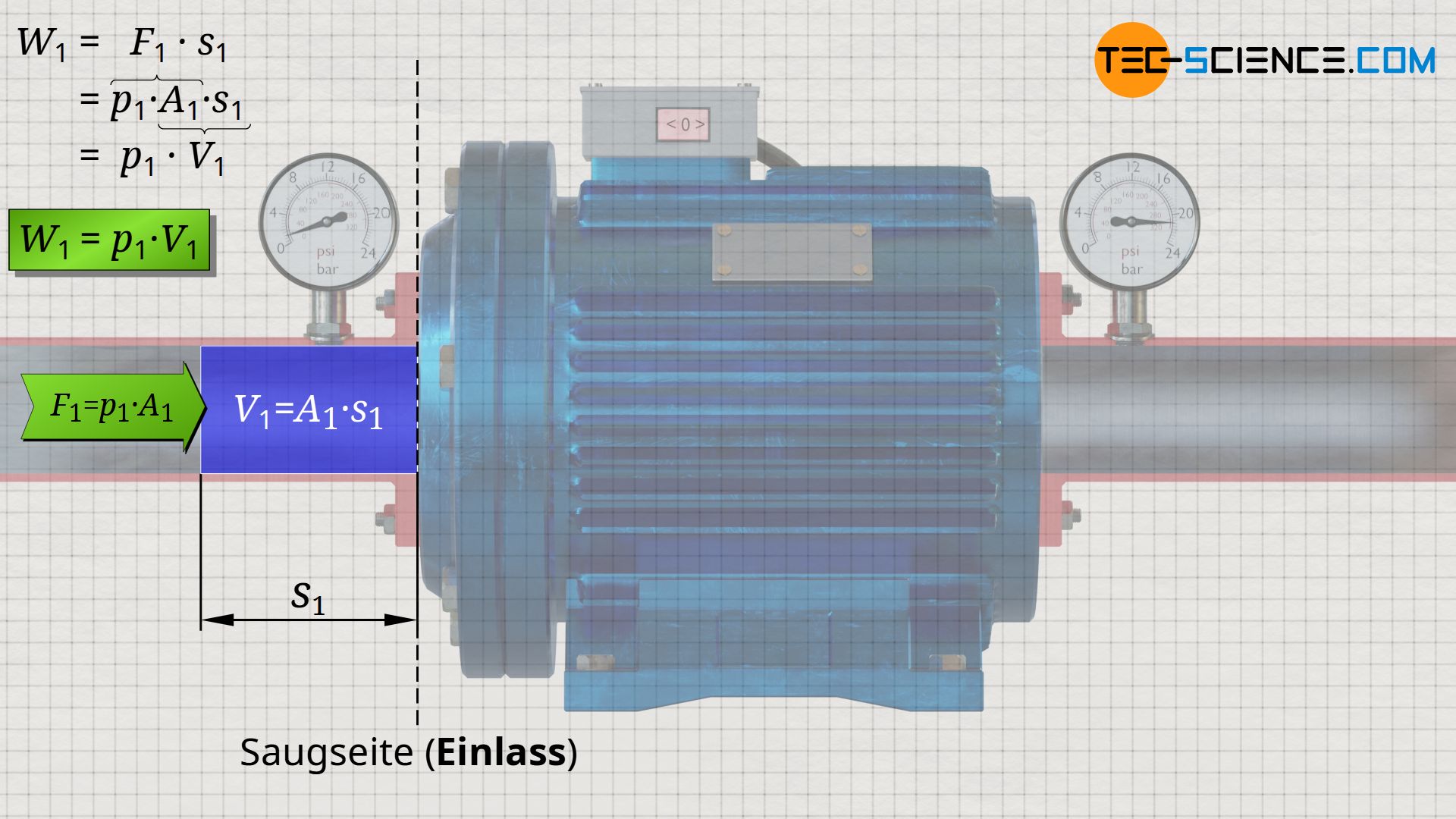
Mit dieser Kraft F1 wird innerhalb einer bestimmten Zeit eine gewisse vor der Öffnung befindliche Wassermasse in die Pumpe geschoben. Man kann sich das Hineinschieben der Wassermasse in die Pumpe auch durch einen Kolben veranschaulicht vorstellen. Dieser drückt mit der Kraft F1 die davor befindliche Wassermasse m entlang der Strecke s1 in die Pumpe. Aus dem Produkt von Kraft und Weg, kann schließlich die Energie W1 bestimmt werden, mit der die Umgebung („Kolben“) die Wassermasse in die Pumpe schiebt. Diese Einschiebeenergie entspricht der Arbeit, die die Umgebung an der Wassermasse verrichtet:
\begin{align}
&W_1 = F_1 \cdot s_1 = p_1 \cdot \underbrace{A_1 \cdot s_1}_{=V_1} = p_1~V_1 \\[5px]
\label{5792}
&\boxed{W_1 = p_1 \cdot V_1} ~~~~~\text{Einschiebeenergie (Einschiebearbeit)}
\end{align}
Das in der oberen Gleichung auftretende Produkt aus Verschiebestrecke s1 und Querschnittsfläche A1 entspricht gerade dem hineingeschobenen Wasservolumen V1 (Einschiebevolumen).
Die Energie, mit der ein Fluid durch einen Querschnitt geschoben wird, ergibt sich aus dem Produkt von Druck und Volumen!
Zahlenbeispiel
Wird der Umgebungsdruck mit 1 bar und die Höhe der Wassersäule mit 1 m angenommen werden, so wirkt zusätzlich zum Umgebungsdruck noch ein (hydrostatischer) Druck von 0,1 bar. Insgesamt wird das Wasser somit mit einem Druck von p1=1,1 bar in die Pumpe gedrückt. Innerhalb einer Zeit von t = 4 s ströme m = 2 kg Wasser durch den Pumpeneingang. Bei einer Wasserdichte von 999,25 kg/m³ besitzt diese Wassermasse somit ein Volumen von V1 =2,0015 Liter. Dieses Wasservolumen wird durch die Umgebung folglich mit einer Energie von W1 = 220 J in die Pumpe eingeschoben:
\begin{align}
&\underline{W_1} = p_1 \cdot V_1 = 1,1 \cdot 10^5 \frac{\text{N}}{\text{m²}} \cdot 2,0015 \cdot 10^{-3} \text{ m³} = \underline{220 \text{ J}}
\end{align}
Ausschiebearbeit an der Druckseite
Nachdem die energetischen Vorgänge am Pumpeneingang geklärt wurden, werden nun im Folgenden die energetischen Prozesse am Pumpenausgang näher betrachtet, der sogenannten Druckseite. Grundsätzlich wird am Pumpenausgang dieselbe Masse an Wasser wieder ausgeschoben wie innerhalb einer bestimmten Zeit am Pumpeneingang hineinströmt, denn schließlich kann sich im stationären Fall kein Wasser in der Pumpe anhäufen oder vernichtet werden. Diese der Massenerhaltung geschuldete Bedingung wird auch Kontinuitätsbedingung genannt. Diese Kontinuitätsbedingung gilt nicht nur für inkompressible Fluide wie Flüssigkeiten, sondern auch für kompressible Stoffe wie Gase.
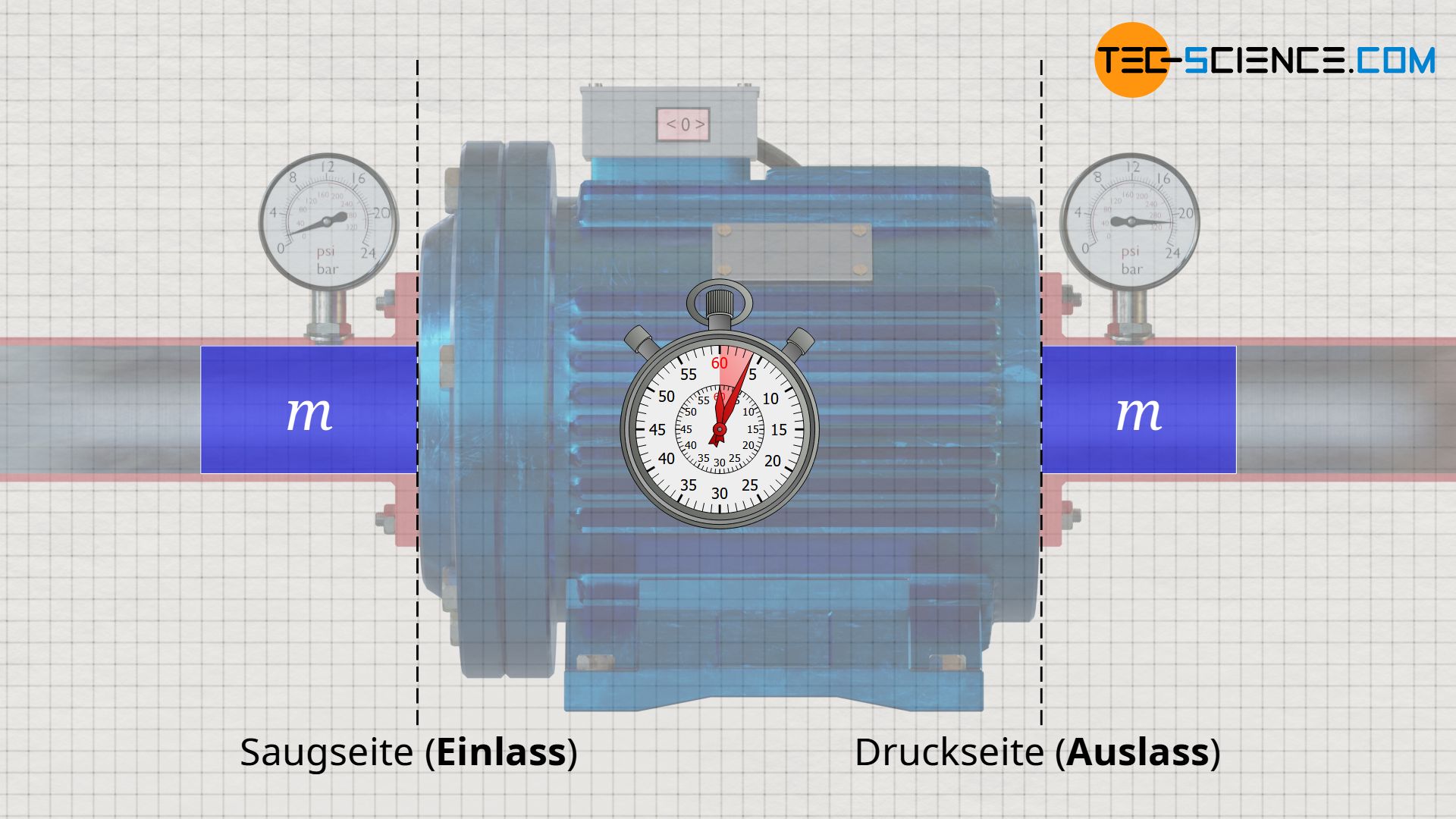
Im Abschnitt zuvor wurde anhand des Zahlenbeispiels berechnet, dass die Umgebung die Wassermasse mit einer Energie von 220 J in die Pumpe drückt. Wäre die Pumpe ausgeschaltet, so würde das Wasser mit dieser Energie durch die Pumpe geschoben werden und würde die Pumpe auch lediglich mit dieser Energie wieder verlassen (Strömungs- und Reibungsverluste vernachlässigt). Die Pumpe sorgt nun allerdings für eine Druckerhöhung, da die Wassermassen durch das rotierende Pumpenrad „zusammengedrückt“ werden. Das Wasser wird also mit einem höheren Druck aus der Pumpe ausgeschoben als es in die Pumpe eingeschoben wurde.
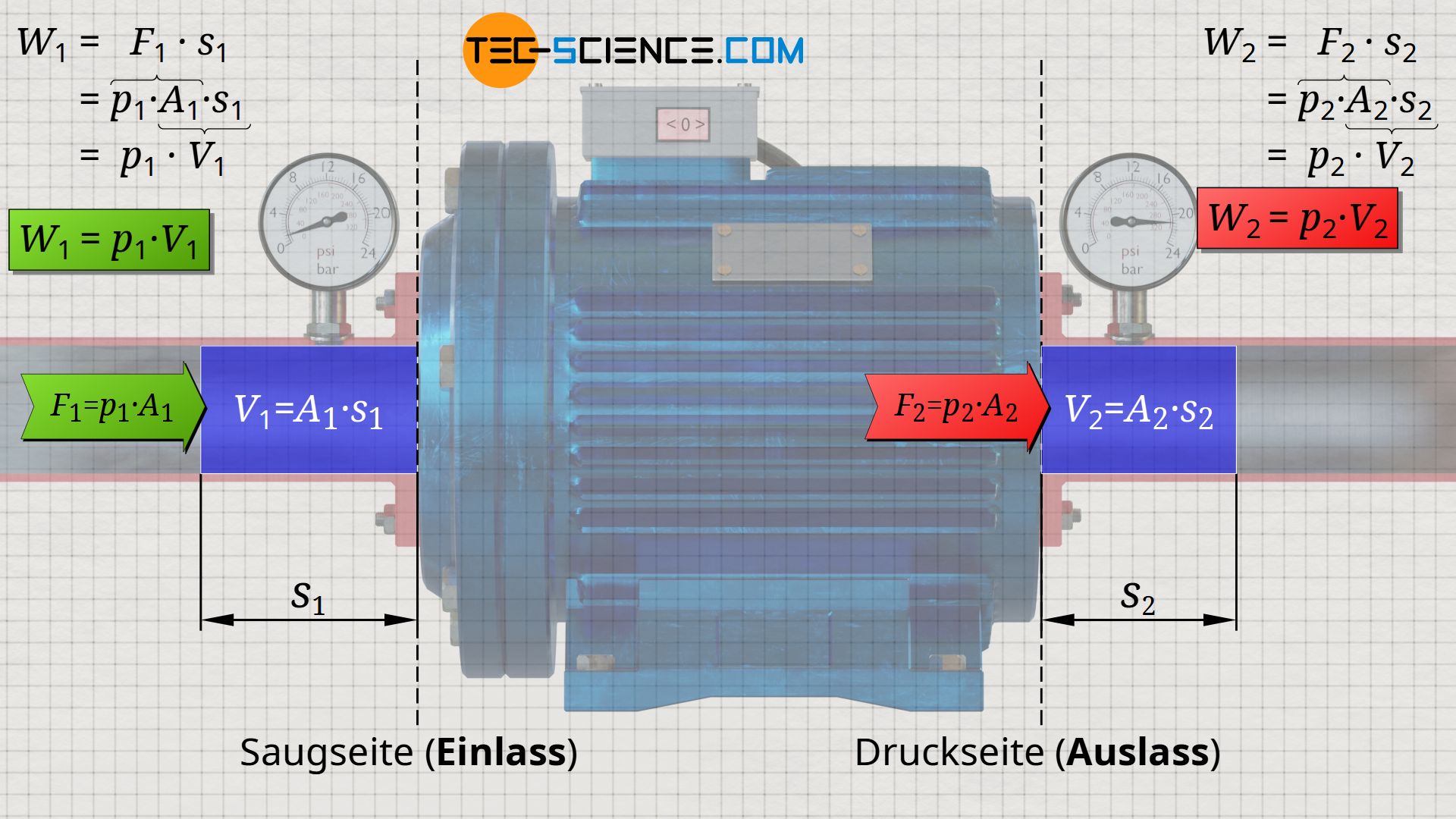
Das Wasser verlässt die Pumpe somit auch mit einer größeren Kraft, was letztlich eine Erhöhung der Energie zur Folge hat mit der das Wasser ausströmt. Diese Energie am Pumpenausgang kann analog zur Einschiebeenergie nach Gleichung (\ref{5792}) hergeleitet werden. So wird die Wassermasse mit der Kraft F2=p2⋅A2 entlang des Weges s2 durch den Querschnitt A2 am Pumpenausgang ausgeschoben. Dies führt entsprechend zur folgender Ausschiebeenergie W2 (Ausschiebearbeit):
\begin{align}
&W_2 = F_2 \cdot s_2 = p_2 \cdot \underbrace{A_2 \cdot s_2}_{=V_2} = p_2 \cdot V_2 \\[5px]
\label{3018}
&\boxed{W_2 = p_2 \cdot V_2} ~~~~~\text{Ausschiebeenergie (Ausschiebearbeit)}
\end{align}
Zahlenbeispiel
Erzeugt die Pumpe bspw. eine Druckerhöhung um Δp = 20 bar, dann erhöht sich der Wasserdruck von p1 = 1,1 bar am Pumpeneingang auf insgesamt p2 = 21,1 bar am Pumpenausgang. Der erhöhte Druck hat wiederum Auswirkungen auf das ausgeschobene Volumen. Aufgrund der Kontinuitätsbedingung sind zwar die innerhalb einer bestimmten Zeit ein- und ausgeschobenen Massen identisch, die jeweiligen Volumina unterscheiden sich aufgrund der unterschiedlichen Drücke jedoch. Die betrachtete Wassermasse von 2 kg weist am Pumpenausgang nicht mehr ein Volumen von V1 = 2,0015 Liter auf, sondern aufgrund des größeren Drucks ein leicht geringeres Volumen von V2 = 1,9996 Liter.
Mit einem Druck von p2=21,1 bar und einem Ausschiebevolumen V2 =1,9996 Liter ergibt sich für die Wassermasse von 2 Kilogramm somit eine Ausschiebeenergie von rund W2 = 4220 J:
\begin{align}
&\underline{W_2} = p_2 \cdot V_2 = 21,1 \cdot 10^5 \frac{\text{N}}{\text{m²}} \cdot 1,9996 \cdot 10^{-3} \text{ m³} = \underline{4220 \text{ J}}
\end{align}
Vergleicht man die Einschiebeenergie von W1 = 220 J mit der Ausschiebeenergie von W2 = 4220 J so wird deutlich, dass die Pumpe offensichtlich dafür sorgt, dass die eintretende Wassermasse mit größerer Energie ausgeschoben wird als sie durch die Umgebung hineingeschoben wurde. Dementsprechend strömt das Wasser mit größerer Wucht aus dem Ende der Rohrleitung im Vergleich zum Fall ohne Pumpe.
Anmerkung: Aufgrund der Inkompressibilität von Flüssigkeiten können die geringen hervorgerufenen Volumenänderungen zwischen Ein- und Ausgang des offenen Systems häufig vernachlässigt werden. Für kompressible Fluide wie Gase, können die Volumenänderungen allerdings sehr groß und damit bedeutsam werden, denn für das Komprimieren eines Volumens ist ein weiterer energetische Aufwand erforderlich (Volumenänderungsarbeit muss dann zusätzlich am Gas verrichtet werden). Hierauf wird im Artikel Druckänderungsarbeit in offenen Systemen näher eingegangen wird.
Verschiebearbeit (Arbeit der Pumpe)
Die um 4000 J höhere Energie, mit der das Wasser ausströmt im Vergleich zur Energie am Eingang der Pumpe kann natürlich nur auf die Pumpe selbst zurückzuführen sein. Dieser Energiebetrag von 4000 J entspricht der Arbeit der Pumpe, die in Form von elektrischer Energie geliefert wird und das Pumpenrad antreibt. Diese Betrachtung ist stark vereinfacht und wird im Artikel zur Druckänderungsarbeit bzw. zur technischen Arbeit noch näher diskutiert.
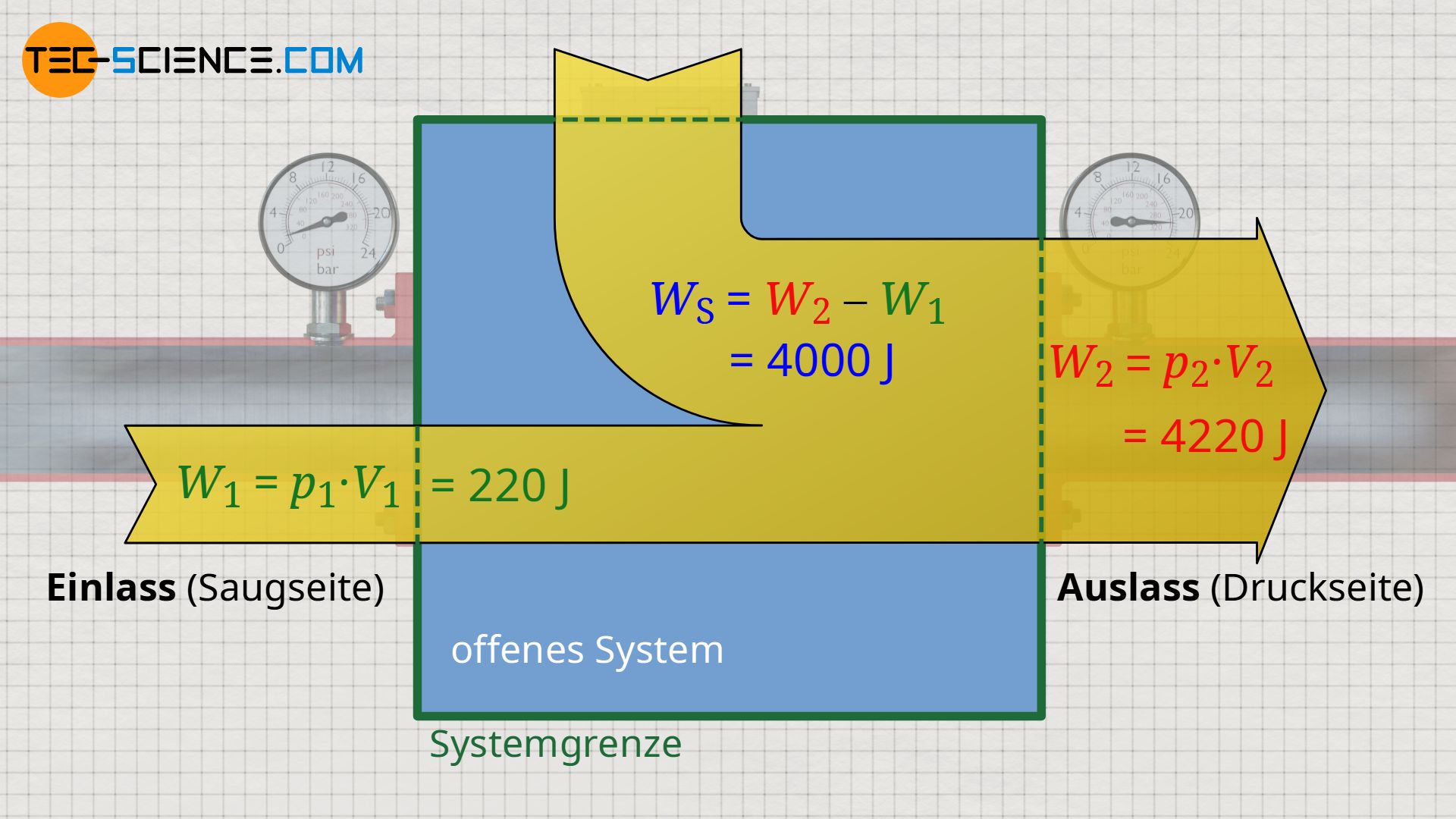
In dieser vereinfachten Betrachtung zeigt sich allerdings, dass sich die Arbeit der Pumpe aus der Differenz zwischen Ausschiebeenergie W2 und Einschiebeenergie W1 berechnet. Diese Arbeit wird bei einem offenen System ganz allgemein als Verschiebearbeit WS bezeichnet (engl. flow work):
\begin{align}
\label{9372}
&W_\text{S} = W_2 – W_1 \\[5px]
\label{7076}
&\boxed{W_\text{S} = p_2~V_2 – p_1~V_1 } = \Delta \left(p~V \right) ~~~~~\text{Verschiebearbeit}
\end{align}
Die Arbeit, die zur Aufrechterhaltung der Strömung entgegen der unterschiedlichen statischen Drücke zwischen Ein- und Ausgang eines offenen Systems erforderlich ist, wird als Verschiebearbeit bezeichnet!
Gleichung (\ref{7076}) macht deutlich, dass sich die Verschiebearbeit eines offenen Systems nur dadurch bestimmt, welchen Zustand eine strömende Masse unmittelbar vor dem System (p1, V1) und nach dem System (p2, V2) aufweist. Dabei spielt es keine Rolle wie die einströmende Masse nun genau vom Ausgangszustand 1 in den Endzustand 2 gelangt. Der thermodynamische Prozess im Inneren des offenen Systems ist also für die Ermittlung der Verschiebearbeit völlig irrelevant. Es handelt sich bei der Verschiebearbeit folglich nicht um eine Prozessgröße wie man anhand des Begriffes Arbeit fälschlicherweise meinen könnte, sondern um eine Zustandsgröße!
Anmerkung: Häufig werden auch lediglich die einzelnen Produkte aus Druck und Volumen als Verschiebearbeit bezeichnet. Denn letztlich ist das Produkt p1⋅V1 auf das Hineinschieben in das offene Systeme und das Produkt p2⋅V2 auf das Hinausschieben aus dem offenen System zurückzuführen. Aus didaktischen Gründen soll im Folgenden mit dem Begriff Verschiebearbeit allerdings immer die Differenz beider Produkte nach Gleichung (\ref{7076}) gemeint sein, d.h. jener Arbeitsumsatz der effektiv für das Durchschieben der Masse durch das offene System verantwortlich ist. Aus diesem Grund wäre der Begriff „Durchschiebearbeit“ wohl besser geeignet, jedoch wie dieser in der Literatur kaum verwendet.
Spezifische Verschiebearbeit
Das in den Abschnitten zuvor erläuterte Pumpenbeispiel zeigte, dass die betrachtete Pumpe für das Fördern einer Wassermasse von 2 kg eine (Verschiebe-)Arbeit von 4000 J aufbringen muss. Soll die Pumpe hingegen die 10-fache Wassermasse von 20 kg fördern, dann muss die Pumpe auch eine entsprechend 10-fache Arbeit von insgesamt 40.000 J verrichten.
Je nach durchströmender Masse ändert sich folglich auch immer die Verschiebearbeit. Deshalb ist es bei offenen Systemen sinnvoller die umgesetzte Energiemenge nicht auf eine willkürliche Masse von 2 kg oder 20 kg zu beziehen, sondern immer auf 1 kg bezogen anzugeben. Demzufolge muss die betrachtete Wasserpumpe pro Kilogramm durchströmenden Wassers eine Energiemenge von 2000 J aufwenden. Man bezeichnet eine solche, auf die Masse bezogene Größe auch als spezifische Größe. In diesem Fall wird sie spezifische Verschiebearbeit genannt und beträgt 2000 J/kg (sprich: 2000 Joule pro Kilogramm).
Die spezifische Verschiebearbeit wS ermittelt sich ganz allgemein als Quotient aus Verschiebearbeit WS und zugehöriger Masse m:
\begin{align}
\label{3475}
&\boxed{w_\text{S} = {W_\text{S} \over m}} ~~~[w_\text{S}] = \frac{\text{J}}{\text{kg}} ~~~~~\text{spezifische Verschiebearbeit} \\[5px]
\end{align}
Mit der Definition der Verschiebearbeit als Differenz der Produkte von Druck p und Volumen V zeigt sich, dass die spezifische Verschiebearbeit auch über die spezifischen Volumina v berechnet werden kann:
\begin{align}
&w_\text{S} =\frac{W_\text{S}}{m} = \frac{p_2 \cdot V_2 – p_1 \cdot V_1}{m} = {p_2 \cdot \underbrace{\frac{V_2}{m}}_{=v_2} – p_1 \cdot \underbrace{\frac{V_1}{m}}_{=v_1}} = p_1 \cdot v_1 – p_2 \cdot v_2 \\[10px]
\label{2070}
&\boxed{w_\text{S} = p_1 \cdot v_1 – p_2 \cdot v_2} ~~~ \text{mit}~~~ \boxed{v={V \over m}} ~~~ [v]=\frac{\text{m³} }{\text{kg}} ~~~\text{spezifisches Volumen} \\[10px]
\end{align}
Das spezifische Volumen gibt anschaulich an, welches Volumen ein Stoff mit einer Masse von 1 kg einnimmt. Das spezifische Volumen v entspricht somit gerade dem Kehrwert der Stoffdichte ρ. So liefert die Stoffdichte genau die umgekehrte Aussage, nämlich welche Masse ein Stoff mit einem Volumen von 1 m³ besitzt. Spezifisches Volumen v und Stoffdichte ρ stehen folglich in umgekehrtem Verhältnis zueinander:
\begin{align}
\label{9579}
&\boxed{v = {1 \over \rho}} \\[5px]
\end{align}
Somit kann die spezifische Verschiebearbeit wie folgt auch anhand der Stoffdichten ermittelt werden:
\begin{align}
\label{2791}
&\boxed{w_\text{S} = \frac{p_2}{\rho_2} – \frac{p_1}{\rho_1} }~~~\text{mit}~~~ \boxed{\rho= {m \over V}} ~~~ [\rho]={\text{kg} \over \text{m³}} ~~~ \text{Dichte} \\[5px]
\end{align}
Der Vorteil der Ermittlung der spezifischen Verschiebearbeit nach Gleichung (\ref{2791}) bzw. (\ref{2070}) ist, dass diese unabhängig der tatsächlich durchströmenden Masse angewendet werden können. Es ist also völlig egal, ob bei der beschriebenen Pumpe nun 2 kg oder 20 kg Wasser hindurchströmen. Die spezifische Verschiebearbeit von 2000 J/kg wird sich hierdurch nicht ändern!
Zahlenbeispiel
Im vorliegenden Beispiel beträgt die Wasserdichte am Pumpeneingang ρ1 = 999,25 kg/m³ (bei p1 = 1,1 bar) bzw. am Pumpenaustritt ρ2 = 1000,19 kg/m³ (bei p2 = 21,1 bar). Aus diesen Größen lässt sich nun die spezifische Verschiebearbeit ermitteln, ohne dass im Vorfeld bekannt sein muss, wie viel Masse tatsächlich durch die Pumpe strömen wird:
\begin{align}
& \underline{w_\text{S} } = \frac{p_2}{\rho_2} – \frac{p_1}{\rho_1} = \frac{12,1 \cdot 10^5 \frac{\text{N}}{\text{m²}} }{1000,19 \frac{\text{kg}}{\text{m³}}} – \frac{1,1 \cdot 10^5 \frac{\text{N}}{\text{m²}} }{999,25 \frac{\text{kg}}{\text{m³}}} = \underline{2000 \frac{\text{J}}{\text{kg}}} \\[5px]
\end{align}
Verschiebeleistung (Leistung der Pumpe)
Besonders bei offenen Systemen ermöglicht die Verwendung von spezifischen Energieangaben die relativ einfache Berechnung von Leistungen. Am Beispiel der bereits betrachteten Wasserpumpe soll davon ausgegangen werden, dass diese auf maximaler Stufe eine Wassermasse von m = 2 kg innerhalb einer Zeit von t = 4 s fördert. Auf eine Sekunde gerechnet, entspricht dies einer Wassermasse von 0,5 kg. Man bezeichnet diese pro Zeiteinheit angegebene Durchflussmenge auch als Massenstrom. In diesem Fall beträgt der Massenstrom folglich 0,5 kg/s (sprich: 0,5 Kilogramm pro Sekunde). Der Massenstrom wird häufig mit einem Punkt über dem Formelsymbol symbolisiert (\(\dot{m}\)) und ermittelt sich ganz allgemein als Quotient aus geförderter Masse m und der hierfür benötigten Zeit t:
\begin{align}
\label{7914}
\boxed{\dot{m} = \frac{m}{t}} ~~~[\dot{m}]=\frac{\text{kg}}{\text{s}} ~~~~~\text{Massenstrom} \\[5px]
\end{align}
Mit diesem Massenstrom kann die Leistung der Pumpe (Verschiebeleistung) relativ einfach ermittelt werden, wie im Folgenden gezeigt wird. So soll die Pumpe laut Beispiel eine Wassermasse von m = 2 kg innerhalb von t = 4 s fördern. Mit einer spezifischen Verschiebearbeit der Pumpe von wS = 2000 J/kg verrichtet diese dann insgesamt eine Verschiebearbeit WS = 4000 J an der Wassermasse; und dies innerhalb einer Zeit von t = 4 s. Aus dem Quotienten von Energie WS und Zeit t ergibt sich schließlich eine Verschiebeleistung der Pumpe von 1000 J/s (1000 W). Im Idealfall entspräche dies der elektrischen Leistung, die der Pumpe von außen zugeführt wird (von Verlusten abgesehen und Inkompressibilität des Wassers vorausgesetzt). Eine solche Verschiebeleistung PS lässt sich also ganz allgemein über den Massenstrom und der spezifischen Verschiebearbeit ermitteln:
\begin{align}
&P_\text{S}=\dot{W_\text{S}}= \frac{W_\text{S}}{t} = \frac{w_\text{S} \cdot m} {t} = w_\text{S}~\underbrace{\frac{m}{t}}_{=\dot{m}} \\[5px]
\label{6526}
&\boxed{P_\text{S} = w_\text{S} \cdot \dot m}
\end{align}
Die prinzipielle Aussage von Gleichung (\ref{6526}) bleibt nicht auf die Verschiebeleistung beschränkt. So gilt auch für andere Formen der Leistung – wie bspw. der Wärmeleistung – ganz allgemein:
\begin{align}
\label{3679}
&\boxed{\text{Leistung = spezifische Energie x Massenstrom}}
\end{align}
Ausblick
Wie in den vorangegangenen Abschnitten bereits mehrfach angedeutet ist die Verschiebearbeit (bzw. Verschiebeleistung) bei inkompressiblen Medien die hauptsächliche Arbeit, die von einem offenen System zu entrichten ist. Handelt es sich jedoch um kompressible Stoffe wie Gase, dann findet sich in einem offenen System noch ein weiterer Energieumsatz statt, da das Volumen unter Energieaufwand zusätzlich zum reinen „Durchschieben“ auch noch komprimiert werden muss (Volumenänderungsarbeit). Hierauf wird im Artikel Druckänderungsarbeit in offenen Systemen näher eingegangen.




