Druckänderungsarbeit in offenen Systemen

Die Druckänderungsarbeit entspricht der Arbeit eines offenen Systems, um ein Fluid an den Systemgrenzen zu verschieben und das Volumen zu ändern.

Energetische Prozesse an den Grenzen des offenen Systems (Verschiebearbeit)

Im Artikel zur Verschiebearbeit wurde am Beispiel einer Wasserpumpe erläutert, dass beim Strömen von Fluiden durch offene Systeme die Verschiebearbeit anfällt. Dies ist auf den Druckunterschied zwischen Eintritt in das System (z.B. Pumpeneinlass mit geringem Druck) und Austritt aus dem System (z.B. Pumpenauslass mit hohem Druck) zurückzuführen. Bei Pumpen wird das Fluid mit geringerer Energie W₁ von der Umgebung eingeschoben und mit höhere Energie W₂ von der Pumpe wieder ausgeschoben.

Die jeweiligen Ein- und Ausschiebeenergien ergeben sich dabei aus dem Produkt von betrachtetem Fluidvolumen V, welches über die Systemgrenze transportiert wird, und dem dort herrschenden Druck p. Die Differenz dieser Energien entspricht dann schließlich der verrichteten Arbeit des Systems, z.B. der Arbeit der Pumpe, und wird ganz allgemein Verschiebearbeit W_S genannt:

\begin{align}
&W_\text{S} = W_2 – W_1 \\[5px]
&W_\text{S} = p_2 \cdot V_2 – p_1 \cdot V_1 \\[5px]
\end{align}

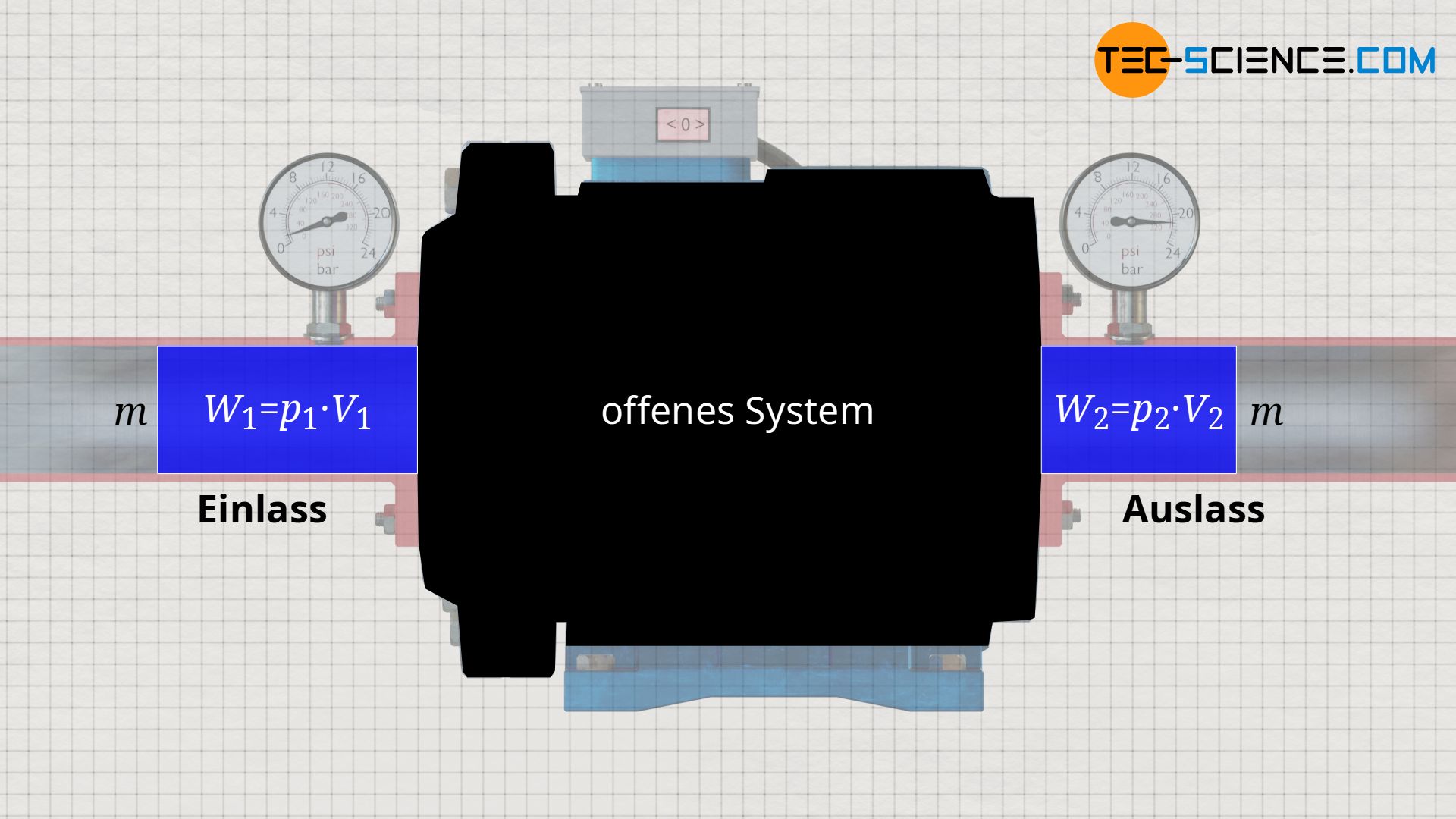
Die am Beispiel der Wasserpumpe gewonnene Erkenntnis der Verschiebearbeit, kann bisher auf jedes offene System übertragen werden. Denn letztlich wird bei jedem offenen System eine gewisse Stoffmasse m mit einem Volumen V₁ und einem Druck p₁ in das System hineingeschoben und mit einem geänderten Volumen V₂ und geändertem Druck p₂ wieder aus dem System ausgeschoben.

Energetische Prozesse im Inneren des offenen Systems (Volumenänderungsarbeit)

Die Verschiebearbeit ist bei einem offenen System allein auf die Tatsache zurückzuführen, dass die Stoffmasse entgegen dem Druckunterschied zwischen Systemeingang und Systemausgang verschoben werden muss. Dabei sind offensichtlich lediglich die energetischen Prozesse an den Systemgrenzen relevant. Unberücksichtigt bleiben bei dieser Betrachtung allerdings die inneren Vorgänge im offenen System selbst, wenn das Fluid durch das System strömt. Das offene System wurde bisher also lediglich als „Blackbox“ betrachtet. Deshalb betrachten wir im Folgenden die energetischen Vorgänge im Inneren eines offenen Systems etwas genauer.

Für eine allumfassende Energiebilanz dürfen nicht nur die energetischen Prozesse an der Systemgrenze betrachtet werden (Verschiebearbeit), sondern es müssen auch die Vorgänge im System selbst näher untersucht werden. So bedingt eine im offenen System vonstattengehende Druckänderung im Allgemeinen auch immer auch eine entsprechende Volumenänderung. Dieser innere Prozess der Volumenänderung wurde in der bisherigen Betrachtung nicht näher diskutiert. Diese Volumenänderung musste am Beispiel der Wasserpumpe auch nicht berücksichtigt werden, da es sich bei Wasser um ein (nahezu) inkompressibles Medium handelt. Bei diesen inkompressiblen Fluiden gibt es keine Volumenänderung.

Bei kompressiblen Fluiden wie Gasen ruft eine druckbedingte Volumenänderung im Systeminneren allerdings die Volumenänderungsarbeit auf den Plan, denn schließlich komprimiert sich ein Gasvolumen nicht von selbst, sondern nur unter Arbeitsaufwand! Neben der Verschiebearbeit, die an den Grenzen des offenen Systems auftritt (beim Massendurchtritt), muss vor allem bei Gasen auch noch die im Inneren umgesetzte Volumenänderungsarbeit (während des Durchströmens) berücksichtigt werden.

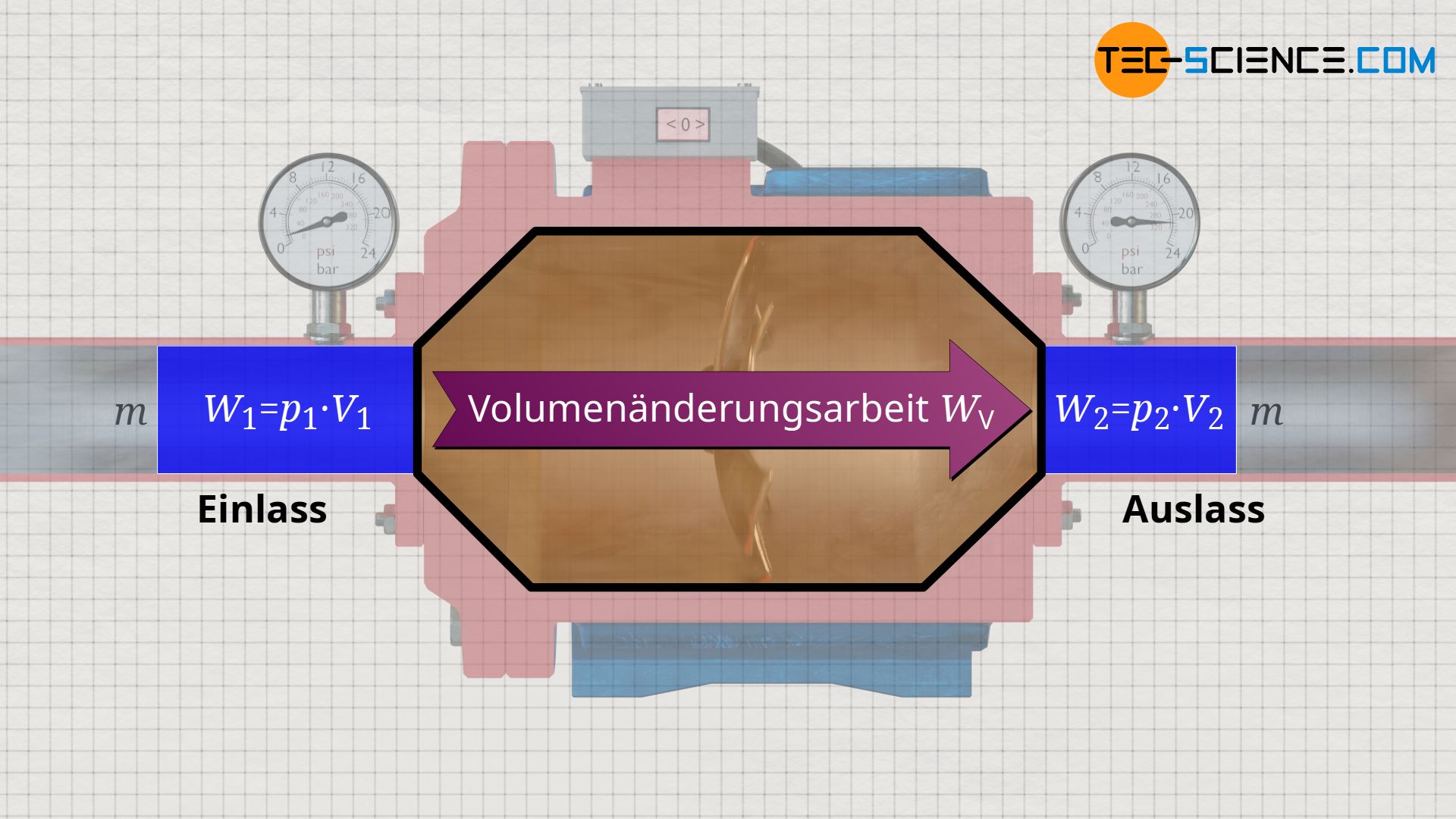
Kontrollvolumen

Man kann sich die in einem offenen System ablaufenden Vorgänge anschaulicher vorstellen, wenn man die eintretende Stoffmasse als geschlossenes System betrachtet. Man denkt sich also eine gedankliche Blase um den eingesaugten Stoff, z.B. eine „Plastiktüte“. Durch die Blase tritt selbst keine Masse, d.h. diese Betrachtung bildet ein geschlossenes System. Dieses geschlossene System – also die darin befindliche Masse – wird nun beobachtet, wie es durch das offene System strömt und welche Zustandsänderungen es dabei durchläuft. Die Pumpe wird in einer solchen Betrachtung dann häufig nicht mehr als offenes System bezeichnet, sondern als sogenannter Kontrollraum. Man betrachtet also ein geschlossenes System der Masse m, wie es sich durch einen Kontrollraum bewegt.

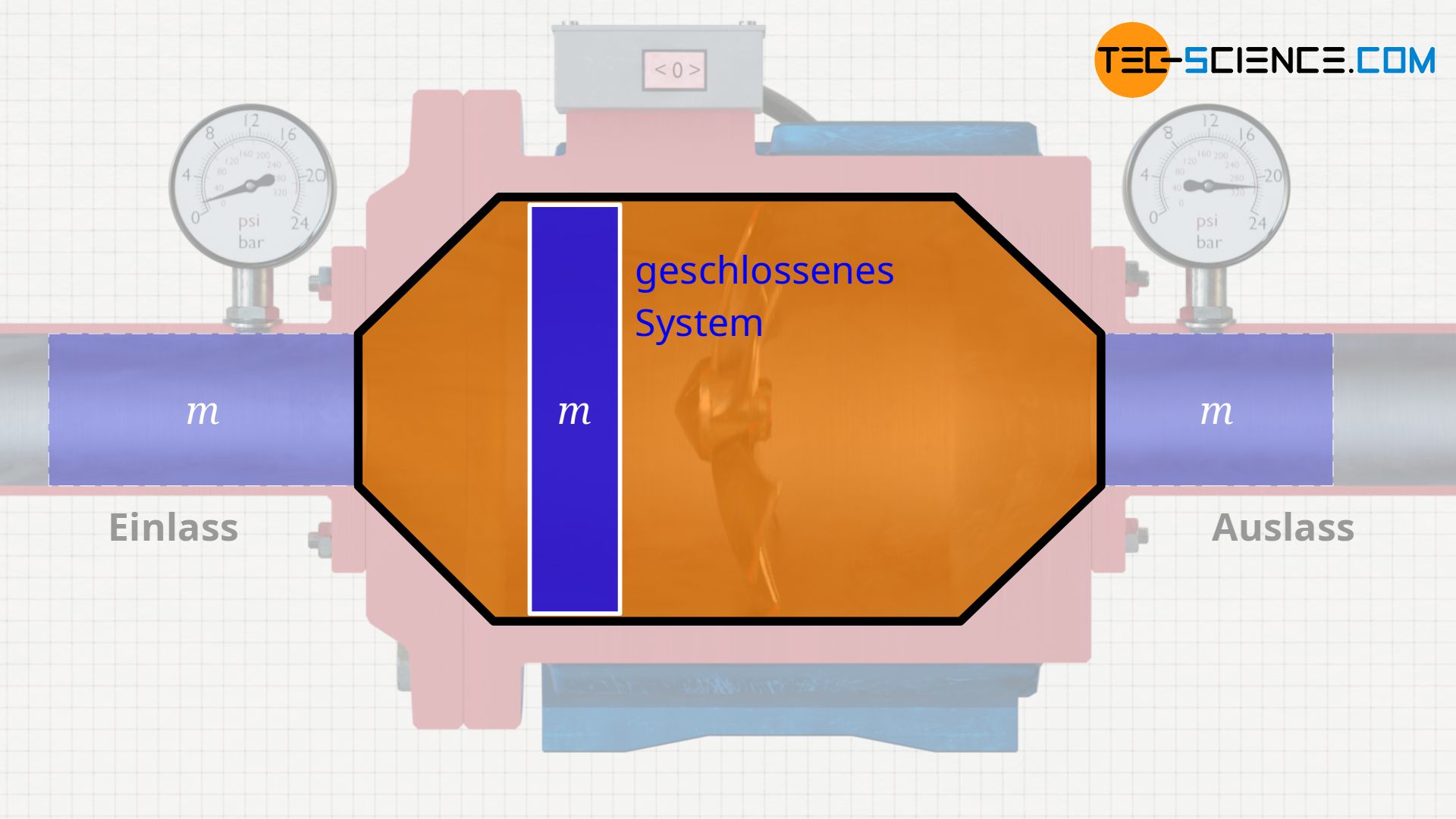
In einer solchen Betrachtungsweise werden nun nochmals die unterschiedlichen Energieumsätze deutlich. Die Verschiebearbeit bezieht sich lediglich auf das Durchschieben der betrachteten Masse aufgrund des wirkenden Druckunterschieds an den Kontrollraumgrenzen. Die Volumenänderungsarbeit hingegen bezieht sich auf den Arbeitsumsatz im Inneren des Kontrollraums, d.h. auf den Arbeitsumsatz der nötig ist, um die betrachtete Masse beim Durchströmen des Kontrollraumes zu komprimieren.

Beide Energieumsätze – Verschiebearbeit und Volumenänderungsarbeit – sind vom offenen System zu erbringen (z.B. vom Motor eines Verdichters bzw. Kompressors). Da sowohl die Volumenänderungsarbeit W_V als auch die Verschiebearbeit W_S aufgrund der Druckänderung während dem Durchströmen entstehen, wird die Summe beider Energieumsätze auch als Druckänderungsarbeit W_D bezeichnet:

\begin{align}
\label{5715}
&W_\text{D} = W_\text{V} + W_\text{S} \\[5px]
\label{4461}
&\boxed{W_\text{D} =~ – \int\limits_{V_1}^{V_2}p(V)~\text{d}V + p_2~V_2 – p_1~V_1 }
\end{align}

bzw. als spezifische Druckänderungsarbeit w_D (Druckänderungsarbeit pro Masseneinheit):

\begin{align}
\label{8858}
&\boxed{w_\text{D} =~ – \int\limits_{v_1}^{v_2}p(v)~\text{d}v + p_2~v_2 – p_1~v_1 }
\end{align}

Dass ein offenes System neben der Verschiebearbeit auch noch Volumenänderungsarbeit umsetzt, kann an einem Verdichter anschaulich nachvollzogen werden. Hält man Ein- und Auslass eines Verdichters für kurze Zeit geschlossen, dann muss für diese Zeit zwar keine Verschiebearbeit mehr vom Verdichter verrichtet werden; das im Inneren befindliche Gas wird aber dennoch komprimiert. Somit fällt weiterhin Volumenänderungsarbeit an. Das offene System wird praktisch zu einem geschlossenen System, in dem lediglich Volumenänderungsarbeit anfällt.

Die Druckänderungsarbeit entspricht der Arbeit eines offenen Systems, um ein Fluid an den Systemgrenzen zu verschieben und das Volumen zu ändern.

Die Druckänderungsarbeit entspricht im einfachsten Fall jenem Arbeitsumsatz, der insgesamt in einem offenen System anfällt. Diese Druckänderungsarbeit muss im Falle einer Pumpe (bei Flüssigkeiten) oder im Falle eines Verdichters (bei Gasen) vom antreibenden Motor bereitgestellt werden. In dieser reibungsfreien Betrachtung sind Änderungen der kinetischen und potentiellen Energie vernachlässigt. Im Abschnitt zur technischen Arbeit wird hierauf näher eingegangen.

Druckänderungsarbeit für inkompressible Stoffe

Beachte, dass in einem offenen System die Verschiebearbeit und die Volumenänderungsarbeit im Prinzip immer gemeinsam auftreten, eben als Druckänderungsarbeit. Schließlich ist eine Druckänderung im Allgemeinen auch immer mit einer Volumenänderung verbunden. Lediglich für den theoretischen Fall eines perfekt inkompressiblen Mediums, würde nur die Verschiebearbeit im offenen System anfallen. Denn ohne Volumenänderung existiert auch kein Volumenänderungsarbeit (dV=0). Somit bliebe als Arbeitsumsatz lediglich die Verschiebearbeit zu verrichten, da der Stoff ja weiterhin in das offene System ein- und bei geändertem Druck wieder ausgeschoben werden muss.

Für diesen inkompressiblen Fall ergibt sich die Druckänderungsarbeit W_D beim Durchströmen des Volumens V=V₁=V₂ durch das offene System lediglich aus Druckänderung Δp, die das offene System erzeugt:

\begin{align}
\label{2394}
&W_\text{D} =~ – \int\limits_{V_1}^{V_2}p(V)~\underbrace{\text{d}V}_{=0} + p_2~\underbrace{V_2}_{=V} – p_1~\underbrace{V_1}_{=V}=p_2~V-p_1~V = V~(p_2-p_1)= V \cdot \Delta p \\[5px]
\label{9679}
&\boxed{W_\text{D} = V\cdot\Delta p}~~~\text{gilt nur für inkompressible Fluide}
\end{align}

bzw. als spezifische Druckänderungsarbeit \(w_D\):

\begin{align}
\label{3376}
&\boxed{w_\text{D} = v\cdot\Delta p}~~~\text{ gilt nur für inkompressible Fluide }
\end{align}

Auch wenn ein solcher inkompressibler Fall praktisch nicht existiert, so kann er dennoch für Flüssigkeiten in sehr guter Näherung als solcher betrachtet werden, da diese als nahezu inkompressibel gelten. Für alle anderen Fälle, insbesondere bei kompressiblen Medien wie Gasen, ist die Druckänderungsarbeit nach Gleichung (\ref{4461}) bzw. Gleichung (\ref{8858}) zu ermitteln. Diese Gleichung lässt sich jedoch in einer wesentlich einfacheren Form darstellen. Dies wird deutlich, wenn man sich den Prozess eines offenen Systems in einem Volumen-Druck-Diagramm veranschaulicht. Im nächsten Abschnitt wird hierauf näher eingegangen.

Druckänderungsarbeit im Volumen-Druck-Diagramm

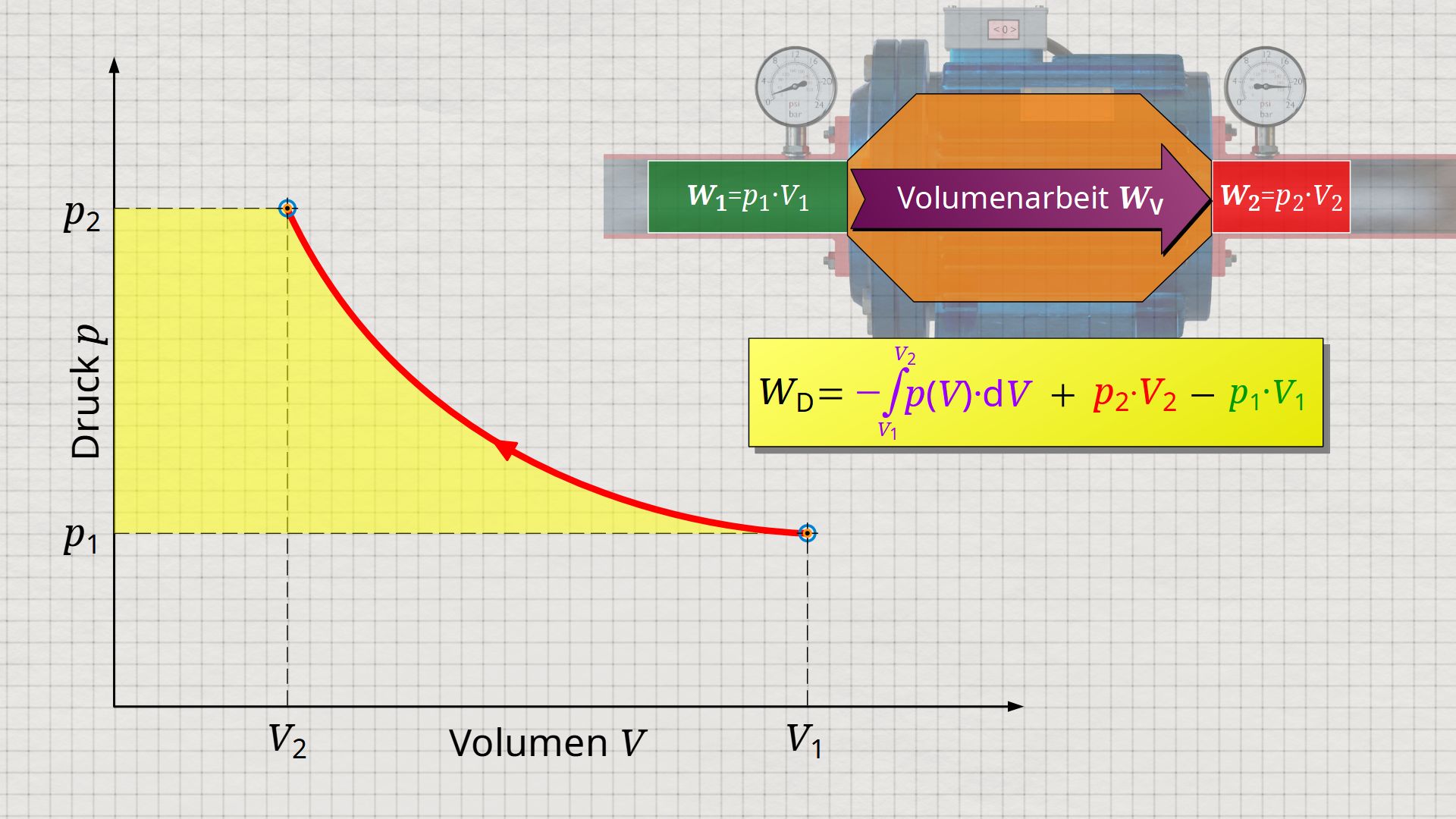
Im Folgenden soll eine wesentlich kompaktere Gleichung für die Druckänderungsarbeit gegeben werden. Hierzu wird ein Gas betrachtet, das vom Kompressor zunächst mit dem Volumen V₁ bei einem Druck p₁ angesaugt wird. Anschließend wird das Gas im Inneren bei ansteigendem Druck auf ein Volumen V₂ komprimiert. Die Zustandsänderung soll gemäß der im p(V)-Diagramm abgebildeten Kurve erfolgen. Nach der Kompression wird das Volumen V₂ bei einem Enddruck p₂ aus dem Kompressor geschoben.

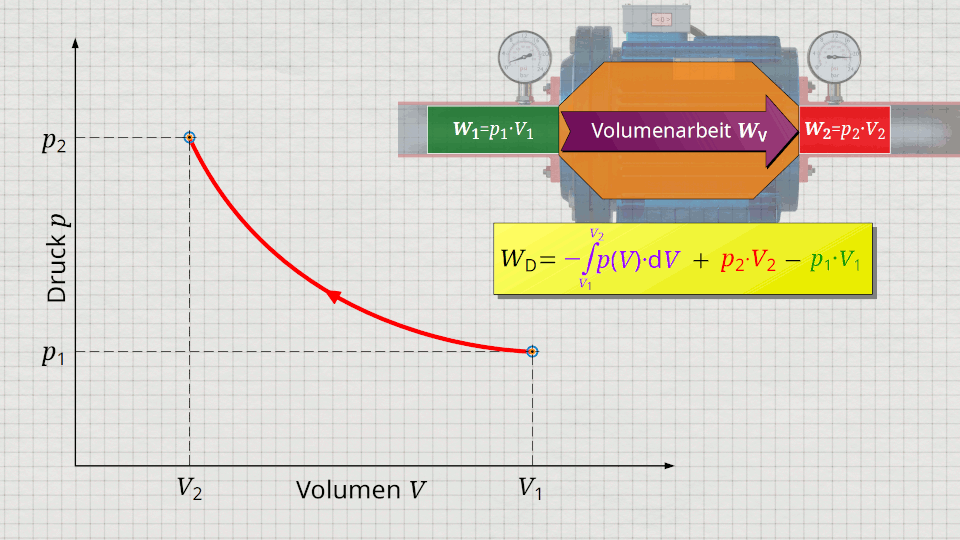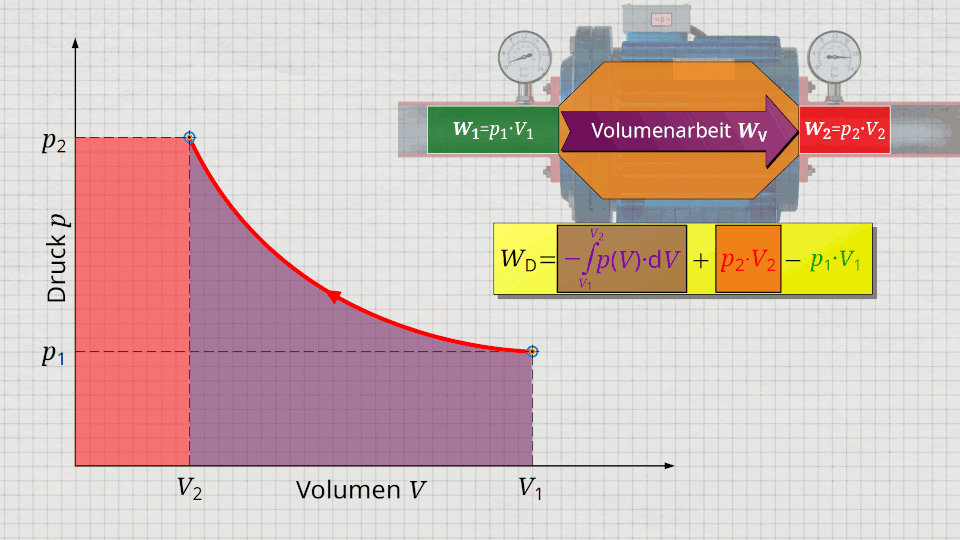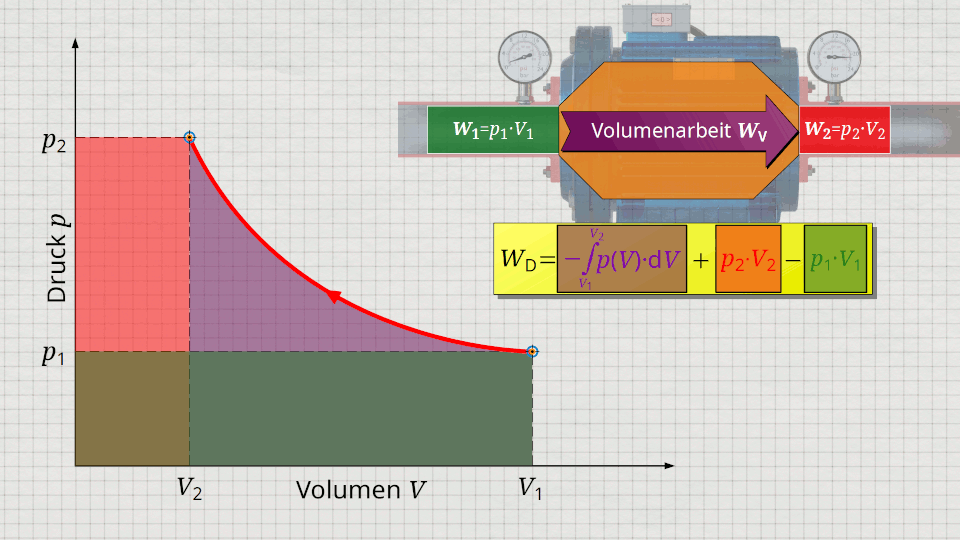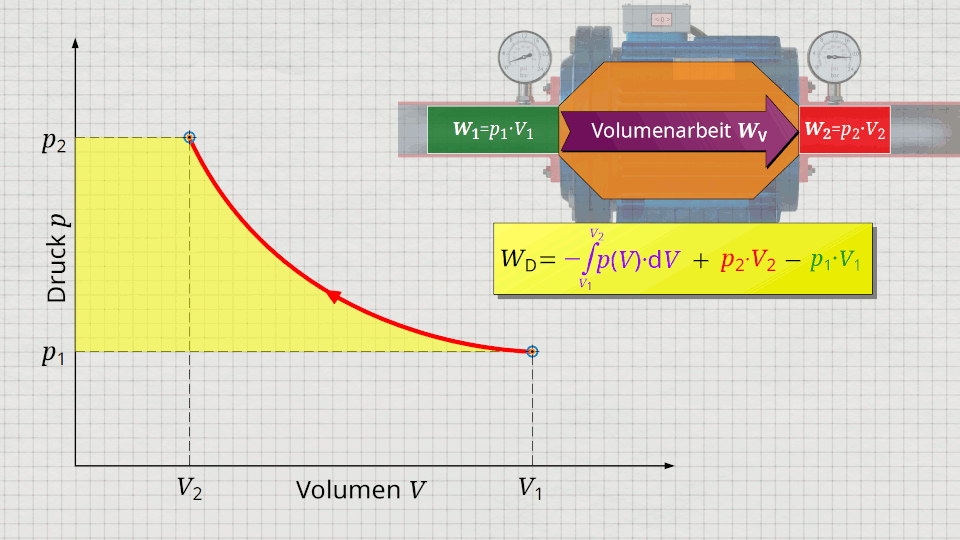
Zur Ermittlung der Druckänderungsarbeit ist die Gleichung (\ref{5715}) heranzuziehen. Darin können die einzelnen Terme im p(V)-Diagramm jeweils als Flächen dargestellt werden. Der Term der Volumenänderungsarbeit W_V = -∫p(V)⋅dV lässt sich als Fläche unter der Zustandskurve abbilden (Beachte, dass dem Gas bei der Kompression Volumenänderungsarbeit zugeführt wird und dieser Arbeitsumsatz somit mathematisch positiv ist)! Addiert wird gemäß Gleichung (\ref{5715}) nun der Term p₂⋅V₂, der sich als Rechteckfläche vom Punkt (V₂|p₂) bis zum Koordinatenursprung (0|0) darstellen lässt („Ausschiebeenergie“). Von dieser Gesamtfläche wird laut Gleichung (ref\{5715}) nun jene Rechteckfläche abgezogen, die sich vom Punkt (V₁|p₁) bis zum Koordinatenursprung (0|0) erstreckt („Einschiebeenergie“).

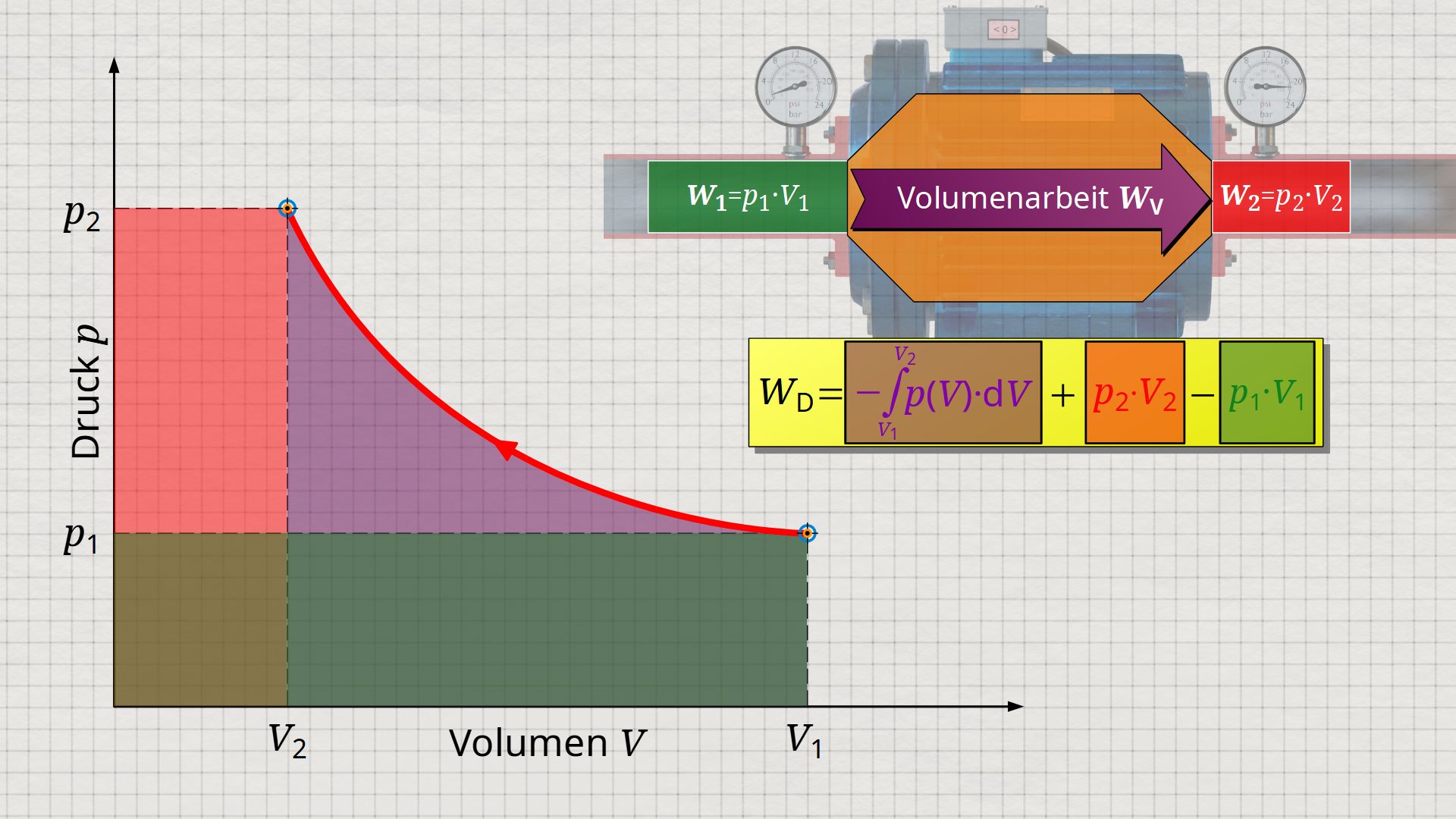
Effektiv übrig bleibt somit lediglich die Fläche links neben der Zustandskurve. Diese seitliche Fläche lässt sich folglich als Druckänderungsarbeit interpretieren!

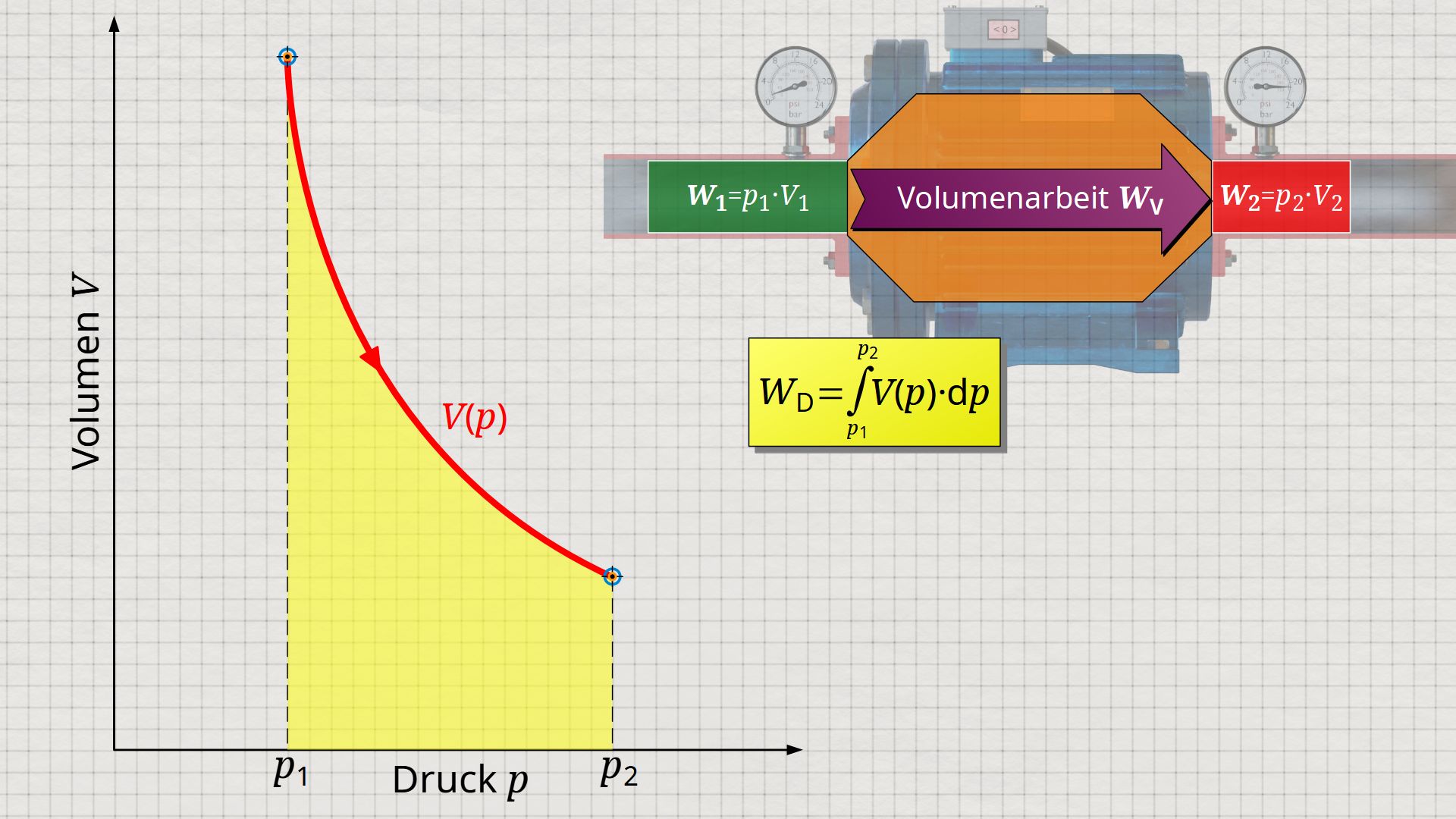
Mathematisch ermittelt werden kann diese Fläche als Integral W_D=-∫V(p)⋅dp innerhalb der Grenzen zwischen p₁ und p₂. Dies wird deutlich, wenn man sich das Koordinatensystem in Gedanken einfach um 90° gedreht und gleichzeitig gespiegelt vorstellt. Die horizontale Achse entspricht dann dem Druck und die vertikale Achse dem Volumen. In diesem Fall ergibt sich dann eine V(p)-Kurve, deren Fläche unter der Kurve der Druckänderungsarbeit W_D entspricht:

\begin{align}
\label{8449}
&\boxed{W_\text{D} = \int\limits_{p_1}^{p_2}V(p)~dp}~~~\text{gilt allgemein für ein offenes System}
\end{align}

Da offene Systeme i.d.R. durch spezifische Größen beschrieben werden, ist es sinnvoll die Zustandsänderungen auch in spezifischer Diagrammform darzustellen. Deshalb wird anstelle des Volumens meist das spezifische Volumen aufgetragen. Anschaulich bedeutet dies nichts anderes, als dass sich das dargestellte Volumen auf eine Masse von 1 kg bezieht. Dementsprechend ergibt sich die spezifische Druckänderungsarbeit w_D als seitliche Fläche in diesem p(v)-Diagramm:

\begin{align}
\label{1956}
&\boxed{w_\text{D} = \int\limits_{p_1}^{p_2}v(p)~dp}~~~\text{gilt allgemein für ein offenes System}
\end{align}

Diese Gleichungen bringen bereits zum Ausdruck, dass für die Ermittlung der Druckänderungsarbeit der Verlauf des (spezifischen) Volumens in Abhängigkeit des Drucks bekannt sein muss. Im Gegensatz zur Verschiebearbeit ist die Druckänderungsarbeit somit vom Weg, auf dem die Zustandsänderung erfolgt, abhängig und damit eine typische Prozessgröße.