Erster Hauptsatz der Thermodynamik für offene Systeme (Herleitung)

Erfahre in diesem Artikel mehr über die Herleitung des ersten Hauptsatzes der Thermodynamik für offene Systeme.

Technische Arbeit in einem offenen System

Im Artikel Technische Arbeit in offenen Systemen wurde gezeigt, dass sich die technische Arbeit W_t im Allgemeinen aus der Druckänderungsarbeit W_D, der Hubarbeit W_H und der Beschleunigungsarbeit W_B zusammensetzt (sowie im reibungsbehafteten Fall Reibungsarbeit W_Diss, auf die zunächst allerdings verzichtet werden soll):

\begin{align}
\label{8918}
&\boxed{W_\text{t} = W_\text{D}+W_\text{H}+W_\text{B}~~~(+W_\text{Diss})} \\[5px]
&~~~W_\text{D} = W_\text{V} + W_\text{S} \\[5px]
&~~~W_\text{S} = \Delta (pV) \\[5px]
&~~~W_\text{H} = mg \cdot \Delta h \\[5px]
&~~~W_\text{B} = \tfrac{1}{2}m \cdot \Delta c^2 \\[5px]
\end{align}

Die Druckänderungsarbeit W_D wiederum kann als Summe von Verschiebearbeit W_S und Volumenänderungsarbeit W_V dargestellt werden. Somit lässt sich die technische Arbeit W_t für den reibungsfreien Fall (W_Diss=0) auch wie folgt ausdrücken:

\begin{align}
\label{9318}
&W_\text{t} = \underbrace{W_\text{V} + W_\text{S}}_{W_\text{D}} + W_\text{H} + W_\text{B} \\[5px]
\end{align}

Strömendes Fluidelement als geschlossenes System

Die Volumenänderungsarbeit W_V in Gleichung (\ref{9318}) ist dafür verantwortlich, dass sich das Volumen der betrachteten Fluidmasse, welche gerade durch das offene System strömt, von V₁ auf V₂ ändert. Diese Volumenänderung kann dabei als in einem geschlossenen System stattfindend betrachtet werden (siehe hierzu auch den Artikel Druckänderungsarbeit).

Man stelle sich hierzu einfach eine gedankliche Blase um ein Fluidvolumen der Masse m und dem entsprechenden Volumen V₁ vor. Diese Blase wird nun angesaugt und auf das Volumen V₂ komprimiert (bei Pumpen) oder expandiert (in Turbinen). Die Hülle der gedachten Blase stellt dabei die Systemgrenze dar, über diese hinweg keine Masseaustausch mit der Umgebung stattfindet. Durch diese Betrachtung kann die Volumenänderung des Stoffes im offenen System (dann auch Kontrollraum genannt) als in einem geschlossenen System stattfindend betrachtet werden.

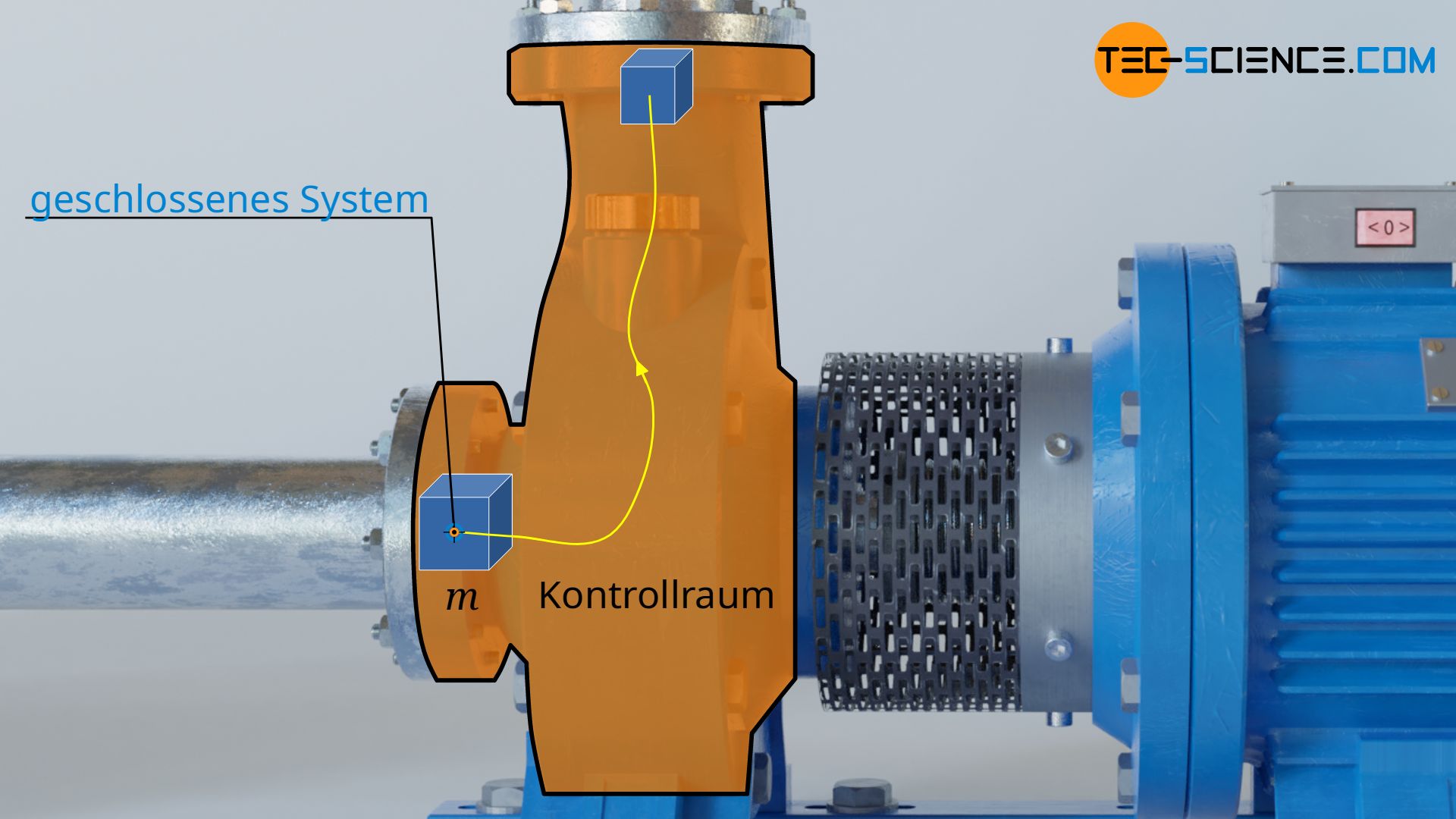
Für die Volumenänderungsarbeit W_V können folglich die Gesetzmäßigkeiten von geschlossenen Systemen zugrunde gelegt werden, insbesondere der erste Hauptsatz der Thermodynamik für ein Stoff in einem geschlossenen System. Dieser besagt, dass für den reibungsfreien Fall die Zufuhr von Volumenänderungsarbeit W_V und Wärme Q zu einer entsprechenden Änderung der innere Energie ΔU des Stoffes führt:

\begin{align}
\label{6682}
W_\text{V} + Q = \Delta U \\[5px]
\end{align}

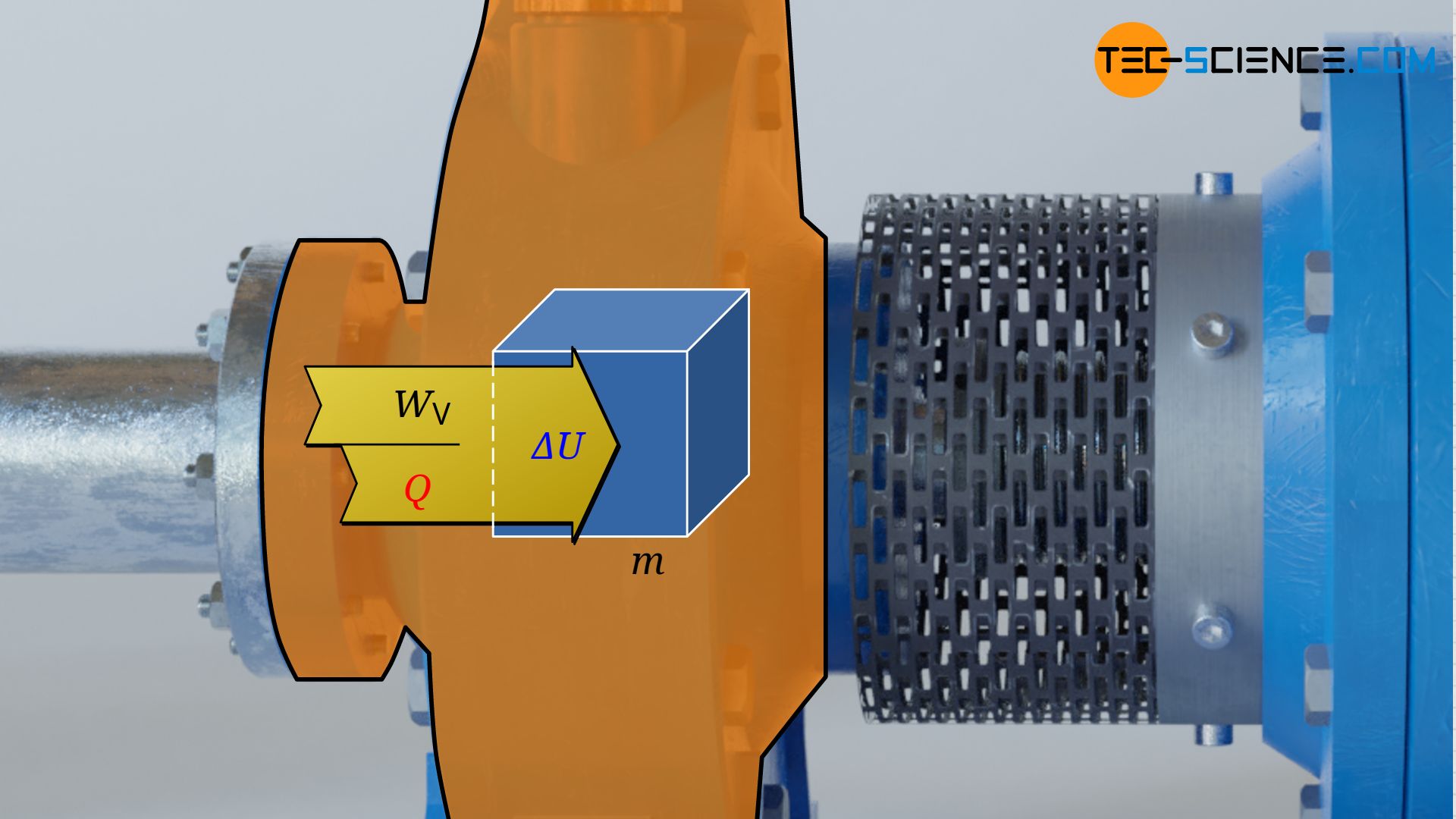
Anmerkung: Prinzipiell müsste bei bewegten geschlossenen Systemen eine Änderung der kinetischen und potentiellen Energie der betrachteten Masse mitberücksichtigt werden. Bei der vorliegenden Betrachtungsweise bewegt man sich aber mit dem Schwerpunkt der Masse mit, während diese durch den Kontrollraum strömt (stofffestes Koordinatensystem). Bezüglich dieser Schwerpunktsbetrachtung ändert sich dann aber weder die potentielle Energie noch die kinetische Energie! Bei der äußeren Betrachtungsweise der strömenden Masse nach Gleichung (\ref{9318}) ist die Änderung der potentiellen und kinetischen Energie ohnehin bereits berücksichtigt (ortsfestes Koordinatensystem).

Gleichung (\ref{6682}) erklärt nun auch weshalb die Luft beim Ausschieben aus einem Kompressor teilweise eine Temperatur von über 100 °C aufweist. Denn während des Kompressionsvorgangs wird dem Gas Volumenänderungsarbeit zugeführt (W_V>0), die ohne Kühlung (Q=0) direkt zur Erhöhung der inneren Energie führt (W_V=ΔU). Da für ideale Gase die innere Energie direkt mit der Temperatur verknüpft ist, steigt die Temperatur folglich an. Um solche, meist unerwünschte Temperaturerhöhungen zu vermeiden, werden Kompressoren in der Regel gekühlt (Q<0)! Aus diesem Grund befinden sich auch in Automobilen häufig sogenannte Ladeluftkühler wieder, sofern die Verbrennungsmotoren mit Kompressoren „aufgeladen“ werden (Motoraufladung).

Erster Hauptsatz der Thermodynamik für offene Systeme

Die Volumenänderungsarbeit W_V kann gemäß Gleichung (\ref{6682}) somit auch anhand der Änderung der inneren Energie ΔU und dem Wärmeumsatz Q ermittelt werden:

\begin{align}
\label{1957}
W_\text{V} = \Delta U – Q \\[5px]
\end{align}

Gleichung (\ref{1957}) kann nun in Gleichung (\ref{9318}) eingesetzt werden. Anschließend werden die Terme nach Prozessgrößen und Zustandsgrößen geordnet. Man erhält so schließlich den ersten Hauptsatz der Thermodynamik für einen Stoff, der durch ein offenes System bewegt wird:

\begin{align}
\label{7962}
&W_\text{t} = \overbrace{\Delta U – Q}^{=W_\text{V}} + W_\text{S} + W_\text{H} + W_\text{B} \\[5px]
\label{6700}
&\underbrace{W_\text{t} + Q}_{\text{Prozessgrößen}} = \underbrace{\Delta U + W_\text{S} + W_\text{H} + W_\text{B}}_{\text{Änderung von Zustandsgrößen}} \\[5px]
\label{6671}
&\boxed{W_\text{t} + Q = \Delta U + \Delta \left(p~V \right) + m~g~\Delta z + \tfrac{1}{2}~m~\Delta c^2} \\[5px]
&\text{erster Hauptsatz für offene Systeme}\\[5px]
\end{align}

Links des Gleichheitszeichens stehen lediglich Prozessgrößen, die dem durchströmenden Stoff von außen zu- oder abgeführt werden. Dies ist zum einen die technische Arbeit W_t, die dem Fluid meist über Wellen zu- oder abgeführt wird, z.B. über die Pumpenwelle oder die Turbinenwelle (deshalb häufig auch als Wellenarbeit bezeichnet). Zum anderen kann Wärme Q zu- oder abgeführt werden, wie zum Beispiel in Turbinen durch das Verbrennen des Treibstoffes (Wärmezufuhr) oder im Falle von Kompressoren durch Kühlrippen (Wärmeabfuhr). Auf der rechten Seite des Gleichheitszeichens stehen hingegen lediglich Zustandsgrößen, die durch diesen äußeren Energieumsatz entsprechend geändert werden.

Beachte, dass sich auch die Verschiebearbeit W_S als Änderung von Zustandsgrößen interpretieren lässt. Die Verschiebearbeit bringt zum Ausdruck, dass der Stoff mit dem Ausgangszustand p₁ und V₁ auf den Endzustand p₂ und V₂ geändert wurde ⇒ Δ(pV). Die Verschiebearbeit ist im eigentlichen Sinne also keine Prozessgröße wie man anhand des Begriffes Arbeit meinen könnte!

Der erste Hauptsatz lässt sich auch in spezifischer Form (d.h. auf die Fluidmasse m bezogen) angeben und ist somit unabhängig von der tatsächlich durchströmenden Masse:

\begin{align}
&\boxed{w_\text{t} + q = \Delta u + \Delta \left(p~v \right) + g~\Delta z + \tfrac{1}{2}~\Delta c^2} \\[5px]
\end{align}

Interpretation des ersten Hauptsatzes für offene Systeme

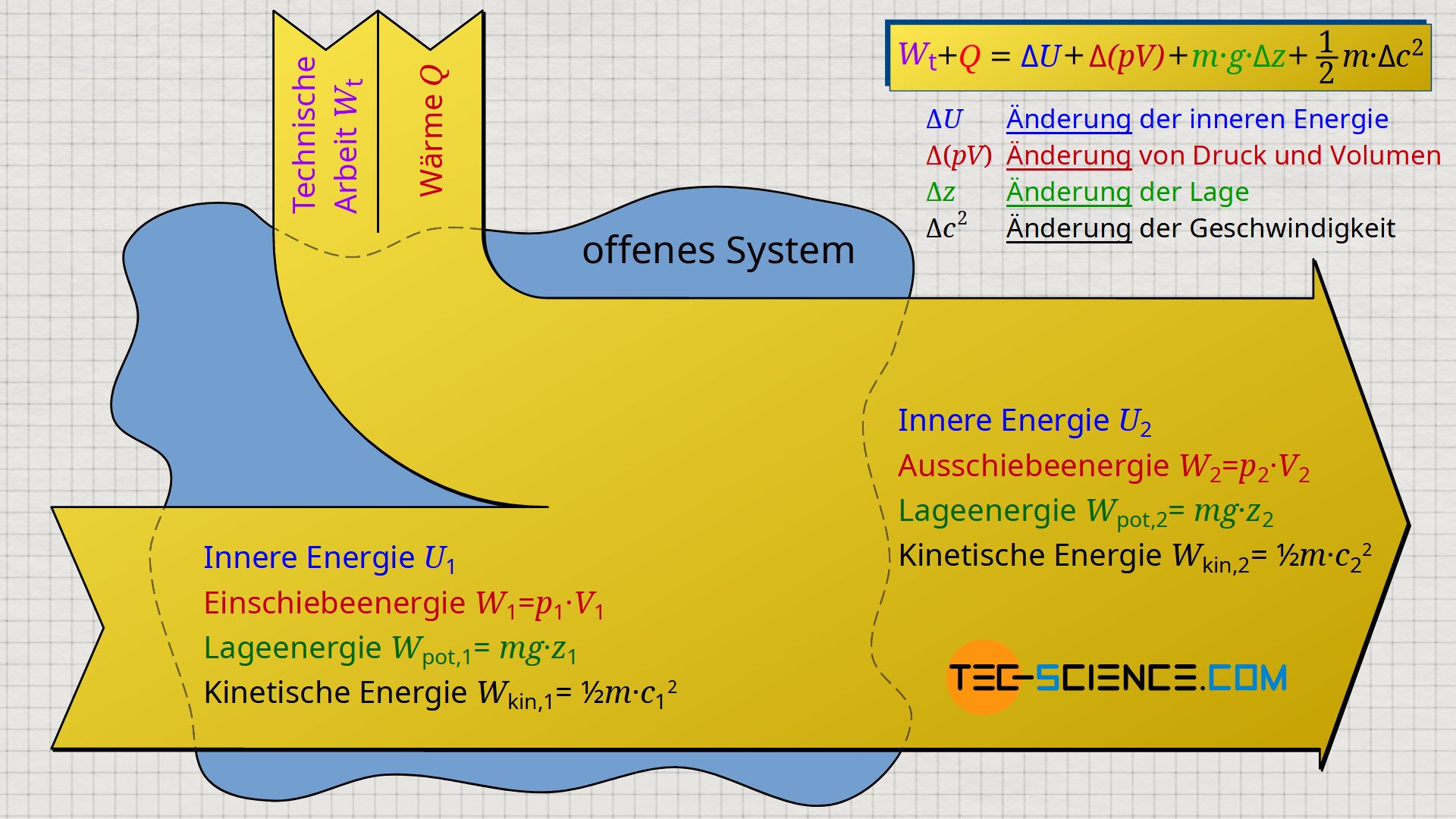
Somit lässt sich der erste Hauptsatz für offene System gemäß Gleichung (\ref{6671}) wie folgt interpretieren: Wird einem Stoff, der durch ein offenes System bewegt wird, von außen die technische Arbeit W_t und die Wärme Q zu- oder abgeführt, so wird der Stoff im Allgemeinen folgenden Änderungen unterliegen:

• ΔU: Zum einen wird sich die innere Energie des Stoffes ändern. Dies resultiert in der Regel in einer entsprechenden Temperaturänderung.
• Δ(pV): Zudem ändert sich die Ausschiebeenergie im Vergleich zur Einschiebeenergie. Dies ist mit einer entsprechenden Änderung im Volumen und im Druck verknüpft.
• Δz: Ebenfalls ändert sich die potentielle Energie der bewegten Masse, wodurch sich die Schwerpunktlage entsprechend ändert.
• Δc²: Außerdem ergeben sich Änderungen in den kinetischen Energien bzw. den damit verbundenen Strömungsgeschwindigkeiten.

In Gleichung (\ref{7962}) wurde der Dissipationsterm W_Diss auf der rechten Seite des Gleichheitszeichens vernachlässigt. Unter Berücksichtigung von Reibung sollte dieser dann zwar prinzipiell auch auf der rechten Seite von Gleichung (\ref{6671}) auftauchen. Jedoch wird die zugeführte Dissipationsenergie früher oder später ohnehin in innere Energie dissipiert, wo sie auch zur Änderung des Drucks p und des Volumens V führt. Eventuell auftretende Dissipationsarbeiten werden also in den Termen ΔU und Δ(pV) bereits berücksichtigt!

Anmerkung: Gleichung (\ref{6671}) wird unter anderem durch die Änderung der inneren Energie ΔU und die Änderung des Drucks bzw. Volumens Δ(pV) ausgedrückt. Es handelt sich dabei um typische thermodynamische Zustandsgrößen. Mit Hilfe der Größe der Enthalpie, lassen sich diese beiden Terme zur sogenannten Enthalpieänderung zusammenfassen.

Exkurs: Bernoulli-Gleichung

Der im vorherigen Abschnitt erläuterte erste Hauptsatz der Thermodynamik für ein offenes System lässt sich auch auf reine Strömungsprozesse von inkompressiblen Stoffen wie Flüssigkeiten übertragen. Hierzu wird eine reibungsfreie Wasserströmung durch ein Rohr mit veränderlichem Querschnitt betrachtet.

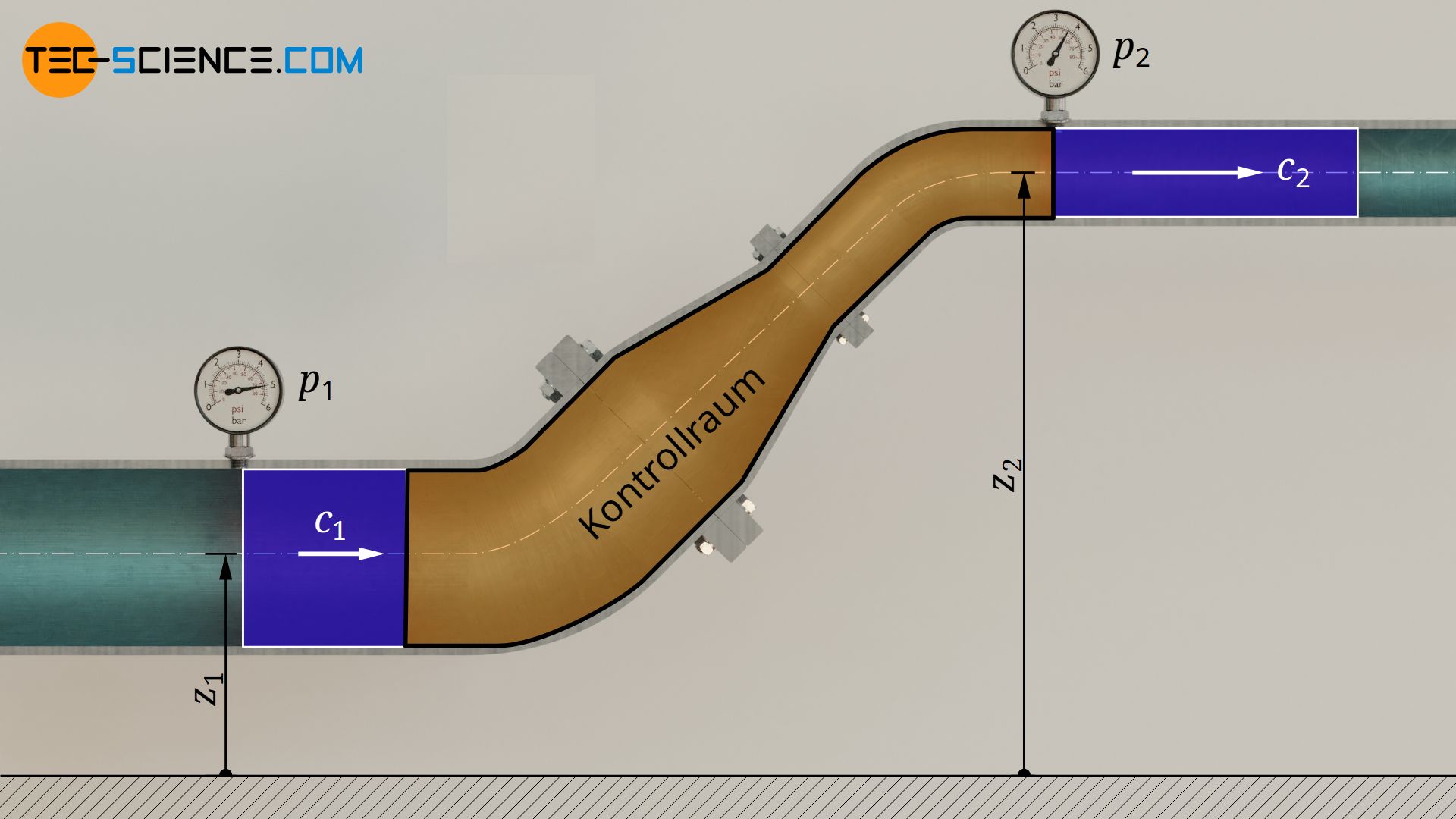
Dem Wasser soll keine Energie in Form von Wärme oder Arbeit zu- oder abgeführt werden. Das Wasser strömt also lediglich durch das Rohr. Somit sind sowohl technische Arbeit W_t als auch Wärmeumsatz Q in Gleichung (\ref{6671}) Null. Auch eine Temperaturänderung kann deshalb vernachlässigt werden, sodass sich die innere Energie nicht ändert ΔU=0. Für diesen Fall ergibt sich der erste Hauptsatz dann wie folgt:

\begin{align}
\label{6570}
\underbrace{W_\text{t}}_{=0} + \underbrace{Q}_{=0} &= \underbrace{\Delta U}_{=0} + \Delta \left(p~V \right) + m~g~\Delta z + \tfrac{1}{2}~m~\Delta c^2 \\[5px]
\label{eq:4700}
0 &= \Delta \left(p~V \right) + m~g~\Delta z + \tfrac{1}{2}~m~\Delta c^2 \\[5px]
\end{align}

Wird der Druck am Eintritt des Rohres mit p₁, das Volumen mit V₁, die Geschwindigkeit mit c₁ und die Eintrittshöhe mit z₁ bezeichnet, sowie die entsprechenden Größen am Austritt mit dem Index „2“ versehen, so gilt:

\begin{align}
\label{7577}
&0 = \underbrace{p_2~V_2-p_1~V_1}_{\Delta \left(p~V \right)} + \underbrace{m~g~z_2-m~g~z_1}_{m~g~\Delta z} + \underbrace{\tfrac{1}{2}~m~ c_2^2-\tfrac{1}{2}~m~ c_1^2}_{\tfrac{1}{2}~m~\Delta c^2} \\[5px]
\end{align}

Beachte, dass für inkompressible Medien grundsätzlich nicht zwischen V₁ und V₂ unterschieden werden muss, da für solche Fälle beide Volumina identisch sind. Das Volumen wird deshalb lediglich mit V (ohne Index) bezeichnet. Ordnet man die Terme noch nach Größen am Ein- und Austritt so folgt:

\begin{align}
\label{8183}
&V~p_1 + m~g~z_1 + \tfrac{1}{2}~m~c_1^2 = V~p_2 + m~g~z_2 + \tfrac{1}{2}~m~c_2^2 \\[5px]
\end{align}

Teilt man die Gleichung durch das Volumen V, so erhält man die sogenannte Bernoulli-Gleichung für Strömungsprozesse inkompressibler Medien:

\begin{align}
\label{4404}
&\boxed{p_1 + \rho~g~z_1 + \tfrac{1}{2}~\rho~c_1^2 = p_2 + \rho~g~z_2 + \tfrac{1}{2}~\rho~c_2^2} ~~~\text{Bernoulli-Gleichung} \\[5px]
&~~~\text{mit: } \rho = \frac{m}{V} \\[5px]
\end{align}