Unterschiedliche Formen des Planck’schen Strahlungsgesetzes

Das Planck’sche Strahlungsgesetz kann in unterschiedlichen Formen dargestellt werden. Auf die wichtigsten wird in diesem Artikel eingegangen.

Einleitung

Mithilfe des Planck’schen Strahlungsgesetzes lässt sich die von schwarzen Körper ausgesendete Strahlung mathematisch beschreiben. Dabei gibt es jedoch unterschiedliche Darstellungsformen, auf die im Folgenden näher eingegangen werden soll. Hauptsächlich sind diese Unterschiede auf die verschiedenen Größen zurückzuführen, die betrachtet werden: z.B. Intensität pro Wellenlänge oder die Intensität pro Raumwinkel oder die Energiedichte. Des weiteren können diese Größe entweder in Abhängigkeit der Wellenlänge der Strahlung oder der Frequenz betrachtet werden.

Verteilung der spektralen Intensität in Abhängigkeit der Wellenlänge

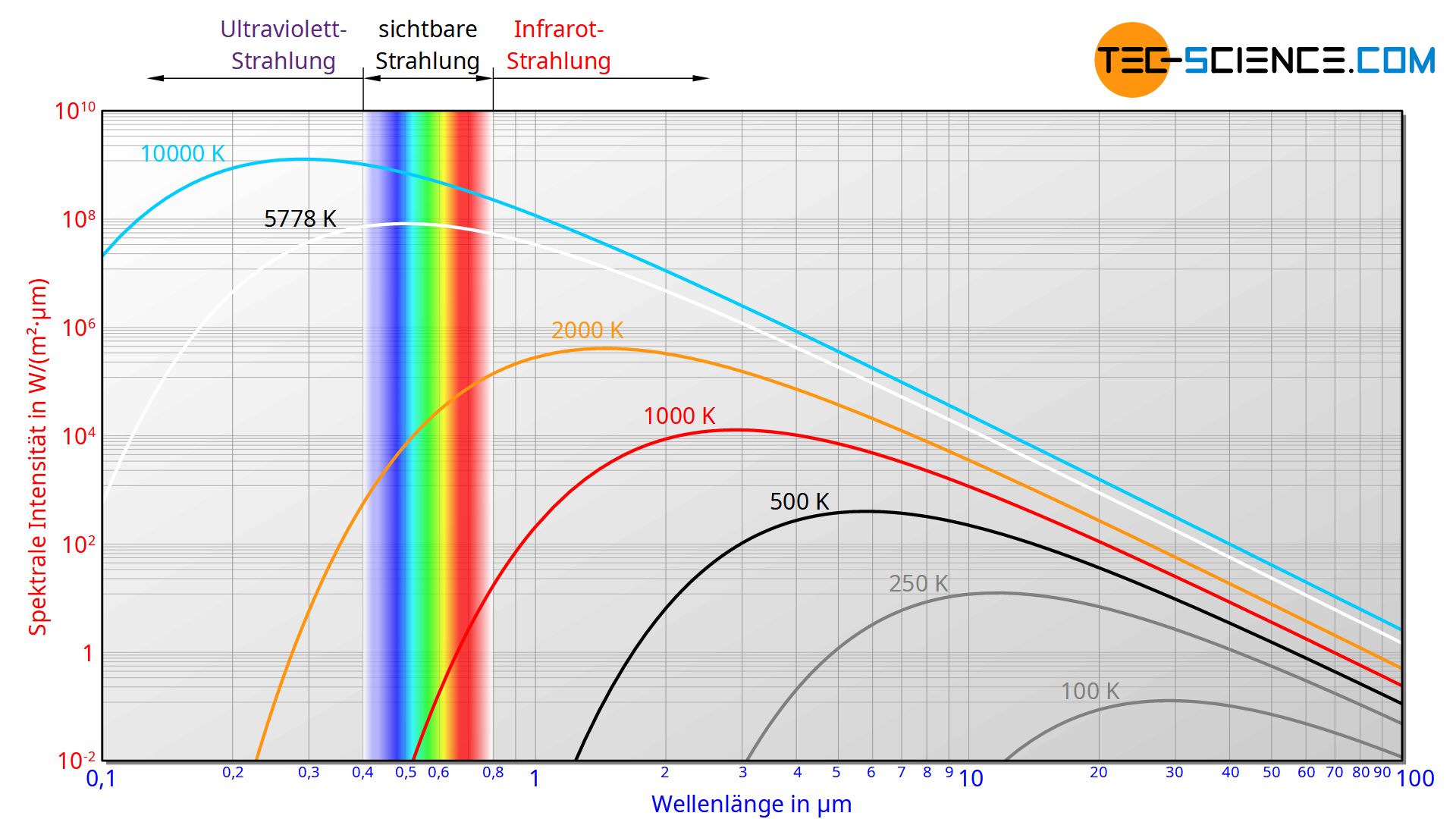
Die untere Abbildung zeigt die sogenannte spektrale Intensität der ausgesendeten Strahlung eines schwarzen Körpers in Abhängigkeit der Wellenlänge für verschiedene Temperaturen. Auf die mathematische Beschreibung dieser Kurven wurde bereits im Artikel zum Planck’sches Strahlungsgesetz etwas detaillierter eingegangen:

\begin{align}
\label{planck}
&\boxed{I_s(\lambda) = \frac{2\pi h c^2}{\lambda^5} \cdot \frac{1}{\exp\left(\dfrac{h c}{\lambda k_B T}\right)-1} } ~~~\text{spektrale Intensität (Wellenlängenform)} \\[5px]
\end{align}

In dieser Darstellungsform handelt es sich bei dem Begriff der Intensität um eine Flächenleistungsdichte. Die Intensität gibt somit die Strahlungsleistung des schwarzen Körpers an, die dieser pro Flächeneinheit aussendet. Am illustrativen Beispiel einer Glühbirne betrachtet, würde dies bedeuten, dass man für die Berechnung deren Intensität, die Strahlungsleistung durch die Oberfläche der Glühbirne teilt. Bei einer Strahlungsleistung von 50-Watt und einer Oberfläche von 100 cm² käme man so auf eine Strahlungsintensität der Glühbirnenoberfläche von 0,5 W/cm² („0,5 Watt pro Quadratzentimeter“).

Eine solche pauschale Angabe der Intensität lässt aber noch keine Aussage zu, ob in der ausgesendeten Strahlung eher kurzwellige oder eher langwellige Strahlungsanteile vorhanden sind. Auf das Beispiel der Glühbirne bezogen würde dies bedeuten, dass anhand der Intensität noch keine Aussage gemacht werden kann, ob die Glühbirne ihre Leistung eher im kurzwelligen Bereich abgibt und somit bläulich erscheint oder verstärkt im langwelligeren Bereich und damit rötlich leuchtet.

Um auch dies darstellen zu können, müsste man bei der experimentellen Untersuchung der Strahlung das gesamte Wellenlängenspektrum zunächst in viele kleine Intervalle aufteilen. Diese Wellenlängenbereiche müsste man nun jeweils getrennt voneinander auf ihre beinhaltende Leistung untersuchen. Mit Hilfe von Filtern könnte man solche Wellenlängenbereiche gezielt von anderen Wellenlängen abgrenzen und untersuchen. Die Intensität mit dem das betrachtete Wellenlängenintervall in der ausgesendeten Strahlung vorhanden ist würde man dann dadurch bestimmen, dass man die gemessene Leistung im betrachteten Wellenlängenbereich durch die Größe der Oberfläche des strahlenden Körpers teilt.

Die gemessene Leistung bzw. Intensität hängt in diesem Fall aber noch entscheidend von der Größe des zugelassenen Wellenlängenintervalls ab. Salopp formuliert bedeutet dies: Lässt man ein doppelt so großes Wellennlängenintervall zu, dann passieren auch doppelt so viele Wellenlängen den Filter und man misst folglich auch eine doppelte so hohe Leistung (zumindest wenn die Intervalle sehr klein gewählt werden). Deshalb bezieht man die gemessene Leistung bzw. die Intensität auf das gewählte Wellenlängenintervall selbst! Man erhält somit unabhängig von der Intervallbreite eine konstante Intensität, die dann als spektrale Intensität bezeichnet wird.

Diese spektrale Intensität wird schlussendlich in Abhängigkeit der Wellenlänge im Diagramm dargestellt. In dieser Darstellungsform entspricht dann die Fläche unter der Kurve der abgestrahlten Intensität im betrachteten Wellenlängenbereich.

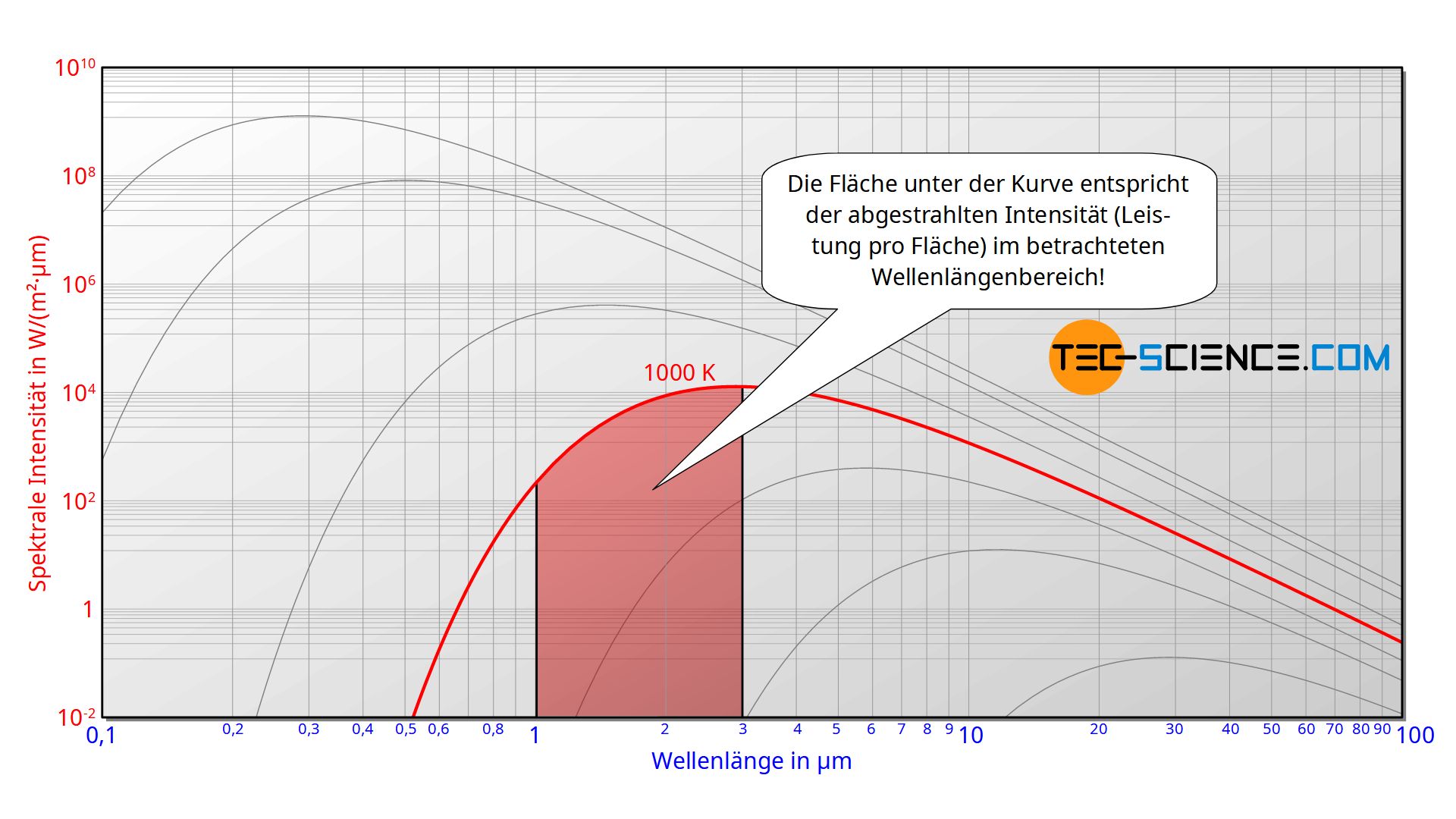
Um die Gesamtintensität I zu bestimmen mit der der schwarze Körper strahlt, muss die spektrale Intensität I(λ) folglich über das gesamte Wellenlängenspektrum von null bis unendlich integriert werden (Gesamtfläche unter der Kurve):

\begin{align}
&\boxed{I=\int \limits_{\lambda=0}^\infty I_s(\lambda) ~\text{d}\lambda } ~~~\text{Strahlungsintensität eines schwarzen Körpers} \\[5px]
\end{align}

Weiterhin bezieht sich die Intensität auf die Leistung pro Flächeneinheit. Die gesamte Strahlungsleistung des schwarzen Körpers P erhält man schließlich durch Integration der Intensität über die Körperoberfläche A. Mathematisch bedeutet dies die Integration der Intensität über die einzelnen Flächenelemente dA:

\begin{align}
&\boxed{P=\int\limits_{(A)} I ~\text{d}A = \int\limits_{(A)} \int \limits_{\lambda=0}^\infty I_s(\lambda) ~\text{d}\lambda ~\text{d}A} ~~~\text{Strahlungsleistung eines schwarzen Körpers} \\[5px]
\end{align}

Sendet der schwarze Körper gleichmäßig über seine Oberfläche verteilt Strahlung aus (isotroper schwarzer Körper), dann ist die Intensität in jedem Punkt der Oberfläche identisch. In diesem Fall ergibt sich die abgestrahlte Gesamtleistung ganz einfach aus dem Produkt von Intensität I und Oberfläche A:

\begin{align}
&\boxed{P=I \cdot A} ~~~\text{Strahlungsleistung eines isotropen schwarzen Körpers} \\[5px]
\end{align}

Die Lösung der oben genannten Integrale führt schließlich Stefan-Boltzmann Gesetz, welches die Strahlungsleistung eines Körpers in Abhängigkeit seiner Temperatur wiedergibt. Im verlinkten Artikel finden Sie speziell zu diesem Thema mehr Informationen.

Verteilung der spektralen Intensität in Abhängigkeit der Frequenz

Da Wellenlänge λ und Frequenz f über die Ausbreitungsgeschwindigkeit c in Zusammenhang stehen (λ=c/f), kann die spektrale Intensität auch in Abhängigkeit der Frequenz ausgedrückt werden. Dabei darf allerdings die Wellenlänge λ nicht einfach nur durch den Ausdruck c/f ersetzt werden. Dies hat damit zu tun, dass es sich bei der spektralen Intensität um eine auf die Wellenlänge bezogene Größe handelt. Man muss also auch die Wellenlängenintervalle dλ in entsprechende Frequenzintervalle df umrechnen!

Wirklich vergleichbar sind nur die abgestrahlten Intensitäten, nicht aber die spektralen Intensitäten. Die abgegebene Intensität dI(λ) in einem Wellenlängenbereich zwischen λ und λ+dλ ergibt sich durch Multiplikation der spektralen Intensität dI(λ) mit dem Wellenlängenintervall dλ („Fläche unter der Kurve“):

\begin{align}
\label{c}
&\text{d} I(\lambda) =I_s(\lambda) \cdot \text{d}\lambda= \frac{2\pi h c^2}{\lambda^5} \cdot \frac{1}{\exp\left(\dfrac{h c}{\lambda k_B T}\right)-1} \cdot \text{d}\lambda \\[5px]
\end{align}

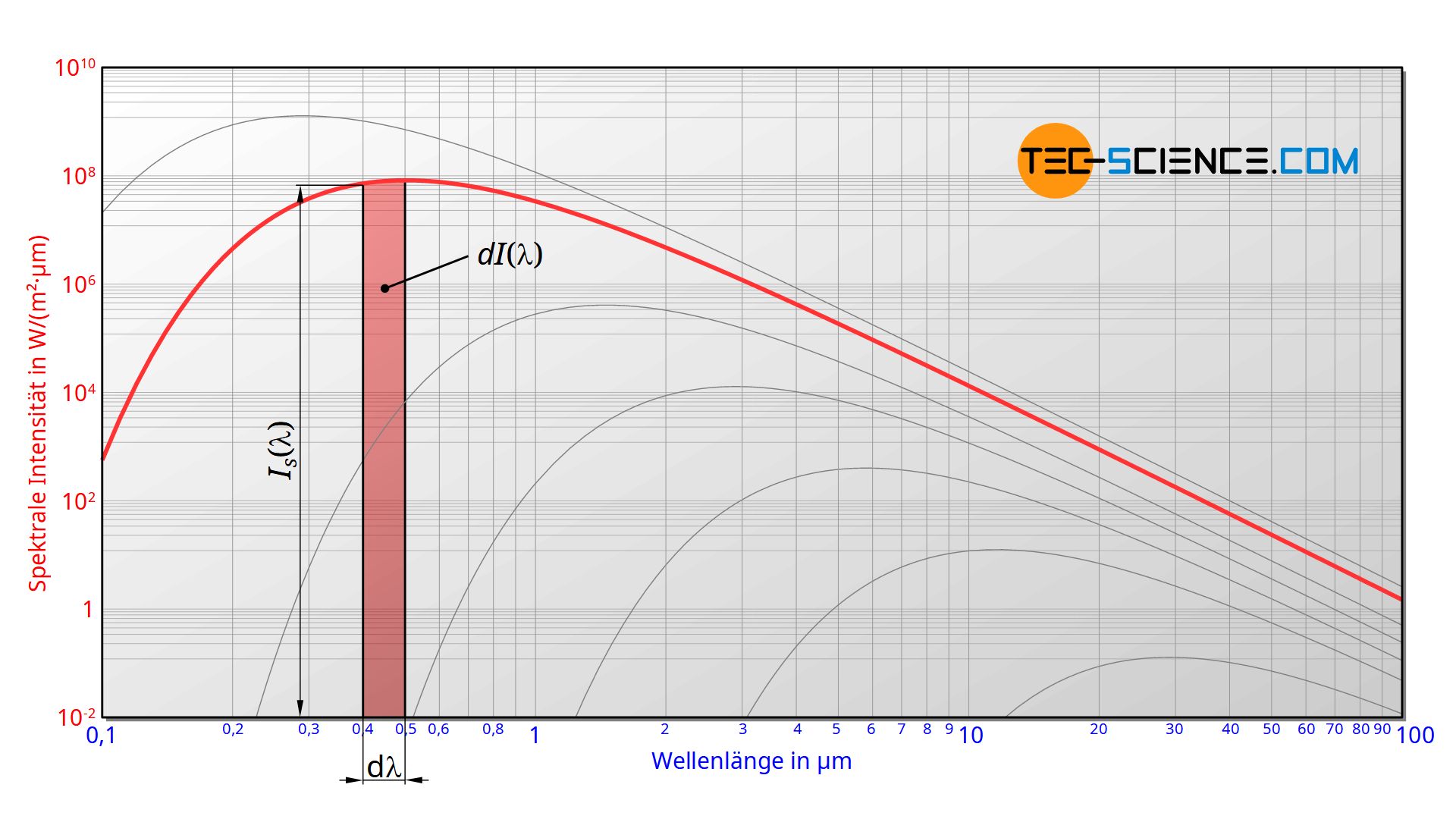
Dem Wellenlängenintervall dλ muss man also ein entsprechendes Frequenzintervall df zuordnen. Dies gescheit über die Ableitung der Funktion f=c/λ nach der Variablen λ:

\begin{align}
\label{a}
&\boxed{f = \frac{c}{\lambda}} ~~~\text{bzw.}~~~\boxed{\color{red}{\lambda=\frac{c}{f}}}\\[5px]
&\frac{\text{d}f}{\text{d}\lambda} = \frac{c}{-\lambda^2} \\[5px]
\label{z}
&\text{d}\lambda = – \frac{\lambda^2}{c} \cdot \text{d}f \\[5px]
\end{align}

Das negative Vorzeichen in Gleichung (\ref{z}) drückt lediglich aus, dass eine Erhöhung der Frequenz um df>0, eine Verringerung der Wellenlänge um dλ<0 zur Folge hat. An dieser Stelle sind allerdings nur die Beträge der Intervalle relevant, sodass auf das negative Vorzeichen verzichtet werden kann. Unter Berücksichtigung von Gleichung (\ref{a}) gilt somit:

\begin{align}
&\text{d}\lambda = \frac{\lambda^2}{c} \cdot \text{d}f = \frac{\left( \color{red}{\frac{c}{f}}\right)^2}{c} \cdot \text{d}f = \frac{c}{f^2} \cdot \text{d}f \\[5px]
\label{b}
&\boxed{\color{blue}{\text{d}\lambda = \frac{c}{f^2} \cdot \text{d}f}} \\[5px]
\end{align}

Werden nun die Gleichungen (\ref{a}) und (\ref{b}) in Gleichung (\ref{c}) eingesetzt, dann folgt für die spektrale Intensität I_s(f) in der Frequenzdarstellung folgender Zusammenhang:

\begin{align}
\text{d} I(f) &= \frac{2\pi h c^2}{\color{red}{\left(\frac{c}{f}\right)}^5} \cdot \frac{1}{\exp\left(\dfrac{h c}{\color{red}{\frac{c}{f}} k_B T}\right)-1} \cdot \color{blue}{\frac{c}{f^2} \cdot \text{d}f} \\[5px]
&= \frac{2\pi h c^2 f^5}{c^5} \cdot \frac{1}{\exp\left(\dfrac{h f}{ k_B T}\right)-1} \cdot \color{blue}{\frac{c}{f^2} \cdot \text{d}f} \\[5px]
&= \underbrace{\frac{2\pi h f^3}{c^2} \cdot \frac{1}{\exp\left(\dfrac{h f}{ k_B T}\right)-1}}_{I_s(f)} \cdot \text{d}f \\[5px]
\label{freq}
&\boxed{I_s(f) = \frac{2\pi h f^3}{c^2} \cdot \frac{1}{\exp\left(\dfrac{h f}{k_B T}\right)-1} } \\[5px]
\end{align}

Für die Umrechnung von der Wellenlängenform in die Frequenzform der spektralen Verteilung gilt also:

\begin{align}
&\boxed{I_s(f) =\frac{\lambda^2}{c} \cdot I_s(\lambda)} \\[5px]
\end{align}

Beachte also, dass bei der spektralen Intensität nicht mehr einfach nur die Wellenlänge gemäß der Formel f=c/λ in eine Frequenz umgerechnet werden darf. Dies liegt daran, dass Wellenlänge und Frequenz sich reziprok zueinander verhalten. Beiden Größen liegen somit unterschiedliche Intervallbreiten zugrunde! Beim Wien’schen Verschiebungsgesetz spielt dies ebenfalls eine Rolle.

Verteilung der spezifischen spektralen Intensität

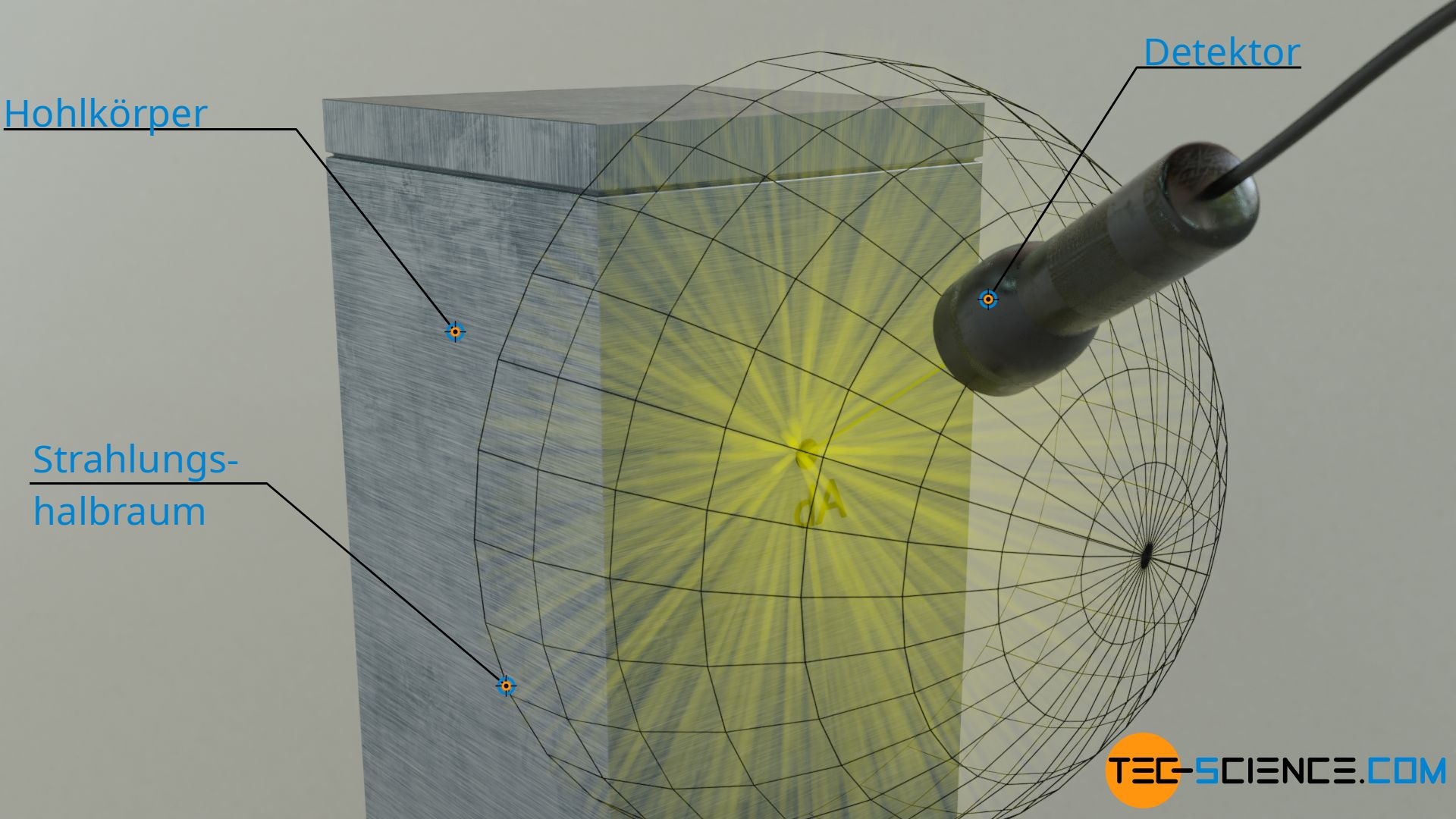
Um die abgestrahlte spektrale Intensität eines Flächenelementes in einem Experiment zu ermitteln, müsste man die gesamte emittierte Strahlung innerhalb des betrachteten Wellenlängenintervalls mit einem Detektor erfassen. Im Artikel Schwarzkörperstrahlung wurde auf die Realisierung eines schwarzen Körpers mithilfe eines Lochs, das in einen Hohlraum führt bereits ausführlich eingegangen (Hohlraumstrahler). In diesem Fall entspräche das zu untersuchende Flächenelement der Fläche des Lochs, welches auftreffende Strahlung vollständig absorbiert und hierdurch selbst Schwarzkörperstrahlung aussendet. Die Strahlung breitet sich dabei kugelförmig in den freien Halbraum hinein aus (siehe Abbildung unten).

Einfluss auf die gemessene Strahlungsleistung: Die „Blickrichtung“

Für die Messung der emittierten Strahlungsleistung genügt es nun allerdings nicht, den Detektor irgendwo einer fixen Stelle zu platzieren, wo nur ein Teil der Strahlung erfasst wird. Man muss die Strahlung über den Halbraum erfassen, um auch tatsächlich die gesamte Strahlungsleistung zu messen. Die Strahlungsleistung des Flächenelementes (hier: Fläche der Öffnung) ist nämlich nicht in alle Richtungen gleich groß ist! Man kann also nicht davon ausgehen, dass die an einer Stelle mit dem Detektor gemessene Leistung an einer anderen Stelle genauso groß ist.

Dass die Strahlungsleistung eines (ebenen) Flächenelementes richtungsabhängig ist, zeigt auch bereits die alltägliche Erfahrung. Man stelle sich hierzu eine große glühende Metallplatte vor. Schaut man frontal auf diese Platte, so wird man eine relativ starke Wärmestrahlung wahrnehmen (diese Wärmestrahlung ist im Übrigen Teil der Schwarzkörperstrahlung!). Die Strahlungsleistung ist mit frontaler Blickrichtung somit relativ hoch. Betrachtet man die glühende Platte allerdings von der Seite, so erscheint die Wärmestrahlung weniger intensiv. Die Strahlungsleistung ist entsprechend geringer. Dies lässt sich damit erklären, dass die Platte von der Seite betrachtet auch deutlich kleiner erscheint und somit weniger effektive Strahlungsfläche besitzt. Offensichtlich hat also die in Blickrichtung erscheinende Fläche, die sogenannte projizierte Fläche, Einfluss auf die wahrgenommene bzw. gemessene Strahlungsleistung.

Man kann sich die projizierte Fläche anschaulich verdeutlichen, indem man sich den Detektor als „Taschenlampe“ vorstellt. Den Schatten, den das angestrahlten Flächenelement dann auf einen dahinter aufgestellten Schirm erzeugt, entspricht der projizierten Fläche.

Einfluss auf die gemessene Strahlungsleistung: Der Raumwinkel

Zum einen ist also die „Blickrichtung“ des Detektors für die gemessene Strahlungsleistung relevant und zum anderen natürlich welche Fläche der Detektor von der gesamten Strahlungshalbkugel einnimmt (sein „Sichtfeld“ sozusagen). Letztere wird durch den sogenannten Raumwinkel ausgedrückt. Ein Raumwinkel Ω gibt ganz allgemein das Verhältnis einer Fläche auf einer Kugel A zum Quadrat des Radius der Kugel r² an:

\begin{align}
\label{r}
&\boxed{\Omega =\frac{A}{r^2}} ~~~\text{Raumwinkel} \\[5px]
\end{align}

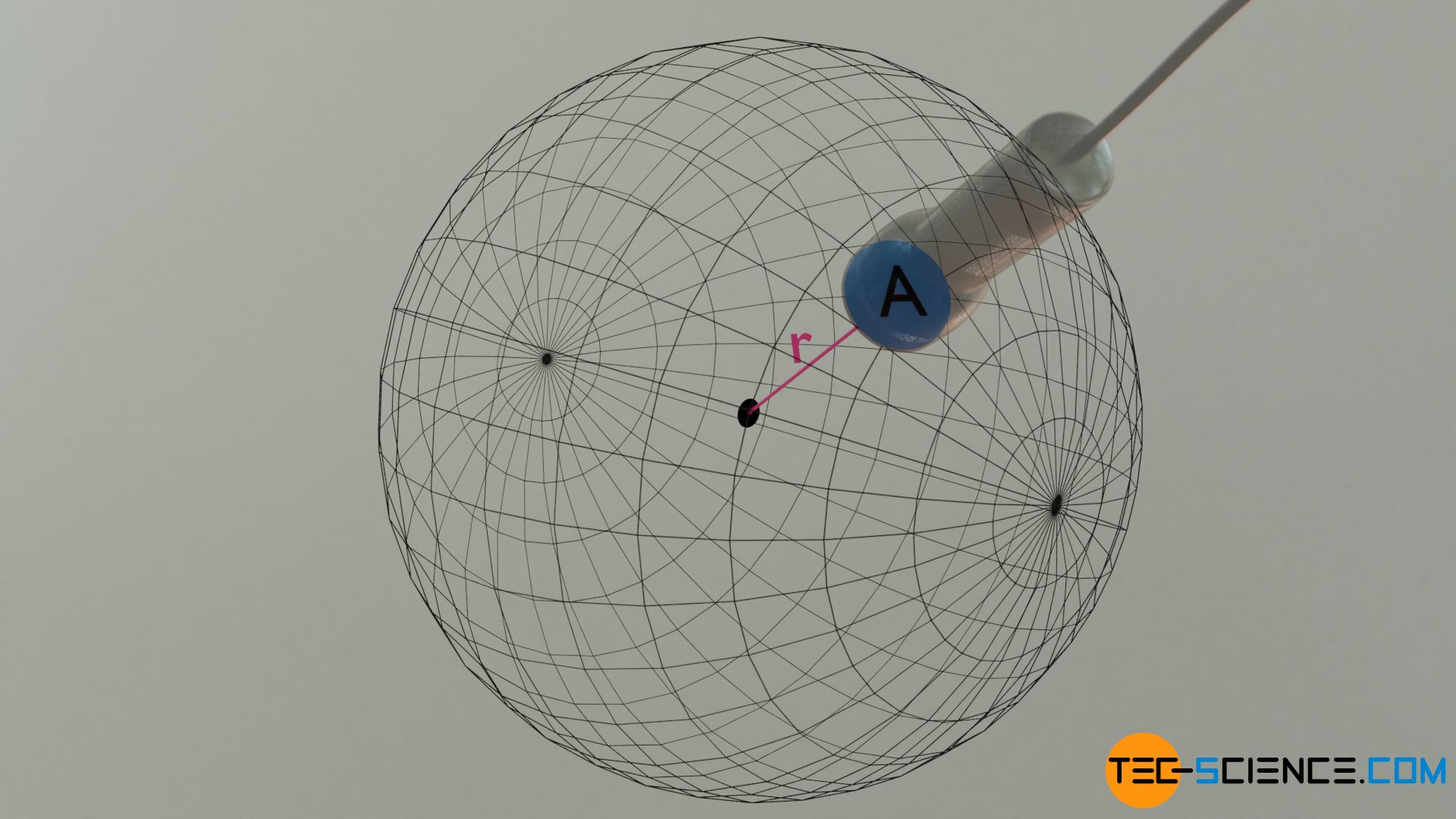
Man kann den Raumwinkel analog zum Bogenwinkel („Bogenmaß“) auffassen. Im zweidimensionalen Raum gibt das Bogenmaß das Verhältnis von Bogenabschnitt zum Radius des Kreises an. Im dreidimensionalen Raum gibt der Raumwinkel das Verhältnis von Kugelabschnitt zum Radiusquadrat der Kugel an.

Umfasst der betrachtete Kugelabschnitt die gesamte Kugeloberfläche mit 4π⋅r², so erhält man folglich einen Raumwinkel von 4π. Der Winkel nimmt sozusagen den gesamten Raum der Kugeln ein. Umfasst die Fläche nur die Hälfte der Kugeloberfläche, dann beträgt der Raumwinkel 2π. Bei diesem Raumwinkel würde der Detektor gerade den gesamten Halbraum umfassen und die gesamte Strahlungsleistung des Flächenelements detektieren. Der Detektor müsste hierzu auch halbkugelförmig gebaut sein.

Beachte: Solange eine betrachtete Fläche Teil einer Kugeloberfläche ist, lässt sich für jede beliebig geformte Fläche gemäß Gleichung (\ref{r}) einen Raumwinkel angeben. Der Umriss der Fläche muss also nicht zwangsläufig einen Kreis bilden wie häufig suggeriert, damit man einen Raumwinkel angeben kann! In anderen Worten: Unser Detektor benötigt keinen kreisförmigen Sensor, er kann auch rechteckig oder sonstig beliebig geformt sein. Er muss lediglich Teil einer Kugeloberfläche sein. Für große Radien und kleine Flächenabschnitte ist die Krümmung der Fläche allerdings so gering, dass man in sehr guter Näherung auch ebene Flächen verwenden kann.

Spektrale Intensität pro Raumwinkel

Untersucht man nun für den oben beschriebenen Fall die emittierte Strahlungsleistung des Hohlraumstrahlers mit einem Detektor, dann stellt man zwei Dinge fest:

1. die gemessene Strahlungsleistung dP ist proportional zur projizierten Fläche in die der Detektor zeigt dA_p),
2. die gemessene Strahlungsleistung dP ist proportional zum Raumwinkel dΩ den der Detektor umfasst (solange kleine Raumwinkel betrachtet werden).

Punkt (1) wurde bereits anschaulich erläutert: Je größer nämlich die Strahlungsfläche ist, die dem Detektor zugewandt ist, desto größer die Leistung. Punkt (2) lässt sich ebenfalls anschaulich nachvollziehen. Stellt man zwei sehr kleine Detektoren direkt nebeneinander auf, dann registrieren beide dieselbe Leistung. Nimmt man beide Detektoren in Gedanken zusammen, die dann den doppelten Raumwinkel einnehmen, dann erhält man auch offensichtlich die doppelte Leistung. Dies gilt strenggenommen nur solange die beiden Raumwinkel sehr klein und dicht beieinander sind, sodass sie sich in der Blickrichtung (fast) nicht unterscheiden. Ansonsten erhielte man gemäß Punkt (1) leicht unterschiedliche Leistungen der beiden Detektoren.

Weiterhin ist natürlich die gemessene Strahlungsleistung von der Größe des Wellenlängenintervalls dλ abhängig, welches der Filter des Detektors passieren lässt. Ein doppelt so großes Wellenlängenintervall bedeutet, dass doppelt so viel Strahlung durch den Filter gelangt. Die gemessene Leistung ist somit doppelt so groß. Diese Proportionalität zwischen Leistung und Wellenlängenintervall gilt nur für sehr kleine Wellenlängenintervalle. Für einen gegeben Wellenlängenbereich zwischen λ und λ+dλ lassen sich die genannten Zusammenhänge mathematisch somit wie folgt darstellen:

\begin{align}
& \text{d}P \sim \text{d}\Omega \cdot \text{d}A_p \cdot \text{d}\lambda \\[5px]
\label{p}
&\frac{ \text{d}P}{\text{d}\Omega \cdot \text{d}A_p \cdot \text{d}\lambda} =\text{konstant} = B_s \\[5px]
\end{align}

Bezieht man also die Strahlungsleistung eines schwarzen Körpers nicht mehr nur auf das Wellenlängenintervall und auf ein bloßes Flächenelement wie bei der spektralen Intensität I_s, sondern neben dem Wellenlängenbereich dλ auf den Raumwinkel dΩ und auf die in „Blickrichtung des Raumwinkels“ projizierte Fläche dA_p dann erhält man für den betrachteten Wellenlängenbereich ebenfalls eine konstante Größe. Diese Größe wird spezifische spektrale Intensität B_s genannt. Die spezifische spektrale Intensität gibt also die ausgesendete Strahlungsleistung pro Einheit Wellenlängenintervall und pro Raumwinkeleinheit sowie pro Flächeneinheit wieder (wobei mit Fläche die projizierte Fläche in Richtung des betrachteten Raumwinkels gemeint ist!).

Als spezifische spektrale Intensität bezeichnet man die Strahlungsleistung eines in Blickrichtung projizierten Flächenelementes pro Raumwinkeleinheit und pro Einheit Wellenlängenintervall!

Auf unser Beispiel übertragen bedeutet dies: Egal in welchem Abstand und unter welcher Blickrichtung der Detektor auf das Flächenelement des schwarzen Körpers blickt, man misst für einen bestimmten Wellenlängenbereich überall dieselbe Größe B_s. Man kann die Strahlung eines schwarzen Körpers somit eben auch durch genau diese Größe B_s charakterisieren. Diese Größe hat in der Praxis den Vorteil, dass man nicht die gesamte emittierte Strahlung eines Flächenelementes zur Charakterisierung der Schwarzkörperstrahlung benötigt, wie dies bei der spektralen Intensität der Fall ist. Bei der spezifischen spektralen Intensität muss nämlich nur nur einen Teil der Strahlung innerhalb eines bestimmten Raumwinkels betrachtet werden.

Für die spezifische spektrale Intensität B_s gilt folgende Formel in Abhängigkeit der Wellenlänge bzw. der Frequenz:

\begin{align}
\label{bs}
&\boxed{B_s(\lambda) = \frac{2 h c^2}{\lambda^5} \cdot \frac{1}{\exp\left(\dfrac{h c}{\lambda k_B T}\right)-1} } ~~~\text{Wellenlängenform} \\[5px]
\end{align}

\begin{align}
&\boxed{B_s(f) = \frac{2 h f^3}{c^2} \cdot \frac{1}{\exp\left(\dfrac{h f}{k_B T}\right)-1} } ~~~\text{Frequenzform} \\[5px]
\end{align}

Zusammenhang zwischen spektraler Intensität und spezifischer spektraler Intensität

Betrachtet man die Formeln (\ref{planck}) und (\ref{bs}), so unterscheiden diese sich offensichtlich nur um den Faktor π. Wie es zu diesem Zusammenhang kommt, soll im Folgenden erklärt werden. Zunächst sei nochmals darauf verwiesen, dass die spezifische spektrale Intensität B_s die Strahlungsintensität pro Raumwinkel angibt, während die spektrale Intensität I_s die gesamte abgestrahlte Intensität eines Flächenelementes umfasst. Da ein (infinitesimales) Flächenelement kugelförmig in den Halbraum abstrahlt, muss zur Berechnung der spektralen Intensität I_s die spezifische spektrale Intensität B_s sozusagen über den gesamten Halbraum aufsummiert werden. Für den kugelförmigen Halbraum beträgt der Raumwinkel 2π. Sollten sich demnach nicht beide Größen um 2π unterscheiden anstatt nur um π?

Beim Aufsummieren über den Halbraum muss beachtet werden, dass sich die spezifische spektrale Intensität nicht auf die volle Fläche des Flächenelementes bezieht, sondern immer nur auf die projizierte Fläche. Beide Flächen sind aber nur für einen speziellen Fall identisch, nämlich dann, wenn frontal auf das Flächenelement geschaut wird. Ansonsten ist die projizierte Fläche stets kleiner. Im Mittel über alle Raumwinkel hinweg ist die projizierte Fläche um die Hälfte kleiner als die Fläche an sich. Dies macht im Ergebnis dann eben nicht 2π, sondern nur π. Im Folgenden soll dies auch mathematisch gezeigt werden.

Mathematisch entspricht das Aufsummieren der Integration der spezifischen spektralen Intensität über die Strahlungs-Halbkugel:

\begin{align}
\text{d}P &= \text{d}P \\[5px]
I_s \cdot \text{d}A \cdot \text{d}\lambda &= \int\limits_{(A)} B_s \cdot \text{d}A_p \cdot \text{d}\Omega \cdot \text{d}\lambda \\[5px]
\label{l}
I_s \cdot \text{d}A &= \int\limits_{(A)} B_s \cdot \text{d}A_p \cdot \text{d}\Omega \\[5px]
\end{align}

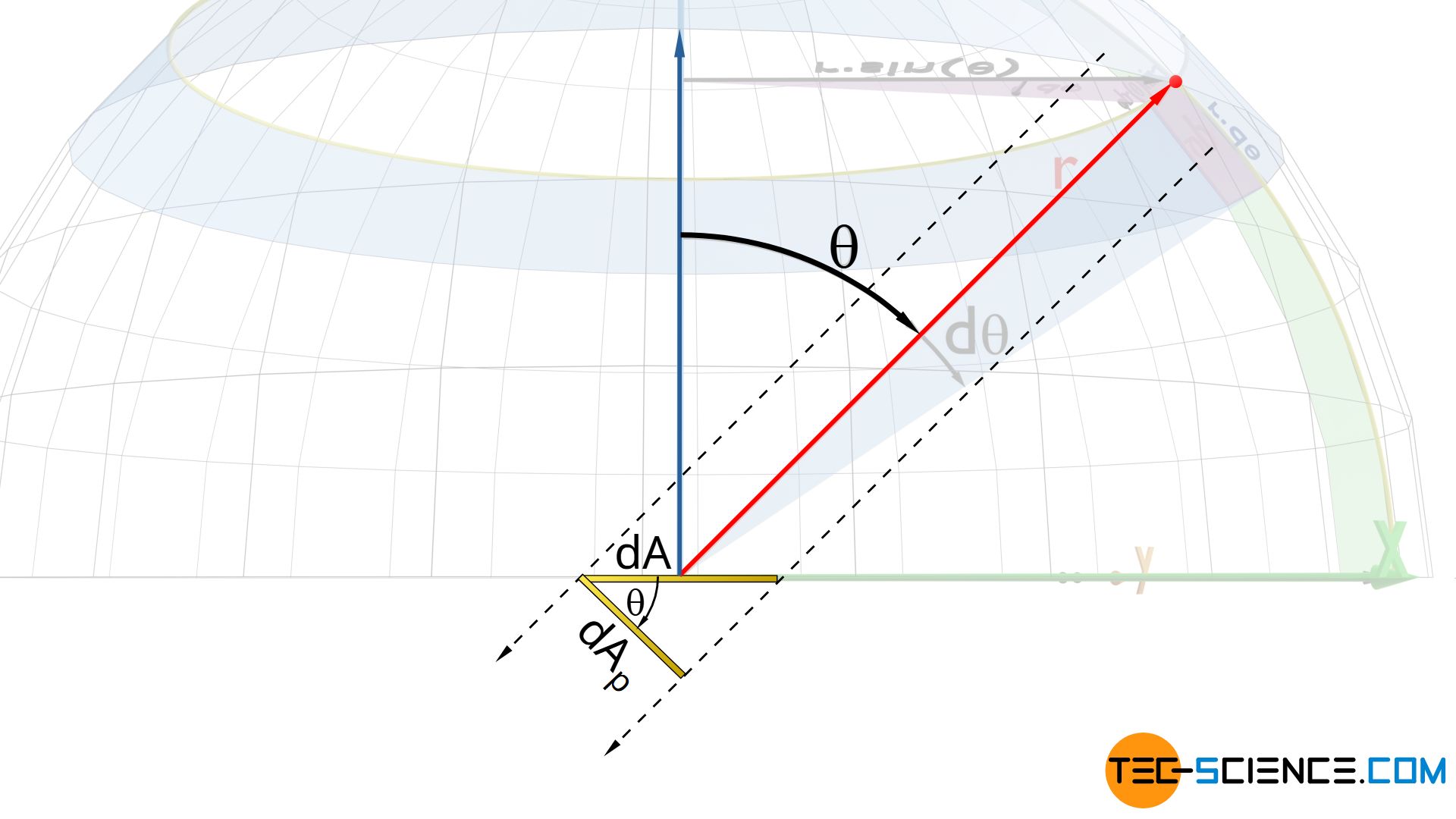
Zunächst muss man einem Raumwinkel dΩ eine entsprechende Richtung zuweisen, damit auch die projizierte Fläche dA_p in diese Richtung ermittelt werden kann. Hierzu beschreibt man die für den Raumwinkel benötigte Fläche dσ am besten durch Kugelkoordinaten. Ein Punkt auf der Oberfläche einer Kugel ist in Kugelkoordinaten durch die Angabe zweier Winkel vollständig definiert. Darin beschreibt der Winkel φ den Winkel in der x-y-Ebene und der Winkel θ den Winkel zur z-Achse.

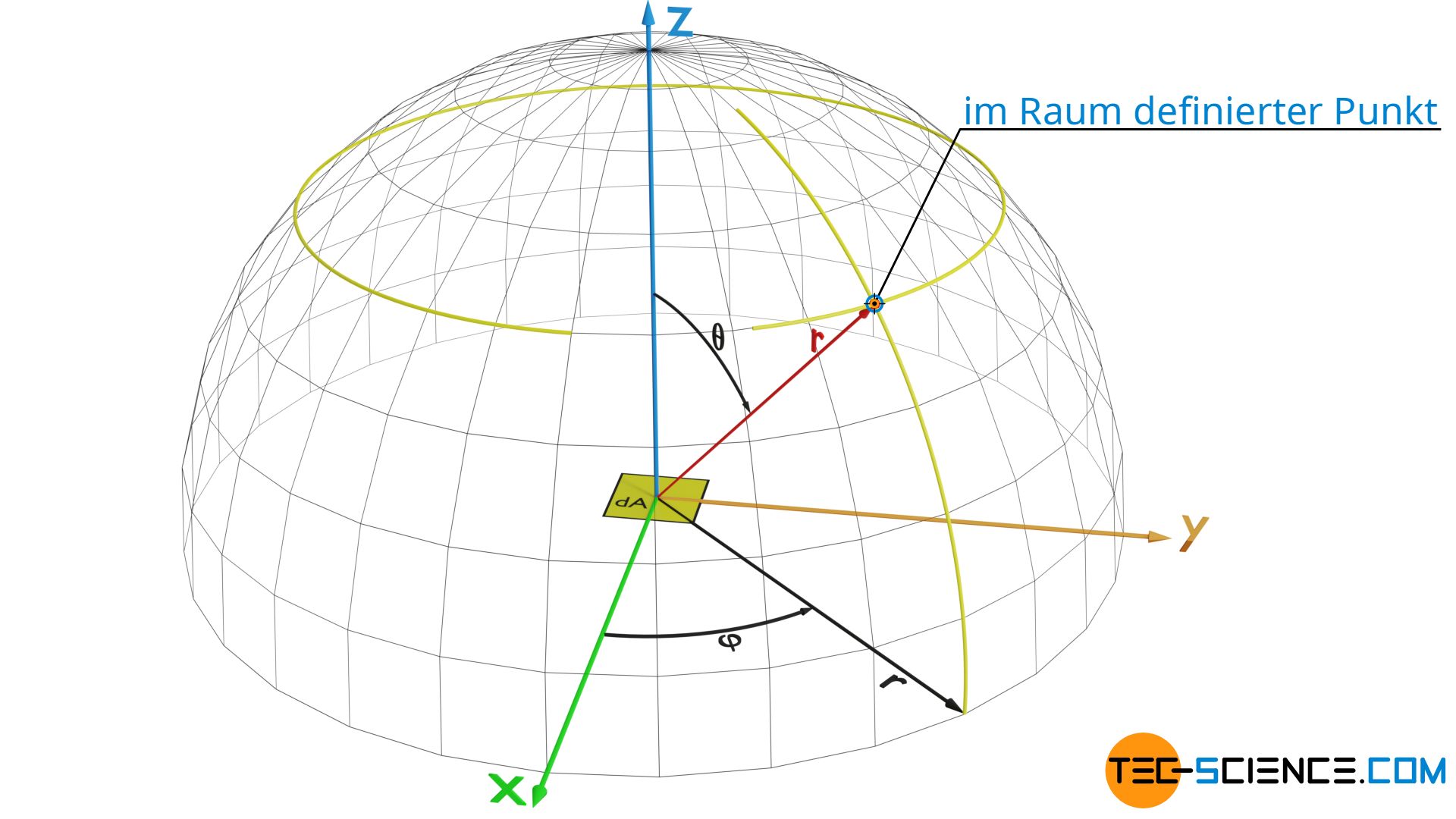
Lässt man nun beide Winkel innerhalb eines Bereichs dφ bzw. dθ variieren, so ergibt sich ein Flächenelement dσ. Der Flächeninhalt dieses Elementes lässt sich anhand geometrischer Überlegungen wie folgt bestimmen:

\begin{align}
& \text{d}\sigma = r^2 \cdot \sin(\theta) ~ \text{d}\theta \cdot \text{d}\varphi \ \\[5px]
\end{align}

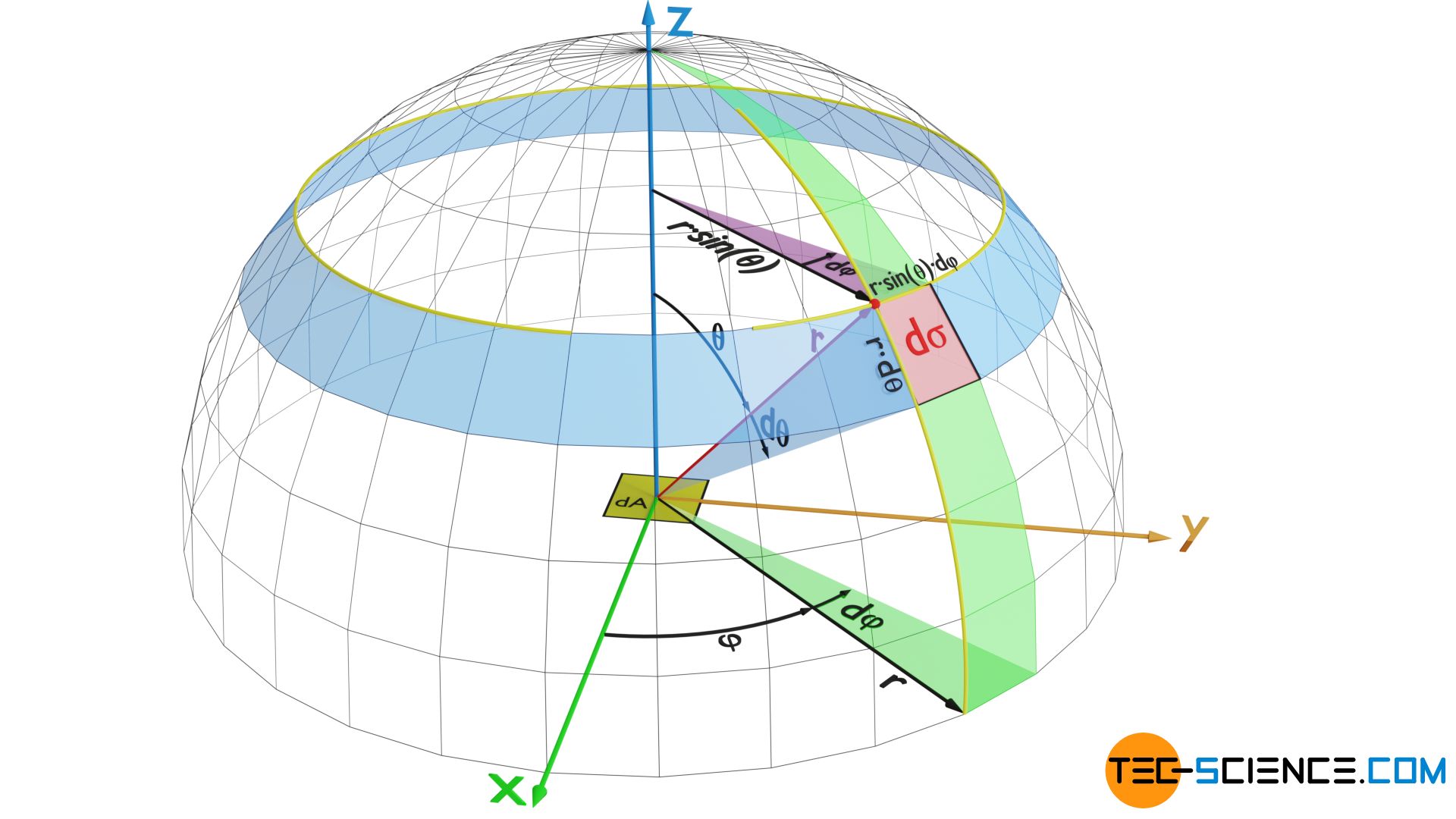
Gemäß der Definition des Raumwinkels dΩ als Verhältnis der Fläche dσ zum Quadrat des Radius r² gilt also:

\begin{align}
\label{x}
& \text{d}\Omega = \frac{\text{d}\sigma}{r^2}= \sin(\theta) ~ \text{d}\theta \cdot \text{d}\varphi \ \\[5px]
\end{align}

Die in Richtung des Ortsvektors projizierte Fläche dA_p ergibt sich über den Kosinus des Winkels θ:

\begin{align}
\label{y}
& \text{d}A_p = \text{d}A \cdot \cos(\theta) \ \\[5px]
\end{align}

Werden die Gleichungen (\ref{x}) und (\ref{y}) in Gleichung (\ref{l}) eingesetzt, dann zeigt sich folgender Zusammenhang:

\begin{align}
\require{cancel}
I_s \cdot \text{d}A &= \int \limits_{(A)} B_s \cdot \text{d}A_p \cdot \text{d}\Omega \\[5px]
I_s \cdot \bcancel{\text{d}A} &= \int \limits_{(A)} B_s \cdot \bcancel{\text{d}A} \cdot \underbrace{\cos(\theta) \cdot \sin(\theta)}_{=\tfrac{1}{2}\cdot \sin(2\theta)} ~ \text{d}\theta \cdot \text{d}\varphi \\[5px]
I_s &= B_s \cdot \tfrac{1}{2} \int \limits_{(A)} \sin(2\theta) ~ \text{d}\theta \cdot \text{d}\varphi \\[5px]
\end{align}

Beachte, dass wie bereits erläutert B_s überall auf der Kugeloberfläche konstant ist und somit bei der Integration über die Halbkugeloberfläche als Konstante zu betrachten ist. Diese konstante Größe kann deshalb vor das Integral geschrieben werden. Nun muss nur noch über die Halbkugel integriert werden, d.h. innerhalb der Grenzen von φ=0…2π und θ=0…π/2:

\begin{align}
I_s &= B_s \cdot \tfrac{1}{2} \int \limits_{\varphi=0}^{2\pi} \int \limits_{\theta=0}^{\tfrac{\pi}{2}} \sin(2\theta) ~ \text{d}\theta \cdot \text{d}\varphi \\[5px]
&= B_s \cdot \tfrac{1}{2} \int \limits_{\varphi=0}^{2\pi} \underbrace{\left[ -\frac{1}{2} \cos(2\theta) \right]_{\theta=0}^{\tfrac{\pi}{2}}}_{=1} \text{d}\varphi \\[5px]
&= B_s \cdot \tfrac{1}{2} \cdot \int \limits_{\varphi=0}^{2\pi} \text{d}\varphi \\[5px]
&= B_s\cdot \tfrac{1}{2} \cdot \left[\varphi \right]_{\varphi=0}^{2\pi} \\[5px]
&= B_s\cdot \tfrac{1}{2} \cdot 2\pi \\[5px]
&= B_s \cdot \pi \\[5px]
\end{align}

Spektrale Intensität I_s und spezifische spektrale Intensität B_s unterscheiden sich also formal nur um den Faktor π. Dies gilt sowohl für die Wellenlängendarstellung als auch für die Frequenzdarstellung:

\begin{align}
\label{gg}
\boxed{I_s = B_s \cdot \pi} \\[5px]
\end{align}

Verteilung der spektralen Energiedichte einer Hohlraumstrahlung

Mithilfe der spezifischen spektralen Intensität lässt auch auf die sogenannte spektrale Energiedichte u_s einer Hohlraumstrahlung schließen. Hierunter versteht man die pro Einheit Wellenlängenintervall im Volumen des Hohlraums enthaltene Strahlungsenergie.

Hierzu betrachten wir wieder einen hohlen Gegenstand mit einem winzigen Loch. Alle Strahlung, die durch die Öffnung einfällt wird bei jeder Reflexion an den Innenwänden absorbiert, bis nach wenigen Reflexionen die gesamte Strahlung absorbiert ist. Das Loch ist definitionsgemäß als schwarzer Körper zu betrachten, dass alle einfallende Strahlung absorbiert. Je nach Temperatur des Hohlraums strahlen die Innenwände aber selbst Strahlung ab. Im thermodynamischen Gleichgewicht absorbieren die Wände genauso viel Strahlungsenergie wie sie emittieren, sodass weder eine weitere Aufheizung noch Abkühlung des Hohlraums bzw. des Körpers erfolgt.

Im Inneren des Hohlraums bildet sich somit eine Art Gas aus Photonen (die Herleitung des Stefan-Boltzmann-Gesetzes basiert genau auf dieser Vorstellung des Photonengases). Die Strahlungsenergie bzw. Energiedichte, die in einem solchen Hohlraum vorhanden ist, lässt sich anhand der austretenden Schwarzkörperstrahlung durch das Loch ermitteln.

Hierzu betrachten wir ein Flächenelement dA in der Öffnung zum Hohlraum. Das Flächenelement ist somit Teil des Photonengases. Wie bei Gasen üblich, so bewegen sich auch die Photonen im Photonengas in unterschiedliche Richtungen. Die Strahlung tritt somit zur Hälfte nach außen in den freien Raum, wo sie detektiert werden kann. Die andere Hälfte der Photonen bewegt sich wieder in Hohlraum hinein.

Unter einem beliebigen Raumwinkel dΩ tritt von der entsprechend projizierten Fläche dA_p Strahlung aus. Die sich mit Lichtgeschwindigkeit c bewegenden Photonen legen dabei innerhalb der Zeit dt die Strecke dl zurück:

\begin{align}
&\text{d}l = c \cdot \text{d}t \\[5px]
\end{align}

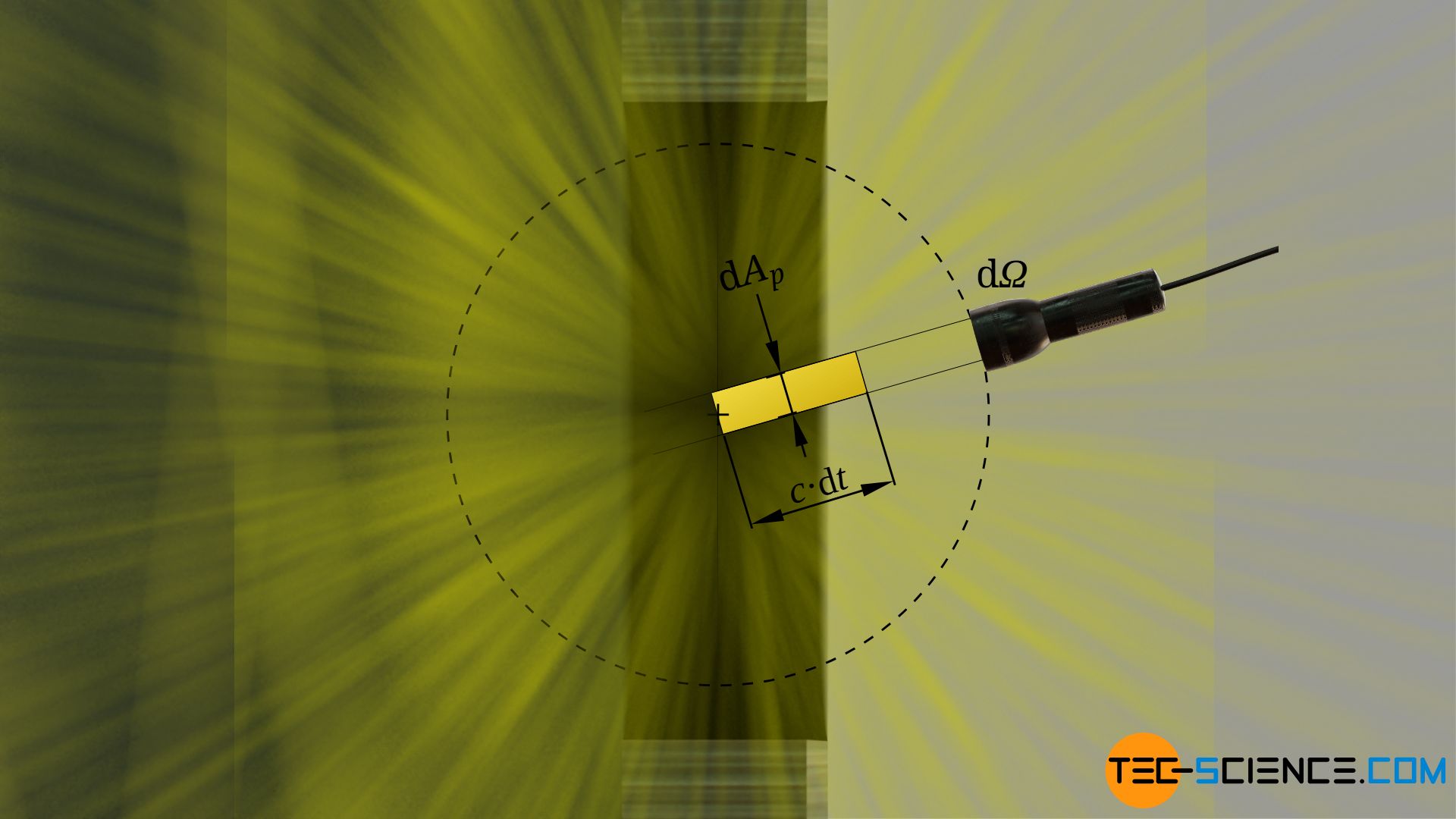
Die Photonen nehmen innerhalb der Zeit dt somit das folgende Raumvolumen dV ein:

\begin{align}
&\text{d}V = \text{d}A_p \cdot \text{d}l = \text{d}A_p \cdot c \cdot \text{d}t \\[5px]
\end{align}

Die Strahlungsenergie dU im Wellenlängenbereich dλ, die sich in der ausgesendeten Strahlung befindet, lässt sich über die spezifische spektrale Intensität B_s und die Zeitdauer dt ermitteln [vgl. Gleichung (\ref{p})].

\begin{align}
\require{cancel}
&\text{d}U = \overbrace{B_s \cdot \text{d}A_p \cdot \text{d}\lambda \cdot \text{d}\Omega}^{\text{d}P} \cdot \text{d}t \\[5px]
\end{align}

Für die Energiedichte u als Verhältnis von Energie dU und Volumen dV gilt somit:

\begin{align}
\require{cancel}
&u = \frac{\text{d}U}{\text{d}V} = \frac{B_s \cdot \cancel{\text{d}A_p} \cdot \text{d}\lambda \cdot \text{d}\Omega \cdot \cancel{\text{d}t}}{ \cancel{\text{d}A_p} \cdot c \cdot \cancel{\text{d}t} } \\[5px]
&u = \frac{\text{d}U}{\text{d}V} = \frac{B_s \cdot \text{d}\lambda \cdot \text{d}\Omega}{c} \\[5px]
\end{align}

Die Energiedichte hängt in dieser Form noch vom Wellenlängenintervall und vom Raumwinkel ab. Deshalb wird die Energiedichte meist als spektrale Energiedichte u_s angegeben, d.h. als Energiedichte pro Einheit Wellenlängenintervall. Ferner ist es bei einem Volumenelement nicht sinnvoll die Energiedichte auf einen bestimmten Raumwinkel zu beziehen. Denn schließlich wird stets das gesamte Volumenelement mit seiner entsprechenden Energiedichte betrachtet. Deshalb wird die Energiedichte über den gesamten „Raum“ angegeben, d.h. die über eine volle Kugeloberfläche (Raumwinkel dΩ=4π):

\begin{align}
&u_s = \frac{u}{\text{d}\lambda} = \frac{B_s}{c} \cdot \text{d}\Omega = \frac{B_s}{c} \cdot 4\pi \\[5px]
&\boxed{u_s = \frac{4\pi}{c} \cdot B_s} \\[5px]
\end{align}

Zwischen der spektralen Energiedichte und der spektralen Intensität existiert schließlich der folgende Zusammenhang [vgl. Gleichung (\ref{gg})]:

\begin{align}
&\boxed{u_s = \frac{4}{c} \cdot I_s} \\[5px]
\end{align}

Diese Beziehung zwischen der spektralen Energiedichte und der (spezifischen) spektralen Intensität gilt nicht nur für die Wellenlängendarstellung, sondern auch für die Frequenzdarstellung. In diesem Fall meint die spektrale Energiedichte dann die Energiedichte pro Einheit Frequenzintervall. In ausgeschriebener Form lässt sich die spektrale Energiedichte für beide Fälle wie folgt bestimmen:

\begin{align}
&\boxed{u_s(\lambda) = \frac{8 \pi h c}{\lambda^5} \cdot \frac{1}{\exp\left(\dfrac{h c}{\lambda k_B T}\right)-1} } ~~~\text{Wellenlängenform} \\[5px]
\end{align}

\begin{align}
&\boxed{u_s(f) = \frac{8 \pi h f^3}{c^3} \cdot \frac{1}{\exp\left(\dfrac{h f}{k_B T}\right)-1} } ~~~\text{Frequenzform} \\[5px]
\end{align}

Die gesamte Energiedichte im Hohlraum eines schwarzen Strahlers würde man schließlich durch Integration dieser Gleichungen über den gesamten Wellenlängenbereich bzw. Frequenzbereich erhalten. Diese Gesamtenergiedichte ist offensichtlich nur von der Temperatur abhängig und im gesamten Hohlraum räumlich konstant. Würde sich die Energiedichte in zwei Punkten unterscheiden, dann wäre in einem Volumenelement offensichtlich mehr Energie enthalten als im anderen. Das Volumenelement mit der höheren Energiedichte würde schließlich „stärker“ strahlen als das andere. Das Photonengas bzw. der gesamte Hohlraum befände sich dann aber nicht im thermodynamischen Gleichgewicht.

Ferner ist die Energiedichte nicht vom Volumen des Hohlraumes abhängig. Die spektrale Verteilung der Energiedichte ist alleinig durch die Temperatur bestimmt. Ob der Hohlraum also klein oder groß ist, spielt für die darin enthaltene (spektrale) Energiedichte keine Rolle!

Die Energiedichte im Hohlraum eines schwarzen Hohlkörpers ist nur von der Temperatur abhängig!

Anmerkung: Planck leitet zuerst die Formel für Energiedichte im Inneren eines Hohlraumstrahlers her. Erst anschließend beschrieb er ausgehend hiervon die austretende Strahlung; also im Prinzip genau die umgekehrte Vorgehensweise wie wir sie in diesem Artikel dargelegt haben.