Förderhöhe und Verlusthöhe

Als Verlusthöhe bezeichnet man den Verlust an Energie einer strömenden Fluidmenge, bezogen auf die Gewichtskraft der Fluidmenge.

Förderhöhe einer Pumpe

Pumpen dienen zur Förderung von Gasen oder Flüssigkeiten. Diese Fluide werden in der Regel von einem tiefer gelegenen Niveau gefördert und auf ein höher gelegenes Niveau gepumpt. Zwischen diesen Niveaus ist die Pumpe angeordnet. Mit Hilfe der Pumpe wird auf der sogenannten Saugseite ein Unterdruck erzeugt, sodass das Fluid angesaugt wird. Anschließend setzt die Pumpe das Fluid unter hohen Druck. Auf der sogenannten Druckseite wird das Fluid nun mit erhöhtem Druck durch die Rohrleitung geschoben und auf das höhere Niveau gefördert. Im Folgenden betrachten wir ausschließlich das Fördern von inkompressiblen Fluiden wie Flüssigkeiten.

Welche Höhendifferenz die Flüssigkeit durch die Pumpe überwinden kann, hängt von der Leistung der Pumpe, der Dichte des zu fördernden Fluids und vom Volumenstrom ab. Um dies zu zeigen, betrachten wir eine vertikale Rohrleitung. Mit Hilfe einer Pumpe wird durch dieses Rohr ein Fluid der Dichte ϱ von einem tiefer gelegenen Becken in die Höhe gepumpt. Am offenen Ende der Rohrleitung tritt das Wasser aus. Die zu überwindende Höhendifferenz betrage H. Reibungs- oder Strömungsverluste werden im Folgenden vernachlässigt.

Die Zeitdauer bis ein Fluidteilchen vom unteren Becken (Höhe Flüssigkeitsspiegel) vollständig durch die Rohrleitung hinauf gepumpt wurde, sei mit t bezeichnet. Innerhalb dieser Zeit t muss offensichtlich einmal die gesamte im Rohr befindliche Flüssigkeit der Masse m=V⋅ϱ um die Höhe H angehoben werden (mit V als Volumen des Fluids im Rohr). Hierzu ist folgende Arbeit W_H erforderlich:

\begin{align}
&W_\text{H} = m \cdot g \cdot H ~~~\text{mit}~~~m =V \cdot \rho \\[5px]
&W_\text{H} = V \cdot \rho \cdot g \cdot H ~~~~~\text{Hubarbeit der Pumpe} \\[5px]
\end{align}

Diese Arbeit wird offensichtlich innerhalb der Zeit t erbracht, sodass sich hieraus folgende Leistung P_H ergibt, die die Pumpe liefern muss:

\begin{align}
&P_\text{H} = \frac{W_\text{H}}{t} \\[5px]
&P_\text{H} = \frac{V \cdot \rho \cdot g \cdot H}{t} \\[5px]
&P_\text{H} = \underbrace{\frac{ V}{t}}_{\dot V} \cdot \rho \cdot g \cdot H\\[5px]
&\boxed{P_\text{H} = \dot V \cdot \rho \cdot g \cdot H} ~~~~~\text{Leistung der Pumpe} \\[5px]
\end{align}

Bei der Herleitung wurde ausgenutzt, dass der Quotient aus Volumen V und Zeitdauer t gerade dem geförderten Volumenstrom V* entspricht.

Umgekehrt bedeutet dies: Bei gegebener Pumpenleistung P_H und zu förderndem Volumenstrom V* ergibt sich die maximale Förderhöhe der Pumpe H in Abhängigkeit der Dichte des Fluids ϱ wie folgt (bei einer größeren Höhe wäre der hydrostatische Druck der Flüssigkeitssäule größer als der erzeugte Druck der Pumpe und das Fluid könnte nicht weiter nach oben gefördert werden):

\begin{align}
&P_\text{H} = \frac{W_\text{H}}{t} \\[5px]
&P_\text{H} = \frac{V \cdot \rho \cdot g \cdot H}{t} \\[5px]
&P_\text{H} = \underbrace{\frac{ V}{t}}_{\dot V} \cdot \rho \cdot g \cdot H\\[5px]
\label{p}
&\boxed{H = \frac{P_\text{H}}{\dot V \cdot \rho \cdot g}} ~~~~~\text{Förderhöhe der Pumpe} \\[5px]
\end{align}

Als Förderhöhe einer Pumpe bezeichnet man die maximale Höhendifferenz die eine Pumpe aufgrund ihrer auf das Fluid übertragenen Leistung bei gegebenem Volumenstrom und gegebener Dichte im verlustfreien Fall maximal überwinden kann!

Beachte, dass die Förderhöhe der Pumpe keine Reibungsverluste im Rohr oder Druckverluste durch eingebaute Komponenten berücksichtigt, sondern nur für den verlustfreien Fall der Rohrleitung gilt. Diese Verluste sind nämlich keine Verluste, die unmittelbar der Pumpe zugeordnet werden könnten, sondern sie sind von der Eigenschaft der Anlage abhängig für die die Pumpe eingesetzt werden soll. Hersteller von Pumpen können solche Rohrleitungsverluste also ohnehin nicht berücksichtigen, da sie die Einsatzbedingungen der Pumpe nicht kennen. Deshalb werden die Rohrleitungsverluste bei der Förderhöhe der Anlage berücksichtigt (später mehr dazu).

Pumpenwirkungsgrad

Die Leistung P_H in den oberen Gleichungen bezieht sich nur auf die Leistung, die die Pumpe effektiv auf das Fluid überträgt, d.h. jene Leistung die tatsächlich für das kontinuierliche Anheben des Fluids auf die Höhe H erforderlich ist! Diese Leistung ist nicht identisch mit dem sogenannten Leistungsbedarf P_B der Pumpe (auch Leistungsaufnahme genannt), d.h. jener Leistung die bspw. eine elektrische Pumpe aus dem Stromnetz entnehmen muss.

Es gilt in diesem Fall Umwandlungsverluste zu berücksichtigen, die bei der Umwandlung der zugeführten elektrischen Leistung in mechanische Leistung entstehen. Ebenfalls müssen Strömungsverluste in der Pumpe durch Turbulenzen berücksichtigt werden, vor allem bei hohen Strömungsgeschwindigkeiten bzw. hohen Volumenströmen. All dies wird in einem Pumpenwirkungsgrad η zusammengefasst:

\begin{align}
&\boxed{P_\text{H} = P_\text{B} \cdot \eta} \\[5px]
\end{align}

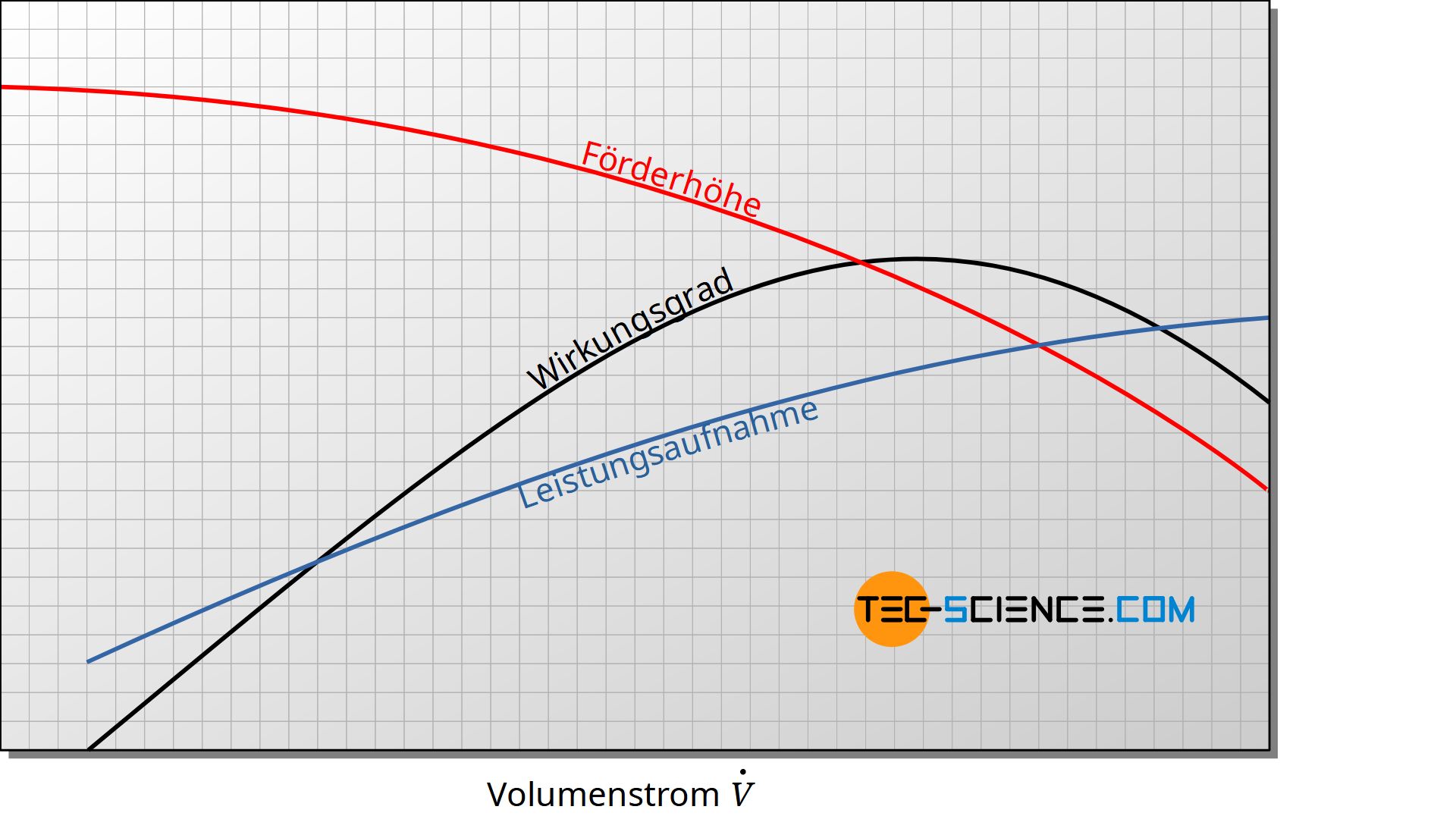
Der Pumpenwirkungsgrad ist keine konstante Größe, sondern vom geförderten Volumenstrom abhängig! Der Wirkungsgrad steigt zunächst mit zunehmendem Volumenstrom an und fällt dann ab einem Maximalwert aufgrund hoher Turbulenzen und den damit verbundenen Strömungsverlusten wieder ab. Typische maximale Wirkungsgrade liegen bei Pumpen zwischen 70 % und 90 %.

Die untere Abbildung zeigt für eine gegebene Drehzahl einer Kreiselpumpe die typischen Verläufe zwischen Förderhöhe, Wirkungsgrad und Leistungsaufnahme der Pumpe in Abhängigkeit des Volumenstroms (Drosselkurve genannt). Beachte, dass solche Kennlinien nur für jeweils eine bestimmte Pumpendrehzahl gültig sind.

Förderhöhe der Anlage

Geodätische Förderhöhe

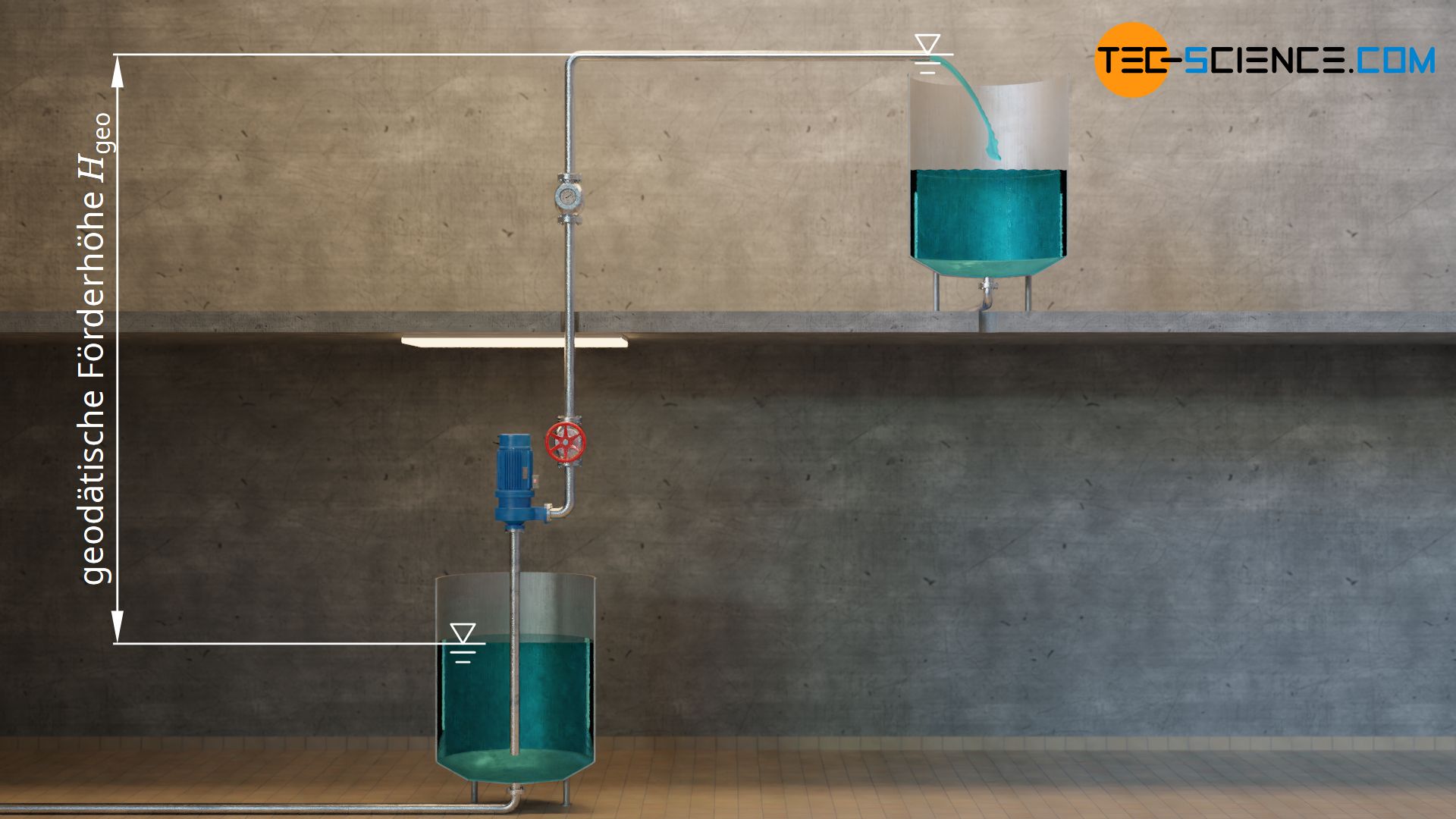
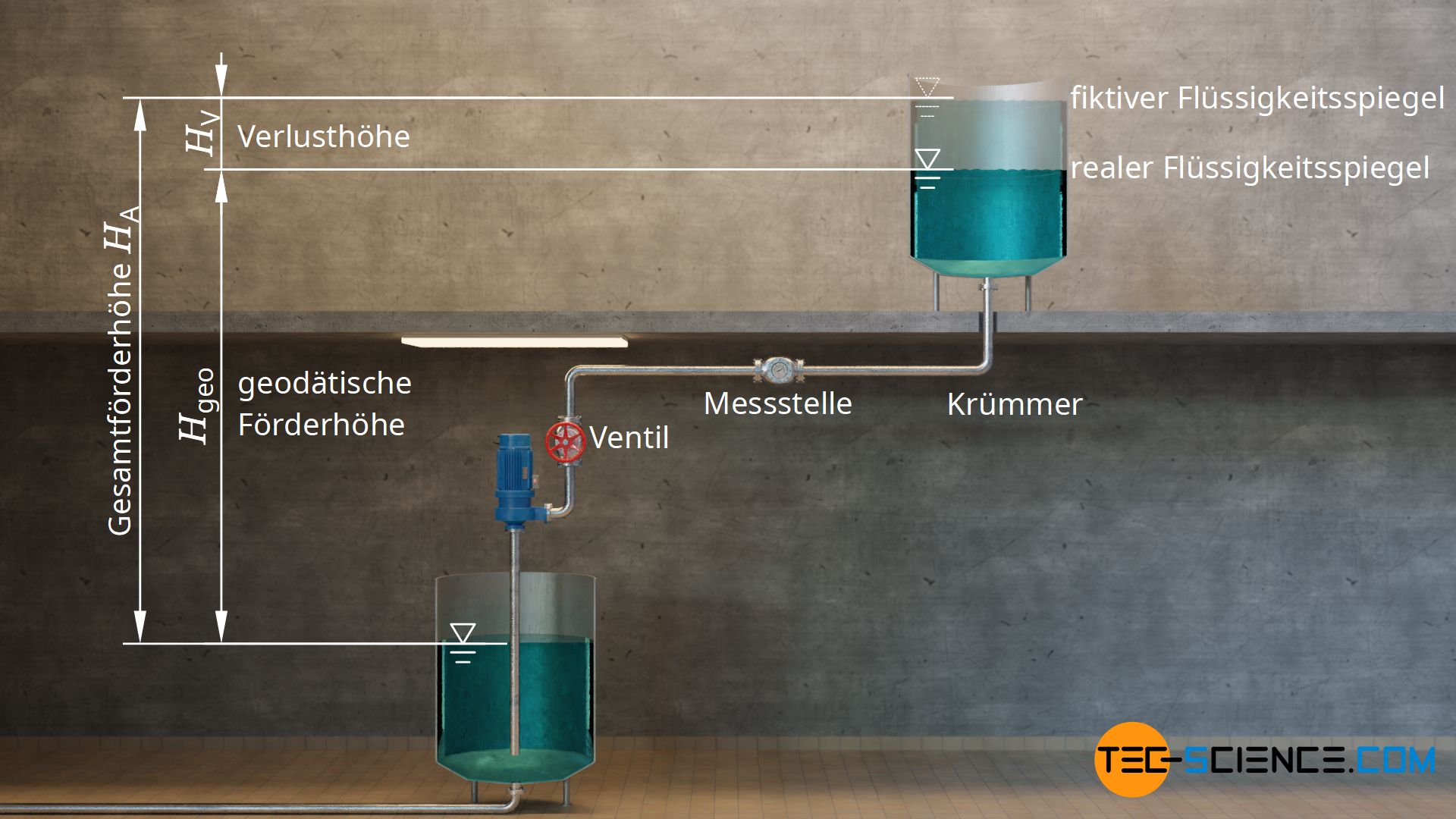
Die Höhendifferenz zwischen einem tiefer und einem höher gelegenen Becken wird als geodätische Förderhöhe der Anlage H_geo bezeichnet. Als Bezugspunkte dienen dabei die jeweiligen Flüssigkeitsspiegel, sofern das höher gelegene Becken von unten befüllt wird. Wird es von oben befüllt, dann ist der Bezugspunkt jener Punkt an dem die Flüssigkeit aus dem Rohr strömt. Für das untere Becken spielt es dabei keine Rolle wie tief der Saugstutzen in die Flüssigkeit eintaucht. Im unteren Becken ist stets die Flüssigkeitsoberfläche zugrunde zu legen, da die Flüssigkeit im Rohr ohnehin von selbst bis auf den äußeren Flüssigkeitsspiegel ansteigt.

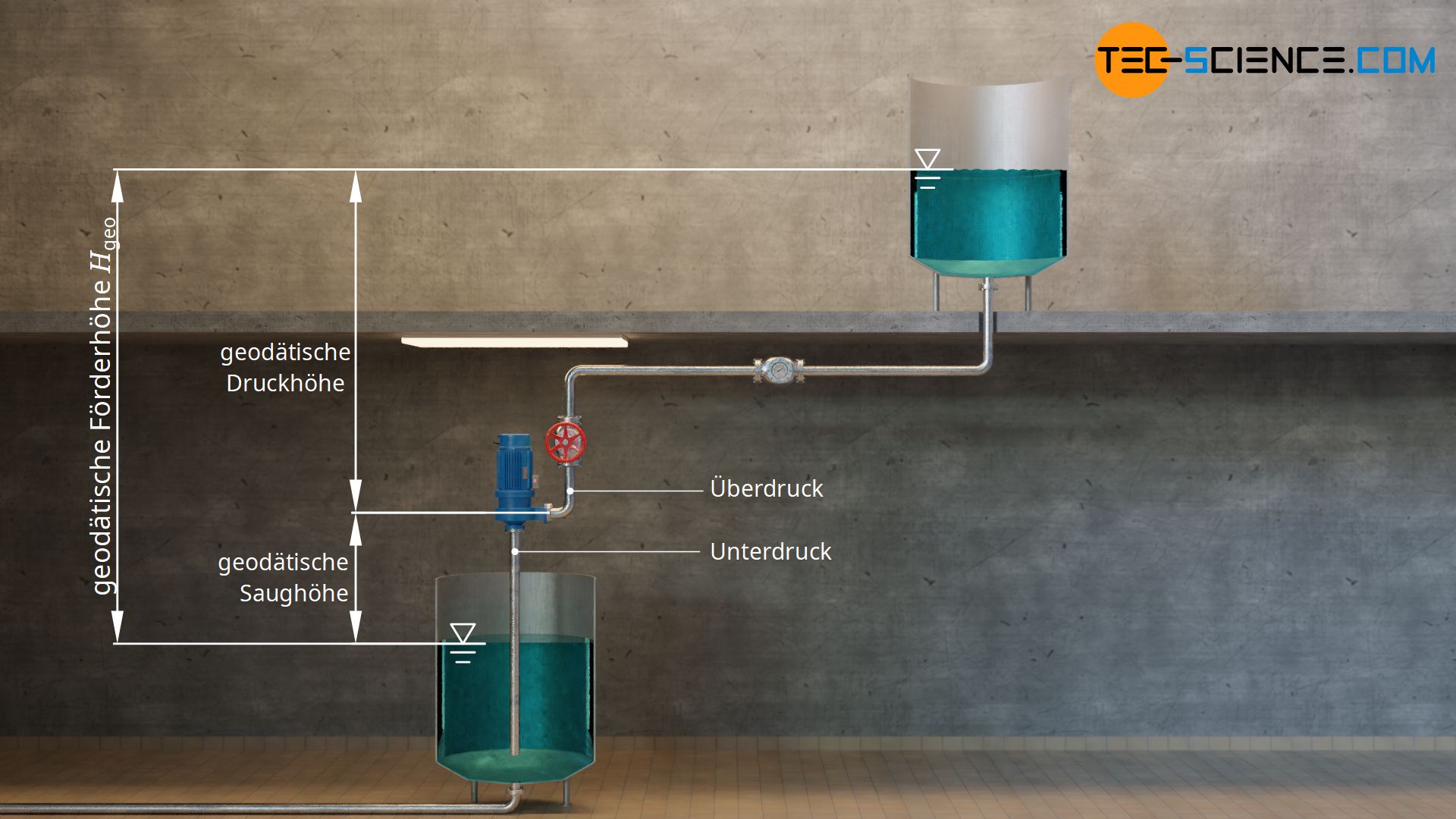
Die geodätische Förderhöhe einer Anlage, lässt sich weiter aufteilen in eine geodätische Saughöhe auf der Saugseite und eine geodätische Druckhöhe auf der Druckseite. Beide Höhen zusammen, bilden die geodätische Förderhöhe der Anlage.

Als geodätische Förderhöhe einer Anlage bezeichnet man die (von einer Pumpe) zu überwindende Höhendifferenz zwischen einem tiefer und einem höher gelegenen Niveau! Sie ergibt sich aus der Summe von geodätischer Saughöhe und geodätischer Druckhöhe.

Damit Flüssigkeiten gefördert werden können, muss die Förderhöhe der Pumpe in jedem Fall größer sein als die geodätische Förderhöhe der Anlage. Dies gilt allerdings nur, wenn im Rohr keine Reibungsverluste oder Strömungsverluste durch eingebaute Komponenten wie bspw. Ventile oder sonstige Messstellen entstehen. Zudem ist die maximale geodätische Saughöhe physikalisch bedingt limitiert.

Maximale geodätische Saughöhe

Auf der Saugseite arbeitet die Pumpe nach dem Trinkhalmprinzip. Es ist demnach also keineswegs so, dass die Pumpe Flüssigkeit einsaugt. Vielmehr drückt der auf der Flüssigkeitsoberfläche lastende (Umgebungs-)Druck das Fluid in die Pumpe. Da der Umgebungsdruck endlich ist, können selbst bei Erzeugung eines perfekten Vakuums keine beliebige Saughöhen überwunden werden. Unter Vernachlässigung von Reibung- und Strömungsverlusten, bestimmt sich die maximale geodätische Saughöhe nach folgender Formel (siehe hierzu den Artikel Wie funktioniert das Trinken mit einem Trinkhalm?):

\begin{align}
\label{hmax}
&\boxed{h_\text{s,max} = \frac{p_0}{\rho \cdot g} } ~~~~~\text{maximale geodätische Saughöhe} \\[5px]
\end{align}

In dieser Formel bezeichnet p₀ den auf der Flüssigkeitsoberfläche lastende (Umgebungs-)Druck und ϱ die Dichte der Flüssigkeit. Für das Fördern von Wasser mit ϱ = 1000 kg/m³ beträgt die maximale geodätische bei einem Umgebungsdruck von 1 bar somit 10 Meter.

Aufgrund der Tatsache, dass jedoch keine Pumpe ein perfektes Vakuum erzeugen kann und aufgrund der Viskosität der geförderten Flüssigkeit unweigerlich Reibungsverluste entstehen, beträgt die maximale geodätische Saughöhe für Wasser in der Praxis nur maximal 8 Meter. Beachte, dass bei geschlossenen Behältern der Umgebungsdruck künstlich erhöht werden kann, sodass dann auch größere Saughöhen möglich werden.

Im Gegensatz zur Saughöhe ist die Druckhöhe auf der Druckseite der Pumpe im Prinzip nicht auf einen Maximalwert beschränkt. Je nach erzeugtem Druck lassen sich im Allgemeinen beliebige Druckhöhen erreichen.

Verlusthöhe

Wie bereits angesprochen, müssen in der Realität Reibungsverluste und Strömungsverluste in der Anlage berücksichtigt werden. Die Pumpe muss also in der Realität eine größere Leistung auf das Fluid übertragen als im reibungsfreien Idealfall. Unter Berücksichtigung der Reibung verhält sich die reale Anlage so, als wäre eine fiktive reibungsfreie Anlage um eine bestimmte Höhe größer. Diese zusätzliche (fiktive) Höhe, in der die Reibungs- und Strömungsverluste zum Tragen kommen, wird Verlusthöhe H_V genannt.

Bezeichnet P_V die Verlustleistung, die beim Strömen des Fluids mit dem Volumenstrom V* entsteht, dann kann die Verlusthöhe H_V gemäß Gleichung (\ref{p}) wie folgt ermittelt werden:

\begin{align}
&\boxed{H_\text{V} = \frac{P_\text{V}}{\dot V \cdot \rho \cdot g} } ~~~~~\text{Verlusthöhe der Anlage} \\[5px]
\end{align}

Die (fiktive) Förderhöhe der Anlage H_A ist somit um den Betrag der Verlusthöhe H_V größer als die geodätische Förderhöhe H_geo:

\begin{align}
&\boxed{H_\text{A} = H_\text{geo} + H_\text{V}} ~~~~~\text{Gesamtförderhöhe der Anlage} \\[5px]
\end{align}

Man muss die Förderhöhe der Pumpe also mit der (fiktiven) Förderhöhe der Anlage vergleichen, wenn es um die Auswahl einer geeigneten Pumpe geht. Die Förderhöhe der Pumpe muss größer sein als diese Förderhöhe der Anlage, damit das Fluid gefördert werden kann. Dabei ist allerdings noch nicht berücksichtigt, dass im oberen bzw. unteren Becken unterschiedliche Drücke herrschen können. Deshalb muss im Allgemeinen auch noch eine Druckhöhendifferenz berücksichtigt werden, auf die im nächsten Abschnitt näher eingegangen wird.

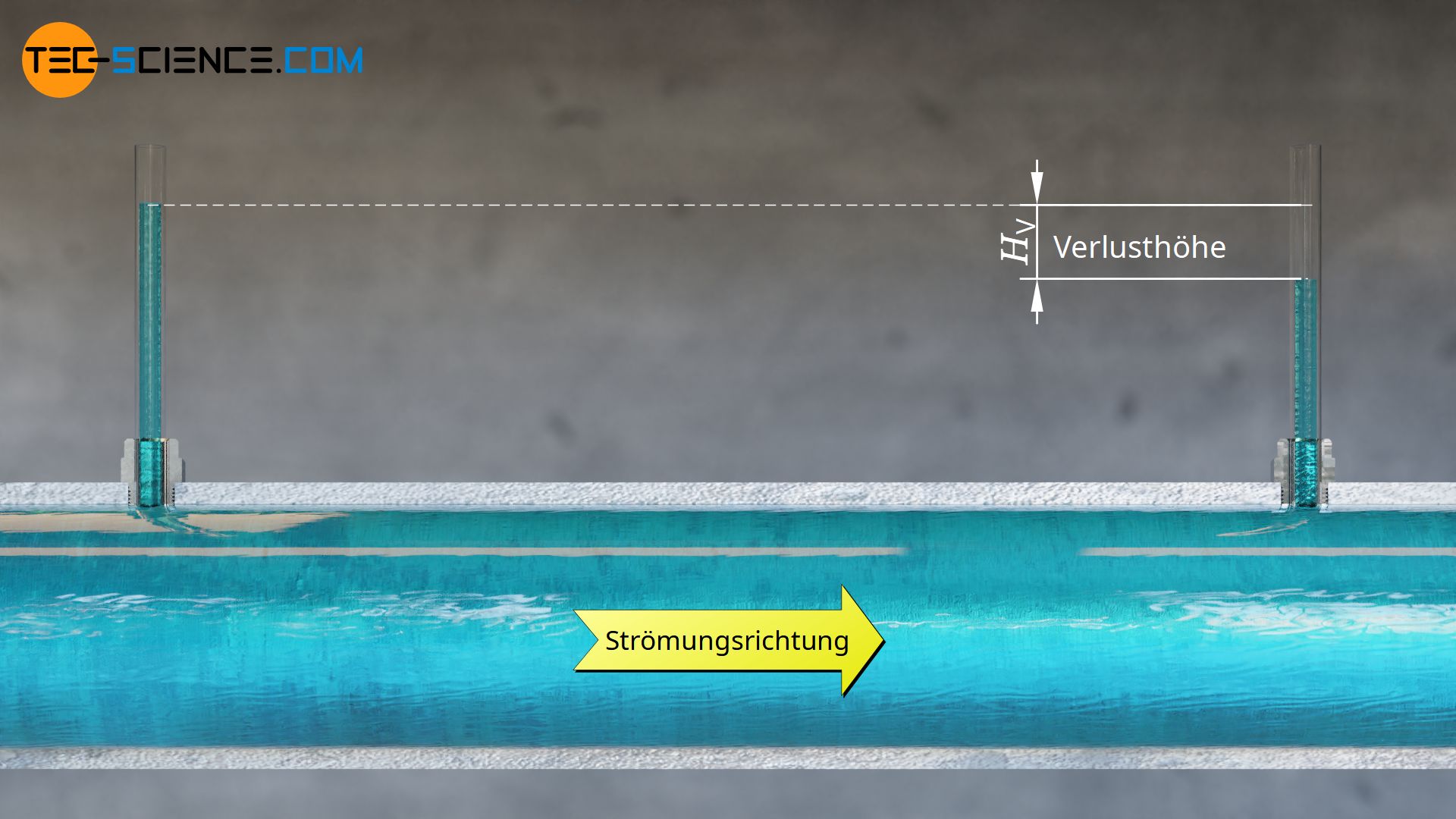
Auch in einem horizontalen Rohr treten aufgrund der Viskosität des darin strömenden Fluids unweigerlich Reibungsverluste auf. Die damit verbundene Verlusthöhe lässt sich in diesem Fall tatsächlich sehr anschaulich zeigen. Hierzu kann man sich kleine Steigrohre am Rohr angebracht vorstellen. Aufgrund des statischen Drucks im strömenden Fluid, wird das Fluid im Steigrohr um einen bestimmten Betrag nach oben gedrückt. Durch die Reibungsverluste im Rohr sinkt der statische Druck stromabwärts jedoch (konstanter Rohrquerschnitt vorausgesetzt). Die Flüssigkeit in einem Steigrohr erreicht an dieser Stelle nur noch eine geringere Höhe. Die Differenz in den Flüssigkeitsspiegeln entspricht anschaulich der Verlusthöhe des horizontalen Rohrs.

Druckhöhendifferenz

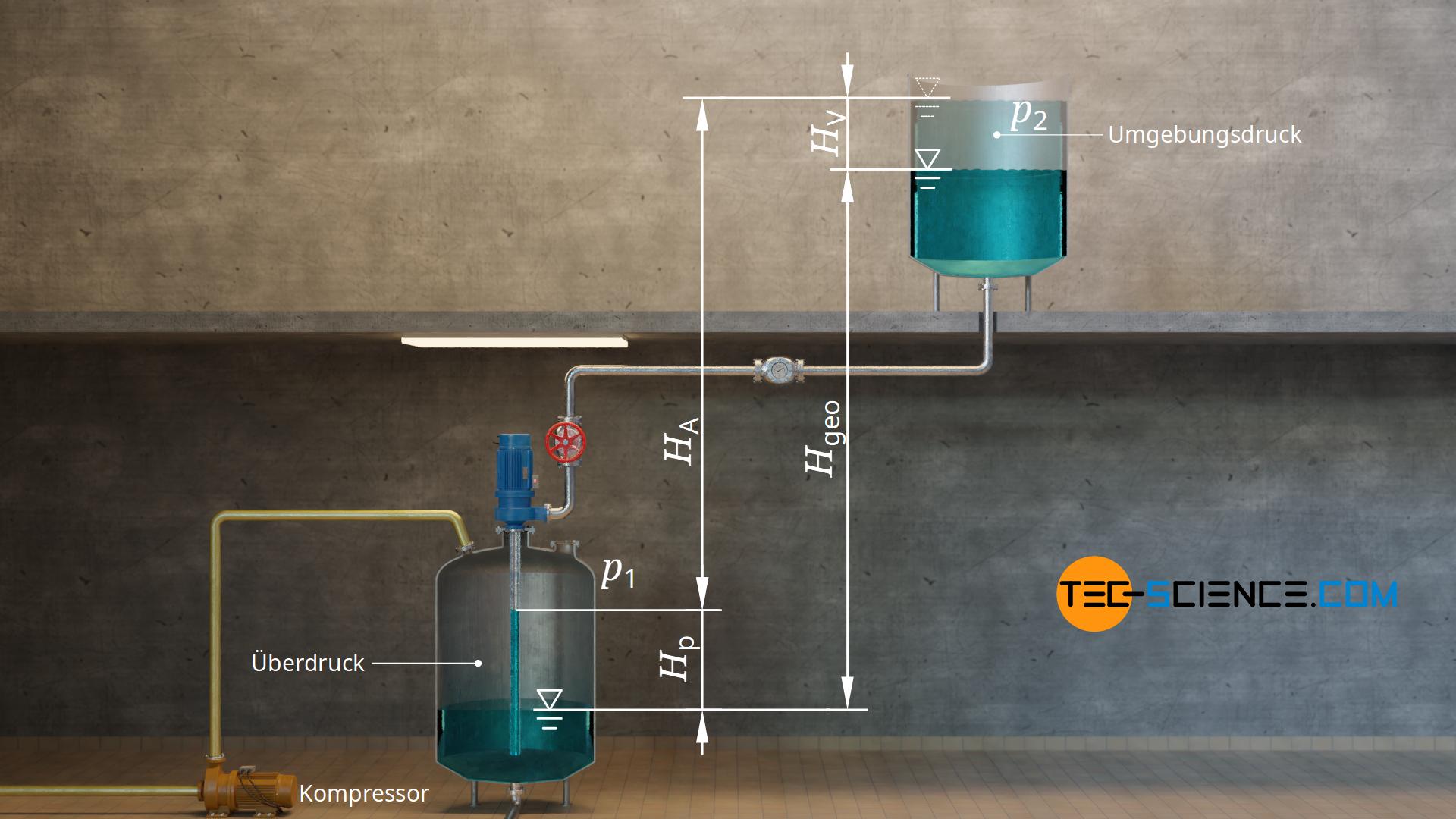
Stellen wir uns folgende Situation vor. Wasser soll von einem geschlossenen Behälter in einen 6 Meter höher gelegenen offene Behälter gefördert werden. Im geschlossenen Behälter wird durch ein Kompressor ein Überdruck erzeugt. Auch ohne das Vorhandensein einer Pumpe wird durch diesen Überdruck das Wasser bereits von selbst ein Stück nach oben gedrückt. Bei einem Überdruck von 0,1 bar steigt das Wasser theoretisch bereits auf eine Höhe von 1 Meter über dem Wasserspiegel an [siehe Formel (\ref{hmax})]. Die Pumpe hat somit nur noch die letzten 5 Meter Höhendifferenz zu überwinden. Energetisch betrachtet, hat die Anlage aus Sicht der Pumpe nur eine Förderhöhe von 5 Metern (ohne Berücksichtigung der Verlusthöhe).

Umgekehrt, erhöht sich die Förderhöhe der Anlage, wenn der untere Behälter offen sich und im höher liegenden Behälter ein Überdruck erzeugt wird. In diesem Fall drückt der größere Druck im oberen Behälter die Wassersäule nach unten. Damit hat die Pumpe nun eine deutlich größere Höhendifferenz zu überwinden. Die Effekte gleichen sich nur dann aus, wenn in beiden Behältern die Drücke gleich groß sind (z.B. Umgebungsdruck in beiden Behältern). Auch ohne externe Kompressoren, kommen in geschlossenen Behältern ohne Entlüftung, Druckunterschiede zustande, da sich das Luftvolumen im Tank bei einer Änderung des Flüssigkeitsstandes ebenfalls ändert, ohne dass Luft entweichen oder nachströmen kann.

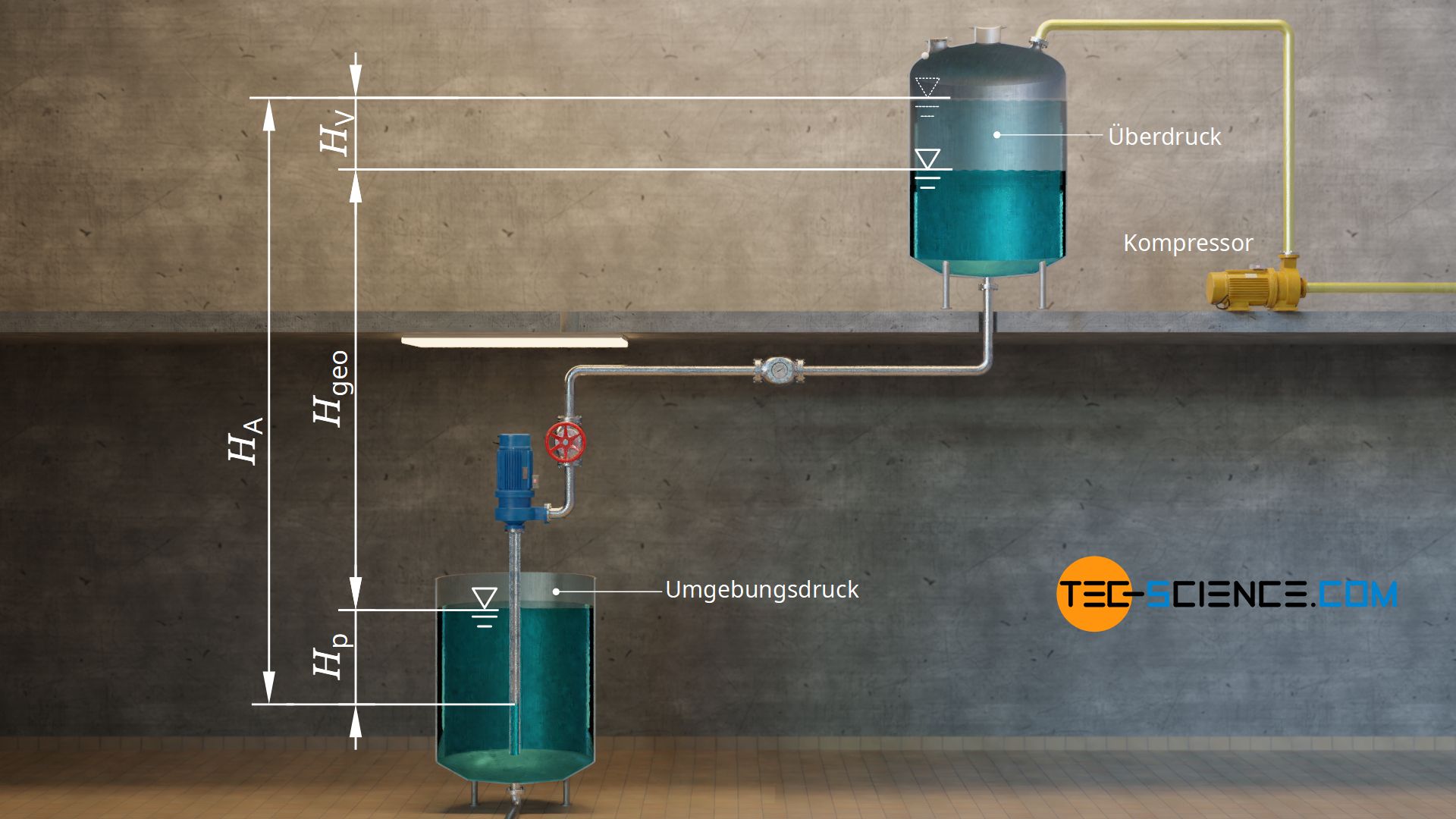
Die zusätzlich Förderhöhe bzw. die verringerte Förderhöhe aufgrund der Druckdifferenz Δp zwischen den beiden Behältern wird als Druckhöhendifferenz H_p bezeichnet. Die Druckdifferenz bestimmt sich dabei über die Differenz zwischen dem Druck im oberen Behälter p₂ und dem Druck im unteren Behälter p₁. Auf diese Weise wird auch das Vorzeichen korrekt wiedergegeben, sodass bei einem Unterdruck im oberen Behälter (bzw. einem Überdruck im unteren Behälter) eine negative Druckhöhendifferenz resultiert, die die Förderhöhe der Anlage verringert.

\begin{align}
&H_\text{p} = \frac{\Delta p}{\rho \cdot g} \\[5px]
&\boxed{H_\text{p} = \frac{p_\text{2}-p_\text{1}}{\rho \cdot g} } ~~~~~\text{Druckhöhendifferenz} \\[5px]
\end{align}

Die Gesamtförderhöhe der Anlage H_A bestimmt sich im Allgemeinen somit aus der Summe von geodätischer Förderhöhe H_geo, Verlusthöhe H_V und Druckhöhendifferenz H_p:

\begin{align}
&\boxed{H_\text{A} = H_\text{geo} + H_\text{V} + H_\text{p} } ~~~~~\text{Förderhöhe der Anlage} \\[5px]
\end{align}

Förderhöhe als eine auf die Gewichtskraft bezogene Energie

An dieser Stelle soll die Förderhöhe nach Gleichung (\ref{p}) nochmals genauer untersucht und etwas anders interpretiert werden. Hierzu wird ausgenutzt, dass sich die Leistung also Arbeit pro Zeit und der Volumenstrom als Volumen pro Zeit darstellen lässt.

\begin{align}
\require{cancel}
&H = \frac{P_\text{H}}{\dot V \cdot \rho \cdot g} ~~~~~\text{mit}~~~P_\text{H}=\frac{W_\text{H}}{t}~~~~~\text{und}~~~\dot V = \frac{V}{t}~~~\text{folgt:}\\[5px]
&H = \frac{\frac{W_\text{H}}{\bcancel{t}}}{\frac{V}{\bcancel{t}} \cdot \rho \cdot g} \\[5px]
&H = \frac{W_\text{H}}{\underbrace{V \cdot \rho}_{m} \cdot g} \\[5px]
&H = \frac{W_\text{H}}{m \cdot g} \\[5px]
&\boxed{H = \frac{W_\text{H}}{F_\text{G}}} \\[5px]
\end{align}

Die Förderhöhe lässt sich als eine auf die Gewichtskraft bezogene Energie interpretieren. Dementsprechend gilt:

• Förderhöhe der Pumpe = Auf ein Fluidelement übertragene Energie der Pumpe (bezogen auf die Gewichtskraft des Fluidelements).
• Förderhöhe der Anlage = Benötigte Energie zum Fördern eines Fluidelements (bezogen auf die Gewichtskraft des Fluidelements).

Anlagenkennlinie

Während die geodätische Förderhöhe und die Druckhöhendifferenz eine konstante Größe einer Anlage ist, ist die Verlusthöhe vom Volumenstrom abhängig. Die Druckverluste nehmen mit zunehmendem Volumenstrom zu. Im Artikel Druckverlust in Rohrsystemen (Rohrreibungszahl) wurde hierzu bereits folgende Gleichung hergeleitet, die den Druckverlust Δp_V einer Rohrleitung mit der Rohrreibungszahl λ, dem Innendurchmesser d und der Länge L beschreibt:

\begin{align}
& \boxed{\Delta p_\text{V} = \lambda \cdot \frac{8\rho~L}{\pi^2} \cdot \frac{\dot{V}^2}{d^5}} ~~~\text{Druckverlust in einem geraden Rohrabschnitt} \\[5px]
\end{align}

Mit diesem Druckverlust ist unweigerlich ein Verlust an mechanischer Energie verbunden und damit eine entsprechende Verlusthöhe. Die Verlust Höhe steigt also (näherungsweise) quadratisch mit dem Volumenstrom an. „Näherungsweise“ deshalb, weil die Rohrreibungszahl wiederum vom Volumenstrom selbst beeinflusst wird. Die untere Abbildung zeigt qualitativ den Verlauf der Förderhöhe einer Anlage in Abhängigkeit des Volumenstroms.

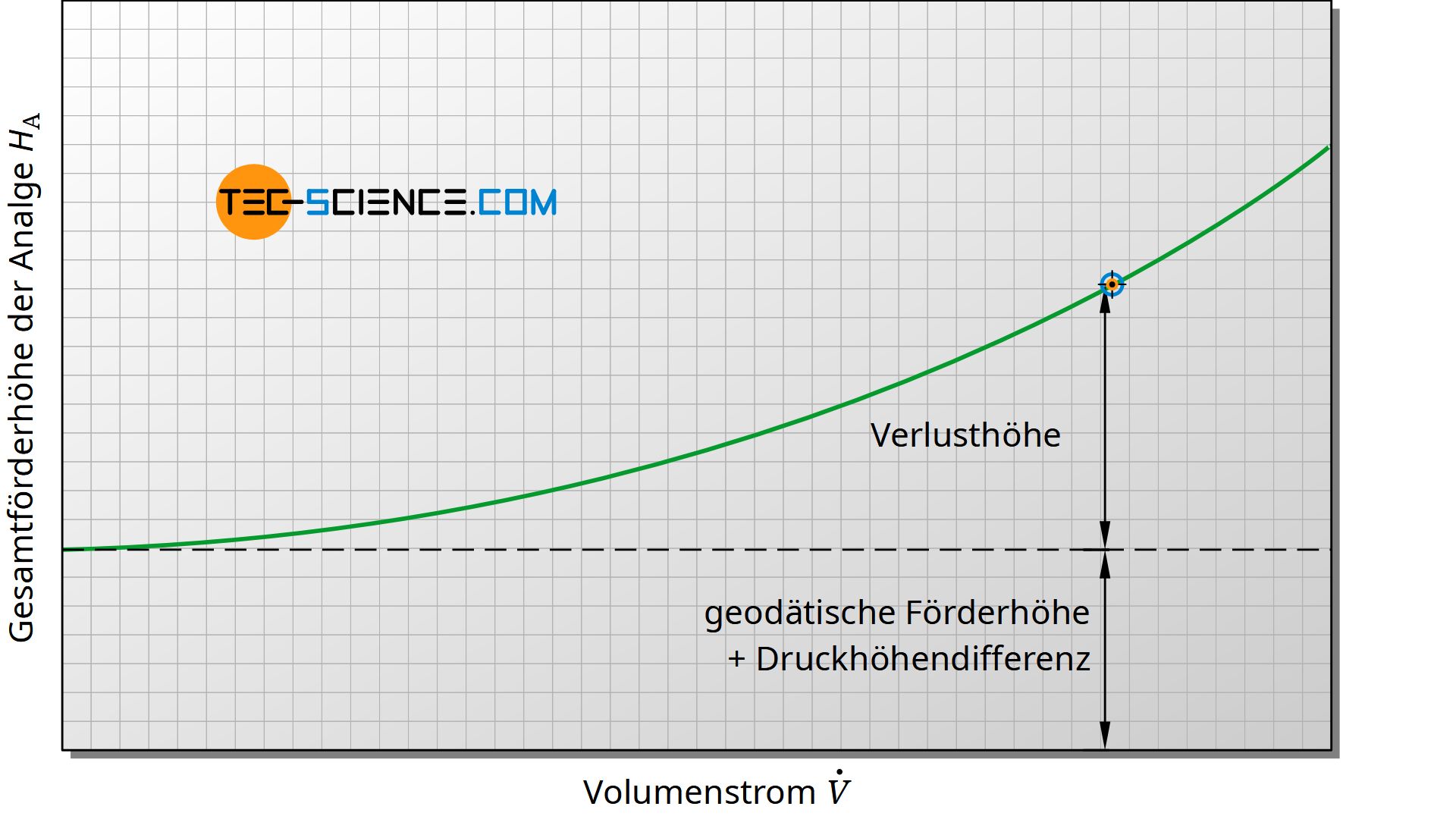
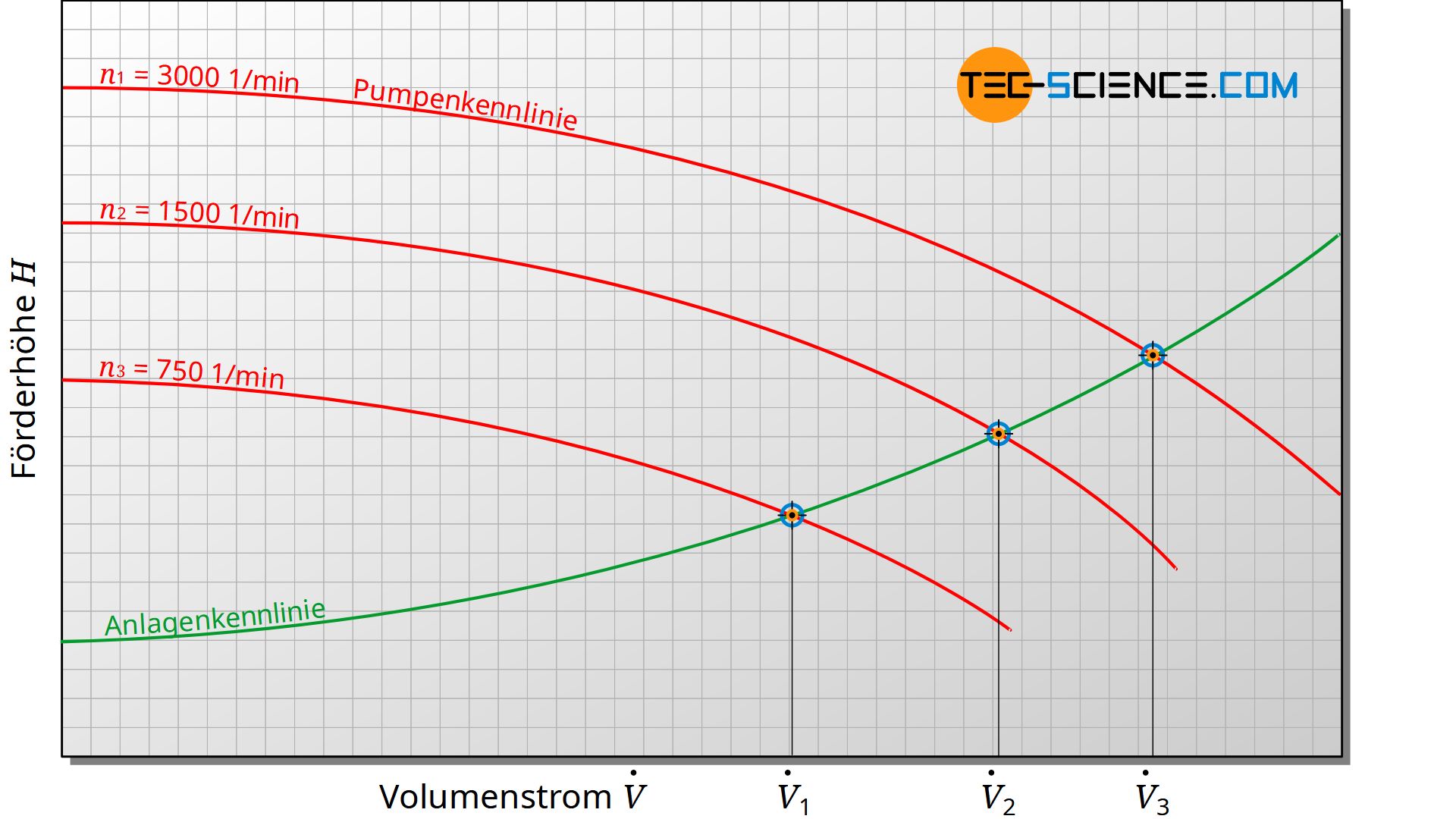
Während also die Förderhöhe der Anlage mit zunehmenden Volumenstrom ansteigt, sinkt (wie eingehend bereits gezeigt) die Förderhöhe der Pumpe aufgrund der zunehmenden Strömungsverluste innerhalb der Pumpe. Im Betrieb der Pumpe stellt sich je nach Volumenstrom ein gemeinsamer Betriebspunkt ein, der dem Schnittpunkt zwischen Pumpenkennlinie und Anlagenkennlinie entspricht.

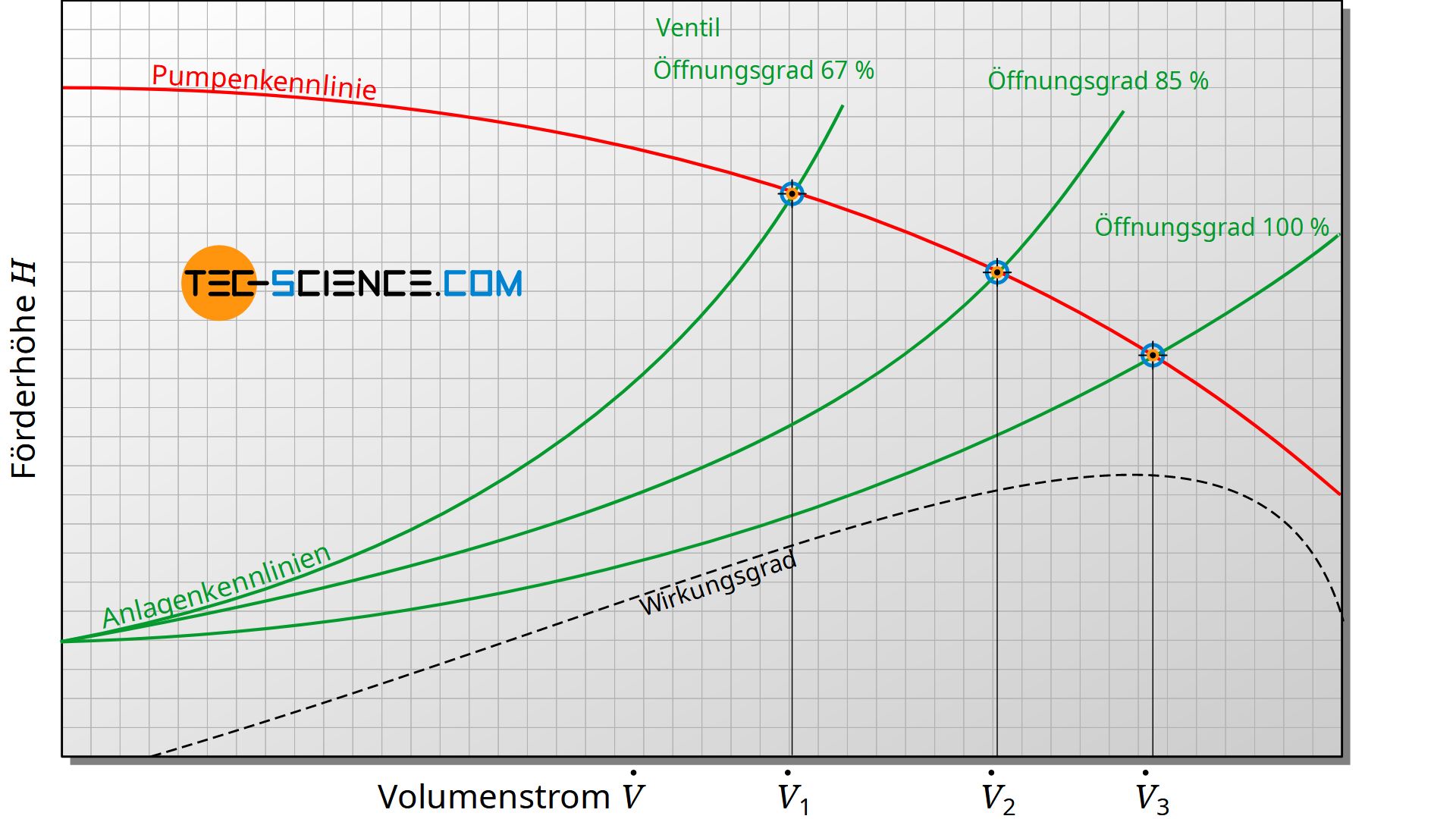
Die Anlagenkennlinie kann durch ein Drosselventil gezielt beeinflusst werden, um den Volumenstrom entsprechend zu steuern. Dabei muss allerdings beachtet werden, dass Kreiselpumpen einen maximalen Wirkungsgrad bei einem bestimmten Volumenstrom aufweisen. Für einen energieeffizienten Betrieb sollte der Betriebspunkt möglichst nahe diesem maximalen Wirkungsgrad liegen. Mit einer Änderung der Anlagenkennlinie durch ein Drosselventil wird der Betriebspunkt in aller Regel jedoch nachteilig verändert. Es resultieren durch die höheren Strömungswiderstände aufgrund der Zustellung geringere Wirkungsgrade. Eine Änderung der Drehzahl der Pumpe zur Steuerung des Volumenstroms kann deshalb an dieser Stelle sinnvoller sein.