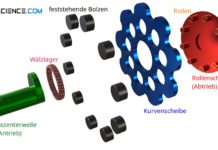
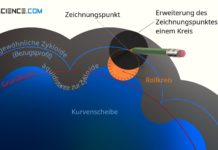
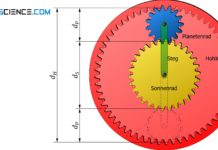
Erfahre in diesem Artikel mehr über die Anwendung der Willis-Gleichung auf Planetengetriebe.
Im Artikel Herleitung der Willis-Gleichung wurde die Grundgleichung für Umlaufgetriebe in der folgenden Form hergeleitet:
\begin{align}
\label{g}
&\boxed{n_P \cdot d_P = n_T \cdot \left(d_P + d_S \right) – n_S \cdot d_S} \\[5px]
\end{align}
Darin bezeichnet nP die Drehzahl und dP den Wälzdurchmesser des Planetenrades. Für das Sonnenrad gilt als Drehzahl entsprechend nS und als Wälzdurchmesser dS. Die Drehzahl des Stegs (Träger) ist mit nT bezeichnet.
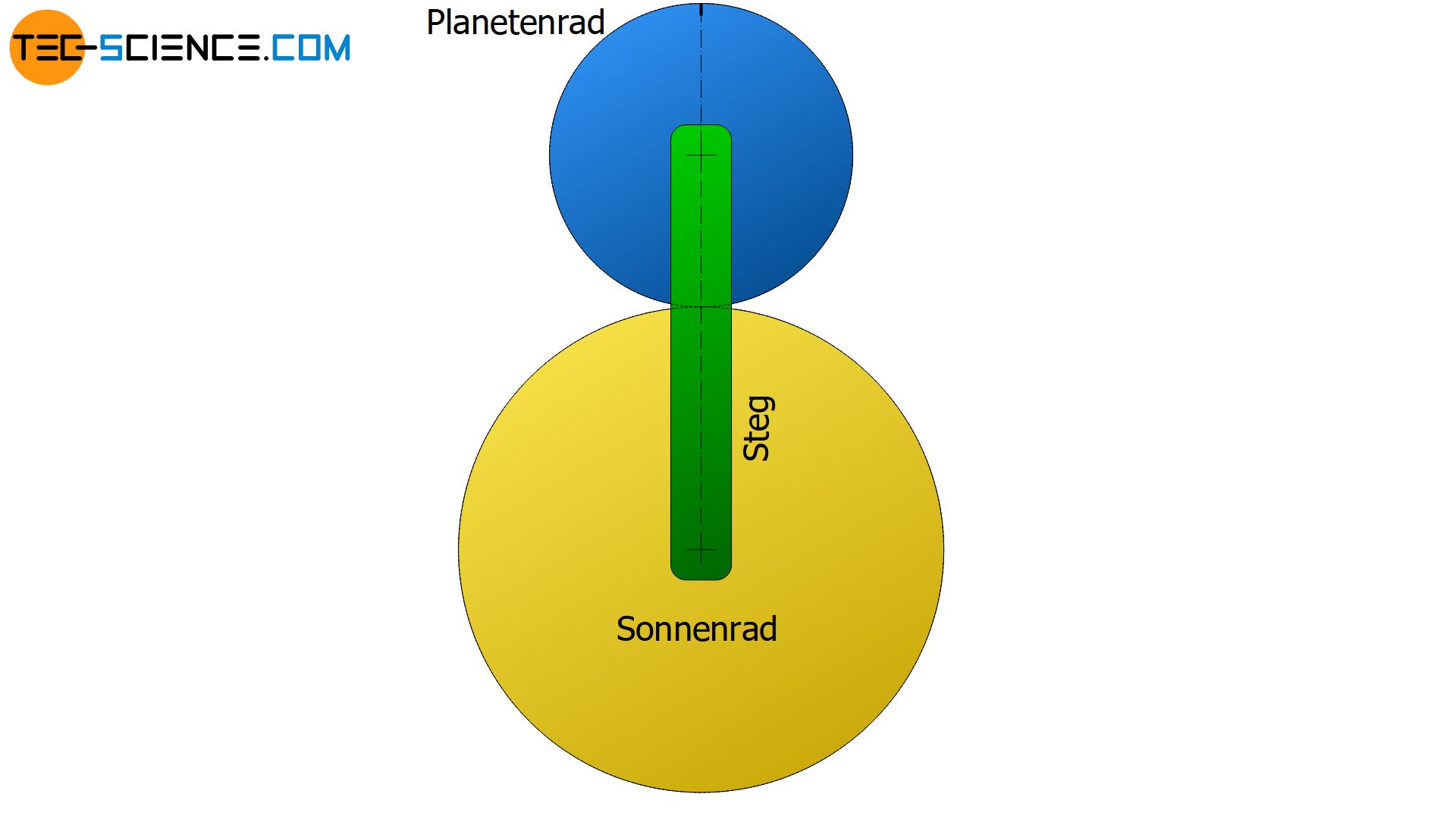
Die Willis-Gleichung (\ref{g}) gilt ganz allgemein für alle Umlaufgetriebe, also im Speziellen auch für Planetengetriebe. Zwar werden die Planetenräder (blau dargestellt) bei einem klassischen Planetengetriebe dabei noch von einem Hohlrad (rot abgebildet) umschlossen, dies ändert jedoch prinzipiell nichts an den hergeleiteten Zusammenhänge zwischen Sonnenrad, Planetenrad und Planetenradträger (Steg; grün dargestellt). Es stellt sich lediglich die Frage, wie die Bewegung der Planetenräder auf das Hohlrad übertragen wird. Dies soll im Folgenden gezeigt werden.
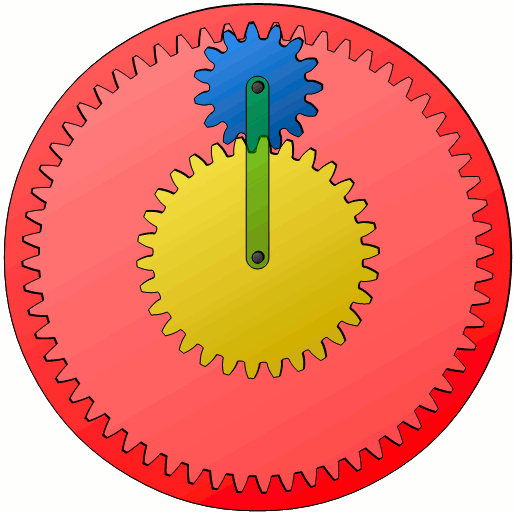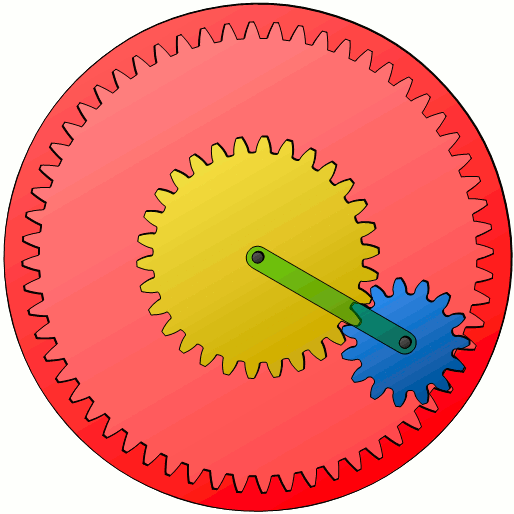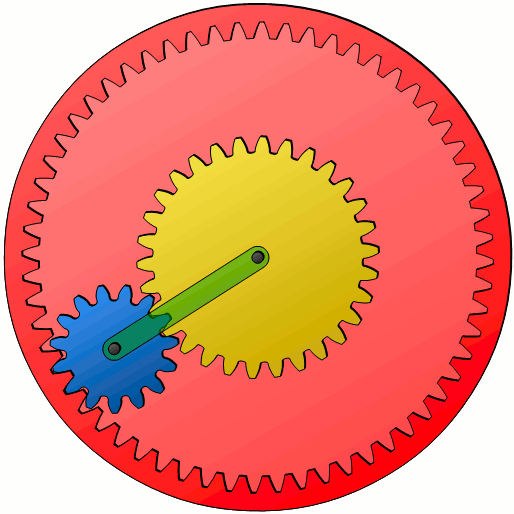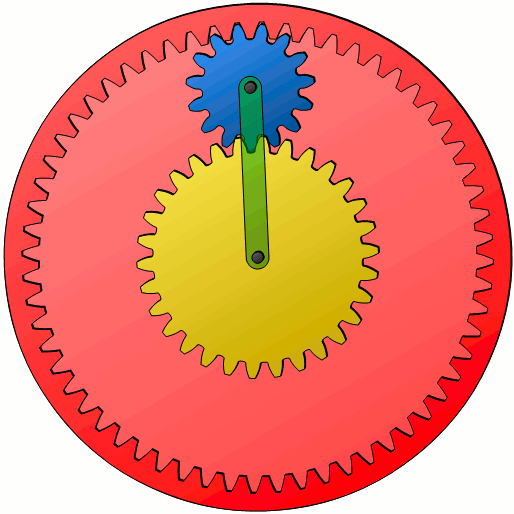
Da zwischen Hohlrad und Planetenrad im Idealfall ein reines Wälzen ohne Gleitung stattfindet, muss die Geschwindigkeit am Wälzpunkt beider Räder identisch sein. Kennt man folglich die Geschwindigkeit vPa mit der sich der äußerste Punkt auf einem Planetenrad bewegt, dann entspricht dies der gesuchten Bahngeschwindigkeit vH des Hohlrades. Über den entsprechenden Wälzkreisradius r (bzw. Wälzkreisdurchmesser d) des Hohlrades kann dann auf dessen Drehzahl n geschlossen werden, da zwischen diesen Größen der folgende allgemeine Zusammenhang gilt:
\begin{align}
\label{o}
&v = \omega \cdot r = \omega \cdot \tfrac{d}{2} ~~~ \text{mit} ~~~ \omega = 2 \pi \cdot n ~~~\text{folgt}: \\[5px]
\label{v}
&\underline{v = \pi \cdot n \cdot d} \\[5px]
\end{align}
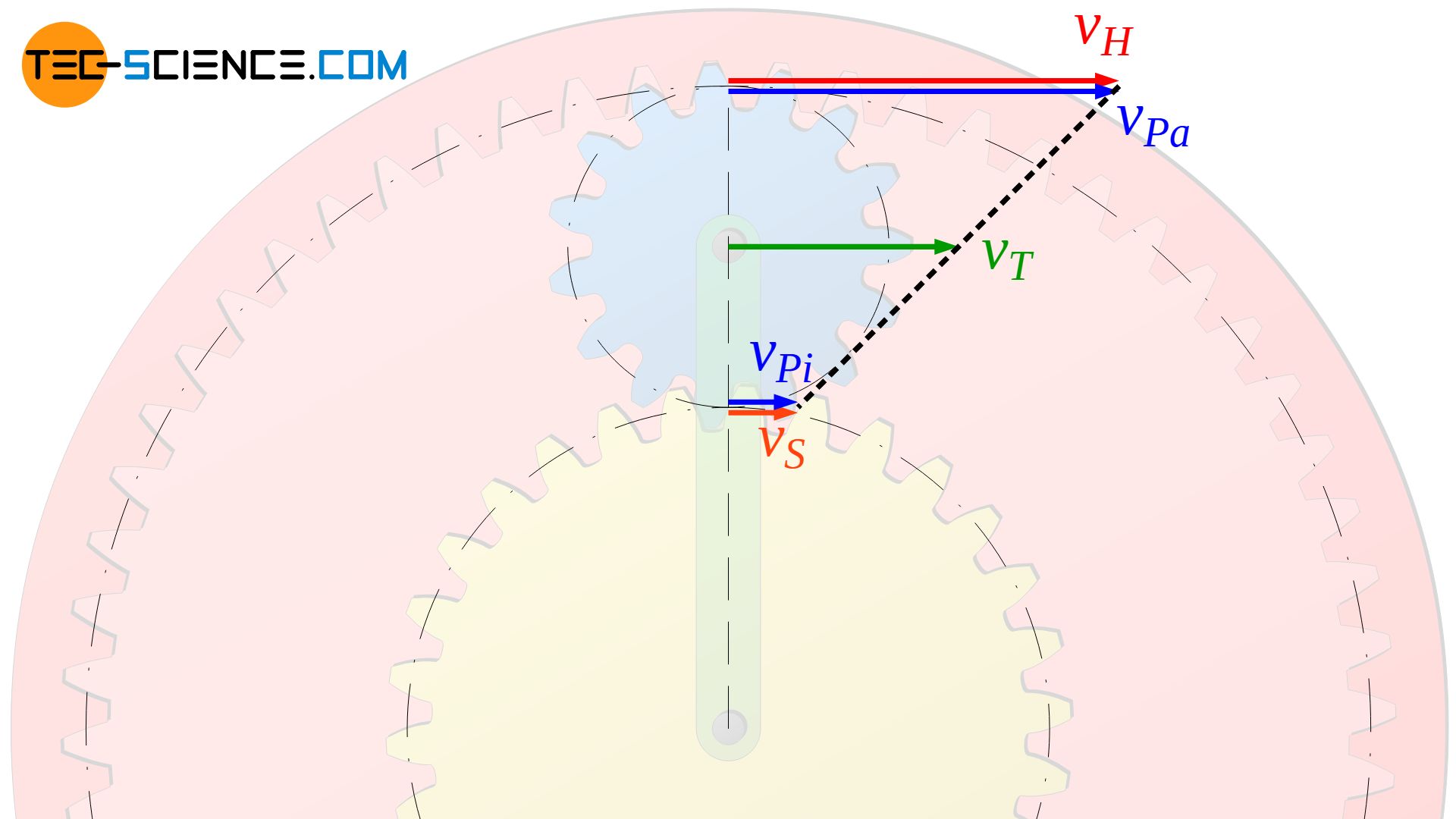
Analoges gilt auch für die Geschwindigkeitsverhältnisse am Berührpunkt zwischen Planetenrad und Sonnenrad. An diesem innersten Punkt muss die Geschwindigkeit des Planetenrades vPi für einen gleitfreien Abwälzvorgang identisch mit der Geschwindigkeit des Sonnenrades vS sein. Der Schwerpunkt des Planetenrades bewegt sich dabei mit der Bahngeschwindigkeit vT des Planetenradträgers. Zwischen diesen Geschwindigkeiten besteht ein linearer Zusammenhang (siehe schwarz gestrichelte Linie in der oberen Abbildung), sodass bei bekannter Bahngeschwindigkeit des Sonnenrades vS und bekannter Umfangsgeschwindigkeit des Planetenradträgers vT die Umfangsgeschwindigkeit des Hohlrades vH ermittelt werden kann.
Warum ergibt sich ein solcher linearer Zusammenhang?
Wie es zu dieser einfachen, linearen Abhängigkeit zwischen den genannten Bahngeschwindigkeiten kommt, soll im Folgenden gezeigt werden. Der einfacheren Darstellung wegen werden die Zahnräder dabei als Wälzzylinder angenommen.
Die Bewegung eines Punktes auf dem Planetenrad lässt als Überlagerung zweier Bewegungen verstehen. Zum einen rotiert das Planetenrad zunächst um seine eigene Achse. In diesem Fall erhält man die typisch symmetrische und lineare Zunahme der Bahngeschwindigkeit gemäß Gleichung (\ref{o}) ausgehend der Drehachse des Planetenrades. Die maximalen Geschwindigkeitsbeträge vP erhält man unmittelbar am Wälzkreis des Planetenrades.
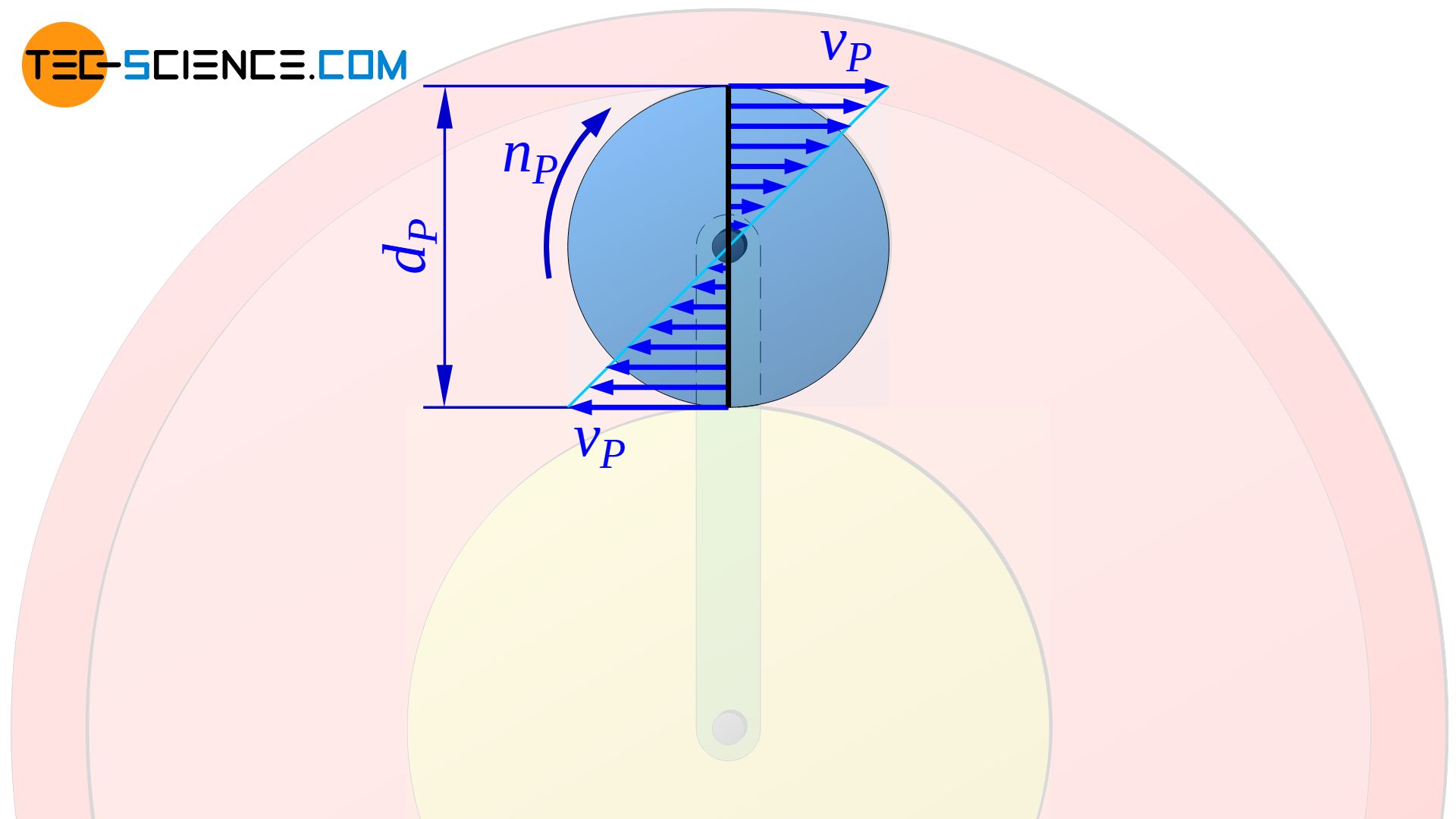
Im Drehzentrum ist die Bahngeschwindigkeit null, solange sich die Planetenradachse nicht bewegt. Nun bewegt sich die Drehachse jedoch mit der Bahngeschwindigkeit des Planetenradträgers vT, d.h. beide Bewegungen können nun zur tatsächlichen Gesamtbewegung überlagert werden.
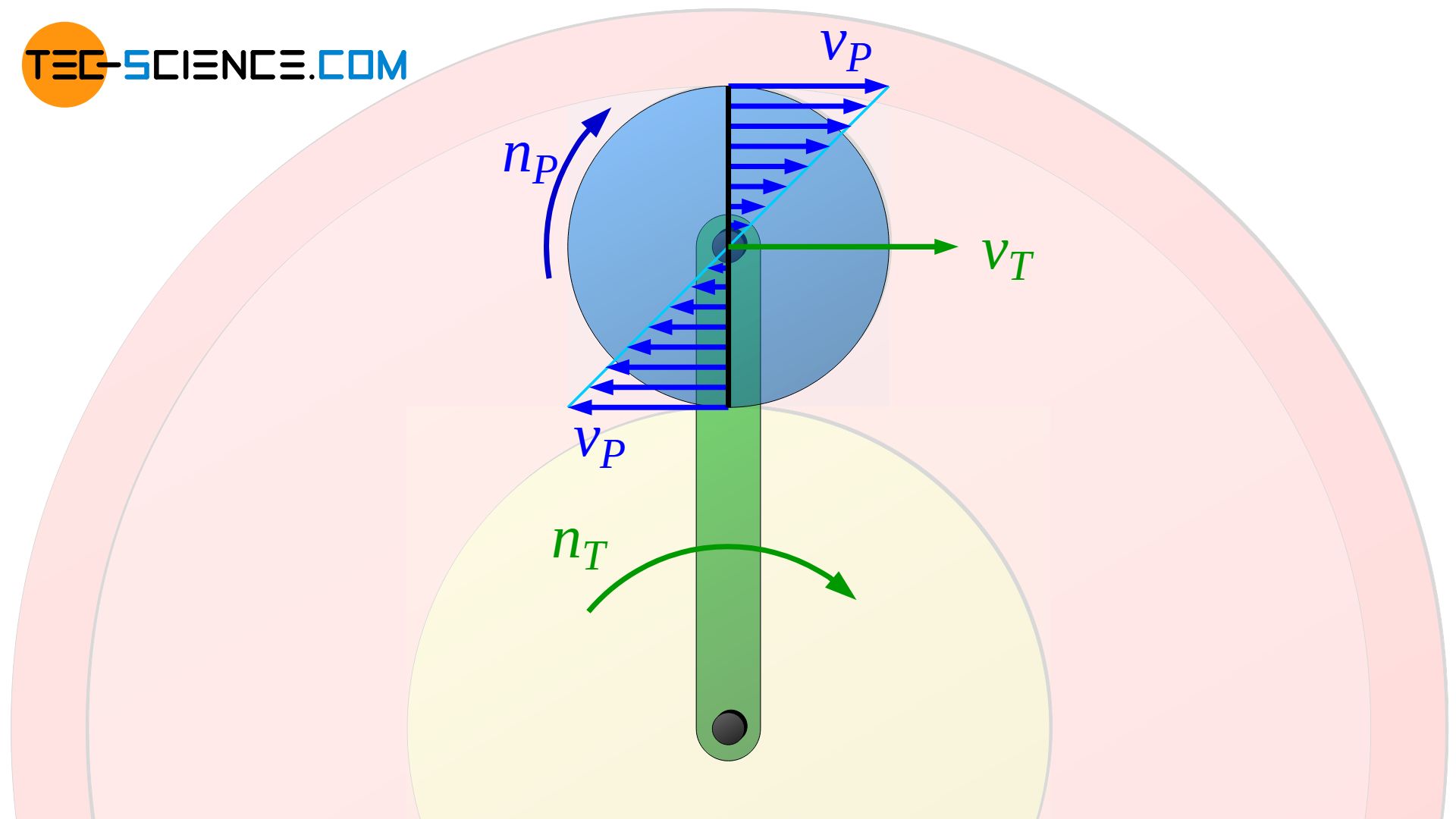
Die Rotationsgeschwindigkeit des Planetenrades ist im oberen Berührpunkt zum Hohlrad mit der Geschwindigkeit des Planetenradträgers gleichgerichtet und am unteren Berührpunkt zum Sonnenrad entgegengesetzt gerichtet. Aufgrund der symmetrischen Geschwindigkeitsverteilung ist die resultierende Gesamtgeschwindigkeit des Planetenrades im äußersten Berührpunkt zum Hohlrad also im selben Maße größer (vPa=vT+vP) wie sie im innersten Berührpunkt zum Sonnenrad geringer ist (vPi=vT-vP).
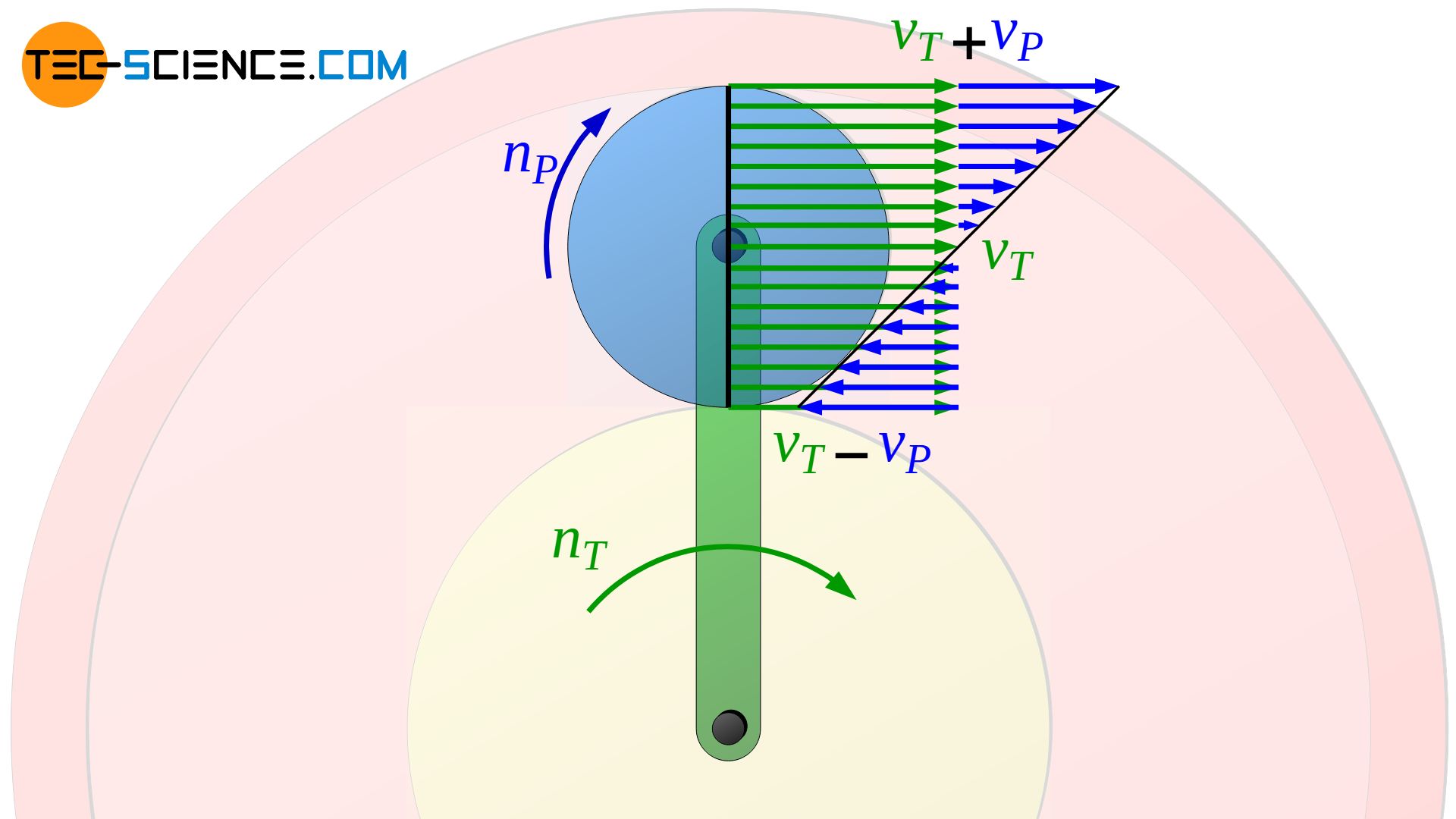
In anderen Worten ausgedrückt: Die Geschwindigkeit eines Punktes auf dem Planetenrad nimmt ausgehend des Berührpunktes zum Sonnenrad linear über die Geschwindigkeit des Planetenradträgers bis hin zum Berührpunkt zum Hohlrad zu. Da die Geschwindigkeit des Planetenradträgers vT als bekannt vorausgesetzt wird, muss lediglich die Geschwindigkeit des Planetenrades am Berührpunkt zum Sonnenrad vS bekannt sein, um die gesuchte Bahngeschwindigkeit am gegenüberliegenden Berührpunkt zum Hohlrad vH bestimmen zu können.
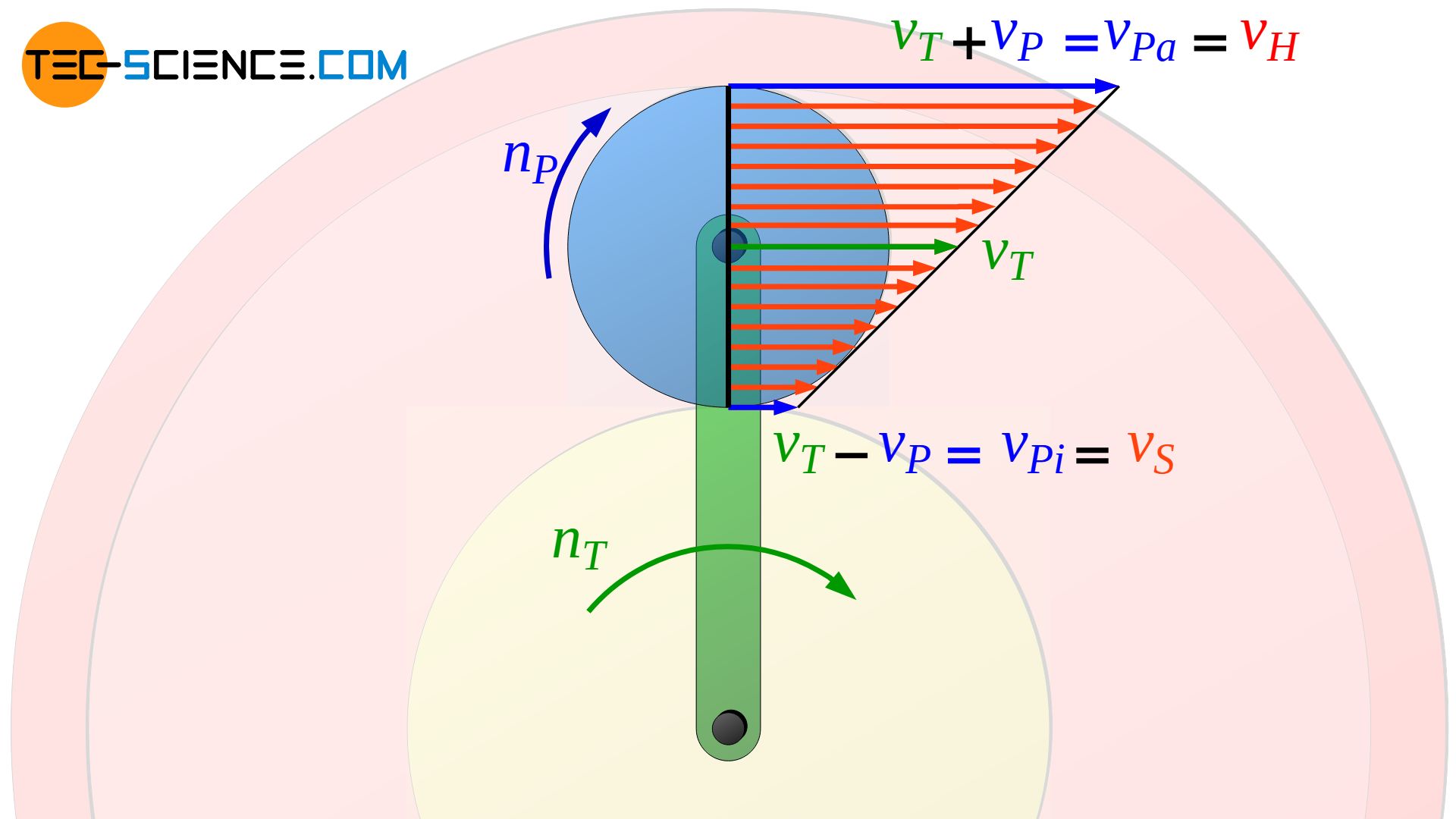
Wie bereits erläutert, muss für einen gleitfreien Abwälzvorgang ohne Relativbewegung die Geschwindigkeit des Planetenrades am Berührpunkt zum Hohlrad (vPa=vT+vP) gleich der Umfangsgeschwindigkeit des Hohlrades vH sein:
\begin{align}
&v_H\overset{!}{=}v_{Pa} \\[5px]
\label{v_H}
&\underline{v_H=v_T+v_P} \\[5px]
\end{align}
Analoges gilt auch für den Berührpunkt zwischen Planetenrad und Sonnenrad. Dort muss die Geschwindigkeit des Planetenrades (vPi=vT-vP) gleich der Umfangsgeschwindigkeit des Sonnenrades vS sein, sofern es sich um einen gleitfreien Abwälzvorgang handelt:
\begin{align}
&v_S\overset{!}{=}v_{Pi} \\[5px]
\label{v_S}
&\underline{v_S=v_T-v_P} \\[5px]
\end{align}
Subtrahiert man nun Gleichung (\ref{v_S}) von Gleichung (\ref{v_H}), dann ergibt sich letztlich folgender Zusammenhang zwischen den Umfangsgeschwindigkeiten des Sonnenrades vS, des Planetenrades vP und des Hohlrades vH:
\begin{align}
&v_H – v_S = v_T+v_P-v_T+v_P \\[5px]
&v_H = 2 \cdot v_P + v_S \\[5px]
\label{vvv}
&\underline{ v_P = \frac{v_H}{2} – \frac{v_S}{2} } \\[5px]
\end{align}
Wird der Zusammenhang aus Gleichung (\ref{v}) in Gleichung (\ref{vvv}) eingesetzt, dann erhält man den Zusammenhang zwischen den entsprechenden Drehzahlen:
\begin{align}
&v_P = \frac{v_H}{2} – \frac{v_S}{2} \\[5px]
&\pi \cdot n_P \cdot d_P = \frac{\pi \cdot n_H \cdot d_H}{2} – \frac{\pi \cdot n_S \cdot d_S}{2} \\[5px]
\label{nn}
&\boxed{n_P \cdot d_P = n_H \cdot \frac{d_H}{2} – n_S \cdot \frac{d_S}{2}} \\[5px]
\end{align}
Der sich aus Gleichung (\ref{nn}) ergebende Zusammenhang kann nun direkt mit der Grundgleichung (\ref{g}) gleichgesetzt werden und man erhält schließlich den folgenden Zusammenhang zwischen den Drehzahlen von Sonnenrad (S), Planetenradträger (T) und Hohlrad (H):
\begin{align}
&n_H \cdot \frac{d_H}{2} – n_S \cdot \frac{d_S}{2} = n_T \cdot \left(d_P + d_S \right) – n_S \cdot d_S \\[5px]
&n_H \cdot d_H – n_S \cdot d_S = 2 \cdot n_T \cdot \left(d_P + d_S \right) – 2 \cdot n_S \cdot d_S \\[5px]
\label{f}
&\underline{n_H \cdot d_H = 2 \cdot n_T \cdot \left(d_P + d_S \right) – d_S \cdot n_S} \\[5px]
\end{align}
Zusätzlich kann noch ausgenutzt werden, dass die Durchmesser von Hohlrad, Planetenrad und Sonnenrad nicht unabhängig voneinander sind. Der Hohlraddurchmesser dH entspricht der Summe aus Sonnenraddurchmesser dS und dem zweifachen Planetenraddurchmesser dP:
\begin{align}
&d_H = d_S + 2 \cdot d_P \\[5px]
&\underline{d_P = \frac{d_H-d_S}{2}} \\[5px]
\end{align}
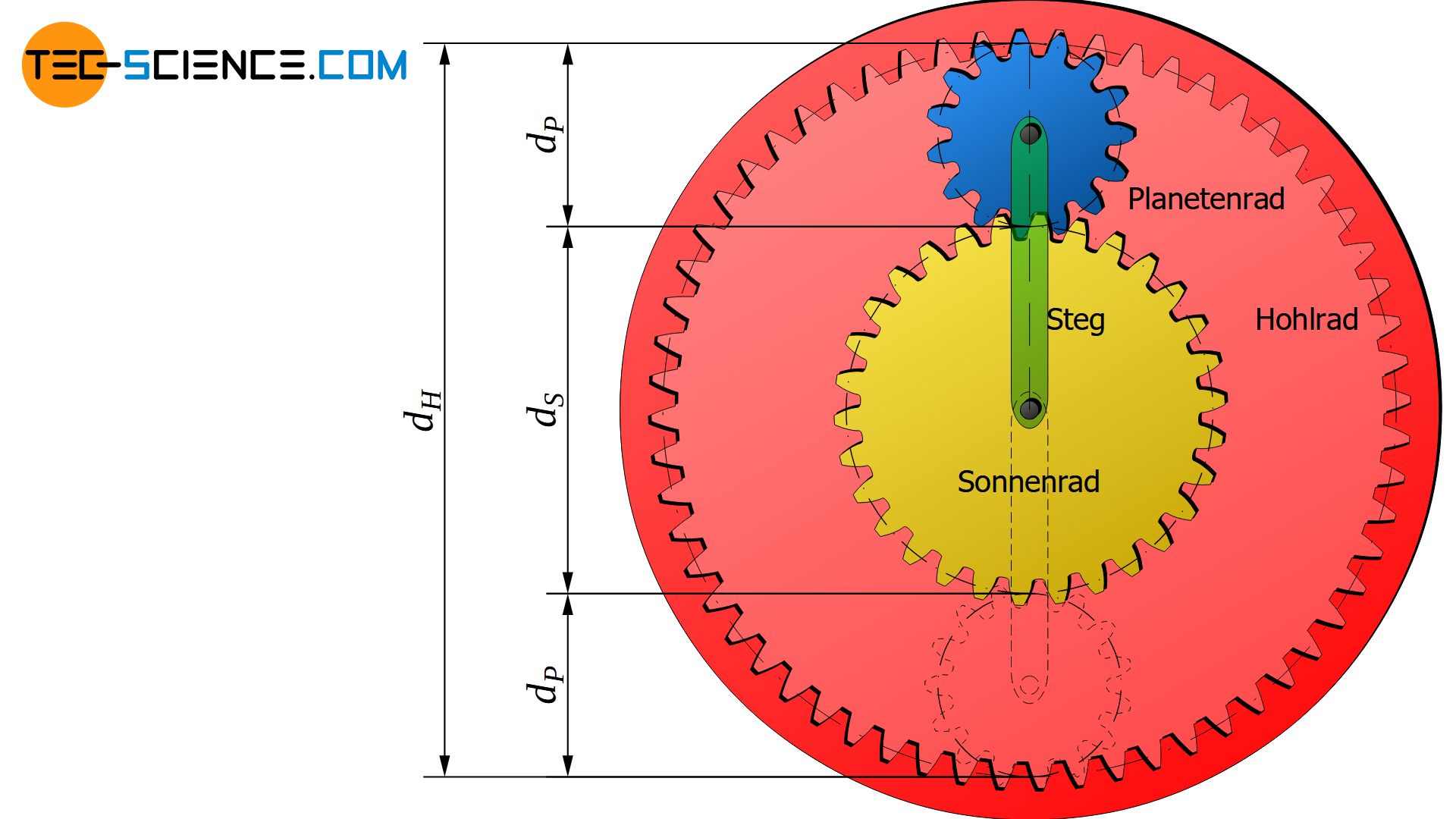
Damit ergibt sich die Planetenradgleichung für klassische einstufige Planetengetriebe, unabhängig von den Eigenschaften der Planetenräder, zu:
\begin{align}
&n_H \cdot d_H = 2 \cdot n_T \cdot \left(\frac{d_H-d_S}{2} + d_S \right) – d_S \cdot n_S \\[5px]
&n_H \cdot d_H =n_T \cdot \left(d_H – d_S + 2 \cdot d_S \right) – d_S \cdot n_S \\[5px]
&\underline{n_H \cdot d_H = n_T \cdot \left(d_H + d_S \right) – d_S \cdot n_S} \\[5px]
\end{align}
Da bei Zahnrädern die Wälzkreisdurchmesser d proportional zu den entsprechenden Zähnezahlen z sind, kann obige Gleichung auch über die Anzahl der Zähne des Hohlrades (zH) und die des Sonnenrades (zS) ausgedrückt werden:
\begin{align}
\label{pl}
&\boxed{n_H \cdot z_H = n_T \cdot \left(z_H + z_S \right) – z_S \cdot n_S} \\[5px]
\end{align}
Mit Hilfe dieser Gleichung lassen sich die unterschiedlichen Übersetzungsverhältnisse von Planetengetrieben erklären. Hierauf wird im Artikel Übersetzungsverhältnisse von Plantengetriebe näher eingegangen.