Übersetzungsverhältnisse von Plantengetriebe (Willis-Gleichung)

Erfahre in diesem Artikel mehr über die Herleitung der unterschiedlichen Übersetzungsverhältnisse von Planetengetriebe.

Willis-Gleichung für Planetengetriebe

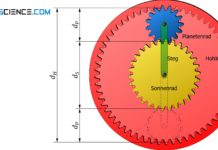
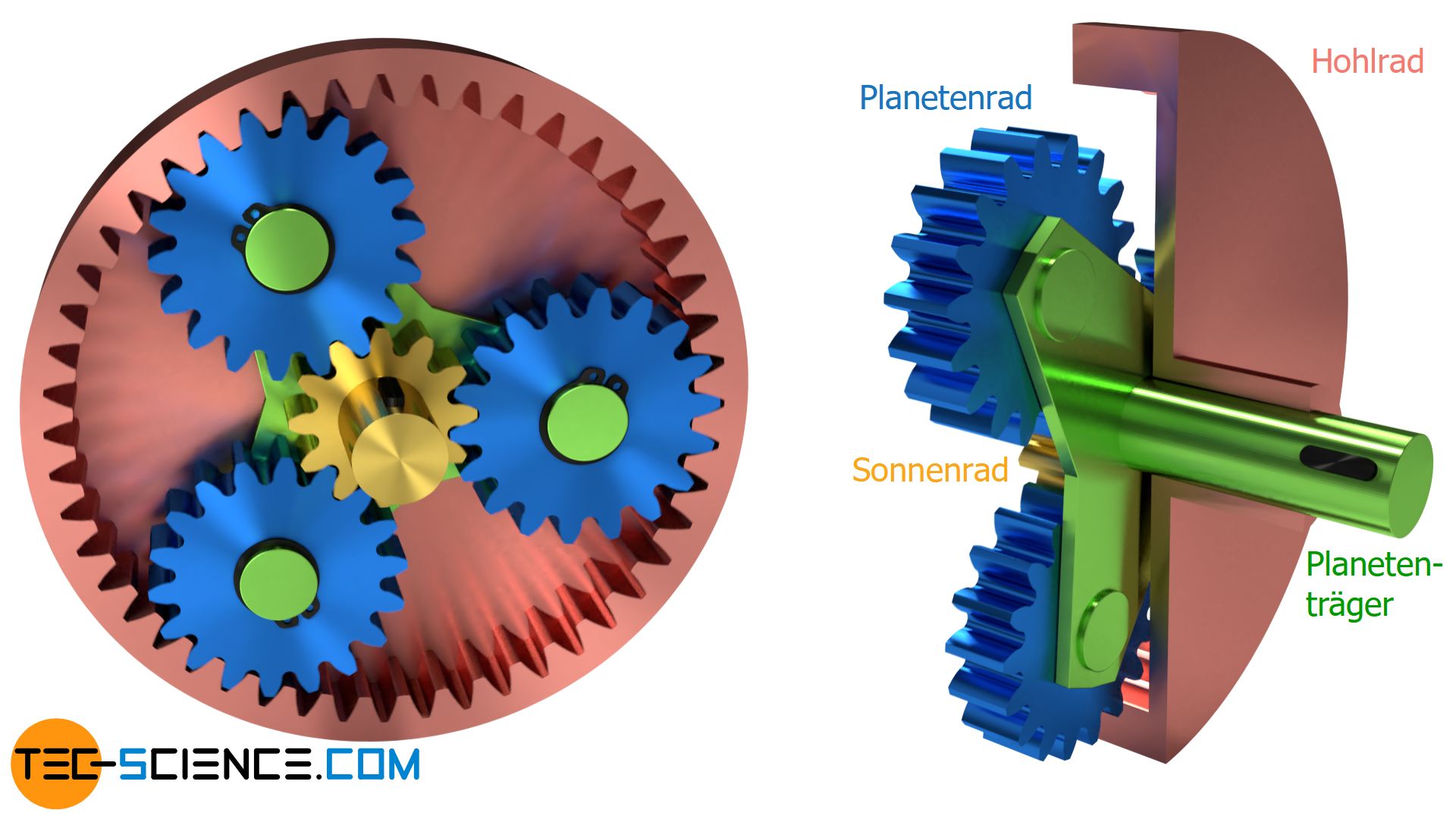
Im Artikel Willis-Gleichung angewendet auf Plantengetriebe wurde folgende Grundgleichung hergeleitet, die die Bewegungen von Sonnenrad (S), Hohlrad (H) und Träger (T) eines Planetengetriebes beschreibt:

\begin{align}
\label{pl}
&\boxed{n_H \cdot z_H = n_T \cdot \left(z_H + z_S \right) – z_S \cdot n_S} \\[5px]
\end{align}

In dieser Gleichung bezeichnet n die Drehzahl und z die Zähnezahl der entsprechenden Zahnräder. Mit dieser Gleichung lassen sich nun die unterschiedlichen Übersetzungsmöglichkeiten von Planetengetriebe zeigen.

Übersetzungsmöglichkeiten

Bei einem klassischen Planetenradgetriebe ergeben sich letztlich drei verschiedene Betriebsmodi, je nachdem welche Komponente (Sonnenrad, Planetenradträger oder Hohlrad) festgestellt wird. Der An- und Abtrieb erfolgt dann über die beiden anderen Komponenten. Welche Übersetzungsverhältnisse sich dabei jeweils ergeben, wird im Folgenden gezeigt.

Festgestelltes Sonnenrad

Für den Fall, dass das Sonnenrad festgestellt wird (n_S=0) und der Antrieb über das Hohlrad und der Abtrieb und den Planetenradträger erfolgt, ergibt sich gemäß Gleichung (\ref{pl}) folgendes Übersetzungsverhältnis i_S=n_H/n_T:

\begin{align}
&n_H \cdot z_H = n_T \cdot \left(z_H + z_S \right) – z_S \cdot \underbrace{n_S}_{=0} \\[5px]
&n_H \cdot z_H = n_T \cdot \left(z_H + z_S \right)  \\[5px]
&\frac{n_H}{n_T} = i_S = \frac{z_H+z_S}{z_H}     \\[5px]
\label{i_S}
&\boxed{i_S = 1+\frac{z_S}{z_H}} ~~~1<i_S<2 \\[5px]
\end{align}

Anhand von Gleichung (\ref{i_S}) zeigt sich, dass bei antreibendem Hohlrad und abtreibendem Planetenradträger das Übersetzungsverhältnis in jedem Fall größer 1 ist, d.h. eine Übersetzung ins Langsame vorliegt. Aber auch nach oben hin ist die Übersetzung begrenzt, da die Zähnezahl des Sonnenrades stets kleiner sein muss als die des Hohlrades (ansonsten wäre das Sonnenrad größer als das umschließende Hohlrad). Im theoretischen Grenzfall, wenn das Sonnenrad genauso groß ist wie das Hohlrad und beide somit identische Zähnezahlen aufweisen, ist das Verhältnis der Zähnezahlen z_S/z_H=1 und das Übersetzungsverhältnis damit maximal 2.

Wird An- und Abtrieb bei feststehendem Sonnenrad vertauscht, d.h. erfolgt der Antrieb über den Planetenradträger und der Abtrieb über das Hohlrad, dann liegen die umgekehrten Verhältnisse vor. Es ergibt sich eine Übersetzung ins Schnelle mit einem reziproken Übersetzungsbereich zwischen 1 und 0,5.

Anwendung finden die vorgestellten  Antriebsvarianten unter anderem bei Drei-Gang-Nabenschaltungen.

Festgestelltes Hohlrad

Eine weitere Möglichkeit zur Übersetzung bietet sich bei festgestelltem Hohlrad (n_H=0), wenn der Antrieb über das Sonnenrad und der Abtrieb über den Planetenradträger erfolgt. Dabei ergibt sich folgendes Übersetzungsverhältnis i_H=n_S/n_T:

\begin{align}
&\underbrace{n_H}_{=0} \cdot z_H = n_T \cdot \left(z_H + z_S \right) – z_S \cdot n_S \\[5px]
&0 = n_T \cdot \left(z_H + z_S \right) – z_S \cdot n_S \\[5px]
&\frac{n_S}{n_T} = i_H = \frac{z_H+z_S}{z_S} \\[5px]
\label{i_H}
&\boxed{i_H = 1+\frac{z_H}{z_S}} ~~~2<i_H<\infty \\[5px]
\end{align}

Im vorliegenden Fall erhält man also ebenfalls eine Übersetzung ins Langsame, dessen Übersetzungsverhältnis in jedem Fall größer 2 sein wird, da die Zähnezahl des Hohlzahnrades stets größer ist als die des Sonnenrades und deren Zähnezahlverhältnis somit größer 1 ist (z_H/z_S>1), d.h. eine Übersetzung ins Langsame vorliegt. Nach oben hin ist das Übersetzungsverhältnis hingegen nicht beschränkt, da das Hohlrad und damit dessen Zähnezahl prinzipiell beliebig groß gewählt werden kann und dann das Übersetzungsverhältnis gegen unendlich strebt.

Erfolgt im umgekehrten Fall der Antrieb nicht mehr über das Sonnenrad sondern über den Planetenradträger, dann erhält man wieder die reziproken Übersetzungsverhältnisse mit einem Wertebereich zwischen 0 und 0,5.

Festgestellter Steg (Planetenradträger)

Eine letzte Möglichkeit der Übersetzung bei klassischen Planetenradgetrieben zeigt sich bei festgestelltem Planetenradträger (Steg), wenn der Antrieb über das Sonnenrad und der Abtrieb über das Hohlrad erfolgt. In diesem Fall ergibt sich folgendes Übersetzungsverhältnis i₀=n_S/n_H:

\begin{align}
&n_H \cdot z_H = \underbrace{n_T}_{=0} \cdot \left(z_H + z_S \right) – z_S \cdot n_S \\[5px]
&n_H \cdot z_H = – z_S \cdot n_S \\[5px]
&\frac{n_S}{n_H} = i_0 = -\frac{z_H}{z_S} \\[5px]
\label{i_0}
&\boxed{i_0 = -\frac{z_H}{z_S}} ~~~\text{„Standübersetzung“}~~~-\infty<i_0<-1 \\[5px]
\end{align}

Auffällig im Übersetzungsverhältnis von Gleichung (\ref{i_0}) ist zunächst das negative Vorzeichen. Es bringt in diesem Fall zum Ausdruck, dass sich der Drehsinn zwischen Antrieb und Abtrieb ändert, d.h. eine Richtungsumkehrung stattfindet („Rückwärtsgang“). Ein solches Getriebe mit Richtungsumkehrung zwischen An- und Abtrieb wird auch als Minusgetriebe bezeichnet; bei gleichsinniger Drehrichtung entsprechend als Plusgetriebe. Im vorliegenden Fall des Minusgetriebes handelt es sich um eine Übersetzung ins Langsame innerhalb eines Übersetzungsbereichs zwischen-∞ und -1. Im umgekehrten Fall bei vertauschtem An- und Abtrieb erhält man folglich eine Übersetzung ins Schnell im Wertebereich zwischen -1 und 0.

Beachte, dass das Planetengetriebe bei diesen Übersetzungsvarianten nicht mehr nach dem Prinzip eines klassischen Umlaufgetriebes arbeitet, da bei festgestelltem Planetenradträger keine umlaufenden Achsen der Planetenräder mehr existieren. Es handelt sich dem Funktionsprinzip nach somit um ein Standgetriebe. Aus diesem Grund wird das Übersetzungsverhältnis bei festgestelltem Planetenradträger auch als Standübersetzung bzw. Standübersetzungsverhältnis i₀ bezeichnet!

Direktantrieb

Ein Planetengetriebe kann auch als Direktantrieb genutzt werden. Dabei werden Steg und Sonnenrad mit dem Hohlrad fest fixiert. In diesem Fall wird dann die Drehbewegung direkt von der Antriebswelle auf die Abtriebswelle übertragen (Übersetzungsverhältnis 1:1).  Ein solcher Direktantrieb kommt bspw. bei Drei-Gang-Nabenschaltungen als „2. Gang“ zum Einsatz.

Standübersetzung

Betrachtet man die Gleichungen (\ref{i_S}), (\ref{i_H}) und (\ref{i_0}), so lassen sich offensichtlich alle Übersetzungsvarianten mithilfe der Standübersetzung i₀=-z_H/z_S ausdrücken. Für ein festgestelltes Sonnenrad ergibt sich das Übersetzungsverhältnis i_S anhand der Standübersetzung dann wie folgt:

\begin{align}
&\boxed{i_S = 1-\frac{1}{i_0}}  \\[5px]
\end{align}

Für ein festgestelltes Hohlrad lässt sich das entsprechende Übersetzungsverhältnis i_H wie folgt mithilfe der Standübersetzung ausdrücken:

\begin{align}
&\boxed{i_H = 1-i_0}\\[5px]
\end{align}

Auch die allgemeine Gleichung (\ref{pl}) der Planetengetriebe kann durch die Standübersetzung i₀ ausgedrückt werden:

\begin{align}
&n_H \cdot z_H = n_T \cdot \left(z_H + z_S \right) – z_S \cdot n_S \\[5px]
&n_H \cdot \frac{z_H}{z_S} = n_T \cdot \left( \frac{z_H}{z_S} + 1 \right) – n_S \\[5px]
& – n_H \cdot i_0 = n_T \cdot \left(1-i_0 \right) – n_S \\[5px]
&\boxed{ n_S = n_T \cdot \left(1-i_0 \right) + n_H \cdot i_0 }~~~\text{mit}~~~\boxed{i_0=-\frac{z_H}{z_S}}~~~\text{Standübersetzung} \\[5px]
\end{align}