Erfahre in diesem Artikel mehr über Aufbau, Funktion und Anwendung eines Differential-Getriebes und die Differentialsperre.
Weshalb benötigt man ein Differentialgetriebe?
In Automobilen werden die Räder in der Regel über ein Kegelradgetriebe vom Motor angetrieben. Dies ermöglicht eine Umlenkung der Drehbewegung vom Motor zu den Rädern um 90°. Wären die anzutreibenden Räder dabei jedoch über eine gemeinsame Welle starr miteinander verbunden, so würde dies bei Kurvenfahrten zu Problemen führen. So muss nämlich das äußere Rad bei der Kurvenfahrt eine größere Strecke zurücklegen als das innere Rad. Da beide Räder die Kurvenfahrt jedoch in derselben Zeit durchlaufen müssen, muss sich das äußere Rad in der Kurve folglich schneller drehen als das innere Rad.

Wären die beiden Räder dabei über eine gemeinsame Welle verbunden, dann würde sich aufgrund der unterschiedlichen Rotationsgeschwindigkeiten die Welle in sich verdrehen. Diese Verdrehung gleicht sich früher oder später durch ein Durchrutschen eines der Räder wieder aus (Schlupf). Dieses Rutschen in der Kurve reduziert nicht nur die Fahrsicherheit sondern führt zu großem Reifenverschleiß und auf Dauer auch zum Bruch der Welle.
Bei Kurvenfahrten muss das äußere Rad schneller rotieren können als das innere Rad!
Aus diesem Grund wurde in den Anfangszeiten des Automobils auch nur eines der Räder angetrieben und das andere Rad frei rotierbar auf der Welle montiert, sodass sich an beiden Rädern unterschiedliche Geschwindigkeiten einstellen konnten. Ein solcher einseitiger Antrieb führ aber dazu dass das Fahrzeug versucht eine leichte Kurve zu fahren. Dies reduziert nicht nur den Fahrspaß sondern auch die Fahrsicherheit. Man musste deshalb eine Lösung finden beide Räder gleichzeitig antreiben zu können und dabei jedoch unterschiedliche Geschwindigkeiten zuzulassen. Dies war die Geburtsstunde des Differentialgetriebes (kurz Differential oder Differenzial genannt).
Die untere Abbildung zeigt das Differentialgetriebe eines LKWs. Zu sehen ist das Ritzel (in der Animation oben gelb dargestellt) und das Kegelrad (in der Animation oben orangefarben abgebildet). Die weiteren Kegelräder sind im Inneren des Gehäuses und nicht von außen zu sehen.

Aufbau eines Differentialgetriebes
Der Aufbau und die Funktionsweise eines Differentialgetriebes ist auf den ersten Blick nicht ganz einfach nachzuvollziehen. Es stellt sich vor allem die Frage wie man auf eine solche Anordnung der Zahnräder überhaupt kommt, die dann den Zweck der unterschiedlichen Rotationsgeschwindigkeiten erfüllt. Um dies zu verstehen ist es sinnvoll zunächst die einzelnen Schritte die hinter der Idee des Differentialgetriebes stecken nachvollziehen zu können.
1. Schritt: Antrieb der getrennten Wellen über Stifte und einen frei rotierbaren Stab
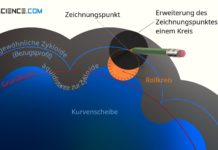
Der Beginn der Idee steckt zunächst darin, dass die gemeinsame Antriebswelle geteilt wird, sodass jedes Rad eine eigene Antriebswelle bekommt. Damit wird sichergestellt, dass es nicht zu einem Verdrehen der Welle kommt, wenn eines der beiden Räder später langsamer bzw. schneller rotieren sollte. An den getrennten Wellen werden nun jeweils zwei Stifte befestigt. Zwischen diesen Stiften treibt ein frei rotierbarer Stab die jeweiligen Radwellen an.

Auf diese Weise wird nun erreicht, dass sich die Räder innerhalb einer gewissen Grenze unterschiedlich stark verdrehen lassen. Wird eines der Räder verlangsamt, so kann das gegenüberliegende Rad durch den drehbaren Stab noch etwas weiter bewegt werden. Zu stark sollte die unterschiedliche Rotation in diesem Schritt jedoch nicht erfolgen, da ansonsten der Stab aus den Stiften gleitet und dann keine Kraft mehr übertragen werden kann.
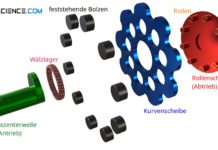
2. Antrieb der Wellen über mehrere Stifte und frei rotierbare Stäbe
Um die eingeschränkte Beweglichkeit zu vergrößern, können nun ganz einfach mehrere Stifte und drehbare Stäbe verwendet werden, sodass diese jeweils nacheinander ineinander gleiten können. Damit ist der Unabhängigkeit des Radantriebs keine Grenzen mehr gesetzt. Eines der Räder kann nun mit gänzlich unterschiedlicher Geschwindigkeit rotieren und sogar stillstehen, während das gegenüberliegende Rad weiter angetrieben werden kann. Eine solche Anordnung stellt im Prinzip bereits ein voll funktionsfähiges Differentialgetriebe dar!

Bei genauer Betrachtung zeigt sich, dass mit einem solchen Differentialgetriebe das verlangsamte Rad im selben Maße abgebremst wird wie das gegenüberliegende Rad beschleunigt wird. Der Geschwindigkeitsverlust auf der einen Radseite wird durch einen gleich großen Geschwindigkeitsgewinn auf der gegenüberliegenden Radseite wieder kompensiert. Hinter diesem Prinzip steckt letztlich nicht anderes als die Energieerhaltung.
Ein solches kinematisches Verhalten der Räder ist genau das, was in Kurvenfahrten von Nöten ist. Bei einer Kurvenfahrt muss nämlich das innen liegende Rad im selben Maße langsamer rotieren wie das äußere Rad schneller rotieren muss. Diese Funktionsweise macht das Differentialgetriebe perfekt geeignet für den Antrieb in Kurven!
Durch ein Differentialgetriebe rotiert in Kurvenfahrten das innere Rad im selben Maße langsamer wie das äußere Rad schneller rotiert!
3. Schritt – Ersetzen der Stifte und Stäbe durch Zahnräder (Kegelräder)
Die Kraftübertragung durch Stifte und Stäbe ist nicht sehr effektiv. Deshalb werden diese durch Zahnräder ersetzt, genauer gesagt durch Kegelräder. Das blau dargestellte, um die Wellen umlaufende Kegelrad, wird auch als Umlaufkegelrad bezeichnet.

4. Schritt – Antrieb der Wellen über weitere Kegelräder
Der Antrieb des Umlaufkegelrades erfolgt in Automobilen natürlich nicht von Hand sondern durch den Motor. Dieses Kegelrad wird wiederum durch ein Kegelradgetriebe angetrieben (meist ein Hypoidgetriebe), bestehend aus dem gelb dargestellten Ritzel (Motorwelle) und dem orangefarbenen Kegelrad. Auf diesem orangefarbenen Kegelrad befindet sich dann das blau dargestellte Kegelrad, das die Räder antreibt. Das das orangefarbene Kegelrad das Umlaufkegelrad „trägt“, wird dieses auch als Umlaufradträger bezeichnet.

5. Schritt – Symmetrische Anordnung der Kegelräder zur Vermeidung von Biegebeanspruchungen
Damit Biegespannungen in den Antriebswellen der Räder vermieden werden, werden diese in der Regel nicht durch ein Umlaufkegelrad sondern durch zwei Umlaufkegelräder angetrieben. Dieses zweite Umlaufkegelrad ist dabei um 180° versetzt angeordnet.

Aus der unteren Abbildung wird nun direkt ersichtlich, dass sich bei der Verwendung zweier Umlaufkegelräder die Kräfte in horizontaler Richtung gegenseitig kompensieren. Die Antriebswellen der Räder werden dann rein auf Torsion beansprucht, aber nicht auf Biegung!

Kinematik des Differentialgetriebes
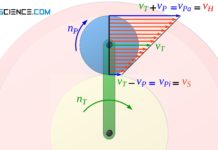
Bei Geradeausfahrten wird im Normalfall keines der Räder gezwungen langsamer oder schneller als das andere zu rotieren. In diesem Fall treiben die Umlaufkegelräder ohne Relativbewegung die Radwellen an. Die Räder rotieren dann mit derselben Geschwindigkeit wie der Umlaufradträger.
Fährt man nun jedoch bspw. in eine Rechtskurve ein, dann wird das innen liegende Rad durch die geringere zu fahrende Wegstrecke verlangsamt. Im selben Maße muss jedoch dann das äußere Rad schneller rotieren, da es im Vergleich zur Mittellinie eine im selben Maße größere Wegstrecke zurücklegen muss. Ein Differentialgetriebe durch seinen speziellen Aufbau erzeugt letztlich genau dies! Der genaue mathematische Zusammenhang wird im nachfolgenden Abschnitt „Differentialgetriebe als Sonderform des Planetengetriebes“ näher erläutert.
Am besten kann man die Kinematik dabei verstehen, wenn man sich eine extreme Kurvenfahrt vorstellt, wo das innere praktisch auf der Stelle stehen bleibt und das äußere Rad ein kreisförmige Bahn um das innere Rad ausführt. Der Umlaufradträger treibt in diesem Fall das Umlaufkegelrad um das stillstehende Kegelrad der Radwelle. Die Umlaufkegelräder beginnen sich dann zu drehen und führen nun Relativbewegungen aus. Das gegenüberliegende Kegelrad der linken Antriebswelle wird durch diese Rotation der Umlaufkegelräder nun zusätzlich zur bereits vorhandenen Rotation des Umlaufradträgers angetrieben und rotiert folglich schneller.
Im Vergleich zum Umlaufradträger rotiert das innen liegende Rad bei Kurvenfahrten im selben Maße langsamer wie das äußere Rad schneller rotiert.
Erst wenn die Kurvenfahrt zu Ende ist und sich die Drehzahlen der Räder wieder angeglichen haben führen beide Radwellen keine Relativbewegung zueinander mehr aus und die Drehzahl des Umlaufradträgers entspricht den Drehzahlen der Räder.
Auch wenn sich die Drehzahlen der Räder in Kurvenfahrten unterscheidet, so werden beide Räder jedoch stets mit demselben Drehmoment angetrieben! Denn bei Getrieben ergibt sich die Drehmomentänderung lediglich über das Verhältnis der Zähnezahlen der Zahnräder. Das Differentialgetriebe ist aber symmetrisch aufgebaut und unterscheidet sich zwischen linker und rechter Antriebswelle nicht in den Zähnezahlen. Zwischen Motor und den Antriebswellen ergeben sich somit stets dieselben Drehmomentwandlungen. Beide Räder weisen deshalb dasselbe Drehmoment auf. Man erhält durch das Differential also an keinem der Räder einen Drehmomentvorteil bzw. -nachteil.
Auch wenn sich das jeweilige Drehmoment an den Rädern also nicht unterscheidet, so weisen diese unterschiedliche Leistungen auf, da sich die Leistung aus der Kombination von Drehmoment M und Drehzahl n bestimmt:
\begin{align}
\boxed{P=2 \pi \cdot M \cdot n} \\[5px]
\end{align}
Beachtet werden muss jedoch, dass wenn das Differential in Kurven aktiv ist, Relativbewegungen der Kegelräder vorhanden sind, die zu einer zusätzlichen Minderung des Getriebewirkungsgrades führen.
Eine Differentialgetriebe teilt zwar die Drehzahlen und damit die Motorleistung auf die unterschiedlichen Räder auf, das Drehmoment ist jedoch an beiden Rädern identisch!
Differentialgetriebe als Sonderform des Planetengetriebes
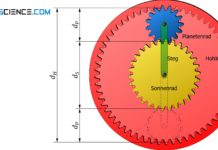
Das Differentialgetriebe gehört zu Gruppe der sogenannten Umlaufgetriebe (Planetengetriebe), da es umlaufende Drehachsen besitzt. In diesem Fall sind es die Drehachsen der Umlaufräder. Die Umlaufräder entsprechen letztlich den Planetenräder in Planetengetrieben. Der Planetenradträger (Steg) wird bei Differentialgetrieben durch den Umlaufradträger gebildet. Eines der Kegelräder kann dabei als Sonnenrad aufgefasst werden. Das gegenüberliegende Kegelrad entspricht dann im übertragenen Sinne dem Hohlzahnrad bei typischen Planetengetrieben.
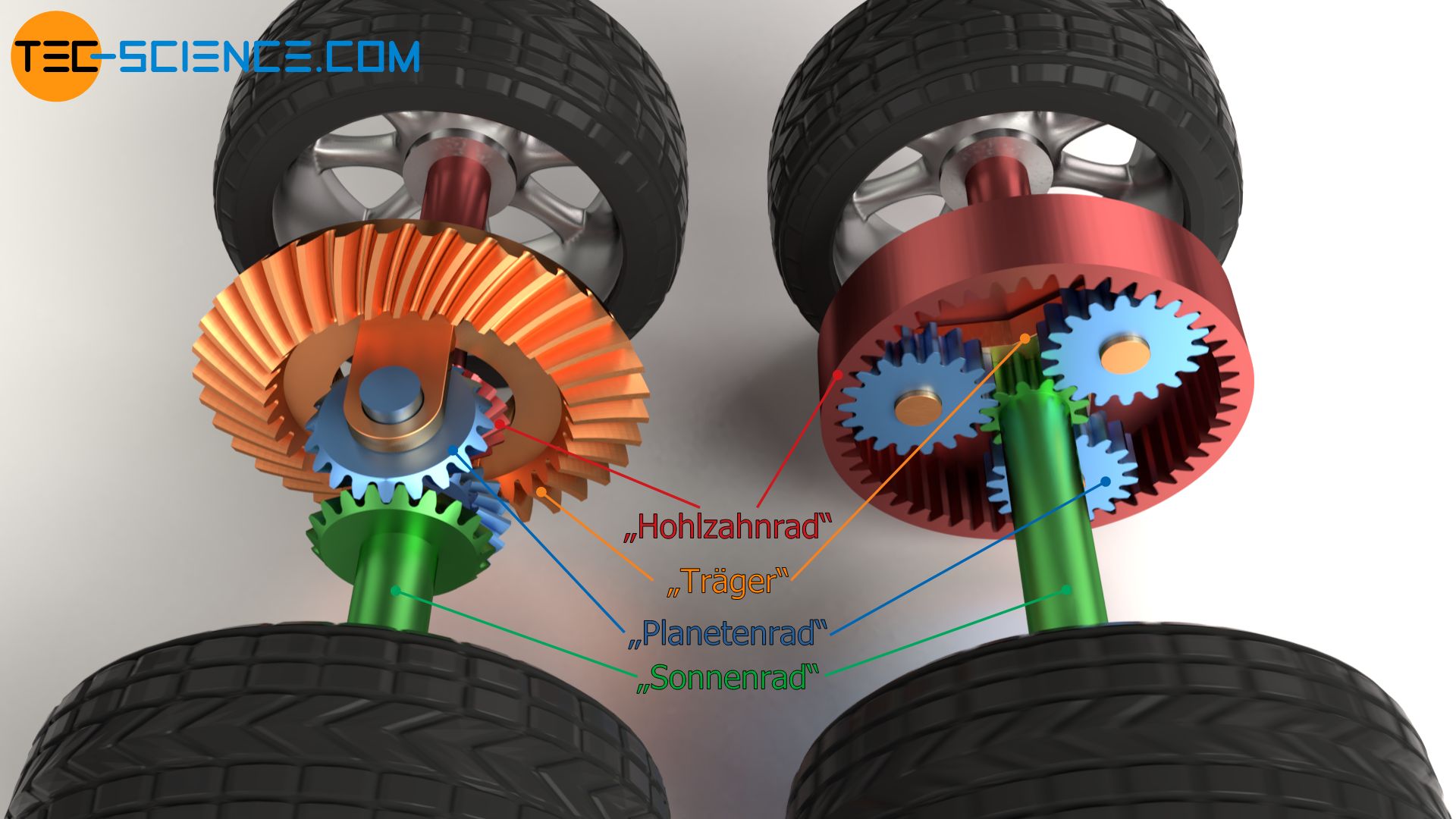
Da das Differentialgetriebe somit eine Sonderform des Planetengetriebes ist, lassen sich die Zusammenhänge der verschiedenen Drehzahlen auch durch die Grundgleichung für Umlaufgetriebe (Willis-Gleichung) beschreiben:
\begin{align}
&\boxed{ n_S = n_T \cdot \left(1-i_0 \right) + n_H \cdot i_0} \\[5px]
\end{align}
Für klassische Planetengetriebe bezeichnet dabei nH die Drehzahl des Hohlzahnrades, nS die Drehzahl des Sonnenrades und nT die Drehzahl des Planetenradträgers (Steg), sowie i0 die sogenannte Standübersetzung, d.h. das Übersetzungsverhältnis bei festgehaltenem Planetenradträger.
Im Falle des Differentialgetriebes entspricht die Standübersetzung dem Übersetzungsverhältnis welches bei stillstehendem Umlaufradträger erhalten wird. Wird in diesem Zustand an einem der Räder gedreht (dem „Hohlzahnrad“), dann rotiert das gegenüberliegende Rad (das „Sonnenrad“) offensichtlich mit derselben Drehzahl, aber in umgekehrter Richtung. Die Standübersetzung des Differentials entspricht damit i0=-1.
Wird die Standübersetzung eines Differentialgetriebes von i0=-1 in die obere Grundgleichung eingesetzt, dann gelten folgende Zusammenhänge:
\begin{align}
& n_S = n_T \cdot \left(1-i_0 \right) + n_H \cdot i_0 ~~~\text{mit}~i_0=-1~~~~\text{folgt:} \\[5px]
&n_S = n_T \cdot \left(1-(-1) \right) + n_H \cdot (-1) \\[5px]
&n_S = n_T \cdot 2 – n_H \\[5px]
&n_H + n_S = 2 \cdot n_T \\[5px]
\end{align}
Da es bei Differentialgetrieben im eigentlichen Sinne kein klassisches Sonnenrad bzw. Hohlrad gibt, werden die entsprechenden Drehzahlen der Räder mit n1 (=nH) bzw. n2 (=nS) bezeichnet. Die Drehzahl des Umlaufradträgers kann jedoch weiterhin mit nT bezeichnet werden. Somit gilt dann folgender Zusammenhang zwischen den Drehzahlen der Räder n1 bzw. n2 und der Drehzahl des Umlaufradträgers nT:
\begin{align}
&\boxed{n_1 + n_2 = 2 \cdot n_T} \\[5px]
\end{align}
Nun wird auch auf mathematischem Wege ersichtlich, dass bei konstanter Motordrehzahl bzw. konstanter Drehzahl des Umlaufradträgers, eine Verringerung der Drehzahl an einem der Räder eine im selben Maße vergrößerte Drehzahl am gegenüberliegenden Rad zur Folge hat. So ist die rechte Seite der Gleichung bei konstanter Drehzahl des Umlaufradträgers stets konstant. Dies gilt dann folglich auch für die Summe der Räderdrehzahlen. Oder anders ausgedrückt: Die Drehzahl des Umlaufradträgers entspricht dem Mittelwert der Räderdrehzahlen:
\begin{align}
&\boxed{n_T = \frac{n_1 + n_2}{2}} \\[5px]
\end{align}
Differentialsperre
Der große Vorteil von Differentialgetrieben besteht also bei Kurvenfahrten durch Aufteilen der Drehzahlen bzw. Leistungen auf die jeweiligen Räder entsprechend ihrem Bedarf. In manchen Situationen kann dies jedoch auch ein Nachteil sein. So kann es bspw. beim Anfahren auf glattem oder rutschigem Untergrund dazu kommen, dass eines der Räder die Haftung verliert und durchrutscht. Das andere Rad bleibt dann auf dem Boden stehen. Das Differentialgetriebe gibt nun die gesamte Leistung auf das durchdrehende Rad, während am stehenden Rad keine Leistung ankommt. Das rotierende Rad dreht nun mit doppelter Geschwindigkeit, während das andere Rad weiterhin stillsteht. Man erhält auf diese Weise kaum eine vorwärts treibende Kraft und wenn dann nur einseitig durch die Gleitreibung des durchdrehenden Rades.
Ein solcher Fall, dass eines der Räder eine geringere Haftung hat als das andere und damit versucht ist durchzudrehen, tritt vor allem bei Geländerfahrten auf, bei denen die Räder je nach Fahrzeuglage unterschiedlich stark belastet werden. Aber auch bei schnellen Kurvenfahrten, bei denen das innere Rad durch die nach außen wirkenden Fliehkräfte stark entlastet wird, steigt die Gefahr des durchdrehenden Reifens und die einseitige Leistungsverteilung droht. Kippt das Fahrzeug im schlimmsten Fall etwas nach außen und das Innenrad verliert die Haftung, dann erhält dieses Rad die volle Leistung und rotiert mit doppelter Geschwindigkeit in der Luft. Das gegenüber liegende Rad, welches die Haftung zum Boden noch hat erhält jedoch keine Leistung und somit ist kein Antrieb des Autos mehr möglich.
In den oben genannten Fällen ist ein Differentialgetriebe also hinderlich. Aus diesem Grund werden vor allem Geländefahrzeuge mit sogenannten Differentialsperren ausgerüstet. Eine solche Differentialsperre verbindet dann die beiden Antriebswellen der Räder wieder starr miteinander und setzt damit das Differential außer Kraft. Jedoch kommt es aber dann zu der bereits eingangs erläuterten Verdrehung der Antriebswelle bei Kurvenfahrten. Differentialsperren sollten also nur in Ausnahmen aktiv werden.