Each type of lattice structure has a different number of slip systems (possibilities of sliding) and is therefore differently deformable.
Slip system
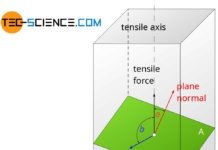
As explained in the article on Fundamentals of Deformation, a plastic deformation processes in metals can be attributed to slippage of atomic blocks on lattice planes. A lattice plane is an arbitrarily imaginary plane which is regularly occupied with atoms. Not only those planes are considered as lattice planes with which the structure of the different lattice types was explained in the chapter Important types of lattice structures!
A lattice plane refers to a plane in a lattice structure that is regularly covered with atoms!
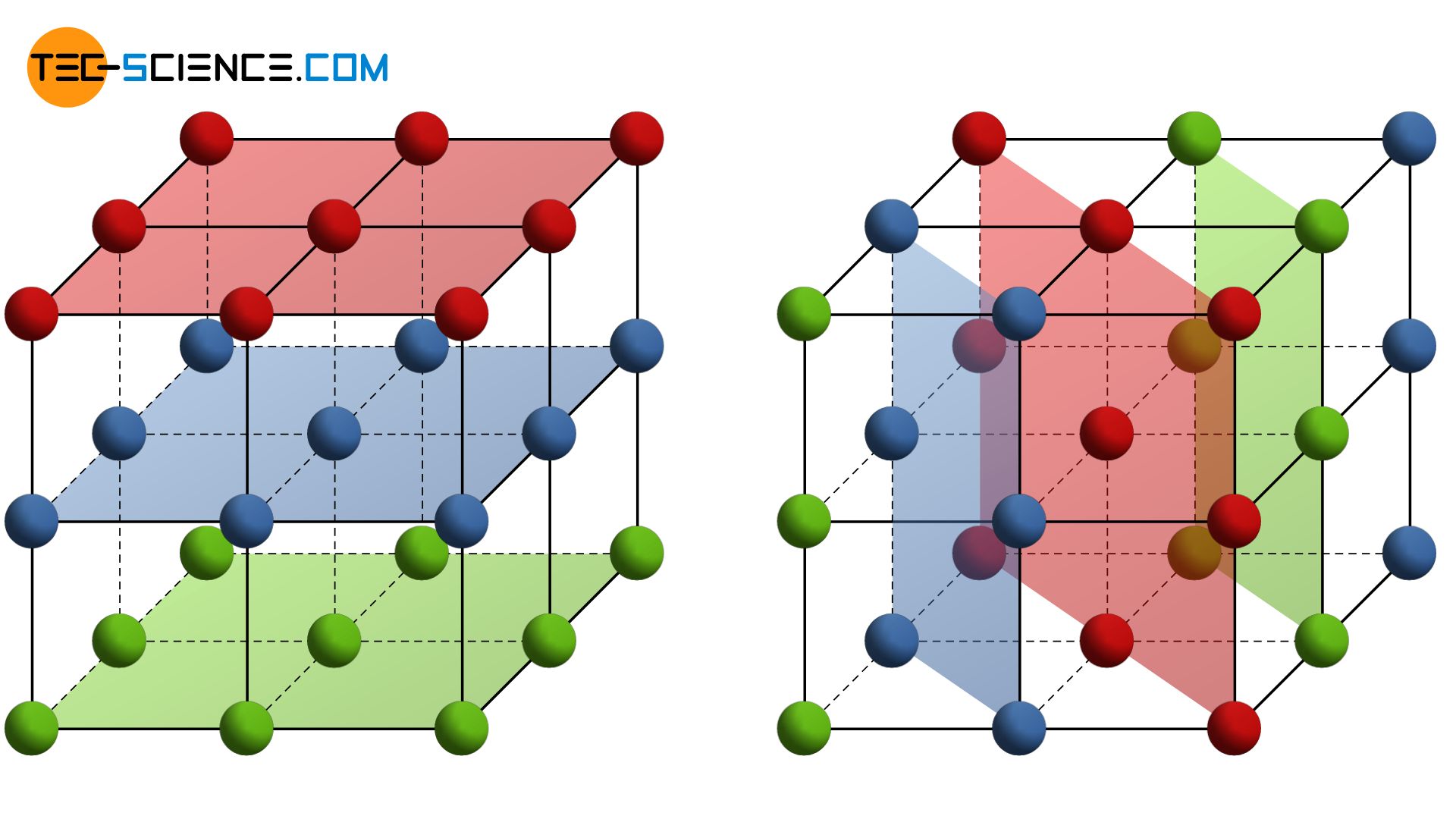
The figure above shows schematically possible lattice planes in a crystal. At this point, it should be expressly mentioned that the “bars” represent no bonds in the imaging of unit cells. Just because two atoms are connected by a bar does not necessarily mean that there is a particularly strong bond between these atoms! Thus, for example, in cubic lattice types not only the outer surfaces of the cubes form lattice planes, but also arbitrarily inclined planes. One should imagine the lattice structure just without the “bars” when it comes to lattice planes.
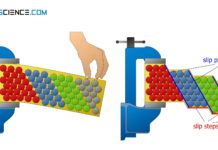
If a shearing of entire atomic layers can take place on such a lattice plane, it is referred to as slip plane.
Slip planes are lattice planes on which entire atomic layers can slide!
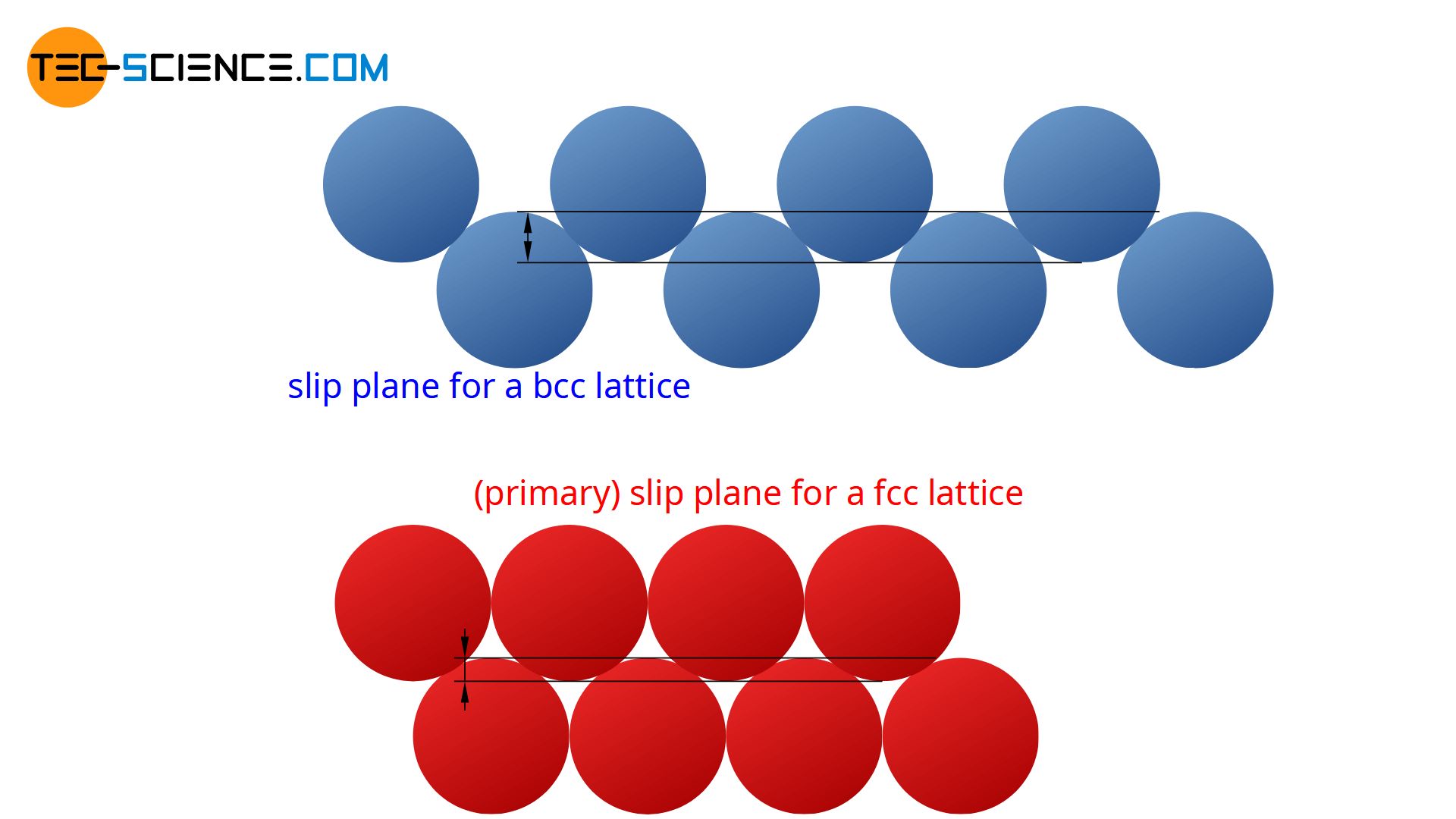
Although there are countless lattice planes in a lattice structure, not all are suitable as slip planes. The reason for this is the electrostatic forces acting between the atoms, which bind the atomic planes more or less strongly to each other. In a lattice structure, those lattice planes preferably serve as slip planes, which have the greatest possible distance from each other (“low attraction forces between the planes”). In addition, the lattice planes should contain as many atoms as possible (“gentle sliding of the planes”).
The displaceability of a slip plane is basically not given in all directions for energetic reasons. Thus, a slip plane is very difficult to move in the direction in which the stacking sequence would change. For then, for example, a face-centered cubic lattice would create a hexagonal one. But finally there are energetic reasons why a lattice crystallizes in a certain lattice type.
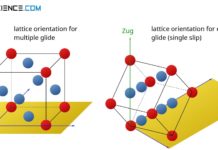
For a good ductility, therefore, a metal must, in addition to a large number of different slip planes, also have the highest possible number of so-called slip directions. It is this combination of slip plane number and number of slip directions that determines the overall slip options and thus the deformability. The combination of slip plane and slip direction is referred to as a slip system.
The number of slip systems describes the sliding possibilities of a lattice structure and is therefore a measure of their ductility.
Note that good deformability does not necessarily mean that a lattice structure must already be deformed by small forces. Good ductility rather means, that the lattice structure should deform without damage (“cracking”). Therefore a lattice structure should have as many slip systems as possible.
Metals and their lattice structures
The different lattice structures (fcc, bcc, hcp, etc.) each have different numbers of slip systems both in quantity and in quality. This is primarily the reason why metals can be deformed to different degrees depending on the type of lattice.
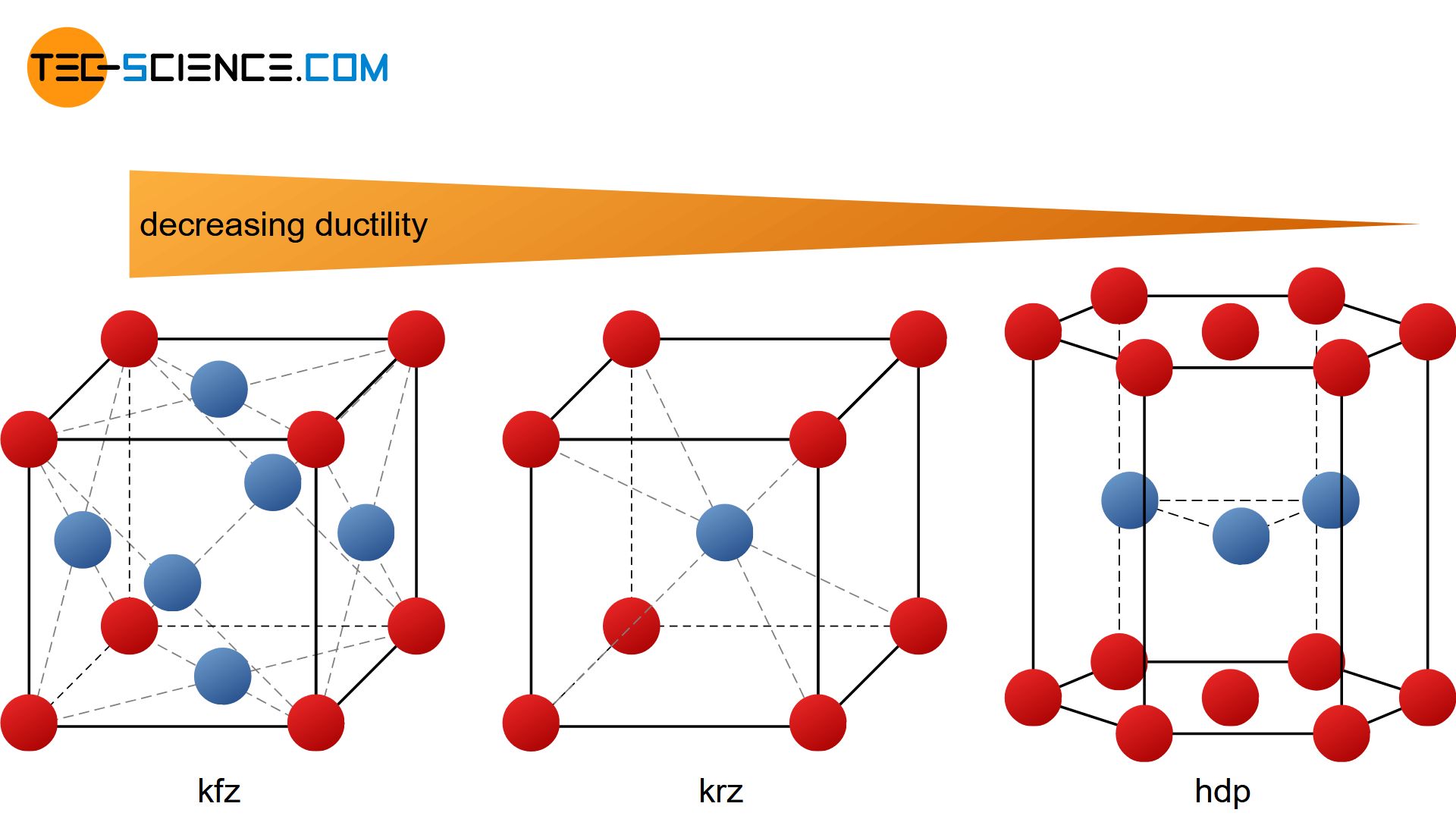
Metals such as magnesium, cobalt, zinc or titanium can hardly be plastically deformed under normal conditions. They would rather crack. All these metals have in common that they are present in a hexagonal closest packed lattice structure (hcp-lattice). This type of lattice obviously offers only a few slip systems.
By contrast, metals such as aluminum, lead, copper and nickel have very good deformability. This is obviously due to their face-centered cubic structure (fcc-lattice), which offers many slip systems.
The ductility of the body-centered cubic lattice (bcc-lattice) lies between the lattice types mentioned above. Typical representatives of this structure are metals such as iron, chromium, molybdenum and vanadium.
The ductility steadily decreases starting from the fcc lattice via the bcc lattice all the way to the hcp-lattice!
Due to the good ductility of the face-centered cubic lattice structure of copper and aluminum (or alloys thereof), these metals are often used as so-called wrought metals. On the other hand, the metals magnesium and zinc are mainly used as cast metals due to their hardly deformable lattice.
Body-centered cubic structure
The body-centered cubic lattice (bcc) has mainly 6 slip planes on which the lattice blocks preferably slide off. This corresponds to the levels which in addition to two atoms on a cube edge also include the body-centered atom as well as the diagonally opposite atoms.
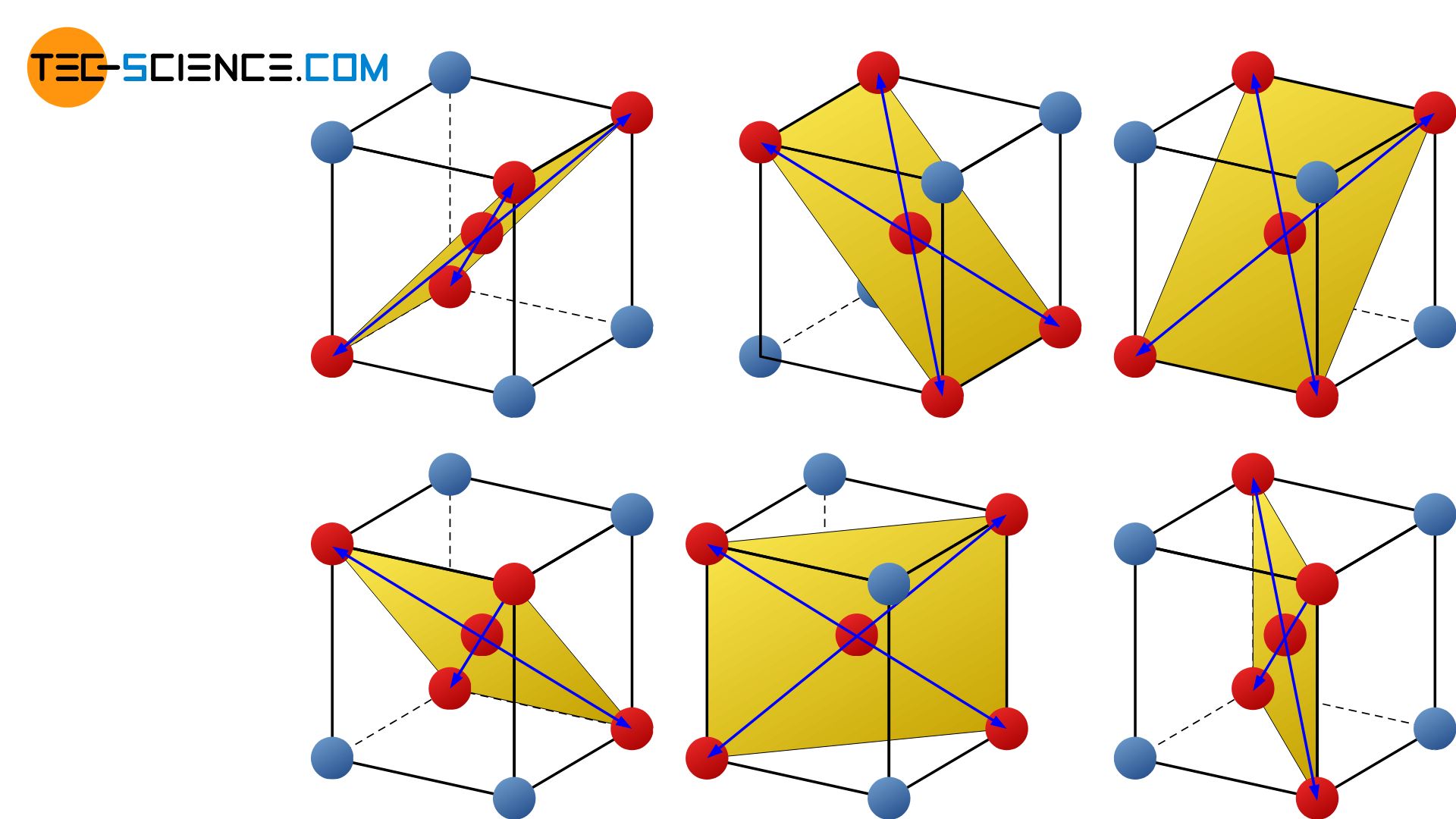
There are 2 possible slip directions for each slip plane. This corresponds to the area diagonals of the defined plane (marked in yellow). Other directions of sliding are out of the question due to the strong forces of attraction. The bcc-lattice thus has mainly 12 sliding possibilities (= 6 slip planes x 2 slip directions), how the atomic blocks can shear one another.
The body-centered cubic lattice structure has mainly 12 slip systems!
Figure: Slip planes and directions in the bcc-lattice
Not only the diagonal planes but also other atomic planes can serve as slip planes if greater forces are applied. However, since these slip planes are activated only with higher forces due to the larger electrostatic attraction, they do not decisively determine the deformability for small forces. So it remains at the 12 mainly operated slip planes in the body-centered cubic lattice. If all sliding options are taken into account, then one would come to a total of 48 slip systems.
At high forces, up to 48 slip systems can be activated in the body-centered cubic lattice!
Face-centered cubic structure
In contrast to the bcc-lattice, a total of 4 four slip planes can be found in the face-centered cubic lattice (fcc), on which atomic blocks preferably slide off. These are the closest packed layers that run diagonally through the unit cell. There are 3 slip directions for each of these slip planes.
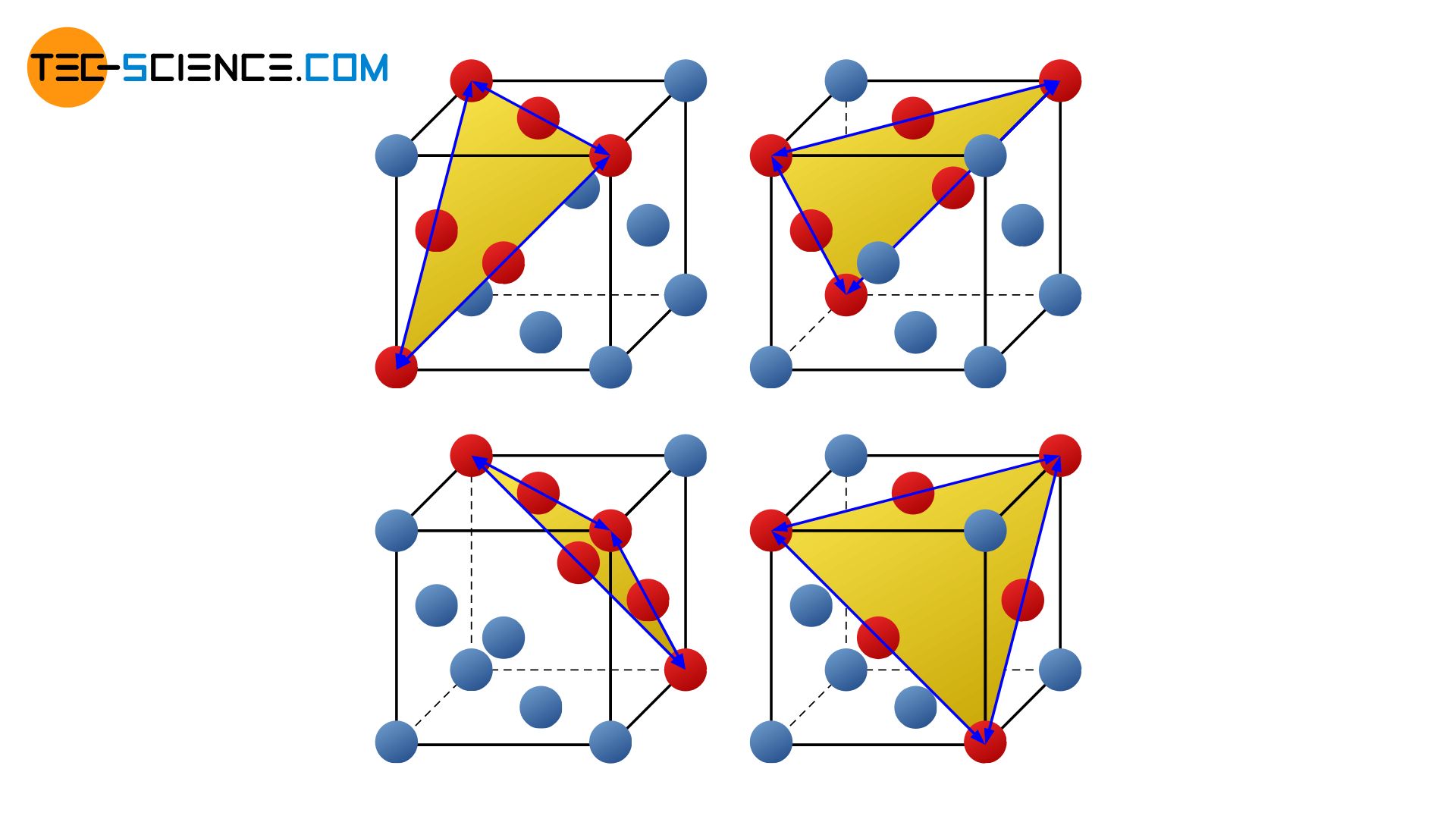
Note that shearing only occurs in the direction in which the stacking sequence (ABCABC …) is maintained. Because by changing the stacking sequence (e.g. in ABAB …), for example, a fcc-lattice would become partially a hexagonal closest packed structure. However, this condition is hardly realizable due to the high forces required. After all, there is an (energetic) reason why the lattice structure is face-centered cubic and not hexagonal.
Like the bcc-lattice, the fcc-lattice therefore has a total of 12 slip systems (= 4 slip planes x 3 slip directions).
The face-centered cubic lattice structure has a total of 12 slip systems!
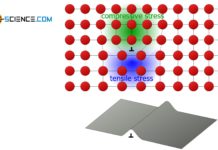
Due to the same number of slip systems, one could prematurely conclude that both lattices (fcc and bcc) are equally deformable. In practice, however, it is found that the fcc-lattice shows a significantly higher ductility.
The reason for this is that the slip planes in the fcc-structure are closest packed compared to the bcc-lattice. The “lifting out” of the atomic blocks from the “hollows” thus requires a significantly lower energy expenditure. Shearing processes therefore take place with less effort.
In addition to the main criterion of the number of slip systems (quantity), the quality of the slip planes also plays a role in ductility.
Due to the closest packed slip planes, the face-centered cubic lattice is more ductile despite the same number of slip systems as the body centered cubic lattice!
Note: Slip planes on which the atoms are closest packed are also called primary slip planes. Such closest packed levels are not present in the bcc-latticed (see article Important types of lattice structures)!
Hexagonal closest-packed lattice structure
In contrast to the fcc-lattice with a total of 4 primary slip planes, the hexagonal closest packed lattice (hcp) has only 1 primary slip plane. It is the hexagonal base of the unit cell. There are 3 slip directions for this slip plane, so that the hcp-lattice has a total of 3 slip systems.
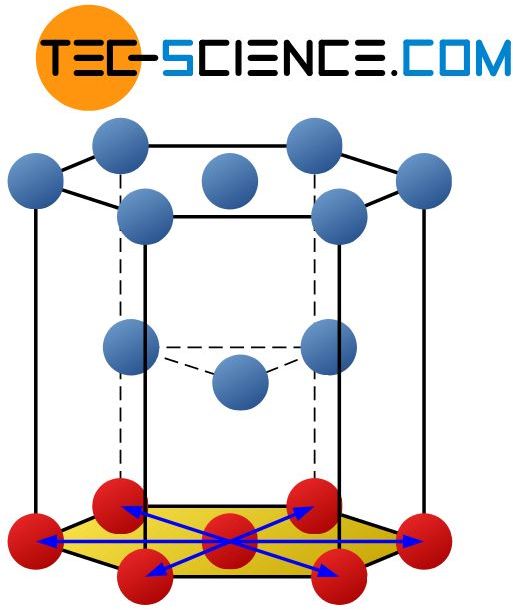
The hexagonal closest lattice structure has only 3 slip systems!
Note that for the determination of the number of slip planes, only non-parallel atomic layers are important, which can thus be activated independently of each other. The atomic levels lying above the base are ultimately identical; they are only shifted against each other. The hcp-lattice thus has only a small ductility compared to the fcc-lattice and the bcc-lattice.
Even in the hcp-lattice, additional slip planes can be activated by greater force. Thus, for example, the outer surfaces of the unit cell can also serve as slip planes. However, this requires very high forces, which is why the deformability of metals with hcp-lattice is very low under normal conditions.
Summary
The most important lattice structures are compared with respect to their ductility in the table below.
| face-centered cubic (fcc) | body-centered cubic (bcc) | hexagonal closest packed (hcp) | |
| lattice structure | 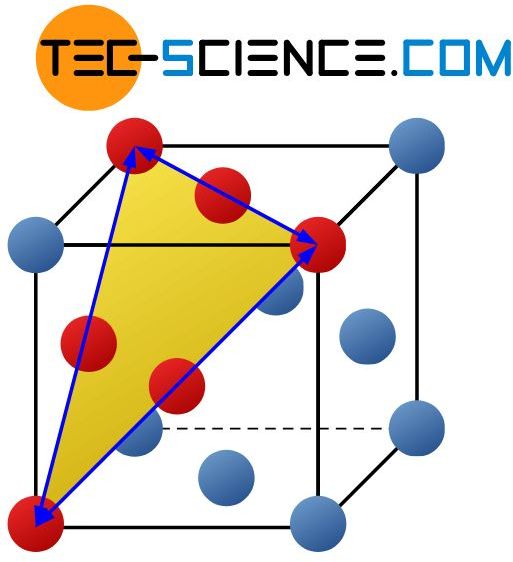 | 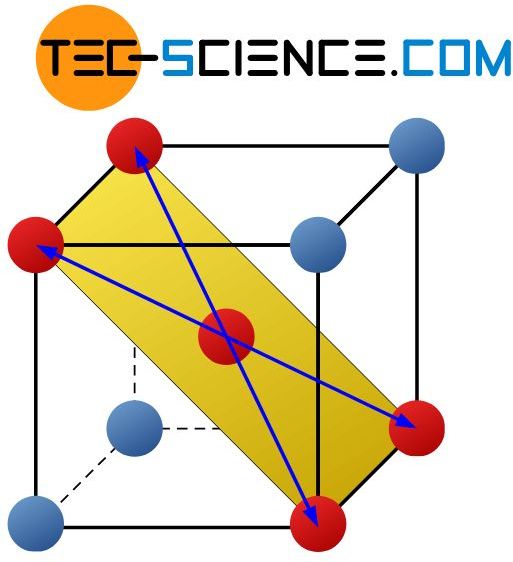 |  |
| number of preferred slip planes | 4 | 6 | 1 |
| number of slip directions | 3 | 2 | 3 |
| number of preferred slip systems | 12 | 12 | 3 |
| packing density | 74 % (densest packed) | 68 % (loosely packed) | 74 % (densest packed) |
| ductility | high | medium | low |
| metals | γ-iron (<1392°C), aluminium, β-cobalt (>417°C), lead, copper, nickel | α-iron (<911°C), chrome, molybdenum, β-titanium (>882°C), vanadium, tungsten | α-cobalt(<417°C), α-titanium (<882°C), zinc, magnesium |
For good deformability, a lattice structure should have at least 5 slip systems to be activated during a deformation process, so that the workpiece can deform in any direction as desired.
For good deformability, a grid structure should have at least 5 slip systems!
Polymorphism (allotropy)
Some metals can change their lattice structure by external thermodynamic influences such as pressure and temperature, whereby only the influence of temperature is relevant for mechanical engineering.
Although iron has a body-centered cubic lattice at room temperature, it is face-centered cubic above 911 °C. At a temperature of 1392 °C, iron reverts to the body-centered cubic lattice modification, before the melting temperature is reached at 1536 °C and the lattice structure dissolves. This transition from the bcc-lattice, which is only moderately deformable, to the much better deformable fcc-lattice is also the reason why iron or steel is heated during forging.
Titanium, too, possesses such a property of changing the lattice structure. At a temperature of 882 °C titanium passes from the hexagonal structure into the body-centered cubic lattice structure.
The property of metals to change their lattice structures, depending on temperature or pressure, is called allotropy or polymorphism.
The cause of allotropy lies in the more favorable energetic conditions at the corresponding temperature, so that the unstable lattice structure “decomposes” into the more stable modification.
The different lattice modification of a polymorphic metal is replaced by Greek letters in front of the element symbol. For example, the hexagonal lattice structure of titanium at room temperature is also known as α-titanium (or \(\alpha\)-Ti). Finally, after the first lattice transformation, \(\beta\)-titanium (or \(\beta\)-Ti). A Further transformation at next higher temperature would be called \(\gamma\) (however, such further lattice conversion does not occur with titanium).