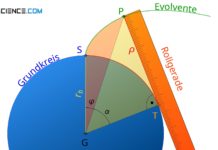
Erfahre in diesem Artikel mehr über den Eingriff der Zahne eines Zahnrades in die Zähne einer Zahnstange.
Einleitung
Die grundlegenden Zusammenhänge beim Eingriff zweier Zahnräder wurden bereits im Artikel Eingriff von Evolventenzahnräder (Kämmen) ausführlich erläutert. In diesem Artikel soll ein Spezialfall eines Zahnrades näher betrachtet werden: die Zahnstange. Die untere Animation zeigt hierzu das Eingreifen eines treibenden Zahnrades in eine Zahnstange.
Eingriffsstrecke
Die Zahnstange ist letztlich ein Spezialfall eines Zahnrades mit unendlich großem Durchmesser. Die gekrümmte Flankenform geht bei der Zahnstange schließlich in eine geradlinige Flankenform über. Die Flanken sind dabei gerade um den Betrag des Normaleingriffwinkels α0 gegen die Senkrechte geneigt. Die Eingriffslinie verläuft hierdurch ebenfalls unter diesem Winkel α0 (= Betriebseingriffswinkel), da die Eingriffslinie senkrecht zu den Zahnstangenflanken steht. Die Eingriffslinie liegt wie üblich als Tangente am Grundkreis des Zahnrades an und ist hierdurch eindeutig festgelegt.
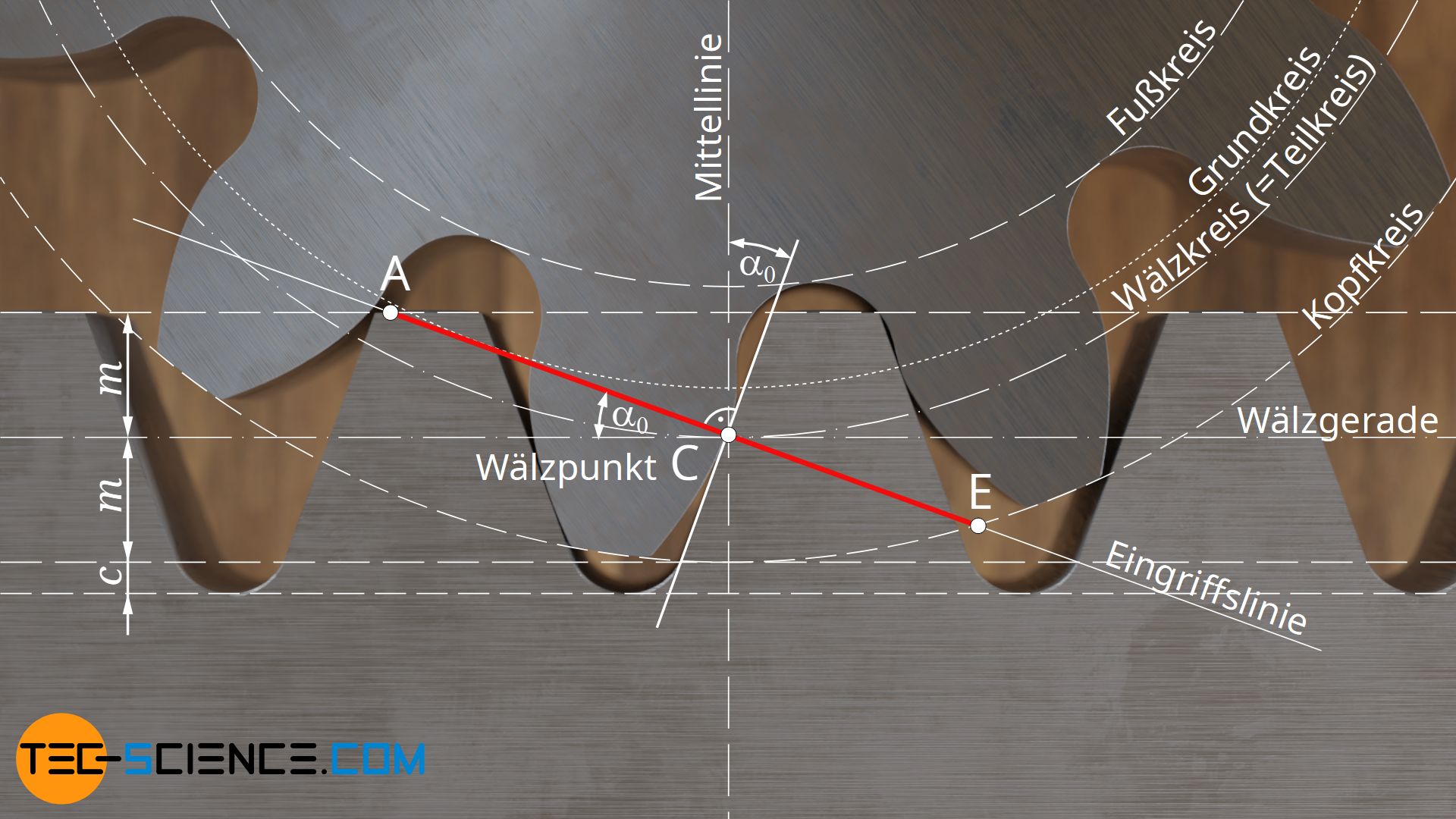
Die Eingriffsstrecke beginnt analog zur Paarung zweier Zahnräder im Schnittpunkt A zwischen Eingriffslinie und Kopflinie der getriebenen Zahnstange (Höhe des Zahnkopfes). Ebenfalls wird das Ende der Eingriffsstrecke wiederum durch den Schnittpunkt E zwischen Eingriffslinie und Kopfkreis des treibenden Zahnrades begrenzt.
Wälzpunkt
Auch der Wälzpunkt C ist analog als Schnittpunkt zwischen Eingriffslinie und Mittellinie zweier Zahnradachsen zu bilden. Da eine solche Mittellinie immer in radiale Richtung eines Zahnrades zeigt und somit stets senkrecht zur Zahnradoberfläche gerichtet ist, steht sie im Falle einer Zahnstange folglich senkrecht zur Zahnstange. Damit ist auch der Wälzpunkt C eindeutig festgelegt.
Bei spielfreier Paarung sitzt die Zahnstange mit beiden Flanken fest an den Zahnflanken des Zahnrades. Ein Verschieben der Zahnstange in radiale Richtung ändert grundsätzlich nichts an der Lage der Eingriffslinie, die sich stets als Flankennormale der Zahnstange und Tangente des Zahnradgrundkreises ergibt. Weder der Grundkreis noch der Flankenwinkel ändern sich in diesem Fall, sodass folglich auch die Eingriffslinie identisch bleibt. Hierdurch ergeben sich auch keine Änderungen in der Lage des Wälzpunktes, da die Mittellinie ebenfalls erhalten bleibt! Einzige Auswirkung einer Abstandsänderung ergibt sich auf die Länge der Eingriffsstrecke, die sich bei einer radialen Verschiebung der Zahnstange weg vom Zahnrad verkürzt.
Die Lage des Wälzpunktes bleibt bei Zahnstangen stets konstant! Die Eingriffsstrecke wird bei einer Vergrößerung des Abstandes zwischen Zahnstange und Zahnrad verkürzt!
Die unveränderliche Lage des Wälzpunktes wird auch anhand dessen Definition sofort ersichtlich. So ist der Wälzpunkt definiert als jener Punkt, in dem die Umfangsgeschwindigkeiten beider „Zahnräder“ identisch sind. Im Falle der Zahnstange handelt es sich jedoch um eine translatorische Geschwindigkeit. Jeder Punkt auf der Zahnstange bewegt sich somit stets mit derselben Geschwindigkeit und dies unabhängig vom Abstand zum Zahnrad. Damit ändert sich auch jener Wälzkreis auf dem Zahnrad nicht, dessen Punkte sich mit derselben Geschwindigkeit wie die Zahnstange bewegen. Der Wälzkreis bleibt identisch und damit auch der Wälzpunkt!
Definition des Teilkreises
Im Gegensatz zur Paarung zweier Zahnräder ist der Wälzpunkt bei Paarung mit einer Zahnstange also unabhängig des Abstandes zwischen Zahnrad und Zahnstange! Die Wälzgerade der Zahnstange und der Wälzkreis des Zahnrades (die beide ja durch den Wälzpunkt verlaufen) ändern sich hierdurch ebenfalls nicht! Dieser Sachverhalt spielt vor allem bei der Zahnradherstellung mithilfe von zahnstangenförmigen Werkzeugen (Wälzfräser) eine besondere Rolle. Hierdurch entstehen auch bei sogenannten Profilverschiebungen (die gleichbedeutend mit dem radialen Verschieben der Zahnstange sind) auf einem Zahnrad stets identische Wälzkreise. Diese werden dann auch als Herstellungswälzkreise bezeichnet.
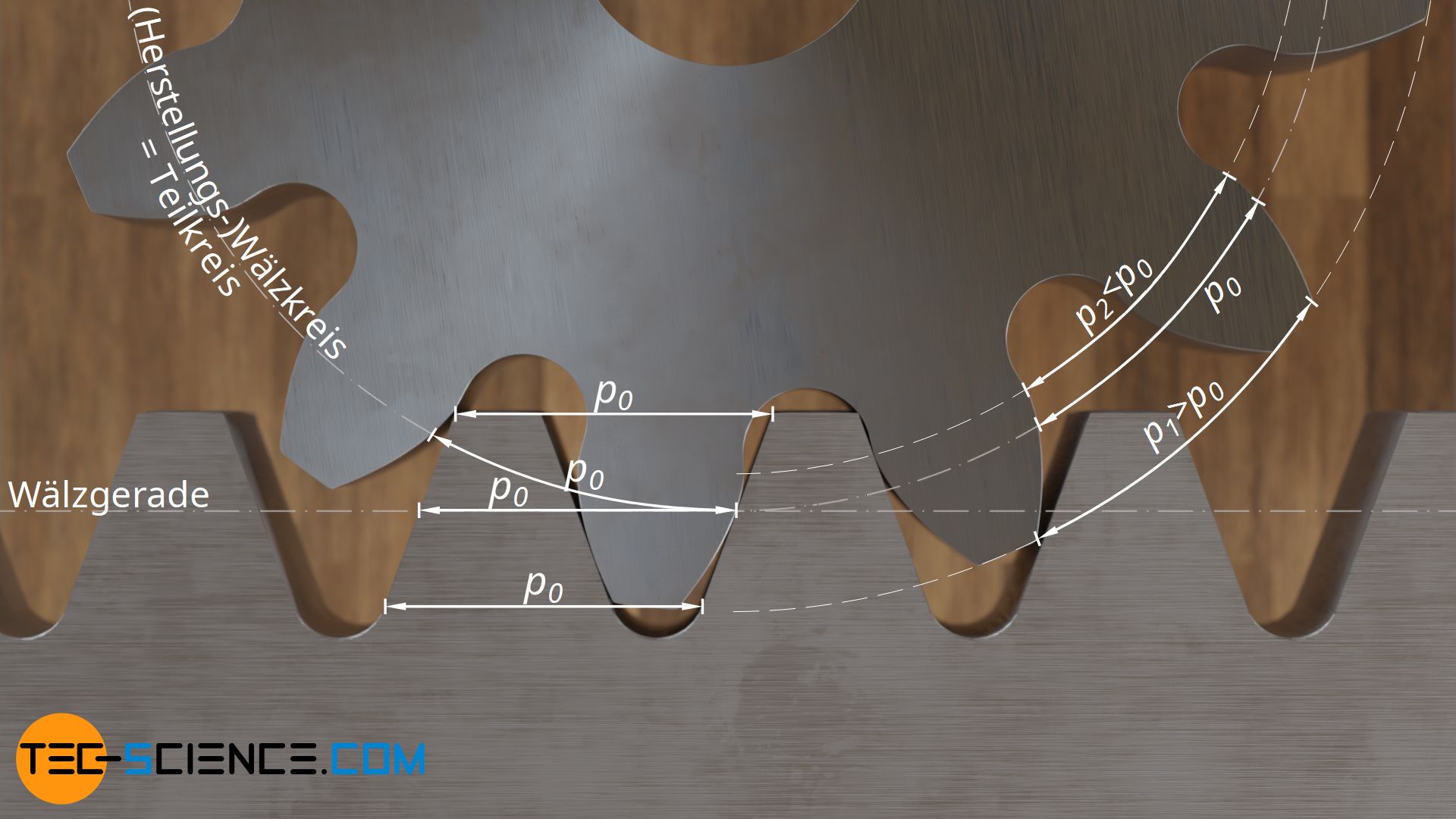
Im Gegensatz zu einem Zahnrad haben zahnstangenförmige Werkzeuge (bzw. Zahnstangen) an jeder Stelle identische Zahnabstände p0. Bei Zahnrädern hingegen hängen diese Zahnabstände vom betrachteten Kreisumfang ab. Mit steigendem Durchmesser der betrachtet wird, verteilen sich auch die Zähne auf einem immer größeren Umfang und der Zahnabstand nimmt folglich zu. Lediglich dort wo die Zähne des zahnstangenförmigen Werkzeuges (bzw. der Zahnstange) unmittelbar auf dem Zahnrad abwälzen finden sich identische Zahnabstände wieder (Umfangsteilungen p0). Dies entspricht per Definition gerade den Herstellungswälzkreisen.
Aus diesem Grund werden die Herstellungswälzkreise auch als Teilkreise bezeichnet, da dort die Umfangsteilungen p0 für alle Zahnräder die mit demselben zahnstangenförmigen Werkzeug gefertigt werden, identisch sind. Der Teilkreis ist als Herstellungswälzkreis folglich eine feste (unveränderliche) Größe eines Zahnrades, die alleine durch das zahnstangenförmige Herstellungswerkzeug bestimmt wird! Deshalb kann die eigentliche Zahnstange auch tatsächlich als Definition für den Teilkreis eines Zahnrades benutzt werden:
Der Teilkreis eines Zahnrades entspricht dem Herstellungswälzkreis bei der Zahnradfertigung durch Wälzfräsen bzw. dem Wälzkreis bei der Paarung mit einer Zahnstange!
Die stets identischen Umfangsteilungen auf den Herstellungswälzkreisen ermöglicht es nicht nur „normale“ Zahnräder (sogenannte Null-Räder) mit profilverschobenen Zahnrädern (V-Räder genannt) zu paaren sondern auch Zahnräder mit beliebiger Größe, d.h. beliebigen Zähnezahlen zu kombinieren, sofern diese mit demselben zahnstangenförmigen Werkzeug hergestellt wurden (dann auch als Satzräder bezeichnet).