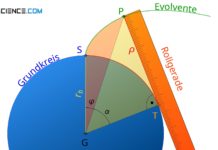
Als Unterschnitt bezeichnet man das Untergraben des Zahnes bei zu geringen Zähnezahlen und führt zur Schwächung des Zahnfußes!
Unterschnitt
Unterschnitt aufgrund des Herstellungsprozesses
Die unten abgebildete Animation zeigt schematisch den Herstellungsprozess dreier Zahnräder mit unterschiedlichen Zähnezahlen durch Wälzfräsen. Es zeigt sich, dass bei zu geringen Zähnezahlen offensichtlich ein Untergraben des Zahnfußes durch den Wälzfräser eintritt. Dies ist der Tatsache geschuldet, dass bei kleinen Zahnrädern die Schneiden des Fräsers relativ weit in das Zahnrad eingreifen (beim roten Zahnrad bis auf rund die Hälfte des Radius). Hierdurch wird der Zahn während der Rotation des Zahnrades sehr stark ausgehöhlt.

Ein solches Untergraben des Zahnes wird auch als Unterschnitt bezeichnet und führt zur Schwächung des Zahnes. Unterschnitte gilt es deshalb stets zu vermieden, d.h. die Anzahl der Zähne darf ein Minimum nicht unterschreiten.
Als Unterschnitt bezeichnet man das Untergraben des Zahnes bei zu geringen Zähnezahlen und führt zur Schwächung des Zahnfußes!

Unterschnitt aufgrund der Funktion
Ein Unterschnitt während der Zahnradfertigung tritt nicht nur beim Wälzfräsen sondern prinzipiell bei allen Wälzverfahren auf, wie bspw. Wälzstoßen oder Wälzhobeln. Zwar ließe sich ein Unterschnitt durch andere Fertigungsverfahren wie bspw. Profilfräsen oder Profilräumen vermeiden, jedoch ist der Unterschnitt auch zur Erfüllung der Funktion zwingend erforderlich. Wäre ein Unterschnitt bei kleinen Zahnrädern nicht vorhanden, dann würden sich die Zahnräder im Eingriff verhaken! Wie die untere Animation zeigt, müssen sich die Zähne des roten Zahnrades von den Zähnen des grünen Zahnrades untergraben lassen, um ein Kämmen zu ermöglichen.
Durch einen Unterschnitt wird der jeweilige Zahnfuß nicht nur geschwächt sondern auch die Eingriffsstrecke verkürzt. So wird nämlich durch den Unterschnitt ein Teil der evolventenförmigen Zahnflanke abgeschnitten. Dieser abgeschnittene Teil steht dann natürlich nicht mehr für die Kraftübertragung zur Verfügung. Die Zahnflanken verlieren somit deutlich vor dem eigentlichen Eingriffsende (Punkt E‘) den Kontakt zueinander (bereits im Punkt E). Die vergrößerte Darstellung in der Abbildung zeigt, dass der Flankenkontakt nach dem Punkt E bereits nicht mehr vorhanden ist. Die Eingriffsstrecke wird dementsprechend verkürzt.
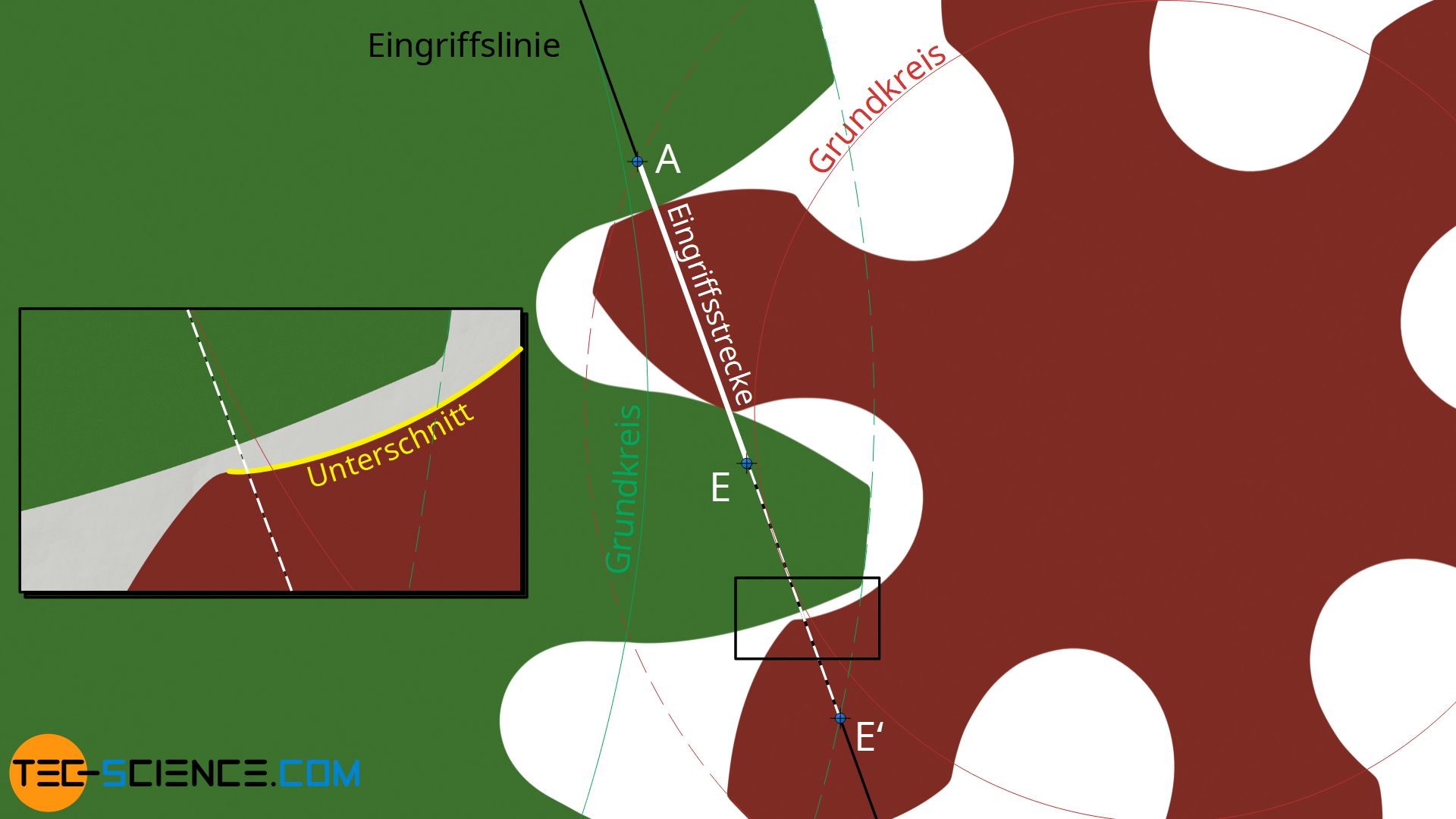
Ein Unterschnitt führt nicht nur zur Schwächung des Zahnes sondern auch zur Verringerung der Eingriffsstrecke!
Mindestzähnezahl (Grenzzähnezahl)
Zur Vermeidung eines Unterschnitts, darf das Zahnrad eine bestimmte Mindestzahl an Zähnen nicht unterschreiten (Grenzzähnezahl genannt). Welche Zähnezahl mindestens vorhanden sein muss, soll im Folgenden gezeigt werden.
Die untere Animation zeigt hierzu das Bezugsprofil des Wälzfräsers wie es in ein zu 6-zahniges Zahnrad eingreift. Dieses Situation kann analog zum Eingriff einer treibenden Zahnstange in ein Zahnrad betrachtet werden (die Grundlagen hierzu sind im Kapitel Zahnstange ausführlich erläutert). Die Eingriffslinie ergibt sich als Tangente an den Grundkreis und verläuft senkrecht zur Flanke des Bezugsprofils. Der Eingriff beginnt im Schnittpunkt A zwischen Eingriffslinie und Kopfkreis des Zahnrades und endet im Schnittpunkt E zwischen Eingriffslinie und Kopflinie des Bezugsprofils (die Verkürzung der Eingriffsstrecke durch den Unterschnitt ist in der Abbildung nicht berücksichtigt).
Wie die Animation zeigt, wird der Zahn ab dem Punkt B untergraben. Dies entspricht dem Punkt ab dem sich die Profilecke über die radiale Linie des Zahnrades schiebt und den Zahn somit untergräbt. Zwischen dem Beginn des Unterschneidens im Punkt B und dem Eingriffsende im Punkt E wird der Zahn innerhalb des grün markierten Bereichs ausgehöhlt und damit geschwächt.
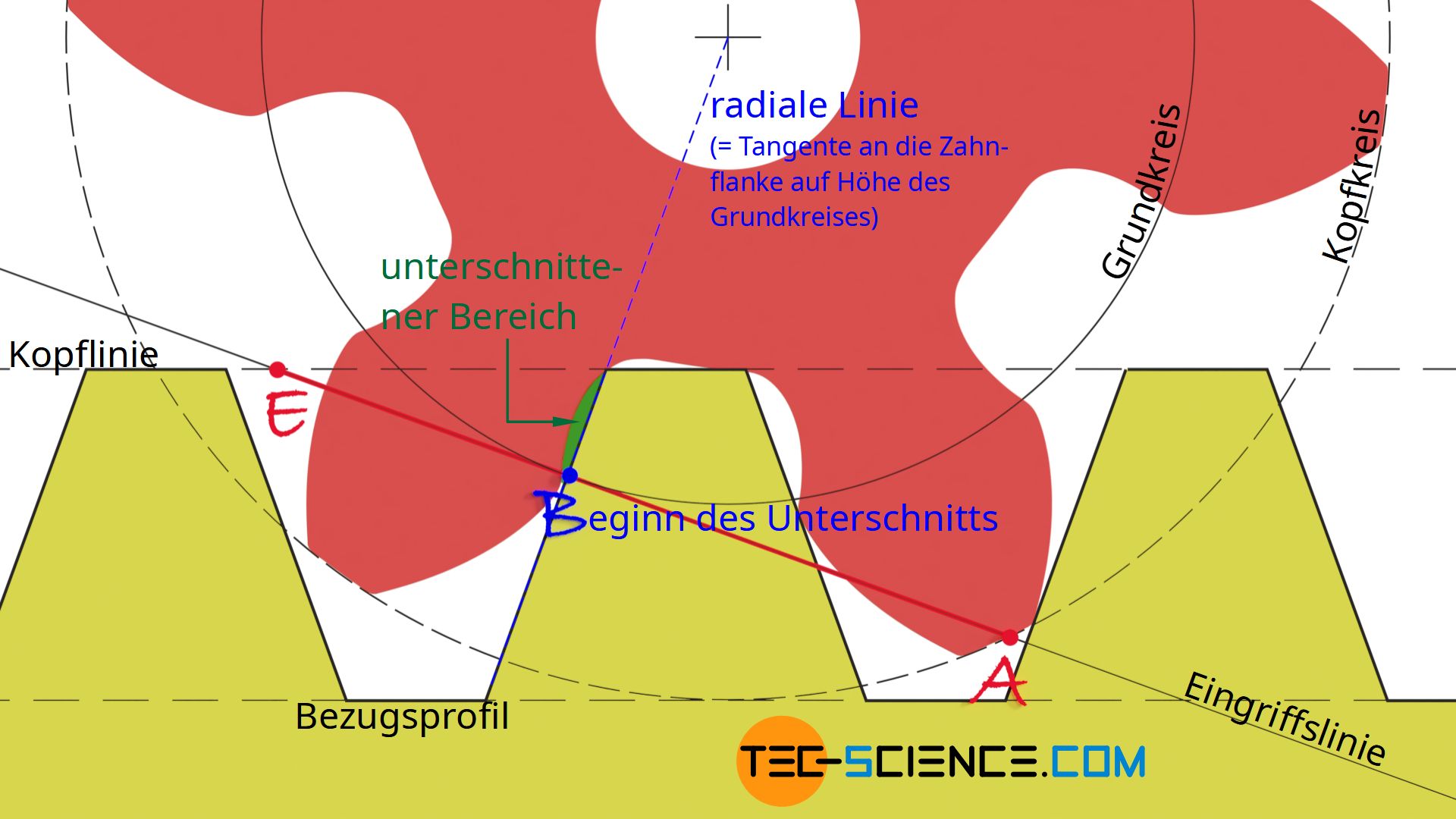
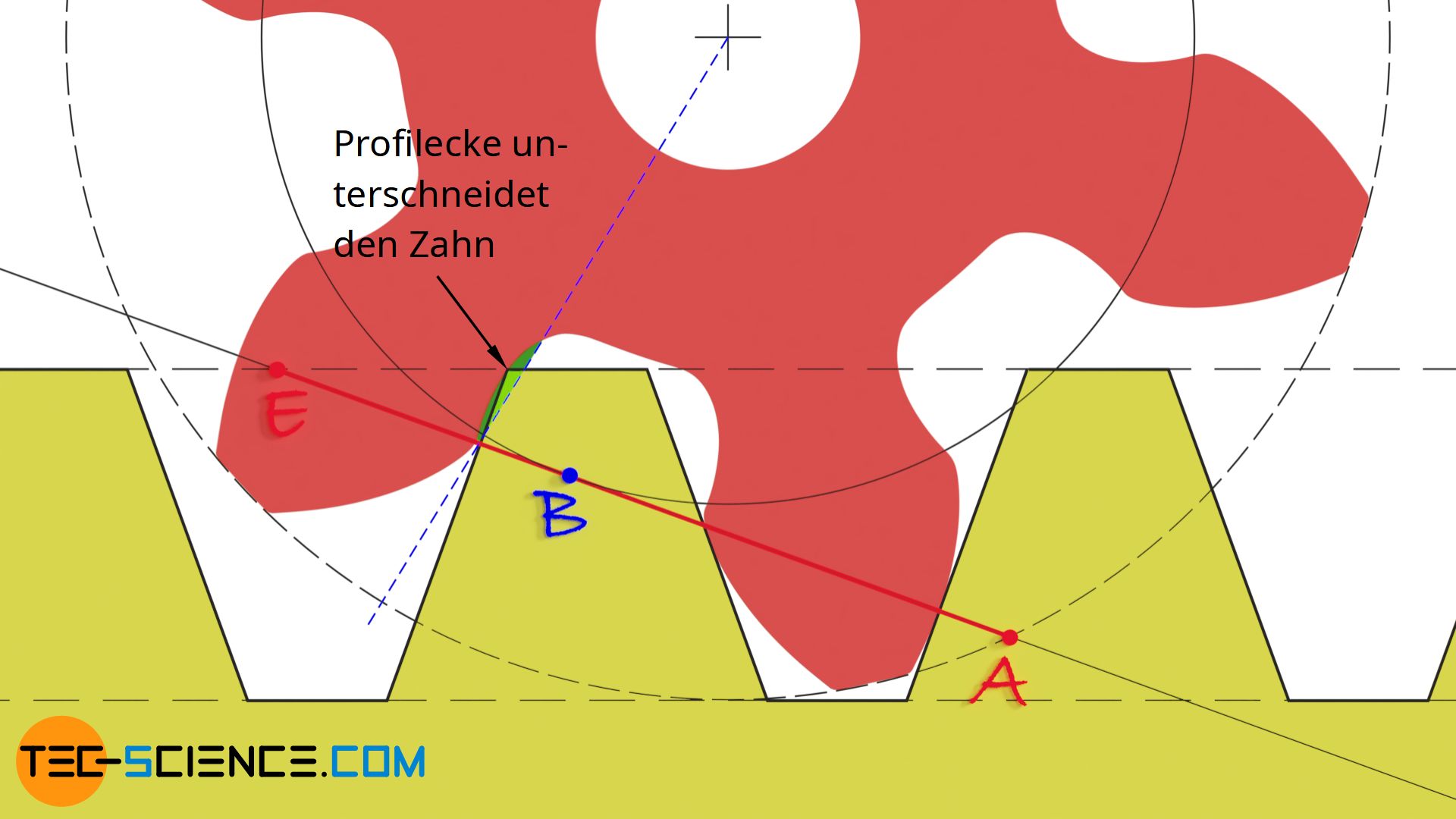
Anmerkung: Die radiale Linie entspricht der Tangente an die Zahnflanke auf Höhe des Grundkreises. Da im Falle eines Unterschnitts ein Teil der evolventenförmigen Zahnflanke jedoch abgeschnitten wird, entsteht eine kleine „Lücke“ zwischen radialer Linie und der tatsächlich vorhandenen Zahnflanke.
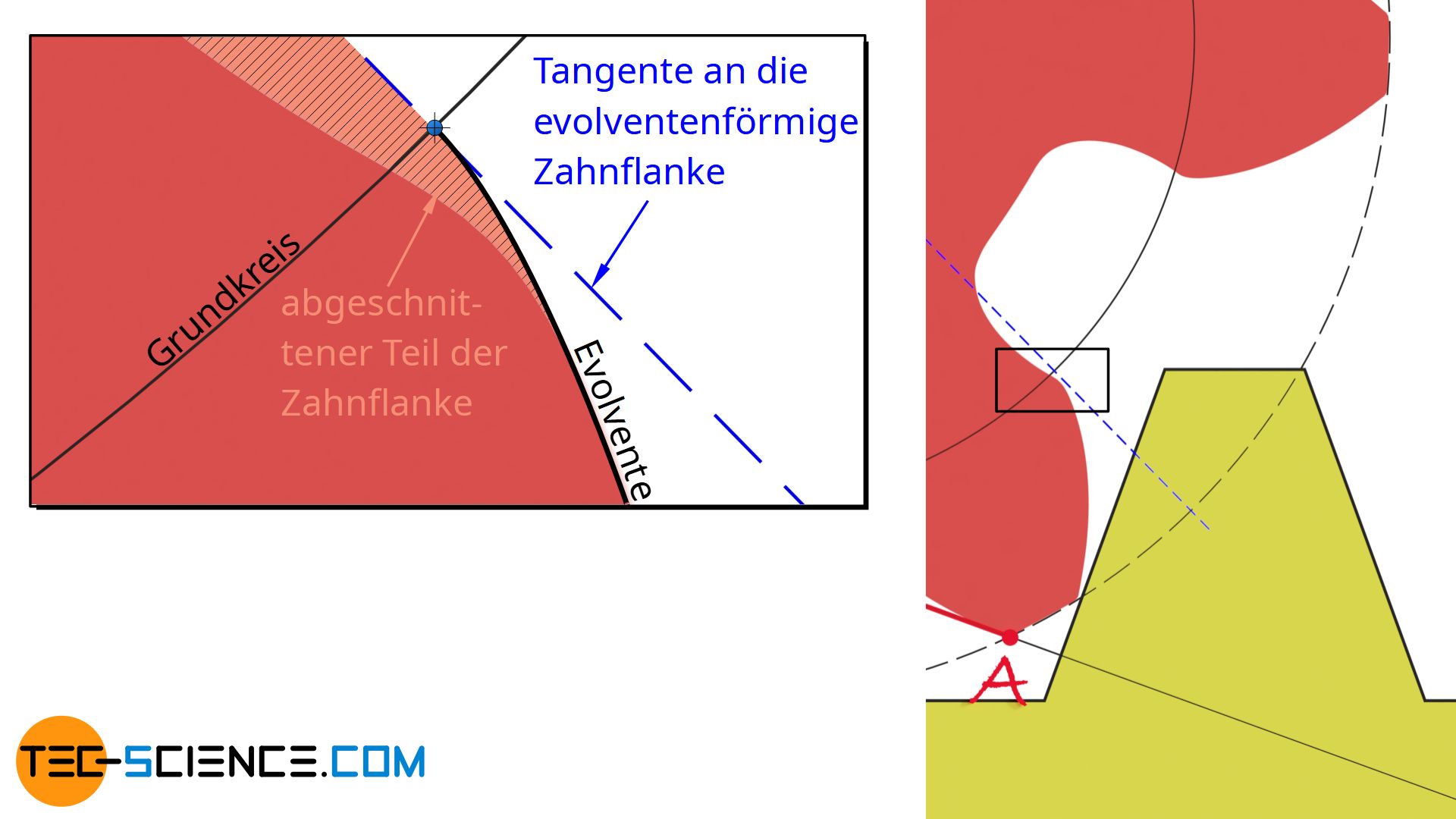
Der Punkt B ab dem ein Unterschneiden auftritt, entspricht ganz allgemein dem Berührpunkt zwischen Grundkreis und Eingriffslinie. In diesem Punkt verläuft die Flanke des Bezugsprofils deckungsgleich mit der radialen Linie des Zahnrades. Über diesen Punkt hinaus wird das Bezugsprofil dann die radiale Linie überschreiten und den Zahn unterschneiden.
Ein Unterschnitt tritt in dem Punkt ein, wo der Grundkreis die Eingriffslinie berührt!
Im Vergleich zum oberen Beispiel zeigt die untere Animation den Eingriff des Bezugsprofils in ein Zahnrad mit 20 Zähnen. Der Punkt B ab dem ein Unterschnitt theoretisch eintritt liegt dabei jedoch außerhalb der Eingriffsstrecke AE. Die Profilecke ist also bereits aus dem Eingriff bevor diese den Zahne hätte unterschneiden können. Die Zähne des Zahnrades werden somit nicht unterschnitten. Ein Unterschnitt wird also immer dann eintreten, wenn der Berührpunkt B von Grundkreis und Eingriffslinie innerhalb der Eingriffsstrecke AE liegt.

Zu einem Unterschnitt kommt es immer dann, wenn der Grundkreis die Eingriffslinie innerhalb der Eingriffsstrecke berührt!
Für den Grenzfall bei dem die Zähne eines Zahnrades gerade noch nicht unterschnitten werden, fällt der Beginn des Unterschneidens im Punkt B mit dem Eingriffsende E zusammen. Wie die untere Animation zeigt ist dies in etwa bei einem Zahnrad mit der Zähnezahl 17 der Fall.
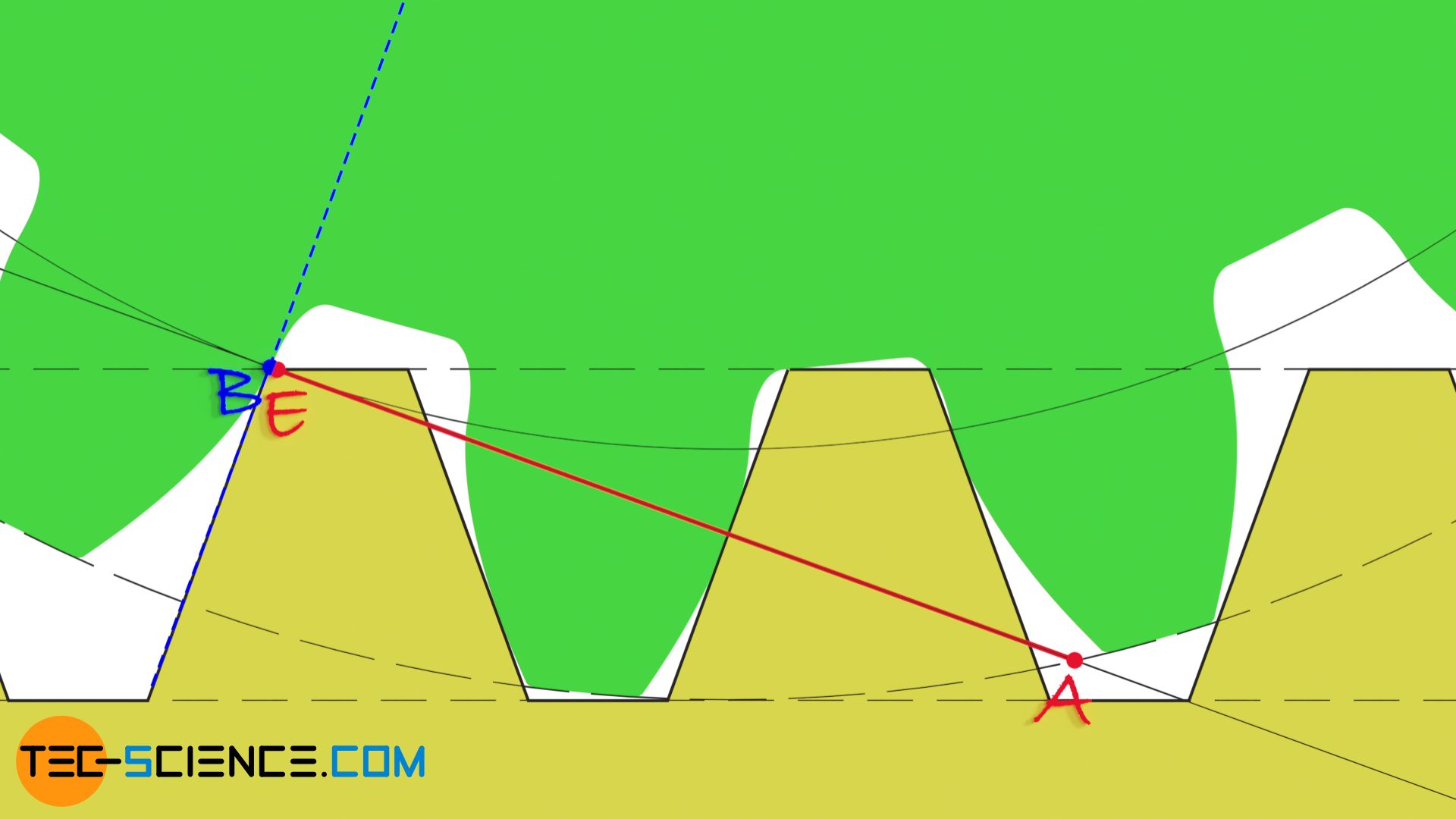
Bei Zahnräder mit Zähnezahlen über 17 tritt kein Unterschnitt mehr auf!
Berechnung der Mindestzähnezahl
Die im Abschnitt zuvor erwähnte Grenzzähnezahl von 17 ist unabhängig des Moduls und gilt somit für jede Zahngröße gleichermaßen! Dies soll im folgenden mathematisch gezeigt werden. Hierzu werden die sich im Grenzfall ergebenden geometrischen Verhältnisse näher betrachtet, d.h. wenn die Punkte B und E theoretisch exakt zusammenfallen.
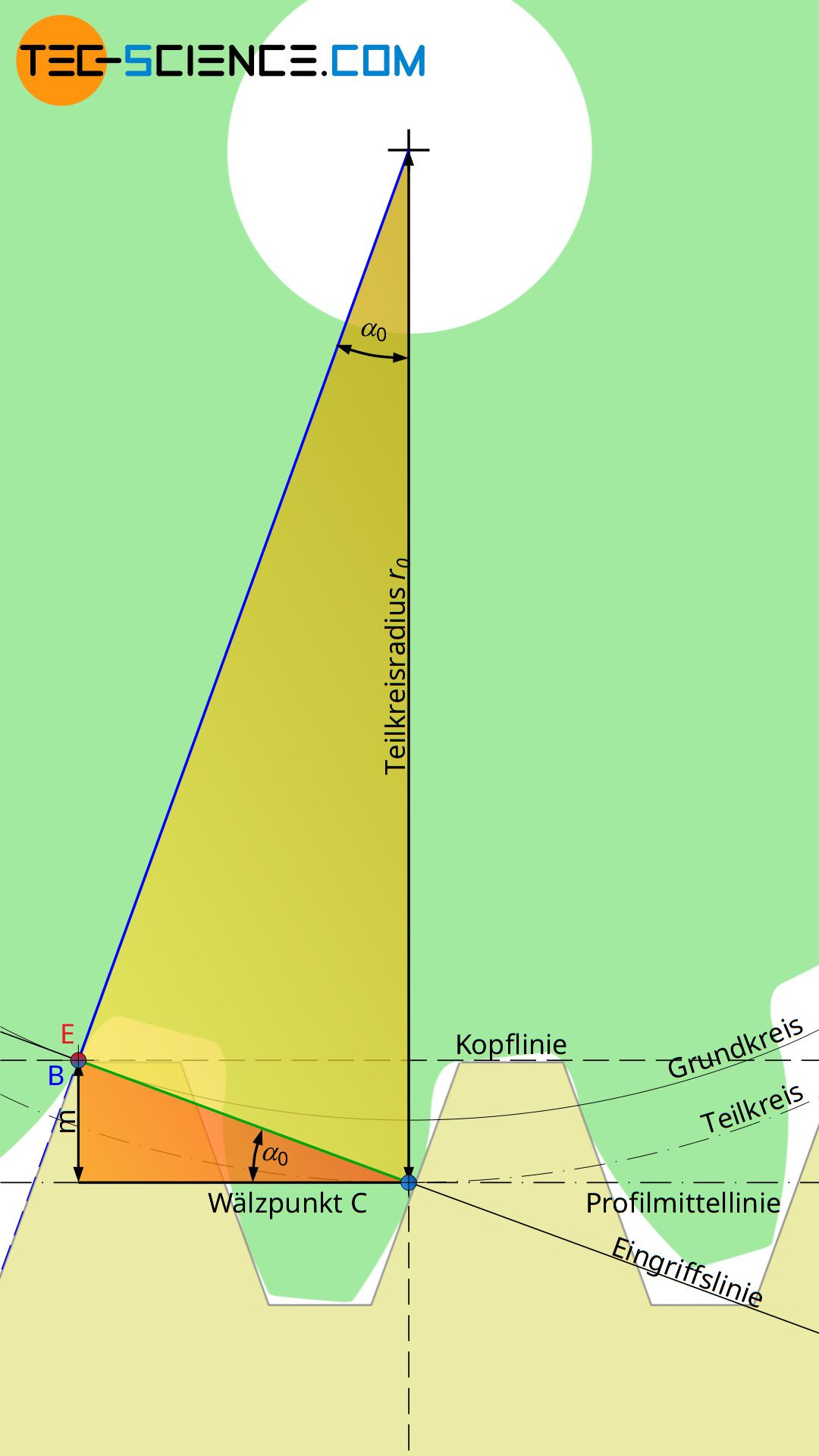
Der Abstand zwischen Profilmittellinie und Kopflinie des Bezugsprofils entspricht ganz allgemein dem Modul m und die Neigung der Flanken dem Normaleingriffswinkel α0 (siehe hierzu auch das Kapitel Zahnradherstellung). Wird in der unteren Abbildung nun das sich ergebende orangefarbene Dreieck betrachtet, so zeigt sich, dass die Gegenkathete bezüglich des Normaleingriffwinkels α0 gerade dem Modul m des Zahnrades entspricht Folglich gilt für die Strecke CB die unten angegebene Beziehung.
\begin{align}
\label{1}
& \overline{CB} =\frac{m}{\sin(\alpha_0)} \\[5px]
\end{align}
Die Strecke CB kann auch aus dem Teilkreisradius r0 bzw. dem Teilkreisdurchmesser d0 ermittelt werden (siehe gelbes Dreieck). Der Teilkreisdurchmesser d0 ergibt sich dabei aus dem Produkt von Modul m und (Mindest-)Zähnezahl zmin (siehe hierzu auch den Artikel Konstruktion von Evolventenzahnräder):
\begin{align}
\label{2}
& \overline{CB} = r_0 \cdot sin(\alpha_0) = \frac{d_0}{2} \cdot \sin(\alpha_0) = \frac{m \cdot z_{min}}{2} \cdot \sin(\alpha_0) \\[5px]
\end{align}
Die beiden Gleichungen (\ref{1}) und (\ref{2}) können nun gleichgesetzt und nach der gesuchten Grenzzähnezahl zmin aufgelöst werden:
\begin{align}
&\overline{CB} = \overline{CB} \\[5px]
&\frac{m}{\sin(\alpha_0)} = \frac{m \cdot z_{min}}{2} \cdot \sin(\alpha_0) \\[5px]
&\boxed{z_{min} = \frac{2}{\sin^2(\alpha_0)} } \\[5px]
\end{align}
Für einen Normaleingriffswinkel von α0 = 20 ° ergibt sich somit eine theoretische Grenzzähnezahl von zmin= 17. In der Praxis geht man bei einer Normverzahnung jedoch von einer Grenzzähnezahl von 14 Zähnen aus, bei der sich ein Unterschnitt dann tatsächlich negativ bemerkbar macht.
Die theoretische Mindestzähnezahl ab der kein Unterschnitt mehr auftritt liegt für eine Normverzahnung von 20° bei 17. In der Praxis geht man meist von einer Mindestzähnezahl von 14 aus!
Tatsächlich lassen sich jedoch auch Zahnräder unter der berechneten Mindestzähnezahl von 17 fertigen; und das ohne Unterschnitt! Hierzu muss jedoch der Fertigungsprozess mit einer sogenannten Profilverschiebung speziell angepasst werden. Auf solche profilverschobenen Zahnräder wird im nächsten Artikel näher eingegangen.