Derivation of the pressure-volume work (displacement work)

Learn in this article why the area under the curve in a volume-pressure diagram corresponds to the pressure-volume work (displacement work).

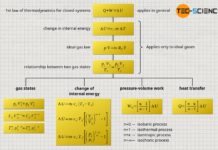
In the article concept of pressure-volume work, it was said without further explanation that the area under the curve in a volume-pressure diagram corresponds to the pressure-volume work (displacement work) done by the gas. In this article, we would therefore like to explain in more detail why the area under the curve corresponds to the displacement work.

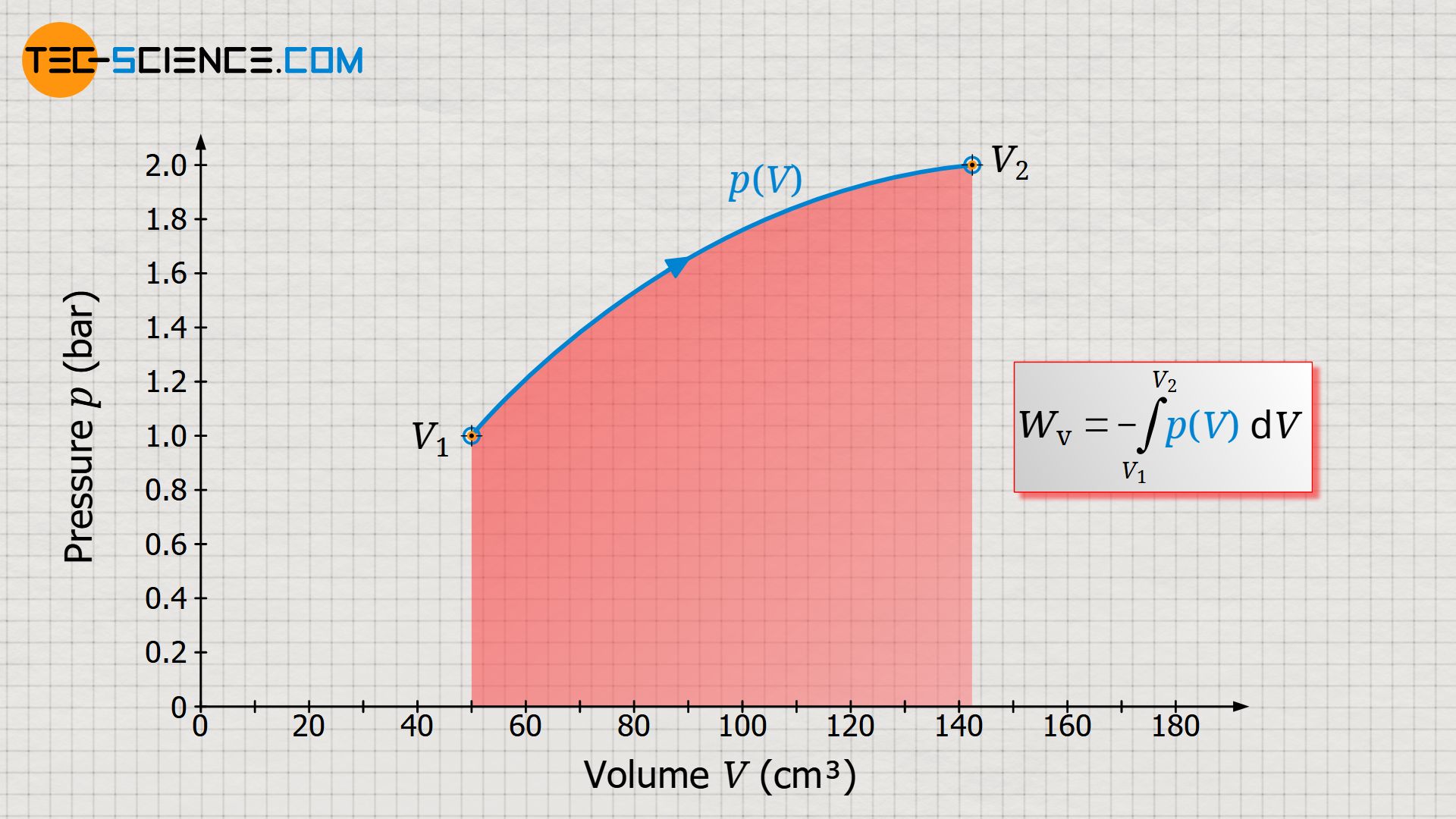
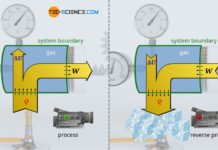
For this purpose, we consider the thermodynamic process of a gas which is enclosed in a cylinder and sealed with a movable piston. The gas is then heated. The gas expands as a result and does work on the piston. This causes a weight to be lifted via a rack and gear. In the volume-pressure diagram, this process is depicted as shown (further explanations of this process can also be found in the article concept of pressure-volume work).

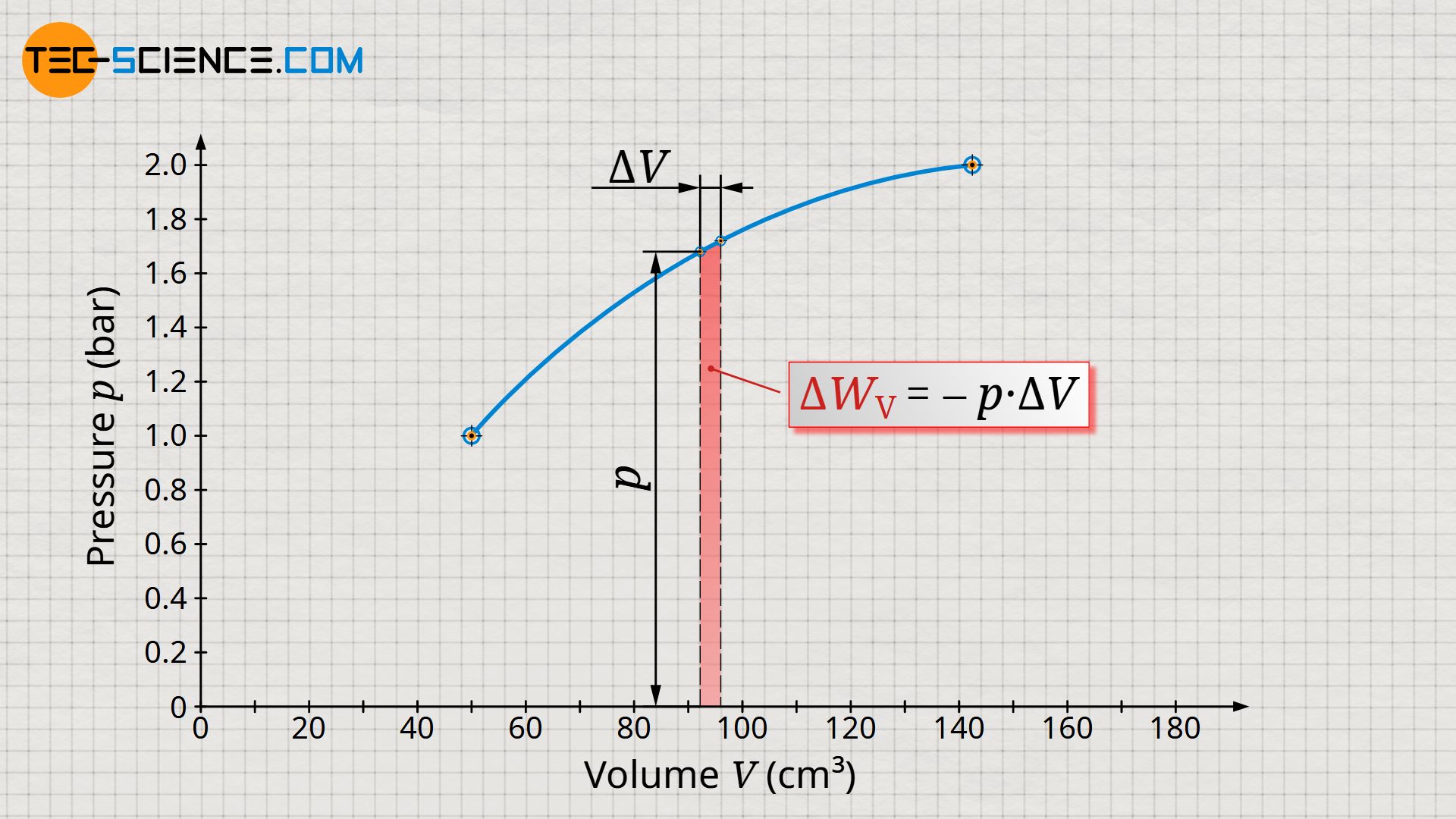
Let us now consider an arbitrary state during the process. This state is characterized by the volume V and the pressure p. Starting from this (initial) state, we now consider the (final) state a short moment later. The volume of the gas will increase only slightly. The change in volume between the two states should be chosen so small that the pressure (almost) does not change and can thus be considered almost constant.

During this very small change in volume, the gas then obviously exerts a (nearly) constant force F. This force is determined from the product of the (nearly) constant gas pressure p and the piston area A on which the pressure acts:

\begin{align}
\label{f}
&F = p \cdot A \\[5px]
\end{align}

The change in volume ΔV that takes place between the two states results from the piston area A and the displacement of the piston Δs. This means that the change in volume can be used to determine the displacement of the piston:

\begin{align}
\label{s}
&\Delta V = A \cdot \Delta s \;\;\; \Rightarrow \;\;\; \Delta s = {{\Delta V} \over A} \\[5px]
\end{align}

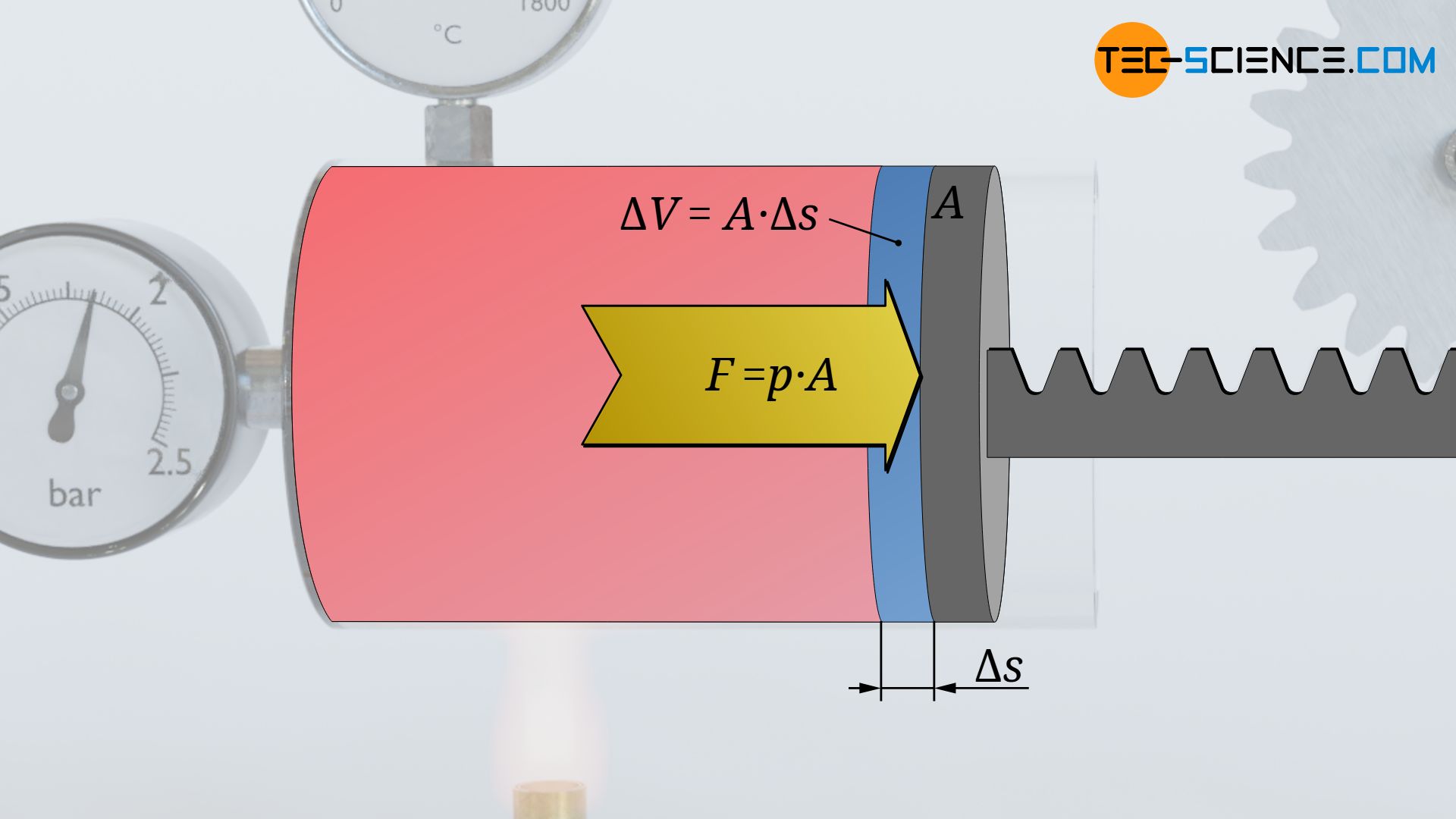
Thus, during the change in volume, the force (almost) constant F=p⋅A acts along the distance Δs=ΔV/A. According to the definition of work as the product of force F and displacement Δs, the (pressure-volume) work ΔW_v performed by the gas within the volume change ΔV can thus be calculated as follows:

\begin{align}
\require{cancel}
\label{w}
&\Delta W_\text{v} = F \cdot \Delta s = p \cdot \bcancel{A} \cdot {{\Delta V} \over \bcancel{A}} = p \cdot \Delta V \\[5px]
\end{align}

Note that when the volume increases (ΔV>0), the gas is obviously doing work. According to the sign convention, the pressure-volume work must therefore be negative (ΔW_v<0). Conversely, the pressure-volume work is positive (ΔW_v>0) if work is done on the gas by compression (ΔV<0). To account for this convention, a minus sign must be introduced in equation (\ref{w}):

\begin{align}
\label{dw}
&\Delta W_\text{v} = – p \cdot \Delta V \;\;\; \text{mit} \;\;\; p= \text{konstant} \\[5px]
\end{align}

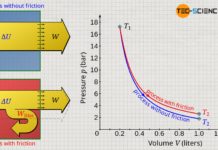
The pressure-volume work within the considered change in volume is therefore the product of the pressure p, which is assumed to be constant, and the change in volume ΔV. In the volume-pressure diagram, this pressure-volume work can be interpreted as a rectangular area, with width ΔV and height p.

In order to determine the total pressure-volume work W_v of the entire process – i.e. from the initial volume V₁ to the final volume V₂ – it would have to be divided into very many small volume intervals. The respective pressure-volume work ΔW_v of each volume interval would then have to be determined and then summed up to the total pressure-volume work W_v:

\begin{align}
\label{ww}
&W_\text{v} = \sum_{V_1}^{V_2} \Delta W_\text{v} = – \sum_{V_1}^{V_2} p \cdot \Delta V  \\[5px]
\end{align}

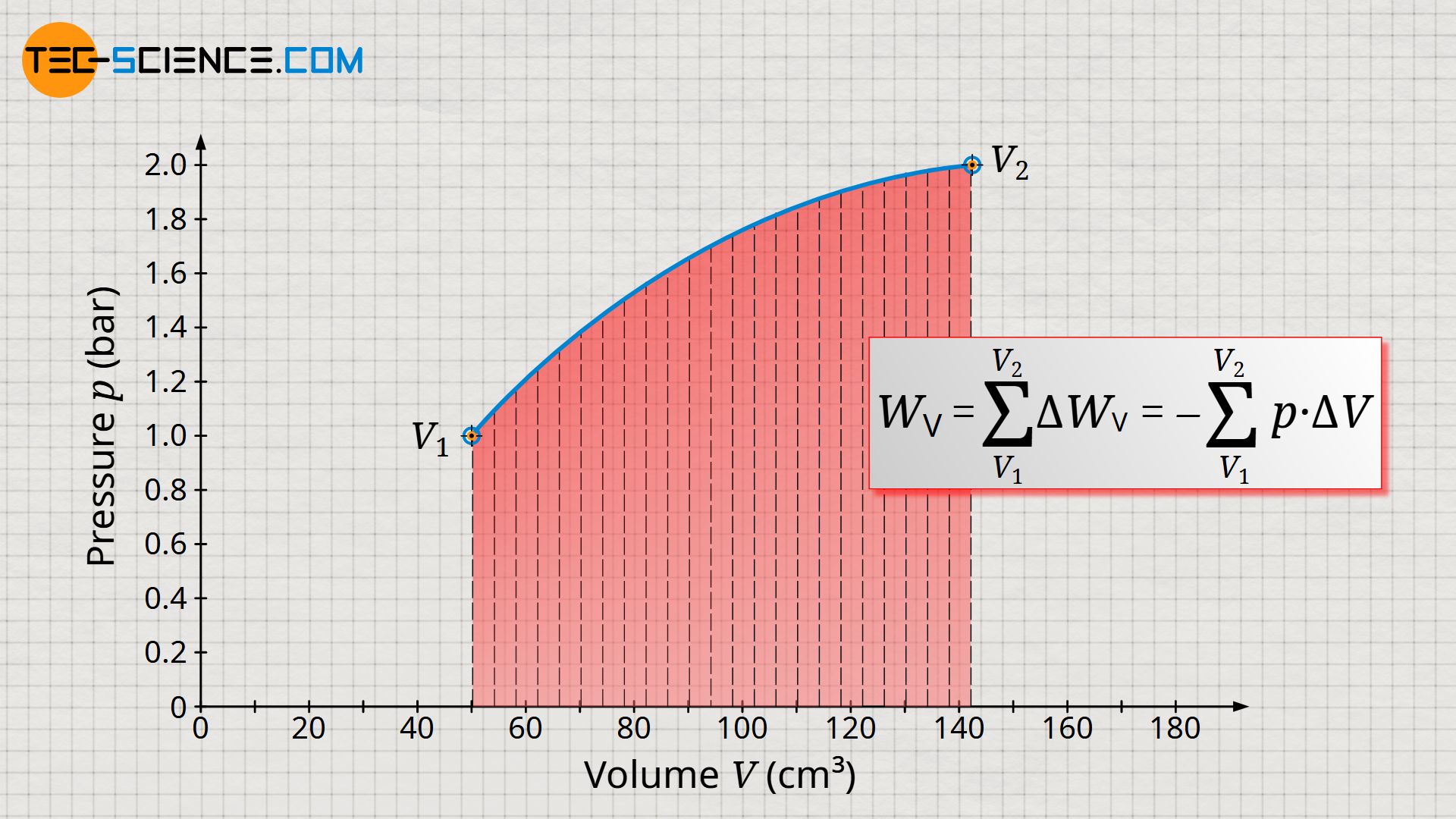
Determining the total pressure-volume work in the way described above would be very time-consuming, and small errors would always be made, since the pressure within the volume intervals ΔV is not constant but varies slightly. Only under the assumption of infinitely small intervals (ΔV→0) would an exact result be obtained.

At this point, mathematics offers a better solution. If the individual volume intervals are considered to be infinitely small, the macroscopic volume change ΔV turns into a infinitesimal volume change dV and the sum sign becomes an integral. If the pressure is known as a function of the volume – i.e. the function p(V) – then the total pressure-volume work W_v can be determined in general by the following integral:

\begin{align}
\label{www}
&\boxed{W_\text{v} = – \int\limits_{V_1}^{V_2} p(V) ~ \text{d}V}\\[5px]
\end{align}

Since an integral determines the area under a curve, this makes it clear once again that the area under the p(V) curve corresponds to the pressure-volume work!