Learn more about applications and examples related to hydrostatic pressure in this article.
Hydrostatic pressure
In the article Pressure in liquids, the formation of hydrostatic pressure and its calculation was explained in detail. It was shown that the hydrostatic pressure ph depends only on the depth hbelow the liquid surface besides the density ϱ of the liquid and the gravitational acceleration g:
\begin{align}
\label{h}
&\boxed{p_h =\rho \cdot g \cdot h} \\[5px]
\end{align}
In the following sections, the importance of hydrostatic pressure for everyday life will be explained in more detail.
Barrel experiment of Blaise Pascal
The following experiment, based on the experiment of Blaise Pascal in the 17th century, demonstrates the mere dependence of hydrostatic pressure on depth. For this purpose, a large glass vessel is completely filled with water. The (hydrostatic) water pressure at the bottom of the bottle can be calculated with equation (\ref{h}). If a height of half a meter is assumed, then the hydrostatic water pressure at the bottom is about 0.05 bar. The glass bottle can still withstand this relatively low water pressure without any problems.

However, if a small vertical tube is attached to the neck of the bottle and filled with water, the hydrostatic pressure increases as the water level rises. If, for example, the tube is run over several storys of a building, the pressure can increase considerably. At a height of 30 meters, the water pressure rises to over 3 bar. After all, the water pressure will eventually be so high that the glass bottle can no longer withstand the enormous forces and breaks.
The impressive aspect of this experiment is that it does not matter which inner diameter the tube has as long as capillary effects can be neglected. A tube with an inner diameter of 4 mm is theoretically sufficient. In order to fill this tube with water, just about 380 ml of water are required. 380 ml of water are therefore completely sufficient to increase the water pressure in the glass vessel more than 60 times, regardless of the capacity of the vessel!
Water pressure in the ocean
The hydrostatic pressure causes the pressure in water to increase more and more with increasing depth. With a water density of around 1000 kg/m³ and a gravitational acceleration of about 10 N/kg, the water pressure increases by around 1 bar per 10 metres of water depth. Note that the pressure values in the figure below refer only to the hydrostatic pressure (water pressure). For the absolute pressure at a certain depth, the ambient pressure of 1 bar (atmospheric pressure) on the water surface must be added.

The water pressure increases by about 1 bar per 10 meters of water depth!
The increasing water pressure during dives, for example, results in more air having to be inhaled from the scuba tanks as the depth increases. In order to balance the surrounding water pressure, the lungs must generate the same pressure through the inhaled air, otherwise the lungs would be compressed by the greater water pressure. Greater lung pressure can only be achieved by inhaling more air, similar to a bicycle tyre where more air needs to be pumped into to increase the pressure. So the air supply in the diving tanks will run out faster the deeper you dive.
Watering can
The fact that hydrostatic pressure only depends on depth is evident in many places in everyday life. It is also the reason why the same water level is found everywhere in vessels connected by pipes (so-called communicating vessels). This can be seen, for example in a watering can that is filled with water. Over time, the same water level will set in the pouring pipe (also called spout) as in the can itself.

Communicating vessels are containers filled with liquid, which are connected to each other by pipes and which have a common liquid level!
This can be explained mathematically as follows. The water in the can leads to a certain hydrostatic pressure pc at the depth hc where the nozzle is welded on:
\begin{align}
&p_{c} =\rho \cdot g \cdot h_{c} ~~~\text{hydrostatic pressure in the can} \\[5px]
\end{align}
In the same way, the hydrostatic pressure in the spout ps at depth hs below the water level can be determined:
\begin{align}
&p_{s} =\rho \cdot g \cdot h_{s} ~~~\text{hydrostatic pressure in the spout} \\[5px]
\end{align}
During the filling of the can, different water levels between the can and the pouring pipe can be observed. After all, the water in the spout is pushed upwards by the greater water pressure in the can.
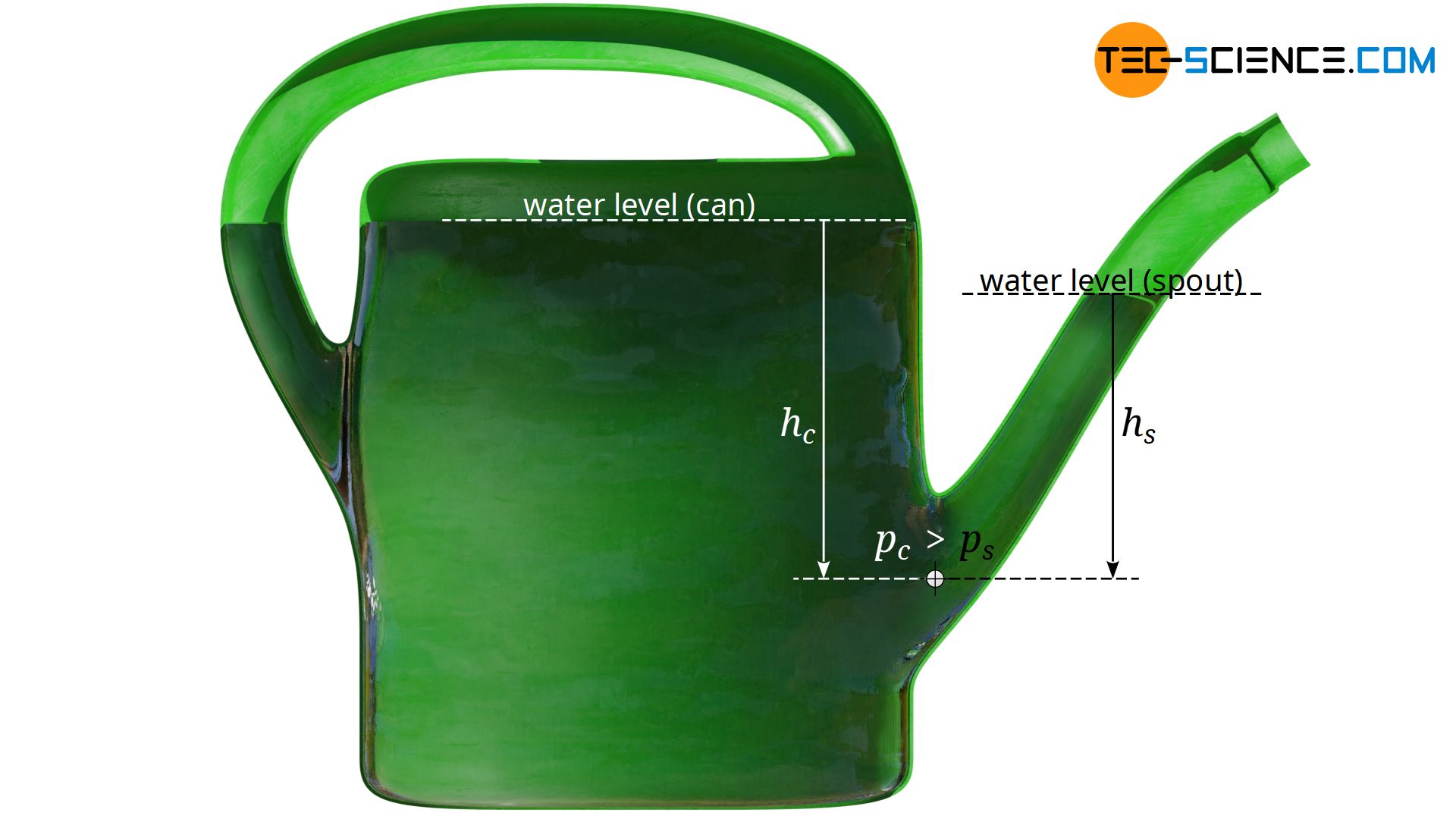
After filling, however, a state of equilibrium is reached and the water is no longer forced through the pipe. In this case, the hydrostatic pressure caused by the water column in the spout must obviously be as high as the hydrostatic pressure caused by the water column in the can. If this were not the case, then the larger of the two hydrostatic pressures would press either the water in the can or in the spout further upwards. In a state of equilibrium, the hydrostatic pressures must inevitably be the same, which is ultimately only the case with a common water level:
\begin{align}
\require{cancel}
p_{c} &\overset{!}{=} p_{s} \\[5px]
\bcancel {\rho \cdot g} \cdot h_{c} &= \bcancel{\rho \cdot g} \cdot h_{s} \\[5px]
h_{c} &= h_{s} \\[5px]
\end{align}
The fact that identical hydrostatic pressures form in the equilibrium state is also shown by the fact that pressures in liquids act equally in all directions. Thus, there cannot be two different hydrostatic pressures at a certain depth. If this were the case, currents would form and there would be no equilibrium.
Water level
The fact that identical water levels form in vessels that are connected to each other is technically used in so-called water level devices. Two vessels are each provided with a scale and connected to each other by a flexible tube filled with water. The water level can be read off the scales.

Since the same water level is reached in both vessels, it is very easy to set the same level even over long distances where simple spirit levels cannot be used. Water levels are used, for example, in construction technology, whereby electronic sensors are mostly used nowadays.

Water tower
Another technical implementation that uses the hydrostatic pressure or the striving for a common liquid level in communicating vessels is the water tower.

In principle, a water tower is an elevated tank that is filled with water by pumps. Due to the resulting hydrostatic pressure, the water can be forced into the lower-lying households without additional pumps. Due to the large water reservoir in the tower, usually several million litres, the water level sinks only relatively slowly. This ensures an almost constant water pressure before water is pumped again when the water level falls below a certain limit.
Nowadays, however, water towers are used less and less. In modern water supply systems, pumps are mostly used to transport the water directly to the consumers.






