Buoyancy is the force directed against gravity that an object experiences when submerged in a fluid (liquid or gas).
Indroduction
Everyone may have tried to lift another person and found that this requires a lot of strength. However, if you try to lift this person in water, it is much easier. The reason for this is due to the so-called buoyancy, which an object experiences as soon as it is submerged in a liquid. This buoyant force is also responsible for the fact that even steel ships weighing tons do not sink but float on the water. The cause of the buoyancy will be discussed in more detail in this article.

Demonstration of buoyancy
The following experiment will demonstrate the effect of the buoyant force. A spring scale (newton meter) is attached to a metal cuboid. Without touching the bottom, the piece of metal is gradually submerged in a glass of water and the newton meter is observed.
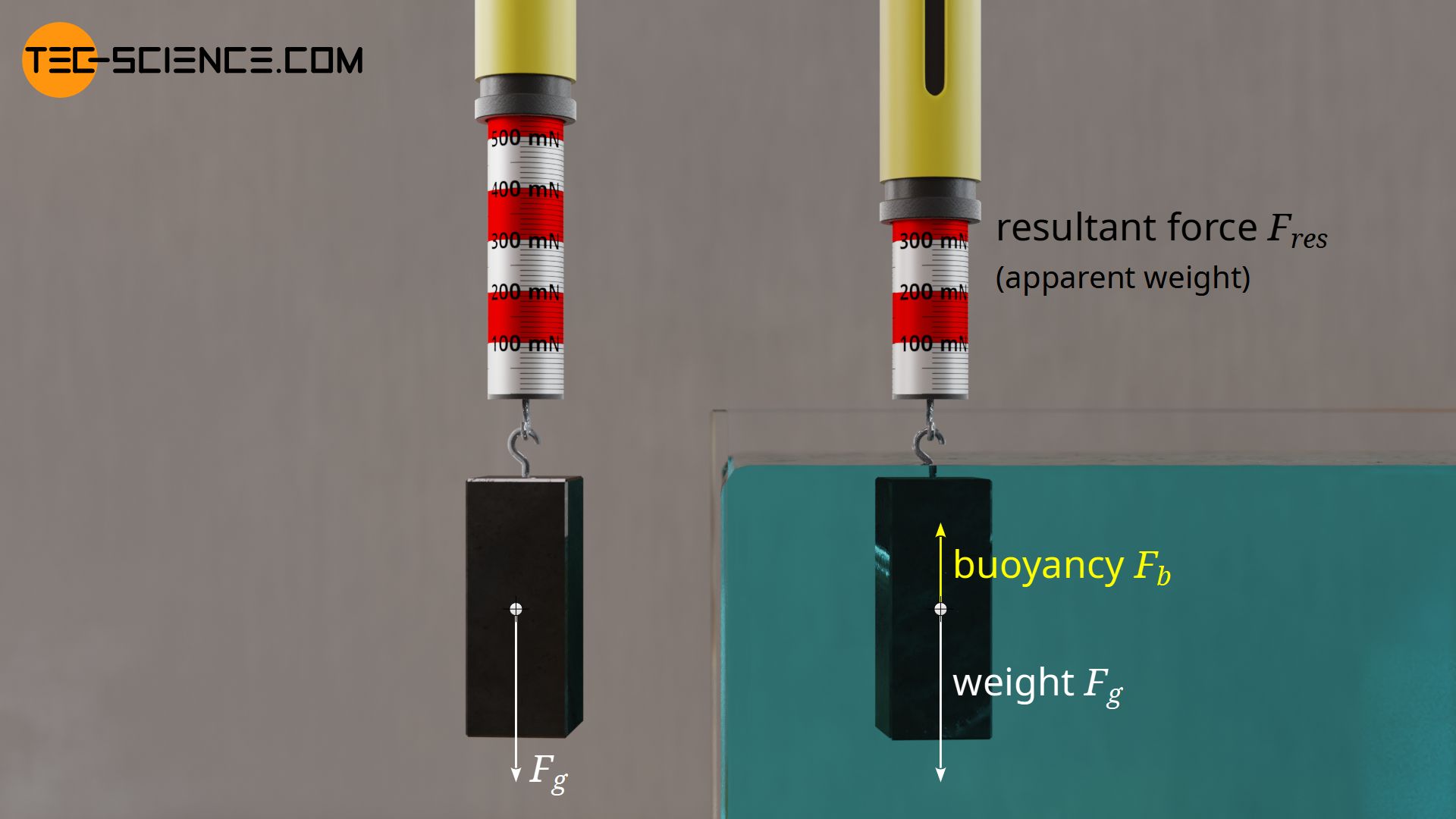
Once the metal piece has reached the water, the indicated value of the newton meter decreases steadily with increasing immersion depth. Only when the cuboid is completely submerged in water does the spring scale show a constant value again. The decreasing force has nothing to do with a decreasing weight, because the mass of the metal block does not change. Rather, the buoyant force acting against gravity increases with increasing immersion depth. The buoyant force corresponds to the amount by which the body appears to have become lighter in water.
The more an object is submerged in a liquid, the greater the buoyancy acting on it! The buoyant force is always directed in the opposite direction to gravity!
The buoyancy: The Archimedes’ principle
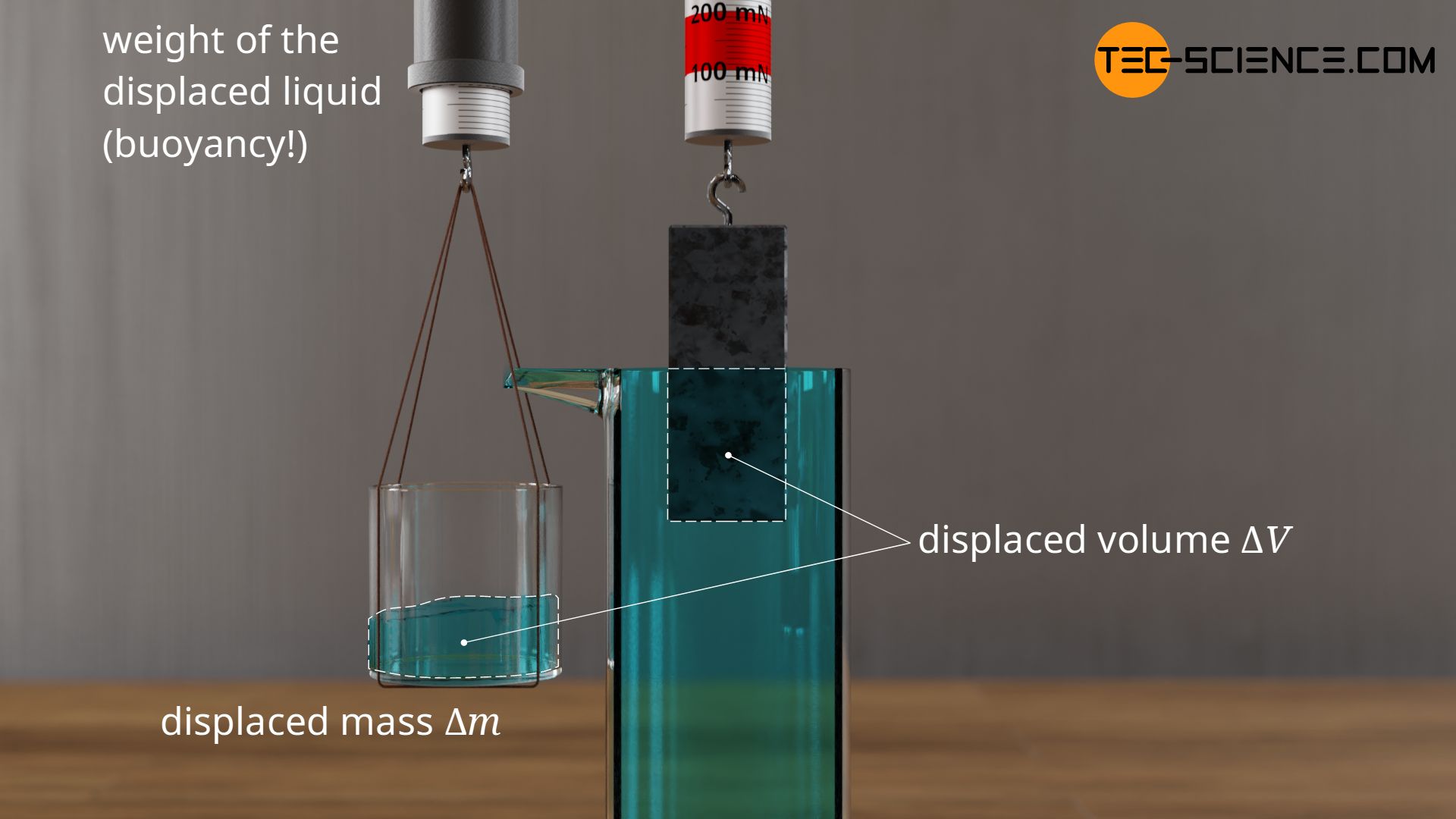
The scientist Archimedes experimented with the phenomenon buoyancy already 250 years B.C. He was able to show that the buoyant force by which a submerged body appears to become lighter corresponds to the weight of the displaced liquid. The term displaced liquid refers to the amount of liquid that has to give way to the body when it is submerged. This is the amount of liquid that theoretically overflows when a glass is full to the brim when a body is submerged. The weight of this overflowed liquid then corresponds to the buoyant force. This statement is also called the Archimedes’ principle.

The Archimedes’ principle states that the buoyant force corresponds to the weight of the displaced liquid!
When an object is completely submerged in a liquid, the volume of the displaced liquid obviously corresponds to the volume of the immersed body. If, for example, the 54 g metal cuboid made of aluminium has a square base area of 4 cm² and a height of 5 cm, this results in a volume of 20 cm³ (20 ml). Consequently, when completely submerged in water, the cuboid displaces a liquid volume of 20 ml. At a water density of 1 g per cm³ this corresponds to a displaced water mass of 20 g. The 54 g metal cuboid therefore feels 20 g lighter under water. A spring scale would therefore indicate only 340 mN instead of 540 mN.
Note that the submersion of the body does not change its weight, but a buoyant force against the weight is now acting, which leads to an reduced resultant force. It is therefore advisable not to argue with the masses (even if this is more descriptive), but with the forces! If the weight of the body is denoted by \(F_g\) and the counteracting buoyant force by \(F_b\), then for the resultant force \(F_{res}\) that the body experiences applies:
\begin{align}
\label{res}
&\boxed{F_{res} = F_g – F_b} \\[5px]
\end{align}
If the metal block is not completely submerged in the liquid, but only partially, then it obviously does not displace as much water. A body will only displace as much fluid as the body volume actually submerges. If only half of the body volume is submerged, the body displaces only half of the water. Accordingly, the buoyancy is only half as great. If \(\Delta V\) denotes the submerged body volume (= displaced liquid volume) and \(\rho_l\) the density of the liquid, then the mass \(\Delta m\) of the displaced liquid can be calculated as follows:
\begin{align}
&\Delta m = \Delta V \cdot \rho_l \\[5px]
\end{align}
For the buoyant force \(F_b\) as the weight of the displaced liquid, then finally applies:
\begin{align}
&F_b = \Delta m \cdot g \\[5px]
\label{arch}
&\boxed{F_b = \Delta V \cdot \rho_l \cdot g} \\[5px]
\end{align}
Derivation of the buoyant force
The buoyancy is due to the different hydrostatic pressures at the top and bottom of a submerged body. For the sake of simplicity, a cuboid object is again considered, which is completely submerged in the surrounding liquid.
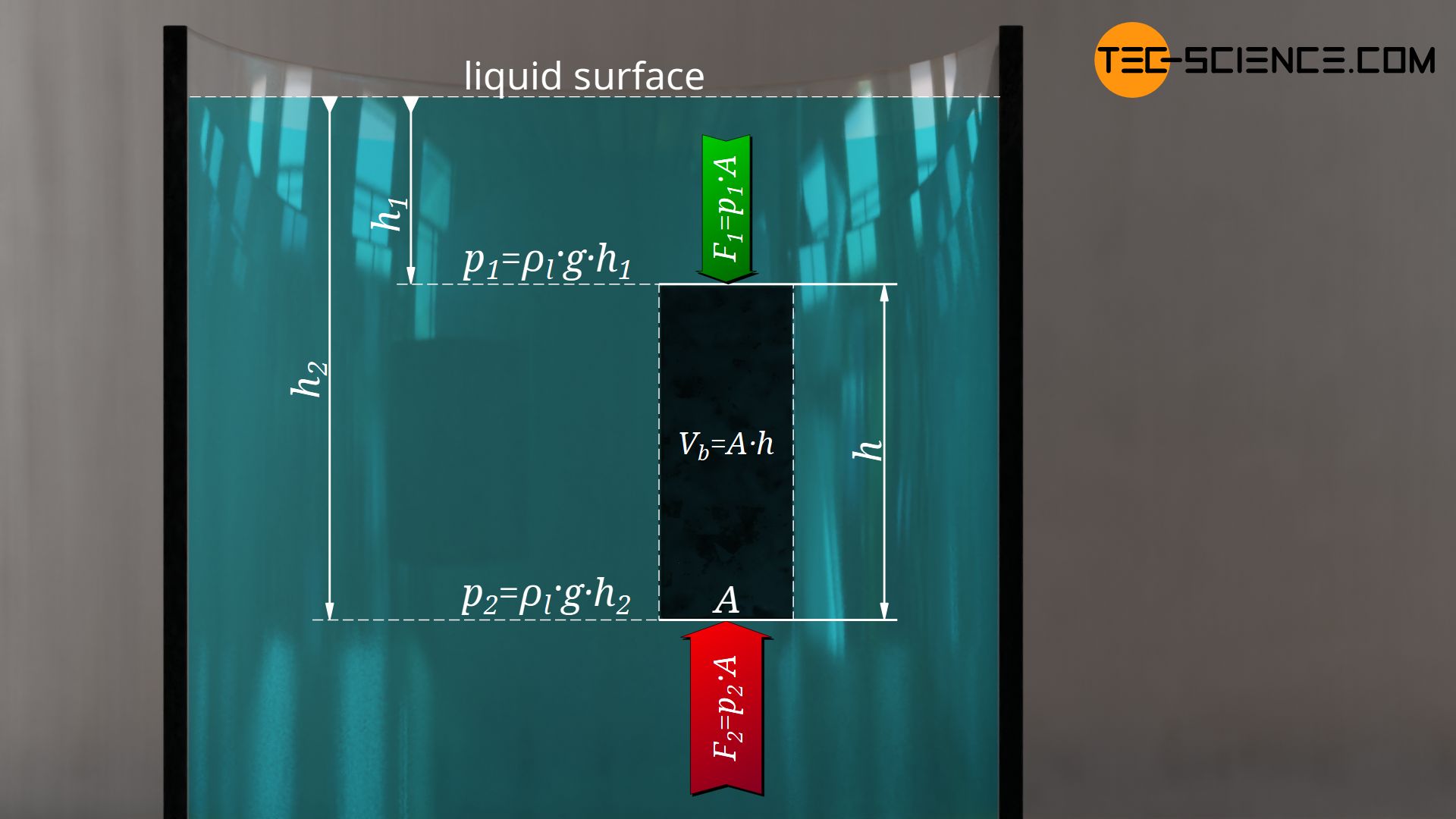
In the article Pressure In Liquids, the cause of liquid pressures has already been explained in detail. They only result from the depth below the liquid surface. The deeper a point lies below the liquid surface, the greater the liquid pressure and the resulting force. In this way, the upward acting force on the bottom of the body is therefore greater than the downward acting force on the top. Thus a force effectively acts upwards, the buoyant force!
The liquid pressure at the bottom of the object is determined from the depth \(h_2\) as follows:
\begin{align}
&p_2 = \rho_l \cdot g \cdot h_2 \\[5px]
\end{align}
In this equation, \(\rho_l\) denotes the density of the liquid. Analogously, for the hydrostatic pressure at the depth \(h_1\) at the top of the cuboid, applies:
\begin{align}
&p_1 = \rho_l \cdot g \cdot h_1 \\[5px]
\end{align}
The respective forces at the bottom and top side of the cuboid are determined according to the Definition Of Pressure by the product of pressure and surface area (\(F=p \cdot A\)). The surface area in this case is the base area \(A\) of the cuboid:
\begin{align}
&\underline{F_2 = \rho_l \cdot g \cdot h_2 \cdot A} ~~~~~\text{or}~~~~~ \underline{F_1 = \rho_l \cdot g \cdot h_1 \cdot A} \\[5px]
\end{align}
The buoyant force \(F_b\), with which the body is effectively pushed upwards, results from the difference of the forces:
\begin{align}
&F_b = F_2 – F_1 \\[5px]
&F_b = \rho_l \cdot g \cdot h_2 \cdot A – \rho_l \cdot g \cdot h_1 \cdot A \\[5px]
\label{d}
&F_b = \rho_l \cdot g \cdot A \cdot \left(h_2-h_1\right) \\[5px]
\end{align}
The difference in the depths corresponds exactly to the height \(h\) of the cuboid. Furthermore, it can be used that the product of height and base area corresponds to the volume \(V_b\) of the submerged body:
\begin{align}
&F_b = \rho_l \cdot g \cdot A \cdot \underbrace{\left(h_2-h_1\right)}_{=h} \\[5px]
&F_b = \rho_l \cdot g \cdot \underbrace{A \cdot h}_{=V_b} \\[5px]
\label{ein}
&\boxed{F_b = V_b \cdot \rho_l \cdot g}~~~~~\text{buoyant force with complete immersion} \\[5px]
\end{align}
Note that the depth at which the object is exactly located is of no importance to the buoyant force. From equation (\ref{d}) it is already clear that only the difference in depth between top and bottom is relevant, i.e. the height of the object*. In combination with the base area of the object, only the dependence on its volume results from this. For simplicity’s sake, this formula was derived from a cuboid, but it applies in principle to any body of any shape as long as its volume \(V_b\) is completely submerged in the liquid (a more general derivation of the buoyant force, which also takes arbitrarily shaped bodies into account, is shown in the next section “Derivation of the Archimedes’ principle“).
*) For this reason, the ambient pressure on the surface of the liquid is also irrelevant, which normally acts in addition to the hydrostatic pressure. This is because the ambient pressure acts equally on both the top and bottom of the body and thus cancel each other out.
If an object is not completely submerged in a liquid (as it was the case in the previous derivation) but is only partially submerged, then the volume \(V_b\) refers only to the actually submerged part of the body volume \(\Delta V\) (= displaced liquid volume). The buoyant force is then generated exclusively by the hydrostatic pressure at the bottom of the body:
\begin{align}
F_b &=p \cdot A \\[5px]
&= \rho_l \cdot g \cdot \underbrace{h \cdot A}_{\Delta V} \\[5px]
\end{align}
\begin{align}
&\boxed{F_b = \Delta V \cdot \rho_l \cdot g} ~~~~~\text{applies in general} \\[5px]
\end{align}
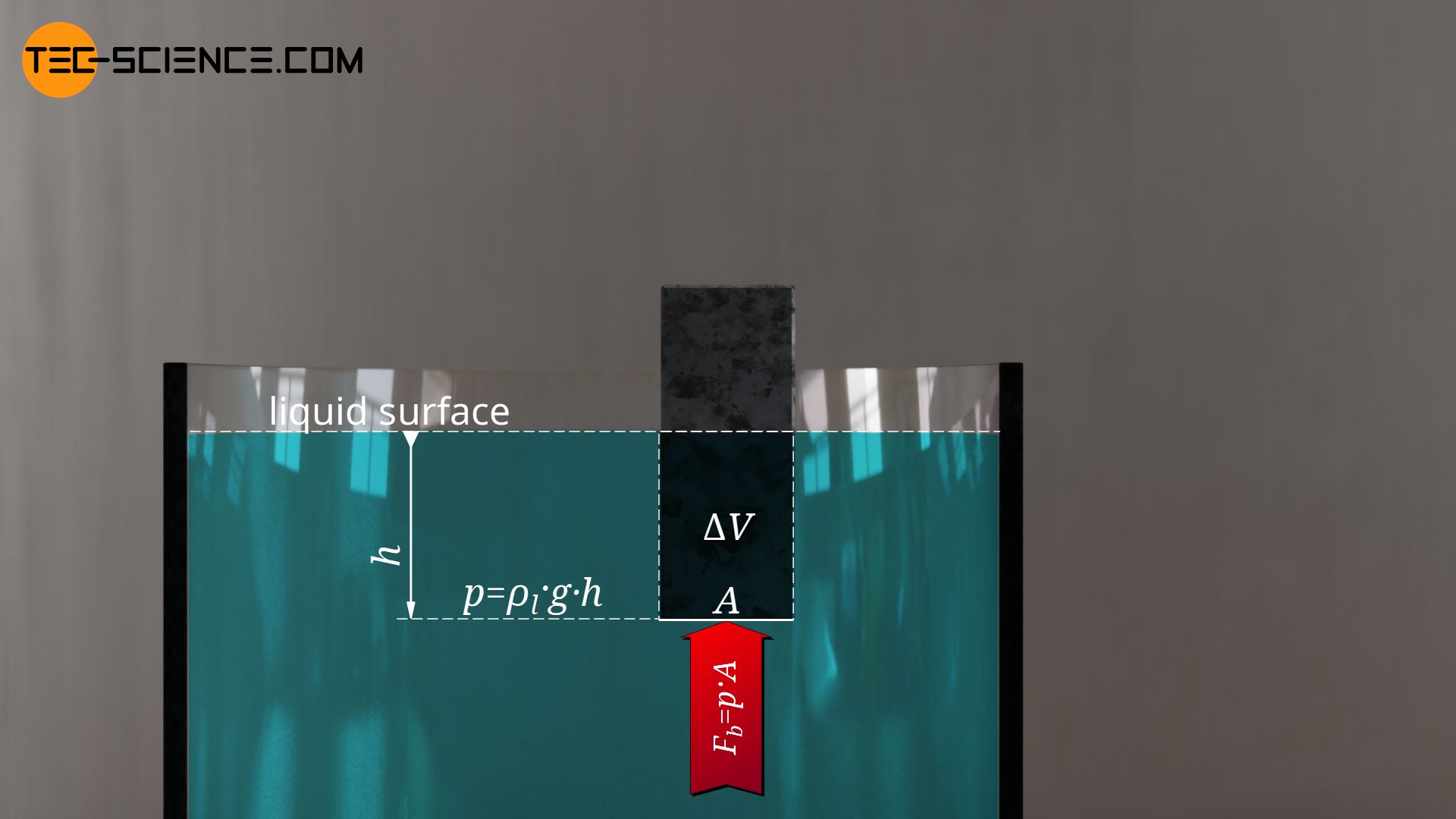
At this point one can now also see the Archimedes’ principle. In the equation above, the product of displaced liquid volume \(\Delta V\) and liquid density \(\rho_l\) can be interpreted as the mass of the displaced liquid. Furthermore, the product of displaced liquid mass \(\Delta m\) and gravitational acceleration \(g\) results in the weight of the displaced liquid \(F_{g,dis}\):
\begin{align}
&F_b = \underbrace{\Delta V \cdot \rho_l}_{\Delta m} \cdot g \\[5px]
&F_b = \underbrace{\Delta m \cdot g}_{F_{g,dis}} \\[5px]
&\boxed{F_b = F_{g,dis}} \\[5px]
\end{align}
Derivation of the Archimedes’ principle for arbitrarily shaped bodies
The derivation of the buoyant force in the previous section was based on an object with a relatively simple geometry on which the acting forces could be calculated relatively easily. That the derived formula can not only be applied to such simple shaped objects, but that the Archimedes’ principle applies to arbitrarily shaped bodies, will be shown in the following.
For this purpose a vessel filled with water is considered. In the Article Pressure In Liquids it has already been explained in detail that the hydrostatic pressure in a liquid is caused by the weight of the liquid column above it. If, for example, the pressure at the bottom of the left vessel is considered, the liquid pressure at the bottom results from the weight of the water mass above (the object has not yet been submerged).

If one immerses now an arbitrarily shaped object into the water, then it experiences a certain buoyant force. According to Newton’s third law (“action = reaction”), the buoyant force exerted by the water on the object corresponds to the force that the object additionally exerts on the water when the situation is viewed from the opposite perspective (i.e. from the water’s point of view)! The force on the bottom of the vessel thus results from the sum of the weight of the water \(F_{g,water}\) and the buoyant force \(F_b\):
\begin{align}
\label{fa}
&F_{bottom} = F_{g,water} + F_b \\[5px]
\end{align}
Note that if the submerged body floats in the liquid, the buoyant force is obviously equal to the weight of the body (otherwise the object would sink to the ground). In this case it becomes clear that not only the weight of the liquid but also the weight of the floating object is acting on the bottom of the vessel. In the general case of a non-floating object (as in the case of the metal cuboid considered above, which was immersed in water by means of a spring scale), however, not the entire weight of the body is applied to the water, but only the weight minus the force with which the object is held. This difference corresponds exactly to the buoyant force (see also the figure Demonstration of the Archimedes’ principle)! Therefore, the resultant force acting on the bottom of the vessel in general results from the sum of the weight of the liquid column and the buoyant force of the submerged object.
In the article Pressure In Liquids it has already been explained in detail that the hydrostatic pressure results only from the considered depth below the water surface. Regarding the pressure at the bottom of the vessel, the water with the submerged object behaves in the same way as a vessel that is only filled with water and thereby has the same water level (principle of communicating vessels) – see the two vessels on the right in the figure above. One can thus imagine the submerged body volume as filled with water; this would obviously have the same effect on the bottom of the vessel.
With this perspective, the force acting on the bottom of the vessel results from the sum of the water weight outside the imaginary immersion volume (\(F_{g,water}\)) and the water weight inside the imaginary immersion volume (\(F_{g,dis}\)). The latter corresponds to the weight of the water which the submerged object displaces in the previous perspective. It therefore applies to the second approach:
\begin{align}
\label{fb}
&F_{bottom} = F_{g,water} + F_{g,dis} \\[5px]
\end{align}
Since both approaches obviously lead to the same force on the bottom of the vessel, equations (\ref{fa}) and (\ref{fb}) can be equated:
\begin{align}
\require{cancel}
&\bcancel{F_{g,water}} + F_b = \bcancel{F_{g,water}} + F_{g,dis} \\[5px]
&\boxed{F_b = F_{g,dis}} \\[5px]
\end{align}
This shows that the buoyancy corresponds directly to the weight of the displaced liquid, regardless of how the submerged object is shaped!
Sinking, rising and floating
Whether a fully submerged object sinks, rises or floats at a given buoyancy depends on the weight of the object.
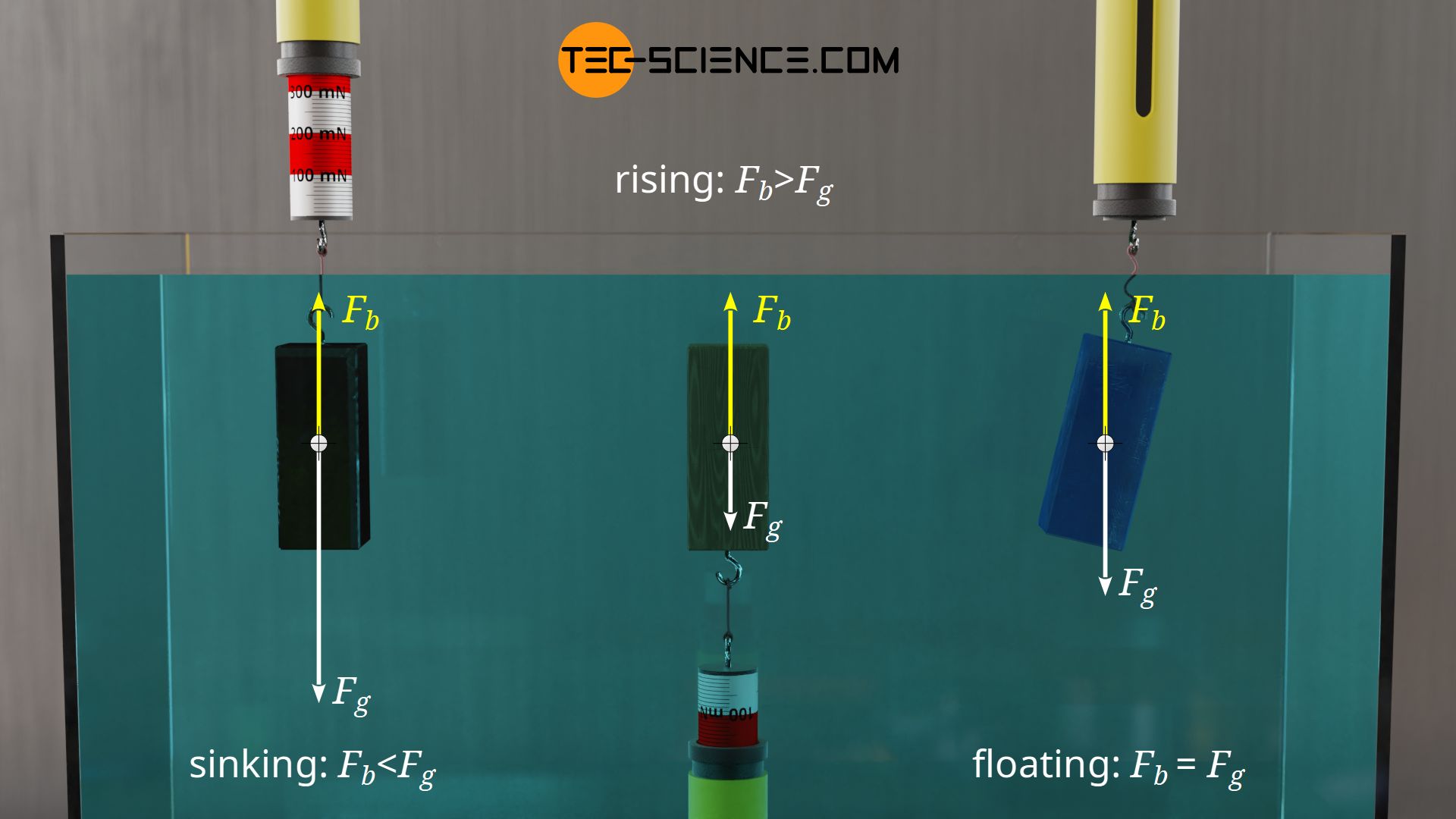
If the weight of a body is greater than the buoyancy, then according to equation (\ref{res}) it will descend with the difference of the forces to the ground. This corresponds to the force indicated by the spring balance when the object is attached to it. If, on the other hand, the buoyancy of a submerged object is greater than its weight, then it will ascend to the surface with the difference of the forces. To display this resultant force, the spring balance would then have to be attached to the object from below. However, if the buoyancy is equal to the weight, the body will appear to float “weightless” in the liquid. An attached spring balance would not indicate a resultant force. This apparent weightlessness in liquids is used, for example, to prepare astronauts for space missions.
For a homogeneous object its weight can be determined by the body volume \(V_b\) and the density of the body \(\rho_b\):
\begin{align}
&F_g = \overbrace{V_b \cdot \rho_b}^{m_b} \cdot g \\[5px]
\end{align}
If at this point the buoyant force according to equation (\ref{ein}) is used, then due to equation (\ref{res}) the following resultant force acts on the completely immersed object:
\begin{align}
&F_{res} = F_g – F_b \\[5px]
&F_{res} = V_b \cdot \rho_b \cdot g – V_b \cdot \rho_l \cdot g \\[5px]
\label{auf}
&\boxed{F_{res} = V_b \cdot g \cdot \left( \rho_b – \rho_l \right)} ~~~\text{resultant force at full immersion}\\[5px]
\end{align}
Using this formula, the conditions for descending, ascending or floating can now be clearly explained. If the density of the submerged body is greater than that of the surrounding liquid, a positive force results which drags the body towards the ground. If, on the other hand, the density of the body is less than that of the liquid, the result is a negative force. This means that the direction of the force is reversed and the submerged object is pulled to the surface. Only in the case that the density of the body corresponds exactly to the density of the liquid, the resultant force disappears. The body seems to float forceless in the liquid.
The considerations of the bodies assumed to be homogeneous can also be extended to inhomogeneous objects, i.e. in particular to objects consisting of different materials and thus different densities. The density \(\rho_b\) of a inhomogeneous body then refers to the mean density, i.e. to the average density which one obtains mathematically, if one refers the total mass of the body \(m_b\) to its total volume \(V_b\):
\begin{align}
&\boxed{\rho_b = \frac{m_b}{V_b}} ~~~~~\text{mean density} \\[5px]
\end{align}
If the mean density of an immersed object is less than that of the surrounding liquid, the object floats to the surface. If the mean density is greater, the object sinks to the bottom. If the densities are the same, the object floats in the liquid.
This also explains why even steel ships weighing tons can float. The average density of a ship is lower than that of the surrounding water. This is achieved by the fact that a ship’s hull is not a massive steel body, but only a steel hull. The interior consists mainly of air. In relation to the volume of the hull, it has a relatively low mass and thus a low mean density, at least a significantly lower (average) density than the surrounding water. Thus the ship’s hull ensures that if it is submerged too much, a large buoyant force is generated which keeps the entire ship above water.

If, on the other hand, water penetrates into the hull, the relatively light air gives way to the penetrating heavy water and the mean density increases. If the mean density is greater than that of the surrounding water (at the latest when the entire hull is full of water), then the ship will sink.
A targeted control of the mean density of a floating body by means of air and water can be found, for example, in submarines. In this way a targeted descending and ascending as well as floating in water is made possible. Depending on the manoeuvre, either water or air is pumped into special ballast tanks. During descending, for example, the air-filled tanks are flooded with water, so that the mean density of the submarine is greater than that of the surrounding water. When the submarine ascends, however, the water in the tanks is pushed out with the aid of compressed air. The mean density of the submarine drops and finally ascends. When floating in water, the tanks are only partially filled with water or air, so that the mean density corresponds exactly to that of the surrounding water.
The fact that substances with lower densities than the surrounding medium rise upwards or substances with higher densities sink downwards also plays a major role in ocean currents. Among other things, these currents are due to the fact that cold and thus heavy water sinks downwards, while warmer and thus lighter water rises upwards. However, these differences in density are not only caused by temperature influences but also by the salt content. The density is higher in waters with a high salt content than in less salty regions.
Immersion depth (draft)
When objects ascend in a liquid, experience shows that they do not emerge completely out of the liquid. A certain part will remain below the liquid surface, while the rest will float above the surface. An everyday example that illustrates this are ships whose hulls are obviously only partially submerged in the water. The question arises, of course, how to determine this depth of immersion, which in the case of ships is also referred to as draught of draft.

If an object floats, it obviously neither sinks nor rises. Consequently, there is no resultant force acting on the object, so there is a balance of forces between the downward acting weight and the upward acting buoyancy:
\begin{align}
&F_{res} = F_g – F_b \overset{!}{=}0 \\[5px]
&\underline{F_b = F_g} \\[5px]
\end{align}
The weight is therefore just as great as the buoyancy. According to the Archimedes’ principle, the buoyancy itself corresponds to the weight of the displaced liquid. So when an object floats on the surface, it will submerge until the weight of the displaced liquid (=buoyancy) corresponds to the weight of the object. If one imagines the volume of the object below the liquid surface to be completely filled with the surrounding liquid, this weight corresponds to the weight of the object. A ship with a mass of 50,000 tons, for example, will sink so deep that the submerged volume displaces 50,000 tons of water.

When floating, the object submerges to such a depth that it displaces as much liquid as it is heavy!
The immersion depth of an object therefore depends not only on its own mass, but also on the density of the surrounding liquid. For example, a ship will have a stronger draft in fresh water than in sea water, i.e. it will submerge deeper. Because of the dissolved salt, seawater has a density that is about 3 % higher than that of freshwater. The ship must therefore immerse more strongly in the “lighter” freshwater in order to displace the same mass of water as in the “heavier” salt water.
For ships, the maximum permissible draught is indicated by a so-called Plimsoll mark depending on the surrounding water (density). This mark is located on the side of the ship’s hull. The upper two lines towards the stern indicate the permitted draft in general freshwater (F) or tropical freshwater (TF). The other four lines towards the bow indicate the permitted draft in saltwater. These are located lower in comparison to the marks of the freshwater, as the ship is more buoyant in saltwater due to the higher water density. A distinction is made between tropical seawater (T), seawater in summer (S) and winter (W) and between waters of the North Atlantic in winter (WNA).

Plimsoll marks on ships indicate the permitted drafts depending on the surrounding water (density)!
This example of the Plimsoll mark also shows that the “heavier” the surrounding liquid is, i.e. the greater the density of the liquid, the stronger the buoyancy is. This can also be seen directly from the equation (\ref{arch}), in which the liquid density directly influences the buoyant force. This fact can also be seen when bathing in the Dead Sea. Due to the very high salt content of more than 30 %, the density of the water in the Dead Sea is about a quarter higher compared to freshwater. Consequently, the buoyancy there is also about 25 % greater than in freshwaters. This leads to the fact that one floats in the Dead Sea without the need to swim.
Outlook
In this article, liquids were considered for the sake of clarity, but not only in liquids but also in gases buoyant forces are acting, which finally are based on same cause. At article Buoyancy In Gases this is discussed in more detail.






